
2023第25卷第6期
2.吉林大学 经济学院, 吉林 长春 130012
新冠疫情爆发以来,中国经济增速走势出现了明显的形态变异,脱离了之前的低波动平稳运行态势,转而进入了高波动不稳定状态。2020年1季度出现了-6.9%的经济增速,2021年1季度经济增速大幅反弹至18.7%,但是这一反弹势头并不稳定,2022年2季度经济增速再次下降至0.4%,2022年全年GDP增长3.0%。即便疫情防控已平稳转变,经济仍呈现出弱复苏态势。诚然,经济增长形态变异的背后有着复杂的机理,但总体来讲可归为如下几方面:第一,百年未遇之变局下的外部冲击与外部不确定性,包括地缘冲突、局部战争、中美博弈、金融危机和“逆全球化”等,在上述因素影响下,全球政治经济格局发生根本性变化,我国经济发展面临的外部环境更加复杂严峻(邓创等,2023)。第二,价格冲击,随着我国经济深度融入全球价值链,国际大宗商品价格对我国价格水平的影响愈发明显,叠加国内供需缺口持续扩张,我国通货膨胀率波动也明显加大(刘金全和刘悦,2022)。例如,2022年实体经济复苏协同俄乌战争引发了一轮成本推动叠加外部输入的复合型通货膨胀,CPI月度涨幅逼近3%,但在2023年上半,国内有效需求不足导致CPI一路下行,经济运行又陷入了通货紧缩困境。第三,金融风险,近年来我国宏观杠杆率再次上升,债务规模持续扩大,地方政府债务问题突出(陈必果等,2023),金融风险更加显性化、透明化、市场化,加之股票市场全面推行注册制,金融市场情绪对经济增长的影响亦将越发强烈。
上述三大因素都是决定经济增长走势的重要因素,这给本文研究带来两点启示:一是对经济增长风险的描述应该具有综合性和全面性,多重因素的复杂变化不仅可以影响经济增长的水平值,而且还可以影响经济增长的波动率,任何因素的改变都可以催生不同的增长分布形态,对经济增长的描述将变得越发复杂化;二是从统计和计量的角度来看,对于经济增长的描述,点估计的意义已明显下降,这是因为任何背景条件的改变都可能直接影响经济增长的点估计值,相比于识别出最优点估计,甄别影响经济增长分布变化的核心条件可能更为重要,这才是全面把握经济增长变异特征和变异方向的关键。为此,本文将以分布估计取代点估计,进而实现经济增长的全面风险管理。从中国经济发展现状来看,后疫情时期经济整体呈复苏势头,长期稳中向好的态势不改,但这并不意味着经济的复苏是线性的和稳定的,尤其是中国经济仍将长期处于不确定的环境之中,增长既可能围绕主体趋势迅速回归,亦可能呈现出短期发散,这将是未来一定时期内经济发展的新特征。因此,有必要从增长分布的角度对经济增长风险进行全面的认知和理解。
本文的边际贡献和创新主要体现在:(1)跳出传统的经济增长率测算思维,以外部不确定性、金融风险、核心通货膨胀等因素为条件,描述经济增长的在险状态,这为全面解析经济增长形态变异提供了新思路;(2)用分布估计取代点估计,计算不同条件下的经济增长遍历在险分布,从风险管理的视角更加全面地描述中国经济增长的分布状态和分布变异。
全文余下部分安排如下:第二部分是文献述评,第三部分是外部不确定性、金融风险和核心通货膨胀指数构建,第四部分是分位数回归分析,第五部分是中国经济增长的在险分布估计,最后一部分是全文的结论与政策建议。
二、文献述评 (一) 经济增长预测方法演进述评经济增长预测一直都是宏观经济学研究的重要分支。从计量模型构建的角度出发,相关研究大致可以归为点估计、长期趋势估计和分布估计三类。早期对于经济增长的预测多使用点估计方法,包括单方程模型和多方程模型。其中,单方程模型包括线性回归模型、自回归移动平均模型(ARMA)以及后续兴起的马尔科夫区制转移模型和混频数据模型等,比如刘金全和隋建利(2010)构建马尔科夫区制转移模型实证检验了货币增长不确定性与经济增长之间的关系,陈守东等(2013)从金融稳定的视角分析了宏观经济走势,郑挺国和尚玉皇(2013)构建混频数据模型对中国经济增长进行了短期预测。多方程模型主要包括传统的联立方程模型和向量自回归类模型,如桂文林和程慧(2021)构建MS-VAR模型分析了资产价格对经济增长的影响,刘金全等(2014)构建TVP-VAR模型分析了经济波动率、金融稳定对经济增长的影响,刘达禹等(2022)采用动态溢出指数进行研究后发现,金融周期波动对实体经济波动的最大溢出效应可达到80%。长期趋势估计方面,常用的方法主要有滤波法和生产函数法。常见的滤波法有H-P滤波、B-K滤波、C-F滤波等。这类方法的优点是便于应用,可以直接分离出GDP等时间序列的长期趋势,但缺点在于对数据频率、参数设定和数据属性比较敏感,同时估计结果缺乏经济意义(Stock和Watson,2020)。相对而言,生产函数法则是从要素贡献的角度出发,运用各类生产要素的数据信息来刻画经济增长的长期趋势,它的优点是富有经济意义,而缺点在于估计结果高度依赖于函数形式选择,也容易造成结果不一致的问题。郭豫媚和陈彦斌(2015)将人力资本因素纳入生产函数模型估算我国1979—2020年的潜在增长率,得出新常态下资本的潜在增长趋势为16.9%,这一结果与刘伟和范欣(2019)的估计结果存在较大差异,表明生产函数法的计量稳定性相对较差。
近期,分布估计逐渐成为经济增长预测的主流方法,其优势是可以计算不同条件下的经济增长在险分布,对经济增长的描述更加全面。Adrian等(2019)运用金融在险分布模型拟合出美国经济增长的偏态t分布函数,发现美国经济增长具有明显的左偏特征,这意味着金融风险将大概率引导经济下行;而宽松的金融环境则可以提升短期内的增长活力并降低经济波动。Kashyap和Stein(2023)将货币政策融入在险分布模型,再度考察了美国经济增长的影响因素,研究表明提高货币政策的预期管理能力可以有效改善金融市场情绪,进而化解经济衰退风险。国内亦不乏相关研究,张晓晶和刘磊(2020)构建在险增长模型将金融风险与经济增长纳入统一框架进行分析,结果显示金融脆弱性上升会抑制经济增长,宽松的经济政策在短期内有效,但在长期同样会抑制经济增长。邓创等(2022)运用Q-VAR模型分析了不同经济增速水平下外部经济和金融不确定性对宏观经济的影响,随后拟合出经济增长的条件分布函数评估了外部不确定性冲击对经济下行风险的影响,结果发现外部经济和金融不确定性对于我国宏观经济具有非线性影响,在经济下行阶段二者的负面影响更大。然而,这些研究都没有考察通胀条件下的经济增长在险分布。根据经典的菲利普斯曲线关系,倘若经济波动主要由实体问题主导,那么通胀和产出之间的权衡关系就会成为主要矛盾,这也是本文要着重关注的内容。
(二) 经济增长冲击因素总结无论在理论上还是实证层面,经济增长的冲击因素都有很多,本文聚焦当前影响经济增长的三大因素,即外部不确定性、价格冲击和金融风险,并对三者的影响进行简要述评。从外部不确定性来看,现有研究主要聚焦于外部不确定性的测度以及外部不确定性的影响。外部不确定性的测度方法主要包括实体经济波动率法(Bloom等,2018)、媒体大数据抓取法(徐宁等,2020)和数理模型估计法(Fernández-Villaverde等,2015)等。外部不确定性对经济增长的负向影响不言而喻,但对宏观调控政策的影响却较为复杂性,邓创等(2023)使用高维动态因子模型和两步加权法测度了中国的外部不确定性冲击,进而考察了不确定性尾部冲击对货币政策的影响,结果表明外部不确定性将通过避险效应和利率渠道来影响我国货币政策调控效果,它会降低货币政策的独立性,在极端分布下会降低货币政策的有效性。
随着国际经济环境日趋复杂,大量研究开始关注输入型通货膨胀对经济增长的影响,认为输入型通货膨胀是经济波动的重要诱因,输入型通货膨胀可以影响国内的产出、消费、净出口与价格水平(Tiwari等,2014;Kleinberg等,2015)。然而在我国,由于物价指数自2012年起持续低迷,这使通货紧缩成为了备受关注的话题。事实上,我国并未发生过严格意义上的通货紧缩,相关研究对通货紧缩的探讨也更多是停留在理论层面和经验对比上。例如根据债务通货紧缩理论——通缩螺旋会带来经济衰退(刘晓光等,2018);而Cruz(2022)针对发达经济体的研究发现,通货膨胀目标制可以提高经济运行稳定性,同时在一定程度上化解通货紧缩风险。需要注意的是,2023年上半,我国PPI跌幅扩大,CPI持续走低,出现了一定的通缩迹象,这很可能是影响经济增长分布的重要因素。最后,从金融风险方面来看,现有研究主要是关注经济周期和金融周期的关联机制,并主要形成了两类观点:一是经济周期与金融周期密切相关且同向运动,其中,金融周期的变化领先于经济周期,是导致经济周期波动的源头之一(Akar,2016;邓创和徐曼,2018;尹筑嘉等,2019);二是总体肯定了二者的正相关性,但同时强调了经济周期和金融周期的关联机制并不稳定(刘达禹等,2022)。
综上所述,现有研究对经济增长的预测更多是采用点估计和趋势估计,仅有少数文献采用了在险分布估计方法,但对于经济增长冲击要素的分析都是基于单一的金融要素展开,缺乏对多重要素的综合考量。事实上,从后疫情时期中国经济运行的现实基础来看,当下经济增长弱复苏态势的成因较为复杂,金融风险、外部不确定性以及物价端的变动都是不容忽视的要素,均会引发增长形态的重大变异。因此,本文的创新在于将外部不确定性、价格冲击和金融风险要素纳入统一框架进行分析,从分布估计的视角全面审视中国经济的在险增长。
三、外部不确定性指数、金融状况指数与核心通货膨胀估计本部分将运用适当的计量模型,分别构建外部不确定性指数、金融状况指数和核心通货膨胀率,进而为估计中国经济增长的在险分布函数奠定基础。参考现有主流研究,使用动态移动平均因子增广时变参数向量自回归模型(TVP-FAVAR-DMA)构建金融状况指数和核心通货膨胀率,使用非预期条件波动率高维因子模型构建外部不确定性指数,两个方法的核心思想都是对高维数据进行降维并提取共同趋势部分。在刻画外部不确定性时并未延续使用TVP-FAVAR-DMA模型的原因在于:外部不确定性是二阶矩过程,采用条件波动率模型进行刻画更加合适。
(一) 计量模型1. TVP-FAVAR-DMA模型。首先给出包含p阶滞后的TVP-FAVAR模型:
| $ {x_t} = \beta _t^y{y_t} + \beta _t^f{f_t} + {\varepsilon _t} $ | (1) |
| $ \left[ \begin{gathered} {f_t} \\ {y_t} \\ \end{gathered} \right] = {c_t} + {\Lambda _{t,1}}\left[ \begin{gathered} {f_{t - 1}} \\ {y_{t - 1}} \\ \end{gathered} \right] + \cdots + {\Lambda _{t,k}}\left[ \begin{gathered} {f_{t - k}} \\ {y_{t - p}} \\ \end{gathered} \right] + {\mu _t} $ | (2) |
其中,
2. 非预期条件波动率高维因子模型。定义
| $ u_{jt}^y(h) = \sqrt {E\left[ {{{\left( {{y_{jt + h}} - E\left[ {{y_{jt + h}}\mid {I_t}} \right]} \right)}^2}\mid {I_t}} \right]} $ | (3) |
其中,
| $ u_t^y(h) = \mathop {p\mathop {\lim }\limits_j }\limits_{{N_y} \to \infty } \sum\limits_j^{{N_y}} {{w_j}} u_{jt}^y(h) = {E_w}\left[ {u_{tj}^y(h)} \right] $ | (4) |
式(3)和式(4)给出了基于非预期条件波动率的经济不确定性指数,其计算方法如下:
首先,估计
| $ {X_{it}} = \Lambda _i^{f^{'}}{f_t} + e_{it}^X $ | (5) |
| $ {y_{jt + 1}} = \phi _j^y(L){y_{jt}} + \gamma _j^f(L){f_t} + \gamma _j^w(L){w_t} + v_{jt + 1}^y $ | (6) |
其中,
综合考虑数据的代表性和可得性后,选取基础指标如下(具体见表1)。金融状况指数方面,选取能够反映货币市场、信贷市场、股票市场、债券市场、房地产市场、外汇市场运行状况的代表性指标。外部不确定性指数方面,选取美国、日本、韩国、德国、澳大利亚、马来西亚、俄罗斯、新加坡、越南、印度等主要发达经济体和发展中国家的核心经济指标(包括产出、消费、投资、价格、对外贸易五方面)。核心通货膨胀方面,选取CPI子类同比增速和PPI子类同比增速指标。对于指标处理过程说明如下:(1)所有指标包括增长率、绝对量、指数三种类型,对增长率指标进行了去百分号处理,在此基础上对所有指标进行了标准化处理,这可以实现不同类型指标之间的无量纲化对比;(2)有部分指标为反向指标,对此我们进行了取倒数处理,从而确保指标含义一致;(3)为便于后续分析,本文将数据频率统一为季度频率,通过加总(总量)或平均(比例)的方式将月度数据转换为季度数据;(4)样本区间均为2003年1季度至2022年4季度,对部分缺失值采取平滑差值进行补充,原始数据来源于中国人民银行网站、国家统计局网站、中国货币网以及WIND数据库。
| 合成指数 | 指标分类 | 基础指标 | 具体指标说明 |
| 金融状况 指数 | 货币金融 总量指标 | 广义货币M2 | 广义货币供应量M2同比增速 |
| 狭义货币M1 | 狭义货币供应量M1同比增速 | ||
| 基础货币 | 基础货币同比增速 | ||
| 人民币存款余额 | 人民币存款余额同比增速 | ||
| 对非金融部门债权 | 对非金融部门债权同比增速 | ||
| 社会融资规模 | 社会融资规模存量同比增速 | ||
| 金融机构资产总量 | 金融机构总资产同比增速 | ||
| 货币市场 | 同业拆借加权平均利率 | 各期限的银行间同业拆借加权平均利率 | |
| 银行间同业拆借利率利差 | 各期限的同业拆借利率利差加权平均值 | ||
| 质押式回购加权平均利率 | 各期限的质押式回购加权平均利率 | ||
| 信贷市场 | 人民币贷款余额 | 人民币贷款余额同比增速 | |
| 实际贷款利率 | 基准贷款利率减去通货膨胀率 | ||
| 股票市场 | 上证综合指数收益率 | 以上一期为基准的上证综合指数收益率 | |
| 沪深300指数收益率 | 以上一期为基准的沪深300指数收益率 | ||
| 基金交易额 | 基金交易额同比增速 | ||
| 债券市场 | 10年期国债收益率 | 10年期国债收益率 | |
| 国债发行余额 | 国债发行余额同比增速 | ||
| 房地产市场 | 房地产价格指数 | 国家统计局公布的房地产价格指数 | |
| 国房景气指数 | 国房景气指数 | ||
| 外汇市场 | 人民币实际有效汇率 | 人民币实际有效汇率指数 | |
| 外汇储备 | 外汇储备余额同比增速 | ||
| 外商直接投资 | 外商直接投资同比增速 | ||
| 外部经济不确定性指数 | 产出指标 | 工业生产指数 | 美国、日本、韩国、德国、澳大利亚、马来西亚、俄罗斯、新加坡、越南、印度工业生产指数 |
| 消费指标 | 零售消费总额或消费支出 | 美国零售和食品服务销售总额;日本商业销售总额;韩国、德国、澳大利亚、俄罗斯零售销售总额;马来西亚、印度最终消费支出;新加坡零售销售指数;越南零售额累计值 | |
| 投资指标 | 固定资产投资总额 | 美国国内私人固定资产投资总额;日本、韩国、德国、澳大利亚、马来西亚、俄罗斯、新加坡、越南、印度固定资本形成总额 | |
| 价格指标 | 居民消费价格指数 | 美国、日本、韩国、德国、澳大利亚、马来西亚、俄罗斯、新加坡、越南、印度居民消费价格指数同比增速 | |
| 对外贸易指标 | 中国对各国家进出口总额 | 中国对美国、日本、韩国、德国、澳大利亚、马来西亚、俄罗斯、新加坡、越南、印度的进出口总额同比增速 | |
| 核心通货 膨胀 | 居民消费 价格指数 | 八大子类CPI同比增速 | 食品、衣着、居住、交通和通讯、娱乐教育文化用品及服务、医疗保健及个人用品、家庭设备用品及维修服务CPI同比增速 |
| 工业生产者出厂价格指数 | 八大子类PPI同比增速 | 采掘、原料、加工、食品、衣着、生产资料、一般日用品、耐用消费品PPI同比增速 |
这里运用上一节的基础指标构建TVP-FAVAR-DMA模型合成金融状况指数和核心通货膨胀率,构建非预期条件波动率高维因子模型合成外部不确定性指数,结果如图1所示。为便于对比,本文将GDP增速和三类指数置于同一图中,图中的灰色部分为本文关注的三次重大危机时期,即国际金融危机时期(2007—2009年)、中美贸易摩擦时期(2017—2019年)以及全球新冠疫情时期(2020—2022年)。其中,外部经济不确定性与GDP的变化趋势相反,为了便于对比分析,本文在图1(b)中将外部经济不确定性指数进行了取相反数处理。由图1(a)可以看出,GDP增速与金融状况指数具有较强的关联性,这说明经济周期和金融周期具有联动特征,同时也说明金融状况指数对经济增长具有一定的预测能力。在国际金融危机时期,经济波动的主要推动因素是金融因素,此时金融状况指数和GDP增速的协动性更强。在贸易摩擦时期,金融状况指数和GDP增速的走势并不一致,表明这一时期推动经济增长的并非金融因素,而是外部冲击。在新冠疫情时期,金融状况指数和GDP增速间再度表现出一定的相关性,且金融状况指数的变动要领先于GDP增速,这主要是因为世纪疫情冲击是全局性冲击,既能通过情绪和预期影响金融体系,也能通过实际经济行为来影响实体经济。

|
| 图 1 GDP增速与三类指标变动趋势的耦合关系 |
由图1(b)可以看出,GDP增速与外部经济不确定性的耦合性十分显著,表明在样本期内外部经济不确定性也是影响我国经济增长的关键因素,同时也意味着外部经济不确定性所包含的信息将对经济增长预测产生重要影响。特别是在国际金融危机时期,全球经济不确定性上升,外部因素传导至我国,致使经济增长短周期下行。从图像上看,该段时期内外部经济不确定性指数和GDP增速的确表现出较强的协动性,外部经济不确定性对GDP增速的变动具有较好的解释力。在贸易摩擦时期,逆全球化和贸易保护主义抬头,外部经济不确定性与我国GDP增速同样具有显性关联。最后在全球新冠疫情时期,外部不确定性再度上升,由此引发的贸易、投资变化以及潜在的产业链断裂风险使GDP增长率快速紧缩,波动率明显上升,这一阶段外部不确定性对GDP增速具有更强的解释力。
再来看图1(c)中核心通货膨胀的表现,核心通货膨胀与GDP增速同样具有较高的耦合性,且GDP增速的变化领先于核心通货膨胀,这一情形符合“产出-物价”型菲利普斯曲线描述的基本规律。在国际金融危机时期,由于宏观经济快速下行,生产、消费、投资、物价等指标同步下降,因此核心通货膨胀和GDP增速的耦合性较强。在贸易摩擦时期,核心通货膨胀的下降幅度明显大于GDP增速,实际经济指标的变化对物价的传导偏弱。在新冠疫情时期,核心通货膨胀和GDP增速再次表现出较强的耦合性,但GDP增速的振幅大于核心通货膨胀,这表明新冠疫情时期的经济波动是一轮典型的实体经济波动。
四、不同分位数水平下的经济增长驱动因素分析本节进一步构建分位数回归模型和分位数向量自回归模型(Q-VAR),分别从静态和动态两个角度分析金融状况指数、外部经济不确定性及核心通货膨胀对经济增长的影响。据此阐明在经济增长的不同分位水平下,三大要素对经济增长预测能力的差异,这将为后文分别以三者为条件刻画经济增长的在险分布奠定基础。
(一) 分位数回归结果分析表2展示了分位数回归结果,其中向前1个季度的预测代表短期预测,向前1年的预测代表中长期预测。总体来看,金融状况指数、外部经济不确定性、核心通货膨胀对经济增长均具有一定的预测能力。从均值来看,外部不确定性对经济增长的解释能力大于金融状况指数和核心通货膨胀,这一结果和上文的直观分析一致,即在样本期内外部经济不确定性是影响经济增长的关键性因素。对于金融状况指数而言,在经济低速增长状态下(对应0.1和0.25分位点),回归系数均不显著,该段样本主要集中在2012—2018年,金融状况指数始终处于波动当中,而经济增长却一路缓和下行,二者不存在明显对应关系,说明金融对增长几乎没有预测能力。该段时期正是中国经济“脱实向虚”的主体阶段,此时金融风险并未对增长产生影响符合客观预期;在经济适速增长状态下(对应0.5和0.75分位数点),也即样本前期和“次贷危机”后的经济复苏阶段,金融状况指数对经济增长存在显著影响,此时金融状况改善明显有助于拉动经济增长;在经济高速增长状态下(对应0.9分位数点),也即2005—2007年,金融状况指数对经济增长的拉动作用更加显著,表明在经济快速增长阶段,金融市场运行是决定经济增长走势的关键,此时金融与经济间能够产生彼此促进的正反馈循环机制。
| 分位数 | 0.1 | 0.25 | 0.5 | 0.75 | 0.9 | 均值 |
| 金融状况指数 | ||||||
| 向前一个季度( | 0.5525 | 0.1583 | 0.2170* | 0.3589*** | 0.3974*** | 0.3082* |
| (0.3471) | (0.1314) | (0.1256) | (0.1288) | (0.1125) | (0.1524) | |
| 0.3094 | 0.4159 | 0.5066 | 0.4405 | 0.3194 | 0.4719 | |
| 向前一年( | 0.9957 | 0.2221 | 0.0451 | 0.6806** | 1.1807** | 0.2012 |
| (0.9342) | (0.3172) | (0.3018) | (0.3203) | (0.5409) | (0.3965) | |
| 0.1292 | 0.1689 | 0.2583 | 0.1924 | 0.1222 | 0.1725 | |
| 外部经济不确定性 | ||||||
| 向前一个季度( | −0.5671*** | −0.2600* | −0.3572*** | −0.6416*** | −1.8620*** | −0.6202** |
| (0.1892) | (0.1459) | (0.1256) | (0.1744) | (0.4969) | (0.2996) | |
| 0.3206 | 0.4265 | 0.5233 | 0.4937 | 0.3515 | 0.4751 | |
| 向前一年( | −1.4058*** | −1.1938*** | −1.6348*** | −2.2033*** | −2.3937*** | −2.0393*** |
| (0.4679) | (0.1181) | (0.3108) | (0.6687) | (0.2872) | (0.3025) | |
| 0.2255 | 0.2809 | 0.3763 | 0.4121 | 0.4483 | 0.4885 | |
| 核心通货膨胀 | ||||||
| 向前一个季度( | 0.4243 | 0.1304 | 0.1299 | 0.4091** | 1.0312** | 0.3313 |
| (0.3050) | (0.1244) | (0.1136) | (0.1588) | (0.4196) | (0.2940) | |
| 0.2778 | 0.4111 | 0.4996 | 0.4587 | 0.3397 | 0.4546 | |
| 向前一年( | 0.7465 | 0.2655 | 0.2587 | 0.9361** | 1.3238** | 0.6819* |
| (0.6936) | (0.1934) | (0.2039) | (0.4147) | (0.5605) | (0.3619) | |
| 0.1115 | 0.1873 | 0.2754 | 0.2062 | 0.1437 | 0.2076 | |
| 注:*、**和***分别代表在10%、5%和1%的水平下显著,括号内数值为标准误。 | ||||||
对于外部经济不确定性而言,在经济低速增长状态、适速增长状态和高增长状态下,外部经济不确定性都会显著影响经济增长,对经济增长均具有预测能力。相比而言,经济高速增长状态下外部不确定性系数的绝对值大于其余两种状态,表明外部经济不确定性同样是在经济繁荣期时对经济增长的影响较大。至于核心通货膨胀,在经济低速增长状态和0.5分位点上,它对经济增长的影响并不显著,这说明当下的弱通缩趋势与经济增长下行之间是割裂的,并非联动紧缩。在0.75分位点和经济高速增长状态下,核心通货膨胀对经济增长具有显著影响,预测能力增强,这意味着高增长通常都会伴随着通货膨胀现象。总体而言,只有在高增长状态下,经济才会出现产出-价格联动效应;而在经济较为疲软时,通胀与增长之间几乎相互独立。这说明中国当下的经济下行是综合性问题,不应当仅归因于需求端。
对比三大影响因素对经济增长的影响可以发现:在经济低速增长状态下,外部经济不确定性对经济增长的影响最为显著,预测能力最强,而金融状况指数和核心通货膨胀对经济增长的影响不明显,不具有预测能力;在经济适速增长状态和高速增长状态下,外部经济不确定性对经济增长的影响强度仍然最大,预测能力最强,体现出外部经济不确定性是影响我国经济运行的关键因素,核心通货膨胀对经济增长的影响强度次之,其预测能力强于金融状况指数,这意味着在经济高速增长状态下,价格冲击是影响经济周期波动的重要因素,而金融状况指数的影响强度最低,对经济增长的预测能力有限。这一结果说明对经济影响最强的要素仍然是外部冲击和实体波动,而非是金融要素。
(二) 基于Q-VAR模型的动态分位数效应分析1. Q-VAR模型和变量设定。该模型可以在经济增长的不同分位数水平下计算变量的脉冲响应函数。首先,给定一个n维向量组
| $ {Q_{{m_t}}}\left( {\tau \left| {{x_{t - 1}}} \right.} \right) = \left\{ {\begin{array}{*{20}{c}} {{q_1}\left( {\tau \left| {{x_{t - 1}}} \right.} \right) = {c_1}{{\left( {{\tau _1}} \right)}^\prime }{q_{ - 1}}\left( {\tau \left| {{x_{t - 1}}} \right.} \right) + {b_1}{{\left( {{\tau _1}} \right)}^\prime }{x_{t - 1}} + {a_1}\left( {{\tau _1}} \right)} \\ \vdots \\ {{q_n}\left( {\tau \left| {{x_{t - 1}}} \right.} \right) = {c_n}{{\left( {{\tau _n}} \right)}^\prime }{q_{ - n}}\left( {\tau \left| {{x_{t - 1}}} \right.} \right) + {b_n}{{\left( {{\tau _n}} \right)}^\prime }{x_{t - 1}} + {a_n}\left( {{\tau _n}} \right)} \end{array}} \right. $ | (7) |
其中,
| $ {Q_{{m_t}}}\left( {\tau \left| {{x_{t - 1}}} \right.} \right) = {\left[ {{I_n} - c\left( \tau \right)} \right]^{ - 1}}\left[ {b\left( \tau \right){x_{t - 1}} + a\left( \tau \right)} \right] = B\left( \tau \right){x_{t - 1}} + {A_\tau } $ | (8) |
本文选取经济增长、金融状况指数、外部经济不确定性以及核心通货膨胀四个变量建立Q-VAR模型,其中经济增长使用我国季度GDP实际同比增速衡量,金融状况指数、外部经济不确定性以及核心通货膨胀使用上文测度的指数衡量。
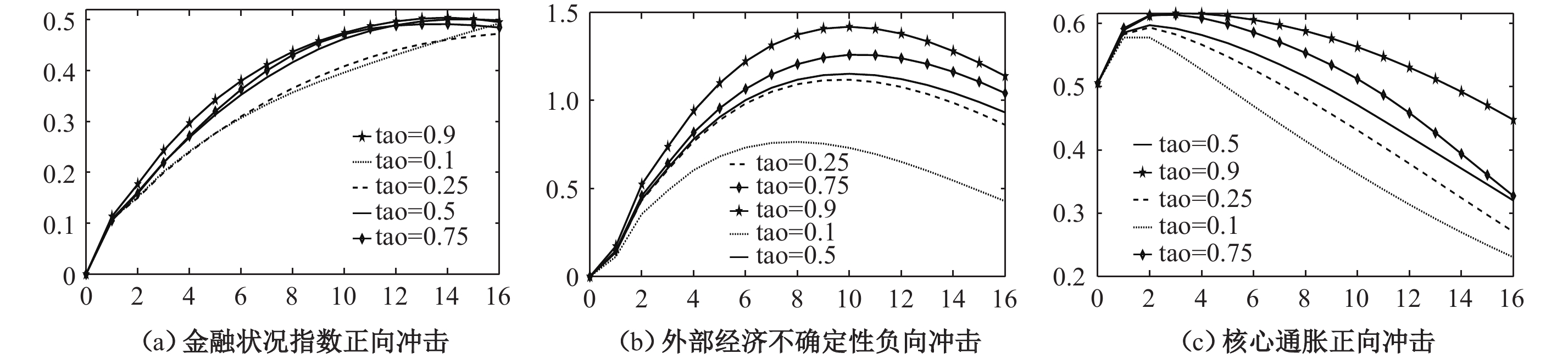
2. 实证结果分析。本文对Q-VAR模型进行估计后,计算了金融状况指数、外部经济不确定性、核心通货膨胀3个指标对经济增长影响的分位数脉冲响应函数。为保持一致性,引入的金融状况指数和核心通货膨胀冲击为一标准差正向冲击,外部经济不确定性引入的是一标准差负向冲击,结果如图2所示。
|
| 图 2 三类指标对经济增长影响的分位数时变脉冲响应函数 |
从图2可以看出随着经济增长由低速转向适速进而再转至高速状态,金融状况指数、外部经济不确定性以及核心通货膨胀对经济增长的影响不断增强,这印证了前文分位数回归的基本结论。总体来看,外部经济不确定性冲击对经济增长的影响明显高于金融状况指数和核心通货膨胀;核心通货膨胀冲击对经济增长的影响次之,略大于金融状况指数,金融状况指数对经济增长的影响最弱,这再次印证了前文的基本观点。此外,可以看出核心通货膨胀冲击的收敛速度最快,外部不确定性冲击的收敛速度次之,金融状况指数冲击的收敛速度最慢,这说明金融状况指数对经济增长的影响更加持久,同样是不能忽视的因素。结合我国自2016年开启的去杠杆征程来看,宏观经济稳增长和金融系统防风险之间的权衡的确是一个漫长的过程,这一结论能够得到经验事实的支持。
五、中国经济增长的在险分布估计 (一) 在险分布估计在险分布估计事实上是估计了一个以分位数回归模型为基础的偏态t分布函数,即将分位数回归结果拟合到一个具有较少参数的概率密度函数中。Azzalini和Capitanio(2003)在传统t分布的基础上加入了表示偏度的参数,提出了偏态t分布函数,其概率密度为:
| $ f(y;\mu ,\sigma ,\alpha ,\upsilon )=\frac{2}{\sigma }· t(\frac{y-\mu }{\sigma },\upsilon )· T(\alpha \frac{y-\mu }{\sigma }\sqrt{\frac{\upsilon +1}{\upsilon +\dfrac{y-\mu }{\sigma }}};\upsilon +1) $ | (9) |
其中
| $ \left. {{{\left\{ {\hat \mu } \right.}_{t + h}},{{\hat \sigma }_{t + h}},{{\hat \alpha }_{t + h}},{{\hat \upsilon }_{t + h}}} \right\} = \mathop {\arg \min }\limits_{\mu ,\sigma ,\alpha ,\upsilon } \sum\nolimits_q {\left( {{{\hat Q}_{{y_{t + h}}\left| {{x_t}} \right.}}\left( {\left. {\underline q } \right|{x_t}} \right) - {F^{ - 1}}\left( {q;\mu ,\sigma ,\alpha ,\upsilon } \right)} \right)} $ | (10) |
其中,h是向前预测的步长,
图3展示了全时点下的条件预测分布,其中短期预测是指向前1个季度预测,长期预测是指向前1年预测。根据图3可以初步得出两点判断:(1)基于不同条件的经济增长分布预测存在明显差异,分布的均值、标准差、峰度、偏度都有不同表现,表明金融状况指数、外部经济不确定性以及核心通货膨胀对经济增长的影响存在本质区别,他们均是改变经济增长水平和波动率的重要条件因素;(2)在不同时点上,基于同一指标预测的经济增长分布也大为不同,比如基于金融状况指数的预测,在早期形态多为左偏,在样本中段多为右偏,近两年更加接近正态,这表明在不同经济发展阶段下,各指标对经济增长的影响机制、影响强度也存在明显差异,具有时变性。从集中离散的角度来看,在样本早期和中期,在不同条件下的经济增长预测均值比较集中,而近几年的预测均值呈发散状态。这表明过去我国经济增长的稳定性较强,分布形态的变异程度低,而在百年未遇之变局、世纪疫情等重大不确定性因素的影响下,我国经济增长的波动性逐渐加大,分布形态的变异程度明显上升。

|
| 图 3 三类指标下全时点条件预测分布图 |
本文还计算了一些代表性时点下的经济增长概率分布(见图4)。代表性时点包括:2008年4季度,代表金融危机时期,主要反映金融状况指数对经济增长的影响;2018年3季度,代表贸易摩擦时期,主要反映外部经济不确定性对经济增长的影响;2020年1季度,代表新冠疫情时期,主要反映核心通货膨胀对经济增长的影响,同时也可以反映外部经济不确定性的影响。在每一个时点,都包含了GDP自分布预测以及GDP的条件分布预测。其中,图4(a)-(c)为GDP增长率的短期在险分布预测,(d)-(f)为长期在险分布预测。

|
| 图 4 典型经济事件时点下的GDP增速概率分布预测 |
在金融危机时期,金融状况指数条件下的GDP分布呈左偏特征,而外部经济不确定性和核心通货膨胀条件下的GDP分布与GDP自分布较为接近,几乎不存在差异。这表明在该段时期内金融状况是主导经济增长分布变异的核心要素。从短期内的GDP增速变化来看,2009年1季度的GDP增速快速下滑至6.4%,出现了阶段性谷底,这恰好是金融在险分布下GDP增速的概率密度峰值,却不是其他三种分布下概率密度的最大值点,这再次印证了金融脆弱性是主导彼时经济增速下行的核心原因。从长期预测看,基于金融状况指数的预测结果明显右偏,这表明基于金融条件进行判断,彼时的金融冲击仅具有短期特征,不会改变中国经济高速运行的基本态势,也即GDP增速将在金融危机后快速反弹。结合后续的事实来看,在1年后的2009年4季度,我国GDP增速快速反弹至11.9%,这仍是金融在险分布的峰值位置,但该值已落于其他三个分布的右侧尾部区间,是其他分布状态下的小概率事件。由此可见,无论是在短期还是在长期,金融条件在险分布都能很好地预测金融危机时期GDP增长率的走势,这一方面肯定了金融要素是彼时主导经济增长的核心因素,另一方面也说明,我们应该高度关注经济增长在险分布的形态变异,这不仅有助于识别影响经济增长的核心要素,而且对精准预测GDP增长率也具有重要意义。
在贸易摩擦时期,从短期预测来看,基于外部经济不确定性条件下的GDP分布预测明显左偏,基于核心通货膨胀的GDP分布预测略有左偏,基于金融状况指数的预测结果基本无偏。上述结果意味着短期以外部确定性和核心通货膨胀为条件的GDP增速预测结果偏低,而基于金融状况指数的预测结果与自分布预测基本无异,这表明金融要素并非催动彼时经济增长变化的主导因素。从实际数据来看,2018年第4季度,我国实际GDP同比增长6.5%,而前3个季度的GDP同比增速分别为6.7%、6.9%和6.9%,第4季度经济增速明显下降,这与基于外部不确定性条件的预测最为一致。由此不难推断,在贸易摩擦时期,外部经济不确定性是影响经济增长的主要因素。当然,核心通货膨胀的持续走低同样也对经济增长产生了一定的下拉作用。2018年下半,随着贸易摩擦不断升级,中美之间的竞争博弈加剧,对我国进出口贸易以及微观主体预期产生了显著影响,外部经济不确定性明显上升,对经济增长产生了负面影响。与此同时,供给端部分供应链、产业链受阻,加征关税使经济运行成本上升,核心通货膨胀出现抬升趋势,因此这一时期的价格因素可以传导至经济增长。从长期来看,基于外部经济不确定性、核心通货膨胀和金融状况指数的GDP分布预测均呈左偏特征,这说明宏观基本面受到了多重负面冲击。结合彼时的情形来看:为缓解资金脱实向虚,金融去杠杆进入深水区和阵痛阶段,生产端PPI持续性陷入通缩,同时中美贸易摩擦不断升级,这些影响均具有长期性。而从一年后的经济数据来看,2019年3季度GDP同比增长5.9%,再度出现明显下降,并且无论从哪种条件下的在险分布来看,实际GDP增长率都较中心位置略有左偏(核心通货膨胀和外部不确定性条件下增长的后验均值为6.2%,金融在险条件下经济增长的后验均值为6.8%),说明三种负面因素产生了叠加效应,这同样与经验判断一致。
在新冠疫情时期,除金融在险分布外,实际GDP增长率的自分布和在险分布均出现了重大形态变异,呈典型的左侧截尾特征。左侧截尾分布具有两方面含义:一是经济下行不会进一步持续,仅具有短期性;二是任何正态条件分布都不具有意义,他们不是导致该变异的核心原因。从短期来看,基于核心通货膨胀的GDP分布预测在−2.5%处截尾,基于外部不确定性的预测和GDP自分布预测在−4%附近截尾。相对而言,基于金融状况指数的预测则呈现出正态分布特征。结合疫情时期的事实来看,由于突然的停产封城政策,经济的确会出现断崖式下跌,但由于中国经济基本面未出现实质性改变,仅是采取了短期应急性政策,因此,截尾分布显然是更具道理的。而金融分布依然呈现正态特征,这显然与彼时的实际状况不符,同时该轮经济下行也的确并非由金融系统变异引致,这基本印证了本文的事前判断。结合具体数据来看,2020年1季度GDP增速为−6.9%,这是疫情冲击负面效应的直接体现,因此基于三类因素对GDP的预测结果均比较悲观。而2020年2季度的GDP增速为3.1%,这与基于核心通货膨胀的预测结果最为接近。相对而言,基于金融条件的预测效果是最差的,这是因为新冠疫情初期,微观主体的预期较为悲观,年初金融市场出现了大幅下行,因此基于金融状况指数的预测结果最为保守,并非是经济基本面的真实反映,存在着太多的非理性因素。由此可见,在新冠疫情时期金融状况指数对GDP的预测能力最弱。反观通货膨胀,2020年1季度我国通胀大幅上升,1月的CPI同比增速高达5.4%,体现出明显的需求激增和供给短缺特征。考虑到疫情主要是影响实体经济,这也便不难理解,彼时通货膨胀为何包含了更多的增长信息。从长期来看,基于外部经济不确定性和核心通货膨胀的GDP分布预测结果在−3%左右截尾,基于金融状况指数的预测结果更加左偏,表明疫情下市场悲观情绪仍在持续蔓延,基于三种因素的长期预测结果均认为经济增长反弹的概率极低。但事实上,在疫情防控取得阶段性胜利后,我国加快复产复工、复商复市,经济增长在短期内大幅反弹,实际经济状况与预测结果存在一定偏差。由此可见,在重大危机事件下,由极度悲观预期引致的预测结果可能会与现实存在较大差距。因此,在重大突发事件和经济非稳态时期,不应过分依赖长期经济预测,短期经济预测一般更为有效。整体来看,无论是以何种要素为条件,经济增长的在险分布相较于自分布均包含了更多有益信息,是估计经济增长走势的有益工具。
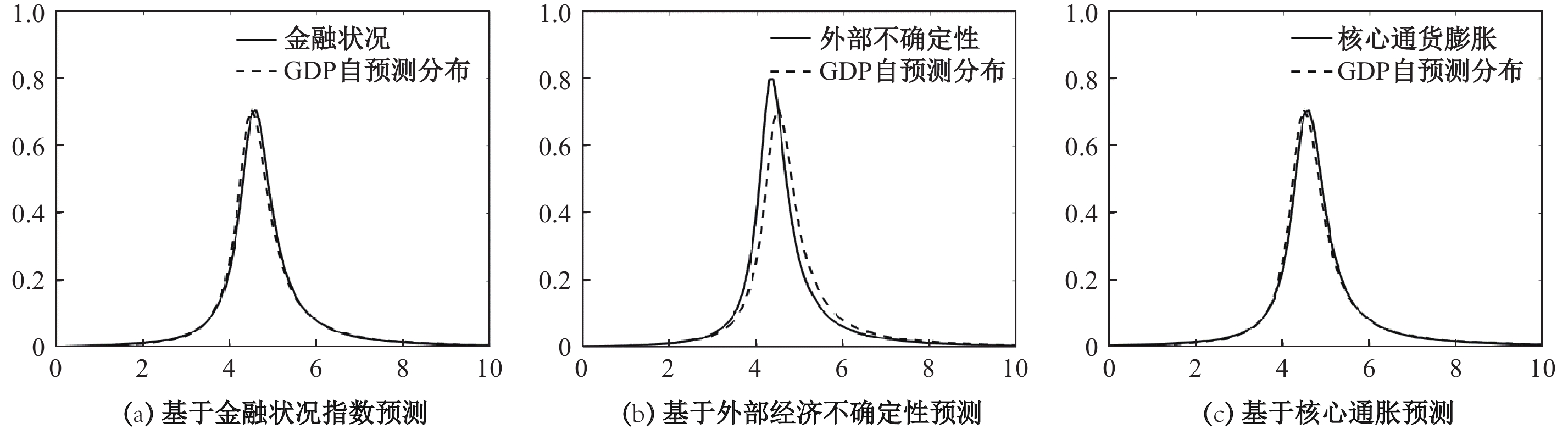
(三) 对未来经济走势的展望随着疫情防控平稳转段,后疫情时期的经济增长走势成为了备受关注的议题。为此,本文以2022年第3季度为基准点,基于三类因素对GDP分布进行短期预测。图5显示,在经济平稳复苏期,由于外部不确定性、金融状况指数以及核心通货膨胀均没有出现异常变化,经济增长更多是依靠其内生动力,因此基于三类因素对GDP分布的预测结果与GDP自预测分布预测比较接近,没有表现出明显的左偏和右偏。其中,GDP自分布预测、基于金融状况指数的预测、基于外部经济不确定的预测和基于核心通货膨胀的预测对应的GDP增速5%分位点分别是3.0%、2.8%、3.0%、2.8%,这意味着未来宏观经济增长的底线将位于2.8%之上。
|
| 图 5 基于不同指标的2022年第3季度 GDP概率分布短期预测(向前一季度) |
事实上,2022年4季度的GDP同比增速为2.9%,与本文的预测结果一致。现阶段,我国经济正处于持续的恢复性增长阶段,外部经济不确定性、金融市场运行、核心通货膨胀等指标都运行得比较平稳,没有遭到金融危机、贸易摩擦、新冠疫情等重大危机事件冲击,因此无论是基于何种要素预测,其分布态势均与GDP的无条件分布比较接近,证明我国经济增长复苏的确定性增强,未来很可能会延续稳中向好复苏。从近期的经济复苏轨迹来看,2023年1季度实际GDP增长4.9%,2季度GDP增速上升至6.3%,呈现出良性温和复苏态势。这表明中国经济将有很大概率以此为起点,破旧立新,重新回归至中高速增长平面。
六、结论和政策建议当前,中国经济发展面临的外部不确定性因素和内部周期性、结构性因素在很大程度上改变了经济增长运行的区位基础和可能的分布形态,造成了经济增长分布的重大变异,这对经济增长预测提出了更高要求。鉴于此,本文跳出传统的点估计和趋势估计思维,综合运用TVP-FAVAR-DMA模型、非预期条件波动率高维因子模型以及分位数回归、Q-VAR模型和在险分布函数刻画我国经济增长的遍历在险分布,从风险管理的视角重新审视了中国经济的在险增长状态。研究显示,金融状况指数、外部经济不确定性与核心通货膨胀对预测我国经济增长分布而言具有重要意义,但不同指标的影响存在差异性,体现出明显的阶段性特征,这揭示了经济增长形态变异的复杂性和多变性。在不同增长状态下,同一指标对经济增长的预测作用也显著不同,具有明显时变性;在金融危机时期金融状况是影响经济增长的主导因素,在贸易摩擦时期外部经济不确定性是影响经济增长的主要因素,在新冠疫情时期核心通货膨胀包含了预测经济增长的有效信息。上述典型事实表明,在预测经济增速时,首先应识别经济增长的核心驱动要素,进而以核心驱动要素为条件识别经济增长的在险分布,据此才能实现最佳的预测效果。最后,考虑到当下经济运行态势渐趋企稳,本文进一步以2022年3季度为基准点,对未来经济增长进行展望,以期识别未来经济增长的核心驱动要素,结果发现无论是基于何种要素进行预测,经济增长的在险分布形态均与GDP的无条件分布十分接近,表明未来的经济增长具有较强的稳定性和确定性,具备了稳中向好复苏的基础。
根据本文的研究结果,提出如下政策建议:
第一,对于经济增长预测而言,条件分布估计所包含的信息更加丰富,应将其作为监测中国经济景气变化的重要参考指标。点估计和趋势估计的结果具有绝对性和刚性,而条件分布从概率的角度给出了经济增长的分布预测,结果更具弹性和容错率,这为宏观调控提供了更多的可能性和政策预案。因此,在监测经济景气变化的过程中,除了考虑传统的宏观经济指标和微观经济运行外,也应对经济增长进行条件分布估计,尤其是短期的分布估计结果更具参考性和实用价值。第二,至于如何识别影响经济增长的核心要素,应当树立动态观念,与时俱进,摒弃僵化的静态认知。基于条件分布的经济增长预测的准确性依赖于条件本身,而在不同的经济运行状态下影响经济增长的核心因素也会不断变化。应在动态的观念下实时跟踪经济增长运行态势,识别不同典型经济阶段下引起经济增长大幅波动和分布变异的关键因素,进而对经济增长的分布函数做出准确描述,确保在不同的经济发展阶段下都可以比较准确地把握经济增长的可能走势,从而做到万全应对。第三,关于如何引导后疫情时期的经济复苏,应充分意识到,当下金融风险、外部不确定性和核心通货膨胀等条件均处于相对稳定状态,这说明未来一定时期内,经济增长的走势将更加依赖于其内生动力。因此,有序引导需求复苏,着力加强供给协调,把经济工作的重心置于提振实体经济活力才是确保经济平稳复苏的根本。一方面,要高度注重后疫情时期的供需结合管理,解决弱有效需求与供给匹配的问题,在需求侧,要坚定不移扩大内需,把培育需求动能置于首要位置,同时还要高度注重提升供给体系对国内消费需求的自适应性,形成以需求牵引供给,以供给激发需求的良性正反馈循环;另一方面,要积极监测金融状况、外部经济不确定性和物价水平等在险条件的变化,积极建立起宏观经济监测预警系统,对可能出现的经济风险进行提前锁定,事前预案,加强宏观经济风险管理意识,树立经济增长底线思维,在激发经济增长动能的同时也要兼顾培育强大的经济韧性。这是在百年未有之大变局下确保经济平稳发展的必要基础,亦是全面建设社会主义现代化强国的必由之路。
| [1] | 陈必果, 夏蜀, 刘志强, 等. 地方政府债务、税负效应与企业投资[J].财经科学,2023(5). |
| [2] | 陈守东, 王妍, 唐亚晖. 我国金融不稳定性及其对宏观经济、非对称影响分析[J].国际金融研究,2013(6). |
| [3] | 邓创, 吴健, 吴超. 外部经济、金融不确定性与我国的宏观经济下行风险[J].统计研究,2022(6). |
| [4] | 邓创, 吴健, 王哲. 外部不确定性冲击的来源甄别及其对中国货币政策有效性的影响[J].数量经济技术经济研究,2023(7). |
| [5] | 邓创, 徐曼. 中国金融周期与经济周期的交互影响作用分析——基于动态溢出指数方法的实证研究[J].上海财经大学学报,2018(6). |
| [6] | 桂文林, 程慧. 杠杆率、资产价格与经济增长时变关联研究——基于混频MS-VAR分析[J].统计研究,2021(7). |
| [7] | 郭豫媚, 陈彦斌. 中国潜在经济增长率的估算及其政策含义: 1979-2020[J].经济学动态,2015(2). |
| [8] | 刘达禹, 向思宇, 宋洋. 中国经济周期与金融周期关联机制的时变特征与不稳定性——基于精准计量视角的重新审视[J].上海财经大学学报,2022(6). |
| [9] | 刘金全, 付卫艳, 刘达禹. 我国经济增长率动态波动机制——基于TVP-VAR模型的实证研究[J].上海经济研究,2014(5). |
| [10] | 刘金全, 刘悦. 输入型通货膨胀的结构性传导与行业异质性[J].中央财经大学学报,2022(5). |
| [11] | 刘金全, 隋建利. 中国货币增长不确定性与经济增长关系检验(1980—2008)[J].中国社会科学,2010(4). |
| [12] | 刘伟, 范欣. 中国发展仍处于重要战略机遇期——中国潜在经济增长率与增长跨越[J].管理世界,2019(1). |
| [13] | 刘晓光, 刘元春, 王健. 杠杆率、经济增长与衰退[J].中国社会科学,2018(6). |
| [14] | 徐宁, 丁一兵, 张男. 经济不确定性冲击与货币政策的时变反馈——基于《人民日报》《光明日报》大数据的研究[J].财经科学,2020(1). |
| [15] | 尹筑嘉, 胡荟, 唐谭岭. 中国朱格拉周期与股价波动关联性研究——基于奇异谱的设备制造业分析[J].上海财经大学学报,2019(6). |
| [16] | 张晓晶, 刘磊. 宏观分析新范式下的金融风险与经济增长——兼论新型冠状病毒肺炎疫情冲击与在险增长[J].经济研究,2020(6). |
| [17] | 郑挺国, 尚玉皇. 基于金融指标对中国GDP的混频预测分析[J].金融研究,2013(9). |
| [18] | Adrian T, Boyarchenko N, Giannone D. Vulnerable growth[J].American Economic Review,2019,109(4):1263–1289. |
| [19] | Akar C. Analyzing the synchronization between the financial and business cycles in Turkey[J].Journal of Reviews on Global Economics,2016,5:25–35. |
| [20] | Azzalini A, Capitanio A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution[J].Journal of the Royal Statistical Society Series B:Statistical Methodology,2003,65(2):367–389. |
| [21] | Bloom N, Floetotto M, Jaimovich N, et al. Really uncertain business cycles[J].Econometrica,2018,86(3):1031–1065. |
| [22] | Cruz C J. Reduced macroeconomic volatility after adoption of inflation targeting: Impulses or propagation?[J].International Review of Economics & Finance,2022,82:759–770. |
| [23] | Fernández-Villaverde J, Guerrón-Quintana P, Kuester K, et al. Fiscal volatility shocks and economic activity[J].American Economic Review,2015,105(11):3352–3384. |
| [24] | Kashyap A K, Stein J C. Monetary policy when the central bank shapes financial-market sentiment[J].Journal of Economic Perspectives,2023,37(1):53–75. |
| [25] | Kleinberg J, Ludwig J, Mullainathan S, et al. Prediction policy problems[J].American Economic Review,2015,105(5):491–495. |
| [26] | Koop G, Korobilis D. A new index of financial conditions[J].European Economic Review,2014,71:101–116. |
| [27] | Stock J H, Watson M W. Slack and cyclically sensitive inflation[J].Journal of Money, Credit and Banking,2020,52(S2):393–428. |
| [28] | Tiwari A K, Suresh K G, Arouri M, et al. Causality between consumer price and producer price: Evidence from Mexico[J].Economic Modelling,2014,36:432–440. |
2.School of Economics, Jilin University, Jilin Changchun 130012, China

