
2023第25卷第5期
2.山东财经大学 高质量发展研究中心, 山东 济南 250014;
3.华中科技大学 经济学院, 湖北 武汉 430074;
4.山东英才学院 商学院, 山东 济南 250104
党的二十大报告明确指出,“统筹推进国际和区域科技创新中心建设,加快建设世界重要人才中心和创新高地,提升国家创新体系整体效能”。党的十八大以来,党中央全面分析国际科技创新竞争局势,坚持把科技创新摆在国家发展全局的核心位置。伴随着数字技术的融合应用,数据要素在实体经济部门的覆盖广度和渗透力度显著提升,逐渐成为科技创新的新动能。在企业经营管理方面,数据要素逐步渗透企业经营管理活动,通过提高企业外部技术信息获取能力与知识整合能力,帮助企业管理者进行有效判断和科学决策,通过大数据分析助力企业制定精准营销策略、生产经营方案,提升企业创新能力(卢剑峰和陈思,2021)。在社会现代化治理方面,大数据在城市交通、数字医疗、城市安全等方面发挥了重要作用,有助于提升社会治理效率,赋能国家治理体系和治理能力现代化(袁韵等,2020;吴朝文等,2021)。为了发挥数据要素的集聚效应,2016年2月25日,国家发改委批复贵州省成为首个国家级大数据综合试验区,随后批复北京、天津、河北、内蒙古、辽宁、河南、上海、重庆、广东9个省份为第二批试验区。大数据综合试验区建设为数据要素流通和数据资源共享提供平台,有效释放数据要素价值,成为试点地区数据要素集聚的重要载体。在数字中国战略背景下,数据要素的集聚效应有助于促进数据要素资源流通与整合应用,对于提高关键核心技术研发能力、提升研发资本配置效率具有重要意义。由此,本文重点关注数据要素集聚能否以及如何赋能科技创新?这种赋能是具有溢出效应还是虹吸效应?
现有研究更多地关注到数据要素的经济效应,探讨数据要素对经济增长的影响。Jones和Tonetti(2020)尝试将数据要素纳入经济增长模型,探讨不同的数据所有权模型如何影响经济增长率。在此基础上,Farboodi和Veldkamp(2021)发现企业通过数据积累可以减少自身面临的不确定性而提高企业生产率。学术界就大数据分析技术对知识更新的影响达成了较为一致的研究结论,认为数据要素通过驱动知识生产提高经济增速(Agrawal等,2019)。与上述观点不同,Aghion等(2019)认为新技术的发展和数据要素的出现将会降低创新活力,造成经济增速下滑。与此同时,也有学者探讨数据要素的市场化配置对经济发展的影响。数据生产要素已渗透到企业生产经营的各环节,数据要素的市场化配置是促进数字经济发展的必然要求(孔艳芳等,2021)。数据要素市场化配置的关键在于确定数据要素的产权,进而识别数据要素的交易机制和市场结构(荣健欣和王大中,2021)。既有研究大多采用定性分析法探讨数据要素的经济增长效应,并未得出一致结论。部分文献阐述了数据要素市场化配置的理论内涵,但尚未定量分析其经济效应。进一步地,有学者通过实证检验发现数据要素市场化促进了区域经济发展(杨艳等,2021)。然而,鲜有文献基于要素集聚视角,揭示数据要素集聚对科技创新的作用机制。
此外,部分文献集中考察数据要素如何赋能创新。作为一种新的生产要素,数据要素赋能提升了企业产品创新绩效(谢康等,2020)。与此同时,大数据赋能企业绿色创新,促进企业技术和商业模式创新,从而推动企业转型升级(陈文和常琦,2022;王鑫等,2022)。然而,部分学者认为,数据要素的创新效应依赖于企业的外部环境。陶长琪和丁煜(2022)指出,当数据要素与人力资本相匹配时,才会通过创新激励效应释放创新红利。企业规模也会影响其创新策略,大企业主要依赖数据要素进行迭代式创新,而其突破性创新动力不足。上述文献为本文奠定了很好的研究基础,但鲜有研究讨论数据要素集聚的科技创新效应,且较少关注两者之间的潜在内生性。事实上,数据要素集聚带来的人力资本和创新资源会提升科技创新水平,同时科技创新又促进了数据要素集聚,互为因果的内生性问题导致回归结果存在偏误。
本文主要的边际贡献如下:第一,现有文献较多关注大数据综合试验区建设对专利授权量等指标的影响,缺乏对科技创新累积效应的研究,而本文采用R&D资本存量作为科技创新的衡量指标,考虑了科技创新的累积性和滞后性。同时采用双重差分法识别大数据综合试验区建设与R&D资本存量的因果关系,拓展了大数据综合试验区实施效果评估的研究范畴。第二,本文根据习近平总书记的重要讲话精神和国家大数据实验区建设目标,锚定科技创新亟需解决的“缺人”和“缺钱”问题,提出人力资本机制、劳动错配缓解机制和研发投入机制,为数据要素高效集聚的研究提供了理论依据和学理支撑。第三,本文在识别数据要素集聚与科技创新的因果关系基础上,厘清数据要素集聚是具有溢出效应还是虹吸效应,为发挥大数据综合试验区的空间效应和梯队式扩容提供参考。
二、理论机制与研究假设数字经济时代经济增长模式由外延式向内涵式转变,数据要素所具备的区别于劳动、资本等传统生产要素的特征对经济高质量发展具有持续推动作用,数据要素是数字经济的微观基础和创新引擎,对于促进科技创新具有重要意义。本文基于“习近平总书记关于科技创新重要讲话”和“国家大数据综合试验区建设的现实问题”,针对“缺人”问题,提出国家大数据综合试验区建设的“劳动力错配缓解机制”和“人力资本积累机制”;针对“缺钱”问题,提出国家大数据综合试验区建设的“研发投入机制”。
(一) 数据要素集聚缓解劳动资源错配大数据综合试验区建设承担通过促进数据要素流通、数据资源共享开放、数据资源应用提升劳动配置效率的重要任务,对于缓解劳动资源错配具有重要作用。数据要素集聚通过以下三个途径缓解劳动力错配。首先,大数据综合试验区建设能够有效促进数据资源的开放和数据要素的高效集聚,数据要素集聚提高了大数据企业和创新型企业对高素质、高质量劳动力的需求。此外,优质的劳动力资源通过大数据了解企业招聘信息,缓解摩擦性失业问题,从而缓解了劳动力错配。其次,大数据综合试验区建设打破了大数据资源的使用壁垒,利用大数据资源有助于高质量劳动要素在高生产效率企业与低生产效率企业之间转移,促进了劳动力的优胜劣汰,从而缓解了劳动资源错配(牛子恒和崔宝玉,2022)。最后,大数据综合试验区建设有利于引导周边地区资本、技术等生产要素向试验区聚集,从而引导大数据企业的劳动力资源的集聚,周边高技能劳动力开始向大数据综合试验区集聚,周边地区高技能劳动力得到有效利用,同时解决了大数据综合试验区内信息技术企业劳动力不足的问题,从而缓解了劳动资源错配(季书涵等,2016)。大数据综合试验区建设通过缓解劳动资源错配,降低新兴产业的高质量劳动力的搜索成本,缓解摩擦性失业,为大数据企业和人工智能企业提供高质量的劳动力,从而提升科技创新水平。据此,本文提出如下假设:
H1:数据要素集聚通过缓解劳动资源错配提升科技创新水平。
(二) 数据要素集聚提升了人力资本积累水平大数据综合试验区建设通过促进公共数据要素的开放共享、大数据创新应用、大数据要素流通、数据中心整合利用等途径促进了大数据产业在综合试验区聚集。数据要素集聚主要通过以下三条途径提升人力资本水平:首先,大数据综合试验区建设带来的大数据产业集聚提高了对高质量人才的需求,有助于促进人力资本的集聚。以数据作为生产要素的信息技术产业和人工智能产业对大数据人才的需求较大,因此,大数据综合试验区建设吸引了大量高技术人才集聚,满足了大数据综合试验区内的高层次人才需求(郑国强等,2023)。其次,数据要素集聚有利于促进人才的流动和配置,促进人力资本提升。大数据信息集聚和共享导致企业对大数据专业人才的争夺更加激烈。大数据专业人才是高新技术企业的重要战略资源,大数据综合试验区使大数据专业人才由分散的、静态性的状态转化为集聚性、动态性的状态,有利于大数据专业人才的优化配置,提升人力资本水平(陶长琪和丁煜,2022)。最后,大数据综合试验区建设有助于促进数字经济发展,能够有效推动高新技术企业的数字化转型,高质量人才团队在“干中学”的过程中,逐渐寻找数据要素与高质量劳动力要素的契合点,从而提升人力资本水平。此外,人力资本在研发过程中具有核心作用,是科技创新的宝贵资源,人力资本优势有利于提升区域科技创新水平,发挥人力资本累积在科技创新过程中的驱动作用(庞瑞芝等,2023)。据此,本文提出如下假设:
H2:数据要素集聚通过提升人力资本积累水平推动科技创新。
(三) 数据要素集聚提高了研发投入水平大数据综合试验区建设促进了大数据产业集聚,由于数据要素和数据产业集聚,吸引了创新型企业进入试点地区,从而缓解了试点地区研发投资不足的问题,提高地区研发投入。大数据综合试验区建设主要通过以下三方面提升研发投入水平:首先,数据要素集聚有助于政府增加研发投入。数据要素集聚推动了数据要素的有序流动,促进了数据开放、数据交易和数据交换(何玉长和王伟,2021),从而引导高新技术企业入驻试点地区,数字化产业集聚带来的数字技术发展有利于促进试点地区的科技创新。为了全面贯彻创新、协调、绿色、开放、共享的新发展理念,地方政府将加大对创新型企业和人工智能企业的研发投入(施锦诚和王迎春,2023)。其次,数据要素集聚有助于企业进行大数据综合分析,帮助企业对创新活动进行有效判断和科学决策,同时利用大数据整合企业内部创新资源,提升企业获取外部技术知识的能力,激励企业加大研发创新投入(毛明芳,2021)。此外,数据要素集聚带来的产业集聚促进了企业间竞争,有利于企业组织优化和效率提升,从而倒逼企业提高研发投入水平,以适应企业竞争需要(徐翔等,2023)。最后,数据要素集聚有助于信息技术企业充分利用多层次资本市场的多元融资渠道,从而缓解企业融资约束,提升创新型企业资金筹集能力和资本配置效率,进而增加企业研发投入。提升科技创新水平需要以研发投入为支撑,吸引科技创新资源集聚,提高重大科技创新产出水平。据此,本文提出如下假设:
H3:数据要素集聚通过增加地区研发投入提升科技创新水平。
三、研究设计与数据说明 (一) 模型构建为了系统识别数据要素集聚对科技创新的影响,本文运用双重差分法识别数据要素集聚与科技创新之间的因果效应。在进行模型设计过程中以大数据综合试验区为背景,将建立大数据综合试验区的试点地区作为处理组,其余地区为控制组。本文构建如下双重差分模型:
| $ Cs{a_{it}} = {\alpha _0} + {\alpha _1}BD{P_{it}} + \phi {X_{it}} + {e_i} + {y_t} + {\varepsilon _{it}} $ | (1) |
其中,Csa表示科技创新,选取地区R&D资本存量作为其代理变量。i、t分别表示地区和年份,BDP为核心解释变量数据要素集聚,若地区i在第t年获批建立大数据综合试验区,其取值为1,否则取值为0。Xit为一系列控制变量,包括经济发展、产业结构、数字基础设施、财政规模、金融发展、科技成果转化、创新能力等一系列变量。此外,ei、yt分别表示地区、时间固定效应。本文重点关注核心解释变量BDP的估计系数α1,其表示数据要素集聚对科技创新的影响。
(二) 变量选取1.被解释变量:采用R&D资本存量作为科技创新的代理指标。从R&D资本存量的内涵来看,R&D资本存量反映了研发创新的知识累积水平,是衡量一个地区创新资源集聚程度和科技创新水平的重要指标(曹跃群等,2022)。因此,R&D资本存量可以反映科技创新水平。对于R&D资本存量的测算,本文借鉴杨骞等(2022)的做法,首先构建R&D价格指数。如何构建R&D价格指数是学术界面临的难题,既有研究在价格指数的选取及其权重的设定方面存在较大争议:一是参考Jaffe的做法,R&D支出价格指数=0.49×非金融企业的工资价格指数+GNP隐含指数;二是选取R&D人员的工资价格指数和设备投资的GNP价格指数,分别赋予0.55、0.45的权重而得到加权平均值。由于R&D支出主要包括固定资产支出和R&D活动人员的消费,本文借鉴朱平芳和徐伟民(2003)构建的R&D支出价格指数,R&D价格指数=0.55×消费物价指数+0.45×固定资产投资价格指数。其次,对R&D经费内部支出进行平减,确定折旧率并计算基期R&D资本存量。利用以2001年为基期的平减指数,对R&D经费内部支出平减得到实际R&D经费内部支出;此外,本文借鉴白俊红和蒋伏心(2015)的做法,选取15%作为R&D资本存量的折旧率。
| $ {K_{i0}} = {E_{i0}}/(g + z) $ | (2) |
其中,Ki0表示基期R&D资本存量,Ei0为基期实际R&D经费内部支出,g是实际R&D经费内部支出的几何平均增长率,z为折旧率。采用永续盘存法核算样本期内R&D资本存量,如式(3)所示。
| $ {K_{it}} = (1 - z) \times {K_{i(t - 1)}} + {E_{i(t - 1)}} $ | (3) |
其中,Kit为R&D资本存量,折旧率z=15%,Ei(t−1)为i地区第t−1期实际R&D经费内部支出。
(2)核心解释变量:数据要素集聚。本文将是否设立大数据综合试验区作为地区数据要素集聚的代理变量,通过设置时间虚拟变量(period)和组间虚拟变量(treat)交乘项表示。若地区i在2001—2019年间获批设立大数据综合试验区,则属于处理组地区,取值为1,否则为0。
(3)控制变量。本文的控制变量包括如下指标:经济发展水平,选取人均实际GDP并取对数;产业结构升级水平采用第三产业与第二产业产值之比来衡量;数字基础设施采用电信业务总量占GDP的比重来表示;财政规模采用财政支出占GDP的比重来表示;金融发展水平选取地区金融业增加值并取对数来衡量;科技成果转化能力采用地区技术市场成交额来表示;创新能力用地区专利申请授权数来度量。
(三) 数据说明与描述性统计本文选取2001—2019年中国30个省级行政区作为研究样本(不含西藏和港澳台地区),数据主要来源于历年《中国统计年鉴》《中国科技统计年鉴》,主要变量的描述性统计见表1。
| 变量 | 变量名称 | 观测值 | 均值 | 标准差 | 最小值 | 最大值 | |
| 被解释变量 | Csa | 科技创新 | 570 | 0.731 | 1.156 | 0.003 | 7.496 |
| 核心解释变量 | BDP | 是否建立大数据
综合试验区 |
570 | 0.072 | 0.259 | 0.000 | 1.000 |
| 中介变量 | M_labor | 劳动资源错配 | 570 | 0.080 | 0.639 | 0.714 | 3.790 |
| R_exp | 研发投入水平 | 570 | 2.755 | 1.035 | 0.970 | 6.040 | |
| H_cap | 人力资本水平 | 570 | 1.065 | 0.208 | 0.652 | 1.867 | |
| 控制变量 | Pgdp | 经济发展水平 | 570 | 10.148 | 0.808 | 8.006 | 12.011 |
| Industry | 产业结构 | 570 | 1.149 | 0.604 | 0.527 | 5.234 | |
| Infra | 数字基础设施 | 570 | 0.053 | 0.031 | 0.010 | 0.231 | |
| Fiscal | 财政规模 | 570 | 0.208 | 0.096 | 0.077 | 0.628 | |
| Finance | 金融发展水平 | 570 | 6.066 | 1.381 | 2.282 | 9.078 | |
| Tech | 科技成果转化能力 | 570 | 3.752 | 1.813 | 0.247 | 8.051 | |
| Innovate | 创新能力 | 570 | 6.915 | 1.819 | 1.792 | 10.998 |
平行趋势检验是双重差分估计的前提,在采用双重差分法对大数据综合试验区的政策效果进行评估时,需要满足处理组与控制组的共同趋势假定。基于此,本文借鉴Beck等 (2010)的做法,采用图示法比较大数据综合试验区建设前后科技创新的变化(见图1)。图1汇报了政策实施之前估计系数的大小及对应的95%置信区间,并且汇报了当被解释变量为Csa时大数据综合试验区建设对科技创新水平的动态影响。从平行趋势检验图中可以看出,在该项政策实施前的2001—2015年,估计系数的变化比较平缓,政策实施之前估计系数的估计值在95%的置信区间内基本没有通过显著性水平检验,不拒绝回归系数为0的原假设,说明在大数据综合试验区政策正式实施之前,处理组与控制组地区的科技创新水平并没有显著差异,满足共同趋势假设的条件。此外,当大数据综合试验区政策实施当年及之后,数据要素集聚对科技创新的估计系数出现明显的上升,表明大数据综合试验区建设显著地促进了处理组科技创新水平的提升。
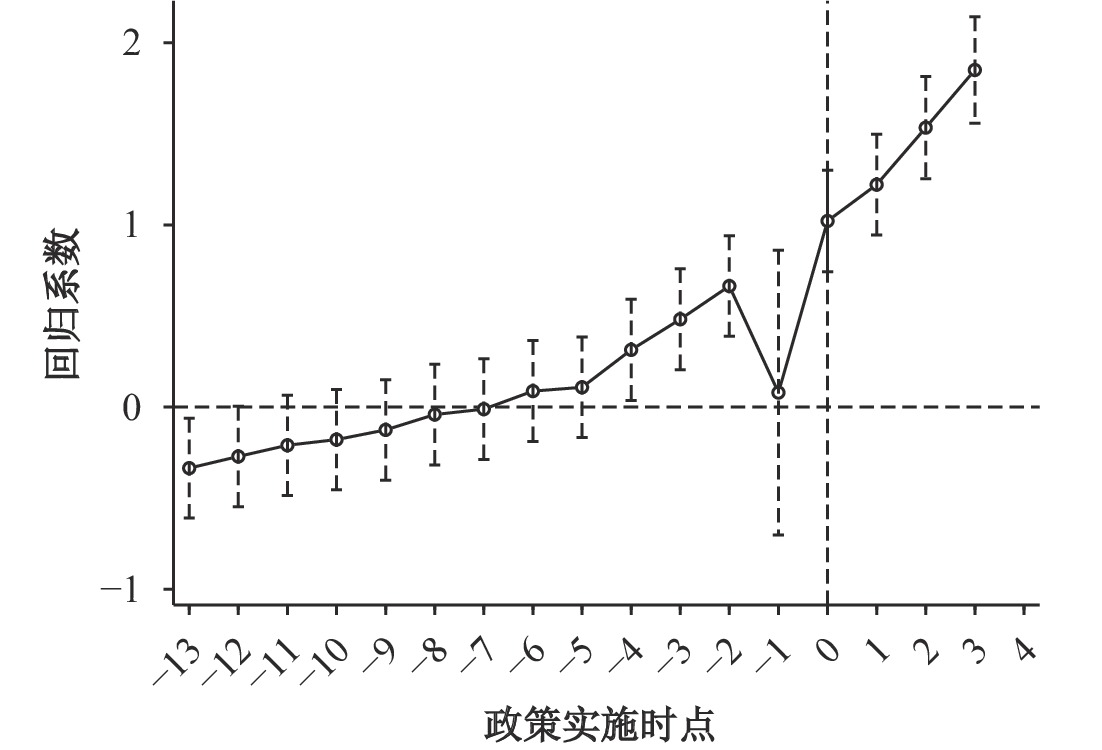
|
| 图 1 平行趋势检验 |
大数据综合试验区建设作为数据要素市场化体制机制建设的重要举措,是打破数据要素流通壁垒、促进数据要素集聚、激活数据要素经济价值与社会价值的关键举措。大数据综合试验区的政策效果如何? 其对科技创新水平的提升作用是否有效?对此,在平行趋势假定满足的前提下,本文运用双重差分法对模型(1)进行估计,考察基于大数据综合试验区建设的数据要素集聚对科技创新水平的影响效应,基准回归结果如表2所示。由模型(1)的基准回归结果可知,列(1)没有加入任何控制变量,可以看到核心解释变量BDP的估计系数显著为正。为了控制其他变量的影响,加入经济发展水平、产业结构、数字基础设施等控制变量之后列(2)的回归系数依然显著。以上结果表明大数据综合试验区建设对科技创新产生显著的正向影响,说明以大数据综合试验区建设为特征的数据要素集聚有效提升了科技创新水平。列(3)、(4)、(5)、(6)在此基础上进一步控制了财政支出规模、金融发展水平、科技成果转化能力等因素对科技创新的影响,核心解释变量BDP的回归系数均在1%的水平上显著为正。列(6)核心解释变量BDP的估计系数为0.354,表明加入控制变量后基准回归结果依然显著,说明数据要素集聚显著提升科技创新水平。
| 变量 | (1) | (2) | (3) | (4) | (5) | (6) |
| BDP | 0.550***(0.137) | 0.432***(0.131) | 0.361***(0.123) | 0.362***(0.124) | 0.356***(0.124) | 0.354***(0.124) |
| 常数项 | 2.044***(0.187) | 2.224***(0.565) | 3.095***(0.541) | 3.128***(0.637) | 3.285***(0.663) | 3.407***(0.669) |
| 控制变量 | 否 | 是 | 是 | 是 | 是 | 是 |
| 城市固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| N | 570 | 570 | 570 | 570 | 570 | 570 |
| R2 | 0.470 | 0.528 | 0.584 | 0.584 | 0.585 | 0.586 |
| 注:***、**和*分别表示1%、5%及10%的显著性水平,括号内为回归系数的标准误;限于篇幅,未汇报控制变量的结果,下同。 | ||||||
根据基准回归结果,本文发现数据要素集聚能够显著提高科技创新水平,为了消除处理组与控制组样本带来的特征差异的干扰,降低估计偏误,本文进一步利用核匹配、半径匹配和近邻匹配法的倾向得分匹配双重差分法(PSM−DID)进行稳健性检验,以保证本文结论的稳健性。具体地,本文运用核匹配方法,首先选择匹配使用的协变量,即匹配处理组与控制组的一系列特征控制变量,计算倾向得分匹配值并进行匹配;然后运用核匹配方法减少处理组和控制组特征变量在匹配前后的标准化偏差,以缓解地区间的特征差异。本文发现处理组和控制组特征变量在匹配前后的标准化偏差基本在0附近(小于10%),表明经过倾向得分匹配之后处理组和控制组的变量差异性得到了平衡,减小了两个样本组在个体特征上的系统性差异。
为了保证匹配结果满足平衡性需要,进一步对匹配变量进行平衡性检验,本文发现匹配后变量的标准化偏差小于10%,而且所有特征变量T检验的结果不拒绝处理组与控制组无系统差异的原假设。对比匹配前的结果,大多数特征变量的标准化偏差均大幅缩小,表明各特征变量基本通过平衡性检验。此外,为了避免匹配方法选取的主观性,本文还采用半径匹配法和K近邻匹配法进行倾向得分匹配。其中,半径匹配法是指首先设定一个半径,找出设定半径范围内的全部观测值作为对照组,将处理组得分值与控制组得分值的差异在半径范围内进行配对;K近邻匹配法是选取距离最近的K个观测值作为对照组,本文选取K=4。表3列(1)−(3)分别报告了核匹配、半径匹配和K近邻匹配的估计结果,我们发现无论选择何种匹配方式,核心解释变量的回归系数均为正,且通过1%水平的显著性检验。该结果说明经过样本匹配后的影响效应依旧较为稳健,样本内地区个体特征差异的影响较小,处理组与控制组地区样本带来的特征差异并未影响数据要素集聚对科技创新的影响,本文的研究结论具有较强的稳健性
| 变量 | 核匹配 | 半径匹配 | K近邻匹配 |
| (1) | (2) | (3) | |
| BDP | 0.346*** (0.130) |
0.383*** (0.131) |
0.383*** (0.130) |
| 常数项 | 1.603** (0.788) |
4.070*** (0.743) |
3.956*** (0.739) |
| 控制变量 | 是 | 是 | 是 |
| 城市固定效应 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 |
| N | 537 | 491 | 495 |
| R2 | 0.782 | 0.578 | 0.576 |
由于本文选取的样本考察期较长,与大数据综合试验区建设无关的其他事件或随机因素也可能会导致科技创新水平产生差异,导致估计结果出现偏误。为了进一步排除不可观测的因素对大数据综合试验区选择的影响,本文参考刘满凤和陈梁(2020)的方法,选取样本考察期内2016年获批建立的大数据综合试验区数量,通过随机分配设立大数据综合试验区的地区进行安慰剂检验,并对安慰剂检验的随机过程重复了500次,对核心解释变量BDP进行估计且对其估计系数进行概率密度分析,将表2中列(6)数据要素集聚的回归系数作为基准估计结果,随机抽取地区样本以确保本文构建的核心解释变量BDP对科技创新水平产生较小的政策效果。图2中报告了被解释变量为Csa时BDP的估计系数的变化及其对应的概率密度分布图。从安慰剂检验的概率密度分布图可知,在随机抽取的样本中BDP的估计系数大多集中分布在0附近,而模型(1)的基准估计结果为0.354,则说明不可观测的其他事件或随机因素对科技创新不存在显著影响,进一步证明数据要素集聚对科技创新有显著的促进作用。以上结果表明未观测到的其他因素不会对科技创新水平产生影响,表明大数据综合试验区科技创新水平的提升来自于大数据综合试验区建设。
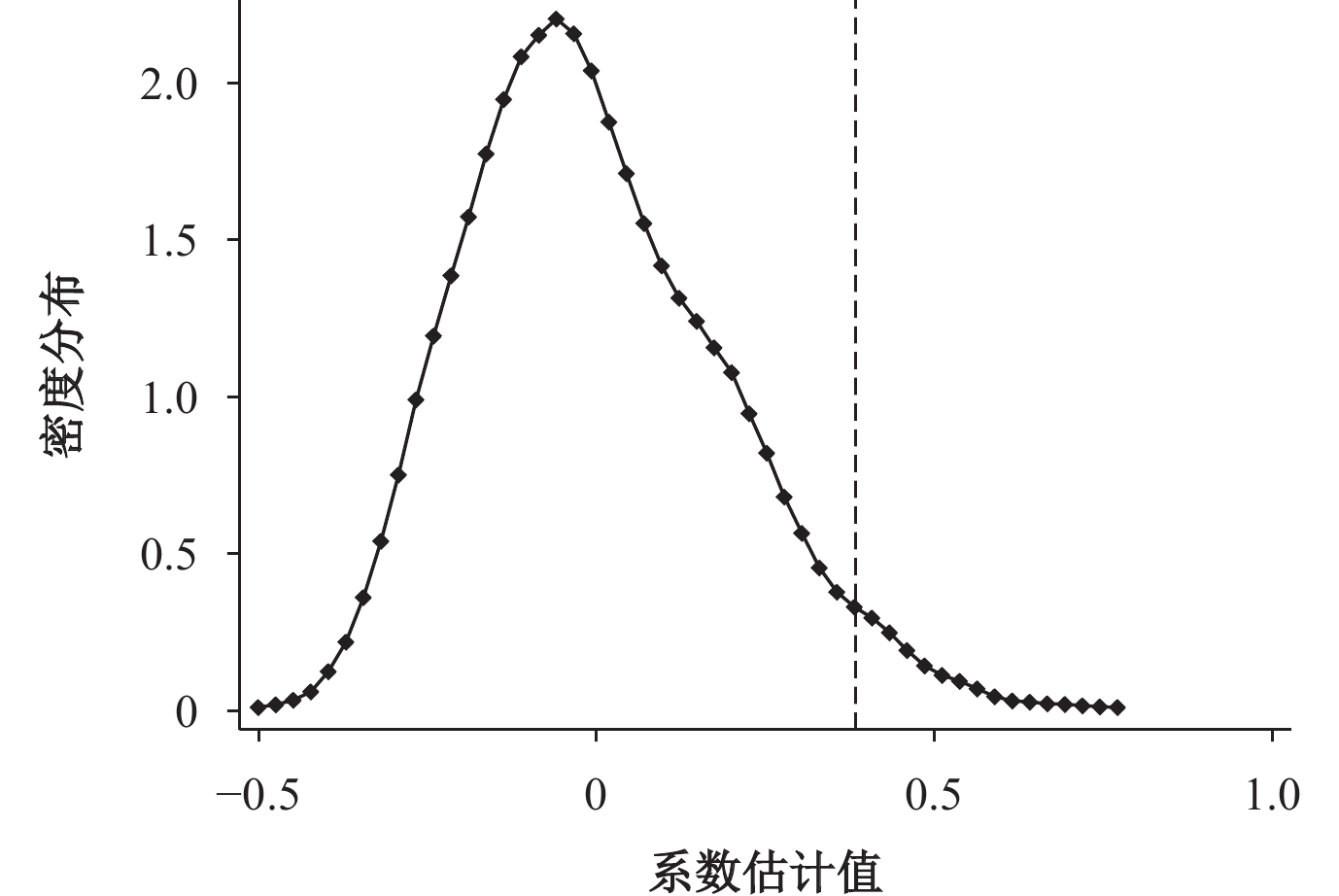
|
| 图 2 安慰剂检验 |
双重差分法通过处理组和控制组的对比能够克服估计过程中的内生性问题,但前提是大数据综合试验区建设试点的地区是随机选择的。然而,事实上并非如此,若处理组地区的大数据产业较为发达,在大数据应用领域拥有巨大的市场优势和发展潜力,这些地区获批大数据综合试验区的可能性较大,双向因果造成的内生性问题会降低研究结论的说服力和精确性。
为了较大程度上缓解内生性问题,亟需寻找一个合适的工具变量识别数据要素集聚对地区科技创新影响的净效应。2016年获批建设大数据综合试验区的地区包括贵州、京津冀、珠三角、重庆、上海、河南、辽宁、内蒙古,主要分布在华北、华南和西南地区,这可能是因为大数据综合试验区的空间分布与信息基础设施能力相关。因此,本文借鉴刘传明和马青山(2020)的做法,选择各地区的地形起伏度作为大数据综合试验区的工具变量。地区地形起伏度同时满足工具变量的相关性与排他性条件。原因在于:一方面,地形起伏度会影响网络基础设施建设,若一个地区的地形起伏度越大,不仅会增加大数据综合试验区基础设施的建设与运行成本,还会影响大数据网络平台的信号质量,进而对大数据综合试验区内数字基础设施的运行产生影响;地区的地形起伏度越小,大数据综合试验区数字基础设施的建设与运行成本越低,则该地区获批大数据综合试验区的概率越大。因此,地形起伏度满足工具变量的相关性要求。另一方面,相对于其他工具变量,将地形起伏度作为一个地区的地理特征变量,与经济社会因素无关,对科技创新水平的影响较弱。综上所述,在控制了其他变量后,选取地区地形起伏度作为工具变量在一定程度上满足排他性约束要求。
本文利用两阶段最小二乘法(2SLS)进行回归分析,估计结果如表4所示。根据表4我们发现无论是否加入控制变量,第一阶段回归中工具变量IV的估计系数均为负且通过5%的显著性检验,表明地形起伏度越小的地区,该地区获批大数据综合试验区的概率越大。第二阶段的工具变量回归中数据要素集聚的估计系数均在1%的水平上显著为正,这与双重差分的基准估计结果一致,说明经过内生性处理之后大数据综合试验区的政策效果依然存在,基准回归结果并未受到自选择偏误造成的潜在内生性问题影响。这一结论表明数据要素集聚显著提升科技创新水平。
| 变量 | 第一阶段回归 | 第二阶段回归 | ||
| (1) | (2) | (3) | (4) | |
| BDP | 11.365*** (4.129) |
5.634*** (1.660) |
||
| IV | −0.131*** (0.041) |
−0.102** (0.046) |
||
| 常数项 | 0.224*** (0.078) |
0.282
(0.218) |
−0.087
(0.319) |
−1.163
(1.549) |
| 控制变量 | 否 | 是 | 否 | 是 |
| 城市固定效应 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 |
| N | 570 | 570 | 570 | 570 |
| R2 | 0.325 | 0.339 | 0.671 | 0.566 |
从前文的理论机制分析可知,大数据综合试验区建设对科技创新水平的影响可能存在劳动资源错配、研发投入及人力资本水平三种主要机制。因此,本文利用中介模型对上述作用机制进行实证检验,并构建以下方程:
| $ Cs{a_{it}} = {w_0} + {w_1}BD{P_i}_t{\text{ + }}{w_2}contro{l_{it}} + {e_i} + {y_t} + {\varepsilon _{it}} $ | (4) |
| $ Cs{a_{it}} = {k_0} + {k_1}BD{P_i}_t + {k_2}{M_{it}} + {k_3}contro{l_{it}} + {e_i} + {y_t} + {\varepsilon _{it}} $ | (5) |
其中,模型(4)是考察数据要素集聚对科技创新的影响,与前文模型(1)一致。模型(5)在模型(4)的基础上加入中介变量,考察数据要素对科技创新影响的作用机制。该模型重点关注估计系数k1和k2。本文考虑的中介变量包括地区劳动资源错配、研发投入及人力资本水平。数据要素集聚对科技创新水平产生的总效应为w1,直接效应为k1。前文模型(1)的基准估计模型中w1的系数显著为正,若k1的回归系数显著为正且k1的系数减少,而k2的回归系数显著为负,则说明劳动资源错配为部分中介变量;而对于地区研发投入及人力资本水平,若k1和k2的回归系数均显著为正且k1的系数减少,则说明研发投入与人力资本为部分中介变量。
(二) 中介效应分析本文从劳动资源错配视角进行作用机制分析,对于地区劳动资源错配水平的测度,本文借鉴陈永伟和胡伟民(2011)的测算方法,选取地区GDP作为产出,三次产业从业总人数作为劳动投入量,地区实际GDP变量以2001年不变价进行核算,通过测算劳动扭曲程度即得到地区劳动资源错配程度,该指标反映一个地区的劳动配置效率。因此,若劳动市场的相对扭曲程度越低,则地区劳动配置效率越高。本文选取地区R&D经费内部支出来衡量研发投入,R&D经费内部支出主要包括地区基础研究、应用研究与试验发展三大领域的研发投入,但地区经济发展水平越高,其R&D经费内部支出也越多。因此,本文选取R&D经费内部支出占GDP的比重来测度地区研发投入水平。此外,对于人力资本水平的测算,本文参考Wang和Yao(2003)的方法,采用各地区6岁及以上人口的平均受教育年限来进行衡量,其计算公式是(16×大专及以上学历人数+12×高中学历人数+9×初中学历人数+6×小学学历人数)/地区6岁及以上人口总数。
表5列(1)汇报了模型(3)的回归结果,从中可见,数据要素集聚有效促进了科技创新。此外,本文将劳动资源配置、研发投入和人力资本水平作为数据要素集聚提升科技创新水平的中介变量,并对模型(4)进一步做中介效应检验,检验结果如表5列(2)−(4)所示。在列(1)基准回归的基础上加入相应的中介变量,如劳动资源错配的回归中k1的系数显著为正且减少,而k2的系数显著为负,劳动资源错配的回归系数为−0.827,通过1%水平的显著性检验。而在研发投入和人力资本水平的机制分析中,k1和k2的系数均显著为正且k1的回归系数有所减少,研发投入强度和人力资本水平的回归系数分别为0.223、0.200,均在5%的水平上显著。从以上中介效应检验的估计结果可以看出,本文选取的三个中介变量均为部分中介,即大数据综合试验区建设通过降低劳动资源错配、提升研发投入和人力资本水平发挥的政策作用提高了科技创新水平。上述机制分析结果表明,数据要素集聚有效缓解了劳动资源错配,提升了研发投入和人力资本水平,从而促进科技创新水平提升,验证了前文理论分析部分提出的假设H1、H2和H3,即数据要素集聚的劳动资源配置效应、研发投入增加效应和人力资本提升效应。
| 变量 | 基准回归 | 劳动资源错配 | 研发投入水平 | 人力资本水平 |
| (1) | (2) | (3) | (4) | |
| BDP | 0.354*** (0.124) |
0.207* (0.122) |
0.330*** (0.124) |
0.322*** (0.124) |
| M_labor | − | −0.827*** (0.134) |
− | − |
| R_exp | − | − | 0.223** (0.094) |
− |
| H_cap | − | − | − | 0.200** (0.081) |
| 常数项 | 3.407*** (0.669) |
4.040*** (0.655) |
1.921** (0.914) |
1.379
(1.059) |
| 控制变量 | 是 | 是 | 是 | 是 |
| 城市固定效应 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 |
| N | 570 | 570 | 570 | 570 |
| R2 | 0.586 | 0.615 | 0.591 | 0.591 |
数据要素集聚对科技创新的影响受到数字基础设施、市场化水平以及数字经济发展等因素的影响。因此,本文将考察数字基础设施、市场化水平、数字经济发展等因素的异质性。
(一) 数字基础设施异质性大数据综合试验区建设实施效果与地区数字基础设施水平密切相关,数字基础设施不仅是支撑科学研究、技术开发的重要平台,同时也为数据要素流动提供安全、快捷的渠道。作为数据要素发挥作用的载体,大数据、人工智能、工业互联网等数字基础设施平台的发展加速了数据在各主体之间的充分流动。由此可见,数字基础设施水平较高的地区,大数据综合试验区建设更有利于提高科技创新水平。本文将数字基础设施水平低于样本期内中位数值的地区定义为数字基础设施水平较低地区,高于中位数值的地区定义为数字基础设施水平较高地区。数字基础设施的异质性分析结果如表6列(1)和列(2)所示,在数字基础设施水平较高的地区中,核心解释变量BDP的回归系数为0.787,且在1%的水平上显著,而数字基础设施水平较低地区的回归系数虽然为正,但并不显著,表明数字基础设施水平较高的地区在大数据综合试验区建设过程中更能取得显著的效果。其原因可能在于,数字基础设施为数据要素集聚提供基础条件,数字基础设施也是数据要素交易与流动的重要载体。数字基础设施水平较高的地区大多在大数据产业发展条件方面具有区位与资源集聚优势,为地区数据要素集聚与产业发展提供支撑。
| 变量 | 高创新基础
设施水平 |
低创新基础
设施水平 |
高市场化程度
|
低市场化程度
|
高水平数字
经济发展 |
低水平数字
经济发展 |
| (1) | (2) | (3) | (4) | (5) | (6) | |
| BDP | 0.787***(0.185) | 0.056(0.147) | 0.370**(0.185) | 0.002(0.036) | 0.497**(0.212) | −0.073(0.048) |
| 常数项 | 1.527(1.096) | 3.630***(0.833) | 2.551*(1.332) | 1.165***(0.164) | 4.146***(1.265) | 1.260***(0.099) |
| 控制变量 | 是 | 是 | 是 | 是 | 是 | 是 |
| 城市固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| N | 285 | 285 | 285 | 285 | 285 | 285 |
| R2 | 0.576 | 0.646 | 0.707 | 0.735 | 0.728 | 0.706 |
大数据作为新型生产要素需要通过数据交易的方式配置到生产和生活领域,即数据要素通过市场机制来实现数据要素需求与供给。因此,区域市场化程度是影响大数据综合试验区政策效果的重要因素。地区市场化程度的差异是否会导致大数据综合试验区科技创新效应的异质性?本文采用樊纲等(2011)构建的市场化指数来衡量地区市场化程度,将市场化指数低于中位数值的地区定义为市场化程度较低地区,将高于中位数值的地区定义为市场化程度较高地区。表6列(3)和列(4)显示,与市场化程度较低地区相比,市场化程度较高地区样本的回归系数为0.370,且通过了5%的显著性检验。表明大数据综合试验区建设在市场化程度更高的地区可以取得显著的政策效果,数据要素集聚在市场化程度较高的地区能够发挥科技创新的提升效应。可能由于过多的非市场因素干预会限制数据要素集聚,此时数据资源配置效率受到非市场因素干预影响,导致大数据综合试验区内数据要素集聚的活跃度下降,数据要素流动与交易受到阻碍,在一定程度上无法有效推动科技创新水平提升。因此,过多的非市场因素干预不利于数据要素流动与集聚,大数据综合试验区建设过程中需要充分发挥市场在数据资源配置中的决定性作用,促进数据要素集聚。
(三) 数字经济发展水平异质性数据要素是数字经济发展的微观基础和创新引擎,促进数据要素的流通和交易是未来数据要素集聚的关键路径。数据要素作为数字经济发展的关键要素,数据要素集聚对科技创新水平的影响与该地区的数字经济发展水平相关。本文采用未受到政策影响的2014年各地区数字经济发展水平作为样本的划分标准,若地区数字经济发展水平高于均值则列入数字经济发展水平较高地区,低于均值则列入数字经济发展水平较低地区,数字经济发展异质性分析结果如表6列(5)和列(6)所示。与数字经济发展水平较低的地区相比,大数据综合试验区建设对科技创新的影响在数字经济发展水平较高的地区可以取得更好的效果,数据要素集聚显著提升数字经济发展水平较高地区的科技创新水平,而数字经济发展水平较低地区的影响系数没有通过显著性检验。这可能是由于数字经济发展水平较高的地区本身具有数据要素集聚的比较优势,这种优势可能通过大数据综合试验区建设被进一步放大,从而更有利于提升科技创新水平。
七、进一步分析前文研究结果表明数据要素集聚显著提升了科技创新水平,值得注意的是大数据综合试验区建设在提升科技创新水平的同时对邻近地区究竟是具有“溢出效应”还是“虹吸效应”?
(一) 模型构建为了识别数据要素集聚对邻近地区科技创新水平的空间效应,本文选择空间Durbin模型考察数据要素集聚对科技创新水平的空间溢出效应。本文在模型(1)的基础上,进一步建立空间Durbin模型考察本地数据要素集聚对邻近地区科技创新水平的影响,具体模型构建如下:
| $ Cs{a_{it}} = \alpha + \rho WCs{a_{it}} + {\sigma _1}BD{P_i}_t{\text{ + }}\sum\limits_{i = 2}^8 {{\sigma _i}{X_{it}}} + \gamma WBD{P_i}_t{\text{ + }}\sum\limits_{i = 2}^8 {{\beta _i}W{X_{it}}} + {u_i} + {v_t} + {\varepsilon _{it}} $ | (6) |
| $ W=\left\{\begin{array}{l}0,i=j\\ \dfrac{1}{{d}^{2}},i\ne j\end{array}\right. $ |
其中,ρ是空间自相关系数,表示本地科技创新对邻近地区科技创新的影响;W是指30×30阶的空间权重矩阵。本文选取省会城市间地理距离平方的倒数作为空间权重矩阵。省际间地理距离采用省会城市之间的球面距离表示。此外,控制变量同模型(1)。本文重点关注系数γ,表示本地数据要素集聚对邻近地区科技创新水平的空间影响,βi表示本地经济发展、产业结构、数字基础设施、财政规模、金融发展、科技成果转化、创新能力等系列控制变量对邻近地区科技创新水平的影响。ui、vt分别表示个体与时间效应,ε为误差项。
(二) 实证结果分析为了分析大数据综合试验区建设的空间效应,本文对模型(6)进行空间面板数据回归。表7中列(1)、(2)分别汇报了随机效应与固定效应模型的估计结果,空间自相关系数ρ均显著为正,说明大数据综合试验区建设产生正向溢出效应;而γ的估计系数显著为正,分别为0.108、0.105,即本地数据要素集聚显著提升了邻近地区科技创新水平。此外,为了进一步提高固定效应模型估计结果的稳健性,列(2)−(4)分别加入时间固定效应、个体固定效应以及双向固定效应进行估计,研究发现无论是空间自相关系数ρ还是γ,其回归系数的大小与作用方向均与列(1)的结果一致。上述分析发现,大数据综合试验区建设带来的数据要素集聚不仅会提高本地科技创新水平,还能明显增强邻近地区的科技创新水平。数据要素集聚产生正向空间溢出效应的原因可能在于,数据要素具有正外部性,在收集和使用的过程中能够累积叠加,形成正反馈效应,同时数据要素会产生明显的溢出效应,对其他部门释放要素价值(徐翔等,2021;张宇和蒋殿春,2021)。因此,这种正外部性给周边邻近地区带来正向溢出效应,从而推动当地科技创新。综上分析,随着数据要素集聚的发展,大数据综合试验区的建设不仅提升了当地科技创新水平,还会对周边地区科技创新水平产生辐射效应,进一步增强了区域创新能力。
| 变量 | 随机效应 | 固定效应 | 时间固定 | 个体固定 | 双向固定 |
| (1) | (2) | (3) | (4) | (5) | |
| W×大数据综合试验区 | 0.108*(0.063) | 0.105*(0.061) | 0.108*(0.063) | 0.108*(0.063) | 0.108*(0.063) |
| W×控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 |
| BDP | 0.021(0.038) | 0.021(0.037) | 0.021(0.038) | 0.021(0.038) | 0.021(0.038) |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 常数项 | 0.783(0.712) | 0.783(0.712) | 0.783(0.712) | 0.783(0.712) | |
| ρ | 0.904***(0.015) | 0.907***(0.015) | 0.904***(0.015) | 0.904***(0.015) | 0.904***(0.015) |
| 观测值 | 570 | 570 | 570 | 570 | 570 |
本文将国家级大数据综合试验区作为一项准自然实验,运用双重差分法探讨数据要素集聚对科技创新的影响效应及作用机制。研究结论表明:第一,数据要素集聚显著提升科技创新水平,这一研究结论在经过安慰剂检验、PSM−DID、工具变量法等一系列稳健性检验后依然成立。第二,数据要素集聚通过降低劳动资源错配程度、提高研发投入及提升人力资本水平促进科技创新水平的提升。第三,数据要素集聚对科技创新水平的提升作用在数字基础设施水平、区域市场化程度、数字经济发展水平较高的地区更明显。第四,数据要素集聚具有明显的正向溢出效应,大数据综合试验区建设能够提升邻近地区科技创新水平,对周边地区产生辐射带动作用。
(二) 政策启示第一,加快推进大数据综合试验区建设,发挥数据要素集聚对科技创新的影响效应。一方面,在大数据综合试验区内,稳步推进数据要素集聚的体制机制建设与实践探索,发挥大数据综合试验区的辐射带动效应与示范引领作用,培育一批具有国际竞争力的大数据综合试验区,激发数据要素集聚对周边地区科技创新的溢出效应。统筹推进数据交易平台建设,培育规范有序的数据要素交易市场,以数据流引领技术流,形成大数据流通、开发、应用的完整产业链和生态链,促进大数据产业集聚发展。另一方面,总结大数据综合实验区建设的实践经验,选择有条件的地区推广大数据综合实验区建设。如实施大数据产业集聚示范工程,在大数据综合实验区内建立国家大数据产业发展集聚区,以大数据产业吸引数据要素集聚,协同推进数据要素开放与大数据融合应用。深入贯彻实施国家大数据战略,发挥政府投资基金作用,设立大数据综合试验区发展专项资金,引导社会资本设立大数据产业发展基金,为大数据综合试验区建设提供资金支持。
第二,发挥市场机制在高素质人才要素配置方面的决定性作用,通过公平竞争和市场供求促进劳动要素的优化配置与合理流动,从而降低劳动要素市场扭曲对科技创新的不利影响。发挥大数据综合试验区带来的数据要素集聚效应与数据要素的融合作用,促进数据要素与劳动要素融合发展,降低劳动要素市场配置扭曲程度。研发投入是科技创新的重要资源,应加大基础研究、应用研究与试验发展的财政支持力度,提升研发投入强度,有效发挥大数据综合实验区带来的科技创新水平的提升效应。此外,发挥人力资本在提升科技创新水平的核心作用,建立培养大数据领域专业型人才和跨界复合型人才机制,引进和培育大数据领域高端领军人才和创新科研团队,提高大数据领域的人力资本竞争力。
第三,完善数字基础设施,深化数据要素市场化配置改革,推动数字经济高质量发展。统筹数字基础设施集约利用,实施新型数字基础设施专项示范工程,加强关键网络基础设施建设,提升网络骨干传输和交换能力,吸引资金、人才等创新资源,为科技创新水平提升效应提供支撑。发挥市场机制配置数据要素资源的关键作用,完善数据要素市场监管机制,规范数据资源交易和流通,将数据要素市场监管纳入市场监管体系。改善数据要素市场流通环境,精准对接市场需求,坚持政府干预和市场配置相结合的原则,充分发挥政府和市场两类资源优势,促进数据要素集聚,提高科技创新水平。大数据综合试验区的建设离不开广阔的数字经济发展前景,获批建立大数据综合试验区的地区需要重塑数字经济发展优势,提高数字经济核心竞争力,为数据要素集聚提供新业态的发展环境,从而发挥数字经济带来的科技创新的协同提升效应。
| [1] | 白俊红, 蒋伏心. 协同创新、空间关联与区域创新绩效[J].经济研究,2015(7). |
| [2] | 曹跃群, 赵世宽, 张晗. 省际R&D资本存量: 框架、检验及空间动态分析[J].科学学研究,2022(8). |
| [3] | 陈文, 常琦. 大数据赋能了企业绿色创新吗——基于国家级大数据综合试验区的准自然实验[J].财经科学,2022(8). |
| [4] | 陈永伟, 胡伟民. 价格扭曲、要素错配和效率损失: 理论和应用[J].经济学(季刊),2011(4). |
| [5] | 樊纲, 王小鲁, 马光荣. 中国市场化进程对经济增长的贡献[J].经济研究,2011(9). |
| [6] | 何玉长, 王伟. 数据要素市场化的理论阐释[J].当代经济研究,2021(4). |
| [7] | 季书涵, 朱英明, 张鑫. 产业集聚对资源错配的改善效果研究[J].中国工业经济,2016(6). |
| [8] | 孔艳芳, 刘建旭, 赵忠秀. 数据要素市场化配置研究: 内涵解构、运行机理与实践路径[J].经济学家,2021(11). |
| [9] | 刘传明, 马青山. 网络基础设施建设对全要素生产率增长的影响研究——基于“宽带中国”试点政策的准自然实验[J].中国人口科学,2020(3). |
| [10] | 刘满凤, 陈梁. 环境信息公开评价的污染减排效应[J].中国人口·资源与环境,2020(10). |
| [11] | 卢剑峰, 陈思. 外部知识搜寻、大数据能力与企业创新[J].科研管理,2021(9). |
| [12] | 毛明芳. 打造具有核心竞争力的科技创新高地——基于区域创新能力建设的视角[J].湖南社会科学,2021(1). |
| [13] | 牛子恒, 崔宝玉. 网络基础设施建设与劳动力配置扭曲——来自“宽带中国”战略的准自然实验[J].统计研究,2022(10). |
| [14] | 庞瑞芝, 刘磊, 张帅. 数字化如何影响企业创新?——基于人力资本和交易成本传导机制的视角[J].南开经济研究,2023(2). |
| [15] | 荣健欣, 王大中. 前沿经济理论视野下的数据要素研究进展[J].南方经济,2021(11). |
| [16] | 施锦诚, 王迎春. 人工智能多元研发模式研究[J].科学学研究,2023(8). |
| [17] | 陶长琪, 丁煜. 数据要素何以成为创新红利?——源于人力资本匹配的证据[J].中国软科学,2022(5). |
| [18] | 王鑫, 刘克春, 曾经纬. 大数据能力如何促进企业转型升级——技术创新与商业模式创新的多重中介模型[J].当代财经,2022(7). |
| [19] | 吴朝文, 景星维, 张欢. 国家治理中大数据智能化的价值、困境与实现路径[J].重庆社会科学,2021(10). |
| [20] | 谢康, 夏正豪, 肖静华. 大数据成为现实生产要素的企业实现机制: 产品创新视角[J].中国工业经济,2020(5). |
| [21] | 徐翔, 厉克奥博, 田晓轩. 数据生产要素研究进展[J].经济学动态,2021(4). |
| [22] | 徐翔, 赵墨非, 李涛, 等. 数据要素与企业创新: 基于研发竞争的视角[J].经济研究,2023(2). |
| [23] | 杨骞, 刘鑫鹏, 孙淑惠. 中国科技创新效率的区域差异及其成因识别——基于重大国家区域发展战略[J].科学学研究,2022(5). |
| [24] | 杨艳, 王理, 廖祖君. 数据要素市场化配置与区域经济发展——基于数据交易平台的视角[J].社会科学研究,2021(6). |
| [25] | 袁韵, 徐戈, 陈晓红, 等. 城市交通拥堵与空气污染的交互影响机制研究——基于滴滴出行的大数据分析[J].管理科学学报,2020(2). |
| [26] | 张宇, 蒋殿春. 数字经济下的国际贸易: 理论反思与展望[J].天津社会科学,2021(3). |
| [27] | 郑国强, 张馨元, 赵新宇. 数据要素市场化如何驱动企业数字化转型?[J].产业经济研究,2023(2). |
| [28] | 朱平芳, 徐伟民. 政府的科技激励政策对大中型工业企业R&D投入及其专利产出的影响——上海市的实证研究[J].经济研究,2003(6). |
| [29] | Aghion P, Bergeaud A, Boppart T, et al. A theory of falling growth and rising rents[R]. Working Paper 26448, 2019. |
| [30] | Agrawal A, McHale J, Oettl A. Finding needles in haystacks: Artificial intelligence and recombinant growth[A]. Agrawal A, Gans J, Goldfarb A. The economics of artificial intelligence: An agenda[M]. Chicago: University of Chicago Press, 2019. |
| [31] | Beck T, Levine R, Levkov A. Big bad banks? The winners and losers from bank deregulation in the United States[J].The Journal of Finance,2010,65(5):1637–1667. |
| [32] | Farboodi M, Veldkamp L. A growth model of the data economy[R]. Working Papers 28427, 2021. |
| [33] | Jones C I, Tonetti C. Nonrivalry and the economics of data[J].American Economic Review,2020,110(9):2819–2858. |
| [34] | Wang Y, Yao Y D. Sources of China’s economic growth 1952−1999: Incorporating human capital accumulation[J].China Economic Review,2003,14(1):32–52. |
2.Research Center for High-quality Development, Shandong University of Finance and Economics, Shandong Jinan 250014, China;
3.School of Economics, Huazhong University of Science and Technology, Hubei Wuhan 430074, China;
4.Business School, Shandong Yingcai University, Shandong Jinan 250104, China

