一、引　言

改革开放以来，中国金融业迎来迅猛发展，金融体制改革和创新亦快速推进：资本市场建立、利率市场化改革、汇率制度转变和系列房改政策为优化资源配置、净化市场环境、维持国际收支平衡和增进人民福祉作出了重要贡献。然而，随着资本市场的蓬勃发展，资本逐利性特征逐渐凸显，大量资金开始涌入房地产、股票和外汇市场，具有典型的投机属性；而资本的生产要素职能渐趋弱化，金融系统运行呈现出“脱实向虚”趋向。由此可见，如何处理好“宏观经济稳增长”和“金融系统防风险”之间的关系已成为新发展阶段下关乎国家发展全局的理论难题和现实挑战。而若想处理好“宏观经济稳增长”与“金融系统防风险”之间的关系，核心要务主要有二：一是对经济增长和金融风险进行准确的度量，即客观描述经济周期与金融周期的变化规律；二是要深入理清经济周期与金融周期之间的传导关系和交互影响。这是认知经济增长与金融风险的变化规律、传导关系以及交互影响的前提和根本，亦是本文研究的逻辑初衷。

事实上，现有研究已对经济周期与金融周期间的关联机制展开大量探讨，却缺乏显性和一致性结论。例如，马勇等 (2016) 发现中国的金融周期通常会先行于经济周期变动，却未能准确测度出领先的时长；邓创和徐曼 (2018) 虽使用DY动态溢出指数测度了经济周期与金融周期间的平均溢出强度，却未对这种溢出效应的显著性和方向进行判断。这一度令相关研究陷入混沌，甚至无法准确地回答一些最基本的问题，例如：经济周期与金融周期间是否具有稳定的关联机制？他们彼此之间表现为共同促进还是相互制衡？二者的变动谁领先于谁，领先的时长有多久？二者之间的交互影响强度又有多大？特别是在当下宏观经济增长一度近乎触及零线的特殊阶段，系统性地量化识别经济周期与金融周期间的时变关联机制已成为宏观经济有效施策的必然前提和客观要求。本文的核心目的和主要贡献即是精准识别经济周期与金融周期间的时变关联机制，具体包括方向性、稳定性、持续性和作用强度四方面。

具体而言，本文将基于精准计量思想，从经济周期与金融周期的刻画、二者间的传导关系和交互影响三方面入手，深入厘清如下几个基本事实和基本关系：(1) 中国的经济周期与金融周期在事实形态上到底具有何种特征，是否出现过耦合抑或是背离等基本表象，这是全文研究的逻辑起点；(2) 经济周期与金融周期的变化是否存在显著的传导关系，倘若有，那么是谁领先于谁，这种关系和机制是否稳定，这是对宏观经济与金融系统间关联机制的深入认识，亦是本文旨在回答的主旨问题；（3）考虑到传导关系的识别仅能反映逻辑上的因果，却不能给以准确的量化描述，而我们最关心的是到底是经济周期变化对金融周期的影响更大，还是金融周期变化对经济周期的影响更强？这种对交互影响强度的刻画能够在直观上回答中国历次典型的经济波动和金融波动在多大程度上是由彼此之间的交互影响所致，且能够为准确把握和识别“宏观经济稳增长”与“金融系统防风险”之间的交叉互渗提供重要的实证基础和量化依据，同时亦是本文研究的逻辑终点。围绕上述问题，全文结构安排如下：第二部分为文献综述，第三部分为中国经济周期与金融周期的事实刻画和现象描述；第四部分采用了基于局部因果推断的时变Granger因果检验对二者之间的领先滞后关系进行了实时测度；第五部分则是基于DY动态溢出指数测度了经济周期与金融周期之间的动态交互影响，最后一部分是全文的研究结论。

二、经济周期与金融周期关联机制研究述评

对于经济周期与金融周期之间关系的研究，最早可以追溯至大萧条时期的“债务-通缩理论”(Fisher, 1933)，该理论认为经济主体的过度负债会与通货紧缩相互作用，形成正反馈循环机制，进而导致经济衰退甚至是经济萧条，这为经济周期与金融周期之间的关联机制奠定了理论基础。随着研究的不断深入，国内外学者对二者之间的关联机制大致形成了两种判断：一种观点认为经济周期与金融周期密切相关，且金融周期领先于经济周期波动，即金融周期是经济周期波动的“晴雨表”。大量实证研究亦支持了这一假说，例如，邓创和徐曼 (2014) 利用主成分分析法测度了中国的金融形势指数，发现中国金融周期的平均长度约为3年，且通常领先于经济周期波动；Shen等 (2018) 通过构建金融周期指数考察了经济周期与金融周期的波动态势及联动关系，结果显示金融周期的波动频率反而低于经济周期，但大幅度的金融周期波动能够显著引领经济周期波动；尹筑嘉等 (2019) 利用奇异谱分析法，考察了投资周期与设备制造业股价波动周期之间的关联性，发现二者间存在较强相关性，且设备制造业股价波动周期领先于投资周期波动。另一种观点则认为经济周期与金融周期之间不具有稳定的关联机制，只有典型的经济周期波动和金融周期波动才会向彼此形成局部传导。董直庆和王林辉 (2008) 利用小波变换和谱分析法，从频域和时域两个角度考察了中国证券市场与宏观经济波动的关联性，发现中周期经济波动要先行于证券市场波动，这为经济周期波动向金融周期波动传导提供了经验证据；苏治等 (2017) 基于GVAR模型和非线性Granger因果检验，在经济全球化背景下重点考察了中国虚拟经济与实体经济的关联性，发现二者在周期波动成分上虽存在双向溢出，但并不存在稳定的Granger因果关系，这表明二者之间的定向溢出效应更多地体现为局部溢出和阶段溢出。

从具体检验层面上看，现有关于经济周期与金融周期之间关联机制的检验可分为三类：第一类是相关性和协同性分析。曹永琴和李泽祥 (2009) 运用恒常条件相关法和动态条件相关法考察了中国经济周期与金融经济周期间的动态关联性，发现二者具有显著的正相关关系，并且随着中国金融市场的不断完善，二者的正相关程度逐步上升；Claessens等 (2012) 通过对44个国家的经济和金融数据进行分析，发现在所有的金融要素中，经济周期与信贷周期间的正相关性最强，且信贷对经济衰退与复苏都具有重要的引导作用；陈雨露等 (2016) 将金融周期划分为高涨期、衰退期与常规期三种状态，并基于系统GMM估计依次考察了三种状态下金融周期对经济周期的影响，发现无论金融周期处于高涨还是衰退状态，经济增长均会受到明显的负向影响，而只有当金融周期处于相对平稳的常规状态时，金融周期与经济周期才会体现为彼此增进。第二类方法是因果推断。马勇等 (2016) 构建包含金融周期、经济周期、货币周期和信贷周期的四变量VAR模型，通过Granger因果检验推断二者之间的领先滞后关系，发现金融周期是其他三个周期成分的Granger原因；丁乙 (2018) 对中国经济增长与股票市场波动之间的传导关系进行了非线性Granger因果关系检验，发现在全样本范围内普遍存在着从经济增长到股票市场波动的非线性传递，而只有在2008年国际金融危机爆发后，股票市场波动才会传导至实体经济，这一研究再次证明了经济周期与金融周期之间的逻辑因果关系并不稳定，须视样本长度、样本区间等因素而定。第三类方法则考察二者间的交互影响。邓创和徐曼 (2018) 基于广义预测误差方差分解得到溢出指数，对中国经济周期与金融周期之间溢出效应的强度进行了捕捉，发现两周期之间的总溢出效应和定向溢出效应都具有明显的时变特征，并且金融周期对经济周期的定向溢出效应要远大于经济周期对金融周期的溢出效应。此外，也有学者从频域视角出发，考察经济周期与金融周期之间的溢出效应。曹强等 (2021) 利用滚动回归BK分解法测度了不同频域下经济周期与金融周期之间的动态溢出效应，发现金融周期对经济周期的影响明显强于经济周期对金融周期的影响，这与时域视角下的判断一致。频域视角下的研究进一步发现，金融周期的高频短期波动成分对经济周期的影响最为强烈。

总体而言，现有关于经济周期与金融周期之间关联机制的研究已较为深入，但相关研究仍留下许多争议有待进一步阐明：第一，就二者之间的领先滞后关系来看，现有文献尚未形成一致结论，其争议主要体现在：(1) 金融周期波动领先于经济周期波动这一基本关系是否成立？(2) 倘若成立这种关系是否稳定？(3) 倘若不成立，在何种情况下易于出现经济周期反向先行于金融周期波动的情形？第二，就二者之间的溢出效应而言，相关争论主要在于：(1) 金融周期向经济周期溢出效应更强的结论是否具有普适性？是否存在经济周期向金融周期的溢出效应强度更高的时点？(2) 在何种条件下，易于出现金融周期对经济周期的强溢出，而又在何种条件下易于出现经济周期对金融周期的强溢出？造成上述困境的根源在于：早期有关经济周期与金融周期关联机制的研究大多着眼于某一特定视角，缺乏系统性和深入的考察。例如，马勇等 (2016) 仅是基于线性Granger因果检验来推断经济周期与金融周期的关联机制，但二者之间很可能本就不存在稳定的因果关系，这就导致变量间的领先滞后时长无法被准确测定；再如，邓创和徐曼 (2018) 虽然测度了经济周期与金融周期之间的溢出效应强度，却未使用与之匹配的滚动相关系数和时变因果推断技术来判断影响方向，导致该研究无法准确判定二者之间的关系到底表现为彼此增进还是相互制约。事实上，关联方向、领先滞后关系和溢出效应都是理解经济周期与金融周期关联机制的核心要素，同时也是制定经济政策时的重要参考。鉴于此，为探究中国经济周期与金融周期的波动态势、传导关系和交互影响，进而从数据层面直观地为“宏观经济稳增长”和“金融系统防风险”之间的权衡提供量化依据，本文将在构建经济周期与金融周期指标的基础上，首先测算两周期的滚动相关系数；随后构建基于局部因果推断的时变Granger因果检验方法，对中国经济周期与金融周期之间的领先滞后关系进行实时判断，从而完成对第一类问题的解答；最后，本文将进一步利用DY动态溢出指数考察两者之间的实时交互影响，进而完成对第二类遗留问题的阐释。

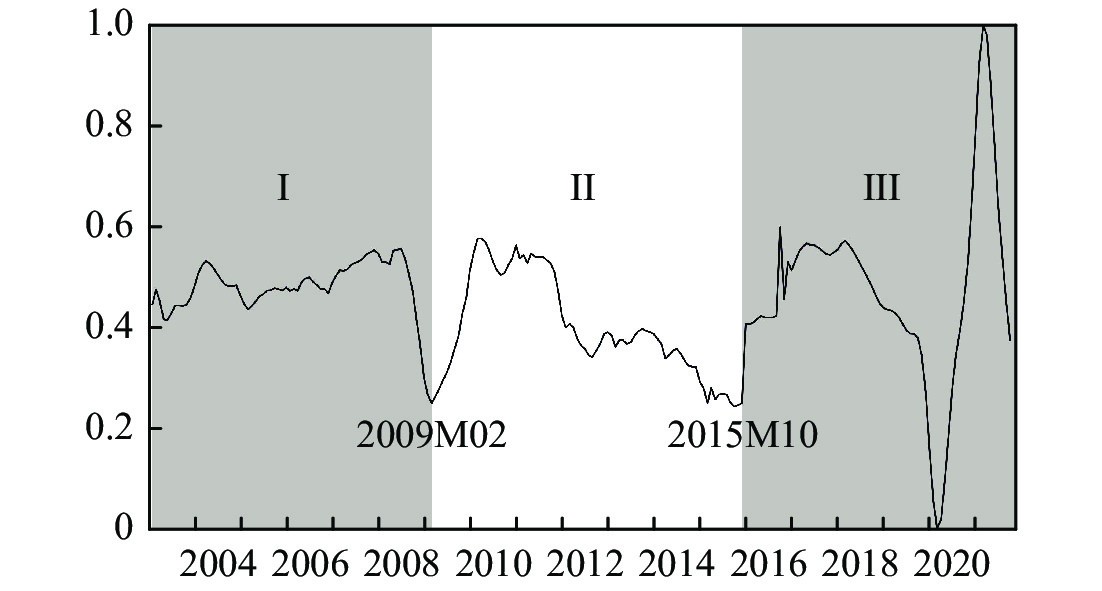
三、中国经济周期与金融周期的刻画及关联现象描述 (一) 中国经济周期刻画与事实描述

本文参照邓创和徐曼 (2018) 以及严佳佳和何梅蓉 (2021)的研究，利用宏观一致合成指数刻画中国经济周期波动。这样做的好处在于：(1) 相较于单一的经济增长率或者实际产出的周期成分，一致合成指数涵盖了社会需求 (消费、投资、外贸)、社会收入 (企业利润、国家税收、居民收入)、工业生产和就业四方面信息，能够更加综合全面地反映经济周期变化；(2) 传统产出类数据均为季度频率，而一致合成指数是月度频率指标，与多数金融指标的频率一致，这样在实证计算中无须进行人为的数据频率转换，从而最大限度地保留了原始数据信息。具体地，指标刻画分两步：第一步，获取序列X，令X=(宏观一致合成指数-100)/100；第二步，利用min—max无量纲化法对序列X进行标准化处理，将标准化后的X序列记作经济周期指数ECI (Economic Cycle Index)，以此度量经济周期变化。得到ECI的走势如图1所示。原始数据来源于中经网统计数据库 (http://db.cei.cn)，样本区间为2003年1月至2021年12月。与此同时，为对比传统经济周期与ECI经济周期之间的差异，本文还绘制了2003—2021年间中国实际GDP同比增长率曲线，如图2所示。观察图1和图2可以初步得到如下两个发现：

第一，传统的经济周期与ECI经济周期间存在系统性差异。如图1所示，参照经典的“谷-谷”分割法 (刘树成, 2000)，图1给出了各轮经济周期的划分状况。不难发现，ECI在样本期间内的变化大致可以归结为3轮典型的周期性波动，各轮经济周期的长度基本相等，约为6–7年。这与传统基于经济增长率划分的经济周期存在显著差异。按照图2中的经济增长率周期划分，2012—2019年间中国经济具有明显的L型拖平长尾特征 (刘金全和周欣, 2022)，期间不存在经济周期转换。而在ECI口径下，第2轮短周期在2015年下半年迅速衰竭，期间恰逢中国资本市场巨幅震荡时段 (上证指数迅速由高点5178衰落)，这一重要事实说明，ECI能够更加全面地反映经济景气变化，且与资本市场和金融周期的关联更加密切，是度量经济周期与金融周期关联机制的适宜指标 (王有鑫等, 2021)。

第二，ECI具有较好的事件反映能力。图1显示，2008年国际金融危机、2015年股灾危机和2020年新冠肺炎疫情爆发时期，ECI均迅速探底，准确地还原了金融冲击和罕见灾难冲击对经济的影响。进一步对比这三次经济周期谷底不难发现，新冠肺炎疫情冲击出现时，ECI探底最深，这与客观事实相符，同时也说明ECI不仅能够准确地捕捉事件冲击的时点特征，也能较为准确地度量事件冲击强度。

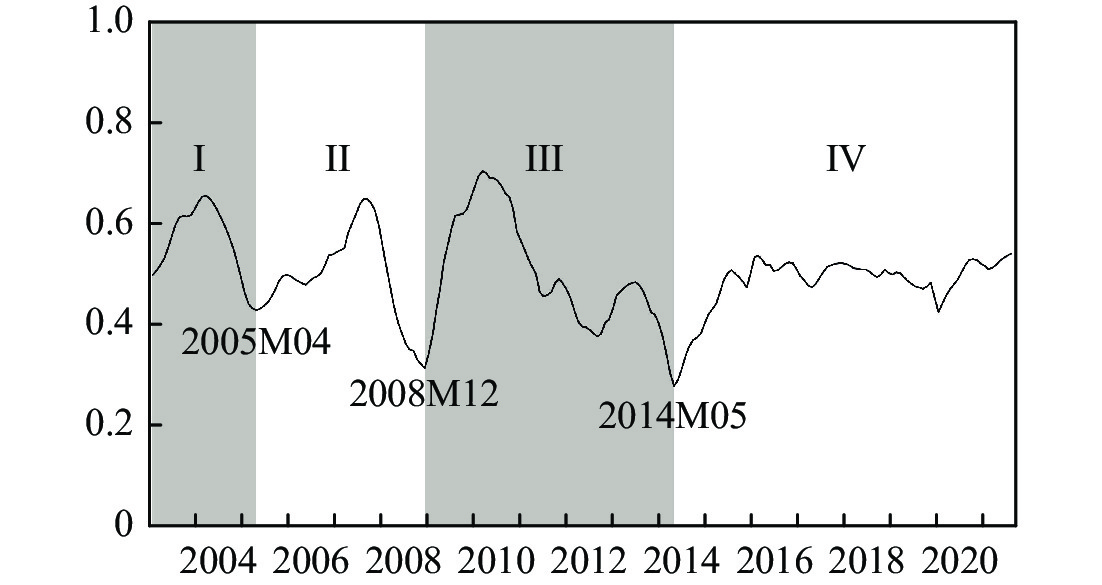
(二) 中国金融周期刻画与事实描述

近期大量研究 (马勇等, 2017; 孙彦林和陈守东, 2019; 钱宗鑫等, 2021) 倾向于从货币市场、股票市场、房地产市场等金融子市场出发，利用利率、汇率、货币供给量、股票价格、房地产价格及信贷规模等变量构建金融周期指数 (Financial Cycle Index, FCI)。这些研究多是通过对各类金融变量加权的方式来进行指数估计。在确定权重方面，又以静态加权、标准化加权、主成分分析、因子分析和动态CRITIC赋权法最为常见。其中，动态CRITIC赋权法主要是通过滚动相关分析来对各金融变量赋以时变权重，它不仅可以有效克服静态类加权法无法随时间和经济状况变化而改变基础指标权重的弊病，同时还能有效解决主成分分析 (邓创和徐曼, 2014; 袁申国和刘兰凤, 2019) 和因子分析 (栾惠德和侯晓霞, 2015) 等方法遗漏信息的问题。鉴于此，本文采用动态CRITIC赋权法进行金融周期指数估计。在基础指标选取层面，本文参照许涤龙和陈双莲 (2015)、刘金全和陈婉莹 (2019) 以及刘金全和廖文欣 (2021) 等研究，兼顾货币市场、外汇市场、资本市场和房地产市场四大金融子市场的运行特征，选取市场利率、汇率、货币供给量、股票价格、房地产价格及信贷规模6个金融变量综合刻画金融周期波动。各金融变量的代理变量分别为银行间存款类金融机构以利率债为质押的7天期回购利率DR007^①、人民币实际有效汇率指数、广义货币供给量M2同比增长率、上证综合指数、国房景气指数以及金融机构各项贷款月末同比增长率，样本区间为2003年1月至2021年12月，各项数据来源于Wind数据库及中经网统计数据库。在合成FCI前，首先对基础数据进行预处理：(1) 对利率进行取倒数处理，这是因为与其他指标相比，利率水平上升代表金融收紧；(2) 对国房景气指数，利用Y=(国房景气指数-100)/100计算其变动率，定义Y为实际房价增长率，以反映房地产市场的周期波动状况；(3) 利用H-P滤波法提取上证综合指数的周期性成分，其中权重参数 $ \lambda $ 取14400^②；(4) 利用min—max无量纲化方法对所有数据进行标准化处理。上述预处理工作均借助Eviews 10完成。 $\mathrm{}$ $ t $ 时刻下指标 $ i $ 的权重为：

$ {w_{it}} = \frac{{{m_{it}}}}{{\sum\nolimits_{i = 1}^n {{m_{it}}} }} , i = 1,2, \cdots ,n $

(1)

其中， $ {m_{it}} $ 代表 $\mathrm{}$ $ t $ 时刻第 $ i $ 个指标所包含的信息，由指标 $ i $ 的标准差 $ {\sigma _i} $ 以及指标 $ i $ 与其余各项指标 $ j $ ( $ j = 1,2, \cdots ,n,j \ne i $ ) 的滚动相关系数 $ {r_{ijt}} $ 计算得到，计算公式为 $ {m_{it}} = {\sigma _i} \cdot \sum\nolimits_{j = 1}^n {\left( {1 - {r_{ijt}}} \right)} $ 。计算出各指标的时变权重后，依据下式即可计算出中国的金融周期指数FCI：

$ FC{I_t} = \sum\nolimits_{i = 1}^n {{w_{it}} \cdot {x_{it}}} $

(2)

为确保滚动相关系数计算既稳定又具有经济意义，本文将滚动时窗设定为3年，即 $ l = 36 $ ，这是因为3年既是完整年度，不存在尾部季节效应，同时又与经验认知下的短周期长度相吻合。金融周期指数的走势如图3所示，由于所有数据均进行了正向同向化处理，因此指数越高表示金融景气越繁荣，反之则代表金融周期收紧。特别地，序列值在均线附近波动幅度越小，表明金融系统越加稳定。观察图3金融周期指数FCI的走势可以得到三个基本判断：第一，金融周期波动较经济周期波动更加频繁。图3显示，样本期间共存在4轮典型的金融周期波动，图中所标注的时点为各轮金融周期的结束时点。不难发现，除最后一轮外，每轮周期的长度都相对较短，这说明相较于经济周期，金融周期的变动更加频繁。这一方面是由金融活动的固有特征所致，另一方面也说明，相较于中国经济稳中向好的基本局面，金融市场的短周期波动特征更加明显。第二，FCI同样具有较强的事件捕捉能力。三次谷值分别出现在2004年信贷收紧时期、2008年国际金融危机时期以及2014年全面降息之前，基本准确地捕捉到了中国金融景气度最低的几个代表性时点。但需要注意的是，2015年股灾危机并未激发金融周期谷值，这一方面说明，此次股灾的影响得到了及时控制，另一方面也表明，这仅是金融市场领域内的一次局部紧缩，对信贷、外汇和货币市场的影响相对有限。第三，末轮金融周期同样出现了典型的形态变异。具体体现在：金融周期出现了明显的长尾特征，并且波动幅度急剧收窄，目前甚至还未走完复苏阶段。这说明近年来国家对金融风险的防控和治理取得了突出效果，随着货币政策回归稳健中性和“三去一降一补”工作的有序开展，金融周期主体与均线几乎重叠，表明中国金融业的整体运行态势处于适宜范围，既不存在金融过热的风险，亦不存在金融过度紧缩的隐患。

(三) 中国经济周期与金融周期关联的现象描述

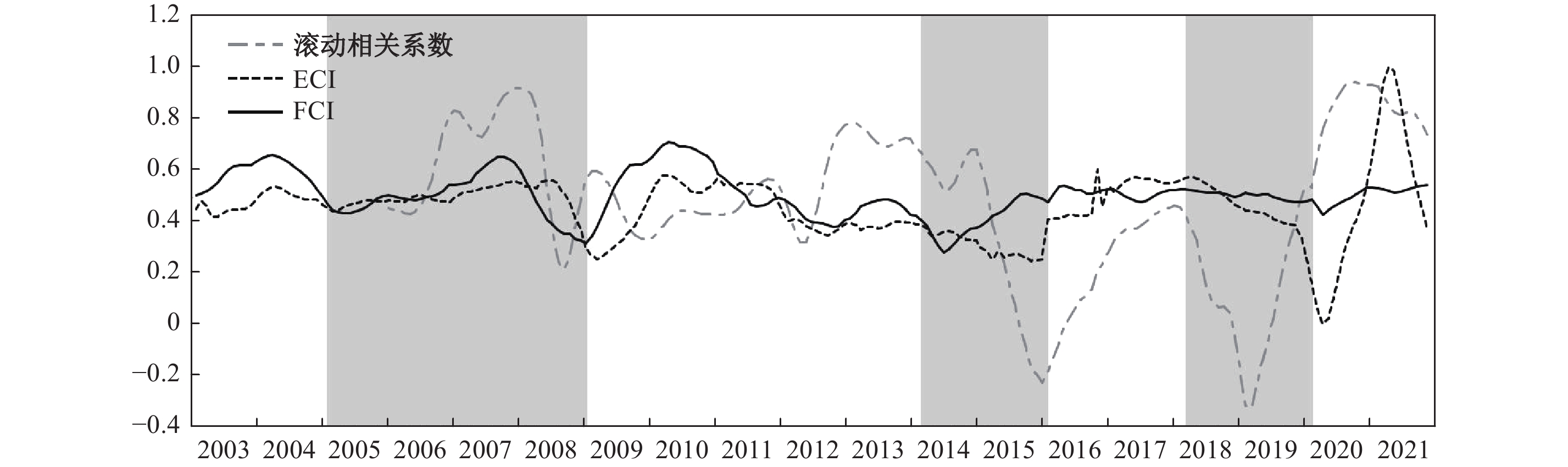
为了从直观上判断经济周期与金融周期之间的领先滞后关系，本文将二者一并置于图4内，并计算了二者之间的滚动相关系数 (滚动时窗依然为36期)。根据图4可得出两点基本判断：

第一，经济周期与金融周期之间存在着典型的周期错配现象。具体体现在：经济周期稳定地以6-7年为一个周期，而前两轮金融周期持续期极短，仅持续2-3年。周期错配的出现很可能意味着经济周期与金融周期之间的领先滞后关系并不稳定。即使金融周期波动领先于经济周期波动的观点成立，但也一定存在着非完全传导抑或是传导受阻的时段。因此，若想准确地判断二者之间的传导关系，还是应该基于实时因果推断。

第二，中国经济周期与金融周期既存在典型的耦合阶段亦存在典型的背离阶段。典型的协同发展阶段为2005—2008年，这一时期内，不仅是ECI与FCI走势高度一致，且滚动相关系数基本保持在0.8以上，二者呈现出典型的协同发展态势。特别值得注意的是，协同时段既包含2005—2007年的资本市场繁荣时期，同时也包括2008年国际金融危机时段，二者之间的强关联关系并未被经济周期和金融周期的更迭所打破，这进一步肯定了此段时期内宏观经济与金融系统之间的联系十分紧密，表现为共荣共退。与之相反，2014—2015年和2018—2019年，经济周期则与金融周期之间出现了典型的阶段性背离，其中在2014—2015年间，经济周期明显处于下行阶段，而金融周期却呈现出典型的逆经济周期上扬之势，彼时正值中国资本市场非理性繁荣阶段，受金融加杠杆影响，资本市场运转出现了明显的“脱实向虚”趋向；而在2018—2019年，受“三去一降一补”政策持续深化的影响，经济周期逐渐下行，但金融风险得到有效控制，金融周期开始逐渐回归至平稳区域。透过现象回归本质来看，这两轮短期背离之间具有显著的对偶性和必然性。倘若不存在2014—2015年间资本市场的“脱实向虚”，那么也便不存在后一轮“脱虚向实”的阵痛纠正。正是这一轮反周期运行和一轮反周期纠正，才使得宏观经济与金融系统之间的匹配关系回归正轨，这在极大程度上确保了后疫情时期经济的稳步复苏和金融安全。

四、中国经济周期与金融周期的领先滞后关系与相依性测度

典型化事实分析表明，经济周期与金融周期之间既存在典型的耦合阶段，又存在显著的背离阶段，同时还可能存在长期的非相关时段 (如：2016—2018年，二者的滚动相关系数基本为0)，这意味着二者之间的领先滞后关系并不稳定，应该使用基于实时预测的方法来推断二者之间的传导关系。为此，本文将分别使用传统Granger因果关系检验和基于局部因果推断的时变Granger因果检验来全面判断二者之间的领先滞后关系。这一方面有利于对二者之间的传导关系进行精准识别，另一方面也有利于纠正由传统Granger因果推断偏差而引发的事实误判。

(一) 基于传统Granger因果检验的传导关系识别

由于传统Granger因果检验要求数据平稳，本文首先选择ADF检验和PP检验对ECI和FCI进行单位根检验。在ADF检验中，选用最常用的SIC准则确定回归模型滞后阶数，相应检验结果如表1所示。观察表1不难发现，ECI与FCI均为平稳的时间序列，可以直接用于Granger因果关系推断。表2进一步给出了传统Granger因果检验的结果，依据BIC准则，确定传统Granger因果关系检验的滞后阶数为3阶。根据表2中的结果不难发现，中国的经济周期指数ECI不是金融周期指数FCI的Granger原因，说明经济周期变化无法预测金融周期变化；而金融周期指数FCI是经济周期指数ECI的Granger原因，这意味着金融周期的变化可以预测经济周期的变化，即金融周期是经济周期变动的“晴雨表”。

然而，从典型化事实中的一些现象来看，这一结果不由得会引发两方面质疑：第一，二者之间明显存在周期错配现象，那么缘何会有稳定的传导关系？第二，从滚动相关分析来看，二者之间既存在耦合时段又存在背离时段，那么缘何会有稳定的传导方向？从学理上讲，产生这两种机制误判的根本原因在于传统Granger因果检验在计量设计上具有明显的局限性。其一，传统的Granger因果检验是基于线性假设进行推断的，它只能用于判断单一机制，本身就不具备识别多重传导关系的功能；其二，ECI和FCI都是月度频率指标，样本期又跨越了19年之长，这意味着样本点有228个之多，虽然这一数据长度并不算是大样本，但是已经绝非小样本范畴，这就导致倘若样本期间内某种领先滞后关系占据主导，那么传统Granger因果检验就会基于多数样本特征形成机制判别，并且样本点越多，机制识别的概率就越大。但事实上，对经济周期与金融周期传导关系的研究并不需要这种较为模糊的机制识别，因为一旦调控失误就会面临极为严重的经济成本。相反，对二者之间传导关系的判断更需要精准的识别，特别是在面临突发金融危机和罕见灾难冲击之时，这种判断极为重要，对风险是否具有传染性以及传染方向的判断直接关乎到后续的危机管理方式，是建立宏观预警系统中不可或缺的一环。为此，下文将使用基于局部因果推断的时变Granger因果检验对二者之间的实时关联机制进行精准推断。

(二) 基于时变Granger因果检验的传导关系识别

为了进行时变Granger因果检验，首先需构建一个用来判别Granger因果关系原假设的Wald统计量，它的计算方法主要有向前滚动、移动平均和递归演进三种。Shi等 (2018) 经过大量的数值模拟后发现，递归演进能够提供最可靠的判别结果，移动平均次之，这两种方法更适用于精准的局部因果推断，能够大幅降低存伪概率。因此，本文主要采用递归演进过程计算Wald统计量，滚动时窗长度设定为24期，并以此作为经济周期与金融周期之间传导关系的判别依据^③。为使前后实证判别标准一致，在进行时变Granger因果检验时，同样依据BIC准则确定因果检验的滞后阶数，最优滞后阶数仍为3阶。这与线性Granger因果关系检验的滞后阶数一致，说明经济周期与金融周期之间的传导通常间隔一个季度左右。最终得到时变Granger因果检验结果如图5 (a)–(b) 所示。

首先来看经济周期对金融周期的传导效应，图5 (a) 清晰地显示，2015年股灾危机过后，中国短暂地出现过经济周期引领金融周期变动的现象，而在其余时段，经济周期均不会对金融周期产生传导效应。这一现象揭示了两个重要事实：第一，在绝大多数情况下，金融周期波动均独立于经济周期波动，也即宏观经济波动并不会引起金融系统内的“传递式反馈”，这说明中国的金融系统运转仍存在着一定的“脱实向虚”趋向，金融系统对宏观经济基本面变动的“反馈效应”仍相对较弱；第二，当经济周期与金融周期产生大幅度背离后，金融周期仍具备向经济周期回归的基本趋向，此时二者间的牵拉表现为反向传递。结合图4和2015—2016年间的经济事实不难发现，2015年股灾危机与2018年国际金融危机存在本质区别，金融危机引发了经济周期与金融周期同步下行，而股灾危机基本是一场纯粹的金融浩劫，彼时宏观经济依然保持着稳中向好的基本态势，这就导致经济周期与金融周期之间产生了大幅背离，同时也迅速形成了宏观经济向金融系统的有效传导。其本质逻辑在于：宏观经济发展越稳定，金融去杠杆的力度和空间就将越大，虽然这在短期内使金融周期迅速探底，但是在很大程度上确保了长期内的金融稳定和金融安全，也使得经济周期与金融周期的关联机制重回正轨。由此可见，尽管中国的金融周期尚不能对宏观经济基本面变化形成精准反应，却具有纠正大幅度偏离的基本属性，说明金融系统已初具“弱有效”特征。

其次来看金融周期对经济周期的传导效应，如图5 (b) 所示，金融周期对经济周期的传导效应主要体现在2020年新冠肺炎疫情冲击出现后的时段。第一个典型化区间是2020年1−2月，彼时受疫情预期影响，资本市场在春节过后发生断崖式下跌，上证指数日跌幅一度高达7.72%。此后，4月发布的1季度实际GDP同比增长率为-6.8%，形成市场经济体制改革以来的首次负增长，二者间隔恰好为3个月 (与时变Granger因果检验的滞后阶数一致)。而在2021年1−2月，上证指数历时一年的修复，一路回升至阶段性高点3731，此后4月发布的2021年1季度实际GDP增长率亦达到本轮周期的峰值18.3%，二者之间的极大值传导再度被时变Granger因果检验确认，这充分地说明时变Granger因果检验能够精确地捕捉到显著的即时传导关系。此外，一个值得注意的现象是，尽管新冠肺炎疫情对宏观经济的影响强度更大、影响范围更广，并且持续时间更长，但是率先对其作出反馈的反而是金融系统，而本轮经济周期与金融周期之间的传导亦具有典型的金融周期波动带动经济周期波动的特征。这深刻地说明，在2015年股灾危机过后，随着资管新规等系列规范措施相继出台，中国资本市场的有效性得以大幅提升，资本市场的“晴雨表”功能渐趋凸显，特别是在对突发性事件的“即时反馈能力”方面有了实质性提高。

最后，结合图5 (a)−(b) 不难发现，倘若是从严格的精准计量角度来看，在绝大多数时期下，经济周期均不是金融周期波动的Granger原因，金融周期也不是经济周期波动的Granger原因，二者之间并不具备稳定的传导关系，仅是在某些特殊情况下才会产生显著的局部传导。这一方面说明，当前中国的经济周期与金融周期仍存在一定的错配现象，资金运转尚未完成“脱虚向实”的转型；但另一方面也说明，从宏观调控的角度来看，“宏观经济稳增长”和“金融系统防风险”的双重目标仍具有较强的独立性，这意味着对二者的调控和治理仍可采用分头治理和双管齐下的方式进行，政策空间层面尚未出现显著的权衡困境。

五、中国经济周期与金融周期的交互影响分析

从中国经济周期与金融周期的相关性及实时因果关系分析中可以看到，ECI与FCI的走势时而一致时而相反，二者之间的滚动相关系数也呈现出正负交替的变化特征。虽然这一结果表明二者之间难以存在稳定的传递关系，却并不代表着经济周期与金融周期之间不存在交互影响。事实上，2005—2007年间，二者之间存在着典型的彼此增进，国际金融危机时期二者又具有明显的协同向下之势，尽管这些事实不能被严格的计量手段确认为传递，但是的确表明经济周期与金融周期间存在着显著的溢出效应。那么，到底是金融周期向经济周期的溢出效应更强，还是经济周期向金融周期的溢出效应更多，便成为了一个亟待阐释的问题。为此，本节还将基于DY动态溢出指数 (Diebold和Yilmaz, 2012)，深入测度中国经济周期与金融周期之间的动态溢出效应，以进一步明晰二者之间的实时交互影响。

(一) 经济周期与金融周期交互影响的DY系统构建

DY动态溢出指数法主要是利用滚动时窗分析对不同周期之间溢出效应的方向和强度进行动态测度，它的本质是一种广义动态方差分解，这一方法存在两方面优势：(1) 能够有效规避传统向量自回归模型进行方差分解时，结果存在变量顺序依赖的问题；(2) 能够依照滚动分解进行实时溢出效应分析。为进一步厘清中国经济周期与金融周期之间的实时交互影响，本文将利用DY动态溢出指数对二者之间的实时溢出效应进行测度。两变量的DY动态溢出指数构建如下：

首先，建立一个协方差平稳的双变量 $ VAR\left( p \right) $ 系统：

$ {Y_t} = \sum\nolimits_{i = 1}^p {{\Phi _i}{Y_{t - i}}} + {\varepsilon _t} $

(3)

其中， $ {Y_t} $ 为包含经济周期与金融周期两个内生变量的向量， $ {\Phi _i} $ 为 $ 2 \times 2 $ 维系数矩阵， $ {\varepsilon _t} \sim \left( {0,\sum } \right) $ 为独立同分布的扰动向量。由于经济周期指数与金融周期指数均是平稳的时间序列，式 (3) 可进一步表示为： $ {Y_t} = \sum\nolimits_{i = 0}^\infty {{A_i}{\varepsilon _{t - i}}} $ 。其中， $ {A_i} $ 为 $ 2 \times 2 $ 维系数矩阵，且满足

$ {A_0} $ 是 $ 2 \times 2 $ 维单位矩阵，且当 $ i < 0 $ 时， $ {A_i} = 0 $ 。在广义 $ VAR $ 框架下，本文依据 $ KPPS $ 法 (Koop等, 1996; Pesaran和Shin, 1998) 对变量 $ {Y_i} $ 的 $ H $ 步预测误差进行方差分解，从而得到 $ {Y_j} $ 对 $ {Y_i} $ 的 $ H $ 步预测误差方差的贡献比例为^④：

$ {d_{ij}}\left( H \right) = \frac{{\sigma _{jj}^{ - 1}{{\sum\nolimits_{h = 0}^{H - 1} {\left( {{e_i}^\prime {A_h}\sum {e_j}} \right)} }^2}}}{{\sum\nolimits_{h = 0}^{H - 1} {\left( {{e_i}^\prime {A_h}\sum {A_h}^\prime {e_i}} \right)} }} $

(4)

其中， $ \sum $ 是扰动向量 $ \varepsilon $ 的协方差矩阵； $ {\sigma _{jj}} $ 是第 $ j $ 个方程误差项的标准差； $ {e_i} $ 代表第 $ i $ 个元素为1，其余元素均为0的选择向量。考虑到在广义 $ VAR $ 系统下进行预测误差方差分解时很难满足 $ \sum\nolimits_{j = 1}^2 {{d_{ij}}\left( H \right)} = 1 $ ，因此本文按式 (5) 对方差分解矩阵进行标准化。

$ {\tilde d_{ij}}\left( H \right) = \frac{{{d_{ij}}\left( H \right)}}{{\sum\nolimits_{j = 1}^2 {{d_{ij}}\left( H \right)} }} $

(5)

对方差分解矩阵进行标准化后， $ \sum\nolimits_{j = 1}^2 {{{\tilde d}_{ij}}\left( H \right)} = 1 $ ， $ \sum\nolimits_{i,j = 1}^2 {{{\tilde d}_{ij}}\left( H \right)} = 2 $ 。

据此，变量 $ {Y_j} $ 向变量 $ {Y_i} $ 的定向溢出指数 (Directional Spillover Index, DSI) 可写为：

$ DS{I_{i \leftarrow j}} = {\tilde d_{ij}}\left( H \right) \times 100 $

(6)

变量 $ {Y_i} $ 接受所有其它变量的定向溢出效应可由标准化后的方差分解矩阵中第 $ i $ 行上除对角线元素外的其他所有元素之和表示，即：

$ DS{I_{i \leftarrow }} = \sum\nolimits_{\begin{subarray}{l} j = 1 \\ j \ne i \end{subarray}} ^2 {{{\tilde d}_{ij}}\left( H \right)} \times 100 $

(7)

特别地，由于本文的广义方差分解中只存在两个变量，因此 $ DS{I_{i \leftarrow }} = DS{I_{i \leftarrow j}}\left( {j \ne i} \right) $ ，并且有 $DS{I_{i \leftarrow }} = 1 - DS{I_{i \leftarrow i}}$ $1-{DSI}_{{i}\leftarrow {i}}$ 。同理，变量 $ {Y_i} $ 对所有其他变量的定向溢出效应则可由标准化后的方差分解矩阵中第 $ i $ 列上除主对角线元素外的其他所有元素之和表示，即：

$ DS{I_{ \leftarrow i}} = \sum\nolimits_{\begin{subarray}{l} i = 1 \\ j \ne i \end{subarray}} ^N {{{\tilde d}_{ij}}\left( H \right) \times 100} $

(8)

系统的总体溢出效应 (Total Spillover Index, TSI)，即所有变量的波动溢出对系统总体预测误差方差的平均贡献，可由标准化后的方差分解矩阵中除主对角线元素外的其他所有元素之和占所有元素之和的比例表示，也可由 $ DS{I_{i \leftarrow }} $ 或 $ DS{I_{ \to i}} $ 的所有元素的平均值表示，即：

$ TSI = \frac{{\sum\nolimits_{\begin{subarray}{l} i,j = 1 \\ j \ne i \end{subarray}} ^2 {{{\tilde d}_{ij}}\left( H \right)} }}{{\sum\nolimits_{i,j = 1}^2 {{{\tilde d}_{ij}}\left( H \right)} }} \times 100 = \frac{{\sum\nolimits_{\begin{subarray}{l} i,j = 1 \\ j \ne i \end{subarray}} ^2 {{{\tilde d}_{ij}}\left( H \right)} }}{2} \times 100 $

(9)

(二) 中国经济周期与金融周期的动态交互影响测度

根据广义预测误差方差分解计算得到整个样本区间内经济周期与金融周期间的溢出效应，如表3所示。观察表3可知,首先，就全样本范围而言，ECI与FCI之间的总溢出效应为27.4%，即经济周期与金融周期的平均交互影响强度为总体波动的27.4%，该指标介于20%−30%之间，说明二者之间具有弱溢出效应，尚未达到强溢出。进一步来看二者的单向溢出情况，经济周期对金融周期的单向溢出效应为20.6%，已接近20%下限，这说明经济周期波动对金融周期的溢出效应相对有限；而反观金融周期对经济周期的溢出效应，该指标高达34.2%，超出了弱溢出上限，达到了强溢出标准。这一现象与经验事实高度相符。据《证券时报网》统计，2020年中国A股 (剔除金融企业) 上市公司投资收益合计高达5528.66亿元，占归属母公司利润的29.19%，创历史新高，而传统核心盈利指标净资产收益率平均仅为7.48%，为历史低点。这说明非金融企业的利润越来越多地来源于金融渠道而非传统的商品生产与贸易渠道，这就导致实体经济对来自金融市场冲击的反应越来越强；同样，资本受逐利性特征驱使，并不关心实体经济的强弱，而是只投资收益更高的领域。

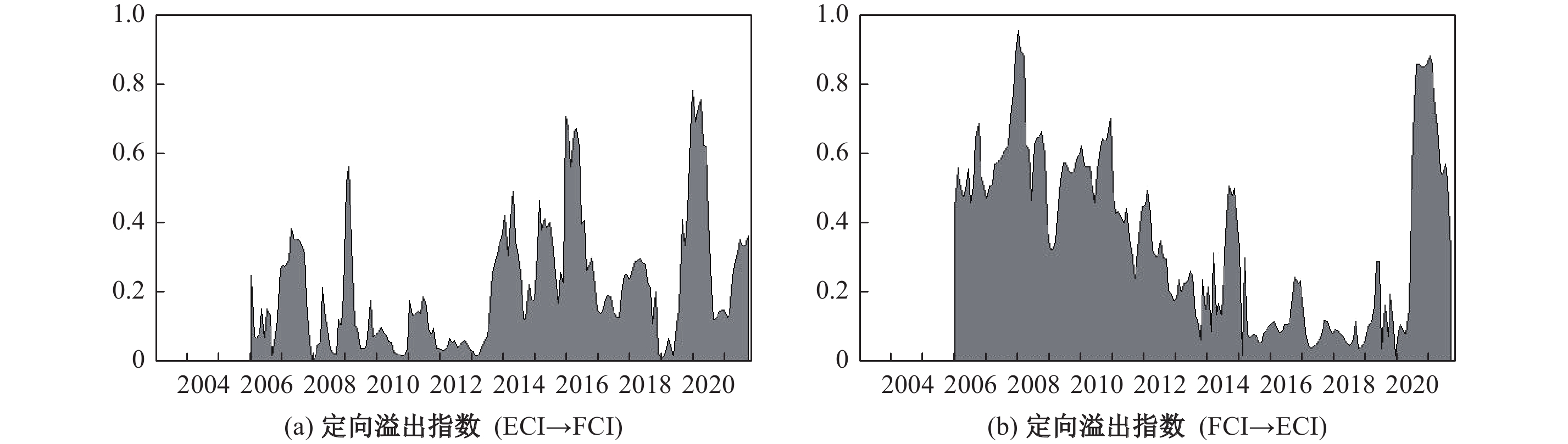
上述结果清晰地反映了一个重要事实：随着中国金融化水平的不断提高，经济运行逐渐呈现出“经济金融化”和“金融脱实化”的趋势，这一结果意味着虚拟经济和资本的地位将越发凸显，同时还会对传统的实体经济产生干预和“挤出”效应。由此可见，在统筹“宏观经济稳增长”和“金融系统防风险”时，正确地认识和把握资本的特性和行为规律至关重要，这是有效提高金融系统对实体经济支持，进而引导资金“脱虚向实”的关键。随后，为刻画经济周期与金融周期之间的动态溢出特性，本文进一步绘制了二者在样本期间内的动态溢出指数，如图6 (a)-(b) 所示。

观察图6 (a)−(b) 可以发现如下几个典型化事实和基本结论：第一，经济周期对金融周期的弱溢出主要体现在2008—2012年，彼时正值后国际金融危机的经济复苏期，宏观经济基本面的快速修复并未使资本市场摆脱恐慌和泥淖，这说明早期的资本市场中投机效应和从众心理仍占据主导地位，资本市场并未向宏观经济基本面和价值投资回归。第二，在2012年后，经济周期向金融周期的溢出效应有所增强，但稳定性仍有待提高。事实上，自2012年后经济周期对金融周期的溢出强度存在显著提升，在部分时段的溢出强度甚至高达80%，形成绝对主导，这是资本市场开始向宏观经济基本面回归的一个积极信号。但需注意的是，这种溢出增进尚不稳定，例如在2018年岁末和2019年初，受资管新规和去杠杆等多重压力影响，经济周期一度进入萧条期，但彼时金融周期却回归至平稳区段，二者几乎呈独立运行态势，而在新冠肺炎疫情期间，经济周期对金融周期的溢出强度显著上升，在新冠肺炎疫情初期甚至达到70%以上，即便是在后疫情经济复苏期，其溢出强度也在40%之上。第三，金融周期对经济周期的定向溢出效应呈现出由强转弱再转强的基本态势。观察样本期内金融周期对经济周期的溢出强度不难发现，金融周期的第一个溢出高峰集中在2006—2012年，期间涵盖了资本市场繁荣期、国际金融危机衰退期和后国际金融危机经济复苏期，而在“新常态”后，宏观经济开始长期陷入“三期叠加”困境。可以说在2012—2019年间，金融周期对经济周期的溢出都相对较弱，而这也是中国经济“脱实向虚”和国家坚定不移治理和化解系统性金融风险的主体阶段。值得注意的是，一个标志性的时点是2014年底，这是该段期间内 (2012—2019年) 金融周期对经济周期溢出效应最强的时段，彼时受中央银行非对称下调金融机构人民币贷款和存款基准利率影响，金融加杠杆曾在一定程度上引起了短期内的经济增长率上行 (2014年第4季度较第3季度上涨0.1%，达到7.3%)，但这种以加杠杆带动经济增长的方式明显不可持续，因为杠杆率不能无限上升，而此时若是加强金融周期对经济周期的溢出效应，那么当杠杆率收缩时，无疑会导致更大的经济风险和经济衰退。后续的资产价格大幅震荡和经济增长率下行也深刻地印证了这一论断。为此，国家坚定不移地走上了去化杠杆道路，并暂时性弱化了金融周期对经济周期的溢出。而在2020年新冠肺炎疫情冲击出现后，金融周期对经济周期再度产生了强溢出效应，说明金融周期再度开始发挥“晴雨表”的基本职能，这与时变Granger因果检验的判断一致，进一步验证了这一结论的稳健性。第四，自2020年后，无论是经济周期向金融周期的溢出效应，还是金融周期向经济周期的溢出效应，二者均达到了一个相对高点，这一方面说明，经过长时间的积极引导和统筹治理，中国经济周期与金融周期的关联性已有了实质性提高，经济运行的“脱实向虚”迹象已有所缓解，另一方面也说明，现阶段宏观经济和金融系统具有明显的协同变化态势，这对宏观经济治理体系的高效性和协同性提出了更高的要求。

六、结论与启示

经济周期与金融周期之间的传导关系和交互影响是现代宏观经济学研究的重要议题，它不仅关系到“宏观经济稳增长”和“金融系统防风险”的协调治理，也是把握和认识资本的基本特征和行为规律的前提，同时更是在长期内引导经济摆脱“脱实向虚”困境的核心和本质。为此，本文基于精准计量思想，在构建中国经济周期指数与金融周期指数的基础上，对经济周期与金融周期的事实形态、传导关系和交互影响进行了详细分析，主要得出如下结论：

第一，就经济周期和金融周期的事实形态而言，2003—2021年间，中国共经历了3轮完整的经济周期和4轮完整的金融周期。这说明经济周期与金融周期间存在着典型的周期错配现象，期间既有典型的耦合区间又有显著的背离时段。

第二，就经济周期与金融周期之间的传导关系而言，使用传统的线性Granger因果检验进行机制识别会产生严重的经验误判，这是因为二者之间无论是在传导关系还是传导方向上都会发生反转。而根据时变Granger因果检验测算，二者之间几乎不存在长期内的稳定传导，只有在罕见灾难危机和周期大幅度背离期间才会产生强牵拉和传导信号。其中，经济周期对金融周期的强传导主要体现在2016年间经济周期与金融周期的强背离阶段，它有效地纠正了资金的“脱实向虚”；而金融周期对经济周期的强传导主要体现在疫情时段，期间资本市场的变化有效地预测了宏观经济基本面的转弱。总体来看，时变Granger因果检验不仅能够准确地捕捉到经济周期与金融周期之间的传导关系，并且对传导时滞的判断也较为精准，可以为完善现代宏观治理体系的危机管理职能提供精准的实时预报。

第三，从经济周期与金融周期的交互影响来看，金融周期对经济周期的溢出效应更强，而经济周期对金融周期的溢出效应较弱，这与经验判断相符。但需要注意的是，自新冠肺炎疫情爆发以来，经济周期和金融周期之间的交互影响明显增强，这一方面说明，中国经济周期与金融周期间的关联性已有了实质性提高，形成了彼此增进、交互渗透的良好态势，经济运行的“脱实向虚”现象已有所缓解；另一方面也对宏观经济治理体系的高效性、协同性和危机管理能力提出了更高要求。

基于此，本文得到如下政策启示：第一，“金融活，经济活；金融稳，经济稳；经济兴，金融兴；经济强，金融强”这一基本理念在新冠肺炎疫情时期已得到深刻印证，这表明国家应长期坚持“引导金融系统回归服务实体经济发展”的基本导向，特别是要注重对小微企业、民营经济的扶植，致力于增强金融资源的可得性、普惠性和基础支持功能。第二，要在把握和认识资本的基本特征和行为规律的基础上，主动适应资本的基本特征和行为规律，着力打造具有发展潜力、盈利能力和就业吸纳力的实体增长点。第三，要充分重视由罕见灾难冲击引发的经济不确定性和周期错配现象，强化宏观治理的实时性，加强政策空间储备。政策当局应充分意识到，疫情时期经济周期与金融周期的协同也可能是阶段表象，从中国经济运行的基本特征和金融发展的一般规律来看，二者在短期内较难实现稳定的协同发展，这就从根本上决定着宏观治理体系必须要强化升级、增加危机时期的政策工具储备、政策组合储备和政策空间储备，全面应对由经济周期与金融周期耦合背离关系变化引致的各类风险。第四，要加强对宏观经济景气和金融风险的实时预测和短期预报功能，实时预报和短期预报精准性的提高不仅有利于应对各种类型的经济金融风险，同时还会对稳定公众预期产生巨大的帮助，这是建立现代宏观治理体系的核心和根本，亦是化解当下“三重压力”的基本诉求。

① 大量近期研究表明，相比于7天期银行间同业拆借利率，DR007数据更能反映市场利率的真实波动状态，故本文选取DR007作为基础指标进行金融周期指数拟合，鉴于DR007数据在2014年开始发布，故前期数据由R007替代，二者具有学理同源性 (刘达禹等, 2021)。

② 这里只对上证综合指数提取周期性成分的原因在于仅上证综合指数是总量指标，具有典型的局部趋势，其他指标均为比率指标，其自身变动就可视为周期变动，这一处理与邓创和徐曼 (2018) 等经典文献一致。

③ Wald统计量的具体构建步骤可参见Shi等 (2018)。

④ 由于本文系统仅涉及两个变量，因此当 $ Y_{i} $ 代表经济周期时， $ Y_{j} $ 即代表金融周期，反之亦然。