
2021第23卷第6期
来自于经济系统外部的各类不确定性冲击,是造成经济波动的重要原因。宏观经济周期理论认为无论是正向冲击还是负向冲击,都可能会对居民福利产生不利影响(Lucas,2003)。长期以来,为了应对各类冲击,中国政府主要采用相机决策型财政政策平抑经济波动。例如,20世纪90年代中期由于经济体制转换,中国政府多次大幅压缩公共投资、抑制经济过热,避免经济“硬着陆”。2008年爆发的国际金融危机,中国及时实施了4万亿元的基础设施投资,为经济复苏提供了内生动力。2020年初,突如其来的新冠肺炎疫情,对中国经济造成了重大负面冲击,为了保障民生、稳定经济,国家出台了以减税降费和扩大支出为特征的积极财政政策。但是,相机决策型财政政策存在一定的时间滞后性,可能会导致顺周期调节,反而放大了经济波动,而扩张型财政政策在降低经济运行风险的同时,财政收支矛盾日益突出,财政自身的风险也在不断积累。展望未来,国外新冠肺炎疫情呈现长期化和反复化,世界政治经济形势也将变得更为动荡不安,中国经济发展面临的不确定性有增无减。后疫情时代,如何在应对外生冲击风险的基础上,化解财政的自身风险,确保财政运行安全、平稳、可持续?如何更加有效地利用财政政策平抑经济波动,保障民生福利?上述问题的解决,一方面需要将产出波动、公共风险、债务风险会同财政支出一并加以考虑,借助于规则型财政政策的约束对上述风险加以权衡;另一方面,需要针对外生冲击的具体性质和作用渠道,给予不同类型的财政支出以不同的应对规则,从而增加财政支出的精准性和灵活性。本研究将公共支出划分为消费性支出、投资性支出和转移支付支出,利用NK-DSGE模型分别研究了这三类公共支出,在平滑规则、盯住产出逆向调节规则、盯住债务逆向调节规则以及同时盯住产出和债务逆向调节规则下的居民福利保障效应,并根据模型运行结果,提出了财政支出规则的优化建议。
一国经济由于外生冲击导致其偏离长期趋势,此种经济波动会对该国的居民福利造成负面影响(Lucas,2003;Alvarez和Jermann,2004;Mukoyama和Şahin,2006)。早在20世纪60年代,凯恩斯学派就指出应当积极运用财政支出手段调控需求,避免通货膨胀或紧缩,并据此提出逆周期赤字型财政政策,又称为相机决策型财政政策;而货币学派和理性预期学派指出,相机决策型财政政策由于市场参与者难以对此理性预期、存在时间滞后性,导致社会福利代价过高,因此应当实施中性的、规则化的财政政策(Kydl和Prescott,1977;Barro,1986),理论界大多认同规则型财政政策优于相机决策型财政政策(Niemann和Pichler,2020),并且在具体的实践中逐步细化为不同的财政规则。近10年来,西方国家经济波动巨大,财政风险持续升高,因此有学者对财政规则的有效性提出了质疑,Jones(2002)对美国战后财政反应函数进行了估计,结果表明财政政策对产出波动并没有起到预期效果。McKay和Reis(2016)研究了自动稳定器对经济波动的影响,结论是采用财政自动稳定机制很难对美国经济波动产生作用。也有文献对不同类型的财政规则做了比较评估,例如,Jalles(2018)的跨国研究发现,平衡预算规则降低了财政政策的逆周期特征,使萧条期经济雪上加霜。Ghosh和Mourmouras(2004)在内生增长模型中讨论了社会福利最大化的财政规则,结论是在严格预算约束规则下能够实现更高的社会福利水平。Alfaro和Kanczuk(2017)指出面对冲击时,设置债务上限的简单债务规则优于复杂的赤字上限规则。实际上,一国制定的财政规则能否有效发挥作用,受到该国实际经济运行环境的影响,Guo和Harrison(2006)的研究表明,财政规则的稳定效应取决于劳动力市场,以及劳动进入家庭效用函数的形式等。Beetsma和Jensen(2005)认为支出产品替代弹性越大、劳动供给弹性越小,则要求财政支出规则越积极。此外,还有文献指出由于法律约束缺失、预警机制失灵等,导致财政规则得不到严格遵循,从而降低了规则的有效性(Reuter,2015)。
国内的学者在这一领域也进行了大量研究。郭庆旺等(2007)、张馨和康锋莉(2007)采用向量自回归模型(VAR)的研究发现,中国相机决策型财政政策不仅没有起到逆周期调节的作用,甚至加大了产出的波动。更多的学者强调当外生冲击发生时,应当通过固定的财政规则平衡公共风险与财政风险(刘尚希,2005;高培勇,2013)。但是对于采用何种规则应对经济波动,结论并不一致。周波(2014)采用面板数据的实证研究认为,财政自动稳定器对平抑产出波动发挥着稳定性作用。尹翔硕等(2020)采用结构向量自回归模型(SVAR)的研究证实,基于广义赤字率制定的支出规则发挥逆周期调控作用,而基于狭义赤字率会得到相反的结果。张佐敏(2014)采用DSGE模型,证实中国的财政调控方式已具有规则属性,盯住产出缺口和政府赤字的财政规则有利于提高福利水平。朱军(2013)基于开放经济环境的模型设定,对中国财政规则进行的研究表明,盯住债务的规则对政策效果具有重要影响。潘敏和张新平(2021)利用DSGE模型考察了新冠肺炎疫情冲击下,中国最优财政规则的选择,认为短期的规则应当关注产出缺口,长期的规则应当关注债务缺口。
综上所述,国内学者在此领域取得了丰硕的研究成果,但是已有的文献大多是从平抑经济波动的视角间接关注居民福利,直接基于居民福利视角,探讨最优财政规则的文献较为缺乏,且大多是对支出的总体考察,忽略了不同类型支出的相互配合。本文可能的贡献在于:基于新凯恩斯模型(NK-DSGE)设定,在假设经济运行受到三类不同性质的外生冲击下,从平抑消费波动和保障居民福利两个视角,对最优支出规则及其组合进行了分析评估。研究发现:在技术正向冲击下,盯住债务规则和同时盯住产出与债务规则,导致私人消费和居民总消费的波动较大;在劳动偏好受到负向冲击时,盯住债务的支出规则对私人消费起到了较好的平滑作用;当投资受到正向冲击时,盯住债务的规则导致私人消费的波动更大。财政支出规则组合对居民长期和短期福利的影响表明:在正向技术冲击下,以居民福利为标准衡量的最优的政策组合为三类支出均采用平滑规则;在负向劳动偏好冲击下,消费性支出采用盯住产出逆向调节,投资性支出与转移支付采用盯住债务与产出逆向调节;在投资效率正向冲击下,最优的规则组合为消费性支出采用盯住产出逆向调节规则,投资性支出采用同时盯住债务和产出逆向调节规则,转移支付支出采用盯住债务逆向调节规则。最后本文证实了,在政府消费偏向民生领域,增加与私人消费的替代弹性后,能够显著提升居民福利水平。
二、标准模型构建与求解本文通过在NK-DSGE模型中引入三类外生冲击,寻找最有利于保障居民福利的财政支出规则。选择的外生冲击包括对技术的正向冲击、对投资效率的正向冲击以及对劳动偏好的负向冲击。选择上述冲击的理由是,技术冲击是最常见的导致经济波动的冲击源,冲击方向一般为正。投资则会对消费、储蓄、生产等造成广泛的影响,理论上投资冲击也一般为正。本文用劳动偏好遭受冲击代表自然灾害以及重大的疫情冲击,上述冲击一旦发生会降低人们的劳动供给意愿,因此其冲击方向为负。本研究构建的NK-DSGE模型具有以下特点:一是将政府支出分为消费性支出、投资性支出以及转移性支出,从而可以更加细致地比较不同类型的财政支出规则及其组合效应;二是将公共消费与居民私人消费组合成居民总消费,并一起纳入居民效用函数中,从而可以更加深入地研究公共消费对居民效用的具体影响;三是引入消费习惯和投资调整成本,使得模型更加符合经济实际运行状况。
(一) 家庭部门将总量为1的代表性居民
| $ {C}_{t}={\left[{\varphi }_{c}{\left({C}_{t}^{p}\right)}^{1-1/{\rho }_{c}}+\left(1-{\varphi }_{c}\right){G}_{t}^{1-1⁄{\rho }_{c}}\right]}^{\frac{1}{1-^{1}/ {{\rho }_{c}}}} $ | (1) |
其中,
| $ u\left({C}_{t},{\bar{C}}_{t},{L}_{t}\right)=\frac{{\left({C}_{t}-{\chi }^{c}\bar{{C}_{t}}\right)}^{1-{\sigma }_{c}}-1}{1-{\sigma }_{c}}-\frac{{\upsilon }_{0}{\epsilon }_{t}^{L}}{1+\frac{1}{{\upsilon }_{1}}}{L}_{t}^{\left(1+\frac{1}{{\upsilon }_{1}}\right)} $ | (2) |
其中,
| $ {b}_{t}+{I}_{t}+\left(1+{\tau }_{c,t}\right){C}_{t}^{p}=\left(1-{\tau }_{l,t}\right){w}_{t}\left(h\right){L}_{t}\left(h\right)+\left(1-{\tau }_{k,t}\right){r}_{k,t}{K}_{t-1}+{\Pi }_{t}+{TR}_{t}+\frac{{R}_{t-1}{b}_{t-1}}{{\pi }_{t}} $ | (3) |
其中,
资本积累方程:
| $ {K}_{t}={\epsilon }_{t}^{I}\left[1-\frac{\varphi }{2}{\left(\frac{{I}_{t}}{{I}_{t-1}}-1\right)}^{2}\right]{I}_{t}+\left(1-\delta \right){K}_{t-1} $ | (4) |
其中,
| $ {E}_{0}{\sum }_{t=0}^{\infty }{\beta }^{t}u\left[{C}_{t},{L}_{t}\left(h\right)\right] $ |
分别求消费、债券、投资和资本存量满足的一阶条件:
| $ {\lambda }_{t}=\frac{{\varphi }_{c}{\left({C}_{t}-{\chi }^{c}{\stackrel-{C}}_{t-1}\right)}^{-{\sigma }_{c}}}{1+{\tau }_{c,t}}{\left({\Xi }_{t}\right)}^{\frac{1}{1-\frac{1}{{\rho }_{c}}}-1}{\left({C}_{t}^{p}\right)}^{-\frac{1}{{\rho }_{c}}} $ | (5) |
| $ {\Xi }_{t}={\varphi }_{c}{\left({C}_{t}^{p}\right)}^{1-1/\rho_c}+\left(1-{\varphi }_{c}\right){G}_{t}^{1-1⁄{\rho }_{c}} $ | (6) |
| $ {\lambda }_{t}=\beta {E}_{t}{\lambda }_{t+1}{(R}_{t}/{\pi }_{t+1}) $ | (7) |
| $ {\lambda }_{t}={Q}_{t}{{\epsilon }_{t}^{I}}_{t}\left\{\left[1-\frac{\varphi }{2}{\left(\frac{{I}_{t}}{{I}_{t-1}}-1\right)}^{2}\right]-\varphi \left(\frac{{I}_{t}}{{I}_{t-1}}-1\right)\frac{{I}_{t}}{{I}_{t-1}}\right\}+\beta {E}_{t}{Q}_{t+1}{\epsilon }_{t+1}^{I}\varphi \left(\frac{{I}_{t+1}}{{I}_{t}}-1\right){\left(\frac{{I}_{t+1}}{{I}_{t}}\right)}^{2} $ | (8) |
| $ {Q}_{t}=\beta {E}_{t}\left[{\lambda }_{t+1}(1-{\tau }_{k,t}){r}_{k,t+1}+{Q}_{t+1}(1-\delta )\right] $ | (9) |
其中,
假定经济中存在最终劳动生产商,将家庭提供的异质性劳动打包:
| $ {L}_{t}={\left[{\int }_{0}^{1}{L}_{t}{\left(h\right)}^{\frac{{\epsilon}_{w}-1}{{\epsilon}_{w}}}dh\right]}^{\frac{{\epsilon}_{w}}{{\epsilon}_{w}-1}},{\epsilon}_{w} > 1 $ | (10) |
其中,
| $ \underset{{L}_{t}\left(h\right)}{\mathit{max}}{W}_{t}{L}_{t}-{\int }_{0}^{1}{W}_{t}\left(h\right){L}_{t}\left(h\right)dh $ |
| $ {L}_{t}\left(h\right)={\left[\frac{{W}_{t}\left(h\right)}{{W}_{t}}\right]}^{-{\epsilon}_{w}}{L}_{t} $ | (11) |
| ${W}_{t}={\left[{\int }_{0}^{1}{W}_{t}{\left(h\right)}^{\left(1-{\epsilon}_{w}\right)}dh\right]}^{\frac{1}{1-{\epsilon}_{w}}} $ | (12) |
采用Calvo定价方法,假定t时期,能够改变工资的家庭占比为
| $ \frac{{W}_{N,t+s}\left(h\right)}{{P}_{t+s}}=\frac{{\prod }_{i=1}^{s}{\pi }_{t+i-1}{W}_{A,t}\left(h\right)}{{\prod }_{i=1}^{s}{\pi }_{t+i}{P}_{t}}=\frac{{\pi }_{t}}{{\pi }_{t+s}}{\stackrel{~}{w}}_{t}\left(h\right) $ |
由于对称性,t期能够设定最优工资的家庭将设定相同的工资水平,即
| $ \begin{aligned} \mathcal{L}= & {E}_{t}{\sum }_{s=0}^{\infty }{\left(\beta {\phi }_{w}\right)}^{s}\{\frac{{\left({C}_{t}-{\chi }^{c}\stackrel{-}{{C}_{t}}\right)}^{1-{\sigma }_{c}}-1}{1-{\sigma }_{c}}-\frac{{\upsilon }_{0}{\epsilon }_{r,t}^{L}}{1+\frac{1}{{\upsilon }_{1}}}{\left[{\left(\frac{\left(\dfrac{{x}_{t}w_t}{{x}_{t+s}}\right)}{{w}_{t+s}^{{-\epsilon}_{w}}}\right)}^{{-\epsilon}_{w}}{L}_{t+s}\right]}^{1+\frac{1}{{\upsilon }_{1}}}\\ &+{\lambda }_{t+s}[\frac{\left(1-{\tau }_{l,t}\right){\pi }_{t}}{{\pi }_{t+s}}{\stackrel{~}{w}}_{t}{\left(\frac{{(\pi }_{t}/{\pi }_{t+s}){\stackrel{~}{w}}_{t}}{{w}_{t+s}^{{-\epsilon}_{w}}}\right)}^{{-\epsilon}_{w}}{L}_{t+s}+RMT\left]\right\} \end{aligned} $ |
其中,
| $ \begin{aligned} 0=&{E}_{t}{\sum }_{s=0}^{\infty }{\left(\beta {\phi }_{w}\right)}^{s}\{{{\upsilon }_{0}{\epsilon }_{t+s}^{L}\epsilon}_{w}{\stackrel{~}{w}}_{t}^{-{\epsilon}_{w}\left(1+\frac{1}{{\upsilon }_{1}}\right)-1}{\left(\frac{\left(\dfrac{{\pi }_{t}}{{\pi }_{t+s}}\right)}{{w}_{t+s}}\right)}^{-{\epsilon}_{w}\left(1+\frac{1}{{\upsilon }_{1}}\right)}{L}_{t+s}^{1+\frac{1}{{\upsilon }_{1}}}\\ &+{\lambda }_{t+s}\left(1-{\tau }_{l,t+s}\right)\left(1-{\epsilon}_{w}\right){\stackrel{~}{w}}_{t}^{-{\epsilon}_{w}}{w}_{t+s}^{{\epsilon}_{w}}{\left(\frac{{\pi }_{t}}{{\pi }_{t+s}}\right)}^{1-{\epsilon}_{w}}{L}_{t+s}\} \end{aligned} $ |
得到最优工资方程的递归方程:
| $ {\stackrel{~}{w}}_{t}=\frac{{\epsilon}_{w}}{{\epsilon}_{w}-1}\frac{{\Delta }_{1,t}}{{\Delta }_{2,t}} $ | (13) |
| $ {\Delta }_{1,t}={\upsilon }_{0}{\epsilon }_{r,t}^{L}{\left(\frac{{\stackrel{~}{w}}_{t}}{{w}_{t}}\right)}^{-{\epsilon}_{w}\left(1+\frac{1}{{\upsilon }_{1}}\right)}{L}_{r,t}^{1+\frac{1}{{\upsilon }_{1}}}+\beta {\phi }_{w}{E}_{t}{\left(\frac{{\pi }_{t}{\stackrel{~}{w}}_{t}}{{\pi }_{t+1}{\stackrel{~}{w}}_{t+1}}\right)}^{-{\epsilon}_{w}\left(1+\frac{1}{{\upsilon }_{1}}\right)}{\Delta }_{1,t+1} $ | (14) |
| $ {\Delta }_{2,t}={\lambda }_{r,t}\left(1-{\tau }_{l,t}\right){\left(\frac{{\stackrel{~}{w}}_{t}}{{w}_{t}}\right)}^{{-\epsilon}_{w}}{L}_{r,t}+\beta {\phi }_{w}{E}_{t}{\left(\frac{{\stackrel{~}{w}}_{t}}{{\stackrel{~}{w}}_{t+1}}\right)}^{{-\epsilon}_{w}}{\left(\frac{{\pi }_{t}}{{\pi }_{t+1}}\right)}^{\left(1-{\epsilon}_{w}\right)}{\Delta }_{r,t+2} $ | (15) |
根据Calvo定价规则,将积分形式的工资方程(12)写成递归形式
| $ {w}_{t}^{1-{\epsilon}_{w}}=\left(1-{\phi }_{w}\right){\stackrel{~}{w}}_{At}^{1-{\epsilon}_{w}}+{\phi }_{w}{\left[\left({\pi }_{t-1}/{\pi }_{t}\right){w}_{t-1}\right]}^{1-{\epsilon}_{w}} $ | (16) |
最终商品生产商
| $ {Y}_{t}={\left[{\int }_{0}^{1}{Y}_{t}{\left(j\right)}^{\frac{{\epsilon}_{y}}{{\epsilon}_{y}-1}}\right]}^{\frac{{\epsilon}_{y}}{{\epsilon}_{y}-1}},{\epsilon}_{y} > 1 $ | (17) |
最终品产商最大化利润,且其利润为零,得到中间产品需求方程(18)和价格方程(19):
| $ \underset{{Y}_{t}\left(j\right)}{\mathit{max}}{P}_{t}{Y}_{t}-{\int }_{0}^{1}{P}_{t}\left(j\right){Y}_{t}\left(j\right)dj $ |
| $Y_t (j)= \left[\frac{P_t (j)}{P_t}\right] ^{-\epsilon_y } Y_t$ | (18) |
| $ {P}_{t}={\left[{\int }_{0}^{1}{P}_{t}{\left(j\right)}^{1-{\epsilon}_{y}}dj\right]}^{\frac{1}{1-{\epsilon}_{y}}}$ | (19) |
中间商品生产商为垄断竞争者,第j个厂商的生产函数:
| $ {Y}_{t}\left(j\right)={\epsilon }_{t}^{A}{\left[{k}_{t-1}\left(j\right)\right]}^{\alpha }{L}_{t}{\left(j\right)}^{1-\alpha }{\left({k}_{g,t-1}\right)}^{{\alpha }_{g}} $ | (20) |
全要素生产率满足方程:
| $ {w}_{t}={\psi }_{t}\left(j\right)\left(1-\alpha \right){\epsilon }_{t}^{A}{\left(\frac{{k}_{t-1}}{{L}_{t}}\right)}^{\alpha }{\left({k}_{g,t-1}\right)}^{{\alpha }_{g}} $ | (21) |
| $ {r}_{k,t}={mc}_{t}{\alpha \epsilon }_{t}^{A}{\left(\frac{{k}_{t-1}}{{L}_{t}}\right)}^{\alpha -1}{\left({k}_{g,t-1}\right)}^{{\alpha }_{g}} $ | (22) |
| $ \frac{{k}_{t-1}}{{L}_{t}}=\frac{\alpha }{1-\alpha }\frac{{w}_{t}}{{r}_{k,t}} $ | (23) |
| $ {mc}_{t}\left(j\right)=m{c}_{t}={\psi }_{t}\left(j\right)=\frac{{w}_{t}}{\left(1-\alpha \right){\epsilon }_{t}^{A}{\left({k}_{g,t-1}\right)}^{{\alpha }_{g}}}{\left(\frac{{k}_{t-1}}{{L}_{t}}\right)}^{-\alpha } $ | (24) |
中间品厂商j实际利润:
| $ \frac{{P}_{t+s}\left(j\right)}{{P}_{t+s}}=\frac{{\pi }_{t}}{{\pi }_{t+s}}{p}_{At} $ |
厂商求解贴现后实际利润最大化:
| $ \underset{{P}_{t}\left(j\right)}{\mathit{max}}{E}_{t}{\sum }_{s=0}^{\infty }{\left(\theta \beta \right)}^{s}\left(\frac{{\lambda }_{t+s}}{{\lambda }_{t}}\right)\left[\frac{{\Pi }_{t+s}\left(j\right)}{{P}_{t+s}}\right] $ |
代入利润方程和产品需求方程:
| $ \underset{{P}_{t}\left(j\right)}{\mathit{max}}{E}_{t}{\sum }_{s=0}^{\infty }{\left({\phi }_{p}\beta \right)}^{s}\left(\frac{{\lambda }_{t+s}}{{\lambda }_{t}}\right)\left\{{\left(\frac{{\pi }_{t}}{{\pi }_{t+s}}{p}_{At}\right)}^{1-{\epsilon}_{y}}{Y}_{t+s}-m{c}_{t+s}{\left(\frac{{\pi }_{t}}{{\pi }_{t+s}}{p}_{At}\right)}^{-{\epsilon}_{y}}{Y}_{t+s}\right\} $ |
关于PAt求一阶条件得到:
| $ {E}_{t}{\sum }_{s=0}^{\infty }{\left({\phi }_{p}\beta \right)}^{s}\left(\frac{{\lambda }_{t+s}}{{\lambda }_{t}}\right)\left[{\left(1-{\epsilon}_{y}\right){\left(\frac{{\pi }_{t}}{{\pi }_{t+s}}\right)}^{1-{\epsilon}_{y}}\left({p}_{At}\right)^{-{\epsilon}_{y}}}{Y}_{t+s}+{\epsilon}_{y}m{c}_{t+s}{\left({p}_{At}\right)}^{-{(\epsilon}_{y}+1)}{\left(\frac{{\pi }_{t}}{{\pi }_{t+s}}\right)}^{-{\epsilon}_{y}}{Y}_{t+s}\right]=0 $ |
写成递归形式:
| $ {p}_{At}=\frac{{\epsilon}_{y}}{{\epsilon}_{y}-1}\frac{{\Gamma }_{1t}}{{\Gamma }_{2t}} $ | (25) |
| $ {\Gamma }_{1t}={\lambda }_{t}{mc}_{t}{Y}_{t}+\left({\phi }_{p}\beta \right){{E}_{t}\left(\frac{{\pi }_{t}}{{\pi }_{t+1}}\right)}^{-{\epsilon}_{y}}{\Gamma }_{1,t+1} $ | (26) |
| $ {\Gamma }_{2t}={\lambda }_{t}{Y}_{t}+\left({\phi }_{p}\beta \right){{E}_{t}\left(\frac{{\pi }_{t}}{{\pi }_{t+1}}\right)}^{1-{\epsilon}_{y}}{\Gamma }_{2,t+1} $ | (27) |
根据Calvo定价规则将价格方程(19)写成递归形式,得到价格的演化方程:
| $ 1={\left(1-{\phi }_{p}\right)p}_{At}^{1-{\epsilon}_{y}}+{\phi }_{p}{\left(\frac{{\pi }_{t-1}}{{\pi }_{t}}\right)}^{1-{\epsilon}_{y}} $ | (28) |
假设货币政策规则采取泰勒规则的形式:
| $ \frac{{R}_{t}}{\stackrel-{R}}={\left(\frac{{R}_{t-1}}{\stackrel-{R}}\right)}^{{\rho }_{r}}{\left[{\left(\frac{{Y}_{t}}{\stackrel-{Y}}\right)}^{{\rho }_{ry}}{\left(\frac{{\pi }_{t}}{\pi }\right)}^{{\rho }_{r\pi }}\right]}^{1-{\rho }_{r}} $ | (29) |
政府的t期收入来自于商品税、劳动税、资本税以及t期发行的债券
| $ {\tau }_{t}^{c}{C}_{t}^{p}+{\tau }_{t}^{l}{w}_{t}{L}_{t}+{\tau }_{t}^{k}{r}_{k,t}{K}_{t-1}+{b}_{t}={G}_{t}+{IG}_{t}+\left(\frac{{R}_{t-1}}{{\pi }_{t}}\right){b}_{t-1}+{TR}_{t} $ | (30) |
政府投资方程:
| $ {K}_{g,t}=\left(1-{\delta }_{g}\right){K}_{g,t-1}+{IG}_{t} $ | (31) |
财政规则分为支出规则和税收规则,因为支出规则是本文研究的重点,在下一节会专门讨论,这里的支出规则仅用平滑规则代表,税收规则采用盯住产出和债务的正向调节规则:
| $ \frac{{X}_{t}}{\stackrel-{X}}={\left(\frac{{X}_{t-1}}{\stackrel-{X}}\right)}^{{\rho }_{x}} $ | (32) |
| $ \frac{{z}_{t}}{\stackrel-{z}}={\left(\frac{{Y}_{t}}{\stackrel-{Y}}\right)}^{\left(1-{\rho }_{tz}\right){\rho }_{tz}^{y}}{\left(\frac{{b}_{t}}{\stackrel-{b}}\right)}^{\left(1-{\rho }_{tz}\right){\rho }_{tz}^{b}} $ | (33) |
其中,
首先,对消费预算方程加总,得到:
| $ {Y}_{t}={I}_{r,t}+{C}_{r,t}^{p}+{G}_{t}+I{G}_{t} $ | (34) |
其次,对中间品厂商的生产函数加总,得到加总的生产函数:
| $ {Y}_{t}=\frac{{\epsilon }_{t}^{A}{\left({k}_{t-1}\right)}^{\alpha }{L}_{t}^{1-\alpha }{\left({k}_{g,t-1}\right)}^{{\alpha }_{g}}}{{d}_{t}^{p}} $ | (35) |
最后,价格离散核
| $ {d}_{t}^{p}=\left(1-\theta \right){p}_{At}^{-{\epsilon}_{y}}+\theta {\left(\frac{{\pi }_{t-1}}{{\pi }_{t}}\right)}^{-{\epsilon}_{y}}{d}_{t-1}^{y} $ | (36) |
按照此类文献的通常做法,对于有着明确经济含义的结构参数,根据中国的实际经济数据计算得到,或者直接取值于权威文献。对于模型中的动态参数,通过贝叶斯估计获得。采用CCER金融数据库2010–2019年个人一年期平均定期存款利率除以4,校准主观贴现因子
| 参数 |
|
|
|
|
|
|
|
|
| 校准值 | 0.988 | 0.5 | 0.9 | 0.25 | 0.907 | 0.5 | 0.903 | 0.025 |
| 参数 |
|
|
|
|
|
|
|
|
| 校准值 | 0.015 | 0.45 | 0.06 | 1.728 | 4.5 | 4.5 | 0.75 | 0.75 |
| 参数 |
|
|
|
|
|
|
|
|
| 校准值 | 0.153 | 0.034 | 0.031 | 0.116 | 0.13 | 0.090 | 0.270 |
对于模型的动态参数,采用中经网统计数据库中2010–2019年月度数据汇总得到季度经济数据,通过RWMH方法进行贝叶斯估计,选择的经济变量包括总产出、居民消费、政府总支出、通货膨胀。对上述季度变量利用季度CPI转换为可比价格,并利用X-12方法进行季节调整,最后计算对数差分转换为增长率。各参数的先验分布设定以及估计出的后验分布,如表2所示③:
| 参数 | 先验
分布 |
先验
均值 |
后验
均值 |
90%置信
区间 |
参数 | 先验
分布 |
先验
均值 |
后验
均值 |
90%置信
区间 |
||
|
|
Beta | 0.5 | 0.5731 | 0.5703 | 0.5760 |
|
Normal | 0.5 | 0.3808 | 0.3349 | 0.4152 |
|
|
Normal | 0.5 | 0.4359 | 0.3813 | 0.4966 |
|
Beta | 0.6 | 0.5213 | 0.4698 | 0.5622 |
|
|
Normal | 0.5 | 0.5275 | 0.4612 | 0.5854 |
|
Normal | 1.2 | 1.0735 | 1.0467 | 1.1050 |
|
|
Beta | 0.5 | 0.4531 | 0.4115 | 0.4944 |
|
Normal | 0.5 | 0.1233 | 0.1018 | 0.1436 |
|
|
Normal | 0.5 | 0.5034 | 0.4335 | 0.5803 |
|
Beta | 0.5 | 0.2286 | 0.1610 | 0.2877 |
|
|
Normal | 0.5 | 0.4943 | 0.4196 | 0.5510 |
|
Normal | 0.5 | 0.3906 | 0.3660 | 0.4150 |
|
|
Beta | 0.5 | 0.4130 | 0.4037 | 0.4206 |
|
Normal | 1.5 | 1.7855 | 1.7347 | 1.8346 |
|
|
Normal | 0.5 | 0.7383 | 0.7094 | 0.7837 |
|
Beta | 0.9 | 0.9648 | 0.9241 | 0.9994 |
|
|
Normal | 0.5 | 0.6907 | 0.6596 | 0.7392 |
|
Normal | 0.5 | 0.8898 | 0.8706 | 0.9032 |
|
|
Beta | 0.6 | 0.9023 | 0.8890 | 0.9127 |
|
Normal | 0.5 | 0.6637 | 0.6578 | 0.6705 |
|
|
Normal | 1.2 | 1.1456 | 1.0897 | 1.1837 |
|
inv_gamma | 0.01 | 0.0035 | 0.0028 | 0.0041 |
|
|
Normal | 0.5 | 0.6834 | 0.6362 | 0.7348 |
|
inv_gamma | 0.01 | 1.0027 | 0.9313 | 1.0736 |
|
|
Beta | 0.6 | 0.7917 | 0.7679 | 0.8141 |
|
inv_gamma | 0.01 | 0.0814 | 0.0698 | 0.0939 |
|
|
Normal | 1.2 | 1.3764 | 1.3331 | 1.4119 | ||||||
| 注:数据来源于中经网月度数据库按季度汇总得到。 |
|||||||||||
政府在预算约束下,可以通过不同的财政支出规则对经济的外生冲击进行调节,这里对标准模型进行变形,将财政支出规则分为四类加以比较研究。具体支出规则按照其与产出和债务关系设定为:
|
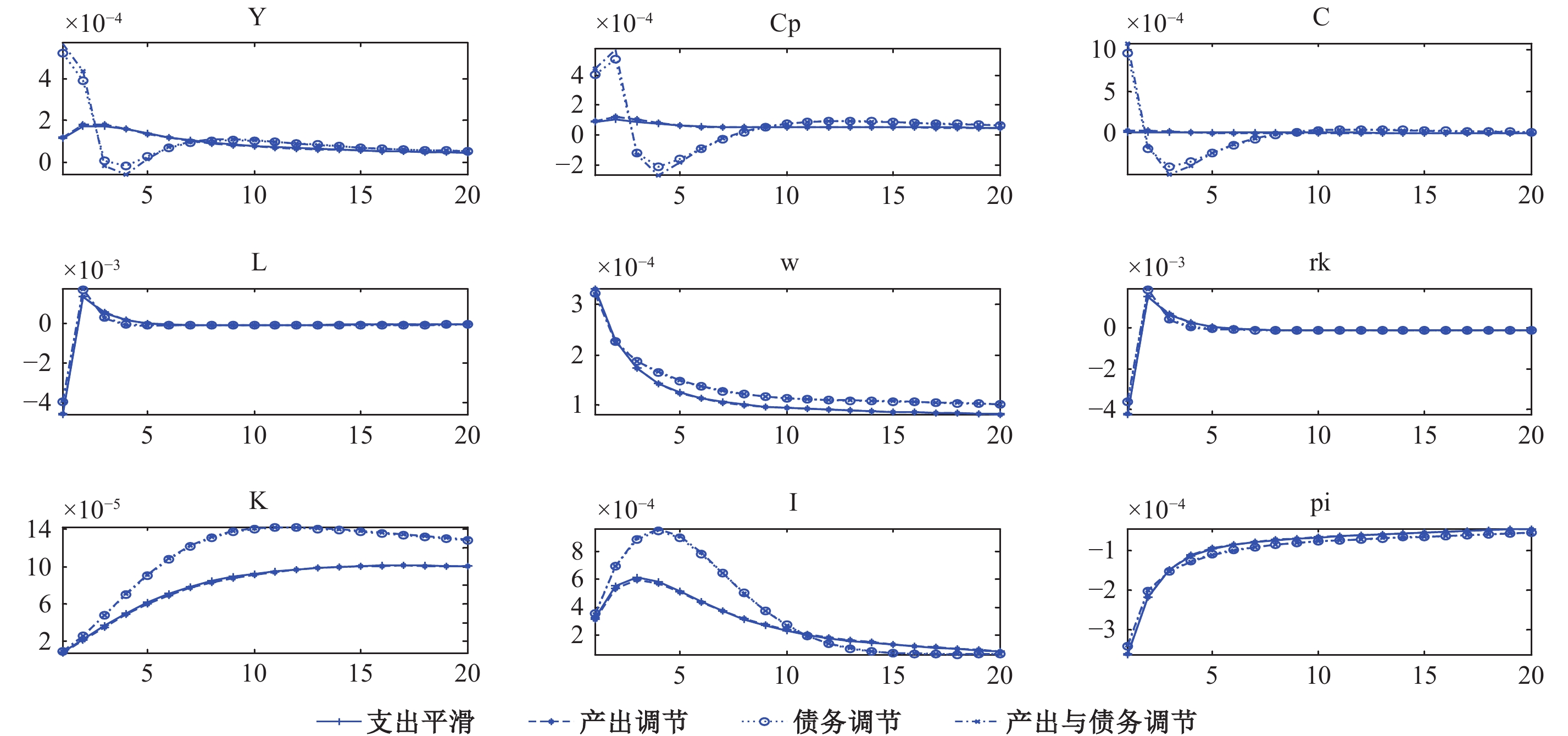
| 图 1 技术冲击在四类支出规则下对宏观经济变量的影响 |
|
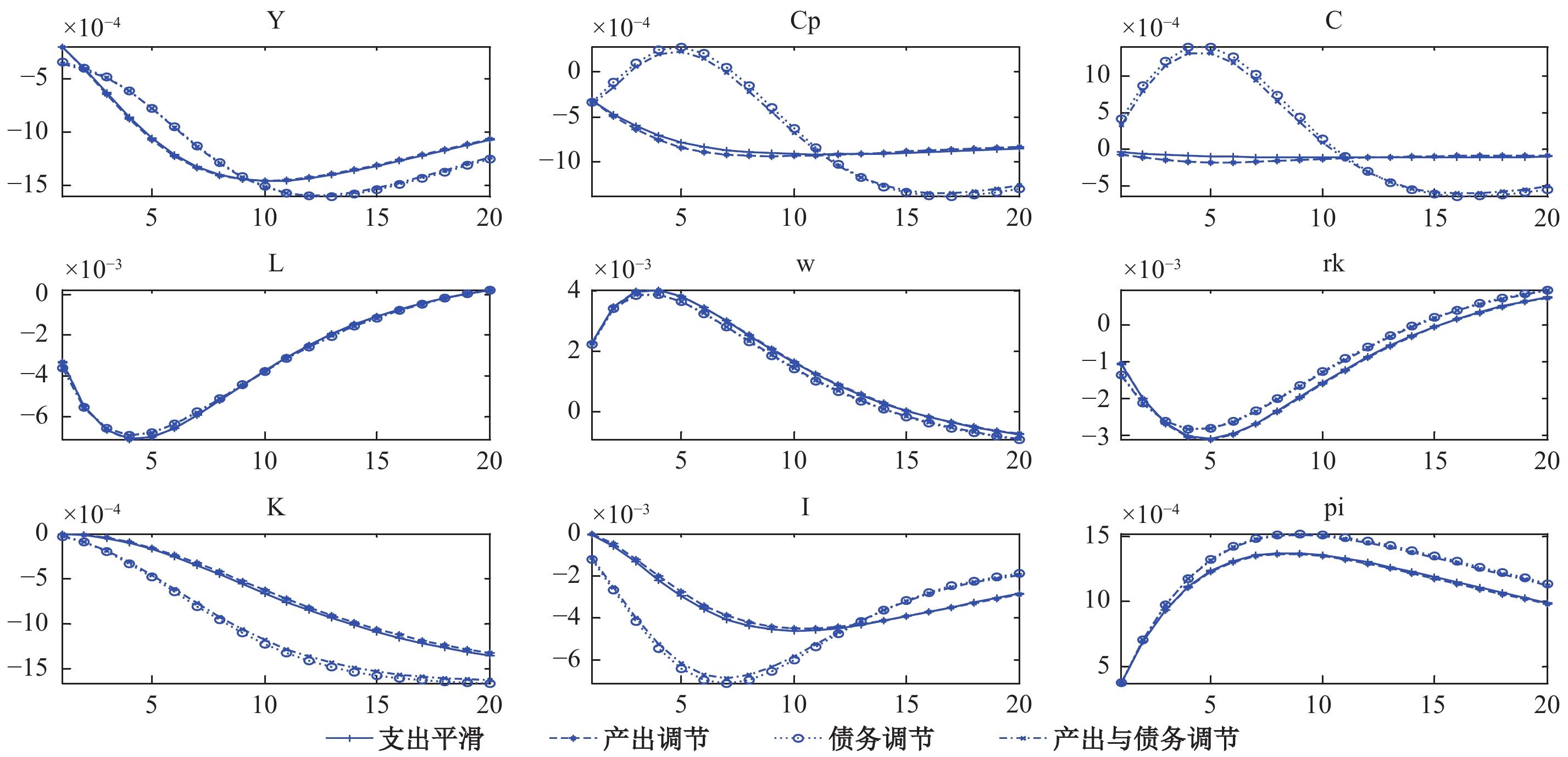
| 图 2 劳动冲击在四类支出规则下对宏观经济变量的影响 |
|
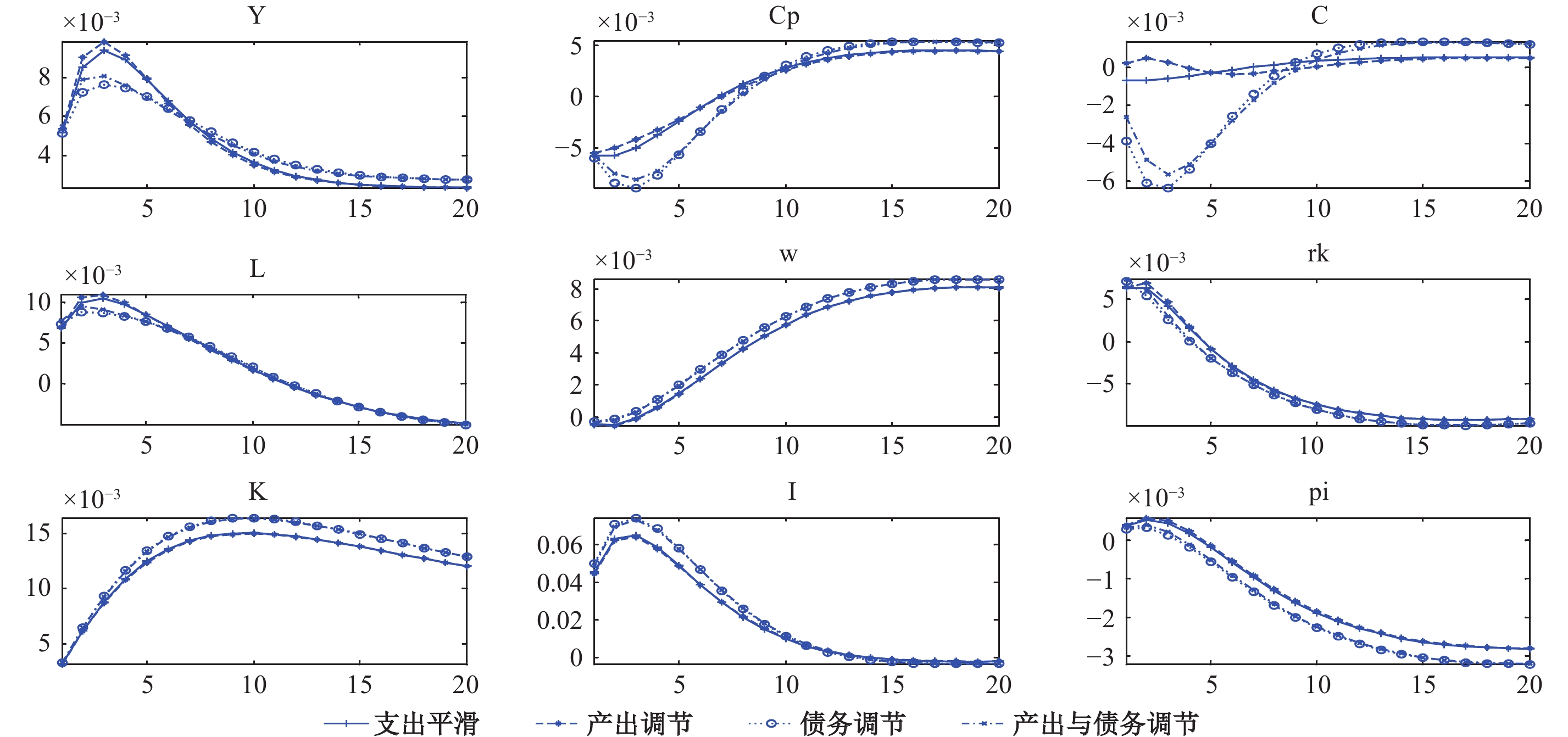
| 图 3 投资冲击在四类支出规则下对宏观经济变量的影响 |
在技术正向冲击下,劳动时间随即下降了0.4%,而后回升并趋于稳态,这是由于生产率提高了,而价格由于粘性不能立即下跌到位,因此总需求不能充分增长,导致厂商必须减少要素的投入,由于大幅度减少投资需要调整成本,因此初期主要是通过减少劳动实现供需平衡。根据资本劳动比方程(23),资本劳动比上升,而工资由于粘性上升不充分,因此资本回报率在初期下降。之后,随着各类因素的调整到位,产出、收入、消费及投资都会提高。但是,盯住债务和同时盯住产出与债务这两种支出规则下,居民私人消费和总消费的波动也较大,这是因为如果消费的增加带来的财政收入超过了劳动和资本回报减少带来的财政损失,则当期政府债务减少,由于逆向调节,导致政府消费、投资和转移支付增加,因此提升了居民收入,拉动了消费增加,反之则降低居民收入,导致消费降低,因此盯住债务的逆向调节规则实际放大了消费波动。
在劳动偏好受到负向冲击下,劳动供给先降低再逐步回归稳态,相应的实际工资先增长之后再逐步降低至稳态,产出也同样表现为先降低,之后再逐步上升。根据资本劳动比方程(23)可知,由于初期资本劳动比上升,而工资由于粘性不能充分增长,因此资本回报率降低,并导致投资和资本存量初期都减少。在盯住债务和同时盯住产出与债务两种支出规则下,劳动偏好的负向冲击,导致政府收入降低,政府债务增加,由于逆向调节,一方面政府的总支出降低,另一方面税率也相应增加,在本研究的贝叶斯估计结果中(表2的系数设定值),总支出降低的效应占优,因此政府实际征税减少,居民的收入维持稳定,所以消费并没有过多降低。总之,当劳动偏好的负向冲击发生时,四类财政支出规则虽然对劳动提升没有明显差异,但是,盯住债务的支出规则对消费起到了较好的平滑作用。
当投资效率受到正向冲击时,资本存量先增长而后逐步下降。由于资本增加提升了生产效率,工资也逐步增加,劳动供给也随之增长。资本收益率初期由于生产效率的提升而提升,但是随着资本存量的增加,资本回报率逐步降低。随着劳动投入与资本存量的增加,总产出也得以增长,因而通货膨胀降低。由于资本回报率增加,在跨期消费替代弹性为2的设定下,人们大幅度减少当前消费,增加投资。在盯住债务和盯住产出与债务的规则下,由于政府债务的减少,刺激了政府消费,但是由于政府消费权重为0.1,替代弹性为0.25,因此政府消费对居民总消费的影响不大,反而由于政府支出增加的效应占优,导致最终税收收入增加,居民消费和总消费减少,因此盯住债务的规则导致了消费波动更大。
五、财政支出规则与居民福利本节进一步分析在系统受到外生冲击后,不同的财政支出规则组合对居民福利的影响。如前所述,不同类型的支出之间存在着规则配合问题,例如消费性支出规则的福利效应可能被投资性支出规则放大或抵消,因此当外生冲击发生后,在选择最优支出规则时,必须考虑不同支出类型的规则搭配问题。DSGE框架下的社会福利度量,比较准确的方法是对模型进行二阶近似,从效应函数中推导出居民福利损失函数,但是此种方法在居民效用函数设定复杂,系统内的摩擦较多时,难以推导出福利损失函数,因此该方法不具有普遍性④。本文采用Schmitt-Grohé和Uribe(2007)提出的消费等价法,即使用基准政策下居民愿意放弃的消费的比例来衡量备选政策导致的社会福利损失,消费等价法适用面广⑤,且测算结果精确,已经成为不同政策的福利水平比较的常用方法。
将三类财政支出规则均为平滑规则,设定为基准福利水平
| $ {W}_{0,t}={E}_{t}{\sum }_{j}^{\infty }{\beta }^{j}U\left({{C}_{0,t+j,}^{*}L}_{0,t+j}^{*}\right)={W}_{i,t}={E}_{t}{\sum }_{j}^{\infty }{\beta }^{j}U\left[\left(1+{\gamma }^{c}\right){{C}_{i,t+j,}^{*}L}_{i,t+j}^{*}\right] $ | (37) |
其中,上标*表示最优选择的消费和劳动。
基于t状态求得的补偿消费
| $ {E(W}_{0})=E{\sum }_{j}^{\infty }{\beta }^{j}U\left[\left(1+{\gamma }^{\mu }\right){{C}_{i,t+j,}^{*}L}_{i,t+j}^{*}\right] $ | (38) |
为了计算补偿消费水平,在本文的标准模型中引入居民福利值函数
| $ {W}_{t}=U\left({C}_{t},{N}_{t}\right)+\beta {E}_{t}{W}_{t+1} $ |
| $ =\frac{{\left({C}_{t}-{\chi }^{c}\stackrel-{{C}_{t}}\right)}^{1-{\sigma }_{c}}-1}{1-{\sigma }_{c}}-\frac{{\upsilon }_{0}{\epsilon }_{r,t}^{L}}{1+\dfrac{1}{{\upsilon }_{1}}}{L}_{t}^{\left(1+\frac{1}{{\upsilon }_{1}}\right)}+\beta {E}_{t}{W}_{t+1} $ | (39) |
因为效应函数具有可分性,引入两个辅助变量:
| $ {W}_{t}={W}_{t}^{C}+{W}_{t}^{L} $ |
其中:
| $ {W}_{t}^{C}={E}_{t}{\sum }_{j=0}^{\infty }\frac{{\left({C}_{t}-{\chi }^{c}\stackrel-{{C}_{t}}\right)}^{1-{\sigma }_{c}}-1}{1-{\sigma }_{c}}=\frac{{\left(C-{\chi }^{c}C\right)}^{1-{\sigma }_{c}}-1}{1-{\sigma }_{c}}+\beta {W}_{t+1}^{C} $ |
| $ {W}_{t}^{N}={E}_{t}{\sum }_{j=0}^{\infty }\frac{{\upsilon }_{0}{\epsilon }_{t}^{L}}{1+\dfrac{1}{{\upsilon }_{1}}}{L}_{t}^{\left(1+\frac{1}{{\upsilon }_{1}}\right)}=\dfrac{{\upsilon }_{0}{\epsilon }_{t}^{L}}{1+\dfrac{1}{{\upsilon }_{1}}}{L}_{t}^{\left(1+\frac{1}{{\upsilon }_{1}}\right)}+\beta {W}_{t+1}^{N} $ |
条件消费的补偿变化:
| $ {\gamma }^{c}={\left[\frac{{W}_{0}-{W}_{i}^{L}+\dfrac{1}{\left(1-\sigma \right)\left(1-\beta \right)}}{{W}_{i}^{C}+\dfrac{1}{\left(1-\sigma \right)\left(1-\beta \right)}}\right]}^{\frac{1}{1-\sigma }}-1 $ | (40) |
在具体计算时,采用模型二阶解的表现形式,假设模型以稳态为起点,无条件福利水平则直接用
| $ W=\bar{W}+\dfrac{1}{2}{g}_{\sigma \sigma } $ | (41) |
政府支出规则组合在技术冲击、劳动偏好冲击和投资效率冲击下的福利水平,具体如表3-表5所示。
| 消费 | 投资 | 无条件福利(长期效果) | 条件福利(短期效果) | ||||
| 转移支付 | |||||||
| 盯住产出 | 盯住债务 | 盯住产出与债务 | 盯住产出 | 盯住债务 | 盯住产出与债务 | ||
| 盯住产出 | 盯住产出 | −0.1449 | −0.1483 | −0.1467 | 0.8214 | 0.9328 | 0.9272 |
| 盯住债务 | −0.0842 | −0.0858 | −0.084 | 0.8653 | 0.9777 | 0.9722 | |
| 盯住产出与债务 | −0.0827 | −0.0842 | −0.0824 | 0.8622 | 0.9746 | 0.9691 | |
| 盯住债务 | 盯住产出 | 6.2947 | 6.821 | 6.8757 | −3.7752 | −3.0774 | −2.9645 |
| 盯住债务 | 6.5019 | 7.0521 | 7.113 | −3.5367 | −2.8242 | −2.6984 | |
| 盯住产出与债务 | 6.5179 | 7.0683 | 7.1303 | −3.4971 | −2.7834 | −2.6557 | |
| 盯住产出
与债务 |
盯住产出 | 7.3354 | 7.9272 | 7.9992 | −0.5251 | 0.319 | 0.4652 |
| 盯住债务 | 7.6513 | 8.2733 | 8.3542 | −0.0703 | 0.8036 | 0.9677 | |
| 盯住产出与债务 | 7.6883 | 8.3115 | 8.394 | 0.01 | 0.8872 | 1.0543 | |
| 注:表中“盯住产出”代表盯住产出的逆向调节规则,“盯住债务”代表盯住政府债务的逆向调节规则,“盯住产出与债务”代表同时盯住产出与债务的逆向调节规则。表中数字是以三类支出均采用平滑规则为基准政策,不同的政策组合与基准政策比较得到的福利水平的相对大小,下同。 | |||||||
| 消费 | 投资 | 无条件福利(长期效果) | 条件福利(短期效果) | ||||
| 转移支付 | |||||||
| 盯住产出 | 盯住债务 | 盯住产出与债务 | 盯住产出 | 盯住债务 | 盯住产出与债务 | ||
| 盯住产出 | 盯住产出 | 0.1226 | 0.1348 | 0.1336 | 0.1807 | 0.2028 | 0.2004 |
| 盯住债务 | 0.1258 | 0.1382 | 0.1371 | 0.1785 | 0.2007 | 0.1983 | |
| 盯住产出与债务 | 0.1256 | 0.1381 | 0.1369 | 0.1787 | 0.2009 | 0.1985 | |
| 盯住债务 | 盯住产出 | −1.6517 | −1.6627 | −1.6621 | −2.4017 | −2.4145 | −2.4135 |
| 盯住债务 | −1.6609 | −1.6718 | −1.6712 | −2.4152 | −2.4284 | −2.4274 | |
| 盯住产出与债务 | −1.66 | −1.671 | −1.6703 | −2.4137 | −2.4268 | −2.4258 | |
| 盯住产出
与债务 |
盯住产出 | −1.5031 | −1.5133 | −1.5128 | −2.2182 | −2.2304 | −2.2295 |
| 盯住债务 | −1.5118 | −1.5219 | −1.5213 | −2.2319 | −2.2444 | −2.2434 | |
| 盯住产出与债务 | −1.511 | −1.5211 | −1.5205 | −2.2303 | −2.2428 | −2.2418 | |
| 消费 | 投资 | 无条件福利(长期效果) | 条件福利(短期效果) | ||||
| 转移支付 | |||||||
| 盯住产出 | 盯住债务 | 盯住产出与债务 | 盯住产出 | 盯住债务 | 盯住产出与债务 | ||
| 盯住产出 | 盯住产出 | −0.1639 | −0.1763 | −0.1742 | −0.0187 | −0.0257 | −0.0226 |
| 盯住债务 | −0.1624 | −0.1749 | −0.1729 | −0.0183 | −0.0255 | −0.0224 | |
| 盯住产出与债务 | −0.1633 | −0.1758 | −0.1738 | −0.018 | −0.0251 | −0.0219 | |
| 盯住债务 | 盯住产出 | 1.703 | 1.7241 | 1.7217 | 0.532 | 0.545 | 0.5407 |
| 盯住债务 | 1.7179 | 1.7392 | 1.7368 | 0.54 | 0.5537 | 0.5492 | |
| 盯住产出与债务 | 1.7159 | 1.7372 | 1.7348 | 0.5377 | 0.5513 | 0.5468 | |
| 盯住产出
与债务 |
盯住产出 | 1.5094 | 1.528 | 1.5268 | 0.4783 | 0.4875 | 0.4855 |
| 盯住债务 | 1.5236 | 1.5424 | 1.5411 | 0.4851 | 0.4951 | 0.4928 | |
| 盯住产出与债务 | 1.5219 | 1.5406 | 1.5394 | 0.4834 | 0.4933 | 0.4911 | |
表3显示,当正向技术冲击发生时,如果政府消费采用盯住产出的逆向调节规则,补偿消费为负值,表明居民福利水平大于基准水平,但是条件福利水平小于基准水平;而政府消费采用盯住债务的逆向调节规则时,居民的无条件福利水平低于基准水平,而条件福利水平高于基准水平;当政府消费采用同时盯住债务和产出时居民福利水平最低。综合来看,无论何种政策组合下,居民总体福利水平均不如基准组合,表明当经济系统受到正向的外生技术冲击时,最优的政策为,三类支出均为平滑规则,而最劣的规则组合是三类支出均为盯住债务和产出逆向调节规则。
表4给出了当经济系统遭受劳动偏好负向冲击后,各类财政支出规则组合的福利水平。当政府消费选择盯住产出的逆向调节规则时,无论政府投资和转移支付采用何种规则,居民的福利水平均小于基准政策组合。当政府消费采用盯住债务和同时盯住债务与产出规则时,居民的福利水平均大于基准政策组合,而且不同的政府投资规则和转移支付规则虽然不改变定性的结论,但都具有定量的影响,按照无条件福利和条件福利的平均值对政策排序,福利水平最高的政策组合为三类支出均采用盯住债务逆向调节规则,福利水平最低的政策组合为,消费性支出-盯住产出逆向调节,投资性支出-盯住债务与产出逆向调节,转移支付-盯住债务逆向调节。上述结论为当前应对新冠疫情冲击提出的“适度扩大公共消费”提供了理论依据,但是还需要其他类型财政支出的进一步配合,方能发挥出政策的最优效能。
当经济系统受到外生的投资冲击时,表5给出了不同的财政支出组合的居民福利的相对大小。表5可见,只有在政府消费规则采用盯住产出逆向调节规则时,居民福利水平方才大于基准政策组合,综合考虑无条件福利和条件福利时,最优的支出组合规则是(补偿消费水平为−0.201),消费性支出−盯住产出逆向调节,投资性支出−盯住债务和产出逆向调节,转移支付−盯住债务逆向调节。最劣的支出组合规则是(补偿消费水平为2.293),三类支出均为盯住债务逆向调节规则。
六、关键性参数的进一步讨论如前文所述,政府消费性支出既包括政府的行政开支,也包括国防支出、一般公共服务支出,以及用于教育、医疗方面的民生性支出,如果民生性支出占比较大,则政府消费性支出和居民消费支出的替代弹性加大。在前面的分析和计算中设定
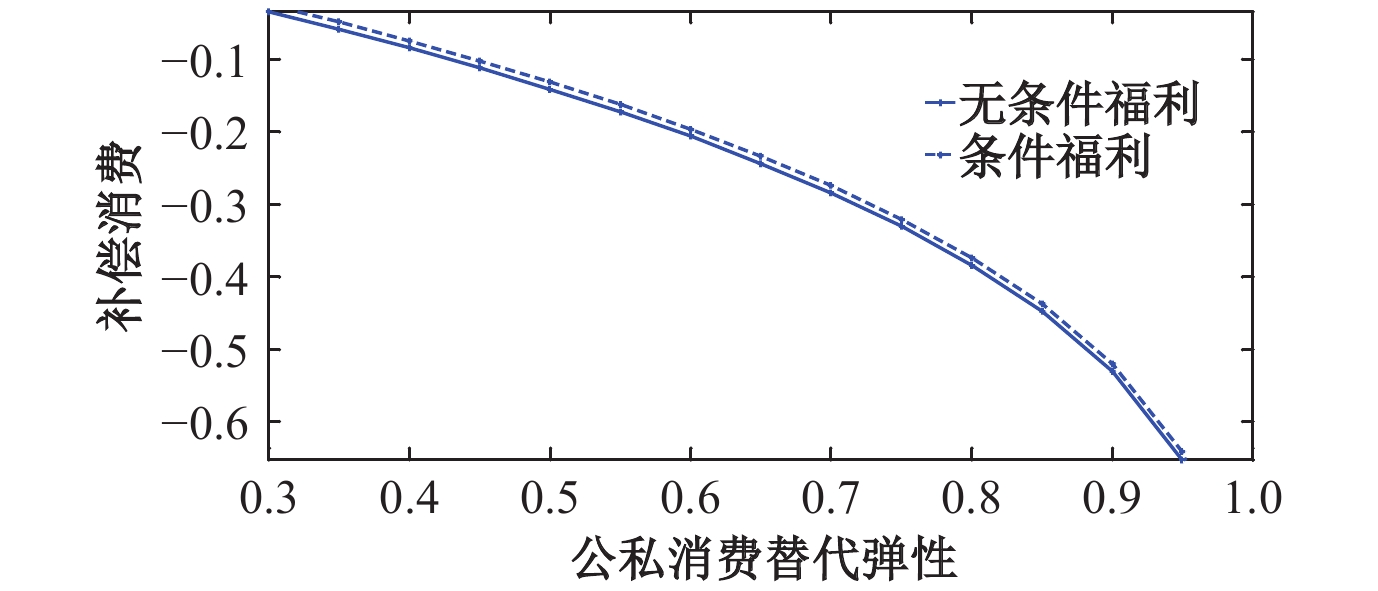
同样,如果保持冲击不变和财政组合规则不变,不同的
|
|
图 4
公私消费替代弹性
|
本文基于NK-DSGE框架,研究了当经济系统遭遇不同的外生冲击时,如何对政府消费性支出、投资性支出以及转移性支出实施差异性的政策规则,通过规则组合降低外生冲击对居民福利的不利影响,主要研究结论如下:(1)从抑制消费波动角度看,在生产技术或投资效率受到正向冲击时,平滑性支出规则为最优选择。在劳动偏好受到负向冲击时,盯住债务的支出规则为最优选择。(2)从居民福利最大化角度看,当发生正的技术冲击时,三类支出均采用平滑规则为最优组合;当发生负的劳动偏好冲击时,消费性支出采用盯住产出逆向调节,投资性支出与转移支付采用盯住债务与产出逆向调节;当发生正的投资效率冲击时,最优的规则组合为消费性支出采用盯住产出逆向调节,投资性支出采用同时盯住债务和产出逆向调节,转移支付采用盯住债务逆向调节。(3)本文验证了当增加公共消费与私人消费的替代弹性时,能够显著提升居民的福利水平。
本文的研究具有如下的政策启示:首先,当外生冲击发生时,需要根据外生冲击的性质,确定主要的财政支出方向及其支出规则,同时还必须考虑其他支出规则之间的相互配合。例如,本文模拟结果显示,当劳动供给受到负向冲击时,公共消费采用盯住产出的逆向调节对保障居民福利最为重要,这实际也为当前应对新冠疫情提出的“适度扩大公共消费”提供了理论依据,但是,研究也证实,投资性支出、转移支付采用盯住债务与产出逆向调节规则加以配合,能够进一步放大公共消费的效益.其次,政府在选择支出规则时,需要将冲击的作用渠道以及主要经济变量的变化方向,结合中国的实际情况加以定量分析。最后,本文对公共消费与私人消费的替代弹性检验表明,公共消费应当向私人消费替代弹性高的领域倾斜,增加环境保护、教育、医疗、养老、育幼等领域的公共消费,这能够直接提升居民福利水平。
① 由于居民劳动和工资存在异质性,因此预算约束方程中工资
② 王立勇和纪尧(2019)的文章中设定消费者风险规避系数为2,消费者风险规避系数与跨期消费替代弹性为倒数关系,即跨期消费替代弹性为0.5。
③
④ 也有一部分文献采用直接设定福利损失函数的方法,将模型直接设定为产出偏离稳态的值与通胀的加权和,此种方法较为简单,但是难以反映摩擦如何影响福利损失,此外权重的设定也具有一定的主观性。
⑤ 只有效用函数是关于消费和劳动可加可分的。
⑥ 由于篇幅所限,这里仅给出了技术冲击的详细结果,劳动冲击和投资冲击的结果,可向作者索取。
| [1] | 卞志村, 杨源源. 结构性财政调控与新常态下财政工具选择[J]. 经济研究, 2016, (3). |
| [2] | 高培勇. 复杂多变经济形势背景下的宏观政策抉择[J]. 财贸经济, 2013, (2). |
| [3] | 郭庆旺, 贾俊雪, 刘晓路. 财政政策与宏观经济稳定: 情势转变视角[J]. 管理世界, 2007, (5). |
| [4] | 刘尚希. 财政风险: 从经济总量角度的分析[J]. 管理世界, 2005, (7). |
| [5] | 吕冰洋, 陈志刚. 中国省际资本、劳动和消费平均税率测算[J]. 财贸经济, 2015, (7). |
| [6] | 潘敏, 张新平. 新冠疫情、宏观经济稳定与财政政策选择——基于动态随机一般均衡模型的研究[J]. 财政研究, 2021, (5). |
| [7] | 王国静, 田国强. 政府支出乘数[J]. 经济研究, 2014, (9). |
| [8] | 王立勇, 纪尧. 财政政策波动性与财政规则: 基于开放条件DSGE模型的分析[J]. 经济研究, 2019, (6). |
| [9] | 尹翔硕, 陈孝东, 肖康康. 财政政策与逆周期调控成效——基于广义财政刺激力度视角[J]. 上海经济研究, 2020, (2). |
| [10] | 张馨, 康锋莉. 中国相机抉择型财政政策: 时间一致性分析[J]. 管理世界, 2007, (9). |
| [11] | 张佐敏. 中国存在财政规则吗?[J]. 管理世界, 2014, (5). |
| [12] | 赵志耘, 刘晓路, 吕冰洋. 中国要素产出弹性估计[J]. 经济理论与经济管理, 2006, (6). |
| [13] | 周波. 基于我国省域面板的财政政策产出稳定效应研究[J]. 管理世界, 2014, (7). |
| [14] | 朱军. 开放经济中的财政政策规则——基于中国宏观经济数据的DSGE模型[J]. 财经研究, 2013, (3). |
| [15] | 朱军, 李建强, 张淑翠. 财政整顿、"双支柱"政策与最优政策选择[J]. 中国工业经济, 2018, (8). |
| [16] | Alfaro L, Kanczuk F. Fiscal rules and sovereign default[R]. NBER Working Paper Series, 2017. |
| [17] | Alvarez F, Jermann U J. Using asset prices to measure the cost of business cycles[J].Journal of Political Economy,2004,112(6):1223–1256. |
| [18] | Barro B J. Reputationina model of monetary policy with incomplete information[J].Journal of Monetary Economics,1986,17(1):3–20. |
| [19] | Beetsma R M W J, Jensen H. Monetary and fiscal policy interactions in a micro-founded model of a monetary union[J].Journal of International Economics,2005,67(2):320–352. |
| [20] | Ghosh S, Mourmouras I A. Endogenous growth, welfare and budgetary regimes[J].Journal of Macroeconomics,2004,26(4):623–635. |
| [21] | Guo J T, Harrison S G. Government size and macroeconomic stability: A comment[J].European Economic Review,2006,50(5):1339–1346. |
| [22] | Heer B. Public economics: The macroeconomic perspective[M]. Berlin: Springer, 2019: 162-163. |
| [23] | Jalles J T. Fiscal rules and fiscal counter-cyclicality[J].Economics Letters,2018,170:159–162. |
| [24] | Ji Y, Xiao W. Government spending multipliers and the zero lower bound[J].Journal of Macroeconomics,2016,48:87–100. |
| [25] | Jones J B. Has fiscal policy helped stabilize the postwar U. S. economy?[J].Journal of Monetary Economics,2002,49(4):709–746. |
| [26] | Kydl F E, Prescott E C. Rules rather than discretion: The inconsistency of optimal plans[J].The Journal of Political Economy,1977,85(3):473–492. |
| [27] | Lucas R E Jr. Macroeconomic priorities[J].American Economic Review,2003,93(1):1–14. |
| [28] | Mckay A, Reis R. The role of automatic stabilizers in the U. S. business cycle[J].Econometrica,2016,84(1):141–194. |
| [29] | Mukoyama T, Şahin A. Costs of business cycles for unskilled workers[J].Journal of Monetary Economics,2006,53(8):2179–2193. |
| [30] | Niemann S, Pichler P. Optimal fiscal policy and sovereign debt crises[J].Review of Economic Dynamics,2020,37:234–254. |
| [31] | Reuter W H. National numerical fiscal rules: Not complied with, but still effective?[J].European Journal of Political Economy,2015,39:67–81. |
| [32] | Schmitt-Grohé S, Uribe M. Optimal simple and implementable monetary and fiscal rules[J].Journal of Monetary Economics,2007,54(6):1702–1725. |

