
2020第22卷第5期
2.吉林大学 东北亚研究院,吉林 长春 130012
作为改善我国收入分配结构的一项重要的制度性安排,最低工资标准对于保障低收入阶层的基本生活水平和改善收入分配格局都具有促进作用(Cuong,2017;马双等,2012)。但不断上调的最低工资标准也在一定程度上改变了我国劳动密集型产业的国际竞争优势,相关产业订单逐渐被东南亚国家分流,国内一些劳动密集型企业开始转移至海外,尤其是在新冠肺炎疫情影响下,各国为了恢复经济会强化产业与投资竞争,低廉的劳动力成本成为一些发展中国家的重要竞争优势,这对我国产业的持续发展形成新的挑战。在此背景下,国家经济发展的战略重点也开始从“人口红利”支撑的劳动密集型产业转变为创新驱动的技术复杂型产业和多学科交叉的知识融合型产业,创新和技术进步正逐渐成为中国经济发展的核心驱动力。那么最低工资标准上浮是否必然倒逼科技创新?存在何种作用路径与微观机制?具有怎样的动态变化特征?厘清上述问题,对于把握创新型经济建设背景下的劳动力市场规制原则,重新认识创新发展与共享发展之间的关系具有重要的理论与实践意义。
最低工资标准会影响企业创新决策。基于要素替代效应(Hicks,1932),一些学者从理论与实证角度证实了最低工资上涨对企业研发的挤入效应。Antonelli和Quatraro(2014)指出,传统要素价格上涨可能会对创新和技术进步起到一定的反推作用;Riley和Bondibene(2017)认为,最低工资标准会迫使企业通过研发和创新活动以及新技术和新设备的引入来提高劳动生产率。要素替代效应、挤入效应和倒逼机制成为以往研究中最低工资标准推动科技创新的理论基础。然而,由于企业研发支出对其当期利润具有较强的敏感性,最低工资标准上浮意味着劳动力成本提升,可能会减少企业利润,并挤出企业研发与创新支出(Klasa等,2009;Matsa,2010)。李后建(2017)基于我国制造业企业数据研究发现,上调最低工资标准会抑制企业创新行为。从宏观角度来看,Koeniger(2007)研究发现,在国际贸易中最低工资规定会扭曲价格机制对创新的激励效应,即最低工资标准会弱化国际市场中非技术劳动密集型产品相对价格下降的创新效应。综上,现有文献对最低工资标准如何影响企业创新行为这一问题仍存在争议,需要进一步研究。
以往文献多基于企业层面数据进行实证分析。企业是科技创新的微观主体,也是创新成果产业化、商业化的重要平台,从企业层面考察最低工资标准对科技创新的影响具有合理性。但是,由于创新活动外部性特征的存在,不同企业创新活动往往存在较强的关联和溢出效应,并且任何企业的创新活动都依托于区域或产业创新系统,政府某项政策对单个企业或某一产业创新水平可能会产生一定的促进或抑制作用,而对整个城市、区域或全产业链创新而言,政府政策可能会产生相反的作用(李政和杨思莹,2018)。从实践层面来看,城市是创新活动的空间载体,城市创新体系建设对国家创新体系建设具有重要的支撑作用,建设创新型国家的前提是城市创新能力的显著增强,因此不能忽视城市层面创新活动的研究。
基于上述分析,本研究将在以下几方面有所创新:第一,从中观(城市)与微观(企业)两个层面更系统地分析最低工资标准的创新效应问题。不同于以往侧重于微观层面的研究,本文从城市层面探讨最低工资标准的创新效应,并通过匹配企业层面数据分析最低工资标准影响城市创新的微观机制,为宏观经济现象找到微观基础与微观证据。第二,探究最低工资标准对城市创新水平影响的持续性特征和动态特征。不同于以往静态分析,本文引入分位数回归模型,探讨随着城市创新水平的提升,最低工资标准对城市创新水平影响的动态轨迹,并且考察了最低工资标准对城市创新影响的持续性特征,丰富了最低工资标准创新效应的研究。第三,厘清最低工资标准对城市创新影响的宏观机制与微观逻辑。分析最低工资标准对科技创新的影响效果固然重要,但只有进一步厘清其内在机制,才能为深化理论研究与指导政策实践提供参考。一方面,本文基于中介效应模型分析了最低工资标准通过影响城市投资要素集聚进而影响城市创新的作用机制,从城市层面揭示了最低工资标准影响科技创新的作用机制;另一方面,通过微观机制分析,本文发现了最低工资标准对企业研发人力资本投入的挤出效应,为最低工资标准抑制城市创新奠定了微观基础。
二、理论基础与观点分歧企业是创新活动的主体,而最低工资标准的制定和调整与企业利润密切相关,并可能进一步影响企业创新决策。因此,以往文献通常将最低工资标准与企业创新结合起来进行考察,并形成了“倒逼论”和“抑制论”两种截然不同的观点。
(一) 最低工资标准倒逼科技创新“倒逼论”形成的重要理论前提是“要素替代效应”,即提高最低工资将导致企业用工成本增加,为此,企业往往用资本或者技术来取代劳动力,通过设备更新改造和研发创新提高企业劳动生产率,以降低最低工资标准对企业利润的挤压(Hicks,1932)。从市场竞争角度来看,面对最低工资标准上涨导致的低技能劳动者用工成本提升,为了保持竞争优势,企业尤其是劳动密集型企业往往投入高技能劳动者以替换低技能劳动者(Neumark和Wascher,1995),用先进技术和装备替代传统技术装备,以提高生产效率,降低生产成本。高技能劳动者和先进设备的投入意味着技术进步和创新可能性的提高。当然,这一作用机制也是建立在企业长期均衡且最低工资标准上浮不存在技能溢价的条件下。从理论上来讲,高劳动力成本提升企业创新激励的观点也有新古典经济理论和内生增长理论等诸多经典理论作为支撑,形成了一种具有坚实理论基础的学术观点。此外,从实证研究来看,Acemoglu(2010)、Vergeer和Kleinknecht(2007)、程晨和王萌萌(2016)等研究均发现,当用工成本提高时,企业倾向于用资本替代劳动力投入,用高技能劳动者替代低技能劳动者,并在这一过程中推动企业创新水平的提升。Broadberry和Cupta(2006)认为,高昂的劳动力成本是19世纪英美等工业国家科技创新和技术进步的重要驱动因素。
效率工资理论或偷懒模型是最低工资标准促进科技创新的另一个重要理论依据(Shapiro和Stiglitz,1984)。效率工资理论强调劳动者工资收入与其效率水平呈正相关关系,较高的工资标准促使工人提高生产效率。一方面,最低工资标准上浮在提高劳动者工资的同时,也会提高劳动者的工作努力程度,并激励低技能劳动者强化自身的技能学习,加强技能培训,以降低失业风险。Owens和Kagel(2010)研究发现,最低工资标准不仅提高了劳动者收入水平,也提高了劳动者工作的努力程度;黄德林和陈永杰(2014)研究发现,提高员工收入水平会使员工更能了解技能培训的重要性,并通过技能培训努力提高自身技能。另一方面,高工资也为劳动者参与职业技能培训创造了物质条件。此外,最低工资标准上浮也会激励企业对员工实施技能培训(Neumark和Wascher,2008)。一方面,企业在加强科技创新、推动技术进步和设备更新的同时,往往也加大了对高技能劳动者的需求,因此会加强员工技能培训;另一方面,为了更加充分利用员工人力资本和获取企业剩余,企业也将积极进行员工技能培训。强化企业员工技能培训能够为企业开展技术创新提供高技能人力资本,对隐性知识外化能力和对显性知识吸收能力具有明显的提升作用,并推动企业研发效率和科技转化效率的提升(Lichtenthaler,2009)。
从宏观层面来看,最低工资标准的制定意味着城市劳动密集型产业发展的不可持续。创新是经济发展的长期动力,为了推动城市经济可持续发展,地方政府往往将创新作为经济转型的重要着力点,从宏观战略方面引导创新型经济发展。Li等(2012)研究发现,中国当前劳动力成本优势逐渐丧失,从发展战略判断,中国更倾向于通过技术进步为经济可持续发展培育动力。由此可见,最低工资标准具有推动城市创新水平提升的微观理论基础与宏观政策取向。事实上,不同国家在上浮最低工资标准以保障低收入劳动者权益的同时,也伴随着国家创新能力的提升。基于上述分析,本文提出如下假设:
假设1a:最低工资标准会倒逼科技创新。
假设2a:最低工资标准会倒逼企业加大研发支出和人力资本投入,促进企业创新。
(二) 最低工资标准抑制科技创新正如许和连和王海成(2016)所指出的,资本和技术对劳动力的替代是有条件的,包括不同要素的供给弹性差异、企业所处的行业特征与市场竞争程度差异、不同产品等产量曲线间差异以及企业所面临的融资约束等。因此,最低工资标准的提升并不一定会倒逼企业创新,在其他条件不变的情形下,最低工资标准上浮会提高企业劳动力工资成本,挤出企业可能用于研发与创新的现金支出,不利于企业创新活动的开展。由于最低工资标准通过提高企业用工成本直接挤压企业利润,出于利润补偿动机,企业管理者可能会降低研发创新相关活动支出来弥补企业利润。出于规避风险的动机,具有风险厌恶特征的企业管理者当面对最低工资标准带来的利润挤压时,也会降低企业研发支出来保障企业现有的利润水平。这是由于创新具有高风险、易被侵权和强外部性等特征,尤其是在我国当前知识产权保护制度建设相对滞后的状态下,某一企业创新成果很容易被行业内部其他企业模仿、应用,减少本企业创新收益,导致企业创新活动的成本收益不匹配,从而抑制企业创新激励。因此,在最低工资标准挤压企业利润的情况下,保守的企业管理者往往会降低创新投入,以克服创新活动风险对企业利润带来的“二次挤压”。
从劳动者角度来看,最低工资制度虽然有利于保障低技能劳动者的收入水平,但在较为严格的监管条件下,最低工资标准的就业效应凸显,即最低工资标准往往导致低技能劳动者失业(Medrano-Adán等,2015)。正如孔东民等(2017)所指出的,一线员工在企业创新中也具有重要作用,一些专利想法多来源于一线员工的生产经验;Bradley等(2017)研究发现,底层员工往往是研发活动的后备支持人员,对企业研发绩效具有重要影响。由此可见,高技能劳动者和低技能劳动者之间存在着显著的知识溢出和技能互补,两者共同促进企业创新水平的提升(Parrotta等,2014)。因此,最低工资标准导致低技能劳动者失业,会使得企业内部不同技能劳动者比例失衡,降低了不同技能劳动者之间的知识互补、交流,不利于企业研发和创新。此外,依据组织公平理论(Adams,1965),最低工资标准强化了对低技能劳动者的保护力度,但也会影响高技能劳动者的组织公平感,降低高技能劳动者创新活动的积极性和努力程度,不利于企业创新水平的提升(王珏和祝继高,2018)。
从城市层面来看,最低工资标准的制定意味着政府对劳动力市场的干预,会在一定程度上扭曲劳动力市场运行机制,对创新要素配置效率产生负面影响。若最低工资标准显著高于城市劳动力市场均衡状态下的工资水平,一方面,这将使企业面临更加高昂的低技能劳动者用工成本,可能致使企业通过解雇部分低技能劳动者降低经营成本。如前所述,即使是低技能劳动者,其在企业创新活动中仍是不可缺少的参与主体,因此,最低工资标准上浮导致的不同技能劳动者就业失衡会抑制企业和城市创新水平提升。另一方面,基于心理攀比效应,最低工资标准的提升具有一定的溢出效应,在提高低技能劳动者工资的同时,也能促进高技能劳动者收入水平的提升(贾朋和张世伟,2013)。因此,最低工资标准的溢价效应抬高了企业创新活动成本,直接抑制企业创新激励,导致企业降低研发人力资本投入,从而不利于创新活动的开展。
此外,对于一个城市来讲,最低工资标准上浮的直接结果是劳动力成本的提高以及随之而来的招商引资难题,导致城市投资要素集聚能力下降,间接抑制城市创新水平的提升。投资为城市科技创新提供了资金保障,大量研究证实,投资能够有效促进创新活动的开展。陈思等(2017)、陆瑶等(2017)研究了风险投资对企业创新活动的影响,发现风险投资显著促进了企业创新水平的提升;李政和杨思莹(2019)研究发现,固定资产投资是企业进行固定资产再生产的重要方式,能够促进固定资产更新和改造,对城市创新活动具有重要的促进作用;Javorcik等(2018)的实证分析结果表明,外商直接投资能够促进东道国产品和技术创新。而最低工资标准上浮弱化了城市区位投资优势和投资集聚能力,甚至导致外资撤离和本地企业出走,进而抑制城市科技创新水平提升。基于上述分析,本文提出如下假设:
假设1b:最低工资标准会抑制科技创新。
假设2b:最低工资标准会挤出企业研发经费投入和人力资本投入,抑制科技创新。
假设3:最低工资标准会抑制城市投资要素集聚,不利于科技创新水平的提升。
三、研究设计 (一) 回归模型本文将就最低工资标准是否会影响科技创新这一问题展开研究。首先,为了对这一问题给出一个整体判断,本文设定如下回归模型:
| innoit=α0+α1wageit+αjXjit+vi+ut+εit | (1) |
式(1)基于城市面板数据考察最低工资标准对城市创新的作用效果。其中,inno表示城市科技创新水平;wage是本文关注的核心解释变量,表示城市最低工资标准额度,其回归系数反映出最低工资标准对城市创新水平的作用效果。X为影响城市创新水平的控制变量集合;
式(1)还考察了最低工资标准对城市创新水平条件期望E(inno|wage)的影响。为了进一步分析最低工资标准对城市创新水平影响的动态变化特征,即随着城市创新水平提升,最低工资标准对城市创新影响的动态轨迹,本文进一步设立如下分位数回归模型:
| innoit,q=α0,q+α1,qwageit,q+αj,qXjit,q+vi,q+ut,q+εit,q | (2) |
其中,q表示分位点,
对于科技创新水平的衡量,以往文献多从投入与产出两个角度进行测算,或基于创新投入指标与产出指标测算创新效率来衡量创新水平。囿于数据可获得性,本文从产出角度,基于城市专利申请数据考察城市创新水平。发明专利往往包含更高的科技与经济价值,并且在申请和授权等方面存在更高的门槛,因此,本文用城市人均发明专利申请量衡量城市创新水平,在稳健性检验中纳入其他专利类型。
最低工资标准是本文的核心解释变量,本文手工检索各地市劳动和社会保障局等政府官方网站,搜集整理了城市市区最低工资标准数据,并按照许和连和王海成(2016)的做法,对其取对数值作为城市最低工资标准的测度指标。若城市当年8月及其之前月份公布新的最低工资标准,则当年最低工资标准为新公布数值;若城市9月及其以后月份公布最低工资标准数据,则当年最低工资标准为年初数值,次年使用新公布的最低工资标准数值。
本文还依据城市创新活动特征,设定了影响城市创新水平的各类控制变量。外商直接投资对东道国科技创新会产生溢出效应和竞争效应两种不同影响,因此用实际利用外商直接投资额占GDP比重测度城市外商直接投资水平。科教资源是城市创新活动赖以开展的要素基础,用高等学校在校生人数占地区户籍人口数比重表示。金融发展既可能缓解城市创新活动所面临的融资约束,也可能对实体经济创新产生挤出效应,本文用银行存贷款余额与GDP的比值测度城市金融发展水平。经济规模扩张为科技创新提供了坚实的经济基础,会保障科技创新活动的要素供给,因此本文用地区生产总值的对数值表示城市经济规模。创业型经济发展为城市创新提供了良好的市场竞争环境,促进科技创新水平的提升,本文用私营和个体从业人员数与该城市户籍人口的比值表示城市创业活跃度。由于创新活动的外部性等特征,市场在配置创新资源过程中面临无效率或低效率问题,需要政府积极参与城市创新活动。因此,本文用财政科技支出占一般预算支出比重测度政府参与创新活动水平。政府规模扩张会在一定程度上挤出城市创新,本文用政府财政一般预算支出占地区生产总值比重表示地方政府规模。
本文样本为我国2003年至2016年278个城市面板数据。构建上述指标所涉及的数据中,城市发明专利申请量来源于中国研究数据服务平台,最低工资标准为手工检索各地政府官方网站并整理得到,其余数据皆来源于EPS数据平台。
四、最低工资标准对城市创新影响的实证检验 (一) 基准回归结果对式(1)进行估计,以检验最低工资标准对城市创新水平的作用效果,结果如表1所示。其中,回归(1)仅将最低工资标准作为解释变量,并基于双向固定效应模型进行估计,结果显示,最低工资标准的系数在1%的水平上显著为负,表明最低工资标准抑制了城市创新,与假设1b的预测一致。在回归(2)至回归(8)中,本文依次加入对外开放水平、人力资本水平、金融发展水平、城市经济规模、城市创业活跃度、政府科技支出和政府规模等指标,发现在所有回归结果中,最低工资标准对城市创新水平的系数始终在1%的显著性水平上为负,同样证实了假设1b。最低工资标准显著抑制了城市创新水平的提升,其原因可能包括诸多方面:第一,最低工资标准上浮挤压企业利润空间,并挤出企业研发创新支出;第二,最低工资标准存在溢价效应,其对研发创新人员等高素质劳动者工资水平也具有较强的提升作用,进而抬高企业创新成本,挤出企业研发人力资本投入,不利于企业创新;第三,从城市层面看,最低工资标准降低了城市投资区位优势,弱化了城市投资集聚能力,不利于城市固定资产新建和更新改造,对城市创新水平提升产生显著的抑制作用。本文将在后续研究中对上述三种机制进行检验。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| wage | −5.395*** | −5.044*** | −4.868*** | −4.867*** | −4.994*** | −3.620*** | −2.781*** | −2.751*** |
| (0.597) | (0.591) | (0.580) | (0.580) | (0.588) | (0.536) | (0.498) | (0.498) | |
| fdi | −34.81*** | −29.49*** | −29.51*** | −29.49*** | −16.72*** | −11.32*** | −10.24*** | |
| (3.497) | (3.467) | (3.469) | (3.469) | (3.182) | (2.959) | (2.969) | ||
| hum | 125.7*** | 125.9*** | 124.0*** | 84.40*** | 57.02*** | 55.20*** | ||
| (10.96) | (11.09) | (11.18) | (10.25) | (9.571) | (9.567) | |||
| finc | −0.0265 | 0.105 | 0.132 | 0.0236 | 0.139 | |||
| (0.199) | (0.223) | (0.202) | (0.188) | (0.190) | ||||
| lngdp | 0.769 | 0.254 | −0.638 | −0.836* | ||||
| (0.583) | (0.529) | (0.492) | (0.494) | |||||
| entre | 33.77*** | 29.03*** | 28.72*** | |||||
| (1.217) | (1.146) | (1.147) | ||||||
| g_tec | 171.5*** | 167.9*** | ||||||
| (7.092) | (7.149) | |||||||
| g_scale | −5.493*** | |||||||
| (1.504) | ||||||||
| constant | 31.39*** | 30.62*** | 28.38*** | 28.43*** | 17.44* | 14.96* | 23.44*** | 26.55*** |
| (3.454) | (3.411) | (3.356) | (3.376) | (8.984) | (8.154) | (7.570) | (7.606) | |
| Observations | 3890 | 3888 | 3888 | 3888 | 3888 | 3888 | 3888 | 3888 |
| R-squared | 0.214 | 0.235 | 0.262 | 0.262 | 0.262 | 0.393 | 0.478 | 0.480 |
| Number of city | 280 | 280 | 280 | 280 | 280 | 280 | 280 | 280 |
| 注:*、**、***分别表示10%、5%和1%的显著性水平,估计过程中控制了时间和个体双向固定效应,后续回归中除特殊说明外,均控制了双向固定效应。 | ||||||||
创新是一个复杂的过程,经济系统中诸多变量会影响科技创新效率和水平,如一个城市经济或政治制度在很大程度上影响科技创新水平,而囿于数据可获得性等原因,本研究无法控制创新系统中所有变量,这会导致本文前述估计结果在一定程度上面临遗漏变量问题。此外,创新水平与最低工资标准之间也可能存在一定的逆向因果关系,创新水平越高的地区,其居民收入水平也越高,并影响城市最低工资标准政策的制定。为了尽可能降低内生性问题对本研究结论造成的影响,本文将从以下方面进行处理:
首先,加入更多控制变量。为了避免遗漏变量问题,本文在前述回归的基础上进一步加入城市产业结构、经济发展水平、地区间竞争程度、信息化水平、城市人口密度、央地间财政关系等变量。具体而言:用非农产业比重衡量城市产业发展水平;用人均地区生产总值作为城市经济发展水平的测度指标;用各地区经济增速近似衡量不同地区间经济竞争程度;用城市人口数量与城市土地面积的比值衡量城市人口密度;用每万人均互联网使用户数近似反映信息化发展水平;用城市人均财政预算内支出占中央、省级和城市三者人均预算内支出之和的比重测度央地间财政关系。将上述变量代入式(1)进行估计,结果如表2中回归(1)所示。从中可见,最低工资标准的回归系数仍在1%的水平上显著为负,与前述结果一致。为了克服城市创新水平与各控制变量间可能存在的逆向因果关系,进一步将所有控制变量滞后一期,并代入式(1)进行估计,结果如表2中回归(2)所示。结果依旧表明最低工资标准显著抑制了城市创新水平的提升。
| (1) | (2) | (3) | (4) | |
| wage | −1.957***(0.466) | −2.184***(0.512) | −0.569***(0.055) | −9.248***(2.042) |
|
innot−1
|
0.969***(0.001) | |||
| constant | 9.233(7.807) | 0.364(8.636) | −1.388***(0.405) | 37.275***(10.717) |
| 更多控制变量 | 控制 | 控制 | 未控制 | 未控制 |
| 控制变量 | 控制 | 控制 | 控制 | 控制 |
| AR(1) | 0.0251 | |||
| AR(2) | 0.5868 | |||
| Anderson LM Stats | 253.207[0.0000] | |||
| Cragg-Donald Wald F Stats | 272.800{16.38} | |||
| Observations | 3878 | 3601 | 3610 | 3532 |
| R-squared | 0.560 | 0.541 | 0.436 | |
| Number of city | 278 | 278 | 278 | 278 |
| 注:回归(4)中,[ ]内为Anderson canon LM统计量的显著性水平,{ }内为Stock-Yogo检验10%的显著性水平临界值。 | ||||
其次,创新活动具有长期性和延续性特征,某一期创新活动往往是以前期创新活动为基础的,因此忽视前期城市创新水平对当期城市创新活动的影响必然会产生重要的遗漏变量问题。为此,本文在式(1)的基础上加入上一期城市创新水平作为解释变量,并使用系统广义矩估计方法进行估计,结果如表2中回归(3)所示。其中,最低工资标准的系数仍旧在1%的显著性水平上为负,表明最低工资标准抑制了城市创新,与前述结论一致。
以往研究中,工具变量法是解决内生性问题较为常用的方法。理想的工具变量要与误差项不相关,而与内生变量具有密切关联。出于区位投资竞争优势塑造等目的,某一地区制定最低工资标准时,除了考虑本城市内部低收入阶层生活水平等自身因素外,往往还会参照省内其他城市最低工资标准,以此作为本地区最低工资标准制定的重要依据。因此,省内其他城市最低工资标准是本城市最低工资标准制定的重要影响因素,但从理论上讲,省内其他城市最低工资标准并不会直接影响本地区城市创新水平,满足外生性要求。因此,本文选择该城市所在省份中城市最低工资标准最高档与最低档的均值作为工具变量,并基于两阶段最小二乘法进行估计,结果如表2中回归(4)所示。其中,最低工资标准的回归系数仍在1%的显著性水平上为负,说明最低工资标准显著抑制了城市创新水平的提升。此外,对工具变量的检验结果显示,不存在不可识别问题和弱工具变量问题。上述结果表明,控制了模型的内生性问题后,最低工资标准抑制城市创新水平的提升这一结论依旧成立。
(三) 稳健性检验1. 替换城市创新水平的测度方式。为了进一步检验最低工资标准抑制城市创新的结论是否稳健,本文首先变换城市创新水平的测度方式,即用人均三种专利申请总量作为城市创新水平的测度指标,结果如表3中回归(1)所示。从表3可以看出,最低工资标准对城市创新水平的回归系数仍在1%的水平上为负,与前述结果一致。此外,不同年龄专利在价值上也存在异质性问题,《中国城市和产业创新力报告2017》通过专利更新模型测算不同年龄专利价值,并加总到城市层面得到城市创新指数,该指数控制了专利年龄差异导致的价值异质性问题(寇宗来等,2017),本文以该指数作为城市创新水平的测度指标进行估计,结果如表3中回归(2)所示。其中,最低工资标准的系数显著为负,可见,最低工资标准在一定程度上抑制了城市创新水平的提升。
| (1) | (2) | (3) | (4) | (5) | |
| wage | −7.873***(1.226) | −13.81***(3.947) | −31.71***(9.674) | −8.348***(2.262) | −2.340***(0.446) |
| constant | 104.6***(18.74) | 102.5*(60.32) | 18.91**(7.619) | 19.74***(4.996) | 30.11***(6.824) |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 |
| Observations | 3888 | 3888 | 3843 | 3558 | 3426 |
| R-squared | 0.506 | 0.170 | 0.480 | 0.407 | 0.420 |
| Number of city | 278 | 278 | 278 | 278 | 245 |
2. 替换最低工资标准的测度方式。前述分析主要用各城市最低工资标准绝对值的对数值作为解释变量,本文将进一步采用相对指标进行估计。具体而言,本文用最低工资标准分别除以各城市城镇居民人均可支配收入和各城市农村居民人均纯收入,以此反映最低工资标准对居民收入的相对水平,并代入式(1)进行估计,结果如表3中回归(3)和回归(4)所示。其中,前者是最低工资标准与城镇居民人均可支配收入的相对水平对城市创新的回归结果;后者是最低工资标准与农村居民人均纯收入的相对水平对城市创新的回归结果。从回归系数可以看出,最低工资标准的相对指标回归系数均显著为负,与前述结论一致。
3. 调整样本。省会城市、直辖市和国家计划单列市相对于一般城市往往具有较高的居民收入水平和较高的创新水平,并且这些城市在创新资源集聚能力、创新政策获取能力、科技创新效率和水平等方面与一般地级市存在较大差异。因此,本文剔除省会城市、直辖市和国家计划单列市样本,并基于调整后的样本重新对式(1)进行估计,结果如表3中回归(5)所示。从中可见,最低工资标准的回归系数仍在1%的水平上为负,与前述结论一致。
(四) 动态特征检验本文还进一步考察最低工资标准对城市创新作用效果的动态变化特征,即选择0.1、0.25、0.5、0.75、0.9五个分位点,对式(2)所示回归模型进行估计,结果如表4所示。从表4可以看出,在不同分位点上,最低工资标准对城市创新水平的回归系数均为负,但在低分位点上该系数并不显著,说明在创新水平较高的城市中最低工资标准会显著抑制城市创新,而对于创新水平较低的城市,最低工资标准对城市创新的抑制作用并不显著。进一步观察不同分位点上的回归系数可以看出,当分位点低于0.75时,随着分位点的提高,最低工资标准对城市创新的回归系数绝对值逐渐增大,说明随着城市创新水平的提升,最低工资标准对城市创新的负面影响逐渐强化;而当分位点高于0.75时,即分位点为0.9时,最低工资标准对城市创新回归系数的绝对值又有所降低。可见,当城市创新达到一定水平时,最低工资标准对城市创新的抑制作用有所弱化。在0.75分位点上,最低工资标准对城市创新的回归系数绝对值最大,说明当城市创新达到该分位点所示创新水平时,最低工资标准对城市创新的负面影响最强。此外,本文还检验了不同分位点上最低工资标准的回归系数在统计上是否具有显著差异,结果显示,F=2.53,P=0.039,拒绝五个分位点上最低工资标准系数相等的假设。由此,本文得出初步结论,即随着城市创新水平的提升,最低工资标准对城市创新的负面影响逐渐增强;而当城市创新水平达到一定程度后,最低工资标准负面效应逐渐减弱。
| (1)
0.1分位点 |
(2)
0.25分位点 |
(3)
0.5分位点 |
(4)
0.75分位点 |
(5)
0.9分位点 |
|
| wage | −0.041(0.057) | −0.085(0.056) | −0.312***(0.081) | −0.365***(0.115) | −0.287***(0.110) |
| constant | 9.894***(3.350) | 12.522*(3.776) | 15.382***(5.783) | 32.878***(12.539) | 42.837***(6.467) |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 |
| Observations | 3888 | ||||
| R-squared | 0.236 | 0.303 | 0.416 | 0.606 | 0.796 |
为了进一步清晰刻画最低工资标准对城市创新水平影响的动态轨迹,本文重新基于分位数回归模型进行估计,并在此基础上画出各分位点最低工资标准对城市创新回归系数的动态变化图,如图1所示。从图1可以看出,当分位点较低时,最低工资标准对城市创新水平的抑制作用较弱;随着分位点提高至约0.65,最低工资标准对城市创新的回归系数逐渐变小,即最低工资标准对城市创新水平的抑制作用逐渐增强;而当分位点高于0.65时,随着城市创新水平提升,最低工资标准对城市创新水平的回归系数基本呈现出逐渐增大的变化特征,说明当城市创新水平超过0.65分位点时,最低工资标准上浮对城市创新的边际抑制作用逐渐减弱。依据图1可以得出如下结论:随着城市创新水平的提升,最低工资标准对城市创新的抑制作用呈现出先增强、后减弱的非对称V字形变化特征。
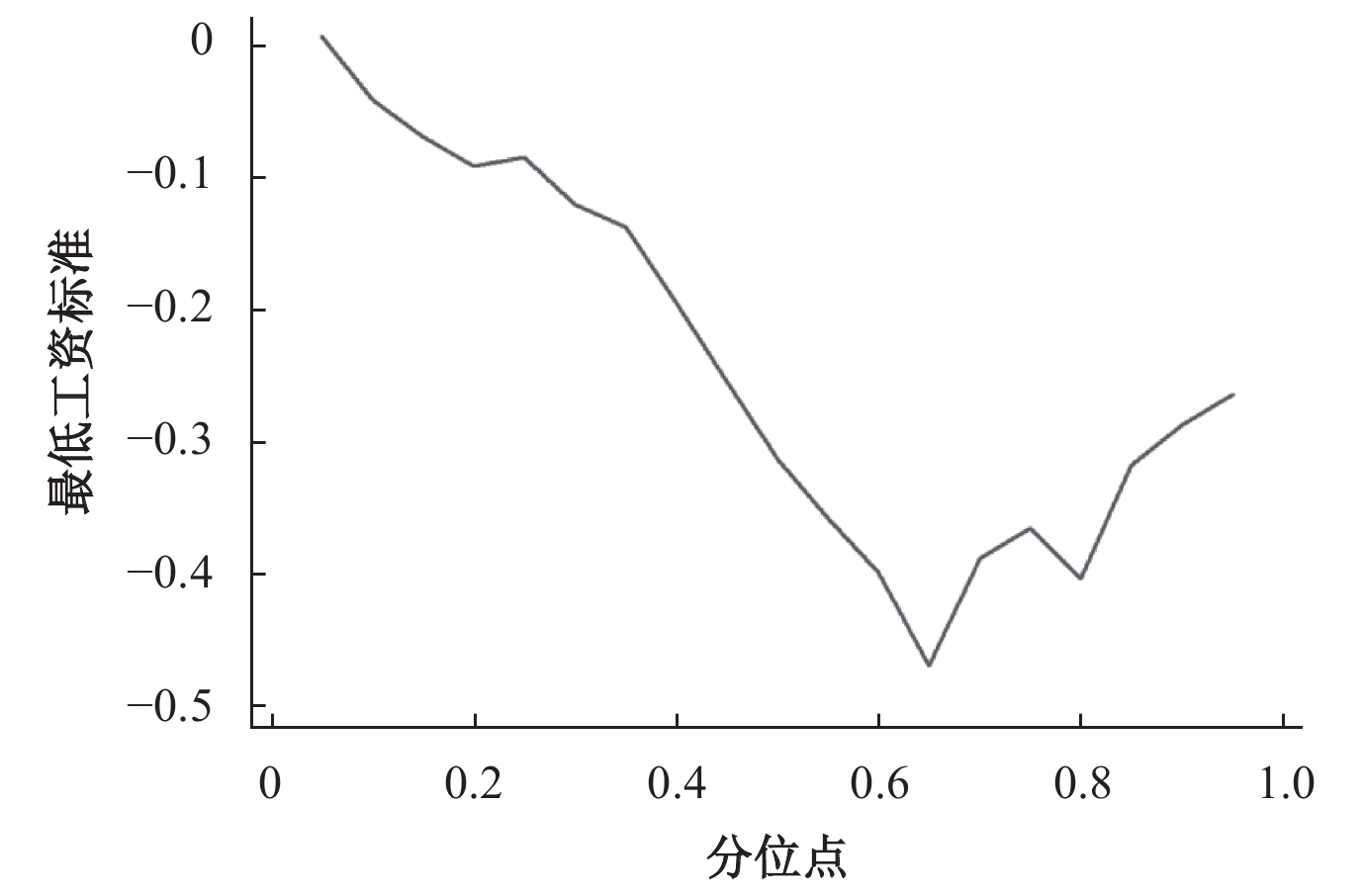
|
| 图 1 不同分位点上的回归结果图示 |
为了检验最低工资标准上浮对城市创新水平的影响是否具有持续性,本文进一步将最低工资标准这一变量做滞后一期处理,代入式(1)进行估计,结果如表5中回归(1)所示。从表5中可以看出,滞后一期的最低工资标准对城市创新水平的回归系数在1%的显著性水平上为负,这可能是由于最低工资标准对城市创新的影响具有滞后特征,或者是延续性特征。进一步控制最低工资标准的当期影响,结果如表5中回归(2)所示。从中可以看出,当期和滞后一期的最低工资标准对城市创新水平的回归系数均显著为负,说明最低工资标准对城市创新水平的影响具有一定的持续性特征。进一步检验滞后两期、滞后三期最低工资标准对城市创新水平的影响,结果如表5中回归(3)至回归(6)所示。从回归结果可以看出,最低工资标准对城市创新的影响具有可持续性特征,而且持续期至少为三年。
| (1) | (2) | (3) | (4) | (5) | (6) | |
| 滞后一期 | 滞后一期 | 滞后两期 | 滞后两期 | 滞后三期 | 滞后三期 | |
| wage | −2.349***(0.595) | −2.998***(0.664) | −3.243***(0.748) | |||
| Waget−1 | −2.628***(0.506) | −1.729***(0.554) | −0.982(0.659) | −1.468**(0.743) | ||
| Waget−2 | −2.845***(0.530) | −2.048***(0.575) | −1.318*(0.687) | |||
| Waget−3 | −2.397***(0.562) | −1.603***(0.597) | ||||
| constant | 25.73***(8.439) | 32.34***(8.585) | 28.60***(9.545) | 45.37***(9.938) | 20.50*(10.72) | 48.11***(11.33) |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| Observations | 3612 | 3612 | 3334 | 3334 | 3058 | 3058 |
| R-squared | 0.461 | 0.464 | 0.434 | 0.441 | 0.405 | 0.416 |
1. 城市产业特征。不同城市之间在产业发展、城市规模、融资约束等方面存在显著差异,并且这些特征差异可能会进一步导致最低工资标准对城市创新水平的作用效果存在空间异质性问题。因此,本文将考察在不同产业发展特征、城市经济规模、金融发展水平和私营企业创业水平下,最低工资标准对城市创新水平影响的差异化特征,结果如表6所示,其中,F表示上述城市特征变量。回归(1)考察了城市劳动密集型产业集聚程度对最低工资标准创新效应的调节作用。由于现有统计资料没有给出各城市劳动密集型产业的比重,因此,本文将城市全员劳动生产率作为城市劳动密集型产业比重的代理变量。其中,用私营和个体从业人员与单位就业人员数之和作为城市就业人口的替代指标,用地区生产总值除以城市就业人口来测算全员劳动生产率。将城市全员劳动生产率及其与最低工资标准交乘项代入式(1)进行估计,结果如表6中回归(1)所示。从表6可以看出,最低工资标准与全员劳动生产率交乘项回归系数在1%的水平上显著为正,说明全员劳动生产率正向调节最低工资标准对城市创新的作用效果,即劳动密集型产业占比越低,最低工资标准对城市创新的抑制作用越弱。这可能是由于以劳动密集型产业为主导产业的城市,其科技创新活动往往更容易受劳动力成本的影响,最低工资标准上浮更容易挤出企业研发投资,并对城市创新产生更大的抑制作用。
| (1) | (2) | (3) | (4) | |
| 城市产业特征 | 城市经济规模 | 金融发展水平 | 私营企业创业水平 | |
| lnincome | −2.691***(0.495) | −43.64***(1.991) | −6.398***(0.532) | −4.521***(0.412) |
| Lnincome×F | 0.003***(0.000) | 2.659***(0.126) | 2.066***(0.129) | 45.04***(1.092) |
| constant | 37.66***(7.738) | 258.6***(13.11) | 68.53***(7.799) | 24.52***(6.265) |
| 控制变量 | 控制 | 控制 | 控制 | 控制 |
| Observations | 3834 | 3888 | 3888 | 3888 |
| R-squared | 0.496 | 0.537 | 0.514 | 0.647 |
| Number of city | 278 | 278 | 278 | 278 |
2. 城市经济规模。一般来讲,城市经济规模越大,其创新型经济发展的经济基础就越好,最低工资标准对城市创新的抑制作用可能就越弱。为了验证这一判断,本文用地区生产总值的对数值测度城市经济规模,构建其与最低工资标准的交乘项,并代入式(1)进行估计,结果如表6中回归(2)所示。从中可以看出,城市经济规模与最低工资标准的交乘项回归系数显著为正,说明城市经济规模扩张会弱化最低工资标准对城市创新水平的抑制作用。这可能是由于大城市内部往往集聚了一大批创新型企业和高技能劳动者,并且创新已成为企业经营发展的主要驱动力,此时企业中高技能劳动者比例远远高于低技能劳动者,企业创新活动对低技能劳动者的工资弹性往往较小。因此,最低工资标准对大城市创新活动的抑制作用往往小于中小城市。
3. 金融发展水平。金融发展水平的提高可以在一定程度上弥补最低工资上浮给企业带来的研发资金缺口。本文将最低工资标准与城市金融发展水平的交乘项代入式(1)进行估计,以考察金融发展水平对最低工资标准创新效应的调节作用,结果如表6中回归(3)所示。其中,金融发展水平与最低工资标准的交乘项对城市创新水平的系数在1%的水平上为正,表明城市金融发展水平越高,最低工资标准上浮对城市创新水平的抑制作用越弱。这可能是由于创新型经济发展离不开金融支持,良好的金融服务能够缓解企业所面临的融资约束;在金融发展水平较高的城市,企业创新活动所面临的融资约束往往较低。当最低工资标准上浮带来的劳动力成本挤出企业可用于研发创新活动的资金时,企业可以通过外部融资方式弥补创新资金缺口,保障企业创新要素供给。因此,最低工资标准对金融发展水平较高城市的创新活动抑制作用较弱,而对金融发展水平较低的城市具有更强的抑制作用。
4. 私营企业创业水平。私营企业与国有企业在创新激励与约束机制上存在差异,并可能进一步导致最低工资标准对创新水平的影响会随着城市私营企业所占比重不同而存在显著差异。本文用私营和个体企业从业人员数占户籍人口比重近似反映私营企业创业水平,并与最低工资标准相乘代入式(1)进行估计,结果如表6中回归(4)所示。从中可以看出,交乘项回归系数在1%的水平上显著为正,说明私营企业创业水平越高的地区,最低工资标准对城市创新水平的抑制作用越弱,这可能是由于国有企业在一定程度上面临委托代理问题,加之企业管理者任期限制及其在剩余索取方面的激励不足(程晨和王萌萌,2016),导致国有企业经营者在创新投入方面更具有成本弹性和风险弹性。而私营企业为了取得市场长期竞争优势,往往具有更强的创新激励,创新投入对企业劳动力成本的弹性相对较小,最低工资标准上浮对企业创新的抑制作用较弱。因此,私营企业创业水平较高的城市,最低工资标准对创新活动的影响较弱。
五、作用机制分析 (一) 微观机制考察最低工资标准影响城市创新的着力点在于其对企业创新决策的影响。为此,本文设立如式(3)所示的回归模型,并匹配我国全部A股上市公司数据与城市层面数据,考察最低工资标准对企业创新决策的影响。
| lnR&Dit=α0+α1wagent+∑γjControljit+vi+ut+εit | (3) |
其中,R&D表示企业研发投入水平,本文重点考察经费(R&D_e)和人员(R&D_p)两个关键要素;
本文选择企业开发支出的对数值、研发人员数量的对数值分别测算企业研发经费和人员投入水平。本文还控制了资产规模、员工数量、股权集中度、资产负债率、盈利能力、企业发展前景、企业现金流、企业所有权性质等影响企业研发决策的微观变量;企业创新的宏观环境变量包含影响城市创新的前述控制变量。企业资产规模、员工数量分别用总资产和员工总数的对数值表示;股权集中度、资产负债率、盈利能力、发展前景、现金流分别用前十大股东持股比例、负债总额与净资产的比值、企业净利润与总资产的比值、每年利润总额增长率、每股经营活动所产生的现金流净额表示;企业所有权性质为虚拟变量,国有企业为1,非国有企业为0。城市层面控制变量设定方式前文已经给出。本文所涉及的企业数据皆来源于Wind数据库。对式(3)进行估计,结果如表7所示。其中,回归(1)至回归(3)考察了最低工资标准对企业研发经费投入的影响,回归(4)至回归(6)考察了最低工资标准对企业研发人员投入的影响。
| 因变量 | (1) | (2) | (3) | (4) | (5) | (6) |
| R&D_e | R&D_e | R&D_e | R&D_p | R&D_p | R&D_p | |
| wage | −0.003(0.610) | 0.185(0.616) | 0.270(0.637) | −0.099**(0.040) | −0.075*(0.040) | −0.071*(0.042) |
| constant | 4.427(4.034) | 21.32***(4.848) | 16.12(14.62) | 0.659**(0.258) | 0.169(0.332) | −0.258(0.843) |
| 企业控制变量 | 未控制 | 控制 | 控制 | 未控制 | 控制 | 控制 |
| 城市控制变量 | 未控制 | 未控制 | 控制 | 未控制 | 未控制 | 控制 |
| Observations | 8087 | 7982 | 7982 | 2023 | 2016 | 2016 |
| R-squared | 0.010 | 0.019 | 0.020 | 0.191 | 0.316 | 0.347 |
回归(1)仅将最低工资标准作为解释变量,并基于双向固定效应模型进行估计,结果发现,最低工资标准对企业研发经费投入的回归系数虽然为负,但并不显著。回归(2)和回归(3)在回归(1)的基础上依次加入影响企业研发决策的企业和城市层面的控制变量,结果依旧显示,最低工资标准对企业研发经费投入的回归系数并不显著。由此可见,最低工资标准对企业研发经费投入并不存在显著的挤出效应。回归(4)仅将最低工资标准作为解释变量,企业研发人员数作为被解释变量,结果显示,最低工资标准抑制了企业研发人员投入的增加。进一步加入影响企业研发决策的企业和城市层面控制变量后发现,回归(5)和回归(6)中最低工资标准的系数依旧在10%的显著性水平上为负,与前述结果一致。上述结果表明,最低工资标准并未显著抑制企业研发经费支出规模,但却对企业研发人员投入产生了显著的挤出效应。这可能源于最低工资标准上浮对高技能劳动者的溢价效应,正如刘贯春等(2017)所指出的,最低工资标准对技能溢价具有正向影响,最低工资标准上浮对高技能劳动者和高学历劳动者的收入具有更大的提升作用。这直接提高了企业研发创新活动成本,抑制了企业研发人力资本投入水平。
综合上述分析可见,最低工资标准会影响企业研发决策,抑制企业研发投入,并且这种抑制作用主要体现在对研发人力资本投入的抑制作用上,即最低工资标准具有溢价效应,提高了研发人员工资,并挤出企业创新相关的人力资本投入;但最低工资标准对企业研发经费投入并不存在显著的挤出效应。上述结论在一定程度上证实了假设2b。
(二) 城市要素集聚的中介效应最低工资标准上浮会影响投资要素的区位选择偏好,可能会导致城市投资集聚能力减弱,影响城市创新活动的要素供给,对城市创新水平产生负面影响。为了检验这一作用机制是否存在,构建如下中介效应模型:
| innoit=α0+α1wageit+αjXjit+vi+ut+εit | (4) |
| investmentit=β0+β1wageit+βjXjit+vi+ut+εit | (5) |
| innoit=γ0+γ1wageit+γ2investmentit+γjXjit+vi+ut+εit | (6) |
其中,式(4)中
| 因变量 | (1) | (2) | (3) |
| inno | investment | inno | |
| wage | −2.750***(0.498) | −0.035***(0.010) | −1.869***(0.438) |
| investment | 24.942***(0.763) | ||
| constant | 40.195***(9.297) | −0.019(0.179) | 39.718***(8.162) |
| 控制变量 | 控制 | 控制 | 控制 |
| Sobel test | −0.881***(0.240) | ||
| Bootstrap test(ind_eff) | −0.881***(0.252) | ||
| Bootstrap test(dir_eff) | −1.869***(0.399) | ||
| Observations | 3886 | ||
| R-squared | 0.809 | 0.860 | 0.853 |
本文基于我国城市与企业两个层面的数据检验了最低工资标准制度对科技创新的影响及其作用机制,并得出以下主要结论:(1)最低工资标准显著抑制了城市创新水平的提升,在控制模型的内生性问题以及通过变换主要变量、调整样本等方法进行估计后发现,这一结论依旧成立;并且随着城市创新水平的提升,最低工资标准对城市创新的抑制作用呈现先增强、后减弱的非对称V字形动态变化特征。最低工资标准对城市创新水平的影响具有一定的持续性特征,且持续期在三年或以上。(2)最低工资标准对城市创新水平的影响存在显著的空间异质性特征,会随着城市产业特征、经济发展规模、金融发展水平以及城市私营企业创业水平等因素的不同而呈现出差异化影响。(3)通过城市层面的机制分析发现,最低工资标准会抑制城市投资要素集聚,进而对城市创新水平产生显著的抑制作用,并且城市投资集聚的中介效应约占总效应的47%;通过企业层面的机制分析发现,最低工资标准会挤出企业研发人力资本投入,对研发和创新活动产生不利影响,而最低工资标准上浮对企业研发经费投入的影响并不显著。
当然,上述结论并非意味着最低工资制度存在的不合理性,相反最低工资标准已经成为改善我国收入分配格局、促进经济共享发展的重要制度保障。本文的启示在于,在追求经济发展成果全民共享的同时,应处理好公平与创新之间的关系,降低最低工资标准对科技创新的负面影响。具体而言:首先,要依据城市经济与科技水平制定适宜的工资政策,适度、循序渐进地推动最低工资制度改革,降低最低工资政策对创新要素配置扭曲的程度,在保障正常科技活动的前提下科学制定最低工资标准;尤其是对以劳动密集型产业为主导产业的城市,以及金融发展水平较低、经济发展规模较小和市场化发展水平较低的城市,更应当审慎制定最低工资政策,工资标准调整幅度不宜过大、调整周期不宜过短。同时还可以通过推动产业转型升级、建立研发扶持基金、做大经济规模以及推动市场化改革等方式降低最低工资标准对城市创新带来的潜在负面影响。其次,应当进一步优化城市营商环境,提高城市引资强度,通过税收优惠、土地价格优惠等差异化政策弥补最低工资政策给城市引资带来的劳动力成本劣势,鼓励创新型企业在城市集聚,为城市科技创新奠定微观基础。最后,给予创新型企业一定的配套扶持政策,通过税收减免、人才补贴、创新奖励等方式缓解最低工资政策给企业带来的工资性成本负担,降低企业研发创新活动的人力成本,为科技创新奠定智力基础。此外,处理好创新与共享之间的关系,还应将提高低收入阶层收入水平内置于创新型经济发展过程中,促进创新成果的全民共享,实现科技创新与低收入阶层增收的有机统一。
| [1] | 陈思, 何文龙, 张然. 风险投资与企业创新: 影响和潜在机制[J].管理世界,2017(1). |
| [2] | 程晨, 王萌萌. 企业劳动力成本与全要素生产率: “倒逼”机制的考察[J].南开经济研究,2016(3). |
| [3] | 贾朋, 张世伟. 最低工资标准提升的溢出效应[J].统计研究,2013(4). |
| [4] | 孔东民, 徐茗丽, 孔高文. 企业内部薪酬差距与创新[J].经济研究,2017(10). |
| [5] | 李后建. 最低工资标准会倒逼企业创新吗?[J].经济科学,2017(5). |
| [6] | 林炜. 企业创新激励: 来自中国劳动力成本上升的解释[J].管理世界,2013(10). |
| [7] | 刘贯春, 张军, 陈登科. 最低工资、企业生产率与技能溢价[J].统计研究,2017(1). |
| [8] | 陆瑶, 张叶青, 贾睿, 等. “辛迪加”风险投资与企业创新[J].金融研究,2017(6). |
| [9] | 马双, 张劼, 朱喜. 最低工资对中国就业和工资水平的影响[J].经济研究,2012(5). |
| [10] | 王珏, 祝继高. 劳动保护能促进企业高学历员工的创新吗?[J].管理世界,2018(3). |
| [11] | 许和连, 王海成. 最低工资标准对企业出口产品质量的影响研究[J].世界经济,2016(7). |
| [12] | Acemoglu D. When does labor scarcity encourage innovation?[J].Journal of Political Economy,2010,118(6):1037–1078. |
| [13] | Adams J S. Inequity in social exchange[J]. Advances in Experimental Social Psychology,1965,2:267–299. |
| [14] | Bradley D, Kim I, Tian X. Do unions affect innovation?[J].Management Science,2017,63(7):2251–2271. |
| [15] | Broadberry S, Gupta B. The early modern great divergence: Wages, prices and economic development in Europe and Asia, 1500-1800[J].The Economic History Review,2006,59(1):2–31. |
| [16] | Cuong N V. Do minimum wage increases matter to firm profitability? The case of Vietnam[J].Journal of International Development,2017,29(6):790–804. |
| [17] | Javorcik B S, Lo Turco A, Maggioni D. New and improved: Does FDI boost production complexity in host countries?[J].The Economic Journal,2018,128(614):2507–2537. |
| [18] | Klasa S, Maxwell W F, Ortiz-Molina H. The strategic use of corporate cash holdings in collective bargaining with labor unions[J].Journal of Financial Economics,2009,92(3):421–442. |
| [19] | Koeniger W. Openness, wage floors and technology change[J]. The B.E. Journal of Macroeconomics,2007,7(1):1–26. |
| [20] | Li H B, Wu S Z, Xiong Y Y, et al. The end of cheap Chinese labor[J].Journal of Economic Perspectives,2012,26(4):57–74. |
| [21] | Lichtenthaler U. Absorptive capacity, environmental turbulence, and the complementarity of organizational learning processes[J].Academy of Management Journal,2009,52(4):822–846. |
| [22] | Matsa D A. Capital structure as a strategic variable: Evidence from collective bargaining[J].The Journal of Finance,2010,65(3):1197–1232. |
| [23] | Medrano-Adán L, Salas-Fumás V, Sanchez-Asin J J. Heterogeneous entrepreneurs from occupational choices in economies with minimum wages[J].Small Business Economics,2015,44(3):597–619. |
| [24] | Neumark D, Wascher W. Minimum-wage effects on school and work transitions of teenagers[J]. American Economic Review,1995,85(2):244–249. |
| [25] | Neumark D, Wascher W L. Minimum wages[M]. Cambridge: MIT Press, 2008. |
| [26] | Parrotta P, Pozzoli D, Pytlikova M. Labor diversity and firm productivity[J].European Economic Review,2014,66:144–179. |
| [27] | Riley R, Bondibene C R. Raising the standard: Minimum wages and firm productivity[J].Labour Economics,2017,44:27–50. |
| [28] | Shapiro C, Stiglitz J E. Equilibrium unemployment as a worker discipline device[J]. American Economic Review,1984,74(3):433–444. |
2.Northeast Asian Studies College,Jilin University,Jilin Changchun 130012,China


