
2019第21卷第6期
2.湖南大学 经济与贸易学院,湖南 长沙 410082
随着改革开放的逐步深入,中国经济已经成为拉动世界经济发展的主要动力,而近年来中国经济又呈现出“新常态”的发展趋势,经济结构加快转型升级。中国在经历市场化去产能调整经济结构后,设备更替和资本投资的增长速度呈现出较明显的朱格拉周期特征,即经济扩张与收缩交替的特征。2016年末,中国设备投资增长速度触底,而2017年设备资本投资增速有明显的回升现象,国泰君安宏观研究团队提出“全球可能正站在新一轮朱格拉周期的起点上”。同年10月,高盛、摩根大通等国际著名投行发布研究报告称,全球资本开支已触底回升。可见,新一轮全球朱格拉周期的判定得到了国际范围的认可,种种迹象表明中国正处于新一轮朱格拉周期的早期。因此,现阶段对中国朱格拉周期及与之相对应的设备制造业股价波动周期的关联性与变化规律进行研究,有望加深学术界对两个周期动态关联的认识,也可以为投资者调整长期投资策略、优化资产组合、提高投资回报提供参考。
国内外研究宏观经济与股票市场之间关系的文献为数不少,但专门研究朱格拉周期和设备制造业股价波动关联性的文献却十分少见。大部分研究宏观经济与股票市场关系的文献通常采用单一的时域或者频域分析方法。在时域分析方面,学者们运用最多的是传统时间序列模型分析法,研究结论主要有两种:第一种结论是宏观经济与股票市场之间存在正相关关系。早期对美国市场数据的研究发现,股票市场和宏观经济之间存在正相关关系(Fama,1990),且随着样本期长度的增加,股票市场波动与未来实际经济活动的相关关系越来越紧密(Schwert,1990)。当研究者进一步将研究对象扩大至44个国家和24个国家(地区),也得到了类似的结果(Demirgüç-Kunt和Levine,1996;Levine和Zervos,1996),而且在单独对英国、中国、印度等国市场的研究中也得到了证实(Morelli,2002;杨高宇,2011;Kumari和Mahakud,2015a;张红伟等,2017)。第二种结论是宏观经济与股票市场之间的相关性在发达国家和发展中国家存在差异。Harris(1997)对49个国家的数据进行研究发现,在发展中国家,股票市场与宏观经济之间没有显著的相关关系,而在发达国家,股票市场对经济增长具有显著影响;Filer(2000)利用64个国家的数据进行研究后也发现,虽然股票市场与宏观经济之间存在正相关关系,但这一特征在高收入国家中更明显,在中等收入与低收入国家则相对较弱;对中国股票市场发展和经济增长之间关系的研究也发现,两者之间不存在显著的相关关系,中国股票市场发展对经济增长的作用极其有限(谈儒勇,1999;朱东辰和余津津,2003)。
在频域分析方面,现有的研究方法主要有小波分析法与谱分析法两类,相关文献数量不多但结论基本一致,均发现宏观经济与股票市场之间具有显著的相关性。其中,董直庆和王林辉(2008a,b)以及黄华继和丁维(2009)均发现中国宏观经济和证券市场周期波动的关联性较高,而且黄继华和丁维(2009)还发现中国股票市场周期领先于经济周期。Uebele和Ritschl(2009)对德国第一次世界大战前的经济周期和股市周期关系的谱分析也发现两者之间具有密切相关性。
总体来看,现有研究成果具有以下几个特点:第一,关于宏观经济与股票市场之间关联性的研究结论,对发达国家的实证研究结果大多是两者之间存在显著的正相关关系,对发展中国家的实证研究结果分歧则较大。第二,现有文献通常以整体经济周期和股票市场为研究对象,极少对细分的经济周期和特定的行业股价波动进行研究,使得实证结论在制定投资策略方面的可操作性不强,影响了研究成果的实践应用价值。第三,绝大多数文献仅选取单一指标代表宏观经济和股票市场波动变化状况,如上述文献大多采用人均GDP、GDP增长率、居民消费价格指数等反映宏观经济波动,用股票市场平均收益率或单一股价指数等反映股票市场波动,而单一指标难以综合全面地反映经济周期或股票市场波动。第四,在实证方法上,大部分文献采用的是单一时域方法或者频域方法,无法避免这两类方法各自的局限性。
相比前人研究,本文主要有以下创新:第一,本文是针对细分的经济周期即朱格拉周期和与之相对应的设备制造业股价波动周期之间的关系进行实证研究,相比以往文献研究内容更具有针对性,在帮助投资者制定投资策略时也更具有可操作性。第二,针对前人采用的人均GDP、GDP增长率、股票收益率等单一指标缺乏针对性、不够全面等缺点,本文构建了全新的朱格拉周期综合指数和设备制造业股价波动周期指数,从宏观、行业、微观三个层面选择指标构建朱格拉周期综合指数,同时选择具有代表性的9个行业设备指数构建设备制造业股价波动周期指数,以确保实证结果更稳健可靠。第三,采用奇异谱分析方法,从时域和频域相结合的角度研究两类周期的特征及其联动关系,相对于传统方法而言,奇异谱分析方法不仅可以用于研究非线性和非稳定的时间序列,还可以从短而具有噪声扰动的数据中提取出更加具有代表性的周期性信号,具有良好的降噪效果,使得实证分析结果更科学准确,本文也是奇异谱分析方法在检验宏观经济周期与股票市场波动关联性上的一次新的尝试。本文余下部分安排如下:第二部分是理论分析;第三部分是朱格拉周期和设备制造业股价波动周期的综合指数构建;第四部分是朱格拉周期和设备制造业股价波动周期的奇异谱分析研究;最后是结论和建议。
二、经济周期和股票市场周期理论分析 (一) 经济周期理论和股市周期理论1. 经济周期理论
经济周期是指宏观经济运行中出现的经济扩张和收缩不断交替反复的周期性波动现象。一个完整的经济周期主要分为衰退、萧条、复苏、繁荣四个阶段,其中衰退和萧条可归为经济收缩期,复苏和繁荣属于经济扩张期,其转折点为峰顶和谷底。经济学家们按照经济周期长度将其分为四类:(1)基钦周期,周期平均长度为40个月,其驱动力是厂商的库存变动以及外生随机因素(Kitchin,1923)。(2)朱格拉周期,其周期长度为8年至10年,这种周期现象以企业设备的大规模更新和资本投资为主要驱动力(Juglar,1862)。(3)库兹涅茨周期,周期平均长度为20年,其周期性波动主要是因为国家房地产等建筑的投资建设推动了国家经济发展(Kuznets,1930)。(4)康德拉季耶夫周期,此循环周期长度为50年,其产生的根本原因被认为是科学技术的创新与进步以及经济中产业结构的变化(Kondratieff,1926)。
2. 朱格拉周期理论
朱格拉周期(Juglar Cycle)又称为中周期,其周期长度为8年至10年,是由法国经济学家Juglar于1862年提出的。他认为朱格拉周期主要由繁荣、危机和萧条这三个阶段构成,并认为这种周期性波动现象主要以国民收入、失业率和通货膨胀率等指标的波动为标志,而且此周期波动现象是以企业设备的大规模更新和资本投资为主要驱动力。固定资产更替使得资本投资增加,以获得企业产能的提高,因此促使企业得到更多的资本投资,更多的资本投资带来更多的需求以出售企业产能,但是由于资本投资的边际效应,每单位所收获的收益愈来愈小,使得企业投资者的积极性愈来愈低,从而减少资本投资,因此使得需求开始下降,导致企业产能过剩,资本投资则进一步减少,从而形成了经济活动有规律地扩张和收缩的周期变化,因此朱格拉周期也称为投资周期。
3. 股市周期理论
股票市场周期是指股票市场整体长期上涨和下跌波动交替出现、不断循环的过程,一般而言,就是牛市与熊市相互交替出现的周期性波动现象,设备制造业股价波动周期也是如此。当利好信息传入市场,股价指数开始上涨,此时买方多于卖方,股市人气不断高涨,股票市场价格上涨,交易额增加,股市随之进入牛市阶段;随着股票价格持续上涨,市场风险开始加大,股价上升空间变得有限,股票成交数量也难以继续增加,市场进入牛熊转换阶段;当利空消息频频传出时,股市人气开始下滑,卖方多于买方,股价不断走低,交易量持续下降,股市进入熊市阶段;股指继续盘桓在周期谷底,市场人气低迷,股价处于低位且波动小,成交量极低,直到股市出现新的生机,下一轮牛市到来。
(二) 朱格拉周期与设备制造业股价波动周期关联性的研究假设关于宏观经济与股票市场之间的相关性研究,目前对发达国家的研究结果基本一致,即两者之间存在显著的正相关关系,但对发展中国家的实证研究结果分歧较大。早期对中国宏观经济与股票市场相关性的研究,大多认为两者之间不存在显著的相关性(谈儒勇,1999;朱东辰和余津津,2003),但近期越来越多的研究发现,随着中国股票市场日渐成熟,两者之间的相关性越来越明显(董直庆和王林辉,2008a,b;杨高宇,2011;张红伟等,2017)。
根据朱格拉周期理论和股市周期理论,朱格拉周期波动对设备制造业股价波动的影响可分为两方面:一是通过直接影响设备制造业上市企业的经营状况及其周期性波动来影响其股票的市场价格(Campbell和Shiller,1989;Fama和French,2015);二是通过改变投资者的心理预期影响其资产的购买行为,从而间接影响设备制造业上市公司股票供需状况,导致股票价格发生周期性波动(Yang和Li,2013;石广平等,2016)。当全社会处于设备大规模更新换代时,企业会加大固定资产投资,朱格拉周期进入复苏繁荣阶段,此时生产力加速增长,设备制造业的产品需求也随之扩大,使得这类上市企业利润提升,股票收益率也随之上升;同时,居民收入增加,投资者对经济发展前景充满希望,从而加大对股票等有价证券的投资,股市交易活跃,股价上升;当企业固定资产等设备更替基本完成后,固定资产投资大幅缩减,朱格拉周期也随之陷入低谷,设备制造业企业利润下降,生产力不足,失业率上升,居民收入下跌,由此影响股票市场投资者信心,对相关上市公司股票的需求减少,导致股价下跌。此外,政府的宏观经济政策也会通过影响宏观经济运行而影响朱格拉周期波动,间接影响股市波动周期(张海波和谢德泳,2014)。
同时股票波动通过两条途径间接影响宏观经济状况。一是通过影响设备制造业上市企业的经营状况对朱格拉周期产生影响(Arellano等,2012;张文菲和金祥义,2019);二是通过影响股票市场投资效率和设备制造业的资源配置而影响全行业劳动生产率,进而影响经济增长质量,带动朱格拉周期波动(Pagano和Pica,2012)。当设备制造业上市公司的股票在市场上表现稳定、股票投资收益良好时,向投资者传递行业发展的积极信号,促使投资者加大对设备制造业股票的投资,充实行业内企业的发展资金,有助于相关企业发展,进而推动朱格拉周期进入繁荣阶段;当设备制造业上市企业的股票价格在市场上表现不佳时,市场收益率下降,投资风险随之增大,投资者对相关企业的股票失去信心,投资意愿下降,使得设备制造业企业融资成本提高,经营风险加大,从而对宏观经济增长产生负面影响,朱格拉周期波动也随之受到影响。Levine和Zervos(1998)指出股票市场流动性越好,越能有效地提高资源配置效率,对经济增长的作用就越显著。段鸿斌和杨光(2009)发现股票市场促进经济增长的基本途径之一是提高股票市场流动性,进而提高全社会投资效率。
综上所述,朱格拉周期是设备制造业股价周期性运行的内在基础,而设备制造业股价周期性的波动可以反映朱格拉周期的变化,并进一步间接影响朱格拉周期的波动。据此,本文提出如下假设:
假设1:中国朱格拉周期与设备制造业股价波动周期之间具有较强的关联性。
关于朱格拉周期与设备制造业股价波动周期之间的领先滞后关系,学界鲜有研究,但对经济周期与股价波动周期的领先滞后关系的研究成果却十分丰富。一类观点认为,宏观经济波动领先于股票市场走势,如Schwert(1989)认为宏观经济波动可以帮助预测股票和债券收益率的波动性;Flad(2006)发现宏观经济变量不仅可以衡量整体股票市场表现,而且还可以预测股票市场的波动性;丁志国等(2007)认为经济会先扩张、后引起股票市场的高波动,然后经济也总会先衰退、后引起股票市场的低波动;Kumari和Mahakud(2015b)利用VAR-GARCH模型研究表明宏观经济可以影响投资者情绪,并进一步对市场波动率形成显著影响。另一类观点却认为股价走势提前反映经济波动,如Fama(1990)认为股票市场对经济变动具有预测作用,而且这种预测作用随着时间的延长而更加显著;Domian和Louton(1997)发现股票收益可以预先反映宏观经济发展的状况,而且在股票市场下跌时,这种预测作用的效果会更显著、更迅速,甚至可以预测到未来经济的变动情况;Levine和Zerovs(1998)、黄华继和丁维(2009)均发现股市波动先于实际经济周期的波动,说明股票市场波动可以提前反映经济周期变化;郭琨等(2012)发现上证指数领先于GDP,而且2006年之后更加明显,说明我国股市已初现经济晴雨表的作用;Croux和Reusens(2013)指出股票价格对未来GDP的预测能力在股市波动平缓的时期较强,在波动剧烈的时期预测能力就较弱。
综上,大多数研究证明了股票市场是一国宏观经济的晴雨表,这一特征在成熟市场表现得更为明显。在中国,由于股票市场成立时间不长,市场发展尚不成熟,早期研究大多认为中国股市未能发挥晴雨表功能(朱东辰和余津津,2003;韩德宗和吴伟彪,2003;晏艳阳等,2004)。但随着市场规模的迅速发展和上市公司治理机制的日渐规范,近期研究发现中国股票市场运行效率不断提高,市场趋于有效(李志冰等,2017),也更能体现出经济的“晴雨表”功能(黄华继和丁维,2009;郭琨等,2012)。过去十年,高技术制造业、装备制造业、战略性新兴产业增加值的增速都持续高于工业整体水平,股权融资规模快速增长,股票市场中设备制造业类上市公司的生产规模和营业收入一直保持较快增长,整体实力也不断增强,涌现出一批优质龙头企业,使得该行业公司股份能够更灵敏地反映实体经济中整个设备制造业的生产和投资情况。据此提出如下假设:
假说2:我国设备制造业股价波动周期可以提前反映朱格拉周期变化状况。
三、朱格拉周期和设备制造业股价波动周期的综合指数构建 (一) 朱格拉周期综合指数的指标选取长期以来,资本投资是中国经济增长的主要动力,经济发展中的朱格拉周期特征较明显,而朱格拉周期主要通过固定资本投资和设备投资增速来揭示制造业在生产设备和基础设施等方面的循环投资活动,其中固定资产投资增速主要反映了宏观经济运行,而设备投资增速更多地反映了产业与微观层面的运行状况。在挑选反映朱格拉周期的经济指标时,以往文献大多是以单一指标描述经济周期甚至细分周期(如朱格拉周期)的波动情况,如Demirgüç-Kunt和Levine(1996)仅采用人均GDP代表宏观经济状况;朱东辰和余津津(2003)选取工业生产增长率作为经济增长指标,并以此反映经济周期;Croux和Reusens(2013)以GDP增速作为经济活动的衡量指标;刘晓曙和王婧(2015)对朱格拉周期的描述与计量也是以GDP增长率的变化来测度的。然而,每个细分经济周期所受到的驱动力不同,以单一指标描述经济周期难免有失偏颇,有必要从多角度、多方面选取指标来建立指标体系。
朱格拉周期波动现象是以企业设备的大规模更新和资本投资为主要驱动力的,而这两方面的活动会在宏观、产业和微观三个层面均有所体现。为更全面准确地刻画朱格拉周期,本文参考前人成果,从这三个层面共选取9个指标构建朱格拉周期综合指数。其中,宏观层面选取固定资产投资完成额、新增固定资产投资完成额和制造业固定资产投资完成额来反映中国固定资产投资增长情况(刘树成,1986;De Long和Summers,1992),这三个指标分别代表固定资产投资规模、发展速度及产业结构,可以较全面地反映宏观层面的固定资产投资总量及其变化情况。产业层面选取金属制品业工业增加值、通用设备制造业工业增加值和专用设备制造业工业增加值,用以体现行业内设备投资增速的具体情况。这是由于根据美国经济分析局和长江证券研究所的统计资料,工业设备作为一个大类可大致分为金属处理机械、通用机械和专业机械三类设备小类,这三类设备可用于制造大多数产品(包括耐用品和非耐用品),因此通过参考上述分类方面,在产业层面选取这三个指标的工业增加值,以体现设备投资增速的具体情况(安宇宏,2013)。微观层面选取金属切削机床产量、工业锅炉产量以及汽车产量,以反映工业设备的产量增速。根据朱格拉周期原理,由于技术创新及进步和原有设备折旧磨损等原因,经济发展过程中伴随着生产设备的更新换代,从而产生对生产设备的大量需求(Juglar,1862),因此工业设备的产量增速可以代表微观层面上制造业资本的支出意愿,而且这三个指标恰好可以与产业层面的三个指标相对应。综合起来,三个层面共9个指标构成了朱格拉周期综合指数的指标体系,能够较全面地描述朱格拉周期的波动状况。具体指标构成及其权重如表1所示。
| 综合指数 | 层面 | 指标 | 序号 | 权重 | 属性 |
| 朱格拉周期综合指数 | 宏观层面 | 固定资产投资完成额 | 1 | 0.129 7 | 正向 |
| 新增固定资产投资完成额 | 2 | 0.100 2 | 正向 | ||
| 制造业固定资产投资完成额 | 3 | 0.155 8 | 正向 | ||
| 产业层面 | 金属制品业工业增加值 | 4 | 0.126 6 | 正向 | |
| 通用设备制造业工业增加值 | 5 | 0.160 8 | 正向 | ||
| 专用设备制造业工业增加值 | 6 | 0.121 9 | 正向 | ||
| 微观层面 | 工业锅炉产量 | 7 | 0.045 8 | 正向 | |
| 金属切削机床产量 | 8 | 0.101 5 | 正向 | ||
| 汽车产量 | 9 | 0.057 6 | 正向 |
本文采用熵值法计算朱格拉周期综合指数中9个指标的权重。熵值法属于客观赋权法,利用各评价指标值之间的差异程度来确定权重系数,相对于主观赋权法,熵值法能够更客观、更准确地反映各指标在综合指数中的重要性,所以在经济学领域得到了广泛应用。由于产业层面的三类工业增加值数据最早可获得的时间为2006年,因此,本文的研究期间为2006年1月–2018年12月共156个月,相关数据为月度数据,所有数据均来源于东方财富Choice数据库和Wind资讯经济数据库。
(三) 朱格拉周期综合指数的测算将样本期间每月朱格拉周期综合指数得分绘制成曲线,如图1所示①。从波动趋势可以看出,在2006–2018年这13年中,考察期间第一个周期低点处于2009年4月,且有文献认为是中国第三轮朱格拉周期的最低点(刘晓曙和王婧,2015;刘金全和刘子玉,2019),对应2008年美国爆发次贷危机后蔓延至全球的金融危机,直接波及中国经济。之后得益于中国政府推出的4万亿投资计划,短期内资本投资迅速增加,设备需求扩张,曲线开始快速回升。考察期间的第二个低点处于2012年10月,在经历了前期4万亿投资计划的刺激后,投资的边际效用逐渐下降,宏观经济增速放缓,综合指数自2012年1月开始快速回落,并一直到2014年全年都保持较低水平,这可能是由于2012年中央八项规定的出台以及第二次地方政府债务审计工作对政府消费和投资形成的负面效应(魏加宁和杨坤,2016)。第三个新的低点出现在2016年6月,是中国第四轮朱格拉周期的最低点,随着4万亿投资计划拉动效应的消失,部分产业甚至出现了产能过剩,宏观经济增速继续放缓,使得综合指数自2014年底开始加速下滑,直到2016年6月降至最低点。随后,综合指数开始回升,在2017年5月达到一个小高点,但很快又逐步回落。这一期间的波动原因可能是由于自2016年开始的供给侧结构性改革实施去产能战略,大量设备更新换代形成了新增需求,而之后又受到设备投资边际收益递减规律的约束,综合指数开始下降。
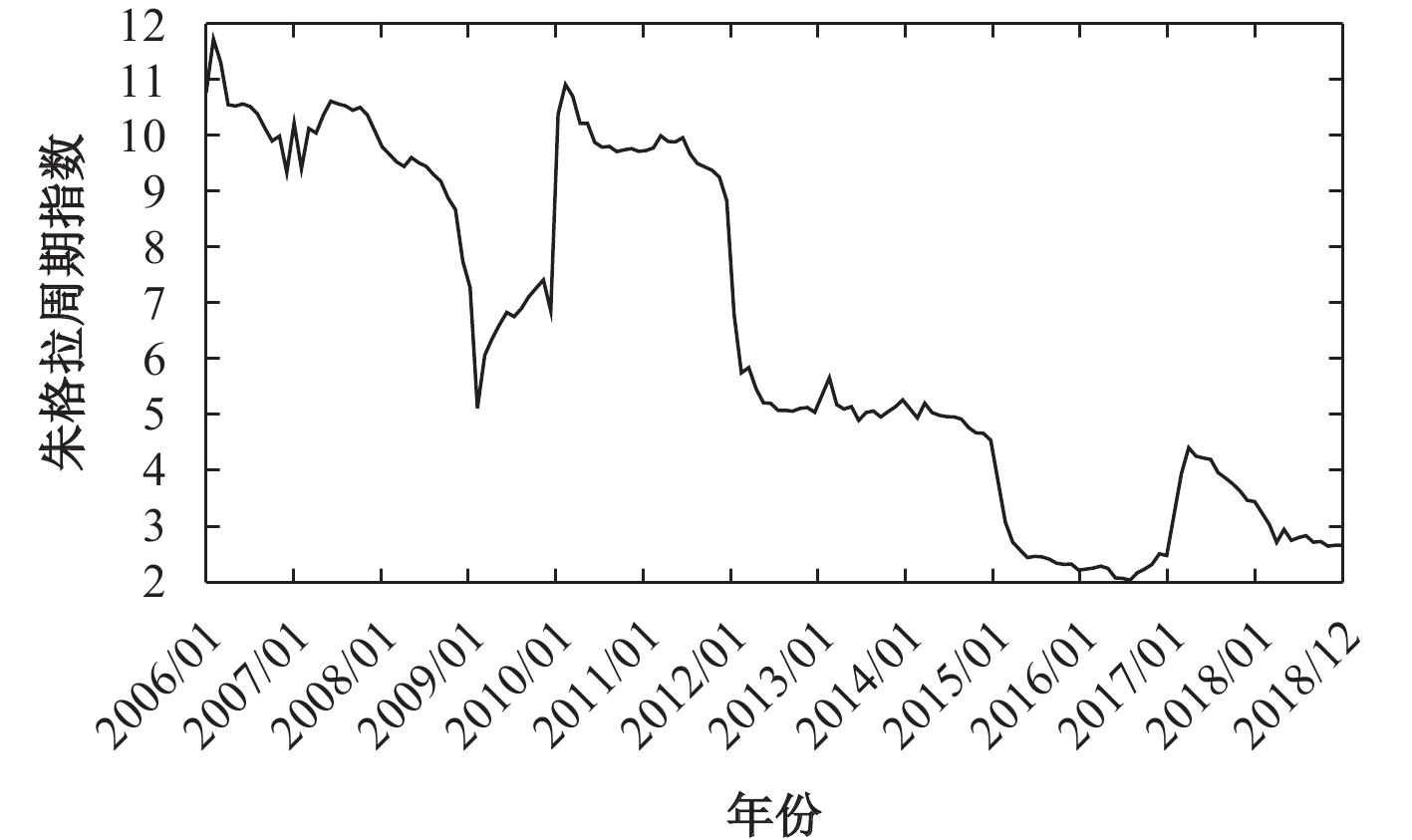
|
| 图 1 朱格拉周期综合指数走势图 |
朱格拉周期是以设备更新换代和资本投资为主要驱动要素的,也称其为设备投资周期,它是衡量宏观经济运行状况的重要指标并影响证券市场的运行轨迹。通常,设备制造业的产品范围主要包括机械、电子和兵器工业中的投资类制成品,依据申银万国行业分类法②,对应的一级行业包括电气设备、机械设备和通信计算机等。为准确描述设备制造业股价波动周期,需要选取有代表性的二级行业股价指数来编制周期综合指数。考虑到数据的可得性、代表性和连续性等问题,本文最终选取了9个设备制造业二级行业指数,仍然采用熵值法计算周期指数中各指标权重。指数名称及权重见表2。
| 综合指数 | 层面 | 指标 | 序号 | 权重 | 属性 |
| 证券周期综合指数 | 行业层面 | 电气自动化设备指数 | 1 | 0.107 0 | 正向 |
| 电源设备指数 | 2 | 0.098 1 | 正向 | ||
| 高低压设备指数 | 3 | 0.130 8 | 正向 | ||
| 通用机械指数 | 4 | 0.110 0 | 正向 | ||
| 专用设备指数 | 5 | 0.125 6 | 正向 | ||
| 运输设备指数 | 6 | 0.132 2 | 正向 | ||
| 其他交运设备指数 | 7 | 0.133 0 | 正向 | ||
| 计算机设备指数 | 8 | 0.067 4 | 正向 | ||
| 通信设备指数 | 9 | 0.096 0 | 正向 |
用熵值法计算得到的设备制造业股价波动周期指数轨迹如图2所示。从图2可以看出,样本期间设备制造业指数的周期性十分明显,经历了数次大涨和大跌,与上证指数的几次大起大落时点基本一致。在2006年全面启动股权分置改革、人民币持续升值的背景下,中国股市进入自市场成立以来的最大一轮牛市,设备制造业指数也快速上涨至历史高位。受到美国次贷危机爆发、股市泡沫破灭等因素的影响,2007年10月以后股市呈现断崖式下跌,设备制造业指数跌幅更深;随后为应对波及全球的金融危机,2008年中国政府推出了4万亿投资计划,促成了新一轮设备制造业牛市;随着投资边际效用的降低以及随之而来的宏观紧缩政策,这一轮牛市很快结束。2014年,中国深化体制改革全面启动,国有上市公司混合所有制改革进入深水区(张云等,2019),驱动大量场外资金涌入股市,设备制造业指数也迎来了新一轮的回升;而2015年年中,受场外配资清理、场内融资以及去杠杆等因素的影响,股市遭受连续暴跌,随后市场一直在低位徘徊。总体而言,在近十余年的几轮涨跌中,设备制造业指数的上涨和下跌幅度在绝大多数时间都大于上证指数的波动幅度,呈现出大起大落的特征。
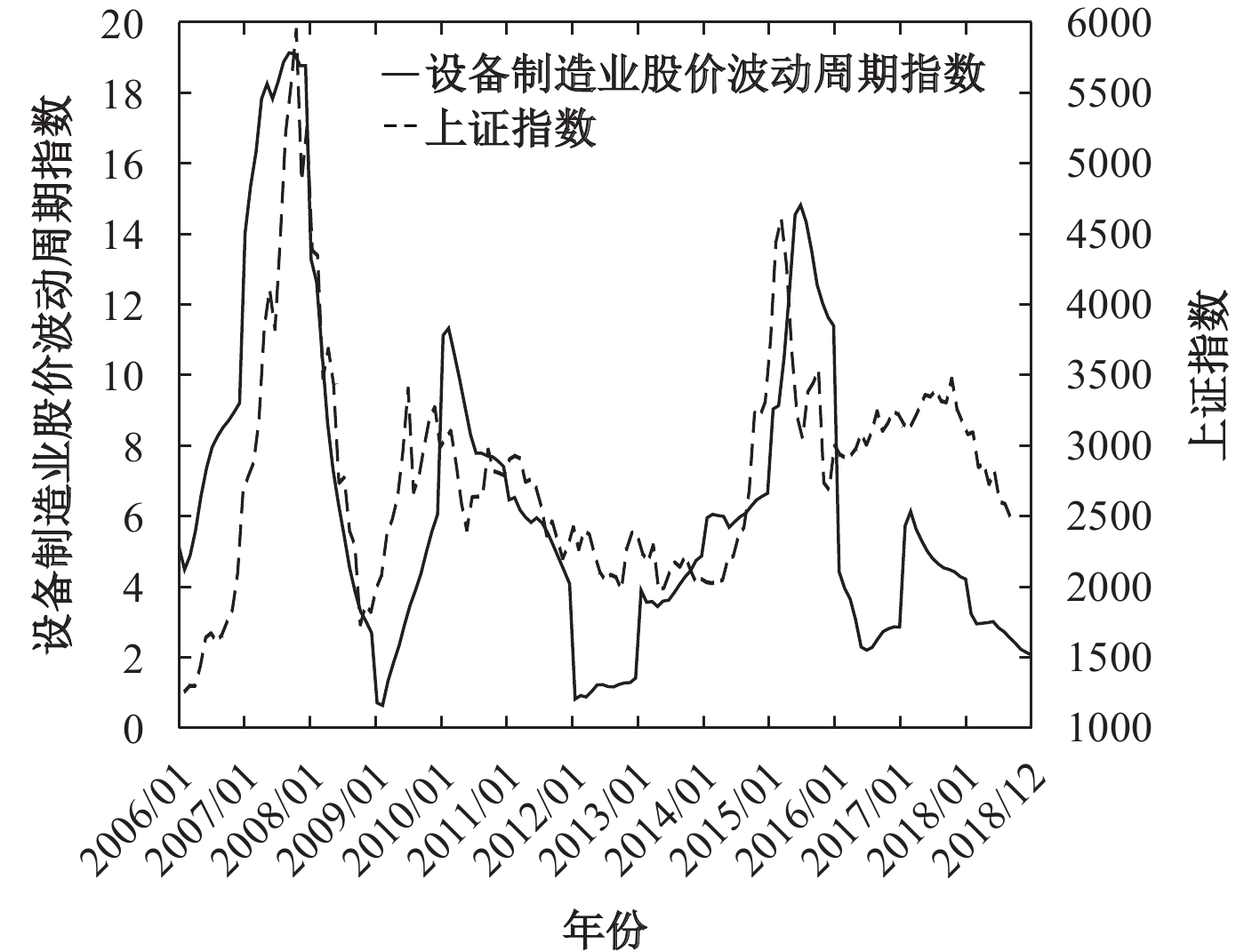
|
| 图 2 设备制造业股价波动周期指数走势图 |
奇异谱分析(Singular Spectrum Analysis,SSA)主要从时间序列中提取有效信息,并分解为不同的独立成分,如趋势项、周期项及噪声项,由此对时间序列的结构进行进一步研究与分析(Golyandina和Zhigljavsky,2013)。
传统的周期结构分析方法主要从时域或频域角度进行研究。虽然传统的纯时域法可以非常方便地测度周期长度、划分周期阶段以及研究周期之间的关系,但是不能区分周期中的不同成分,难以揭示经济周期与证券市场周期关联波动的本质。而传统的纯频域法可以研究不同频率阶段的各周期长度以及各周期之间的动态关系,弥补时域方法的不足,但是频域角度的方法对时间序列的要求比较严格,其要求所研究的时间序列是线性且平稳的,而经济周期和证券市场周期通常是一个非线性与非平稳的波动过程。
奇异谱分析方法是近年来发展起来的一种研究非线性与非平稳时间序列数据的时频域方法,它结合了时域和频域两种方法的优点,同时也弥补了两种方法的不足,具有以下优点:一是对时间序列的线性和平稳性不作强制要求;二是不需要提前设定时间序列的滤波周期,而是依据数据本身确定周期长度;三是不仅可以测算周期长度,而且可以描述周期的波动状况;四是此方法适用于期限短且噪声多的时间序列(Gonzalez等,2015);五是可以将时间序列依据不同的频率波动分解为趋势项、周期项和噪声项,并且可以测算不同的周期分量对原始时间序列的方差贡献率,重构分解后的周期序列,具有良好的降噪效果。目前,奇异谱分析主要应用于信息学、气象学等领域,经济领域应用较少,但近年来已有学者开始尝试。Patterson等(2011)利用奇异谱分析方法对英国GDP数据进行分析和预测。De Carvalho和Rua(2017)在奇异谱分析方法的基础上延伸拓展,对美国GDP进行实证研究与预测。郑小琴(2018)基于奇异谱理论对中国金融周期进行了测度。桂文林等(2018)运用奇异谱分析估计了中国实际季度GDP产出缺口,并比较了该方法与传统方法的优缺点。
奇异谱方法适合研究周期波动性行为,其算法的详细过程可参考文献(Vautard等,1992),主要分为以下四个步骤:建立轨迹矩阵、奇异值分解、分组、对角重构信号平均化。限于篇幅,这里不一一介绍四个步骤的具体算法,为便于读者理解实证部分两个周期相关系数的由来,这里仅说明奇异值分解原理。
奇异值分解(Singular Value Decomposition,SVD)为奇异谱分析四个步骤中的第二步,主要被用于提取两个要素场的耦合信号,研究两者的相关关系。奇异值分解原理如下(Kalman,1996):
设有两个要素场
| $ {C_{XY}} = X{Y^T} $ | (1) |
分别由左场
| $A = {L^T}X$ | (2) |
| $B = {M^T}Y$ | (3) |
使得两组新变量
| $\operatorname{cov} (A,B) = {L^T}CM = Max$ | (4) |
依据条件极值算法可以证明:
| ${C_{XY}}M = \delta L$ | (5) |
将式(5)写成矩阵形式为:
| ${C_{XY}}M = L\left( {\begin{aligned} & \Sigma &0 \\ & 0&0 \end{aligned}} \right)$ | (6) |
其中,
为了反映两个要素场的整体相关性,定义
| $R = \sum\limits_{i = 1}^r {\delta _i^2} $ | (7) |
并且定义第
| $SC{F_j} = \frac{{\delta _j^2}}{{\sum\limits_{i = 1}^r {\delta _i^2} }}$ | (8) |
1. 朱格拉周期和设备制造业股价波动周期的周期性分析
首先对原始序列利用X12方法进行季节性调整,去除季节性因素。然后对季节性调整后的时间序列进行对数增长化处理,以此研究经济和股市的增长率波动,再进行奇异谱分析。通过设定窗宽长度L=48,对中国朱格拉周期和设备制造业股价波动周期的时间序列分别建立轨迹矩阵,并进行奇异值分解,得到两者的奇异值和奇异向量,具体见表3和表4。由于序列过长,因此只展示累计至90%的奇异值。
| 序号 | 特征值 | 方差贡献率(%) | 累计方差贡献率(%) | 序号 | 特征值 | 方差贡献率(%) | 累计方差贡献率(%) | |
| 1 | 1.574 9 | 14.754 1 | 14.754 1 | 8 | 0.510 3 | 4.780 1 | 72.265 1 | |
| 2 | 1.418 7 | 13.290 2 | 28.044 3 | 9 | 0.441 7 | 4.138 3 | 76.403 4 | |
| 3 | 1.122 0 | 10.511 2 | 38.555 5 | 10 | 0.414 5 | 3.883 3 | 80.286 7 | |
| 4 | 1.057 8 | 9.909 9 | 48.465 4 | 11 | 0.397 1 | 3.720 0 | 84.006 7 | |
| 5 | 0.920 9 | 8.627 2 | 57.092 7 | 12 | 0.338 5 | 3.171 2 | 87.177 9 | |
| 6 | 0.558 9 | 5.235 6 | 62.328 3 | 13 | 0.249 8 | 2.340 6 | 89.518 4 | |
| 7 | 0.550 5 | 5.156 7 | 67.485 0 | 14 | 0.214 3 | 2.007 2 | 91.525 7 |
| 序号 | 特征值 | 方差贡献率(%) | 累计方差贡献率(%) | 序号 | 特征值 | 方差贡献率(%) | 累计方差贡献率(%) | |
| 1 | 4.320 2 | 11.514 1 | 11.514 1 | 10 | 1.635 2 | 4.358 0 | 73.699 3 | |
| 2 | 4.137 8 | 11.028 1 | 22.542 2 | 11 | 1.231 7 | 3.282 7 | 76.982 0 | |
| 3 | 3.811 2 | 10.157 5 | 32.699 6 | 12 | 1.158 0 | 3.086 2 | 80.068 2 | |
| 4 | 3.479 4 | 9.273 2 | 41.972 9 | 13 | 0.905 0 | 2.412 0 | 82.480 1 | |
| 5 | 2.517 8 | 6.710 5 | 48.683 3 | 14 | 0.867 3 | 2.311 4 | 84.791 5 | |
| 6 | 2.339 2 | 6.234 5 | 54.917 8 | 15 | 0.831 1 | 2.215 1 | 87.066 6 | |
| 7 | 1.906 2 | 5.080 3 | 59.998 2 | 16 | 0.803 9 | 2.142 6 | 89.149 1 | |
| 8 | 1.841 0 | 4.906 5 | 64.904 6 | 17 | 0.662 9 | 1.766 7 | 90.915 9 | |
| 9 | 1.664 7 | 4.436 7 | 69.341 3 |
依据奇异值和奇异向量提取周期成分并进行分组,通过借鉴De Carvalho等(2012),运用分解序列的周期波动性,结合朱拉格周期与设备制造业股价波动周期的周期性特点,以平均周期长度大于128个月的视为趋势项;在18个月至128个月之间的分解序列视为周期项;小于18个月的则作为噪声项。
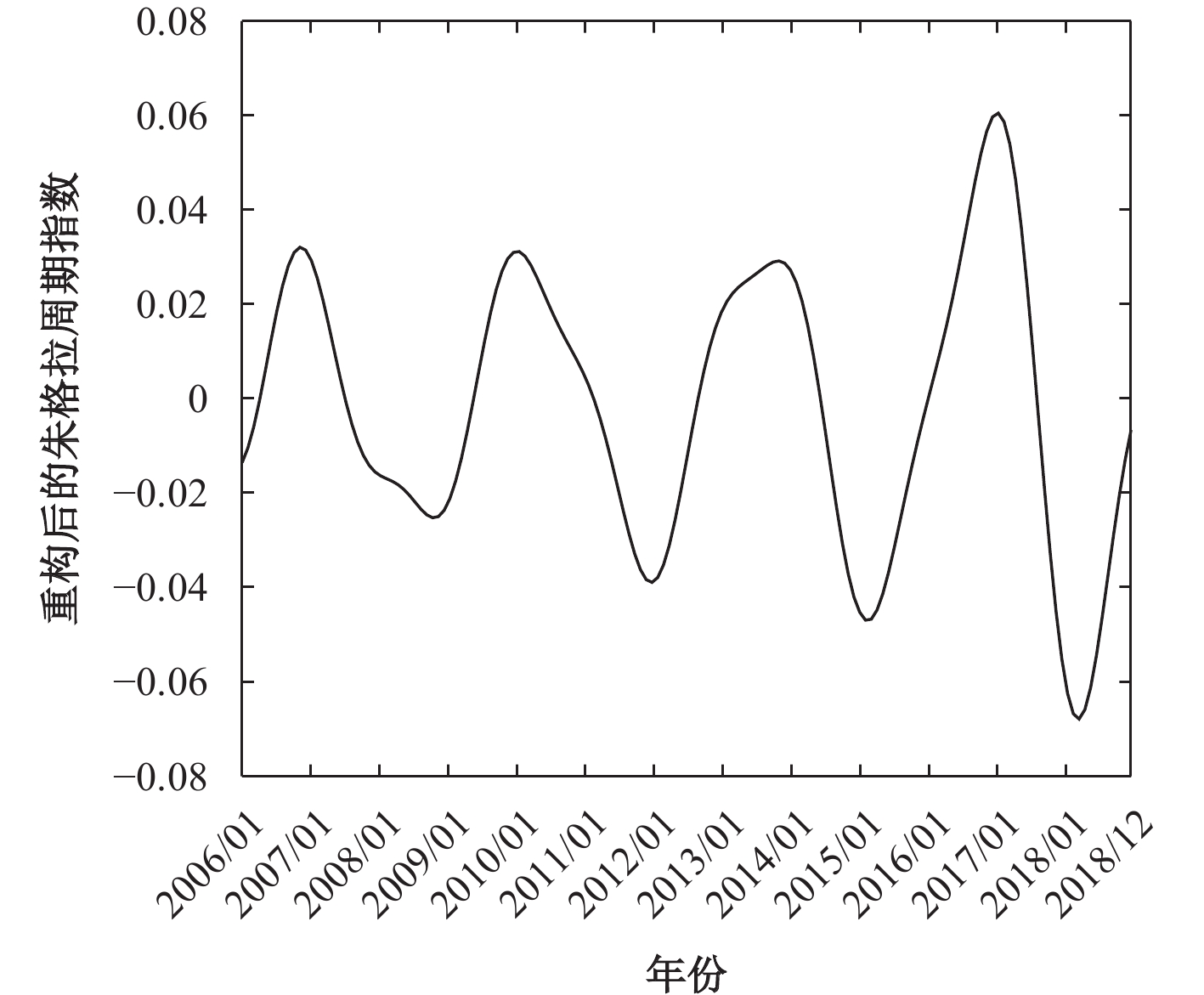
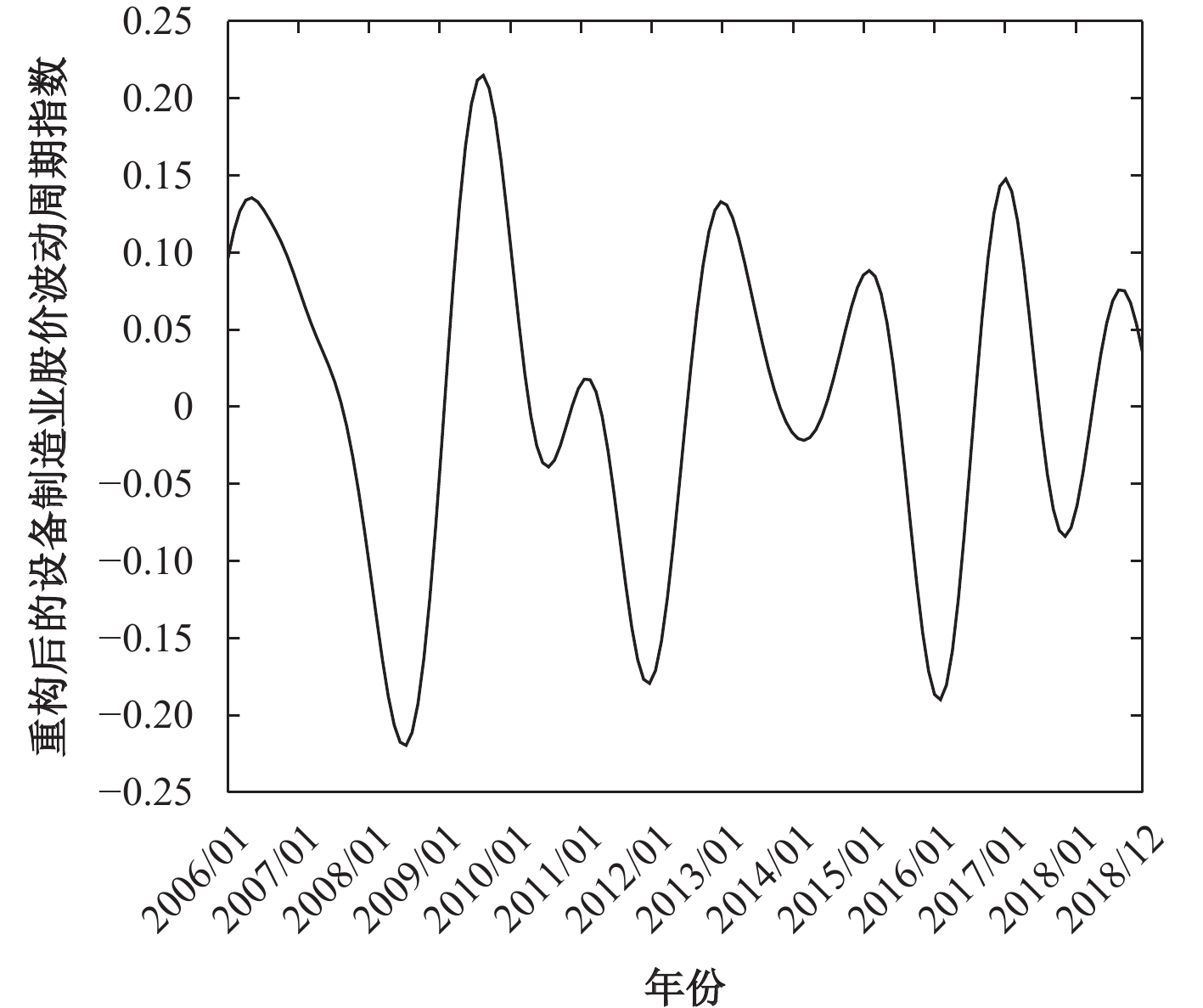
结合表5和图3可知,在朱格拉周期的前14个分解序列中,第5个分解序列的平均周期长度为155个月,大于128个月,所以将其作为趋势项,第1、2个分解序列的平均周期长度在18个月到128个月之间,因此将它们作为周期项,而剩余的分解序列则作为噪声项。结合表6和图4可知,在设备制造业股价波动周期的前17个分解序列中,第1、2、3、4、11个分解序列的平均周期长度在18个月到128个月之间,因此将它们作为周期项,而其他分解序列的周期长度小于18个月,故作为噪声项。通过对周期成分的分解序列进行对角平均化,得到朱格拉周期和设备制造业股价波动周期的周期序列,其周期项都具有一定规律的波动性,具体见图5和图6。
| 序列 | 均值 | 标准差 | 平均周期长度(月) |
| 1 | −0.002 0 | 0.019 33 | 38.750 0 |
| 2 | 0.000 3 | 0.011 9 | 38.750 0 |
| 3 | 0.001 3 | 0.009 7 | 17.222 2 |
| 4 | −0.000 6 | 0.009 2 | 17.222 2 |
| 5 | −0.008 7 | 0.004 7 | 155.000 0 |
| 6 | 0.000 1 | 0.005 0 | 9.117 6 |
| 7 | −0.000 0 | 0.005 4 | 9.117 6 |
| 8 | −0.000 3 | 0.003 9 | 9.117 6 |
| 9 | −0.000 0 | 0.003 5 | 14.090 9 |
| 10 | 0.000 0 | 0.003 5 | 7.381 0 |
| 11 | −0.000 0 | 0.002 6 | 7.381 0 |
| 12 | 0.000 0 | 0.003 3 | 14.090 9 |
| 13 | −0.000 0 | 0.001 8 | 11.923 1 |
| 14 | −0.000 0 | 0.001 9 | 11.071 4 |
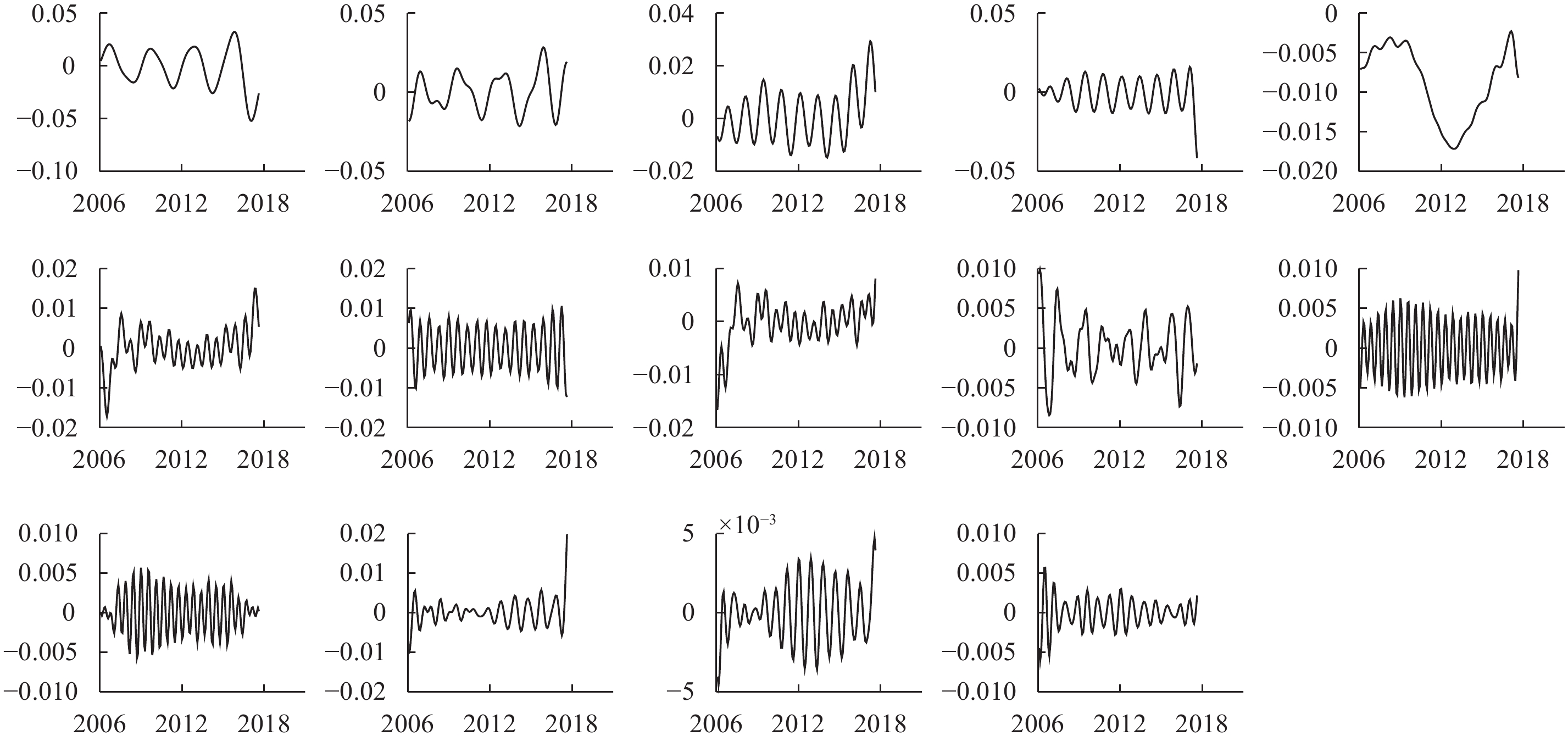
|
| 图 3 SSA方法对朱格拉周期的前14个分解序列 |
| 序列 | 均值 | 标准差 | 平均周期长度(月) |
| 1 | 0.005 5 | 0.044 7 | 38.750 0 |
| 2 | −0.000 6 | 0.032 4 | 22.142 9 |
| 3 | 0.003 7 | 0.035 6 | 22.142 9 |
| 4 | −0.002 3 | 0.021 3 | 51.666 7 |
| 5 | −0.005 1 | 0.023 1 | 17.222 2 |
| 6 | −0.000 1 | 0.016 3 | 15.500 0 |
| 7 | −0.000 4 | 0.017 3 | 9.117 6 |
| 8 | −0.000 0 | 0.012 4 | 9.117 6 |
| 9 | 0.000 0 | 0.011 2 | 7.045 5 |
| 10 | −0.000 0 | 0.011 9 | 7.045 5 |
| 11 | −0.004 7 | 0.009 1 | 77.500 0 |
| 12 | −0.001 0 | 0.006 0 | 14.090 9 |
| 13 | −0.000 0 | 0.006 5 | 6.200 0 |
| 14 | 0.000 0 | 0.005 2 | 6.200 0 |
| 15 | −0.000 2 | 0.005 5 | 11.923 1 |
| 16 | −0.000 2 | 0.004 7 | 10.333 3 |
| 17 | −0.000 2 | 0.003 5 | 5.961 5 |
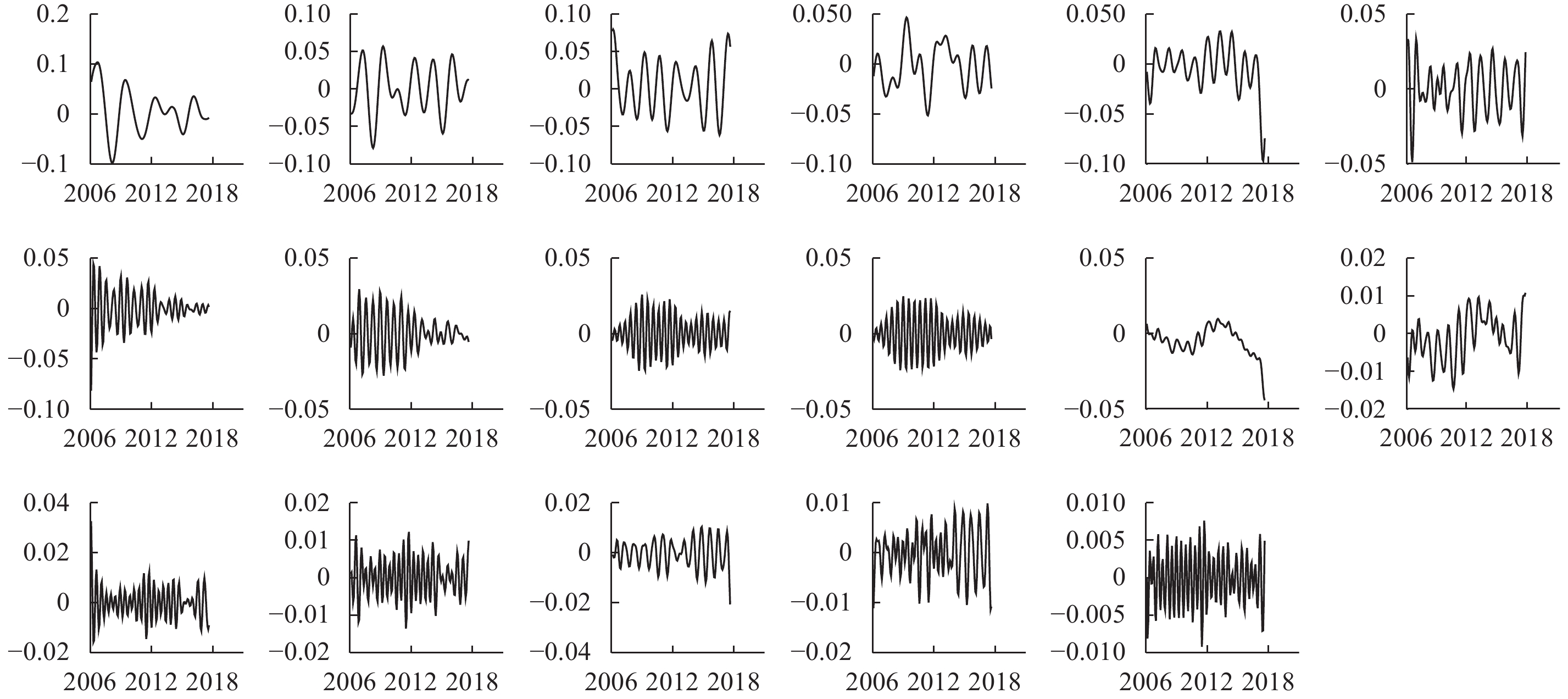
|
| 图 4 SSA方法对设备制造业股价波动周期的前17个分解序列 |
|
| 图 5 朱格拉周期重构后的周期项 |
|
| 图 6 设备制造业股价波动周期重构后的周期项 |
2. 朱格拉周期和设备制造业股价波动周期的相关性分析
根据前文的奇异值分解原理和相关系数推导公式(1)−(7),计算得出朱格拉周期综合指数与设备制造业股价波动周期指数的整体相关系数为0.635 2,说明两者具有较强的相关关系,证明了假设1。但这一相关性水平尚未达到高度相关,从侧面反映出中国朱格拉周期的周期性波动除了受设备制造业波动的影响外,还受到其他因素的影响。
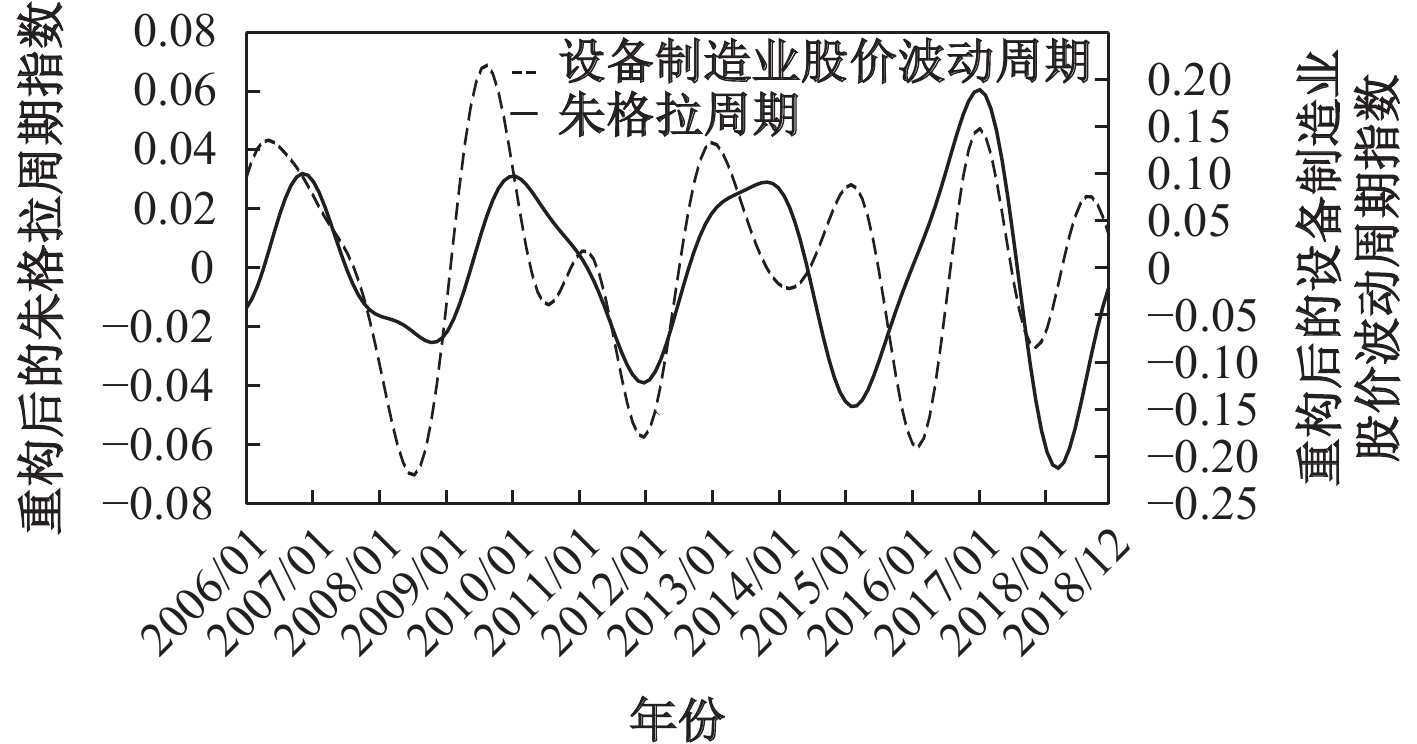
为了进一步观察两个周期的相关性特征,将两个周期指数走势图置于同一坐标图中,如图7所示。从波动幅度来看,朱格拉周期重构序列的耦合周期振荡相对平稳,但振荡幅度在2015年之后有所增强,而设备制造业股价波动周期在2009年前后最强,之后有所减弱。同时,设备制造业股价波动周期的振荡幅度大于朱格拉周期,说明中国的证券市场股价波动与宏观经济基本面变化相比更灵敏也更剧烈。从两个周期发生波动的先后关系来看,朱格拉周期指数的波动滞后于设备制造业股价波动周期指数,即设备制造业股价会提前反映朱格拉周期的未来走势。例如,在2006年6月、2008年8月、2009年9月、2013年1月、2017年11月等月份均为设备制造业股价波动周期的波峰或波谷③,而2006年12月、2008年11月、2010年2月、2013年11月、2018年3月等月份均为对应的朱格拉周期的波峰或波谷。可以发现,设备制造业股价波动周期波峰或波谷大多比朱格拉周期波动的波峰或波谷提前3−6个月出现,符合假设2的预期。例如,设备制造业股价波动周期于2006年6月达到样本期间的第一个波峰,朱格拉周期的第一个波峰则出现在2006年12月;2008年8月,设备制造业股价波动周期指数首次达到波谷,朱格拉周期指数的首个波谷出现在2008年11月等。可见,设备制造业股价波动周期指数提前3−6个月反映了朱格拉周期的未来趋势。从近两年来看,中国政府持续推进制造业转型升级,强调要增强制造业技术创新能力,以推动经济高质量发展,设备制造业股价波动周期指数在2017年年中降至低位后开始逐渐上升,2018年9月之后又出现小幅回落,而朱格拉周期指数在2018年初开始从谷底回升,全年都保持了持续上升。可见,中国宏观经济总体上已经度过了前两年经济探底时最低迷的时期,开始显示出回暖迹象,但设备制造业股价波动周期指数在2018年的回落也预示着宏观经济的回暖过程可能不会一帆风顺,是否会出现二次探底还有待观察。
|
| 图 7 重构后的朱格拉周期和设备制造业股价波动周期组合图 |
3. 结合奇异谱分析(SSA)与自回归分析(AR)进行周期波动预测
奇异谱分析(SSA)与自回归分析(AR)结合法是利用基于奇异谱分析方法分解重构后的周期项,再结合自回归分析方法构建预测模型,以此来预测周期在未来一段时期内的走势。由于通过SSA分解重构后的时间序列具有周期性强、噪音小等优点,据此构建的预测模型受随机扰动项的影响较小,具有良好的预测效果(高文婷等,2017)。
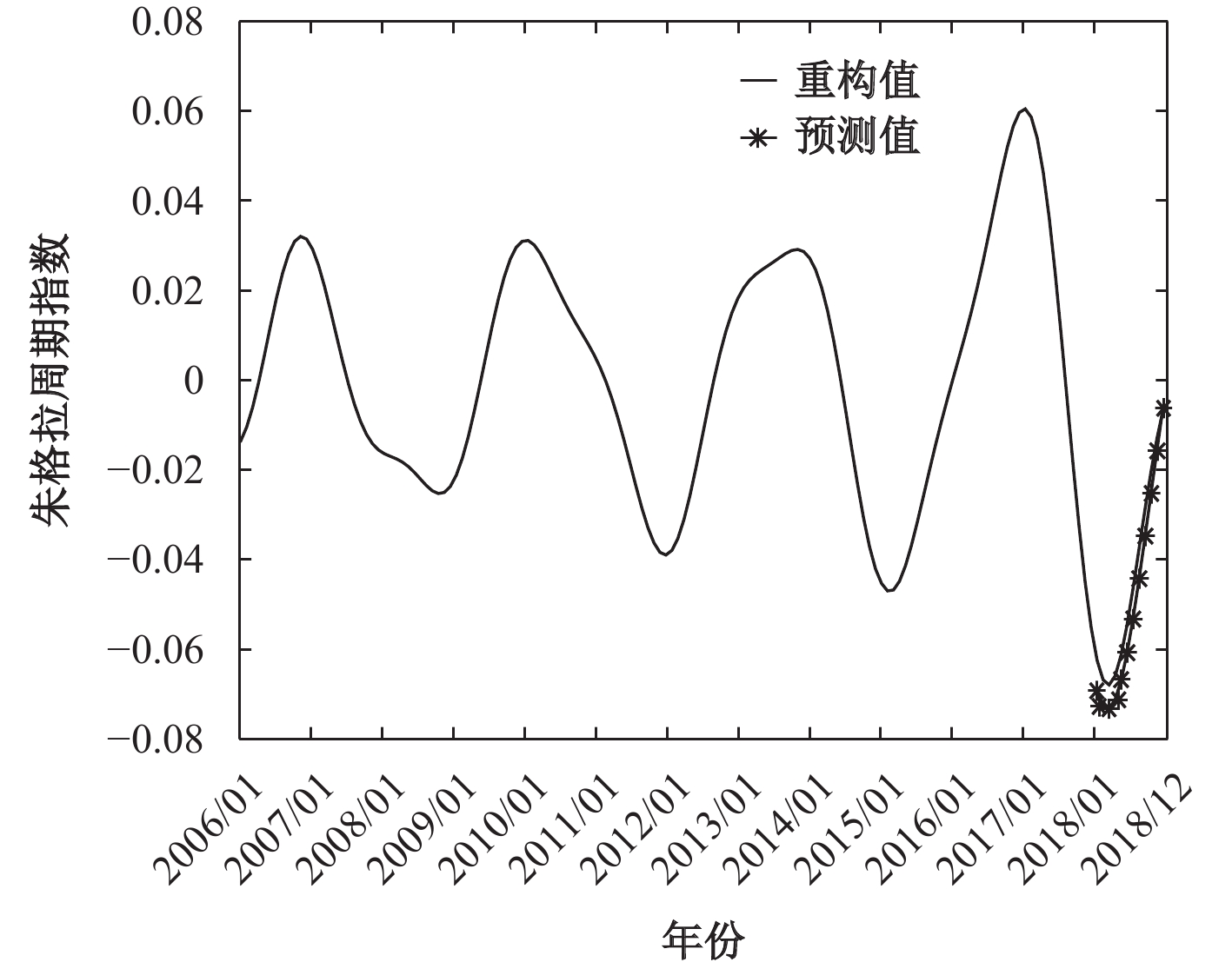
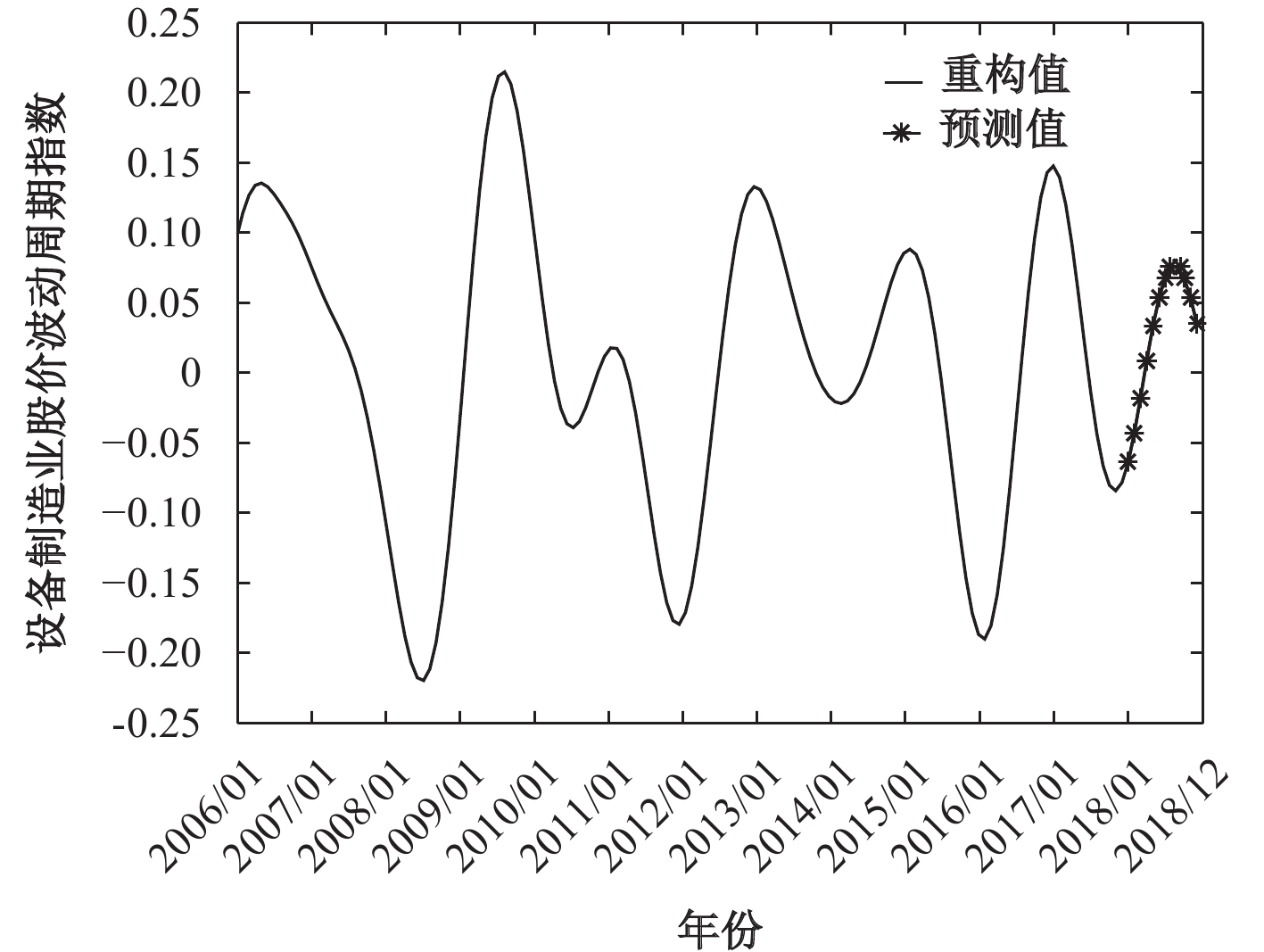
本节采用这一方法,将样本期间分为训练期和预测期,来检验预测模型的预测效果。样本期仍为2006年1月–2018年12月共156个月,为保证预测模型的效果,预测时期不宜过长,因此将2006年1月–2017年12月作为训练期,期间的周期项数据作为历史样本数据用于建立预测模型,2018年1月–2018年12月作为预测期,期间的数据作为独立样本用于检验模型的预测效果。利用上述方法构建了预测模型,实现周期序列的外推预测,结果得到了两个周期指数在2018年全年12个月的趋势预测值。将它们的实际数据测算值和预测值分别绘制成图8和图9,可以发现,朱格拉周期和设备制造业股价波动周期在2018年的预测趋势与实际趋势基本一致。
|
| 图 8 基于自回归模型的朱格拉周期重构序列及2018年趋势预测 |
|
| 图 9 基于自回归模型的设备制造业股价波动周期重构系列及2018年预测趋势 |
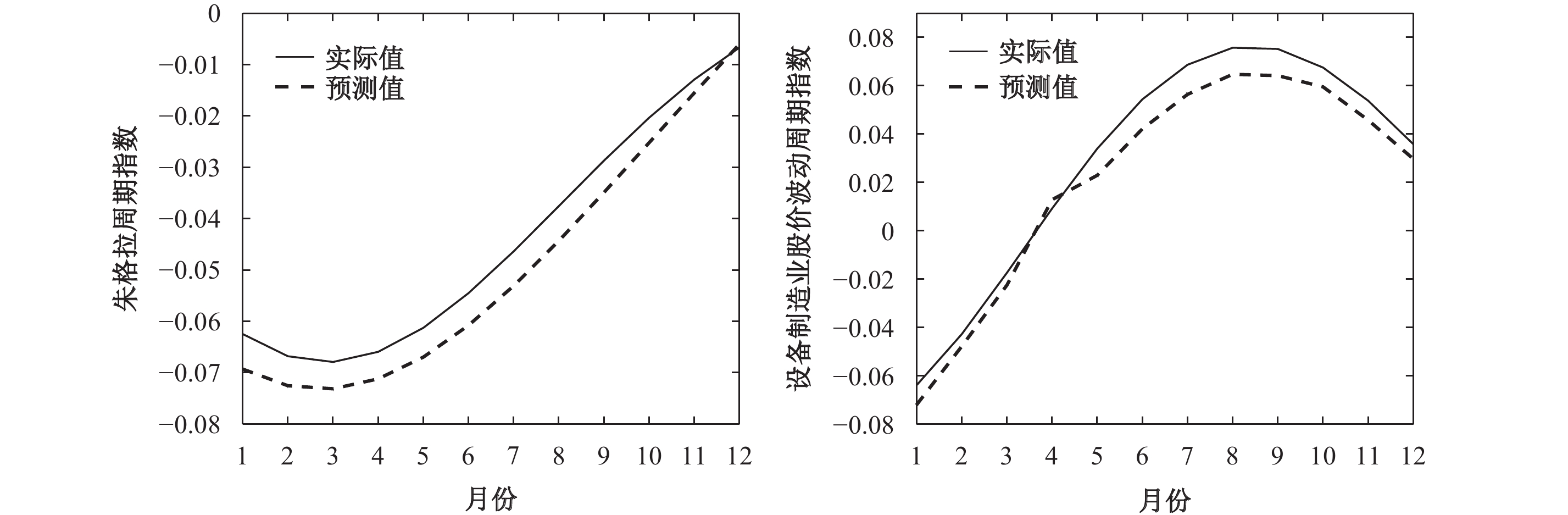
为更清楚地观察模型的预测效果,将2018年的预测趋势与实际趋势放大后绘制于同一图中,如图10所示。可以看出,图10中左侧朱格拉周期综合指数的预测走势和实际走势非常接近,均为先下降再上升,12个月的指数实际结果与预测结果的误差均在0.01以内,并且最后2个月误差近乎为0;右侧设备制造业股价波动周期指数的预测走势也和实际走势基本一致,且12个月的预测值误差都在0.01以内。
|
| 图 10 2018年周期指数预测值与实际值对比 |
我们进一步通过计算预测值和实际值的均方根误差(RMSE)和平均绝对误差(MAE)来检验周期指数的预测效果(张一和惠晓峰,2012),具体见表7。由表7可知,朱格拉周期和设备制造业股价波动周期的均方根误差(RMSE)和平均绝对误差(MAE)均近似于0,也反映出预测结果与实际结果非常接近。而且,依据预测结果计算出来的朱格拉周期和设备制造业股价波动周期的相关系数为0.603 2,与实际相关系数0.635 2十分接近。同时,通过观察两个周期指数预测值的波动状况可以发现,设备制造业周期指数从2018年1月便呈上升趋势,而朱格拉周期指数却自3月才开始逐渐上升,说明预测结果也证明了设备制造业周期指数的走势领先于朱格拉周期指数,与之前的结论完全一致。因此,从整体上来看,结合SSA与AR方法构建的模型预测的波动趋势与实际趋势基本一致,说明预测结果基本准确,预测效果良好。
| 朱格拉周期 | 设备制造业股价
波动周期 |
|
| 均方根误差(RMSE) | 0.010 6 | 0.009 8 |
| 平均绝对误差(MAE) | 0.008 2 | 0.007 6 |
本文基于中国2006–2018年间的月度数据,依据朱格拉周期和设备制造业股价波动周期的内涵分别构建了两个周期的综合指数,再通过熵值法分别计算出综合指数水平,并利用奇异谱分析方法,从时域和频域相结合的角度实证研究了两者的周期性特征及其关联性,验证了理论分析部分提出的两个假设。同时,将奇异谱分析与自回归分析两种方法结合起来对两个周期指数进行了预测,主要得到以下结论:第一,基于奇异值分解原理测算得到的朱格拉周期和设备制造业股价波动周期的整体相关系数为0.635 2,说明两者的走势具有很强的相关性。但这一相关性水平还未达到高度相关,从侧面反映出中国朱格拉周期的周期性波动除了受设备制造业波动的影响外,还受到其他因素的影响。第二,中国设备制造业股价波动周期领先于朱格拉周期3–6个月,说明中国股票市场设备制造业的股价波动状况在一定程度上可以提前反映朱格拉周期的未来走势,体现了股票市场是宏观经济晴雨表这一重要功能。第三,结合奇异谱分析与自回归分析方法可以较准确地预测两个周期的波动趋势。在将样本期间分为训练期和预测期后,对2018年的朱格拉周期和设备制造业股价波动周期的走势进行预测,结果表明,该方法对两个周期趋势的预测与实际趋势基本一致,误差值近似于0;而且预测期两个周期的相关关系为0.603 2,与实际相关系数0.635 2也十分接近。
本文的实证研究发现对于股票市场投资者制定投资策略和政府部门制定宏观调控政策均有重要的参考价值。中国朱格拉周期与设备制造业股价波动周期之间具有较高的相关关系,而且设备制造业股价波动周期领先于朱格拉周期3–6个月,波动幅度也更大,说明设备制造业股价能够对宏观经济运行状况作出较灵敏的反应,从而提前反映出朱格拉周期的波动。因此,当两条周期曲线的走势开始出现背离时,投资者可考虑调整投资策略。以近两年为例,2017年8月至2018年7月,设备制造业股价指数经历了一波上升,但2018年下半年开始调整向下,而此间朱格拉周期曲线一直稳步回升,似乎已经进入了复苏阶段,两个周期指数呈现出一定程度的背离。这说明目前股票市场已提前显示中国宏观经济正从底部进入回升阶段,但在上升过程中仍呈现出一定的不确定性,导致市场信心不足,设备制造业股价指数出现回落。虽然在经济复苏阶段股价指数会有较大波动,但股价普遍已处在低位,对于长期投资者而言是配置股票资产的良机,可以择机低价购入设备制造业股票。随着宏观经济对产能的需求进一步提高,设备投资将进一步扩大,朱格拉周期会明确进入经济景气周期,设备制造业指数也将停止回落转而上升,为投资者带来丰厚回报。当然,本文的实证结果对制定设备制造业股票投资策略的参考还较粗略,如何根据设备制造业周期与朱格拉周期的相关关系制定细化的投资策略,正是本研究未来努力的方向。
① 此处限于篇幅,未能将样本期内两个周期指数月度值一一列出,有需要的读者可来信索取。
② 常见的上市公司行业分类标准主要有《上市公司行业分类指引(2012修订版)》和申银万国、WIND、MSCI明晟等投资机构编制的行业分类法。本文之所以选择申银万国证券研究所编制的行业分类标准,是由于该行业分类标准是从投资管理的角度设置的,主要供投资者进行投资价值分析以调整资产配置,与本文研究目的一致;而且此分类方法考虑了实际研究需求,兼顾了政府及行业管理部门的行业分类,因此和现有的行业数据具有较好的匹配性,与其他行业分类标准具有互通性;此外,该行业指数可将所有细分行业全部覆盖,且是目前可用的指数里时间跨度最长的指数。
③ 限于篇幅,本文未一一列出样本期间两个周期指数在各月份的重构序列值,有需要的读者可来信索取。
| [1] | 安宇宏. 朱格拉周期[J].宏观经济管理,2013(4). |
| [2] | 丁志国, 苏治, 杜晓宇. 经济周期与证券市场波动关联性——基于向量SWARCH模型的新证据[J].数量经济技术经济研究,2007(3). |
| [3] | 董直庆, 王林辉. 我国通货膨胀和证券市场周期波动关系——基于小波变换频带分析方法的实证检验[J].中国工业经济,2008a(11). |
| [4] | 董直庆, 王林辉. 我国证券市场与宏观经济波动关联性: 基于小波变换和互谱分析的对比检验[J].金融研究,2008b(8). |
| [5] | 段鸿斌, 杨光. 股票市场与经济增长: 基于中国的经验分析[J].中央财经大学学报,2009(12). |
| [6] | 高文婷, 陈心怡, 包云轩, 等. 奇异交叉谱分析方法在中国南方稻纵卷叶螟发生预测中的应用[J].中国农业气象,2017(9). |
| [7] | 桂文林, 李建兰, 刘权盼. 基于奇异谱的中国季度GDP分解和产出缺口估计[J].统计与信息论坛,2018(7). |
| [8] | 郭琨, 周炜星, 成思危. 中国股市的经济晴雨表作用——基于热最优路径法的动态分析[J].管理科学学报,2012(1). |
| [9] | 韩德宗, 吴伟彪. 中国股市是宏观经济的" 晴雨表”吗?[J].数量经济技术经济研究,2003(5). |
| [10] | 黄华继, 丁维. 我国股市与经济周期互动关系的谱分析[J].产业经济研究,2009(6). |
| [11] | 李志冰, 杨光艺, 冯永昌, 等. Fama-French五因子模型在中国股票市场的实证检验[J].金融研究,2017(6). |
| [12] | 刘金全, 刘子玉. 中国经济新常态下的经济周期更迭与驱动因素转换研究——兼论新周期的形成与识别[J].经济学家,2019(5). |
| [13] | 刘树成. 我国固定资产投资周期性初探[J].经济研究,1986(2). |
| [14] | 刘晓曙, 王婧. 中国朱格拉周期现象分析: 来自1978−2013年的实证研究[J].制度经济学研究,2015(4). |
| [15] | 石广平, 刘晓星, 魏岳嵩. 投资者情绪、市场流动性与股市泡沫——基于TVP-SV-SVAR模型的分析[J].金融经济学研究,2016(3). |
| [16] | 谈儒勇. 中国金融发展和经济增长关系的实证研究[J].经济研究,1999(10). |
| [17] | 魏加宁, 杨坤. 有关当前经济下行成因的综合分析[J].经济学家,2016(9). |
| [18] | 晏艳阳, 李治, 许均平. 中国股市波动与宏观经济因素波动间的协整关系研究[J].统计研究,2004(4). |
| [19] | 杨高宇. 中国股市周期与经济周期的动态关联研究[J].工业技术经济,2011(10). |
| [20] | 张海波, 谢德泳. 股市收益率、货币政策与宏观经济变化关系的实证检验[J].统计与决策,2014(13). |
| [21] | 张红伟, 杨琨, 向玉冰. 宏观经济周期、企业生产与股票资产定价——基于沪市上市公司的经验研究[J].国际金融研究,2017(5). |
| [22] | 张文菲, 金祥义. 金融市场发展对企业生存期限影响研究——基于银行与股票市场的数据分析[J].财经理论与实践,2019(2). |
| [23] | 张一, 惠晓峰. 基于奇异谱分析的汇率预测研究[J].统计与决策,2012(6). |
| [24] | 张云, 刘丽娟, 尹筑嘉. 股权结构特征与混合所有制企业效率[J].会计与经济研究,2019(3). |
| [25] | 郑小琴. 测度我国的金融周期: 基于奇异谱的分析[J].金融理论与实践,2018(8). |
| [26] | 朱东辰, 余津津. 中国股市波动与经济增长关系的实证分析[J].经济科学,2003(2). |
| [27] | Arellano C, Bai Y, Zhang J. Firm dynamics and financial development[J].Journal of Monetary Economics,2012,59(6):533–549. |
| [28] | Campbell J Y, Shiller R J. The dividend ratio model and small sample bias: A Monte Carlo study[J].Economics Letters,1989,29(4):325–331. |
| [29] | Croux C, Reusens P. Do stock prices contain predictive power for the future economic activity? A Granger causality analysis in the frequency domain[J].Journal of Macroeconomics,2013,35:93–103. |
| [30] | De Carvalho M, Rodrigues P C, Rua A. Tracking the US business cycle with a singular spectrum analysis[J].Economics Letters,2012,114(1):32–35. |
| [31] | De Carvalho M, Rua A. Real-time nowcasting the US output gap: Singular spectrum analysis at work[J].International Journal of Forecasting,2017,33(1):185–198. |
| [32] | De Long J B, Summers L H, Abel A B. Equipment investment and economic growth: How strong is the nexus?[J].Brookings Papers on Economic Activity,1992(2):157–211. |
| [33] | Demirgüç-Kunt A, Levine R. Stock market development and financial intermediaries: Stylized facts[J].The World Bank Economic Review,1996,10(2):291–321. |
| [34] | Domian D L, Louton D A. A threshold autoregressive analysis of stock returns and real economic activity[J]. International Review of Economics & Finance,1997,6(2):167–179. |
| [35] | Fama E F. Stock returns, expected returns, and real activity[J].The Journal of Finance,1990,45(4):1089–1108. |
| [36] | Fama E F, French K R. A five-factor asset pricing model[J].Journal of Financial Economics,2015,116(1):1–22. |
| [37] | Filer R K, Hanousek J, Campos N F. Do stock markets promote economic growth?[R]. CERGE-EI Working Paper Series No.151, 2000. |
| [38] | Flad M. Do macro-factors help forecasting stock market volatility?[J]. Finance and Monetary Economics,2006,8:1–35. |
| [39] | Golyandina N, Zhigljavsky A. Singular spectrum analysis for time series[M]. New York: Springer, 2013. |
| [40] | Gonzalez R B, Lima J, Marinho L. Business and financial cycles: An estimation of cycles’ length focusing on macroprudential policy[R]. Working Papers 385, 2015. |
| [41] | Harris R D F. Stock markets and development: A re-assessment[J].European Economic Review,1997,41(1):139–146. |
| [42] | Juglar C. Des crises commerciales et leur retour periodique en France, en Angleterre et aux Etats Unis[M]. Paris: Guillaumin, 1862. |
| [43] | Kalman D. A singularly valuable decomposition: The SVD of a matrix[J].The College Mathematics Journal,1996,27(1):2–23. |
| [44] | Kitchin J. Cycles and trends in economic factors[J].The Review of Economics and Statistics,1923,5(1):10–16. |
| [45] | Kondratieff N D. Die langen wellen der konjunktur[J]. Archiv für Sozialwissenschaft und Sozialpolitik,1926,56(3):537–609. |
| [46] | Kumari J, Mahakud J. Relationship between conditional volatility of domestic macroeconomic factors and conditional stock market volatility: Some further evidence from India[J].Asia-Pacific Financial Markets,2015a,22(1):87–111. |
| [47] | Kumari J, Mahakud J. Does investor sentiment predict the asset volatility? Evidence from emerging stock market India[J].Journal of Behavioral and Experimental Finance,2015b,8:25–39. |
| [48] | Kuznets S S. Secular movements in production and prices: Their nature and their bearing upon cyclical fluctuations[M]. Boston: Houghton Mifflin and Company, 1930: 177-179. |
| [49] | Levine R, Zervos S. Stock market development and long-run growth[]. Washington, DC: The World Bank, 1996. |
| [50] | Levine R, Zervos S. Stock markets, banks, and economic growth[J]. The American Economic Review,1998,88(3):537–558. |
| [51] | Morelli D. The relationship between conditional stock market volatility and conditional macroeconomic volatility: Empirical evidence based on UK data[J].International Review of Financial Analysis,2002,11(1):101–110. |
| [52] | Pagano M, Pica G. Finance and employment[J].Economic Policy,2012,27(69):5–55. |
| [53] | Patterson K, Hassani H, Heravi S, et al. Multivariate singular spectrum analysis for forecasting revisions to real-time data[J].Journal of Applied Statistics,2011,38(10):2183–2211. |
| [54] | Schwert G W. Why does stock market volatility change over time?[J].The Journal of Finance,1989,44(5):1115–1153. |
| [55] | Schwert G W. Stock returns and real activity: A century of evidence[J].The Journal of Finance,1990,45(4):1237–1257. |
| [56] | Uebele M, Ritschl A. Stock markets and business cycle comovement in Germany before World War I: Evidence from spectral analysis[J].Journal of Macroeconomics,2009,31(1):35–57. |
| [57] | Vautard R, Yiou P, Ghil M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals[J].Physica D: Nonlinear Phenomena,1992,58(1-4):95–126. |
| [58] | Yang C P, Li J F. Investor sentiment, information and asset pricing model[J].Economic Modelling,2013,35:436–442. |
2.School of Economics and Trade, Hunan University, Hunan Changsha 410082, China

