
2019第21卷第5期
2.中央民族大学 管理学院,北京 100081
伴随着人口的世代更迭,中国1950年代和1960年代出生的婴儿潮一代将陆续退出劳动市场,1990年代和2000年代出生的低谷一代陆续进入劳动力市场,这种超大规模世代的退出和超小规模世代的进入,导致适龄劳动人口断崖式下降,老年人口急剧攀升,老龄潮扑面而来。有学者预测,到21世纪中叶,中国65岁及以上人口占比将处于20%−24%,并长期维持在这一较高的水平上(董克用和张栋,2017)。在老龄化提速的背景下,自2008年以来,中国经济增速不断下行,尤其是近3年来,国内生产总值增长率始终低于7%。面对来势汹汹的人口老龄化对经济社会系统的冲击,适龄劳动人口增速下降,社会抚养比的上升引致储蓄率下降,以及人力资本提升和产业结构升级缓慢,经济增速不断下降。为推动中国经济的持续稳定发展,顺利实现两个百年目标,对企业减税,降低企业负担,尤其是降低企业养老保险缴费率成为重要的政策抓手。国务院办公厅2019年4月4日发布了关于印发降低社会保险费率综合方案的通知,并规定自2019年5月1日起将城镇职工基本养老保险单位缴费率降至16%。在此背景下,降低企业养老保险缴费率是否以及多大程度上会促进未来中国实际潜在经济增长率成为当前亟需回答的问题之一。
关于降低企业养老保险缴费率对经济增长的影响,国内外学者均进行了积极的探索。国外学者关于降低企业养老保险缴费率对经济增长的影响研究更多集中在探讨现收现付制和基金制养老制度对经济增长的影响。因为企业缴纳养老保险金是统筹账户养老金,而统筹账户养老金占比越高,养老保险制度越倾向于现收现付制的养老保险制度,否则倾向于基金制的养老保险制度。Aaron(1966)认为,只要市场利率小于人口和工资增长率之和,现收现付制养老保险制度就会优于基金制养老保险制度;Diamond(1997)进一步佐证了上述观点。Friedrich(1989)把上述结论进一步推广后发现,要用基金制的养老保险制度取代现收现付制的养老保险制度,而使得其他代的福利不降低,同时使得转轨的第一代的福利损失得以补偿,通常是不可能的。这个结论不仅适合开放的经济,也适合封闭的经济;不仅适合资本回报外生的情景,也适合资本回报内生的情景。相对于上述学者的研究发现,也有诸多学者持不同的观点,如Feldstein(1999)、Sinn(2000)、Ginn(2004)、Kaganovich和Zilcha(2012)以及Yang(2016)认为,从现收现付制的养老保险制度过渡到基金制的养老保险制度,会导致社会的总福利提升,其逻辑是,基金制的养老保险制度在老龄化的社会里可以增进社会储蓄和资本存量,进而提高社会产出和福利。
关于降低企业养老保险缴费率对经济增长影响的国内文献多集中在关于养老制度变轨对经济增长影响上。部分学者认为从现收现付制转向基金制不利于经济增长或者促进经济增长是有条件的。封进(2004)基于理论分析认为,在人口增长率与工资增长率之和大于市场利率的情况下,现收现付制可以在代际间实现帕累托改进。彭浩然和申曙光(2007)、彭浩然等(2018)指出,虽然降低企业养老保险缴费率可以促进经济增长,但是政府只有在降低养老保险缴费率的同时加大公共教育投资,才可能实现促进经济增长和维持养老金替代率不变两大目标。张熠和卞世博(2012)认为,老龄化社会存在向基金制转变的语境,提升名义个人账户有利于改善社会福利。国内学者也从理论和经验上证明了此观点。万春和许莉(2006)、万春(2008)、李时宇(2010)、汪伟(2012)、高彦等(2015)、洪丽和曾国安(2017a,b)基于理论分析发现,由现收现付制转化为基金制会促进经济增长和社会福利的提升。王兴化和李金凤(2012)、杨艳东和车凯丽(2018)、赵健宇和陆正飞(2018)基于经验分析发现,企业较高的缴费率会限制企业和员工对培训的投入,制约全要素生产率的提升和高端产业的形成,进而对经济发展存在负面影响。
虽然学者在降低企业养老保险缴费率对经济增长的影响上进行了有意义的探索,但是在以下几个方面还存在可以拓展的空间。其一,在研究问题上,关于降低企业养老保险缴费率,或者从现收现付制养老保险制度转为基金制养老保险制度,对经济增长是促进还是抑制,或是在一定条件下是促进作用,在另一些条件下是抑制作用,关于这个问题的回答依然存在异议。比如彭浩然等(2018)认为,中国政府只有在降低养老保险缴费率的同时,加大公共教育投资,才有可能实现促进经济增长和维持养老金替代率不变两大政策目标。其二,在研究内容上,多数研究没有结合中国2019年5月1日起开始执行的降低企业养老保险缴费率至16%的最新政策背景。首先精确定量地回答降低企业养老保险缴费率至16%会在多大程度上影响经济增速;其次为规避降低企业养老保险缴费率可能产生的负面影响,以及该如何安排相应的配套政策等问题。其三,在研究方法上,上述研究要么基于过去的历史经验,要么基于OLG模型进行理论上的分析,但是从一个可计算的动态一般均衡框架分析降低企业养老保险缴费率对经济增速影响的研究还不多;同时在模型设定上,相比前人的研究,本文新增加了降低企业养老保险缴费率通过影响人力资本和劳动生产率进而作用于经济增长的机制。
基于此,本文通过构建一个可计算、可推广的动态一般均衡框架,通过模拟尝试回答降低企业养老保险缴费率至16%以及进一步降低企业养老保险缴费率可能对未来中国实际潜在经济增长率的影响。结果显示,虽然降低企业养老保险缴费率至16%无法改变未来中国经济增速下降的趋势,但是的确可以提升未来中国实际潜在经济增长率,且降低企业养老保险缴费率不是越低越好,而是存在一个最优的缴费率。本文的边际贡献在于:(1)在研究问题和研究内容上,其一,定量地评估企业养老保险缴费率降至16%对未来实际潜在经济增长率的影响;其二,进一步模拟在16%基础上再继续降低企业养老保险缴费率可能对经济增长率的影响;其三,对比分析了降低企业养老保险缴费率和个人账户养老保险缴费率对经济增长影响的异质性,这可能会为公共政策的制定提供数值依据和决策参考。(2)在研究方法上,模型设定除考虑到降低企业缴费率通过影响储蓄和资本作用经济增长的机制外,还新增加了降低企业缴费率通过影响人力资本积累和劳动生产率,进而作用经济增长的机制。这可能会为学者提供一个分析降低企业养老保险缴费率对经济增长影响的可延拓理论框架。本文的结构安排如下:第二部分是模型和参数设定,第三部分是基本结果和讨论,第四部分是在考虑到OECD国家经验后,进一步模拟降低企业养老保险缴费对未来中国实际潜在经济增长率的影响,以及提升个人账户养老金缴费率等降低企业养老保险缴费率的配套性政策对未来中国实际潜在经济增长率的影响。
二、模型与参数设定 (一) 模型构建在模型构建上主要借鉴了Becker和Barro(1988)、Liao(2013)、Yang(2016)、Li和Lin(2016)以及杨华磊(2019)等学者的做法。与多期OLG模型不同的是,决策者不再追求一生的效用最大化,而是从当年和下一年来看当年产出带来的效用最大化,以期实现对历年经济增长的可计算模拟和程序上的简化。第t期的消费、工资、青少年人口数量以及第t+1期的消费分别记为Ct1、wt、Ht以及Ct2;如果抚养一个孩子占工资的比例记为μ,则抚养孩子的总支出就为Htμwt;跨期替代弹性、利他因子以及未来消费的折现因子分别记为σ、γ和β。在中国,抚养孩子不仅是对养老的投资,还具有传宗接代的利他属性,即还是一种消费行为,所以抚养孩子支出Hiμwi要进入决策者的效用函数,并在当期发生效用流。借鉴Becker和Barro(1988)的工作,则目标函数设定为:
| $ {U_t} = {\left( {C_t^1} \right)^\sigma } + \gamma {\left( {{H_t}\mu {w_t}} \right)^\sigma } + \beta {\left( {C_t^2} \right)^\sigma } $ | (1) |
如果企业和个人缴纳的社会养老保险费率分别记为τ1和τ2,则相应缴纳的总养老保险费用分别为τ1Ltwt和τ2Ltwt;如果家庭赡养一个老人支出占工资的比例记为ϕ,同时结合抚养比例μ,则总赡养老人支出和总抚养子女支出分别为Otϕwt和Htμwt;如果第t期的总产出和储蓄分别记为Yt和St,则在第t期决策者面临的约束为:
| $ {Y_t} = C_t^1 + {S_t} + {H_t}\mu {w_t} + {O_t}{w_t} + {\tau _1}{L_t}{w_t} + {\tau _2}{L_t}{w_t} $ | (2) |
如果第t+1期的利率记为rt+1,则在第t+1期个人账户养老金和储蓄的回报为(St+τ2Ltwt)(1+rt+1);如果临近退休人口数量和死亡率分别记为Jt和πr,第t期的劳动人口数量和老年人口数量分别记为Lt和Ot,则第t期的抚养和赡养支出在第t+1期给决策者带来
| $ C_t^2 = \left( {{S_t} + {\tau _2}{L_t}{w_t}} \right)\left( {1 + {r_{t + 1}}} \right) + \left( {\frac{{{O_{t + 1}} + {\tau _1}{L_{t + 1}}}}{{{O_{t + 1}}}}{\pi _r}{w_{t + 1}} - \frac{{{H_t}\mu + {O_t}\phi + {\tau _1}{L_t}}}{{{L_t}}}{w_t}} \right){J_t} $ | (3) |
如果要知道青少年人口数量、劳动人口数量、老年人口数量以及将要退休的人口数量等人口结构变量,则需要知道未来历年分年龄的人口数据。参照王广州(2018)的人口预测方法,未来各年龄段上人口数量以及新生人口数量计算公式如下:
| $ \left\{ \begin{aligned} & P_{t + 1}^{female}\left( {j + 1} \right) = \left[ {1 - d_t^{female}\left( j \right)} \right]P_t^{female}\left( j \right)\\ & P_{t + 1}^{male}\left( {j + 1} \right) = \left[ {1 - d_t^{male}\left( j \right)} \right]P_t^{male}\left( j \right)\\ & P_t^{female}\left( 0 \right) = s{r_t}\mathop \sum \nolimits_{j = 15}^{49} TFR_t^{female}\left( {j + 1} \right)P_t^{female}\left( {j + 1} \right)\\ & P_t^{male}\left( 0 \right) = \left( {1 - s{r_t}} \right)\mathop \sum \nolimits_{j = 15}^{49} TFR_t^{female}\left( {j + 1} \right)P_t^{female}\left( {j + 1} \right) \end{aligned} \right. $ | (4) |
其中srt为女性婴儿占总出生婴儿的比例,变量dtv(j)、P(j)以及TFRtfemale(j)分别为第t年性别为v、年龄为j的死亡率、人口数量以及育龄妇女的生育水平。为分析方便,假设超过100岁的个体将不出现在未来的人口结构方程中。考虑到中国法律规定16岁以前的人口进入劳动力市场属于违法行为,约定青少年为0–15岁人口;根据《国务院关于工人退休、退职的暂行办法》(国发〔1978〕104号)文件的规定,即“城乡居民养老保险中年满60岁方可领取养老金,男职工年满60周岁,女干部年满55周岁以及女工人年满50周岁可领取养老金”,以及未来可能延长退休年龄的情景,约定领取养老金的老年人为60岁及以上人口;再根据2010年第六次人口普查中各年龄段上的劳动参与率数据,假设未来分年龄劳动参与率LPRt(j)不变,则未来青少年、适龄劳动人口以及老年人口数量的计算公式如下:
| $ \left\{ \begin{aligned} & {H_t} = \mathop \sum \nolimits_{j = 0}^{15} \left[ {P_t^{female}\left( j \right) + P_t^{male}\left( j \right)} \right]\\ & {L_t} = \mathop \sum \nolimits_{j = 16}^{100} LP{R_t}\left( j \right)\left[ {P_t^{female}\left( j \right) + P_t^{male}\left( j \right)} \right]\\ & {J_t} = P_t^{female}\left( j \right) + P_t^{male}\left( j \right)\\ & {O_t} = \mathop \sum \nolimits_{j = 60}^{100} \left[ {P_t^{female}\left( j \right) + P_t^{male}\left( j \right)} \right]\\ & {P_t} = \mathop \sum \nolimits_{j = 0}^{100} \left[ {P_t^{female}\left( j \right) + P_t^{male}\left( j \right)} \right] \end{aligned} \right. $ | (5) |
人口结构变量Ht、Lt、Ot以及Jt已知,参数σ、γ、β、μ、ϕ、τ1、τ2和πr外生给定,要求解上述动态优化模型,还需要知道约束条件中的工资wt和利率rt+1。要求工资和利率,还需要知道生产部门决策。如果生产函数是C-D形式,资本贡献份额、劳动、资本、人力资本以及全要素生产率相应记为α、Lt、Kt、ht和At,则生产函数为Yt=At(Kt)α(htLt)1-α。需要说明的是,消费会促进经济增长,经济增长也会提升消费,消费和经济增长存在互为因果关系。但是消费和经济增长存在何种互为因果的关系,不同的学者有不同的设定。为避免自身设定的主观性以及学者们对哪一种设定最优的争议,也为了降低设定误差可能扩大预测结果的误差,在此从GDP核算的生产法出发,核算GDP的潜在产出。把一年一个国家生产部门生产的最终产品和服务进行加总,核算出历年的GDP,这样可以规避消费和经济增长的双向因果关系给模型求解带来的难度,突出了研究问题,也简化了模型。
全要素生产率At如何决定呢?根据Liang 等(2014)、Jones和Schoonbroodt(2016)、陆铭(2017)以及杨华磊(2019)的研究发现,当期多生育,未来有更多更年轻的人聚集在一起就更能促进创新和全要素生产率的提升。在此设定全要素增长率与20年前的出生人数正相关,基于历史上的经验关系,通过对出生人数预测来估计未来的全要素生产率。
资本存量Kt如何决定呢?其等于扣除折旧后的上一期资本存量加上本期个人账户养老金和本期储蓄。如果每期资本的折旧率均设为δ,则第t期的资本量为:
| $ {K_t} = (1 - {\rm{\delta }}){K_{t - 1}} + {S_{t - 1}} + {\tau _2}{L_t}{w_t} $ | (6) |
人力资本 ht如何决定呢?参照黄晨熹(2011)以及陆旸和蔡昉(2014)的研究设定,同时为了便于比较,把基准年份下的人力资本进行归一化处理,则第t期的人力资本为:
| $ {h_t} = {e^{\varphi \left( {{s_t}} \right) - \varphi \left( {{s_{2018}}} \right)}} $ | (7) |
考虑到不同教育阶段的教育回报不同,特别是初等教育回报大于高等教育回报,参照陆旸和蔡昉(2014)、Psacharopoulos(1994)以及Barro和Lee(2013)的做法,进一步设定φ(st)为:
| $ \varphi \left( {{s_t}} \right) = \left\{ {\begin{aligned} & {0.134 \times \left( {4 - {s_t}} \right),{s_t} \leqslant 4}\\ & {0.134 \times 4 + 0.101 \times \left( {{s_t} - 4} \right),4 < {s_t} \leqslant 8}\\ & {0.134 \times 4 + 0.101 \times 4 + 0.068 \times \left( {{s_t} - 8} \right),8 < {s_t}} \end{aligned}} \right. $ | (8) |
在劳动市场和资本市场有效的情景下,生产者利润最大化条件为:
| $ \left\{ {\begin{aligned} & {{w_t} = {A_t}\left( {1 - \alpha } \right){{({K_t})}^\alpha }{{\left( {{h_t}{L_t}} \right)}^{ - \alpha }}}\\ & {{w_{t + 1}} = {A_t}\left( {1 - \alpha } \right){{({K_{t + 1}})}^\alpha }{{\left( {{h_{t + 1}}{L_{t + 1}}} \right)}^{ - \alpha }}}\\ & {{r_{t + 1}} = {A_t}\alpha {{({K_{t + 1}})}^{\alpha - 1}}{{\left( {{h_{t + 1}}{L_{t + 1}}} \right)}^{1 - \alpha }}} \end{aligned}} \right. $ | (9) |
综合家庭和生产者决策,建立一个可计算的动态一般均衡模型。在这个框架下家庭实现效用最大化,生产者实现利润最大化。每年决策者面临的决策是如何把产出在消费、储蓄、养老保险缴费、抚养孩子以及赡养老人之间进行最优分配,以确保当年产出实现效用最大化,动态一般均衡模型如下:
| $ \begin{aligned} & \mathop {\max }\nolimits_{C_t^1,C_t^2,{S_t}} {U_t} = {\left( {C_t^1} \right)^\sigma } + \gamma {\left( {{H_t}\mu {w_t}} \right)^\sigma } + \beta {\left( {C_t^2} \right)^\sigma }\\ & s.t.\left\{ \begin{aligned} & C_t^1 = {Y_t} - C_t^1 - {S_t} - {H_t}\mu {w_t} - {O_t}\phi{w_t} - {\tau _1}{L_t}{w_t} - {\tau _2}{L_t}{w_t}\\ & C_t^2 = \left( {{S_t} + {\tau _2}{L_t}{w_t}} \right)\left( {1 + {r_{t + 1}}} \right) + \left( {\frac{{{O_{t + 1}} \phi+ {\tau _1}{L_{t + 1}}}}{{{O_{t + 1}}}}{\pi _r}{w_{t + 1}} - \frac{{{H_t}\mu + {O_t}\phi + {\tau _1}{L_t}}}{{{L_t}}}{w_t}} \right){J_t}\\ & {w_t} = {A_t}\left( {1 - \alpha } \right){({h_t})^{1 - \alpha }}{({K_t})^\alpha }{\left( {{L_t}} \right)^{ - \alpha }}\\ & {w_{t + 1}} = {A_t}(1 - \alpha ){({h_{t + 1}})^{1 - \alpha }}{({K_{t + 1}})^\alpha }{\left( {{L_{t + 1}}} \right)^{ - \alpha }}\\ & {r_{t + 1}} = {A_t}\alpha {\left( {{h_{t + 1}}} \right)^{1 - \alpha }}{\left( {{K_{t + 1}}} \right)^{\alpha - 1}}{\left( {{L_{t + 1}}} \right)^{1 - \alpha }}\\ & 0 \leqslant \sigma ,\beta ,{\tau _1},{\tau _2},\phi ,\mu ,{\pi _r} \leqslant 1 \end{aligned} \right. \end{aligned} $ | (10) |
已知初始的资本存量、人口运动方程、人力资本运动方程、资本运动方程、未来全要素生产率以及模型中的其他参数,根据方程(10)即可模拟降低企业养老保险缴费率对2018-2050年间中国实际潜在经济增长率的影响。同时根据资本运动方程来实现模型的动态化,即考察降低企业养老保险缴费率对未来历年经济增长率的影响。
(二) 参数设定若已知σ、β、γ、τ1、τ2、ϕ、μ和πr等参数,通过上述动态一般均衡模型,利用MALTAB软件优化工具箱中fmincon函数,即可模拟出未来不同降低养老保险缴费率情景下历年的实际潜在经济增长率。在进行数值模拟前,根据中国的实际情况和相关文献,表1给出了变量Kt和Lt的初值以及σ、β、γ、τ1、τ2、ϕ、μ和πr等参数的取值。
根据人口预测模型、人力资本方程以及资本运动方程等,模型中未来历年人口结构变量、人力资本变量、资本变量进而工资、利率以及经济增速等变量是可测的,与此同时,我们假设模型中的参数保持不变。这些参数代表一定时期的社会、经济以及文化等环境,这些环境变量会随着时间而发生变化,比如折现因子和跨期替代弹性等,但是其未来如何变化,演进的路径是什么?不同的学者有不同的看法。其一,为避免人为设定参数演进路径的主观随意性;其二,为避免参数预测值设定可能会引致经济增长率预测误差的扩大化,使得经济增速趋势性特征发生变化。在此本文设定这些参数是不变的。为尽可能地保证结论的稳健性,本文也将对可能影响结论的核心参数进行敏感性分析。
| 参 数 | 取 值 | 设定依据 |
| K2018(亿元) | 1 351 028 | 基于李宾和曾志雄(2009)的方法进行资本盘存得到 |
| L2018(人) | 778 782 529 | 基于2010年人口普查数据和队列要素法加以推算 |
| α | 0.5 | 借鉴Zhu等(2014)的设定 |
| A | 0.0145 | 根据2018年总产出加以校准 |
| σ | 0.5 | 借鉴Liao(2013)的设定 |
| β | 0.95 | 借鉴康传坤和楚天舒(2014)的设定 |
| μ | 0.8 | 根据Liao(2013)的数据和劳动贡献份额加以计算 |
| 0.6 | 基于(国发〔1997〕26号)文件中的基本养老金目标替代率 | |
| γ | 0.9 | 借鉴彭浩然等(2018)的设定 |
| τ1 | 0.2 | 基于(国发〔2000〕42号)文件中企业养老保险缴费率设定 |
| τ2 | 0.08 | 基于(国发〔2000〕42号)文件中个账养老保险缴费率设定 |
| δ | 0.05 | 借鉴陈昌兵(2014)的设定 |
| srt | 0.52 | 借鉴贺丹等(2018)的设定 |
最后对于折现因子β的设定作说明。与OLG模型不同的是,决策者不再是追求一生的效用最大化,而是追求历年产出带来的效用最大化,本模型对每年的劳动者进行一次规划,来适应变化的人口结构,也就是在2050年前需要求解模型22次左右。通常在OLG模型下折现因子取值很低,因为OLG模型中一期是20–30年,意味着此处折现因子的取值应是OLG模型下折现因子取值的20–30次方。本文的折现因子不是相对上一代,而是相对上一年。参考彭浩然等(2018)的研究,决策者对本年消费赋予的权重β通常在90%以上,同时为了与初始2018年的经济增长率保持一致,参考康传坤和楚天舒(2014)的研究工作,设定本文中的折现因子等于0.95。
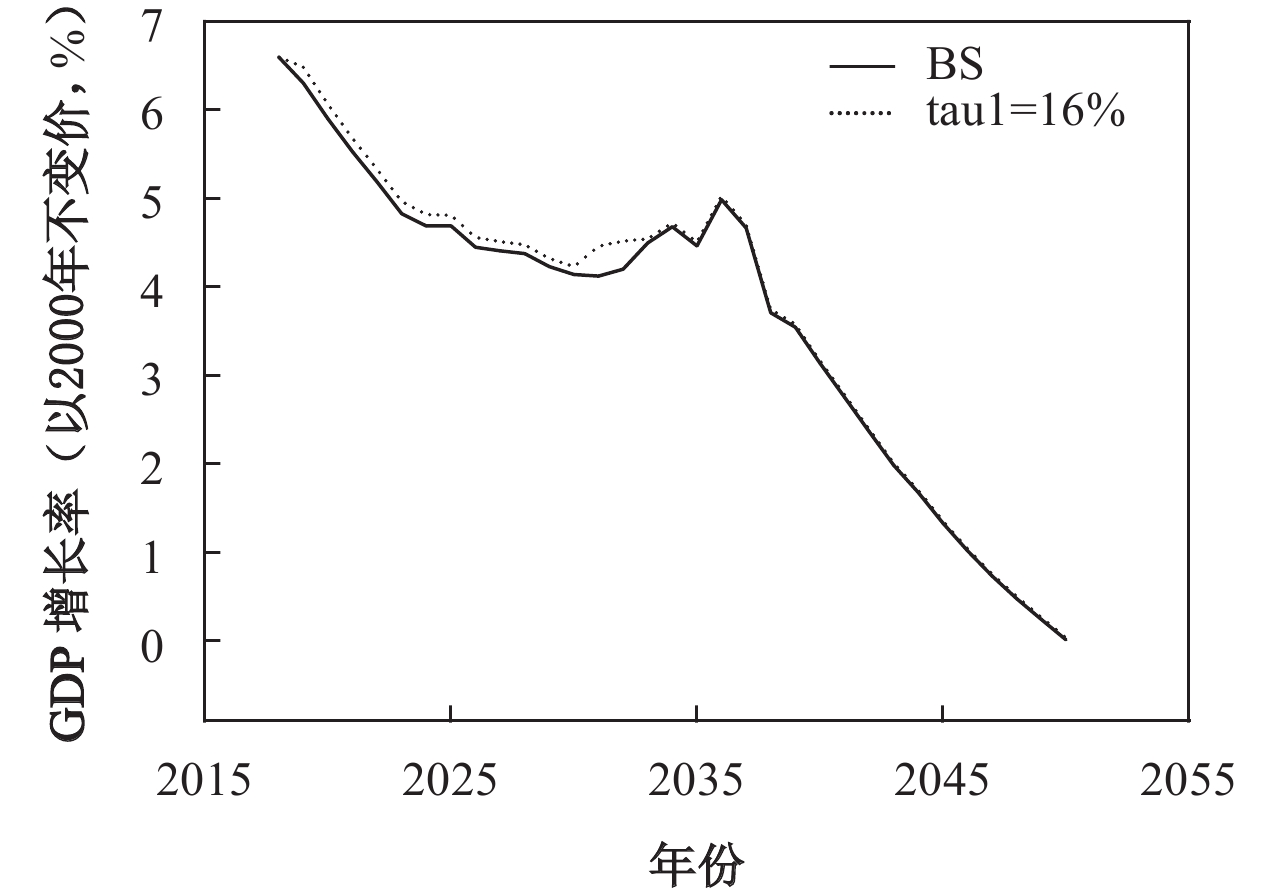
三、基本结果与讨论 (一) 结果讨论在不改变个人账户养老保险缴费率的情况下,为定量考察降低企业养老保险缴费率至16%对未来中国实际潜在经济增长率的影响,在此设定两种政策情景:其一,企业养老保险缴费率为20%(简称BS);其二,企业养老保险缴费率为16%(简称tau1=16%)。依据现实可行参数进行数值模拟,从图1可以看出,如果企业养老保险缴费率从20%下调至16%,虽然没有改变未来中国实际潜在经济增长率阶梯式下降的趋势,但是减缓了经济增长率下降的幅度。在实现两个百年目标期间内,降低企业养老保险缴费率至16%,可使2019–2021年、2022–2050年间的平均经济增速分别提升0.167%和0.077%,在2019–2050年间可使平均经济增速提升0.085%,其中长期效果甚微,短期效果明显,尤其在2033年之前使得平均经济增速提升0.148%。
|
| 图 1 降低企业养老保险缴费率下的经济增长率 |
为什么降低企业养老保险缴费率可以提升未来中国经济增长率呢?根据中国统账结合养老保险制度的特点,企业当前上缴的养老金划入统筹账户,直接赡养当前的老年人,当前劳动人口上缴的个人账户养老金类似储蓄,为自己的将来养老。过高的企业养老保险缴费率,意味着当前老年人口养老金支出较大,考虑到这部分养老金具有现收现付的特点,故企业养老保险缴费率越高,越可能会挤占社会储蓄,进而降低资本,在其他条件不变的情况下,经济增长率就可能越低。相反,如果我们降低企业养老保险缴费率,意味着储蓄和资本增加,资本增加会导致经济增长。为什么长期作用效果会减弱呢?原因在于,随着资本存量的扩大,适龄劳动人口的减少,经济体量以及历年储蓄份额的增加,对总劳动人口征收的企业养老保险基金挤占储蓄的比例越来越低,其对经济增长的长期作用降低。
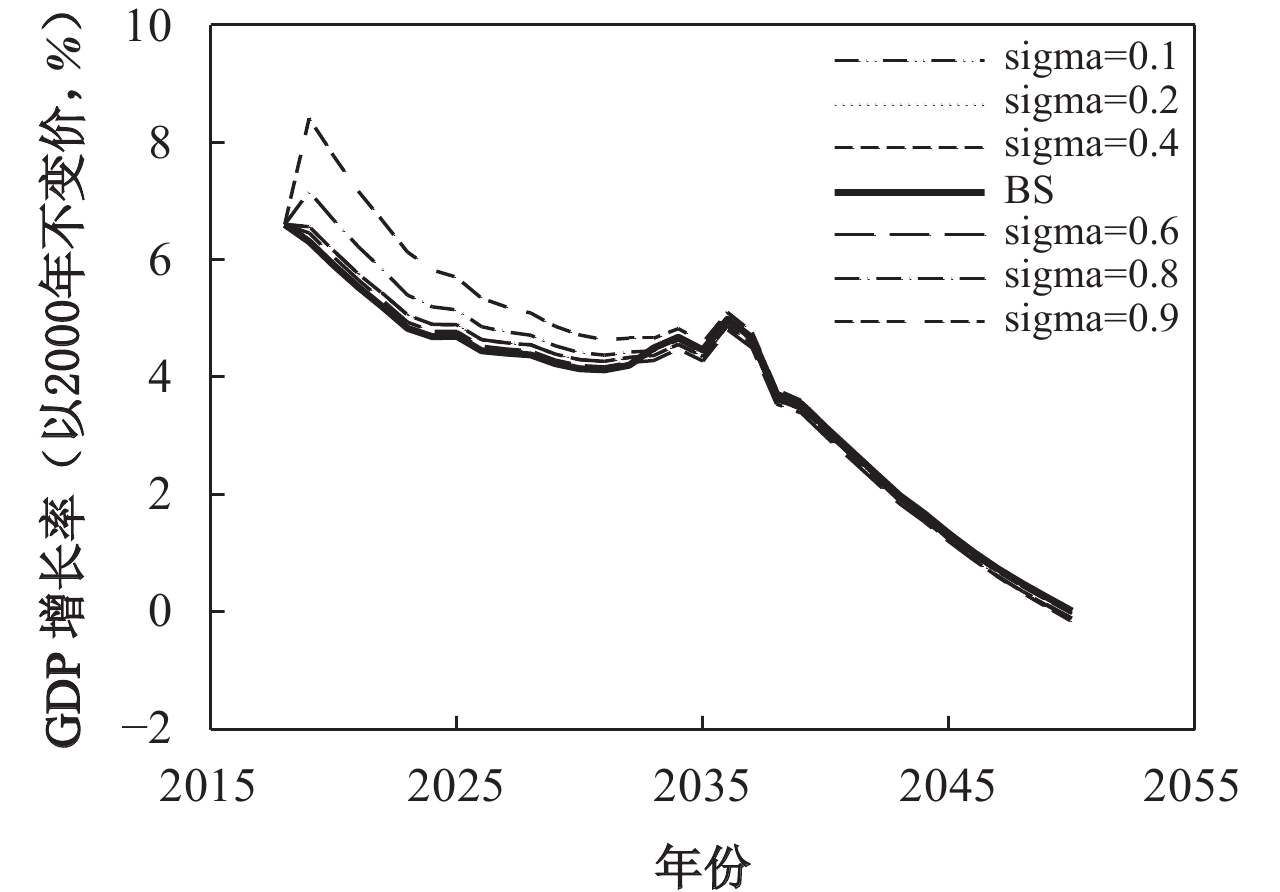
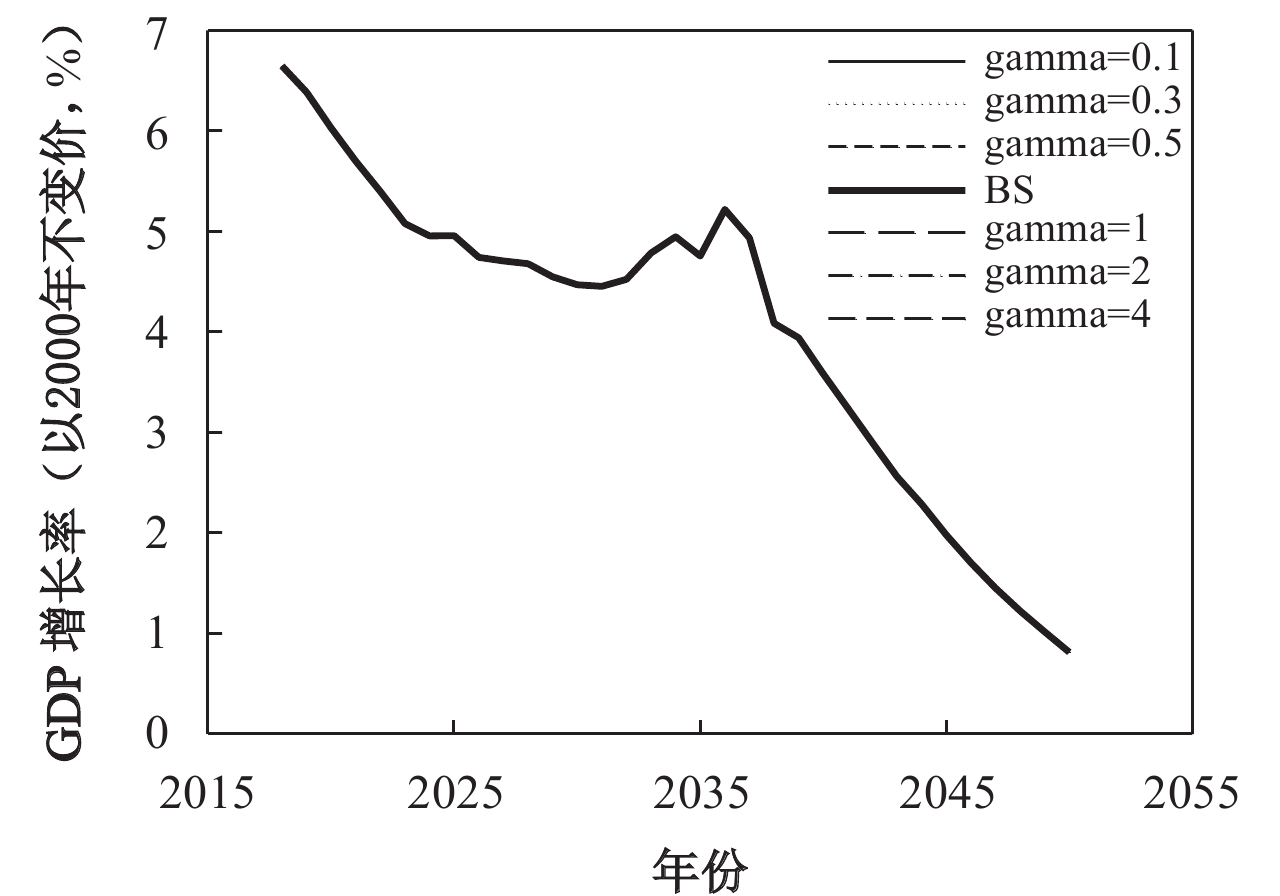
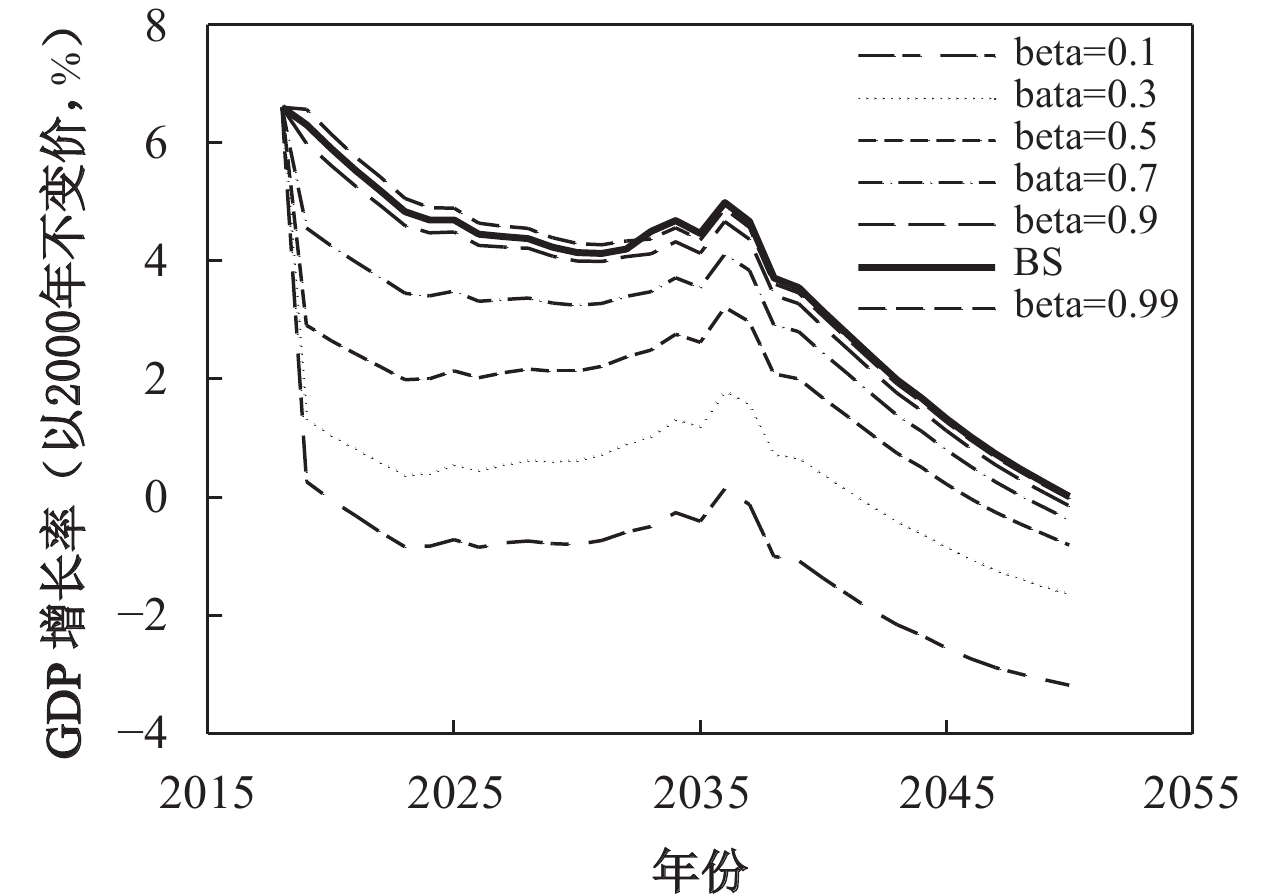
(二) 稳健性分析这里要观察模型中的一些核心参数,比如跨期替代弹性以及折现因子等变化是否影响上述模拟结果的可靠性。考虑到跨期替代弹性σ取值在0–1之间,基准情景下σ=0.05,在此选取σ=0.1、0.3、0.7和0.9 4种情景;考虑到折现因子β取值在0–1之间,基准情景下β=0.95,在此选取σ=0.1、0.5、0.7和0.99 4种情景;考虑到利他系数γ取值大于0,基准情景下γ=0.9,在此选取σ=0.1、0.5、1和2 4种情景,稳健性分析结果如图2至图4所示。
|
| 图 2 关于参数σ的敏感性分析 |
|
| 图 4 关于参数γ的敏感性分析 |
从图2至图4可以看出,跨期替代弹性的变化并没有从根本上改变降低企业养老保险缴费率对经济增长率的提升作用,仅略微改变了对经济增长率的提升幅度,其中跨期替代弹性取值越高,经济增长率越高;消费折现因子大体上同样没有改变降低企业养老保险缴费率对经济增长率的提升作用,同时也只是改变了不同取值情景下经济增长率的绝对值,其中消费折现因子越高,经济增长率越高;降低企业养老保险缴费率对经济增长率的提升作用对利他系数的改变更是稳健,不仅没有改变趋势性特征和比较特征,也没有改变经济增长率的绝对值。综上,从上述稳健性分析结果可以发现,趋势性特征和比较特征不会随参数的改变而产生明显变化。
|
| 图 3 关于参数β的敏感性分析 |
降低企业养老保险缴费率除通过影响储蓄和资本机制进而影响经济增长外,在现实中,降低企业养老保险缴费率还可能通过影响当前劳动人口人力资本积累和劳动生产率影响经济增长。短期企业养老保险缴费率的降低意味着当前老年人养老福利的降低,也意味着当前劳动人口未来养老福利的减少。根据心理学中的叶克斯—道森定律,焦虑和工作效率之间呈倒U形关系,当焦虑处于中等水平时,人的工作效率最高,焦虑过高或者过低都不利于效率的提升和任务的完成。降低企业养老保险缴费率意味着当前劳动人口未来养老福利的减少,企业养老保险缴费率越低,当前劳动人口越可能感受到未来养老福利无法得到保障。在一定范围内,对未来养老无法保障的焦虑可能会有利于督促劳动者努力工作和提升工作效率。但是如果继续降低企业养老保险缴费率,未来较低的养老保障会使当前劳动人口过度焦虑,最终影响当前劳动人口的人力资本积累以及劳动生产率,进而影响经济增长。根据叶克斯—道森定律在经济学中的体现,企业养老保险缴费率应该存在某个门槛值或最优值,高于这个值时,降低企业养老保险缴费率有助于经济增长率的提升;低于这个值时,降低企业养老保险缴费率可能不利于经济增长率的提升。
考虑到降低企业养老保险缴费率可能会通过影响当前劳动人口的未来养老保障预期进而影响当前和未来的经济增长率,在此设定企业养老保险缴费率作用于经济增长率的另一渠道是通过影响人力资本积累,进而影响经济增长。在此引入系数函数Z(τ1),根据上述论述,系数函数Z(τ1)应是二次多项式函数。如果最优缴费率是τ1*,则公式(7)可重写为:
| $ {h_t} = \frac{{Z\left( {{\tau _1}} \right)}}{{Z\left( {0.2} \right)}}{e^{\varphi \left( {{s_t}} \right) - \varphi \left( {{s_{2018}}} \right)}} $ | (11) |
如何估计系数函数Z(τ1)呢?考虑到中国各地区企业养老保险缴费率的差异性不太明显,并且企业养老保险缴费率相对稳定,通过中国经验数据计算出最优的企业养老保险缴费率不太可行。国际上各个国家的企业养老保险缴费率存在较大的差异性,进而通过国际经验寻找最优缴费率是可行的。如果对于经济增长率存在一个最优的企业养老保险缴费率,企业养老保险缴费率与对应经济增长率应该呈现一个倒U形关系。考虑到社会养老保险制度是伴随着城镇化和工业化而发展起来的,所以社会养老保险对经济增速的影响更多存在于社会养老保险制度成熟的地区,这些地区社会养老保险覆盖面广、保障水平高。
城镇化水平高且已完成工业化的OECD国家,其工业化和城镇化程度较高,社会保障制度也较为完善,对中国的未来具有重要的借鉴意义,OECD国家现在走的路,正是中国将要走的路。中国已经初步完成工业化,城镇化过半并不断提高,截至2018年底,中国社会养老保险覆盖率超过90%且养老保障制度日趋完善。通过观察OECD国家企业养老保险缴费率与经济增长率的经验关系,推断中国企业养老保险缴费率与经济增长率之间的关系,可以为中国经济改革提供经验。
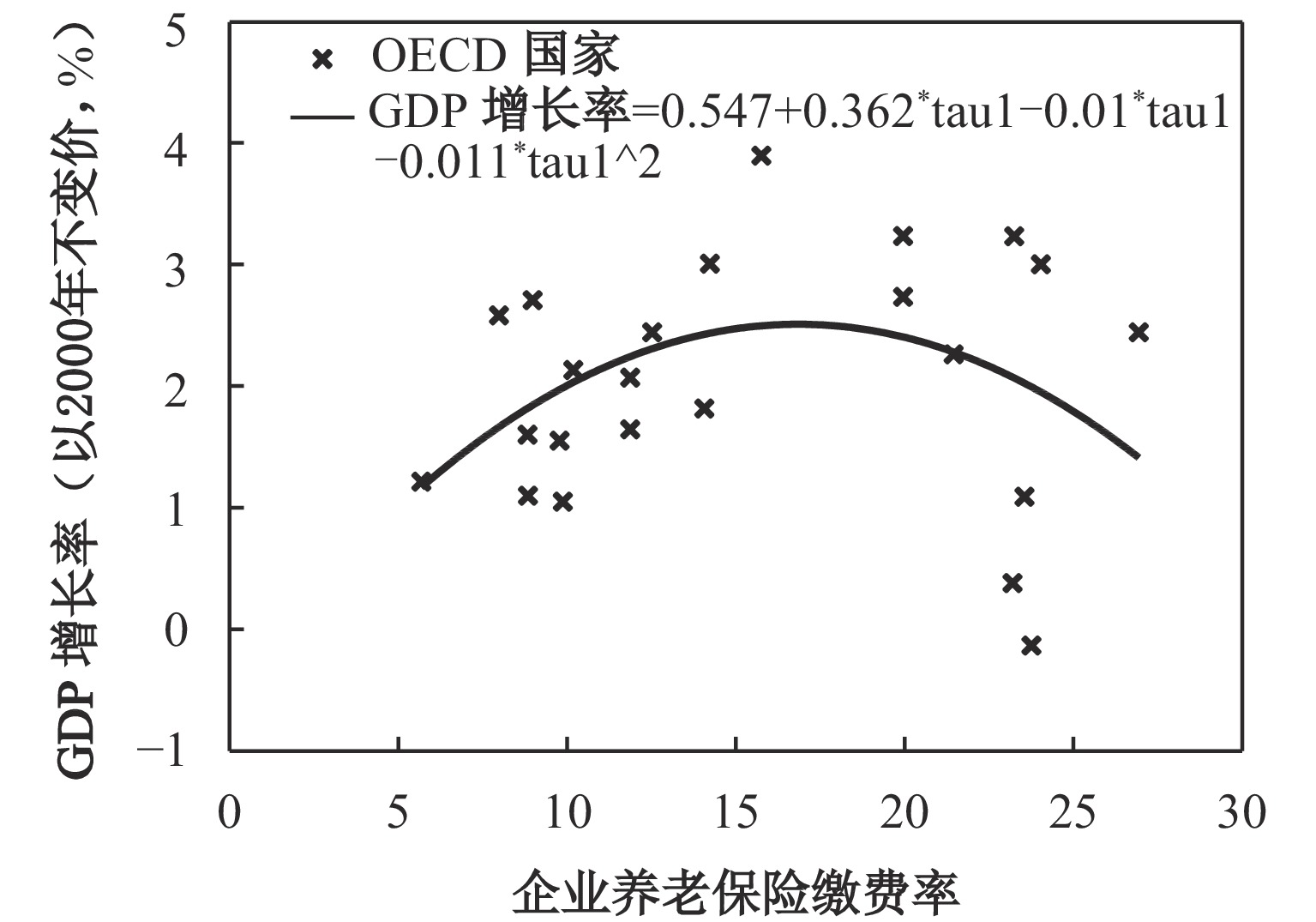
根据2011年的《世界社会保障报告》,可以获取2011年OECD中各个国家的企业养老保险缴费率。考虑到企业养老保险缴费率对经济增速影响具有滞后性以及企业养老保险缴费率相对稳定,各国对应的经济增长率为2012–2017年间平均GDP增速,在剔除非欧洲OECD国家的数据后,绘制企业养老保险缴费率与经济增速的散点图并做非线性统计拟合(见图5)。
|
| 图 5 OECD国家企业养老保险缴费率与2012–2017年间经济增长率 |
从图5可以看出,OECD国家的企业养老保险缴费率与经济增速大体上呈现倒U形的关系,基本符合前述的推断和叶克斯—道森定律。这意味着企业养老保险缴费率不是越少,经济增长率就越高,也不是企业养老保险缴费率越高,经济表现就越好,而是存在一个最优的企业养老保险缴费率。为估计最优的企业养老保险缴费率,这里采用多项式拟合。通过图5中的拟合结果公式可以算出经济增长率取最大值时的企业养老保险缴费率为16.454%,此值与中国此次降低企业养老保险缴费率至16%相对吻合。根据OECD国家的经验和叶克斯—道森定律,降低企业养老保险缴费率不是无限制的,而是存在一个最优值。当前中国把企业养老保险缴费率从20%降至16%是有利于经济增速的提高的。但是如果在16%的基础上继续降低,根据OECD国家经验和前述理论推断,可能会不利于经济增长率的提升。
根据OECD国家的历史经验,把方程(11)代入方程(10)。在不改变个人账户养老保险缴费率的情况下,为考察降低企业养老保险缴费率对未来中国实际潜在经济增长率的影响,在此设定三种情景:其一,企业养老保险缴费率为20%(简称BS);其二,企业养老保险缴费率为16%(简称tau1=16%);其三,企业养老保险缴费率为12%(简称tau2=12%)。
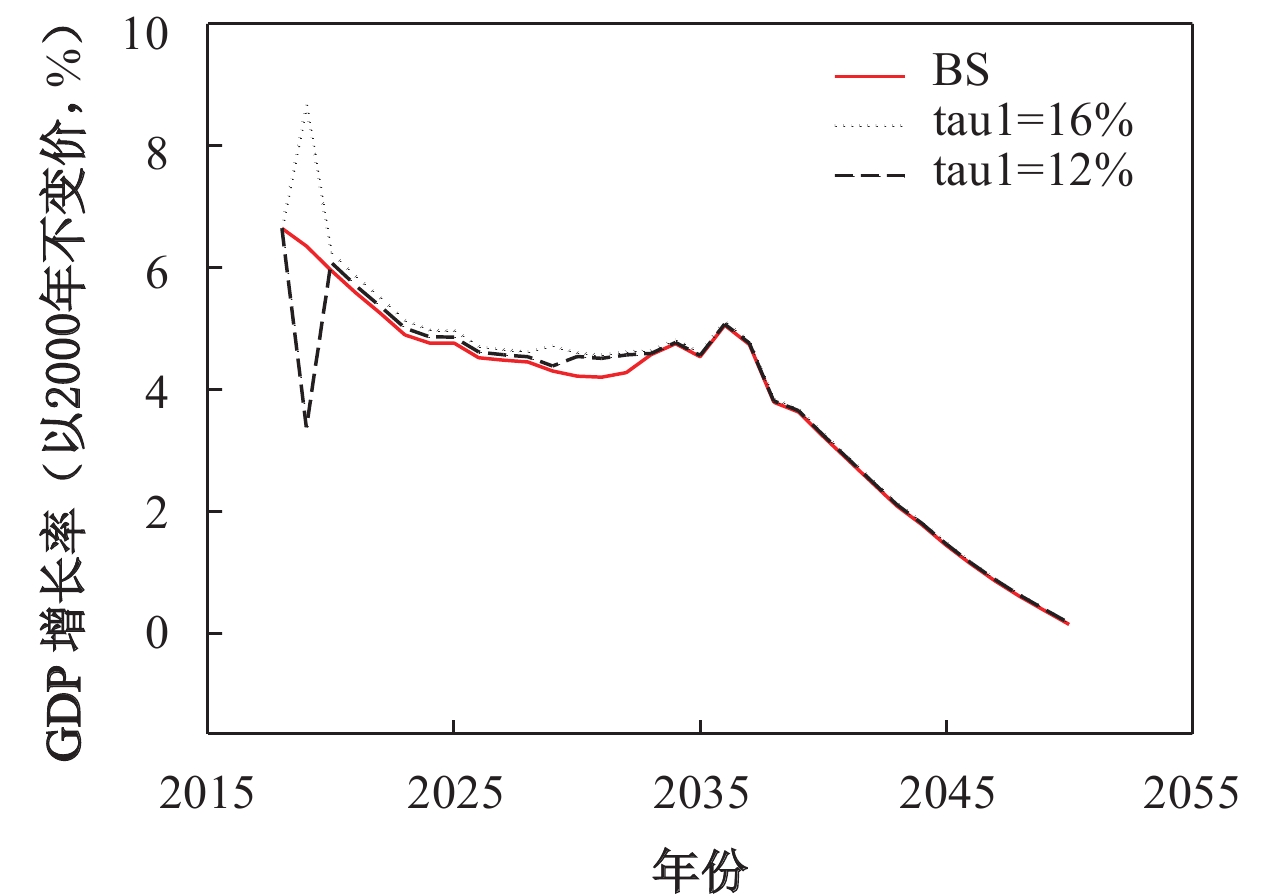
依据现实可行参数进一步模拟发现(见图6):其一,相比企业养老保险缴费率20%,如果把企业养老保险缴费率降至16%,的确可以提升未来中国实际潜在经济增长率且短期效果较好,长期效果微弱。在实现两个百年目标的2019–2021年、2022–2050年和2019–2050年间,相对于企业养老保险缴费率保持不变情况下的平均经济增速分别为5.913%、3.299%和3.544%,企业养老保险缴费率降至16%后的平均经济增速则分别为6.885%、3.431%和3.755%,分别平均提升经济增速0.912%、0.132%和0.211%,这与前述研究结果是一致的。其二,如果在企业养老保险缴费率16%的基础上继续降低企业养老保险缴费率,比如降低至12%,相比当前企业养老保险缴费率16%,则此情景会有损经济增长率,但依然可以得出短期影响较大、长期效果不太明显的结论。
|
| 图 6 降低企业养老保险缴费率下的潜在经济增长率 |
综上,至少从OECD国家的历史经验来看,这次中国企业养老保险缴费率降至16%是有效率的;同时企业养老保险缴费率不是越少越好,企业养老保险缴费率与经济增长率之间呈现倒U形关系,企业养老保险缴费率存在一个最优值16.454%。
(二) 提升个人账户缴费率根据上述模拟研究我们发现,降低企业养老保险缴费率至16%,虽然促进了未来中国实际潜在经济增长率的提高,但是同时也表明降低企业养老保险缴费率会导致当前劳动人口未来养老福利的降低,此外,降低企业养老保险缴费率的长期效果有限。2050年是中国两个百年目标的关键期,保障老年人福利又是两个百年目标的重要内涵和组成部分。我们如何在利用降低企业养老保险缴费率促进短期经济增长的同时,构建降低企业养老保险缴费率的配套性政策,规避其对当前和未来老年人福利的负面影响以及保障其长期的效果呢?
根据中国现收现付制占主导的统账结合养老保险制度的特点,企业当前上缴的统筹账户养老金供养当前的老年人,劳动人口上缴的个人账户养老金类似储蓄,为自己的将来养老。劳动人口未来的养老金来自未来劳动人口上缴的统筹账户养老金和自身当前上缴的个人账户养老金。基于当前中国统账结合的养老保险制度,为保障当前劳动人口未来的养老福利,我们需要在降低劳动人口未来统筹账户提供的养老金的同时,增加个人账户的养老金。在降低企业养老保险缴费率的同时,我们提升个人账户养老保险缴费率,能否在保障劳动人口未来养老福利的同时,不降低未来中国实际潜在经济增长率,甚至还提升未来中国实际潜在经济增长率,尤其是提升未来中国长期实际潜在经济增长率呢?
为回答上述问题,在此设计三种情景:其一,企业养老保险缴费率为20%,个人账户养老保险缴费率为8%(简称BS);其二,企业养老保险缴费率为16%,个人账户养老保险缴费率为8%(简称tau1=16%+tau2=8%);其三,企业养老保险缴费率为16%,个人账户养老保险缴费率为12%,此时在总养老保险缴费率上达到不降低之前的28%水平(简称tau1=16%+tau2=12%)。
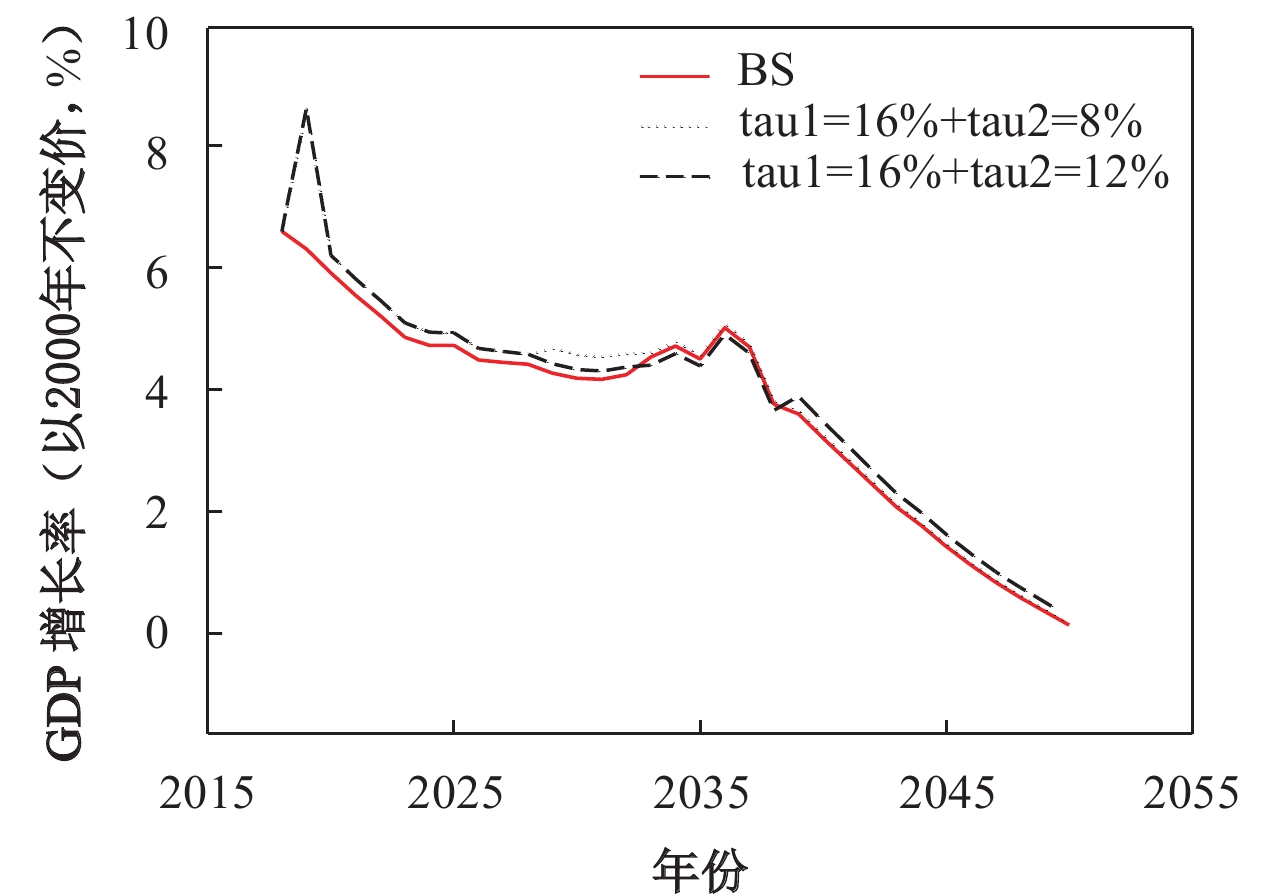
从图7可以看出:其一,相比把企业养老保险缴费率降至16%,同时不提升个人账户养老保险缴费率,如果我们在降低企业养老保险缴费率的同时增加个人账户养老保险缴费率,并且使其达到不降低之前的总缴费率水平,在保障当前劳动人口未来养老福利不降低的情况下,此政策虽然无法改变未来经济增长率下降的趋势,但是整体上略微提升了未来中国的实际潜在经济增长率,大约提升了0.001%,进而实现了政策的帕累托改进。其二,在降低企业养老保险缴费率的同时增加个人账户养老保险缴费率,短期政策效果微弱,但是长期较好地提升了未来中国实际潜在经济增长率,尤其是2038年以后,平均提升历年实际潜在经济增长率约0.171%。
|
| 图 7 提升个人账户养老金缴费率下的潜在经济增长率 |
为什么在降低企业养老保险缴费率的同时,提升个人账户养老保险缴费率能够提升未来中国实际潜在经济增长率,并且长期来看效果更好呢?相比统筹账户养老金的现收现付特征,企业缴纳的养老金当期收取,当期支付,没有积累和增加储蓄,进而没有增加资本变量;由于个人账户养老金具有积累制特征,提升个人账户养老保险缴费率意味着储蓄增加,会引致资本变量增加,在劳动等其他要素不变的情况下,可提升经济增速。
为什么长期效果会更好呢?其一,在家庭决策模型中个人账户养老保险缴费率增加,短期会挤占储蓄,降低资本存量,但是随着个人账户养老保险缴费率的提升,个人账户养老金累积效应凸显,长期来看可以慢慢地弥补对社会储蓄的挤占,进而提升经济增速;其二,相比降低企业养老保险缴费率,即通过减少历年所有老年人的支出,进而促进经济增长,历年提升个人账户养老保险缴费率仅影响劳动人口中临近退休的一个队列,所以直到劳动人口中较多的队列进入老年后,其作用效果才逐渐显现。
五、结论与政策启示为回答降低企业养老保险缴费率至16%是否以及多大程度上会提升未来中国的实际潜在经济增长率的问题,本文通过构建动态可计算一般均衡框架,根据现实可行参数,进行模拟后发现:虽然降低企业养老保险缴费率无法改变中国未来实际潜在经济增长率下降的趋势,并且长期效果甚微,但是降低企业养老保险缴费率至16%的确可以提升未来中国实际潜在经济增长率,短期来看效果更显著。从长远看,降低企业养老保险缴费率至16%,可使2019–2021年、2022–2050年和2019–2050年间的平均实际潜在经济增长率分别提升0.912%、0.132%和0.211%,且这一提升作用对于参数的改变以及考虑到国际OECD国家经验后依然是稳健的。
无论基于模拟分析,还是考虑到国际经验,目前降低企业养老保险缴费率至16%均是有利于经济增长的,而降低企业养老保险缴费率促进经济增长的关键是:其一,各地区落实且各企业执行了降低企业养老保险缴费率政策。如果降低企业养老保险缴费率政策没有真正贯彻落实,则不会如模型展示的那样很好地促进经济增长。其二,如果因降低企业养老保险缴费率而使企业增加的留存没有用于企业生产活动、增加储蓄和提升员工的人力资本等,降低缴费率政策也将不会如模型展示的那样很好地促进经济增长。
上述研究的政策启示在于,为释放企业活力,贯彻落实降低企业养老保险缴费率政策,国家应该建立相应的激励措施,督促各地区和各企业尽快制定相关降低企业养老保险缴费率的实施细则,构建降低企业养老保险缴费率的政策路径,并且真正把这项政策落实。降低企业养老保险缴费率可通过增加储蓄和资本存量来促进经济增长,还可通过未来老年养老保障的不确定性,督促员工进行人力资本积累和提升劳动生产率来促进经济增长。这意味着要实现降低企业养老保险缴费率来促进经济增长,需要将降低企业养老保险缴费率所增加的企业储蓄用于增加资本存量、技术研发、员工培训、员工福利等有利于资本和人力资本提高的生产活动中。
考虑到OECD国家的经验,进一步统计和模拟发现,如果在企业养老保险缴费率16%的基础上,继续降低企业养老保险缴费率可能会抑制经济增长。这说明企业养老保险缴费率不是越低越好,越低意味着劳动人口的未来养老越缺乏保障,进而会影响工作期间的人力资本积累和劳动生产率。因此,应该把企业养老保险缴费率保持在一个合理的范围内,从OECD国家来看,当前中国的16%是一个较为合理的企业养老保险缴费率。考虑到降低企业养老保险缴费率长期效果有限且不可能无限制降低,在降低企业养老保险缴费率来提升短期经济增长率的同时,国家也应该积极寻找其他更有效的促进经济增长的举措。
考虑到降低企业缴费率会损害当前劳动人口未来的养老福利,进一步研究表明,如果在降低企业缴费率的同时,提升个人账户养老保险缴费率至12%,使得总养老保险缴费率达到不降之前的28%,不仅保障了劳动人口未来的养老福利,还提升了未来的经济增长率,从长期来看效果更好,最终实现政策的帕累托改进。这给我们的政策启示在于,从长期来看,降低企业养老保险缴费率不易单独实施,为实现政策的帕累托改进,需要在降低企业养老保险缴费率的同时,尝试提升个人账户养老保险缴费率。降低统筹养老保险缴费率和提升个人账户养老金缴费率均能有效地促进经济增长,前者短期有效,后者长期有效。如果两者组合就是当前的养老制度转轨,在老龄化的社会下从现收现付制的养老制度转轨为基金制的养老制度,能够在尽可能少地降低老年人福利损失的同时,提升中国未来实际潜在经济增长。
| [1] | 陈昌兵. 可变折旧率估计及资本存量测算[J].经济研究,2014(12). |
| [2] | 董克用, 张栋. 高峰还是高原?——中国人口老龄化形态及其对养老金体系影响的再思考[J].人口与经济,2017(4). |
| [3] | 封进. 中国养老保险体系改革的福利经济学分析[J].经济研究,2004(2). |
| [4] | 高彦, 杨再贵, 曹园. 调整养老保险缴费率对内需和养老金待遇的影响[J].当代经济管理,2015(8). |
| [5] | 贺丹, 张许颖, 庄亚儿, 等. 2006–2016年中国生育状况报告——基于2017年全国生育状况抽样调查数据分析[J].人口研究,2018(6). |
| [6] | 洪丽, 曾国安. 养老保险缴费率调整与经济增长: 理论模型与数值模拟[J].社会保障研究,2017a(2). |
| [7] | 洪丽, 曾国安. 现收现付制、降低缴费率与经济增长——基于中国省际面板数据的经验研究[J].统计与信息论坛,2017b(4). |
| [8] | 黄晨熹. 1964−2005年我国人口受教育状况的变动——基于人口普查/抽查资料的分析[J].人口学刊,2011(4). |
| [9] | 康传坤, 楚天舒. 人口老龄化与最优养老金缴费率[J].世界经济,2014(4). |
| [10] | 李宾, 曾志雄. 中国全要素生产率变动的再测算: 1978–2007年[J].数量经济技术经济研究,2009(3). |
| [11] | 李时宇. 从现收现付制转轨为基金积累制的收益研究——隐性债务下世代交叠一般均衡模型的理论分析及模拟[J].财经研究,2010(8). |
| [12] | 陆旸, 蔡昉. 人口结构变化对潜在增长率的影响: 中国和日本的比较[J].世界经济,2014(1). |
| [13] | 陆铭. 城市、区域和国家发展——空间政治经济学的现在与未来[J].经济学(季刊),2017(4). |
| [14] | 彭浩然, 申曙光. 现收现付制养老保险与经济增长: 理论模型与中国经验[J].世界经济,2007(10). |
| [15] | 彭浩然, 邱桓沛, 朱传奇, 等. 养老保险缴费率、公共教育投资与养老金替代率[J].世界经济,2018(7). |
| [16] | 万春, 许莉. 养老保险缴费率变动的经济增长效应分析——基于资本视角[J].财经理论与实践,2006(6). |
| [17] | 万春. 我国混合制养老金制度缴费率的经济效应分析[J].数量经济技术经济研究,2008(5). |
| [18] | 王广州. 中国人口预测方法及未来人口政策[J].财经智库,2018(3). |
| [19] | 汪伟. 人口老龄化、养老保险制度变革与中国经济增长——理论分析与数值模拟[J].金融研究,2012(10). |
| [20] | 王兴化, 李金凤. 我国养老保险制度的经济效应分析——基于中低收入群体的经济刺激策略[J].财经问题研究,2012(2). |
| [21] | 杨华磊. 世代更迭、人口政策调整与经济增速[J].经济科学,2019(3). |
| [22] | 杨艳东, 车凯丽. 养老保险费率对地方民营经济发展的影响[J].浙江社会科学,2018(2). |
| [23] | 张熠, 卞世博. 我国最优混合养老保险体制的选择: 收益和风险分析[J].财经研究,2012(8). |
| [24] | 赵健宇, 陆正飞. 养老保险缴费比例会影响企业生产效率吗[J].经济研究,2018(10). |
| [25] | Aaron H. The social insurance paradox[J].The Canadian Journal of Economics and Political Science,1966,32(3):371–374. |
| [26] | Barro R J, Lee J W. A new data set of educational attainment in the world, 1950-2011[J].Journal of Development Economics,2013,104:184–198. |
| [27] | Becker G S, Barro R J. A reformulation of the economic theory of fertility[J].The Quarterly Journal of Economics,1988,103(1):1–25. |
| [28] | Diamond P A. A framework for social security analysis[J]. Journal of Public Economics,1997,8(3):275–298. |
| [29] | Feldstein M. Social security pension reform in China[J].China Economic Review,1999,10(2):99–107. |
| [30] | Friedrich B. On the intergenerational pareto efficiency of pay-as-you-go financed pension systems[J]. Journal of Institutional and Theoretical Economics,1989,145(4):643–658. |
| [31] | Ginn J. European pension privatisation: Taking account of gender[J].Social Policy and Society,2004,3(2):123–134. |
| [32] | Jones L E, Schoonbroodt A. Baby busts and baby booms: The fertility response to shocks in dynastic models[J].Review of Economic Dynamics,2016,22:157–178. |
| [33] | Kaganovich M, Zilcha I. Pay-as-you-go or funded social security? A general equilibrium comparison[J].Journal of Economic Dynamics and Control,2012,36(4):455–467. |
| [34] | Li S Y, Lin S L. Population aging and China’s social security reforms[J].Journal of Policy Modeling,2016,38(1):65–95. |
| [35] | Liang J, Wang H, Lazear E P. Demographics and entrepreneurship[R]. NBER Working Papers No. 20506, 2014. |
| [36] | Liao P J. The one-child policy: A macroeconomic analysis[J].Journal of Development Economics,2013,101:49–62. |
| [37] | Psacharopoulos G. Returns to investment in education: A global update[J].World Development,1994,22(9):1325–1343. |
| [38] | Sinn H W. Why a funded pension system is needed and why it is not needed[J]. International Tax and Public Finance,2000,7(4-5):389–410. |
| [39] | Yang H L. The choice of pension and retirement systems when post-1960s baby boomers start to retire in China[J]. China Finance and Economic Review,2016,4(1):1–11. |
| [40] | Zhu X, Whalley J, Zhao X L. Intergenerational transfer, human capital and long-term growth in China under the one child policy[J].Economic Modelling,2014,40:275–283. |
2.School of Management, Minzu University of China, Beijing 100081, China

