文章信息
 | 上海财经大学 2018年20卷第6期 |
- 杨振兵, 王乐琦
- Yang Zhenbing, Wang Leqi
- 中国制造业部门创新网络扩散的酵母效应研究
- A Research on the Yeast Effect of Innovation Network Diffusion in China’s Manufacturing Sector
- 上海财经大学学报, 2018, 20(6): 29-43.
- Journal of Shanghai University of Finance and Economics, 2018, 20(6): 29-43.
-
文章历史
- 收稿日期:2018-05-02

2018第20卷第6期
2.上海财经大学 城市与区域科学学院,上海 200433
技术进步是经济增长的原动力。亚当•斯密在古典经济增长理论的代表性著作《国富论》中指出,劳动生产率的提高是决定国民财富增长的重要因素之一;新古典增长理论则将经济长期增长归因于外生的技术进步;而罗默等著名的经济学家又将技术进步内生化,提出了内生经济增长理论。从经济学理论的发展历程来看,技术进步对经济可持续增长具有决定性作用。
技术进步主要来源于创新。约瑟夫•熊彼特(1912)提出的技术创新理论很好地诠释了创新活动与经济增长的关系,对于大多数国家而言,提升技术水平的重要方式在于自主技术创新,并指出企业家的创新是一个国家技术进步的重要原因。技术创新作为经济增长的引擎,这种引擎作用的强弱取决于创新自身的内部结构,因此,诸多学者普遍认为:创新更多的应该以R&D活动为主,实质性创新应该达到一定的比重,而且要充分发挥创新网络扩散的作用。雷家骕等(2005)指出创新植入增长是率先创新、模仿扩张与创新更替的动态过程。明显地,创新植入增长后的网络扩散活动,不仅有利于整个经济体生产技术水平的提升,而且有利于增长潜能的发挥,这类似于酵母发酵现象,被一些学者形象地称为“酵母效应”(Harberger,1998;张军等,2009)。
在当前中国大力提倡加快实施创新驱动发展战略和《中国制造2025》的背景下,如何准确地把握创新驱动因素对中国制造业的影响,对全面建设创新型国家意义重大。尽管现有研究对创新网络扩散进行了系列研究,但是对酵母效应的关注仍然不足。例如姚云浩和高启杰(2014)认为旅游企业网络的强关系有利于提升企业的创新绩效;沈飞和吴解生(2015)研究发现,创新网络式转换及传播是通过结构化效益差异机制实现的。Sgrignoli等(2015)研究发现创新的网络效应被创新单元的集中度影响,而Bertotti等(2016)则通过一个异质性的网络结构模型考察了创新的扩散时间问题。马永红等(2016)考察了空间约束下的新企业不同合作伙伴搜寻方式对创新扩散效率的影响,发现全局搜寻是更利于集群创新扩散的新进企业合作伙伴搜寻方式。由此可见,尽管这些研究集中于创新网络的扩散机制,但是尚未关注创新网络扩散的酵母效应,即对创新全要素生产率的影响效果。
基于此,本文以中国制造业为研究样本,通过建立实证分析模型,考察创新网络扩散效应对创新效率的影响。相对于现有研究,本文的贡献在于以下几点:(1)基于超越对数生产函数的随机前沿分析方法,在充分考虑了创新活动技术效率损失的前提下,测算了中国制造业创新活动的全要素生产效率;(2)利用中国投入产出协会提供的投入产出表,在技术转移依附于中间品投入的假设下,测算了中国制造业不同行业创新网络的扩散效应指数;(3)采用可以有效控制内生问题的系统广义矩估计方法,考察了创新网络扩散效应对于创新效率的影响,并进一步验证中国制造业创新网络扩散酵母效应的存在。
二、文献回顾与理论机制 (一) 创新扩散效应创新扩散效应即为创新扩散的S形曲线。如果一个封闭的经济体中产生了一项技术创新,一旦有一家企业进行模仿性创新,由示范效应与群体效应导致的模仿者成倍增加,并且在某一时期达到顶峰,表现出创新扩散S形曲线。林雄二郎(1986)以日本转炉炼钢技术的普及为研究对象,对S形创新扩散曲线进行了佐证。
国内的一些学者也纷纷通过理论模型对创新扩散现象进行了考察。陈欣荣和蔡希贤(1996)研究指出创新成果的扩散不仅受经济环境的制约和影响,同时这些创新成果还对经济活动产生影响,进一步影响创新环境。方世建(2001)通过显性和隐性两类创新技术的扩散现象,研究发现技术创新扩散是一个马尔科夫随机过程。楚俊国(2001)采用案例研究的主因素分析方法考察了技术创新扩散速度的影响因素,发现效益是影响扩散速度最为关键的因素。
雷家骕等(2005)研究指出技术扩散方式通常有独立性转移与依附性转移两种方式,前者主要指技术发明者将持有的技术直接转移至厂商等技术需求者;而后者是指技术依附于生产要素或者中间投入产品的转移。本文的研究主题为技术扩散的酵母效应,限于数据与研究样本的可得性,只考察依附性转移的技术扩散方式,即生产技术的转移是依附于产品而进行的。
(二) 创新活动的网络扩散效应将网络模型与创新扩散效应相结合,可以更加准确地了解创新技术在不同行业之间的传递过程。与工业部门从要素投入到产品产出的生产环节类似,创新活动也经历了由创新要素投入到创新产品产出的过程(杨振兵,2016)。而现有研究仅对创新活动的生产效率及其决定因素进行了研究与探讨(白俊红等,2009;肖文和林高榜,2014)。
Acemoglu等(2015)建立了一个商品交易网络与宏观经济发展的理论模型,其指出一个企业生产的产品不外乎两种用途:一是被用作最终产品进行消费;二是被其他企业购买用作中间投入产品。因此,一个企业的生产率的变化也通常来自于两个方面:一是企业自身的技术进步;二是上游行业通过提供中间投入品而实现的技术传递。Acemoglu等(2015)特别指出生产技术进步只会影响下游行业的生产率,而对上游行业的影响不大。
与之类似,创新产出增长效应也可以分为两部分:自身增长效应与网络扩散增长效应。同时还说明,一个行业创新活动生产效率的改善,不但可能源于本行业自主的创新技术进步,也可能源于上游研发技术进步对下游企业进行传递的影响。这是因为上游行业提供的中间投入品,包含着较为先进的创新技术,会通过网络扩散效应传递至下游行业,并对其创新全要素效率水平产生影响。
(三) 创新网络扩散酵母效应的形成机制创新活动的网络扩散效应说明创新技术会从上游行业传递至下游行业,然而这并不能完全解释中国工业部门整体的创新提升现象。与创新扩散理论比较而言,酵母效应理论产生与发展的时间并不长。Harberger(1998)将经济增长形象地概括为两种过程:一种称为蘑菇效应,指生产投入要素不断地从低生产率行业配置到高生产率行业,最终导致不同行业的生产能力具有较大差异;另一种为酵母效应,指对于不同的行业来讲,由于受宏观经济基本面的影响因素相同,最终导致不同行业表现相似的增长状况。
酵母效应理论很好地解释了中国工业部门不同行业之间在增长方式、生产技术进步等方面所表现出惊人的相似度。张军等(2009)曾在研究中指出中国工业部门的轻工业行业和重工业行业的技术进步水平、全要素生产效率增长等方面都表现出相似的演化轨迹,工业部门整体增长的酵母效应十分明显。这说明一些宏观影响因素影响了某些行业之后,这种影响同时也扩展至其他行业,这种由于不同行业之间存在技术溢出导致的效率改善,如同酵母发酵过程一样,最终促进中国工业整体的经济发展。
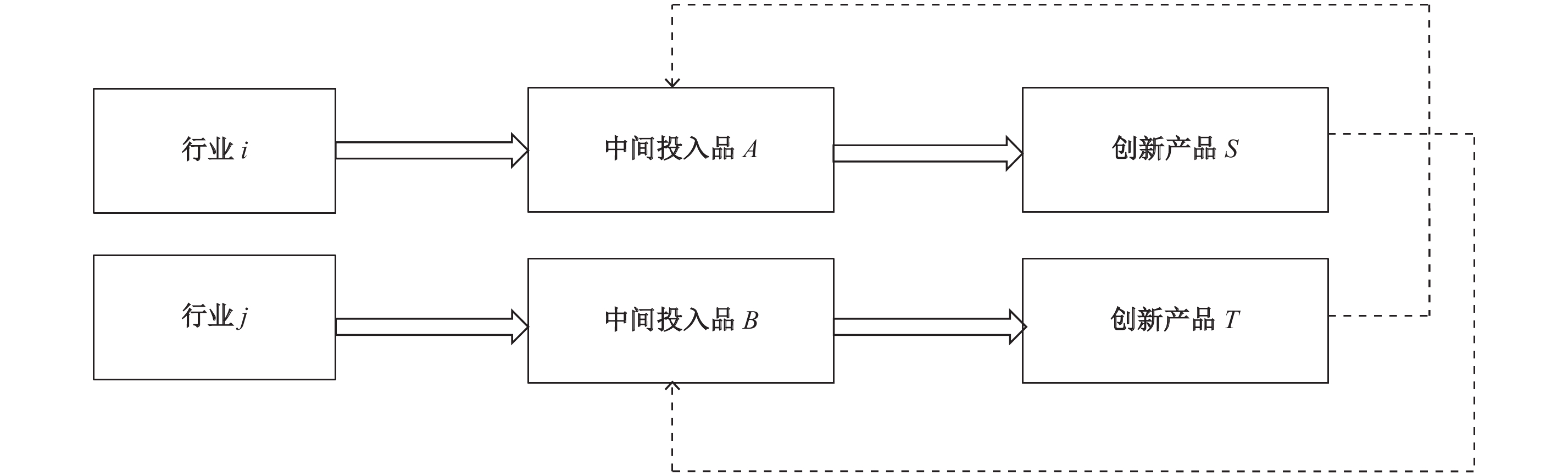
创新活动同样可以产生酵母效应。在生产技术依附于产品转移与扩散的假设下,由于不同行业之间相互提供中间投入品,于是创新活动导致的技术进步会通过中间投入品的使用进行传递与扩散,导致制造业整体生产技术水平的提升,即创新活动的酵母效应。创新活动的酵母效应具体表现为创新成果的扩散导致制造业整体创新效率的提升。以两个行业i与j为例(如图1所示),行业i在生产过程中采购中间投入品A,并且生产创新产品S;而行业j在生产过程中采购中间投入品B,生产创新产品T。由于部分创新产品T被行业i进行采购,因此新的生产技术伴随着产品T转移至行业i的生产过程中;同时部分创新产品S中的领先技术被转移至行业j的生产过程中,这种创新扩散效应最终引起整个制造业整体的技术进步,表现出创新活动扩散的酵母效应。
|
| 图 1 创新扩散酵母效应形成机制 |
考虑到现有文献仅从理论模型的角度论证创新网络扩散的现象,对于实证研究的文献尚且少见。因此,本文将通过设定实证考察模型,分析创新网络扩散效应对中国制造业创新全要素生产效率的影响,从而进一步检验创新网络扩散酵母效应的存在。
三、研究设计 (一) 模型设定本文进一步通过建立实证模型考察创新网络扩散对制造业行业创新活动全要素生产效率的影响效果,以期准确评估不同行业之间创新网络扩散的酵母效应,基本模型设定如下:
| $I\!t\!f\!{p_{it}} = {\alpha _0} + {\alpha _1}Idif\!{f_{it}} + {\alpha _2}C{V_{it}} + {\varepsilon _{it}}$ | (1) |
其中,
这样,模型的具体形式如下:
| $I\!t\!f\!{p_{it}} = {\alpha _0} + {\alpha _1}Idif\!{f_{it}} + {\alpha _2}FD{I_{it}} + {\alpha _3}GO{V_{it}} + {\alpha _4}Ente{r_{it}} + {\alpha _5}K{L_{it}} + {\varepsilon _{it}}$ | (2) |
针对各变量的计算方法我们做出如下说明:
1. 创新效率。与一般的生产活动的过程类似,创新活动也经历了由创新投入到创新产出的过程,与现有研究一致(白俊红等,2009),我们将创新活动的全要素生产效率作为创新效率的替代变量。本文采用随机前沿分析(SFA)方法(Aigner等,1977;Meeusen和van den Broeck,1977)对创新活动的tfp进行测算。相对于柯布道格拉斯(C-D)生产函数与不变替代弹性(CES)生产函数而言,由于超越对数生产函数进一步放松了替代弹性固定的严格假设,可以充分反映投入要素之间的替代效应和交互作用,同时还可以加入时间因素来反映不同投入要素技术进步的差异性,因而能够揭示经济系统的更多内在特征(涂正革和肖耿,2005;杨振兵等,2015)。因此,本文设定的生产函数如下:
| $\begin{array}{c}\ln {Y_{it}} = {\alpha _0} + {\alpha _1}t + \displaystyle\frac{1}{2}{\alpha _2}{t^2} + {\alpha _3}\ln {K_{it}} + {\alpha _4}\ln {L_{it}} + {\alpha _5}t \times \ln {K_{it}} + {\alpha _6}t \times \ln {L_{it}}\\ + \displaystyle\frac{1}{2}{\alpha _7}\ln {K_{it}} \times \ln {L_{it}} + \frac{1}{2}{\alpha _8}{(\ln {K_{it}})^2} + \frac{1}{2}{\alpha _9}{(\ln {L_{it}})^2} + {v_{it}} - {u_{it}}\end{array}$ | (3) |
其中,Y为创新产出;i为行业;t为时间;K为创新活动的资本投入,即R&D资本存量;L为创新活动的劳动投入。v为随机误差项,是不可控的影响因素,作为具有随机性的系统非效率计算,且有
创新活动的技术效率即创新活动实际产出与生产前沿期望的比值为:
| $T{E_{it}} = \frac{{E[f({{\bf{x}}_{it}},{\bf{\beta }})\exp ({v_{it}} - {u_{it}})]}}{{E[f({{\bf{x}}_{it}},{\bf{\beta }})\exp ({v_{it}} - {u_{it}})\left| {{u_{it}} = 0} \right.]}} = \exp ( - {u_{it}})$ | (4) |
根据Battese和Coelli(1992)对生产无效率项的设定,
参考现有研究(Kumbhakar等,2000),创新活动的tfp计算方式如下:
| $I\!t\!f\!{p_{it}} = T\!{C_{it}} + T\!E{C_{it}} + S\!{E_{it}}$ | (5) |
其中,等号后面三项的含义依次是技术进步、技术效率变化与规模效率。其中,技术进步(TC)的计算方式为:
| $T\!{C_{it}} = \frac{{\partial \ln f{\rm{(}}{{\bf{x}}_{it}}{\rm{,}}{\bf{\beta }}{\rm{)}}}}{{\partial t}} = {\alpha _1}{\rm{ + }}{\alpha _2}t + {\alpha _5}\ln K + {\alpha _6}\ln L$ | (6) |
技术效率变化(TEC)的计算方式为:
| $T\!E{C_{it}} = \frac{{\partial \ln T\!{E_{it}}}}{{\partial t}} = \frac{{\partial \ln \exp ( - {u_{it}})}}{{\partial t}} = - \frac{{\partial {u_{it}}}}{{\partial t}}$ | (7) |
规模效率(SE)的计算方式为:
| $S\!{E_{it}} = (RT{S_{jit}} - 1)\sum\nolimits_j {{\lambda _{jit}}} {\dot x_{jit}}$ | (8) |
其中,
2. 创新网络扩散指数。创新活动引致技术水平的提升最终体现在产品上,而制造业部门不同行业之间创新型中间投入品的投入与使用,可以实现先进技术水平的传递与扩散。如图1所示,行业i生产过程中所需的中间投入品A包含部分来自其他行业的创新产品。根据Acemoglu等(2015),一个行业生产技术改进只会对下游行业生产率的变化产生影响,这意味着本文的创新网络扩散指数需要测度本行业消耗的其他行业提供的中间投入品中创新产品的数量比重。因此,为了准确地刻画该创新网络扩散效应,本文借鉴Javorcik(2004)关于不同行业间外资企业生产技术溢出的思路,并采用如下创新网络扩散指数的计算公式:
| $Idif\!{f_{it}} = \sum\limits_{j,i \ne j} {{\xi _{ij}}\frac{{{Y_{jt}}^T}}{{{Y_{jt}}}}} $ | (9) |
其中,
3. 控制变量。本文中所有控制变量的选择依据与计算方法见表1。
| 变量 | 选取理由 | 计算方法 | 单位 |
| FDI | 外资企业通常生产技术水平较高,且存在对本土企业的技术溢出效应(张诚等,2001;陈涛涛和陈娇,2006),从而对工业企业的创新行为具有一定的影响 | 行业外资企业产值/行业总产值 | % |
| GOV | 白俊红等(2009)指出,政府对企业创新活动的资助会影响创新投入要素的价格,并影响创新投入与产出的数量,从而进一步影响创新效率 | 企业创新活动经费来源中政府资金所占比重 | % |
| Enter | 企业自有资金对创新活动的支持,由于将创新研发的沉没成本纳入成本收益核算,可能将有利于企业创新能力的改善,并进一步对创新全要素生产效率产生影响(杨振兵,2016) | 企业创新活动经费来源中企业自有资金所占比重 | % |
| KL | 根据现有研究结论(如杨振兵,2016),即创新投入的要素结构影响创新投入与产出水平,进一步对创新全要素生产效率产生影响 | 创新资本投入/创新劳动投入 | 万元/人 |
式(2)的设定意味着各变量对被解释变量的影响都是瞬间发生的,忽略了创新活动的效果滞后性。由于创新活动的开展往往需要大量的知识沉淀,前期的创新全要素生产效率会对当期产生一定的影响,因此创新活动的全要素生产效率往往存在一定的路径依赖特征,因此,本文将式(2)进一步修改为:
| $It\!f\!{p_{it}} = {\alpha _0} + \chi Itf\!{p_{it - 1}} + {\alpha _1}Idi\!f{f_{it}} + {\alpha _2}F\!D{I_{it}} + {\alpha _3}GO{V_{it}} + {\alpha _4}Ente{r_{it}} + {\alpha _5}K{L_{it}} + {\varepsilon _{it}}$ | (10) |
其中各变量的统计性描述与相关系数矩阵我们报告于表2与表3。从表3来看,各个变量之间的相关系数均不超过0.4,因此可以忽略多重共线性的问题。
| 变量 | 样本容量 | 均值 | 标准差 | 最小值 | 最大值 |
| Idiff | 308 | 0.130 5 | 0.068 2 | 0.018 6 | 0.329 8 |
| FDI | 308 | 0.255 2 | 0.119 7 | 0.000 0 | 0.743 7 |
| GOV | 308 | 0.029 5 | 0.021 8 | 0.001 1 | 0.155 2 |
| Enter | 308 | 0.895 9 | 0.064 2 | 0.638 4 | 0.990 7 |
| KL | 308 | 59.186 6 | 37.552 2 | 2.556 0 | 402.117 0 |
| 变量 | Idiff | FDI | GOV | Enter | KL |
| Idiff | 1 | 0.320 2 | 0.135 2 | 0.184 0 | 0.085 8 |
| FDI | 0.320 2 | 1 | –0.131 7 | 0.186 3 | –0.144 0 |
| GOV | 0.135 2 | –0.131 7 | 1 | –0.278 4 | 0.383 0 |
| Enter | 0.184 0 | 0.186 3 | –0.278 4 | 1 | –0.093 9 |
| KL | 0.085 8 | –0.144 0 | 0.383 0 | –0.093 9 | 1 |
式(10)中被解释变量与解释变量之间可能存在由于双向因果关系而产生的内生性问题。例如创新网络扩散效应有利于将不同行业的创新型中间投入品的先进技术应用到某一行业,从而提升了该行业的创新全要素生产效率;而某一行业创新全要素生产效率的提升,将生产更多的创新产品,提高创新产品在总产值中的比重,从而有利于创新网络扩散效应的发挥,二者存在双向因果关系。因此,为规避模型中可能由此而导致的内生性问题,我们选择系统广义矩估计方法(GMM)对式(10)进行参数估计②。
(三) 数据说明本文采用中国制造业2001–2012年的创新投入与产出数据,计算得出2002–2012年创新活动的全要素生产率,所建立的动态面板数据模型的样本区间亦为2002–2012年。式(9)中的直耗系数来自于各年份投入产出表中的列向量,由于样本区间内中国投入产出协会只提供了2002年、2005年、2007年和2012年的投入产出表,而其余诸多年份的投入产出表缺失,囿于数据可得性,按照现有研究的做法(杨亚平,2007;Yang等,2017),本文采用相近年份的投入产出表进行计算,2002–2003年的创新网络扩散指数计算过程采用2002年的投入产出表,2004–2006年的创新网络扩散指数计算过程采用2005年的投入产出表,剩余年份采用2007年的投入产出表。2012年尽管公布投入产出表,但是并未公布直耗系数,而且利用现有资料无法计算获取,因此亦采用相近年份2007年的投入产出表。式(7)中的超越对数生产函数的投入产出数据来自历年的《中国科技统计年鉴》。由于中国投入产出表中的行业分类与《中国科技统计年鉴》中行业分类不完全一致,根据杨振兵等(2015)提供的行业合并法则,某个年份某些行业的直耗系数是相同的。此外,本文中所有含价格因素的变量全部平减为2000年不变价格序列,具体的投入产出数据指标说明如下:
(1)创新产出(Y)。现有研究选择了专利授权数量作为创新产出(白俊红等,2009),然而,仍有很多权威研究指出由于专利质量的差异,无法准确体现创新成果的经济价值(Griliches,1990;吴延兵,2006),加之工业行业的专利数据并不规整,某些年份缺失较多。我们参考Zhang等(2003)、朱有为和徐康宁(2006)的做法,采用新产品产值作为创新产出变量。
(2)创新R&D资本存量(K)。R&D 经费支出是一项流量指标,参考吴延兵(2006)、白俊红等(2009),我们用永续盘存法计算R&D资本存量,具体的计算方法为:
(3)创新劳动投入(L)。由于R&D 人员全时当量的数据缺失年份较多,我们选取报告期内R&D人员数予以度量。
由于相关年鉴中的统计口径有所调整,我们对制造业行业样本的选取也进行了相应的整理,年鉴中后来出现的“工艺品及其他制造业”“废弃资源和废旧材料回收加工业”“金属制品、机械和设备修理业”三个行业没有包含在本研究范围之内。2012年“交通运输设备制造业”数据为“汽车制造业”与“铁路、船舶、航空航天和其他运输设备制造业”之和,“橡胶制品业”与“塑料制品业”的数据由“橡胶和塑料制品业”根据2011年两个行业各自所占比重求得。为方便描述,本文所考察的剩余28个制造业细分行业(包含14个轻工业,14个重工业)按照统计年鉴中出现的先后顺序依次标记为S1、S2、S3、…、S28,限于篇幅,轻重工业的划分结果请参考Fan等(2015),此处不再赘述。
四、基本结果讨论 (一) 创新活动tfp的估算结果1. 超越对数生产函数估计结果。式(1)的参数估计结果如表4所示。从表4可以看到,绝大多数参数是显著的,且很多是在1%的水平上显著,说明模型变量设置具有很强的合理性。从模型整体的诊断性指标和生产无效率的检验结果来看,极大似然估计值和单侧LR检验值同样表明模型的解释力较为理想。总体方差
| 变量 | 系数 | t值 | 变量 | 系数 | t值 |
| α0 | 3.954 6***(0.681 1) | 5.806 2 | α5 | –0.022 1* | (0.013 5)–1.639 9 |
| α1 | –0.069 9(0.093 3) | –0.749 6 | α6 | –0.014 5***(0.003 0) | –4.758 7 |
| α2 | 0.031 6***(0.008 6) | 3.681 2 | α7 | 0.226 3***(0.089 2) | 2.538 1 |
| α3 | –0.043 1**(0.020 6) | –2.092 9 | α8 | 0.337 6***(0.094 5) | 3.571 5 |
| α4 | 0.655 3**(0.307 9) | 2.128 6 | α9 | –0.297 9**(0.169 9) | –1.753 6 |
| σ2 | 0.196 8***(0.036 5) | 5.399 3 | μ | 1.244 0***(0.321 4) | 3.870 0 |
| γ | 0.939 1***(0.124 5) | 7.542 8 | |||
| 对数似然函数(log likelihood function)值 | –484.27 | ||||
| LR检验值 | 327.44 | ||||
| 注:括号中是回归系数标准误;***、**和*分别表示1%、5% 、10% 的显著性水平。下同。 | |||||
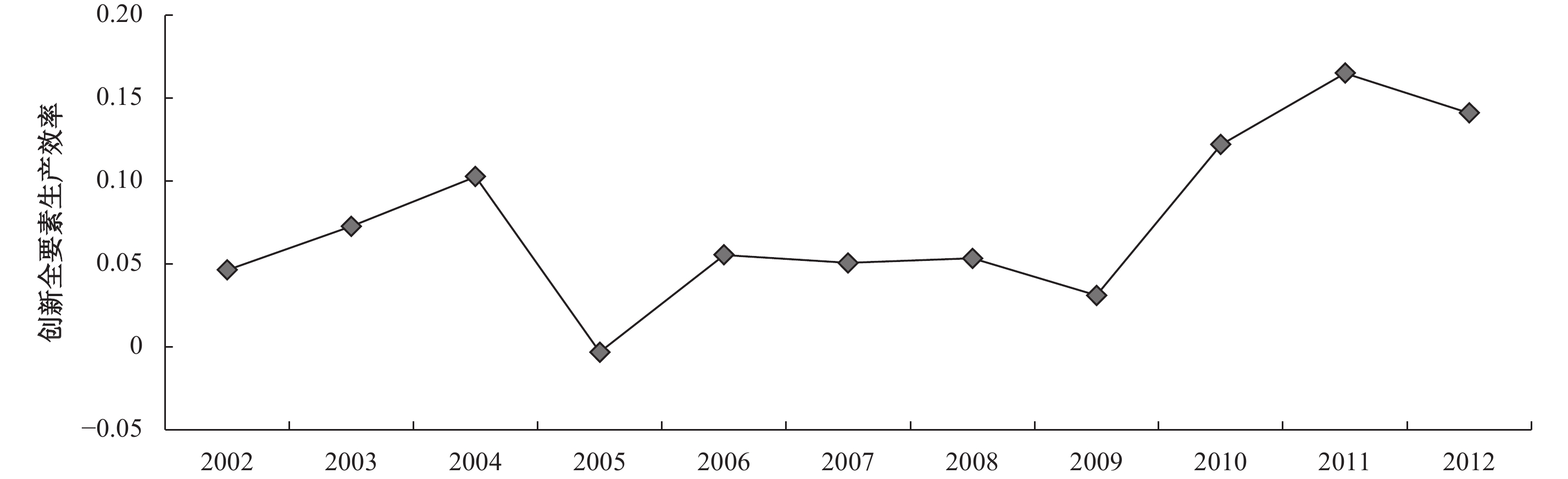
2. 创新全要素生产效率测算结果。本文的创新全要素生产效率结果如图2所示。从图2可以看出,虽然总体来看中国创新全要素生产效率起伏波动,但大致呈现先降后升的趋势。可以看出2005年是明显且短暂的下降拐点,这是由于相比2004年而言,2005年的创新资本和创新劳动投入均保持高速增长,但是创新产出的增长幅度却较小③。根据计算结果,2005年比2004年的创新资本投入增长23.13%,创新劳动投入增长17.58%,而创新产出的增长率仅为4.33%。明显地,这最终导致2005年创新全要素生产效率的下降,甚至为负。
|
| 图 2 中国制造业总体创新全要素生产效率 |
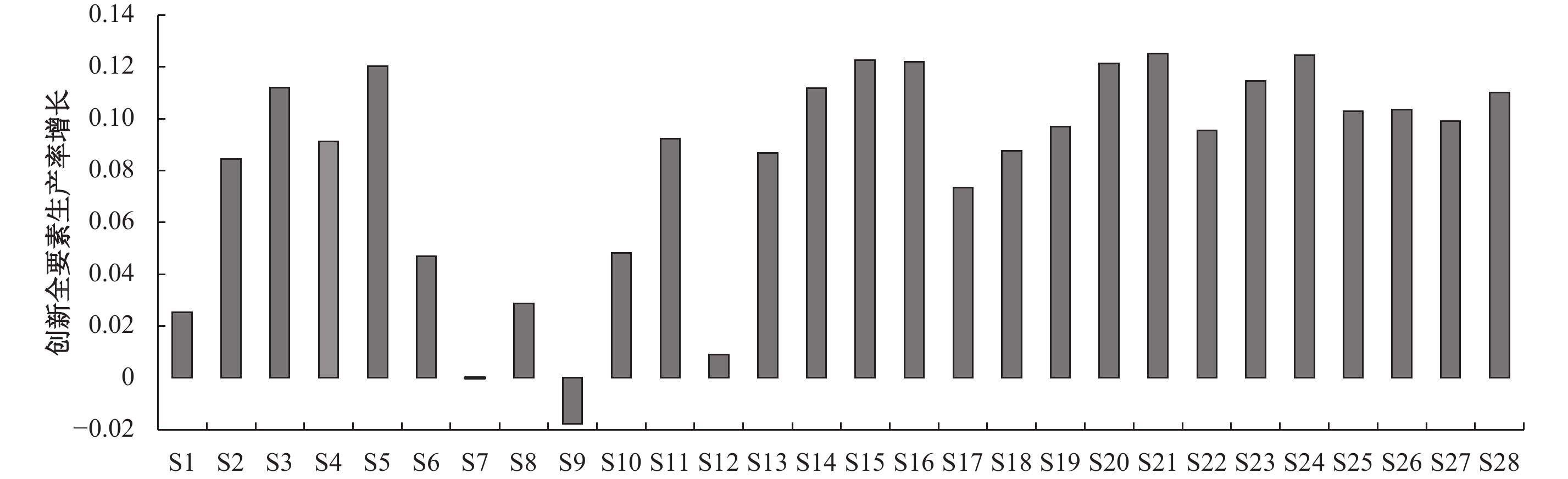
从行业层面来看(如图3所示),中国制造业部门不同行业的创新全要素生产效率增长具有较大的差异,创新全要素生产效率增长幅度较高的典型行业有有色金属冶炼及压延加工业(S21)和专用设备制造业(S24),增长率分别为12.51%和12.4%;而创新全要素生产效率增长幅度较低的行业为皮革毛皮羽绒制品业(S7)和家具制造业(S9),增长率分别为0.02%和–1.77%。特别地,对于家具制造业来讲,2009年之前创新全要素生产效率增长率一直为负,直到近些年才转为正值,说明如果该行业可以优化创新要素投入结构,提升创新投入的产出效率,那么该行业的创新全要素生产率可能会有较大提升。因此,该行业仍然具有巨大的创新潜力。
|
| 图 3 中国制造业28行业创新全要素生产效率增长率 |
我们将式(10)的估计结果报告于表5,模型1–5为逐次加入各变量的估计结果,其中模型1只考虑创新网络扩散指数,而模型2–5依次加入了外资比重、企业自有资金支持、政府资金支持、创新投入要素结构。从各模型Arellano-Bond检验与Sargan检验的结果来看,我们所选择的滞后期数与工具变量也都是合理的。
| 变量 | 模型1 | 模型2 | 模型3 | 模型4 | 模型5 |
| L.Itfp | 0.668 0*** | 0.675 0*** | 0.695 0*** | 0.697 0*** | 0.699 0*** |
| (0.000 7) | (0.001 6) | (0.004 9) | (0.005 7) | (0.006 2) | |
| Idiff | 0.901 0*** | 1.004 0*** | 1.087 0*** | 1.080 0*** | 1.038 0*** |
| (0.017 4) | (0.034 8) | (0.053 6) | (0.055 5) | (0.033 2) | |
| FDI | 0.529 0*** | 0.449 0*** | 0.474 0*** | 0.479 0*** | |
| (0.015 5) | (0.048 2) | (0.060 4) | (0.061 9) | ||
| Enter | 0.144 0*** | 0.140 0*** | 0.107 0*** | ||
| (0.022 0) | (0.026 7) | (0.030 6) | |||
| Gov | –0.216 0** | –0.272 0*** | |||
| (0.085 5) | (0.088 5) | ||||
| KL | –0.009 8*** | ||||
| (0.003 4) | |||||
| 常数项 | 0.191 0*** | 0.035 5*** | 0.159 0*** | 0.144 0*** | 0.120 0*** |
| (0.002 3) | (0.004 7) | (0.028 4) | (0.032 7) | (0.035 8) | |
| AR(1)检验 | –3.009 8 | –2.908 1 | –2.841 4 | –2.880 5 | –2.954 5 |
| (0.002 6) | (0.003 6) | (0.004 5) | (0.004 0) | (0.003 1) | |
| AR(2)检验 | –1.385 9 | –1.400 7 | –1.501 7 | –1.518 4 | –1.482 6 |
| (0.165 8) | (0.161 3) | (0.131 8) | (0.128 9) | (0.138 2) | |
| Sargan检验 | 27.949 8 | 27.774 4 | 27.715 6 | 27.656 0 | 27.292 4 |
| (0.467 1) | (0.476 4) | (0.479 6) | (0.482 8) | (0.502 4) | |
| 工具变量个数 | 31 | 32 | 33 | 34 | 35 |
| 样本容量 | 308 | 308 | 308 | 308 | 308 |
| 注:各变量的括号中为回归系数标准误;Arellano-Bond检验与Sargan检验中括号内为相伴概率。下同。 | |||||
模型5中L. Itfp的系数显著为正,说明前期的创新全要素生产效率水平对当期水平具有积极影响,意味着创新全要素生产效率存在明显的动态延续性特征,由于创新活动是一个由知识积累到成果产生的漫长过程,前期的技术沉淀与创新经验将对后期的创新活动具有重要帮助,因此,创新全要素生产效率表现出一定的路径依赖特征。
模型5中Idiff的系数显著为正,意味着创新网络扩散指数对行业创新全要素生产率具有积极影响,说明创新网络扩散程度的提高有利于提升制造业整体的创新全要素生产效率。这是由于生产技术往往依附于产品而进行转移与扩散,当某行业采购其他行业提供的中间投入品时,如果这些中间投入品采用了较为先进的生产技术,那么该行业所生产的最终产品的技术含量也随之提升,这将有利于该行业内企业的生产技术进步,在提升整体生产效率的同时,也使得产品质量与效益得到进一步改善。需要说明的是,创新网络扩散效应并不仅仅发生于一个行业而终止,生产技术得到改善的行业同样也为其他行业提供中间投入品,其先进的生产技术将会再次进行转移,使得创新技术蔓延至整个制造业部门,如同酵母发酵过程一样,导致整个制造业部门整体的创新效率不断改善。根据Acemoglu等(2015),技术冲击虽然只影响了下游行业的全要素生产率,但是对于中国制造业行业而言,每个行业均处于其他行业的下游位置,这意味着所有行业均可以得到来自其他行业的创新技术供给,最终导致整体创新效率的改善。我们的实证研究结果证明,创新网络扩散有利于提升创新全要素生产效率,这进一步说明创新网络扩散的酵母效应十分明显。
对于各控制变量的估计结果我们作出如下解释:(1)FDI的系数显著为正,说明外资企业比重的上升,有利于制造业行业创新全要素生产效率的提升。诸多学者已经指出,跨国公司对本土企业存在技术溢出效应(张诚等,2001;陈涛涛和陈娇;2006),这有利于本土企业技术水平的提升,当然对于本土企业创新活动来讲也是有益的。(2)Enter的系数显著为正,说明企业自有资金支持有助于创新全要素生产效率的提升,这是由于企业自有资金支持作为研发投入的一项沉没成本纳入企业成本核算,增加了企业的创新研发动力。(3)Gov的系数显著为负,意味着政府对企业创新项目的支持不利于创新效率的提升,该结论与白俊红等(2009)研究结论一致,其解释为政府的创新活动资助行为会挤出企业R&D投资,且有可能提升创新投入的成本。而我们认为,政府通过税收抵扣、补贴等方式对企业创新活动的支持之所以对创新全要素生产效率产生消极影响,是因为工业企业没有将这部分创新研发成本纳入自己的盈亏核算而丧失了创新动力。(4)KL的系数显著为负,说明创新投入要素结构的资本化程度的提升将对创新全要素生产效率产生消极影响。这说明如果创新要素投入结构只重视资本投入而忽略了创新研发人员的投入,将不利于创新全要素生产效率的提升,在一定程度上这与党的十八大提出的“创新驱动的关键在于人”的指导方针不谋而合。
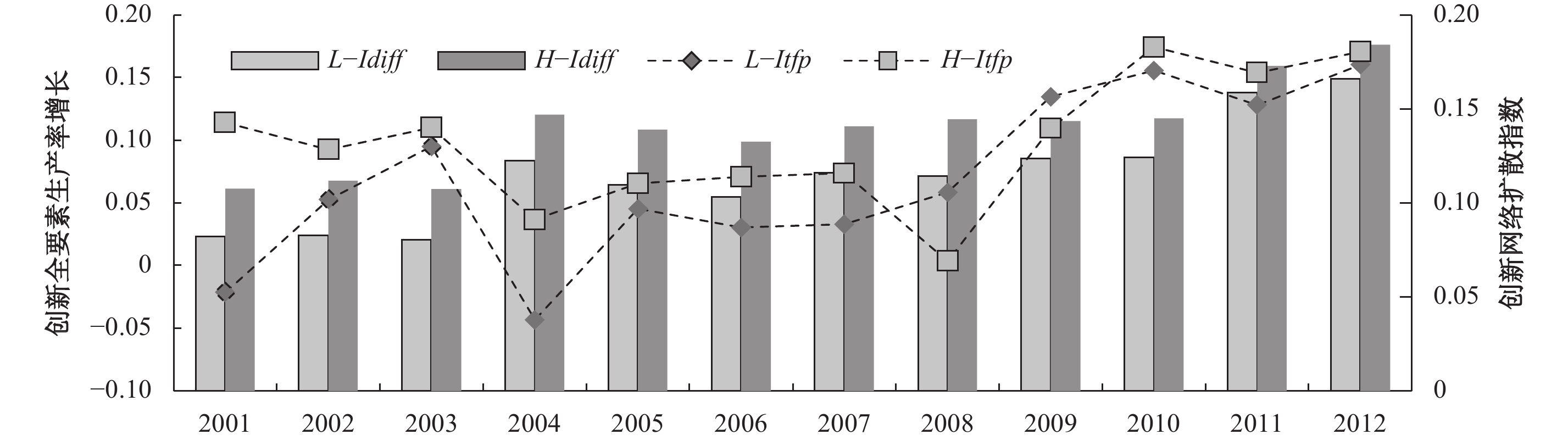
五、稳健性检验:轻工业与重工业的分析前文考察了中国制造业整体的创新网络扩散效应,接下来,我们通过对轻工业部门与重工业部门单独考察以对前文的估计结果进行稳健性检验,本文参考Fan等(2015)的做法,将整体的制造业行业划分为轻工业与重工业。从图4可以看出,在样本区间内,重工业各年创新网络扩散指数均大于轻工业,这是由于这两类行业对国民经济的贡献有差别,轻工业行业的产品主要用于居民生活消费,整体而言技术水平相对较低(杨智峰等,2016),因此其采购的中间投入品中创新产品数量相对较少;而重工业行业的产品为各部门提供物质资本支持,整体而言技术水平相对较高(朱劲松和刘传江,2006),其采购的中间投入品中创新产品数量相对较多。因此重工业行业的扩散指数要普遍高于轻工业行业。
|
| 图 4 轻工业与重工业的创新网络扩散指数与全要素生产率增长 注:L(H)-Idiff表示轻(重)工业创新网络扩散指数;L(H)-tfp表示轻(重)工业创新全要素生产率增长。 |
而就创新全要素生产效率增长率来看,除少数年份外(2008年和2009年),重工业的创新全要素生产效率增长率要高于轻工业水平。这两者的关系与轻重工业的创新网络扩散指数差异比较接近。因此,从直观上可以看出,重工业的创新网络扩散效应大于轻工业,从而导致重工业的创新全要素生产效率增长大于轻工业。为此,我们需要进行进一步的实证检验。
根据式(10)的模型,本文依然采用可以控制内生性问题的系统广义矩估计(GMM)方法分别对轻工业样本与重工业样本进行考察,并将估计结果报告于表6。从两个模型的相关检验(Arellano-Bond 检验与Sargan检验)可以发现,本文的滞后期数与工具变量也都是合理可行的。后面,我们将重点对于创新网络扩散指数(Idiff)的系数符号进行讨论。
| 变量 | 轻工业 | 重工业 | ||
| 系数 | t值 | 系数 | t值 | |
| L.Itfp | 0.149 2*(0.077 6) | 1.92 | 0.280 6***(0.067 0) | –4.19 |
| Idiff | 0.224 2*(0.135 2) | 1.66 | 0.645 8**(0.289 4) | 2.23 |
| Enter | 0.033 5(0.145 9) | –0.23 | 0.506 1***(0.133 8) | 3.78 |
| Gov | –1.039 9**(0.505 0) | 2.06 | –1.963 4***(0.754 4) | –2.6 |
| FDI | 0.064 7**(0.035 1) | –1.85 | 1.051 8***(0.206 4) | –5.1 |
| KL | –0.000 8***(0.000 3) | 2.61 | –0.001 8***(0.000 3) | –6.88 |
| Constant | 0.010 2(0.132 0) | 0.08 | –0.021 1(0.142 7) | –0.15 |
| AR(1)检验 | –21.28(0.000 0) | –2.27(0.023 0) | ||
| AR(2)检验 | 1.24(0.216 0) | 1.32(0.186 0) | ||
| Sargan检验 | 122.29(0.400 0) | 62.20(0.157 0) | ||
| 工具变量个数 | 32 | 32 | ||
| 样本容量 | 154 | 154 | ||
| 注:各变量的括号中为回归系数标准误;Arellano-Bond检验与Sargan检验中括号内为相伴概率。下同。 | ||||
从表6中可以看出,尽管两个样本中创新网络扩散指数(Idiff)的系数符号均为正,但是重工业样本中Idiff的系数不仅绝对值明显大于轻工业水平,而且显著程度有所提升,意味着重工业行业创新网络扩散的酵母效应更加明显。明显地,这是由于重工业行业的产品通常技术含量较高、资本深化程度较强,因此必然对来自于其他行业的中间投入品中的创新产品需求水平较高,从而加速了创新技术在重工业行业中的扩散。因此,重工业行业创新网络扩散的酵母效应更加明显。
根据Acemoglu等(2015),行业产出从用途上来讲最终分为私人消费、政府消费与其他行业采购的中间投入品三种,即
需要说明的是,在轻工业样本中,企业自有资金支持(Enter)的系数并不显著,这与之前的研究有所区别。我们初步怀疑这是由于轻工业的产品多属于技术含量较低的居民消费品,一方面这些行业利润率较低,研发资本较为稀缺,而且资金管理水平有限,创新资本使用效率不高;另一方面这些行业创新产品的市场需求相对较小,创新动力不强。当然,模型中的其他相关系数的符号、显著性等与之前的模型均没有太大的差异,本文在此不再重复讨论。
六、结论与政策含义基于点扩展到面的创新网络扩散过程所形成的酵母效应,有利于中国制造业部门整体创新全要素生产效率的提升,但是现有研究未给出经验证明。本文基于超越对数生产函数的随机前沿分析方法,测算了2001–2012年中国制造业行业创新活动全要素生产效率增长率,并采用可以控制内生性问题的系统广义矩估计方法,考察了创新网络扩散效应对创新全要素生产效率增长率的影响,以此来检测中国制造业部门酵母效应的存在。我们将得出的结论报告如下:
(1)中国创新全要素生产效率在震荡调整后经历了上升的趋势,其中2005年是明显且短暂的下降拐点,这在统计层面上源于该年创新资本和创新劳动投入增长速度远远高于创新产出的增长速度。制造业部门不同行业的创新全要素生产效率增长具有较大的差异,有12个行业的创新全要素生产效率增长率超过10%,而家具制造业是所有行业中唯一创新全要素生产效率增长率年均值为负的行业。
(2)中国制造业创新网络扩散指数在经历了震荡调整后,也呈现稳步上升的趋势。由于2005年创新产品占行业总产值的比重有所下降,创新网络扩散能力下降,进一步导致创新网络扩散总体趋势出现下降拐点。尽管由于直耗系数相同导致某些行业的扩散指数相同,但是不同行业之间仍然具有较大差异,化学工业创新网络扩散指数最高,而石油加工及炼焦业创新网络扩散指数最低。
(3)中国制造业创新全要素生产效率具有明显的路径依赖特征,这是由于前期的知识沉淀可以为后期的创新活动提供丰富的经验支持。由于技术依附于产品进行转移与扩散,因此创新网络扩散指数越高,意味着生产过程中所需的来自其他行业的中间投入品中创新产品的比重越高,也越有利于本行业的创新全要素生产效率的提升。重工业行业的创新网络扩散的酵母效应比轻工业更为明显,这是由于重工业行业的中间投入品对创新产品需求更高。
近年来,我国政府先后提出了《中国制造2025》和创新驱动发展战略,制造业领域的技术创新突破已成为中国制造业和经济增长转型升级的关键。对于如何提升中国制造业整体的创新效率,结合本文的相关研究结论,我们提出如下政策建议:
(1)鼓励创新型中间投入品的广泛使用。由于创新活动网络扩散效应是通过中间投入品的使用而实现,政府应积极主动地通过出台财政、金融等政策鼓励和引导企业尤其是重工业企业采购使用创新型中间投入品,这将加速创新技术在制造业中的扩散。例如对企业采购创新型中间投入品进行财政补贴,或者允许先进生产技术设备的采购商进行采购成本税收抵扣,以此促进创新型中间投入品的广泛使用,推动制造业整体创新活动的开展。
(2)政府应该优化调整对企业创新活动的资助方式。根据控制变量的估计结果,政府对创新活动的资金支持并不有利于创新全要素生产率的改善。为了充分调动企业的创新积极性,政府需要调整当前的研发补贴方式(巫强和刘蓓,2014)。此外,还可以实行差额补贴方式,对于高质量的创新成果提高奖励金额。鼓励企业将源自政府的资金创新支持纳入成本核算,以此充分调动企业的创新积极性。
(3)提高外资引进质量,提升科研人员待遇。外资比重的提高有利于创新全要素生产效率,因此对于具有较高创新能力的外资企业而言,可以在政策允许的范围内提供一系列优惠措施,并且鼓励内资企业与外资企业创新技术成果方面的交流;而由于创新要素的资本化程度(即要素结构)的提升会降低创新全要素生产率,因此,可以通过提高创新劳动投入比重来改善创新全要素生产率,即提高科研人员的现有待遇,充分调动科研人员的创新积极性,增加人力资本投资,通过筑巢引凤等方法,吸引人才集聚,全面打造创新型科研高地。
① 本文之所以没有加入出口变量,是因为出口与外商直接投资(FDI)的相关系数较高。
② 对于式(10)而言,除创新网络扩散效应(Idiff)之外,其余变量均从不同方面反映行业的自我创新效应。例如,Itfp的滞后项可以反映自我创新的积累效应(路径特征),而其他变量也分别从不同方面反映对行业自我创新效应的影响。
③ 创新全要素增长率描绘了创新活动中要素投入转化为产出的能力,如果创新产出不变,而要素投入上升,那么便意味着创新全要素生产效率的下降。在此对审稿专家的提示表示感谢。
④ 根据我国官方统计标准,轻工业指主要提供生活消费品和制作手工工具的工业,重工业指为国民经济各部门提供物质技术基础的主要生产资料的工业,因此重工业为其他行业提供更多的中间投入品,意味着重工业创新扩散强度更大。
| [1] | 白俊红, 江可申, 李婧. 中国地区研发创新的相对效率与全要素生产率增长分解[J].数量经济技术经济研究,2009(3). |
| [2] | 陈涛涛, 陈娇. 行业增长因素与我国FDI行业内溢出效应[J].经济研究,2006(6). |
| [3] | 楚俊国. 技术创新扩散时间模式及其实证研究[J].数量经济技术经济研究,2001(3). |
| [4] | 方世建. 技术创新扩散的随机过程模型[J].数量经济技术经济研究,2001(3). |
| [5] | 雷家骕, 程源, 杨湘玉. 技术经济学的基础理论与方法[M]. 北京: 高等教育出版社, 2005. |
| [6] | 林雄二郎. 科学技术•经济•社会[M]. 北京: 科学技术文献出版社, 1986. |
| [7] | 马永红, 张帆, 周文, 等. 新进企业合作伙伴搜寻模式、网络结构与创新扩散效率[J].系统管理学报,2016(6). |
| [8] | 沈飞, 吴解生. 知识密集型服务业创新扩散溢出能力、效应及其网络质量评价研究[J].科技进步与对策,2015(8). |
| [9] | 涂正革, 肖耿. 中国的工业生产力革命——用随机前沿生产模型对中国大中型工业企业全要素生产率增长的分解及分析[J].经济研究,2005(3). |
| [10] | 巫强, 刘蓓. 政府研发补贴方式对战略性新兴产业创新的影响机制研究[J].产业经济研究,2014(6). |
| [11] | 吴延兵. R&D存量、知识函数与生产效率[J].经济学(季刊),2006(4). |
| [12] | 肖文, 林高榜. 政府支持、研发管理与技术创新效率——基于中国工业行业的实证分析[J].管理世界,2014(4). |
| [13] | 杨振兵. 中国制造业创新技术进步要素偏向及其影响因素研究[J].统计研究,2016(1). |
| [14] | 杨振兵, 邵帅, 张诚. 生产比较优势、棘轮效应与中国工业技术进步的资本偏向[J].数量经济技术经济研究,2015(9). |
| [15] | 杨智峰, 汪伟, 吴化斌. 技术进步与中国工业结构升级[J].财经研究,2016(11). |
| [16] | 姚云浩, 高启杰. 网络关系嵌入、创新扩散与旅游企业创新绩效[J].旅游科学,2014(5). |
| [17] | 约瑟夫•熊彼特. 经济发展理论[M]. 美国哈佛大学出版社, 1912. |
| [18] | 张诚, 张艳蕾, 张健敏. 跨国公司的技术溢出效应及其制约因素[J].南开经济研究,2001(3). |
| [19] | 张军, 陈诗一, Jefferson G H. 结构改革与中国工业增长[J].经济研究,2009(7). |
| [20] | 朱有为, 徐康宁. 中国高技术产业研发效率的实证研究[J].中国工业经济,2006(11). |
| [21] | 朱劲松, 刘传江. 重新重工业化对我国就业的影响——基于技术中性理论与实证数据的分析[J].数量经济技术经济研究,2006(12). |
| [22] | Acemoglu D, Akcigit U, Kerr W. Networks and the macroeconomy: An empirical exploration[R]. Harvard Business School Working Paper, No. 16–006, 2015. |
| [23] | Aigner D, Lovell C A K, Schmidt P. Formulation and estimation of stochastic frontier production function models[J].Journal of Econometrics,1977,6(1):21–37. |
| [24] | Battese G E, Coelli T J. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India[J].Journal of Productivity Analysis,1992,3(1-2):153–169. |
| [25] | Bertotti M L, Brunner J, Modanese G. Innovation diffusion equations on correlated scale-free networks[J].Physics Letters A,2016,380(33):2475–2479. |
| [26] | Fan M T, Shao S, Yang L L. Combining global malmquist-luenberger index and generalized method of moments to investigate industrial total factor CO2 emission performance: A case of Shanghai(China) [J].Energy Policy,2015,79:189–201. |
| [27] | Griliches Z. Patent statistics as economic indicators: A survey[J]. Journal of Economic Literature,1990,28(4):1661–1707. |
| [28] | Griliches Z. R & D and the productivity slowdown[J].The American Economic Review,1980,70(2):343–348. |
| [29] | Harberger A C. A vision of the growth process[J]. The American Economic Review,1998,88(1):1–32. |
| [30] | Javorcik B S. Does foreign direct investment increase the productivity of domestic firms? In search of spillovers through backward linkages[J].The American Economic Review,2004,94(3):605–627. |
| [31] | Kumbhakar S C, Denny M, Fuss M. Estimation and decomposition of productivity change when production is not efficient: A paneldata approach[J].Econometric Review,2000,19(4):312–320. |
| [32] | Meeusen W, van den Broeck J. Efficiency estimation from cobb-douglas production functions with composed error[J].International Economic Review,1977,18(2):435–444. |
| [33] | Sgrignoli P, Agliari E, Burioni R, et al. Instability and network effects in innovative markets[J].Mathematics and Computers in Simulation,2015,108:260–271. |
| [34] | Zhang A M, Zhang Y M, Zhao R. A study of the R & D efficiency and productivity of Chinese firms[J].Journal of Comparative Economics,2003,31(4):444–464. |
2.School of Urban and Regional Science,Shanghai University of Finance and Economies,Shanghai 200433,China
 2018, Vol. 20
2018, Vol. 20



