文章信息
 | 上海财经大学 2018年20卷第5期 |
- 邢红卫, 刘维奇
- Xing Hongwei, Liu Weiqi
- 换手率:流动性还是不确定性
- Turnover: Liquidity or Uncertainty
- 上海财经大学学报, 2018, 20(5): 58-71.
- Journal of Shanghai University of Finance and Economics, 2018, 20(5): 58-71.
-
文章历史
- 收稿日期:2018-01-28

2018第20卷第5期
2.山西财经大学 财政与金融学院,山西 太原 030006
自1990年12月19日上海证券交易所正式营业至今,我国股票市场在拓宽融资渠道、促进资本形成、优化资源配置、分散市场风险等方面发挥了不可替代的作用,也成为当前支持我国产业结构调整、自主创新发展的重要平台。活跃的股票市场能够积极发挥促进实体经济发展的助推器作用,然而21世纪以来,作为描述市场活跃程度的重要指标,我国股票市场的换手率却呈现剧烈变动。从2002年的0.07一路上升至2007年的1.10,短短数年间增加了15倍,之后又迅速下降至2012年的0.09,锐减12倍。2000年1月至2015年6月期间,股票市场换手率呈现出W形,平均值仅为0.30,却有高达0.20的标准差和1.57的分布偏度①。那么,如此大起大落、激昂崩溃的换手率究竟蕴含着怎样的风险?
Datar等(1998)、Rouwenhorst(1999)、苏冬蔚和麦元勋(2004)、Eckbo和Norli(2005)、Avramov和Chordia(2006)、Liu(2006)、梁丽珍和孔东民(2008)认为换手率代表了流动性,高的换手率意味着高的流动性和低的流动性风险载荷,低的换手率意味着流动性枯竭和高的流动性风险载荷。依据Acharya和Pedersen(2005)、Liu等(2016)关于流动性风险定价的研究,流动性风险低的股票有低的预期收益,因而换手率与股票预期收益之间应该是负向关系。然而,在市场微观结构和行为金融学研究中,换手率也常被用来衡量股票的不确定性或由于股票不确定性而产生的投资者意见分歧程度(Diether等,2002;Jiang等,2005;Barinov,2014、2015)。股票的不确定性越高,投资者持有股票所承担的风险就越大,未来会要求更高的风险补偿,因而换手率应该正向预测股票收益。Harris和Raviv(1993)、Blume等(1994)的理论模型证明交易量与股票价格变化的绝对值之间正相关。股票价格变化的绝对值越大表明蕴含的风险越高,未来要求的风险报酬也越高,因而也证明换手率与股票预期收益之间是正向关系②。Gervais等(2001)发现交易量高(低)的股票会有高(低)的预期收益,控制股票规模后依然成立,也表明换手率与股票预期收益之间存在正向关系。徐浩峰和朱松(2012)在研究机构投资者的交易风格时也发现高的换手率会使股票价格短期内上涨。
换手率既被作为股票流动性的代理指标,也被用来衡量股票的不确定性程度,这两者对于换手率风险信息的解读存在显而易见的冲突。然而,对此至今难以给出合理的解释,使得借助换手率进行其他相关研究也难以令人信服。张峥和刘力(2006)的研究表明,在中国股票市场换手率与股票预期收益之间的负向关系不能完全由流动性溢价理论所解释,换手率与其他流动性指标的相关性较弱,更侧重于反映投资者的意见分歧程度,并且认为换手率越高,投资者意见分歧程度越大,股价被高估的程度越大,从而有低的预期收益。然而,Chen等(2013)表明当投资者意见分歧较大时,股价也有被低估的可能,从而未来有高的预期收益。Barinov(2014、2015)发现换手率与股票预期收益之间的负向关系并不能被流动性或流动性风险所解释,换手率代表了股票的不确定性程度,而且总波动率越大,不确定性越高。然而,Ang等(2006)表明总波动率与股票预期收益之间的负向关系本身就是违背“高风险预期高收益”的市场异象。目前,大量文献都在试图解释换手率对股票收益的负向预测能力,却鲜有文献深入剖析换手率本身所包含的风险信息。
本文基于理性定价的角度,选择Amihud(2002)流动性指标、Pástor和Stambaugh(2003)流动性指标来度量流动性,以总波动率和特质波动率来度量股票的不确定性,以分析换手率的风险溢价为手段,探究换手率究竟代表流动性风险还是不确定性风险。通过股票组合的特征分析和横截面相关性分析,发现换手率与流动性、不确定性之间都存在显著的正相关关系。投资组合分析和Fama-MacBeth(1973)横截面回归分析表明,换手率低的股票整体而言比换手率高的股票有更高的风险溢价,即使在控制规模、交易量、贝塔系数、动量、收益短期反转、流动性和不确定性之后,结果依然稳健。然而,换手率与股票预期收益之间并非单调的负向关系。在换手率较低的股票中换手率与股票预期收益成正向关系,而在换手率较高的股票中换手率与股票预期收益成负向关系,即换手率与股票预期收益成先增后降的倒U形关系。
在换手率处于较低水平时,依据市场微观结构理论,投资者通过订单流了解股票价格内在信息的可能性降低,正如Gervais等(2001)的研究所表明的,此时股票对于投资者的可见度较低,换手率更多反映由于信息不对称所产生的不确定性,并且换手率越高,投资者预期所获得的不确定性风险补偿越高。当换手率超过某个阈值后,交易成本、交易摩擦和信息不对称程度降低,换手率更多反映股票的流动性,而且换手率越高,股票的流动性风险越低,未来要求的风险报酬也越低(Liu,2006;Acharya和Pedersen,2005)。
以换手率的二次模型进行横截面回归,将换手率的收益预测能力发生方向性转变作为换手率水平的分界点,并据此进行实证检验。结果表明,对于换手率低于横截面分界点的股票,以总波动率和特质波动率作为代理变量的不确定性能够显著解释换手率与预期收益的正向关系,而对于换手率高于横截面分界点的股票,流动性能够显著解释换手率与预期收益的负向关系。因此,较低水平的换手率更多包含了股票的不确定性信息,而较高水平的换手率则更多包含了股票的流动性信息。由于换手率与股票预期收益之间的倒U形关系并不对称,较高水平的换手率与股票预期收益之间的负向关系更强,或者说换手率更多地代表了股票的流动性水平,因此整体上换手率高的股票相对于换手率低的股票有低的风险溢价。由于在研究样本期中国股票市场交易机制发生了重大变革,因此依据变革事件将样本期划分为四个阶段,稳健性检验表明不同子样本期并不会对换手率的风险信息产生显著影响。明确换手率的风险信息,不仅为借助换手率进行其他相关研究提供了理论支撑,而且对依据换手率进行投资实践具有直接的指导意义。
二、数据及指标计算 (一) 数据来源选择中国沪深两市A股作为实证研究对象,原始数据均来自国泰安CSMAR金融数据库。为了保证以月内日数据估计月度Pástor和Stambaugh(2003)流动性、特质波动率等指标的有效性,剔除月内交易日少于10的当月股票数据。由于中国股票市场在1999年2月只有7个交易日,基于研究的时间连贯性考虑,我们的样本期选择从2000年1月1日至2015年6月30日。由于创业板在上市门槛、监管制度、信息披露、交易者条件、投资风险等方面和主板市场有较大区别,因此也剔除其中的创业板股票,最终得到2 380只股票的数据,共计6 069 096条样本。
(二) 指标计算Roll(1984)、Hasbrouck(2009)、Corwin和Schultz(2012)以买卖价差测量股票的流动性,Amihud(2002)、Pástor和Stambaugh(2003)从对价格影响的角度测量流动性。由于Roll(1984)和Hasbrouck(2009)的指标也能度量流动性对价格的影响,而Roll(1984)的指标类似于Pástor和Stambaugh(2003)的指标,Hasbrouck(2009)的指标类似于Amihud(2002)的指标,因此本文以Amihud(2002)、Pástor和Stambaugh(2003)的指标作为流动性测度。
Barinov(2014)的研究中,以特质波动率、分析师预测分歧、分析师预测误差、盈利波动和现金流波动度量股票的不确定性,同时表明总波动风险对不确定性有显著的解释作用。由于分析师预测、盈利和现金流数据频率的限制,我们以总波动率和特质波动率作为不确定性的度量指标。依据Ang等(2006),以Fama-French三因子(FF3)模型无法解释的收益残差的标准差作为特质波动率。
剔除股票在月内的交易日少于10的当月股票数据,在此基础上以月内日数据回归CAPM模型得到股票月度的贝塔系数,以股票月内日收益的标准差作为月度总波动率,以月内日数据回归FF3模型的收益残差序列计算月度特质波动率。以流通市值的自然对数值作为股票的规模,以交易金额的自然对数值作为股票的交易量,以股票t-6至t-2的累积收益作为股票t月的6个月动量指标,以t-1的收益衡量t月的收益短期反转。分别以月内日度换手率的算术平均值和日度Amihud流动性测度的算术平均值作为月度换手率和月度Amihud流动性测度。
三、实证分析 (一) 股票特征的相关性分析换手率(TUR)与股票规模、交易量、风险载荷以及历史表现密切相关,因此我们对股票的规模(SIZE)、交易量(VOLU)、贝塔系数(BETA)、6个月动量(MOM)、短期反转(REV)、Amihud非流动性、PS非流动性、总波动率(TV)和特质波动率(IV)进行分析。首先,将所有股票按照个股月度换手率构建10分位组合,平均加权计算组合规模、交易量等,结果见表1。表1显示,(高)换手率股票组合的规模小(大),交易量高(低),动量、当月收益、贝塔系数、总波动率和特质波动率都低(高),Amihud非流动性高(低),而PS非流动性呈现明显的单调变化。
| 组合 | TUR | SIZE | VOLU | BETA | MOM | REV | Amihud | PS | TV | IV |
| 低 | 0.114 4 | 15.847 2 | 20.048 1 | 0.885 6 | 0.073 5 | –0.002 8 | 0.053 5 | –0.009 4 | 0.020 9 | 0.013 1 |
| 2 | 0.189 0 | 15.102 1 | 20.070 4 | 0.996 4 | 0.064 7 | –0.001 3 | 0.026 0 | –0.008 7 | 0.022 8 | 0.014 0 |
| 3 | 0.239 5 | 14.901 5 | 20.117 1 | 1.034 4 | 0.066 9 | 0.001 1 | 0.023 9 | –0.008 3 | 0.023 9 | 0.014 7 |
| 4 | 0.285 5 | 14.766 7 | 20.169 4 | 1.063 7 | 0.073 4 | 0.003 8 | 0.022 1 | –0.008 8 | 0.024 9 | 0.015 4 |
| 5 | 0.333 5 | 14.656 8 | 20.229 1 | 1.079 5 | 0.077 6 | 0.008 2 | 0.020 9 | –0.010 1 | 0.025 8 | 0.016 3 |
| 6 | 0.387 2 | 14.580 6 | 20.317 5 | 1.102 2 | 0.083 8 | 0.012 7 | 0.019 5 | –0.009 3 | 0.026 8 | 0.017 2 |
| 7 | 0.452 8 | 14.523 3 | 20.435 2 | 1.112 6 | 0.092 7 | 0.018 9 | 0.018 7 | –0.009 7 | 0.027 8 | 0.018 3 |
| 8 | 0.541 0 | 14.449 5 | 20.561 3 | 1.129 7 | 0.105 9 | 0.028 6 | 0.017 3 | –0.010 6 | 0.029 3 | 0.019 6 |
| 9 | 0.682 8 | 14.363 2 | 20.733 4 | 1.156 5 | 0.121 4 | 0.038 6 | 0.015 0 | –0.009 3 | 0.031 2 | 0.021 5 |
| 高 | 1.147 7 | 14.237 4 | 21.155 0 | 1.172 0 | 0.179 4 | 0.079 1 | 0.014 0 | –0.009 8 | 0.037 2 | 0.027 4 |
为了进一步探究换手率与其他股票特征的相关性,我们进行横截面相关性分析。首先在横截面上计算股票各个特征的相关系数,然后在时间序列上检验相关系数的显著性,括号内为相应的t统计量,结果见表2。表2显示,换手率与规模的相关系数为–0.233 3,与交易量的相关系数为0.394 7,且t统计检验显著,这显然符合换手率的定义方式。换手率与贝塔的相关系数为0.127 2,t统计检验显著,表明换手率高的股票风险载荷也高,相应的当期风险报酬也高。换手率与Amihud非流动性的相关系数为–0.096 7,与PS非流动性的相关系数为–0.009 1,虽然t统计检验都显著,然而两者之间却相差甚远。梁丽珍和孔东民(2008)认为中国股票市场PS非流动性指标在捕捉流动性方面要远差于Amihud非流动性指标。换手率与总波动率的相关系数为0.519 1,与特质波动率的相关系数为0.508 6,与其他特征相比,换手率与股票不确定性高度相关。Amihud、PS与总波动率、特质波动率的相关系数较弱,表明流动性与不确定性之间几乎不存在共有风险。
| TUR | SIZE | VOLU | BETA | MOM | REV | Amihud | PS | TV | IV | |
| TUR | 1 | |||||||||
| SIZE | –0.233 3 | 1 | ||||||||
| (–20.45) | ||||||||||
| VOLU | 0.394 7 | 0.706 7 | 1 | |||||||
| (30.33) | (88.83) | |||||||||
| BETA | 0.127 2 | –0.036 5 | 0.116 1 | 1 | ||||||
| (14.84) | (–2.96) | (11.72) | ||||||||
| MOM | 0.108 9 | 0.127 8 | 0.185 9 | –0.044 9 | 1 | |||||
| (9.46) | (8.87) | (19.64) | (–3.25) | |||||||
| REV | 0.241 1 | 0.054 5 | 0.167 6 | –0.100 4 | –0.037 6 | 1 | ||||
| (22.00) | (3.75) | (14.88) | (–6.00) | (–3.14) | ||||||
| Amihud | –0.096 7 | –0.284 4 | –0.383 4 | –0.082 7 | 0.016 3 | 0.018 3 | 1 | |||
| (–14.62) | (–25.48) | (–30.17) | (–14.73) | (2.13) | (1.66) | |||||
| PS | –0.009 1 | 0.053 5 | 0.042 4 | 0.006 8 | 0.016 6 | –0.014 8 | –0.044 3 | 1 | ||
| (–3.74) | (12.77) | (8.05) | (1.58) | (5.96) | (–4.40) | (–2.77) | ||||
| TV | 0.519 1 | –0.112 8 | 0.298 2 | 0.404 4 | 0.092 6 | 0.264 5 | 0.004 6 | –0.023 8 | 1 | |
| (49.47) | (–9.92) | (27.48) | (20.33) | (5.05) | (12.47) | (0.63) | (–6.82) | |||
| IV | 0.508 6 | –0.085 3 | 0.292 0 | 0.004 8 | 0.138 2 | 0.346 9 | 0.033 8 | –0.027 0 | 0.847 1 | 1 |
| (49.91) | (–10.63) | (28.77) | (0.30) | (10.14) | (19.29) | (5.56) | (–8.62) | (108.87) |
我们通过检验换手率对股票收益的预测能力,进一步探析换手率所包含的信息。在每个月以换手率从低到高对所有股票进行排序,按分位点将股票分成5个组合,以流通市值加权计算组合当月的换手率,持有组合一个月,以流通市值加权(value-weight,VW)、平均加权(equal-weight,EW)计算组合的收益率,检验高、低换手率组合在持有期的收益率之前是否存在差异。为了避免系统性风险报酬对换手率风险溢价的影响,进一步以FF3模型对组合收益率进行回归,过滤其中的系统性风险溢价,比较高低组合之间常数项Alpha的差异。
在表3中,第二列是以流通市值加权计算的组合换手率,低换手率组合的流通市值加权换手率为0.12%,高换手率组合的流通市值加权换手率为0.88%。第三列和第四列分别展示了以流通市值加权和等权计算的组合预期收益率时间序列平均值。低换手率组合的流通市值加权收益为1.08%,高换手率组合的流通市值加权收益为0.28%,高、低换手率组合之间的收益差为–0.80%,相应的Newey-West-t统计量(括号内)为–4.17,表明高、低换手率组合的预期收益之间存在显著差异,且低换手率组合未来有高收益,高换手率组合未来有低收益。以FF3模型回归组合收益率,发现高、低换手率组合的常数项差异为–0.41%,且相应的Newey-West-t统计量为–3.40,表明调整系统性风险后高、低换手率组合的异常收益之差依然显著为负。以等权计算换手率组合的预期收益率,发现高、低换手率组合的预期收益之差为–1.43%,相应的Newey-West-t统计量为–7.42,经FF3模型调整系统性风险后的高、低换手率组合的异常收益之差为–1.07%,相应的Newey-West-t统计量为–6.69。表3的结果表明,换手率低的股票比换手率高的股票有更高的风险溢价。以二维投资组合分析方法检验换手率组合的预期收益差异,结果依然稳健。
| 组合 | TUR | VW加权组合收益 | EW加权组合收益 |
| 低 | 0.12 | 1.08 | 1.95 |
| 2 | 0.26 | 1.71 | 2.23 |
| 3 | 0.36 | 1.52 | 1.93 |
| 4 | 0.49 | 1.09 | 1.55 |
| 高 | 0.88 | 0.28 | 0.52 |
| 组合收益之差 | –0.80 | –1.43 | |
| (–4.17) | (–7.42) | ||
| 常数项之差 | –0.41 | –1.07 | |
| (–3.40) | (–6.69) |
为了同时检验多个控制变量对换手率风险溢价的影响,以换手率及其他控制变量对股票预期收益进行Fama-MacBeth(Fama和MacBeth,1973)横截面回归:
| ${R_{i,t + 1}} = {a_i} + {b_i} TU{R_{i,t}} + {c_i} Control{s_{i,t}} + {\varepsilon _{i,t + 1}}$ | (1) |
其中Ri,t+1为股票在t+1期的收益,TURi,t为股票在t期的换手率,Controlsi,t为股票在t期的控制变量。模型中的所有变量被调整为0到1之间的值,样本期从2000年1月至2015年6月,结果见表4。
模型1中换手率的系数为–0.14,相应的Newey-West-t统计量为–6.56,表明换手率显著负向预测股票收益,即使在模型2中加入规模(SIZE)、交易量(VOL)、贝塔系数(BETA)、动量(MOM)、收益反转(REV)作为控制变量,换手率与预期收益的负向关系依然显著,且没有减弱。在此基础上,模型3加入Amihud流动性和PS流动性作为控制变量,换手率与预期收益的负向关系依然显著且没有减弱。相反,Amihud流动性的系数为0.02,相应的Newey-West-t统计量为0.23,PS流动性的系数为0,相应的Newey-Westt统计量为–2.96,表明流动性溢价被换手率完全解释甚至逆转,表明流动性溢价并不能完全解释换手率对股票收益整体上的负向预测能力,这与张峥和刘力(2006)的研究结论相一致。
模型4在模型2的基础上加入总波动率(TV)和特质波动率(IV)作为控制变量,换手率的系数变为–0.11,表明换手率与股票预期收益之间的负向关系有所减弱,可见不确定性对换手率与股票预期收益整体之间的负向关系有一定程度的解释能力,然而也并不能完全解释。模型3和模型4的结果表明,换手率并不单纯包含流动性信息或不确定性信息,因此模型5将Amihud、PS、总波动率(TV)和特质波动率(IV)都纳入控制变量,发现换手率的回归系数为–0.11,相应的Newey-West-t统计量为–7.86,换手率与股票预期收益之间的负向关系依然显著,表明换手率并不仅仅包含流动性信息或不确定性信息,或者换手率与股票预期收益之间并不是简单的线性关系。
| 模型 | TUR | SIZE | VOLU | BETA | MOM | REV | Amihud | PS | TV | IV |
| 1 | –0.14 | |||||||||
| (–6.56) | ||||||||||
| 2 | –0.14 | 0.03 | –0.03 | –0.01 | 0.02 | –0.00 | ||||
| (–7.36) | (1.09) | (–1.64) | (–0.08) | (0.83) | (–0.43) | |||||
| 3 | –0.14 | 0.03 | –0.02 | –0.01 | 0.02 | –0.00 | 0.02 | –0.00 | ||
| (–7.84) | (0.98) | (–1.34) | (–0.09) | (0.70) | (–0.69) | (0.23) | (–2.96) | |||
| 4 | –0.11 | 0.02 | –0.02 | –0.01 | 0.03 | 0.02 | 0.35 | –0.42 | ||
| (–6.94) | (0.51) | (–1.44) | (–1.41) | (1.31) | (0.43) | (2.11) | (–2.65) | |||
| 5 | –0.11 | 0.02 | –0.01 | –0.01 | 0.03 | 0.02 | 0.02 | –0.00 | 0.36 | –0.42 |
| (–7.86) | (0.48) | (–1.15) | (–1.32) | (1.21) | (0.26) | (0.51) | (–3.07) | (2.17) | (–2.70) |
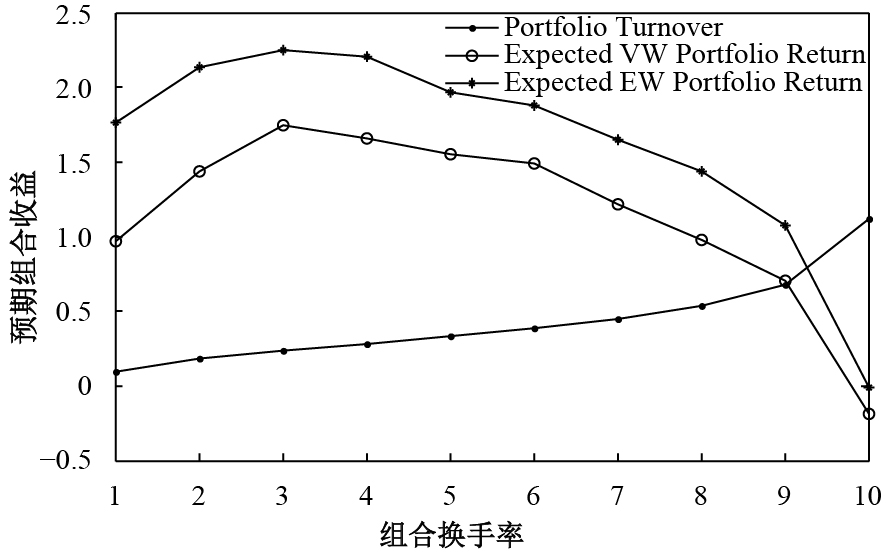
以换手率构建10分位组合,以流通市值加权计算组合换手率,分别以流通市值加权和等权计算组合下个月的收益率。图1展示了换手率从低到高的组合预期收益的变化趋势。随着组合换手率从低到高,组合的流通市值加权预期收益和等权预期收益都呈现出先增高后降低的非单调性趋势。对于换手率较低的第1至第3个组合,换手率越高,预期收益也越高;而对于换手率较高的第3至第10个组合,换手率越高,预期收益越低。
|
| 图 1 不同换手率组合的预期收益率 |
为了检验不同程度的换手率与股票预期收益之间的关系,基于图1的直观结果,在表5的Panel A将所有股票按照换手率的高低划分为30%、40%、30%三组,分别在换手率较低的30%股票和换手率较高的30%股票中进行组合分析。对于低换手率的股票,以换手率构建5分位数组合,发现高、低换手率组合的市值加权预期收益率之差为0.78%,相应的Newey-West-t统计量为2.96;经FF3模型调整系统性风险后的溢价为0.95%,Newey-West-t统计量为3.64,等权的预期收益率也类似,表明在换手率较低的股票中,低的换手率股票有低的预期收益,高的换手率股票有高的预期收益。对于高换手率的股票,发现高、低换手率组合的市值加权预期收益率之差为–1.17%,相应的Newey-West-t统计量为–5.18;经FF3模型调整系统性风险后的溢价为–1.01%,Newey-West-t统计量为–4.66,等权的预期收益率也类似。显然与换手率较低的股票不同,在换手率较高的股票中换手率低的股票有高的预期收益,换手率高的股票有低的预期收益。
表5的Panel B和Panel C分别按照换手率的高低将股票划分为40%、20%、40%三组和50%、50%两组,分别在换手率较低的股票中和换手率较高的股票中检验换手率对收益的预测能力。与Panel A的结果类似,较低的换手率可以正向预测股票收益,而较高的换手率可以负向预测股票收益。由此可见,较低水平的换手率更多包含了股票的不确定性信息,较低水平换手率对股票收益的正向预测能力证明了对不确定性风险的补偿。较高水平的换手率更多反映了股票的流动性信息,较高水平换手率对股票收益的负向预测能力验证了由于频繁交易产生的流动性风险溢价。
| 换手率较低的股票 | 换手率较高的股票 | |||
| VW组合收益 | EW组合收益 | VW组合收益 | EW组合收益 | |
| Panel A:30%、40%、30% | ||||
| 组合收益之差 | 0.78 | 0.49 | –1.17 | –1.45 |
| (2.96) | (2.61) | (–5.18) | (–7.62) | |
| 常数项之差 | 0.95 | 0.53 | –1.01 | –1.31 |
| (3.64) | (2.62) | (–4.66) | (–7.47) | |
| Panel B:40%、20%、40% | ||||
| 组合收益之差 | 0.69 | 0.45 | –1.40 | –1.66 |
| (2.29) | (1.93) | (–5.41) | (–7.58) | |
| 常数项之差 | 0.92 | 0.56 | –1.19 | –1.37 |
| (3.04) | (2.27) | (–5.03) | (–7.06) | |
| Panel C:50%、50% | ||||
| 组合收益之差 | 0.59 | 0.20 | –1.68 | –1.89 |
| (1.71) | (0.76) | (–5.60) | (–7.84) | |
| 常数项之差 | 0.77 | 0.29 | –1.38 | –1.56 |
| (2.33) | (1.07) | (–4.70) | (–7.29) | |
苏冬蔚和麦元勋(2004)对中国股票市场的研究表明,预期收益率是换手率的分段线性和整体凸性减函数,即换手率与股票预期收益率是单调负向关系,并且负向关系随换手率渐弱,这与本文对低水平换手率的分析结果存在方向性差异。苏冬蔚和麦元勋(2004)基于换手率5分位组合的结果表明低水平的换手率对预期收益率的回归系数为负,然而统计检验都不显著,并不能说明预期收益率是换手率的整体减函数,而且5个组合换手率系数的绝对值并非一致单调递减,不足以说明预期收益率是换手率的凸性函数。本文借鉴苏冬蔚和麦元勋(2004)的方法,在每个横截面将所有股票按照换手率分为5个组合,在每个组合内进行换手率对预期收益率的Fama-MacBeth横截面回归,并且将规模(SIZE)、交易量(VOL)、贝塔系数(BETA)、动量(MOM)、收益反转(REV)作为控制变量,结果见表6,括号内为相应的Newey-West-t统计量。表6显示,换手率较低的前3个组合中换手率对预期收益率的回归系数都不显著,换手率较高的后2个组合中换手率对预期收益率的回归系数都显著为负,这与苏冬蔚和麦元勋(2004)的结果基本一致。然而,对于换手率较高的后2个组合,我们发现换手率的系数分别为–0.04和–0.16,其绝对值递增,因此更不能说明预期收益率是换手率的凸性函数。
| 组合 | 常数项 | TUR | SIZE | VOLU | BETA | MOM | REV |
| 低 | –0.05 | 0.00 | 0.06 | –0.08 | 0.02 | 0.01 | 0.00 |
| (–3.38) | (1.28) | (1.26) | (–1.55) | (1.52) | (1.02) | (0.25) | |
| 2 | –0.12 | 0.00 | –0.03 | 0.03 | 0.00 | 0.05 | 0.00 |
| (–2.12) | (–0.22) | (–0.16) | (0.16) | (0.14) | (1.39) | (0.31) | |
| 3 | –0.10 | 0.03 | 0.45 | –0.46 | 0.01 | 0.04 | 0.00 |
| (–3.37) | (1.22) | (2.68) | (–2.73) | (0.61) | (3.30) | (–0.31) | |
| 4 | –0.05 | –0.04 | 0.11 | –0.16 | 0.02 | 0.01 | –0.02 |
| (–1.96) | (–2.32) | (0.72) | (–1.02) | (1.13) | (0.54) | (–0.97) | |
| 高 | –0.06 | –0.16 | 0.00 | –0.02 | 0.05 | 0.03 | 0.01 |
| (–2.50) | (–7.39) | (0.07) | (–0.45) | (2.83) | (1.57) | (0.34) |
为了进一步分析不同水平的换手率与股票预期收益率之间的关系,在每个横截面将所有股票细分为10个换手率组合,再次进行Fama-MacBeth横截面回归分析,结果见表7。表7显示,对于换手率较低的前3个组合,换手率对预期收益率的回归系数都为正,且第3个组合的换手率系数统计显著。对于换手率处于居中水平的第4至第6个组合,换手率的回归系数统计检验不显著。对于换手率较高的后4个组合,换手率的回归系数都显著为负。显而易见,将横截面所有股票按换手率细分为10个组合后,换手率与股票预期收益率之间呈现先增后降的非单调关系,即预期收益率是换手率的凹性函数,并且不同水平换手率的回归系数表明低水平换手率与股票预期收益的正向关系强于高水平换手率与股票预期收益的负向关系。
| 组合 | 常数项 | TUR | SIZE | VOLU | BETA | MOM | REV |
| 低 | –0.08 | 0.01 | 0.10 | –0.11 | 0.03 | 0.02 | 0.01 |
| (–3.39) | (1.04) | (1.19) | (–1.37) | (1.43) | (1.52) | (0.40) | |
| 2 | –0.25 | 0.03 | 0.37 | –0.34 | 0.01 | 0.07 | 0.01 |
| (–1.51) | (1.37) | (1.31) | (–1.18) | (0.34) | (1.08) | (0.41) | |
| 3 | –0.32 | 0.10 | 0.43 | –0.39 | –0.04 | 0.04 | 0.02 |
| (–2.68) | (2.63) | (0.69) | (–0.62) | (–0.94) | (0.63) | (0.96) | |
| 4 | 0.10 | –0.06 | 0.31 | –0.38 | 0.01 | –0.07 | –0.05 |
| (0.42) | (–1.67) | (0.57) | (–0.72) | (0.31) | (–0.84) | (–1.14) | |
| 5 | –0.10 | –0.02 | –0.12 | 0.14 | 0.00 | 0.03 | 0.00 |
| (–0.99) | (–1.17) | (–0.20) | (0.22) | (–0.06) | (2.19) | (–0.29) | |
| 6 | –0.15 | 0.02 | 1.02 | –1.06 | 0.00 | 0.07 | 0.00 |
| (–1.40) | (0.27) | (2.19) | (–2.34) | (–0.06) | (2.03) | (0.09) | |
| 7 | –0.05 | –0.06 | 0.09 | –0.13 | 0.01 | 0.01 | –0.01 |
| (–0.97) | (–2.19) | (0.27) | (–0.38) | (0.55) | (0.85) | (–0.49) | |
| 8 | –0.12 | –0.08 | –0.62 | 0.59 | –0.01 | 0.01 | –0.01 |
| (–1.45) | (–2.97) | (–0.71) | (0.67) | (–0.28) | (0.41) | (–0.25) | |
| 9 | 1.17 | –0.40 | –2.53 | 2.37 | –0.14 | 0.10 | 0.12 |
| (1.07) | (–2.94) | (–0.92) | (0.89) | (–0.89) | (0.40) | (1.04) | |
| 高 | –0.23 | –0.22 | –0.05 | –0.01 | 0.08 | 0.02 | 0.11 |
| (–1.59) | (–4.36) | (–0.56) | (–0.10) | (2.67) | (0.95) | (1.02) |
本文的结果之所以不同于苏冬蔚和麦元勋(2004)的发现,究其原因可能有以下几方面:第一,与我们的样本期相比,苏冬蔚和麦元勋(2004)选择的样本期为1999年1月至2003年7月,时间跨度很短。第二,苏冬蔚和麦元勋(2004)样本期内的换手率均值为0.236 0,方差为0.022 4,而我们样本期的换手率均值为0.299 7,方差为0.037 8,换手率的分布有很大不同。第三,苏冬蔚和麦元勋(2004)缺失了重要的风险度量指标贝塔系数作为横截面回归的控制变量。第四,苏冬蔚和麦元勋(2004)将横截面股票划分为5个换手率组合,而我们细分为10个换手率组合,能够更为清晰地分析不同水平换手率组合的预期收益率。
为了进一步分辨不同水平换手率的风险信息,我们计算换手率对收益预测方向发生改变的转折点,即是换手率风险信息发生转变的分界点。由于股票预期收益是换手率的先增后降凹性函数,因此以换手率与换手率平方项对股票预期收益进行横截面回归,结果见表8。模型1表明换手率平方项的系数为–0.18,相应的Newey-West-t统计量为–2.59,表明股票预期收益是换手率的开口向下凹性函数。换手率的系数为0.13,由二次函数的性质可知,股票预期收益对换手率的凹性函数具有正的对称轴,为0.36。由于将所有变量以最大值标准化为0到1之间的值,因此这意味着当换手率低于横截面换手率最大值的36%时,换手率与股票预期收益之间是正向关系,更多地反映了由于股票交易频率匮乏、可见度低的不确定性风险;当换手率超过横截面换手率最大值的36%时,换手率与股票预期收益之间是负向关系,更多地反映了股票的流动性风险。以每个横截面换手率的最大值乘以0.36,得到换手率风险信息发生转变的平均绝对分界点为0.24。
| 模型 | TUR | TUR2 | SIZE | VOLU | BETA | MOM | REV |
| 1 | 0.13 | –0.18 | |||||
| (3.48) | (–2.59) | ||||||
| 2 | 0.21 | –0.12 | 0.02 | –0.02 | 0.01 | 0.02 | 0.00 |
| (4.57) | (–2.71) | (0.67) | (–1.19) | (0.00) | (0.90) | (–0.34) |
摒除转折点附近的换手率对结果的影响,选择换手率较低的30%股票和换手率较高的30%股票进行横截面回归,结果见表9。表9显示,对于Panel A换手率较低的股票,模型1换手率对股票预期收益回归的系数为0.01,相应的Newey-West-t统计量为2.01,换手率与股票预期收益之间有显著的正向关系,模型2加入控制变量后也表明较低水平的换手率可以稳定地正向预测股票收益。模型3加入总波动率(TV)和特质波动率(IV)作为控制变量,换手率的系数为0.01,且不显著,因此较低水平的换手率与股票预期收益的正向关系可以被不确定性完全解释,验证较低水平的换手率更多包含了股票的不确定性信息。
对于Panel B换手率较高的股票,模型4中换手率对股票预期收益回归的系数为–0.16,相应的Newey-Westt统计量为–7.07,换手率与股票预期收益之间存在显著的负向关系,加入控制变量后也表明较高水平的换手率也可以稳定地负向预测股票收益。模型6加入Amihud流动性和PS流动性作为控制变量,换手率的系数变为–0.12,因此流动性可以在一定程度上减弱换手率与股票预期收益之间的负向关系,进而说明横截面上较高水平的换手率包含了部分股票的流动性信息。在剔除月度换手率小于1%分位点和大于99%分位点的异常值,以及股票IPO当月的收益后,结果依然稳健。
| 模型 | TUR | SIZE | VOLU | BETA | MOM | REV | Amihud | PS | TV | IV |
| Panel A:换手率较低的股票 | ||||||||||
| 1 | 0.01 | |||||||||
| (2.01) | ||||||||||
| 2 | 0.01 | –0.02 | 0.01 | 0.02 | 0.01 | 0.00 | ||||
| (1.97) | (–0.50) | (0.33) | (1.27) | (0.83) | (0.05) | |||||
| 3 | 0.01 | –0.02 | 0.00 | 0.03 | 0.03 | 0.02 | –0.04 | –0.06 | ||
| (1.06) | (–0.35) | (0.03) | (1.41) | (2.04) | (1.27) | (–1.02) | (–2.26) | |||
| Panel B:换手率较高的股票 | ||||||||||
| 4 | –0.16 | |||||||||
| (–7.07) | ||||||||||
| 5 | –0.16 | 0.03 | –0.06 | 0.03 | 0.01 | 0.01 | ||||
| (–7.76) | (0.87) | (–1.42) | (1.65) | (0.75) | (0.32) | |||||
| 6 | –0.12 | 0.01 | –0.02 | 0.04 | 0.02 | 0.01 | 0.02 | –0.00 | ||
| (–7.52) | (0.11) | (–0.36) | (2.57) | (1.21) | (0.51) | (0.98) | (–0.21) | |||
在我们选择研究的样本期中,中国股票市场的交易机制发生了重大变革,如《合格境外机构投资者境内证券投资管理暂行办法》出台后于2003年7月9日完成了第一单交易;2005年9月4日中国证监会发布《上市公司股权分置改革管理办法》;2010年3月31日起正式开通融资融券交易系统。不同时期的交易机制变革可能会对换手率的风险信息产生显著影响,因此以上述事件为分割点,将样本期划分为四个阶段,检验交易机制变革是否会改变换手率的风险信息。
表10以换手率构建5分位组合并持有组合一个月,检验高、低换手率组合的预期收益率是否存在显著差异,并且剔除系统性风险溢价后,换手率的风险溢价是否依然显著。结果表明在2000年1月至2003年6月,在股权分置改革之前的2003年7月至2005年8月,由于中国股票市场经历了长期的熊市,5个换手率组合都有负向预期收益。而在2005年9月至2010年3月期间,中国股票市场蓬勃发展,出现了大牛市,5个换手率组合都有较高的正向预期收益。在2000年1月至2003年6月、2003年7月至2005年8月、2005年9月至2010年3月三个子样本期间,高、低换手率组合的预期收益率之间存在显著的负向差异。在2010年4月至2015年6月期间,高、低换手率组合的预期收益率之差为–0.42,然而Newey-West-t检验(括号内)不显著,剔除系统性风险溢价后负向差异显著,表明这期间高、低换手率组合预期收益率之差的方向不稳定主要是由系统性风险引起。由此,尽管股票市场交易机制在不断改革和完善,换手率整体上依然具有显著的负向溢价。
| 组合 | 2000.01–
2003.06 |
2003.07–
2005.08 |
2005.09–
2010.03 |
2010.04–
2015.06 |
| 低 | 0.04 | –1.44 | 3.30 | 0.86 |
| 2 | 0.22 | –0.42 | 4.07 | 1.49 |
| 3 | –0.12 | –0.76 | 4.10 | 1.27 |
| 4 | –0.11 | –1.03 | 3.48 | 0.68 |
| 高 | –0.96 | –2.38 | 2.28 | 0.44 |
| 组合收益之差 | –1.00 | –0.93 | –1.02 | –0.42 |
| (–4.20) | (–3.94) | (–2.08) | (–1.58) | |
| 常数项之差 | –1.24 | –0.89 | –0.17 | –1.14 |
| (–6.09) | (–4.04) | (–2.17) | (–2.61) |
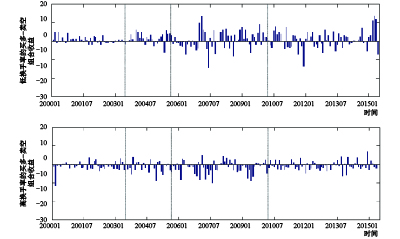
按照换手率风险信息发生改变的分界点,分别计算换手率较低的30%股票(图2之上图)和换手率较高的30%股票(图2之下图)中高、低换手率组合流通市值加权的预期收益率之差。在图2的上图,对于换手率较低的股票,高、低换手率组合预期收益率之间的正向差值明显多于负向差值,且正向差值的幅度明显大于负向差值,表明对于换手率较低的股票,高的换手率预期高的股票收益。对于不同的子样本期,高、低换手率组合预期收益率之间的正向差值都明显占优。而在图2的下图,对于换手率较高的股票,高、低换手率组合预期收益率之间的负向差值明显多于正向差值,且负向差值的幅度明显大于正向差值,表明对于换手率较高的股票,高的换手率预期低的股票收益。对于四个子样本期,负向差值在数量和幅度上也都明显多于正向差值。
|
| 图 2 不同水平的换手率组合预期收益之差的时序直方图 |
进一步检验对于不同水平的换手率,在不同子样本期高、低换手率组合的预期收益率是否存在显著差异,结果见表11。对于Panel A换手率较低的股票,在四个子样本期间,高、低换手率组合的预期收益率都存在正向差异,经FF3模型剔除系统性风险溢价后的正向超额收益都显著,表明尽管市场交易机制在不断变革和完善,较低水平的换手率却具有稳定的正向风险溢价,反映了股票的不确定性信息。对于Panel B换手率较高的股票,在四个子样本期间,高、低换手率组合的预期收益率都存在负向差异,剔除系统性风险溢价后的负向超额收益依然显著,表明对于不同的子样本期,市场交易机制的变革并没有使较高水平的换手率丧失反映股票流动性的能力。
| 2000.01–2003.06 | 2003.07–2005.08 | 2005.09–2010.03 | 2010.04–2015.06 | |
| Panel A:换手率较低的股票 | ||||
| 组合收益之差 | 0.53 | 1.43 | 0.61 | 0.81 |
| (2.40) | (2.47) | (1.06) | (2.61) | |
| 常数项之差 | 0.36 | 1.94 | 1.55 | 0.30 |
| (2.25) | (3.15) | (2.58) | (2.56) | |
| Panel B:换手率较低的股票 | ||||
| 组合收益之差 | –0.97 | –1.33 | –1.78 | –0.70 |
| (–2.51) | (–1.83) | (–3.94) | (–2.62) | |
| 常数项之差 | –0.96 | –1.63 | –1.91 | –0.97 |
| (–2.35) | (–2.79) | (–4.31) | (–2.27) | |
换手率可以作为股票流动性的代理指标,因而换手率应该负向预测股票收益。同时,换手率也可以用来衡量股票的不确定性程度,或者由于不确定性而引起的投资者意见分歧程度,因而换手率应该正向预测股票收益,以补偿不确定性风险。这两者之间的矛盾显然令人费解,因此有必要通过剖析换手率与股票预期收益之间的关系,明确换手率所包含的信息。
本文通过投资组合分析和横截面回归分析等实证方法,发现换手率低的股票确实比换手率高的股票有更高的预期收益。然而,换手率与预期收益整体上的负向关系并不是单调线性的,而是呈现先增后降的不对称倒U形。对于横截面上换手率较低的股票,换手率越高,股票预期收益越高;而对于换手率较高的股票,换手率越高,股票预期收益却越低。基于流动性或不确定性为控制变量的横截面回归表明,较低水平的换手率更多包含了由于股票交易频率匮乏、可见度低的不确定性风险,而较高水平的换手率更多包含了股票的流动性信息。换手率与股票预期收益之间之所以整体表现负向关系,是因为较高水平的换手率与股票预期收益之间的负向关系更强,或者说换手率更多地代表了股票的流动性水平。通过换手率与换手率平方项对股票预期收益进行横截面回归,发现换手率风险信息发生转变的分界点为横截面换手率的36%分位点。当换手率低于分界点时,依据换手率构建组合有助于买多投资;当换手率高于分界点时,依据换手率构建组合则有助于卖空投资。依据中国股票市场几次重大的交易机制变革将样本期划分为四个阶段,发现实证结果依然显著,表明交易机制变革并没有从根本上改变换手率的风险信息。
明确换手率的风险信息,不仅可以为流动性风险溢价研究提供更为详尽的证据,而且可以为当前投资者异质信念定价研究的不一致结论提供合理解释,为借助换手率进行其他相关研究提供了理论支撑。与全球其他国家的股票市场相比,我国股票市场的换手率明显更为不稳定。通过明确不同水平的换手率的风险信息,一方面有助于降低投资者对资产价格的认知偏差,提升投资实践中的资产配置效率;另一方面对强化监管股票市场系统性风险,早识别、早预警、早发现重点行业风险,完善金融风险应急处置机制具有指导意义。
① 对个股的月度换手率进行流通市值加权,得到2000年1月至2015年6月的市场换手率。
② 价格变化的绝对值与二阶矩波动率指标类似,也是衡量资产风险的重要指标。由于股票规模效应的普遍存在,流通股与股票预期收益之间是负相关,因而流通股的倒数与股票预期收益之间是正相关,那么交易量与流通股倒数的乘积(即换手率)与股票预期收益之间也应是正向关系。
| [1] | 梁丽珍, 孔东民. 中国股市的流动性指标定价研究[J].管理科学,2008(3). |
| [2] | 苏冬蔚, 麦元勋. 流动性与资产定价: 基于我国股市资产换手率与预期收益的实证研究[J].经济研究,2004(2). |
| [3] | 徐浩峰, 朱松. 机构投资者与股市泡沫的形成[J].中国管理科学,2012(4). |
| [4] | 张峥, 刘力. 换手率与股票收益: 流动性溢价还是投机性泡沫?[J].经济学(季刊),2006(3). |
| [5] | Acharya V V, Pedersen L H. Asset pricing with liquidity risk[J].Journal of Financial Economics,2005,77(2):375–410. |
| [6] | Amihud Y. Illiquidity and stock returns: Cross-section and time-series effects[J].Journal of Financial Markets,2002,5(1):31–56. |
| [7] | Ang A, Hodrick R J, Xing Y H, et al. The cross-section of volatility and expected returns[J].The Journal of Finance,2006,61(1):259–299. |
| [8] | Avramov D, Chordia T. Asset pricing models and financial market anomalies[J].The Review of Financial Studies,2006,19(3):1001–1040. |
| [9] | Barinov A. Turnover: Liquidity or uncertainty?[J].Management Science,2014,60(10):2478–2495. |
| [10] | Barinov A. Why does higher variability of trading activity predict lower expected returns?[J]. Journal of Banking & Finance,2015,58:457–470. |
| [11] | Blume L, Easley D, O’Hara M. Market statistics and technical analysis: The role of volume[J].The Journal of Finance,1994,49(1):153–181. |
| [12] | Chen C R, Lung P P, Wang F A. Where are the sources of stock market mispricing and excess volatility?[J].Review of Quantitative Finance and Accounting,2013,41(4):631–650. |
| [13] | Corwin S A, Schultz P. A simple way to estimate bid-ask spreads from daily high and low prices[J].The Journal of Finance,2012,67(2):719–760. |
| [14] | Datar V T, Naik N Y, Radcliffe R. Liquidity and stock returns: An alternative test[J].Journal of Financial Markets,1998,1(2):203–219. |
| [15] | Diether K B, Malloy C J, Scherbina A. Differences of opinion and the cross section of stock returns[J].Journal of Finance,2002,57(5):2113–2141. |
| [16] | Eckbo B E, Norli Ø. Liquidity risk, leverage and long-run IPO returns[J]. Journal of Corporate Finance,2005,11(1–2):1–35. |
| [17] | Fama E F, MacBeth J D. Risk, return, and equilibrium: Empirical tests[J].Journal of Political Economy,1973,81(3):607–636. |
| [18] | Gervais S, Kaniel R, Mingelgrin D H. The high-volume return premium[J].The Journal of Finance,2001,56(3):877–919. |
| [19] | Harris M, Raviv A. Differences of opinion make a horse race[J].The Review of Financial Studies,1993,6(3):473–506. |
| [20] | Hasbrouck J. Trading costs and returns for U.S. equities: Estimating effective costs from daily data[J].The Journal of Finance,2009,64(3):1445–1477. |
| [21] | Jiang G H, Lee C M C, Zhang Y. Information uncertainty and expected returns[J]. Review of Accounting Studies,2005,10(2–3):185–221. |
| [22] | Liu W M. A liquidity augmented capital asset pricing model[J].Journal of Financial Economics,2006,82(3):631–671. |
| [23] | Liu W M, Luo D, Zhao H N. Transaction costs, liquidity risk, and the CCAPM[J]. Journal of Banking & Finance,2016,63:126–145. |
| [24] | Pástor L, Stambaugh R F. Liquidity risk and expected stock returns[J].Journal of Political Economy,2003,111(3):642–685. |
| [25] | Roll R. A simple implicit measure of the effective bid-ask spread in an efficient market[J].The Journal of Finance,1984,39(4):1127–1139. |
| [26] | Rouwenhorst K G. Local return factors and turnover in emerging stock markets[J].The Journal of Finance,1999,54(4):1439–1464. |
2.Faculty of Finance and Banking,Shanxi University of Finance and Economics,Shanxi Taiyuan 030006,China
 2018, Vol. 20
2018, Vol. 20


