文章信息
 | 上海财经大学 2018年20卷第3期 |
- 刘伯凡, 刘叶
- Liu Bofan, Liu Ye
- 高等教育的婚姻效应:推迟结婚还是选择不婚?——来自合成控制法的新证据
- Does Higher Education Enrollment Expansion Really Reduce the Marriage Rate in China? New Evidence from Synthetic Control Method
- 上海财经大学学报, 2018, 20(3): 93-109.
- Journal of Shanghai University of Finance and Economics, 2018, 20(3): 93-109.
-
文章历史
- 收稿日期:2017-12-25

2018第20卷第3期
新中国成立以前,中国总体教育水平低下,总人口中文盲的比例约为80%①。新中国成立后,政府针对中国人口众多,但基础教育薄弱、文盲率高的特点,展开了大量的基础教育普及工作。中国基础教育普及程度不断提升,2010年人口普查数据显示,中国文盲率仅为4.08%。在此期间,高等教育虽然也得到一定程度的发展,但由于起步晚、水平低、人口基数大等原因,其整体水平一直落后于欧美等发达国家,甚至落后于一些发展中国家。1994年,中国大学入学率仅为4.6%,远低于当年的世界平均水平(13%)。改革开放后,大量廉价劳动力带来的人口红利推动了中国经济的快速发展。随着经济水平的迅速增长和生活水平的日益提升,人民对高等教育的渴望也越来越大。为了满足人们对高等教育的迫切需求,也为了提高社会的人力资本水平,摆脱低端产业的束缚,推动经济的转型与升级,1999年中国开始大幅扩大高等教育的招生规模。至2013年,全国普通高等学校(本专科)招生人数达681.5万人,约是1998年的6.3倍。如此大规模的教育扩展,在提升全社会的人力资本存量与劳动生产率,为经济转型和劳动力就业提供动力的同时,也不可避免地冲击了中国的婚姻市场。特别是在当前人口增长缓慢以及老龄化程度不断加深的背景下,高等教育对初婚年龄和结婚率的影响也受到了社会的广泛关注。其中,高等教育推迟初婚年龄的观点基本得到了国内外学者的一致认可,但高等教育对结婚率的影响尚存争议。一些学者认为,高等教育带来的结婚年龄的推迟以及女性社会地位的提高,降低了人们(尤其是女性)结婚的可能性(Lichter等,1991;吴要武和刘倩,2015);还有一些学者认为,高等教育带来的经济优势将会提高人们进入婚姻的概率(Ono,2003),并且随着社会经济压力的上升,这种促进作用更为显著(於嘉和谢宇,2013)。
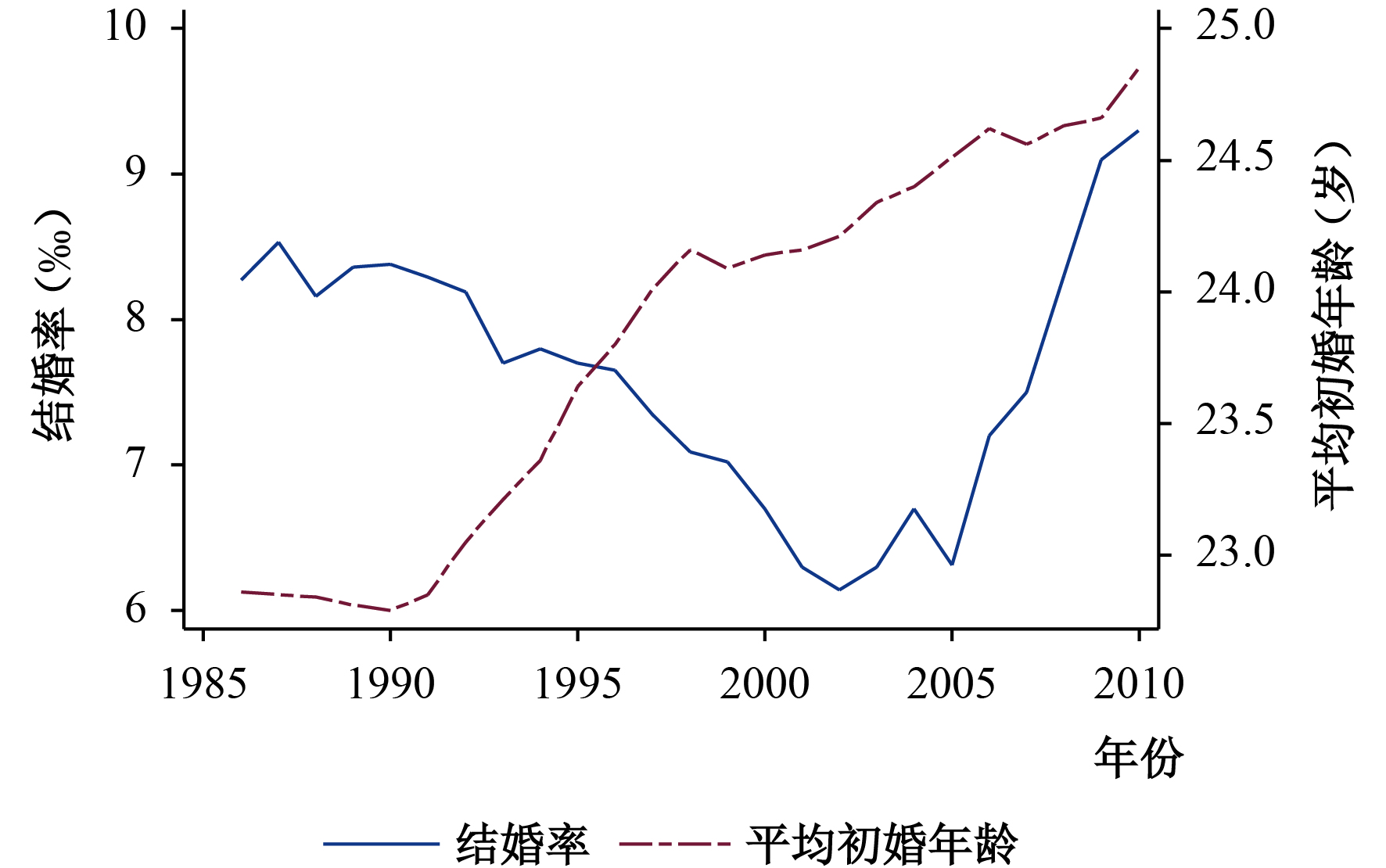
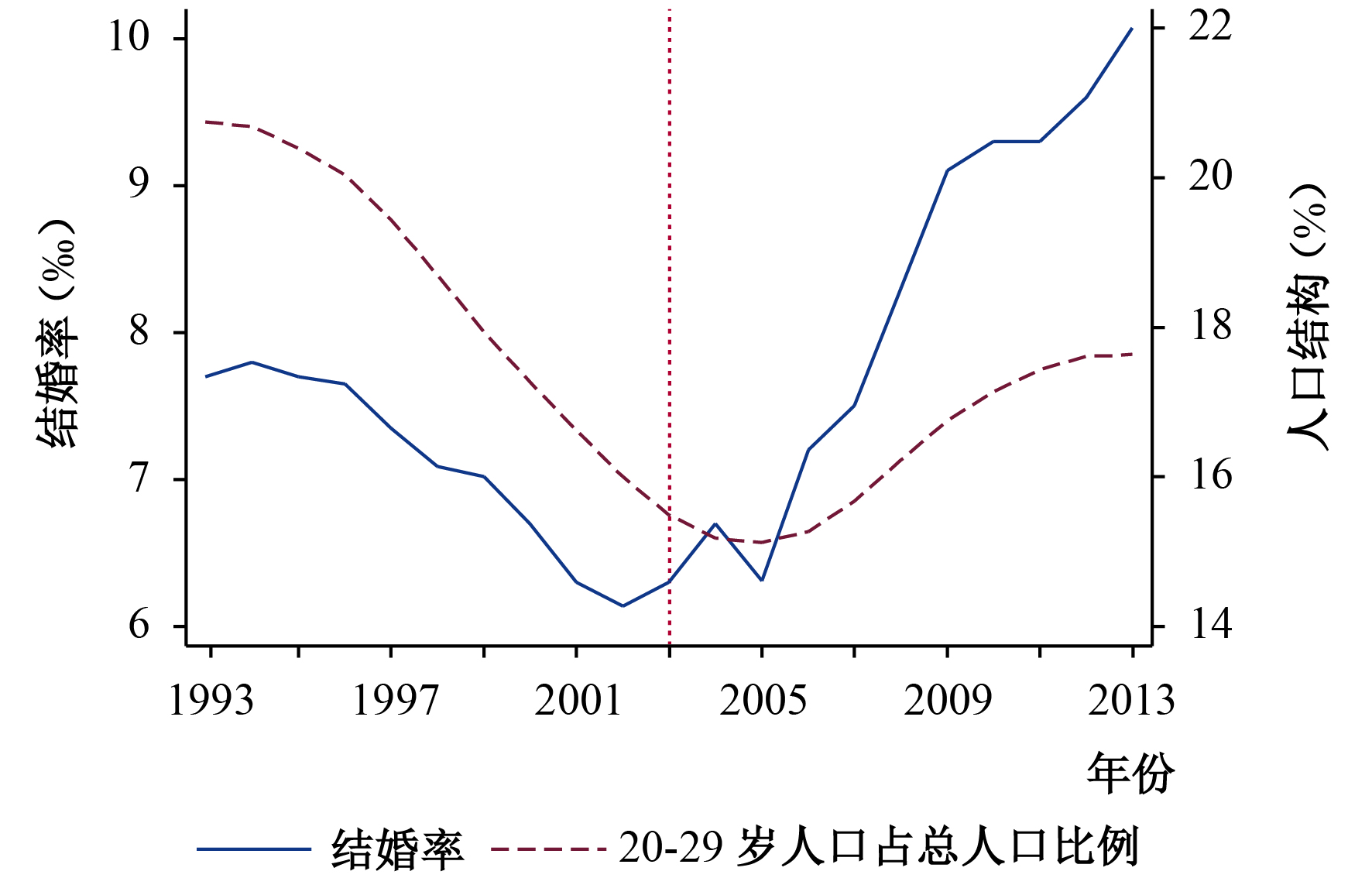
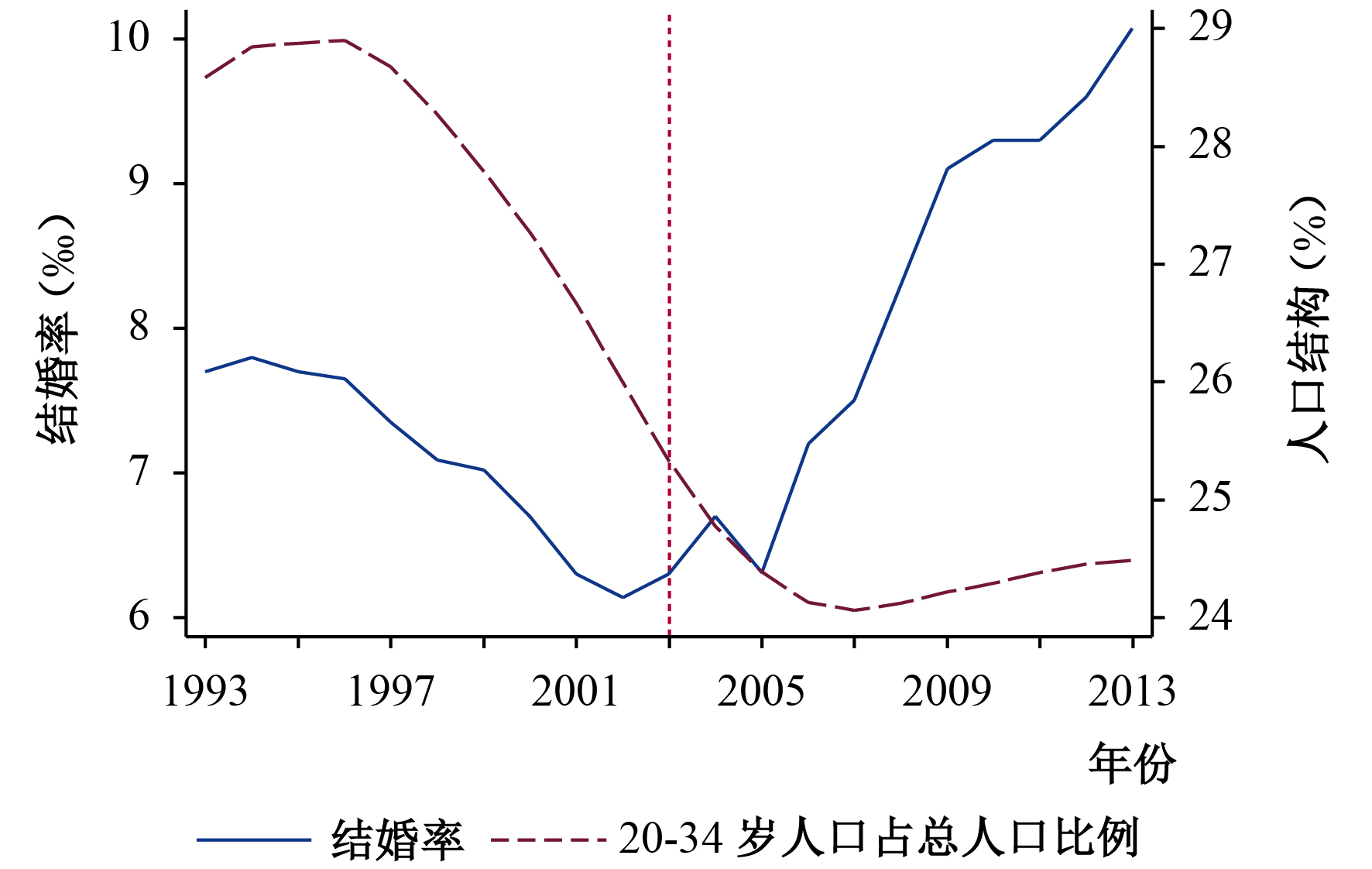
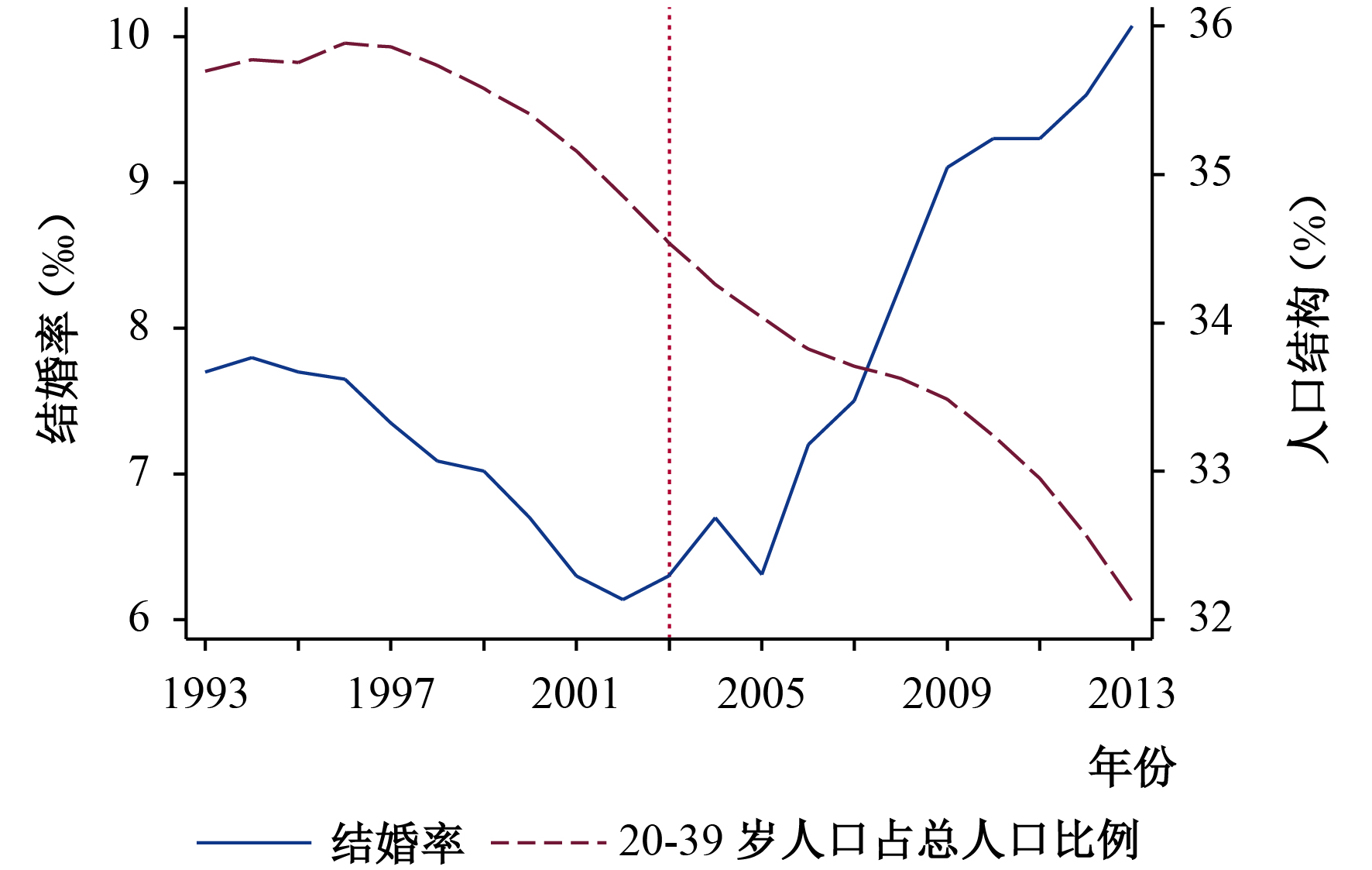
进入21世纪,中国经济、社会的迅速发展以及国民受教育水平的普遍提高,使得年轻人群的婚恋观与以往相比产生了巨大差别。那么受高等教育的影响,中国年轻人群究竟是选择不结婚保持单身,还是仅推迟了进入婚姻市场的时间呢?根据可获得的人口普查数据和民政局公布的婚姻数据,本文计算出中国人口的平均初婚年龄和粗结婚率②,如图1所示。如果多数年轻人口选择不结婚,那么中国的结婚率应该保持下降趋势;如果多数选择的是推迟结婚,那么平均初婚年龄会保持上升趋势,但结婚率变动的趋势不确定。从图1可以看出,中国人口的平均初婚年龄总体呈现先下降后上升的趋势。其中,1986–1991年的平均初婚年龄下降主要与中国1980年新《婚姻法》的颁布有关。虽然《新婚姻法》相对于1950年《婚姻法》将中国男女的法定婚龄各自提高了2岁,但在20世纪70年代实施计划生育的过程中,各地政府以行政规定的形式将男女婚龄提高了5岁左右③(王忠,2003)。也就是说,新《婚姻法》的颁布事实上引起了人口平均初婚年龄的短期下降;1992–2010年平均初婚年龄总体呈上升趋势,除了受中国经济市场化改革的影响外,还可能与中国高等教育的扩招有关(王鹏和吴愈晓,2013;刘昊,2016)。接着,从图1中有关粗结婚率的变动来看,1986–2002年间中国结婚率呈下降趋势,但2003年开始呈现上升趋势。当然,粗结婚率的上升很有可能是人口结构的变化导致的。为了排除人口结构因素的影响,我们分析了各适婚年龄段的人口比重变化趋势(见图2至图4)。从中可以看出,在2003年以前,各适婚年龄段人口比重整体呈下降趋势的同时,结婚率也呈现下降趋势;2003年之后,这种共同下降的趋势开始发生改变,2003–2005年间结婚率开始出现上升趋势;2005年之后,20–29岁和20–34岁年龄段人口比重虽然也开始上升,但结婚率上升斜率更大,甚至在20–39岁人口占比下降的情况下依旧上升。这就是说,人口数量的增加无法完全解释中国结婚率上升的现象。
那么,年轻人口究竟是推迟了结婚还是选择不婚?人们的普遍观点是高等教育推迟了年轻人口的初婚年龄,进而导致其更容易不婚。但在排除了人口结构因素的影响之后,中国结婚率依旧上升的事实表明,高等教育虽然推迟了中国人口的结婚年龄,但可能并未导致更多的人选择不婚。我们知道,2003年是第一批扩招生(1999年入学)进入社会的年份,如果教育水平的提高真的不利于婚姻匹配,那么在扩招的冲击下,中国结婚率应该以更快的速度下降,至少不应该上升。但实际数据显示,2003年以后中国的结婚率却呈上升趋势。那么,高校扩招真的降低了中国结婚率吗?为了回答这一问题,本文尝试利用Abadie和Gardeazabal(2003)提出的合成控制法进行分析与验证。首先,我们挑选世界上若干国家并对其进行适当的线性组合(反事实组),构造出一个最优“合成中国”④;接着,通过对这个没有实施扩招政策的“合成中国”与“真实中国”的结婚率进行比较,分析高校扩招政策对中国婚姻率的影响。这对推动社会形成更加多元化和更具包容性的婚姻观念具有重要的现实意义。
|
| 图 1 1986–2010年平均初婚年龄和结婚率变动趋势 |
|
| 图 2 1993–2013年结婚率与20–29岁人口占比 |
|
| 图 3 1993–2013年结婚率与20–34岁人口占比 |
|
| 图 4 1993–2013年结婚率与20–39岁人口占比 |
第二次世界大战以来,工业化国家的平均初婚年龄普遍呈上升趋势(於嘉和谢宇,2013)。进入20世纪90年代,中国人口的平均初婚年龄也开始逐年增加(见图1)。在分析高等教育对结婚率的影响时,一些学者通常以初婚年龄的推迟作为判断中国结婚率下降的依据(於嘉和谢宇,2013;吴要武和刘倩,2015)。但初婚年龄是否能够很好地度量结婚率呢?理论上讲,个体教育主要从两方面影响初婚年龄:一方面,受教育时间的延长,导致绝大多数在校学生因时间、精力和经济独立性等因素的限制,在难以兼顾学业与家庭的情况下,选择完成学业之后再去承担家庭责任(Thornton等,1995;Raymo,2003;王鹏和吴愈晓,2013),客观上推迟了初婚年龄(Blossfeld和Huinink,1991;Sweeney,2002;刘爽和高华,2015);另一方面,受教育程度的提高,提升了女性的经济地位,推迟了她们进入婚姻的时间。一些以性别角色专业化理论为基础的经验研究发现,女性经济地位的提升会降低她们进入婚姻的动力(White,1981;Cready等,1997)。一是由于受过高等教育的女性在劳动力市场上有更大的竞争力,相应地她们在婚姻市场上的预期收益就越低(王鹏和吴愈晓,2013);二是由于男女平等程度的提高和晚育风险的降低,使女性有了更多的时间和机会去追求自我价值的实现,进而推迟了她们进入婚姻的时间,甚至不结婚。但之后有学者对这一观点进行了修正,指出只有在性别角色分工严重的社会,女性受教育程度才与其结婚机会呈负相关关系,而在性别分工不那么明显的国家或地区,教育水平的提高带来的经济优势会增加其进入婚姻的概率(Ono,2003)。随着社会经济压力的上升,这种促进作用将更加明显(於嘉和谢宇,2013)。也就是说,在这些地区人们受教育水平的提高虽然会导致晚婚,但未必会导致结婚率的下降。还有一些学者的研究表明,高学历女性中的大多数人只是推迟了结婚,并不是选择不婚(Goldstein和Kenney,2001;Isen和Stevenson,2010)。此外,作为一个“普婚”的国家,中国人的婚姻家庭观念很强,终身未婚率很低(刘昊,2016)。基于以上分析,本文认为初婚年龄的推迟不足以说明结婚率的下降,利用初婚年龄来衡量结婚率的做法也是有待商榷的。
(二) 高校扩招真的降低结婚率了吗?虽然一些研究认为女性受教育程度和社会经济地位的提高,会降低其结婚的动力(White,1981;Cready等,1997)和可能性(Lichter等,1991;吴要武和刘倩,2015);但婚姻寻找理论指出,现代社会中女性的经济潜力在婚姻形成中的作用越来越重要(Oppenheimer,1988)。尤其,在当前社会结构激烈变动的大环境下,经济上的压力⑤使得仅靠男性收入难以负担整个家庭的情况越来越普遍,那么在经济实力(或经济潜力)上具有优势的女性进入婚姻的几率将会变得更大。一些利用“事件史分析法”(Lichter等,1992;Thornton等,2016)和“世代比较法”(Lichter等,2002)进行的经验研究也都证实了这一观点。另外,研究现代美国女性婚姻行为的文献发现,与过去相比,现在大学毕业的女性选择结婚的人越来越多(Goldstein和Kenney,2001),且有大学文凭女性的结婚率和再婚率都要高于受教育年份较少的女性(Isen和Stevenson,2010)。从婚姻回报率的角度来看,受教育程度的提高可以使女性从婚姻中获得更高的收益⑥,同时男性还可以从具有较高教育水平的妻子那里获得多方面的好处,如子女的教育和健康(Currie和Moretti,2003;Liu和Nordstrom Skans,2010)。还有一些研究中国高等教育对婚姻市场影响的研究显示,作为普婚国家,中国接受高等教育的人口更多的是推迟结婚而非不婚,并指出高等教育提升了中国女性的人力资本,使其可以更加耐心地寻找合适的婚姻,但在30岁之前仍会较为普遍地进入婚姻(刘昊,2016)。此外,受教育程度高的女性由于结婚较晚、生育孩子更少且将结婚作为一种经济保证的可能性更小,从而更加享受婚姻和家庭生活,其婚姻质量和稳定性也就越高(Isen和Stevenson,2010)。这些无疑也提高了高学历女性进入婚姻的可能性。
综上所述,虽然教育推迟初婚年龄的观点受到了国内外学者的广泛肯定,但关于教育对结婚率的影响尚未取得一致意见。那么,扩招政策的实施究竟对中国结婚率的变动带来什么样的影响呢?下文展开实证分析。
三、中国的现实情况分析:扩招与婚姻 (一) 初婚年龄与结婚率的关系从中国的现实情况来看,1999年高校扩招以来,大批年轻人口进入大学接受高等教育。至2013年,中国普通高等院校本专科及研究生招生人数达783万,约占适龄人口的50%。教育时间的延长客观上推迟了中国人口的平均初婚年龄。由于以往中国女性进入结婚的年龄相对较小,高等教育对其初婚年龄推迟的影响可能要大于男性(刘爽和高华,2015)。但是,作为性别分工不明显⑦和相对传统的普婚国家,选择推迟结婚并不意味着以后一定不结婚。根据吴要武和刘倩(2015)给出的有关中国各年龄阶段研究生有配偶比例的数据,我们发现虽然随着时间的推移,各年龄段有配偶的比例都呈下降趋势。但年龄段越大这种差距就越小,考虑到当下人们普遍选择推迟进入婚姻的现状,本文认为仅通过比较不同时点同一年龄段有配偶比例的下降来判断结婚率下降是不合理的。事实上,如果比较45–49岁年龄段有配偶的数据,可以发现不同调查年份中有配偶的人口比例都趋于一致,没有呈现明显的下降趋势。因此,综上所述,虽然当下人们的结婚年龄推迟了,但是婚姻市场可能并未出现结婚率下降的现象。
实际上,由于高等教育的推广,年轻人有足够的机会对自身进行人力资本投资,以期未来获得更高的收入。加之,接受了高等教育之后,年轻人思想更加开放,比其父辈对婚姻年龄的容忍度更高,也更有可能推迟进入婚姻市场。与此同时,高校扩招不仅会影响接受高等教育的人群,那些没有接受高等教育的人群也有可能受到这些人示范效应的影响而选择推迟进入婚姻市场。也就是说,年轻人推迟进入婚姻能够解释中国初婚年龄的上升,但这并不一定就表明婚姻市场的匹配率下降了。人们到了一定的年龄就会进入婚姻市场,而这个“一定的年龄”是在不断变化的。所谓“剩男剩女”的概念都是建立在过往的思想观念之上,认为现在很多年轻人早已应该进入婚姻市场,而那些过了“一定的年龄”还没有搜寻到配偶的人,是婚姻市场中的“被剩下”的失败者,于是便根据初婚年龄的推迟来推断结婚率出现了下降。那么,初婚年龄和结婚率呈现负相关关系这样的判断是否成立呢?事实上,通过图1至图4我们发现,在1990–2003年间,这种判断基本成立,但在2003年前后,这种负相关关系就不存在了,甚至呈现出了一定的正相关关系。我们知道,扩招会在客观上导致平均初婚年龄上升。如果扩招同时导致结婚率下降,那么这种负相关关系就不应该在2003年前后瓦解,反而会更加明显。考虑到2003年前后是扩招后第一批本专科学生毕业的年份⑧,那么是否扩招导致了这种负相关关系的瓦解呢?
(二) 高校扩招对结婚率的影响从理性人角度出发,人们之所以有意愿结婚是因为组成家庭生活比自己单独生活所得到的效用更大。因此,人们在进入婚姻市场时会寻找那些能够使自己效用水平提升的伴侣。那么,结婚率的高低将主要取决于“婚姻市场中满足以上条件的异性数量”⑨和“寻找满足以上条件异性的难易程度”。本人认为,高校扩招正是通过影响这两大因素进而对中国整体结婚率产生正面影响的,具体来讲:
第一,高校扩招政策扩大了婚姻市场中满足以上条件的异性数量。一方面,从20世纪末开始,中国婚姻市场上的择偶模式逐渐出现教育同质性回潮,即夫妻双方具有同等教育水平的家庭比重上升的现象(李煜,2008;潘丽群等,2015)。由于长久以来,中国男性的平均受教育水平要高于女性,这无疑限制了中国男性的择偶范围。但高校扩招政策的实施,大大提高了在校大学生中女性的占比,男性择偶范围得以扩大,这可能会促进结婚率的上升。另一方面,婚姻观念的转变以及性别比例的失衡,使得中国夫妻之间的婚龄差发生了较大变化,“女大男小”的婚配比例明显增加,并与“男大女小”的比例基本持平(刘爽和梁海艳,2014)。这意味着接受过高等教育的大龄女性的择偶范围也得以扩大。
第二,高校扩招政策降低了寻找满足以上条件异性的难度。高等教育虽然挤占了原本用于婚姻市场搜寻的时间(推迟了初婚年龄),但是扩招使得大批同龄年轻人口集聚在一起,长年累月的学习与生活使他们有足够的机会和时间去接触、认识和了解彼此,这可能会使其积累一定的人际交往经验,进而提高其未来进入婚姻市场的搜寻效率;与此同时,扩招也加大了中国的人口流动,提高了人们之间的接触频率,使得进入婚姻市场的搜寻者更容易找到理想的目标。
我们知道,扩招最大的影响在于扩大了受过高等教育人群的比例。根据现有文献和本文的分析,在当前社会经济背景下,增加的这部分人群在婚姻市场中会受到更多的青睐,人们为了提高婚姻价值,会期望寻找教育水平更高的配偶,因而扩招的冲击不仅仅局限于接受高等教育的群体,还会对整个婚姻市场造成冲击。当然,接受高等教育的人群对配偶的要求也更高,这将不利于婚姻市场的匹配。总的来看,高校扩招对于结婚率的影响并不能确定。
综合现有研究和上文分析,我们认为高校扩招确实是导致中国初婚年龄普遍上升的因素之一,但初婚年龄的上升未必意味着结婚率的下降。同时,扩招对中国结婚率的影响是双向的,但仅从理论角度无法探知其综合影响的正负。因此,高校扩招对中国结婚率产生的净影响需要通过精确的实证方法进行研究。接下来,我们将利用控制合成法进行探究。
四、模型设置与实证策略 (一) 模型设置与参数估计方法一般而言,可以利用DID方法(双重差分法)来测度扩招影响中国结婚率的平均效应。但是传统的DID方法需要有合适的控制组才能得到理想的效果。随着时代的发展,人们的婚姻观在逐渐改变,不同时期的人们对于适婚年龄的定义是在不断变化的。无论是使用不同时期同一年龄段的人群,或是使用同一时期不同年龄段的人群作为对照组,都是将具有不同婚姻观念的两组人进行比较。考虑到扩招对不同婚姻观念的两组人影响显然是不同的,而利用DID方法无法解决对照组和控制组的异质性问题,进而无法准确估计出扩招对结婚率的影响。此外,传统的双重差分模型假设所有个体的时间趋势均相同⑩,但在实际操作中很难找到符合这一假设的对照组。
为了解决以上问题,本文基于Abadie和Gardeazabal(2003)提出的“合成控制法”(synthetic control method)思想,采用Abadie等(2010)的方法,通过数据特征构造出一个反事实对照组,从而更加合理地推测出扩招对中国结婚率的影响。与传统的DID方法相比,该方法具有两大优势:第一,将“冲击”发生前处理组和各对照组的各预测变量进行对比,而后利用最小化预测变量差值的方法,将各对照组赋予不同的权重,并以此为基础构建出一个全新的反事实对照组。该方法是根据数据来选择线性组合的最优权重,避免了研究者主观选择控制组的随意性(王贤彬和聂海峰,2010;刘甲炎和范子英,2013)。此外,又由于合成控制法的权重必须非负,可以避免使用回归法时权重可能出现负值的情况,从而避免了过分外推问题(Abadie等,2015)。第二,该方法是一种非参数估计方法对基于双向固定效应模型的双重差分法进行的推广,放松了过于严格的平行趋势假设,允许互动固定效应存在,可以体现面对冲击的异质性反应。
具体而言,假设可以观测的样本为N+1个地区,一共T期的面板数据,我们记
| ${\alpha _{1t}} \equiv M_{1t}^I - M_{1t}^N = {M_{1t}} - M_{1t}^N (t = {T_0} + 1, \cdots ,T)$ | (1) |
如果扩招冲击对于我国结婚率没有影响,则
| $M_{it}^N = {\delta _t} + {\beta _t}'{z_i} + {\lambda _t}'{\mu _i} + {\varepsilon _{it}}$ | (2) |
其中,
接着,建立一组N×1阶权重向量:
| $W \equiv {({w_2}, \cdots ,{w_{N + 1}})'}$ | (3) |
其中,
| $\sum\limits_{i = 2}^{N + 1} {{w_i}} M_{it}^N = {\delta _t} + {\beta _t}'\sum\limits_{i = 2}^{N + 1} {{w_i}} {z_i} + {\lambda _t}^\prime \sum\limits_{i = 2}^{N + 1} {{w_i}} {u_i} + \sum\limits_{i = 2}^{N + 1} {{w_i}} {\varepsilon _{it}}$ | (4) |
用
| $E\Biggr(M_{1t}^N - \sum\limits_{i = 2}^{N + 1} {{w_i}} M_{it}^N\Biggr) = E\Biggr({\beta _t}\prime \Biggr({z_1} - \sum\limits_{i = 2}^{N + 1} {{w_i}} {z_i}\Biggr)\Biggr) + E\Biggr({\lambda _t}\prime \Biggr({u_1} - \sum\limits_{i = 2}^{N + 1} {{w_i}} {u_i}\Biggr)\Biggr) + E\Biggr(\sum\limits_{i = 2}^{N + 1} {{w_i}} \left({\varepsilon _{1t}} - {\varepsilon _{it}}\right)\Biggr)$ | (5) |
由于式(5)中
| ${z_1} \approx \sum\limits_{i = 2}^{N + 1} {{w_i}} {z_i}, {M_{1t}} \approx \sum\limits_{j = 2}^{N + 1} {{w_i}} {M_{it}}(1 {\text{≤}} t {\text{≤}} {T_0})$ | (6) |
就会有,
| ${u_1}{\rm{ = }}\sum\limits_{j = 2}^{J + 1} {{w_j}} {u_j}$ | (7) |
于是,为估计
| ${\hat \alpha _{1t}} \equiv {M_{1t}} - \sum\limits_{i = 2}^{N + 1} {w_i^*} M_{it}^N (t = {T_0} + 1, \cdots ,T)$ | (8) |
也就是说,得到
| $\left\| {{X_1} - {X_0}W} \right\| = \sqrt {{{({X_1} - {X_0}W)}'}V({X_1} - {X_0}W)} $ | (9) |
其中,((
考虑到任意满足条件的矩阵
| $\mathop {\min }\limits_v \tfrac{1}{{{T_0}}}{({M_1} - {M_0}{W^*}(V))'}({M_1} - {M_0}{W^*}(V))$ | (10) |
其中,M1为地区1由第1期到第T0期结婚率组成的(T0×1)阶列向量,
由此可知,在通过数据得到最优权重矩阵时,结果变量的线性组合和预测变量起到了至关重要的作用⑫。因此,本文对结果变量的线性组合和预测变量做了如下选择:首先,按照一般惯例,结果变量的线性组合直接使用冲击发生之前结果变量的均值,本文中为扩招对结婚率发生冲击前结婚率的均值。其次,确定了以下预测变量:(1)女性人口比例。男女比例会对婚姻匹配产生直接影响,无论是男多女少,还是女多男少,都会导致数量相对较少的性别成为稀缺资源,从而不利于婚姻匹配,合适的男女人口比例则有利于提高结婚率,本文使用女性人口占总人口比例来度量男女人口比例。(2)生育率。生育和婚姻密切相关,一个地区人们的生育观往往和婚姻观存在着紧密联系,但由于难以找到一个度量地区婚姻文化的合适变量,因而本文考虑用女性人均生育率来度量当地的生育观,并将其作为度量当地婚姻观念的代理变量。(3)男女失业比。很多地区存在男女不平等的现象,会影响人们的婚姻选择行为。考虑到男女就业差异可在一定程度上体现这种不平等,本文将使用男女失业比来度量男女不平等程度。(4)适龄人口比重。一个地区的年轻人越多,结婚率自然就越高,为了尽可能减少不同地区平均结婚年龄存在较大差异可能带来的影响,本文使用20–29岁、20–34岁、20–39岁人口占总人口比例三个指标来度量适龄人口比重。(5)人均受教育程度。人们的婚姻观念往往会受教育水平的影响,因此本文使用25岁及以上人口的平均受教育年限来度量⑬。最后,我们选用粗结婚率作为结婚率的度量指标⑭。此外,为了解决可能的遗漏变量问题,我们还将1993年、1998年和2002年三个年份的结婚率纳入预测变量中,以期获得更加准确的估计效果。
(二) 扩招冲击时间节点的确定自1999年起,中国大规模增加了普通高校本专科院校招生人数,更多的年轻人进入了大学校园。但是,考虑到目前中国年轻人在大学期间结婚的事例非常罕见,在毕业之前扩招可能只是推迟了他们结婚的年龄,未必降低了他们的结婚概率,因此将1999年作为扩招对结婚率冲击时间点是不合适的。鉴于第一批受到扩招冲击的专科生在2002年毕业,而本科生在2003年毕业,将冲击时点定在2002年或者2003年更为合适。又由于到2003年,第一批受到冲击的大学生才可基本全部毕业,扩招冲击的影响才能开始全部显现,故本文最终选择2003年作为扩招对中国结婚率产生影响的时间节点。
五、实证结果与分析 (一) 数据来源及相关说明合成控制法需要利用其他未受到冲击的地区拟合出一个反事实的未受冲击的处理组地区,就本文而言,我们需要用其他国家拟合出一个未受冲击的“合成中国”。由于各国的实际婚恋市场均存在一定差异,且难以被清晰地观测出来,所以我们需要尽可能多的对照组数据用来合成处理,以求能够找到更为精确的矩阵进行拟合。出于数据可得性的限制,本文选取了以下35个具有代表性的国家和地区,作为用于合成对照组的样本:澳大利亚、阿根廷、巴西、白俄罗斯、保加利亚、波多黎各、波兰、韩国、丹麦、德国、俄罗斯、法国、菲律宾、哈萨克斯坦、荷兰、加拿大、捷克、立陶宛、卢森堡、罗马尼亚、美国、蒙古、墨西哥、挪威、日本、西班牙、土耳其、委内瑞拉、乌克兰、新加坡、新西兰、意大利、英国、中国澳门、中国香港。此外,我们选取的指标均为比例型指标,也无须担心绝对面积或人口数量造成的影响。考虑到时间跨度的限制,本文选取了1993–2013年为研究的时间跨度,自1993年到扩招冲击节点2003年共10年时间,可以保障我们确定的权重矩阵合理有效。其中,结婚率的数据主要来源于《国际统计年鉴》(中文)和联合国《人口统计年鉴》(英文);女性人口比例、生育率、男女失业比以及三个度量适龄人口比重指标的数据都来源于世界银行数据库;人均受教育程度指标的数据来源于联合国发布的人均受教育年限数据。
(二) 实证结果分析首先,表1给出了对照组样本的权重赋值表,从中可以看出韩国和菲律宾的权重赋值最高。这两个国家都属于东亚文化圈范围,婚恋文化与中国相似,且经济发展趋势也与中国相似,故权重最高。
然后,表2给出了扩招冲击发生之前(1993–2002年),中国、合成中国以及对照组样本的预测变量平均值之间的对比。由表2可以看出,对照组的各个预测变量的平均值,特别是1993年、1998年和2002年的结婚率,与中国相差较大,并非一个合适的对照组,而合成中国与中国的各预测变量中除了生育率的平均值差距相对较大,其他的都非常接近。本文认为,这主要是由于中国实行了计划生育政策所致。总体来讲,合成中国很好地复制了中国婚姻市场的特征,这也意味着本文利用合成控制法得到的结果是合理有效的。
| 预测变量 | 中国 | 合成中国 | 用于合成对照组的35个样本 |
| 女性人口比例 | 48.60 | 50.32 | 50.74 |
| 生育率 | 1.59 | 2.32 | 2.17 |
| 男女失业比 | 1.35 | 1.21 | 1.12 |
| 平均受教育年限 | 7.07 | 8.53 | 7.45 |
| 20–29岁人口占比(%) | 18.78 | 17.36 | 16.70 |
| 20–34岁人口占比(%) | 27.99 | 25.49 | 24.50 |
| 20–39岁人口占比(%) | 35.57 | 33.23 | 31.97 |
| 结婚率1993(‰) | 7.70 | 7.72 | 7.24 |
| 结婚率1998(‰) | 7.09 | 7.04 | 6.48 |
| 结婚率2002(‰) | 6.14 | 6.18 | 5.68 |
| 资料来源:作者计算整理所得。 | |||
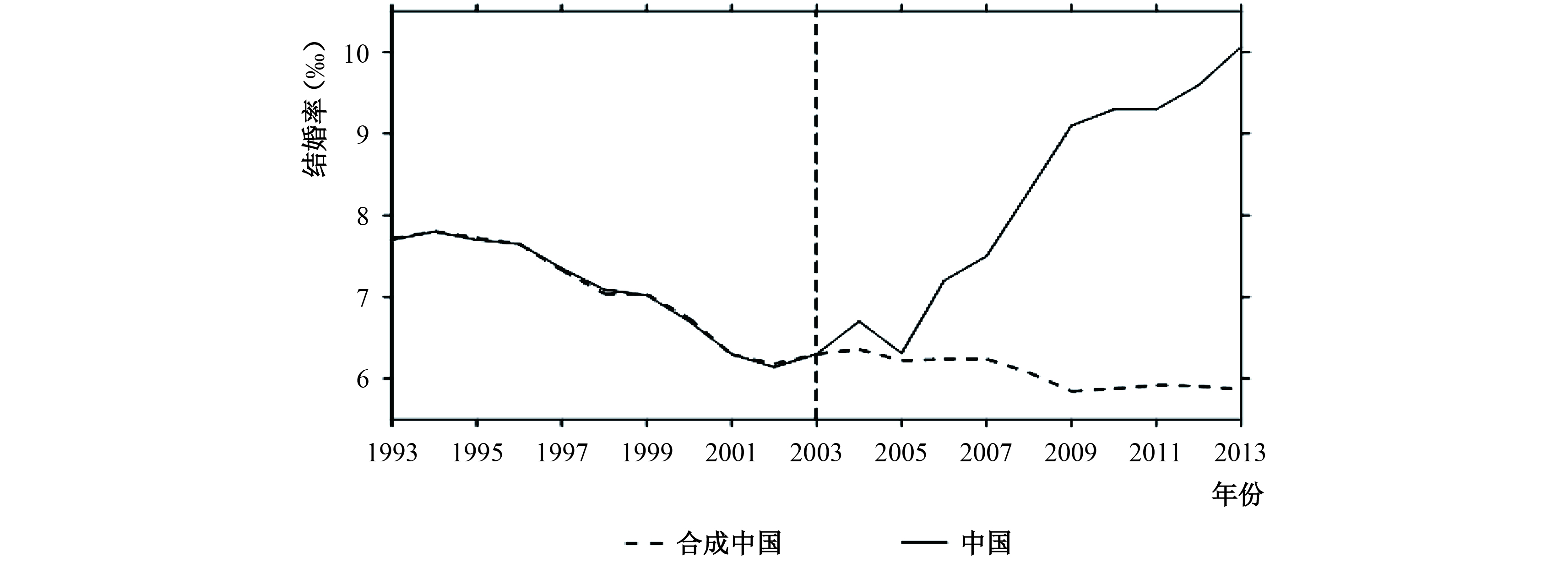
接下来,具体分析高校扩招对中国结婚率的影响。首先,我们计算出了1993–2013年间中国与合成中国的结婚率变动趋势⑮(见图5)。可以看出,在2003年以前,两者相差不大;而在2003年以后,中国的结婚率开始明显高于合成中国的结婚率,且这一差距随着时间的推移不断扩大。
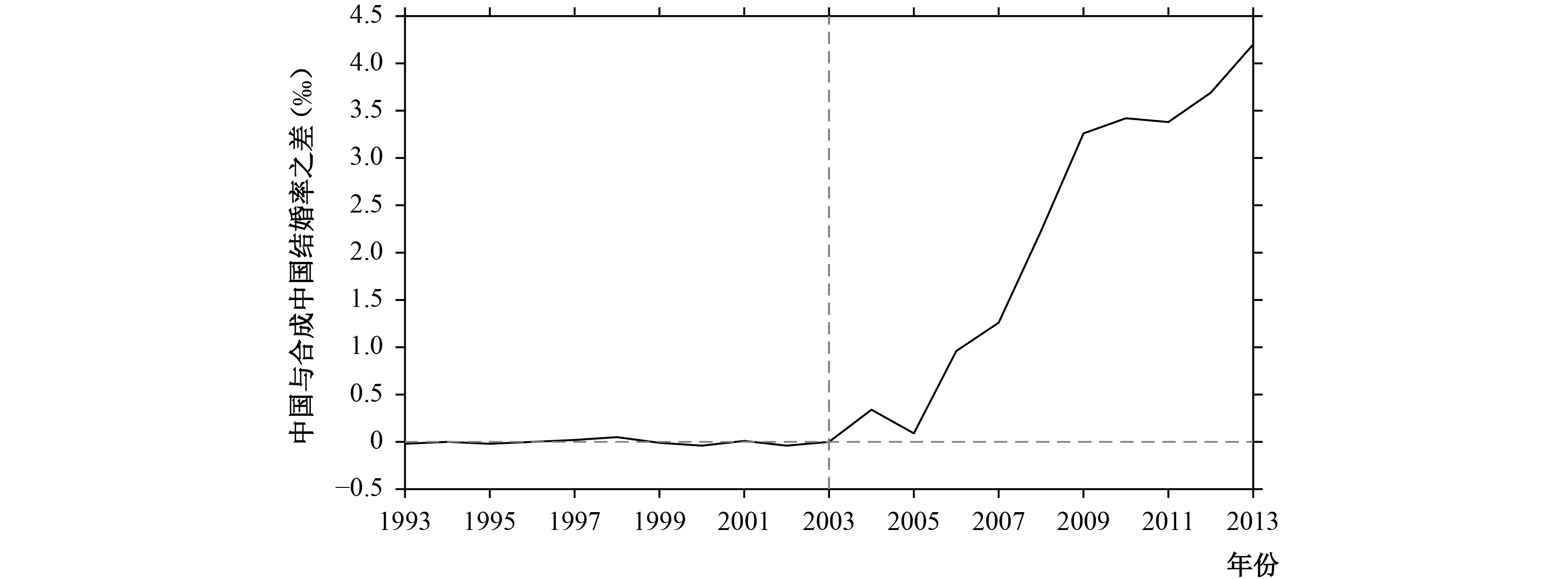
为了更直观地分析这一影响,我们又计算了中国与合成中国的结婚率之差⑯,并据此画出两者差距的变化趋势(见图6)。不难看出,2003年以前,两者的差值一直在0附近,表明合成中国很好地复制了中国婚姻市场的特征,合成控制法是合理有效的;2003年以后,两者每一年的差值始终为正,即处理效应为正,表明扩招冲击不仅没有降低中国结婚率,反而促进了中国结婚率的上升。于是,可以确定扩招冲击对于中国结婚率的影响是正向的。
此外,由图6还可以看出,2003年之后(2005年和2011年除外)的每一年,扩招冲击所带来的正向影响总是比上一年的影响更大。很显然,扩招冲击对于中国结婚率的影响是非线性的,这种正向影响在不同年份之间存在一定差异,且影响程度随着时间的推移不断扩大。这一现象并不难以理解,首先扩招并非一步到位,普通高校本专科院校招生人数是在1999年以后逐渐增加的;其次,扩招之后随着时间的推移,社会中直接受到扩招影响的人数也越来越多,其示范作用也得到更广泛传播。此外,这种非线性的影响效果也表明,使用合成控制法比传统的DID方法更加准确有效。
|
| 图 5 1993–2013年中国与合成中国结婚率变动趋势图 |
|
| 图 6 1993–2013年中国与合成中国结婚率的差值变动趋势 |
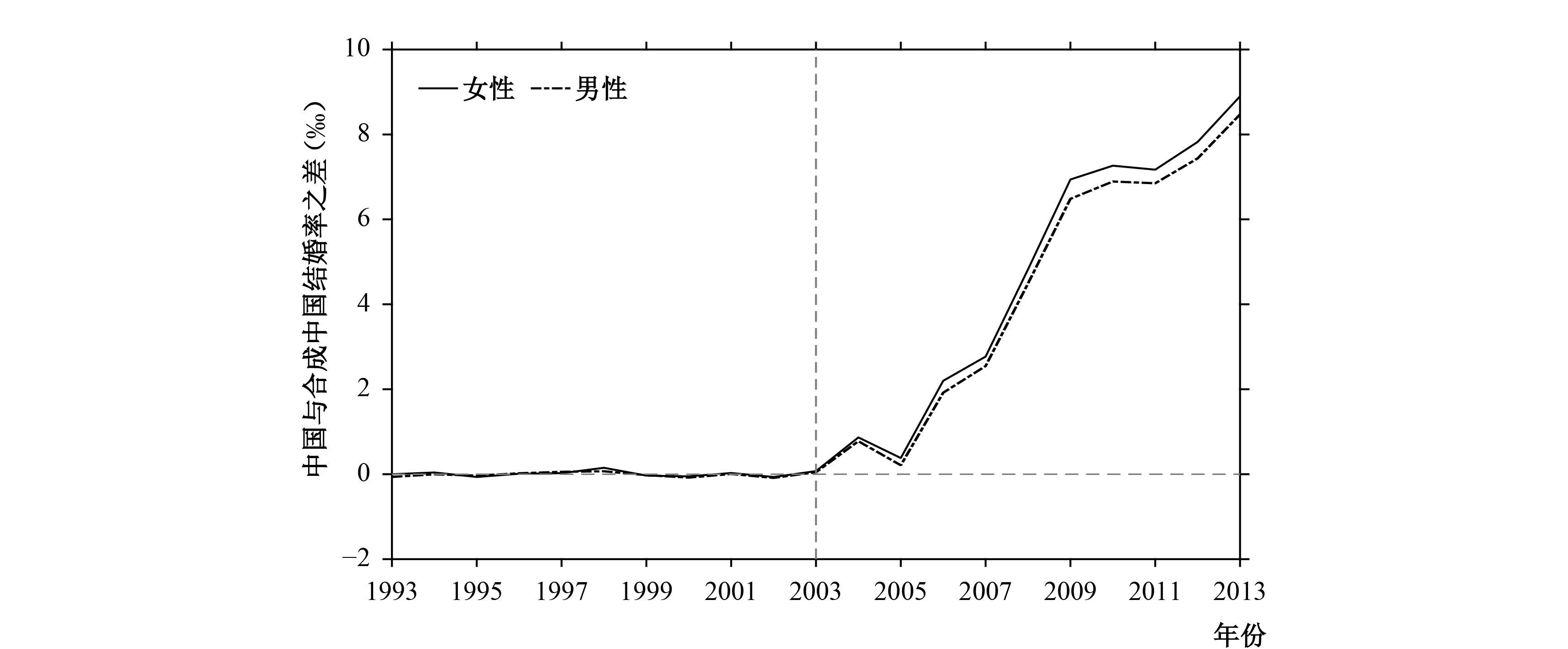
一般认为,扩招会使得男女在教育方面的不平等问题得到改善,受过高等教育的人群中男女比例会随着扩招而不断接近(Goldin等,2006)。因此,扩招对于两性结婚率的影响可能有所不同。于是,我们利用合成控制法分别测算了扩招冲击对中国男性和女性结婚率的影响,计算出中国与合成中国在男性和女性结婚率上的差值,并画出了相应的变化趋势图(见图7)。
结果显示,无论从女性角度还是男性角度,中国与合成中国的变化趋势基本保持一致,扩招冲击对女性和男性的结婚率都存在一个明显的正向影响。但是,扩招冲击对女性结婚率的正向影响要略大于男性,这一结论与主流的观点不同。一般认为,一个地区扩大教育规模时,受教育水平的提高会导致女性收入提高并使女性经济更加独立,因此会选择不婚,进而导致女性不婚比例上升乃至整体结婚率下降。但本文认为,女性经济独立不代表会选择不婚。根据理性人假设,个人之所以选择结婚,是因为两个人组成家庭生活所获得的效应水平比一个人生活的效应水平高。虽然受过高等教育的女性独居生活效应水平相对更高,但这并不意味着她无法找到可使其获得比独居更大效应水平的婚姻伴侣。事实上,有研究显示,婚姻双方越来越多的呈现出同质性特征,即人们越来越倾向于寻找和自己教育背景相似的异性伴侣组成家庭(Sweeney,2002;潘丽群等,2015)。此外,虽然中国劳动力市场仍存在性别歧视,但是相当一部分家庭都属于夫妻双方同时为家庭贡献收入的双收入模式⑰。这种分工条件下,通常女性的经济条件越好越有利于其婚姻匹配(Lichter等,1992)。不仅如此,还有一些研究表明婴儿的健康程度(Currie和Moretti,2003)和教育(Liu和Nordstrom Skans,2010)均与母亲的受教育水平正相关。根据理性人假说,男性理应更愿意将接受过高等教育的女性作为配偶。基于以上分析,我们认为,在中国受过高等教育的女性理应更加“抢手”,而扩招使得受高等教育的女性人口增长,这无疑会对女性结婚率的提高产生更大的正向影响。
|
| 图 7 中国女性/男性结婚率与合成中国女性/男性结婚率之差 |
1. 基于地区的安慰剂检验
虽然实证结果表明扩招冲击对中国结婚率有正向影响,但上述实证结果无法确定这种正向影响是源于扩招而非其他因素,且这种正向影响的显著性也需要进一步验证。因此,本文借鉴Abadie等(2010)所提出的“安慰剂检验”(placebo test)来进行统计检验。我们先将对照组中的国家或地区进行合成控制分析,即假定其中一个国家或地区像中国一样进行了高等教育扩招,且扩招冲击时间点同样是2003年。然后再使用合成控制法,利用对照组中剩余的样本构造出该样本的合成控制对象,并得到该样本与未实施扩招的合成控制对象的结婚率差异,这种差异即为“安慰剂效应”。最后,依照以上方法,依次计算对照组中每个国家的“安慰剂效应”。需要指出的是,在进行安慰剂检验时,如果某个国家或地区在扩招冲击产生影响之前的均方误差(MSPE)特别大,则表明合成控制法的效果很差,扩招冲击产生影响之后的处理效应也会特别大,那么该“安慰剂效应”就不可信。
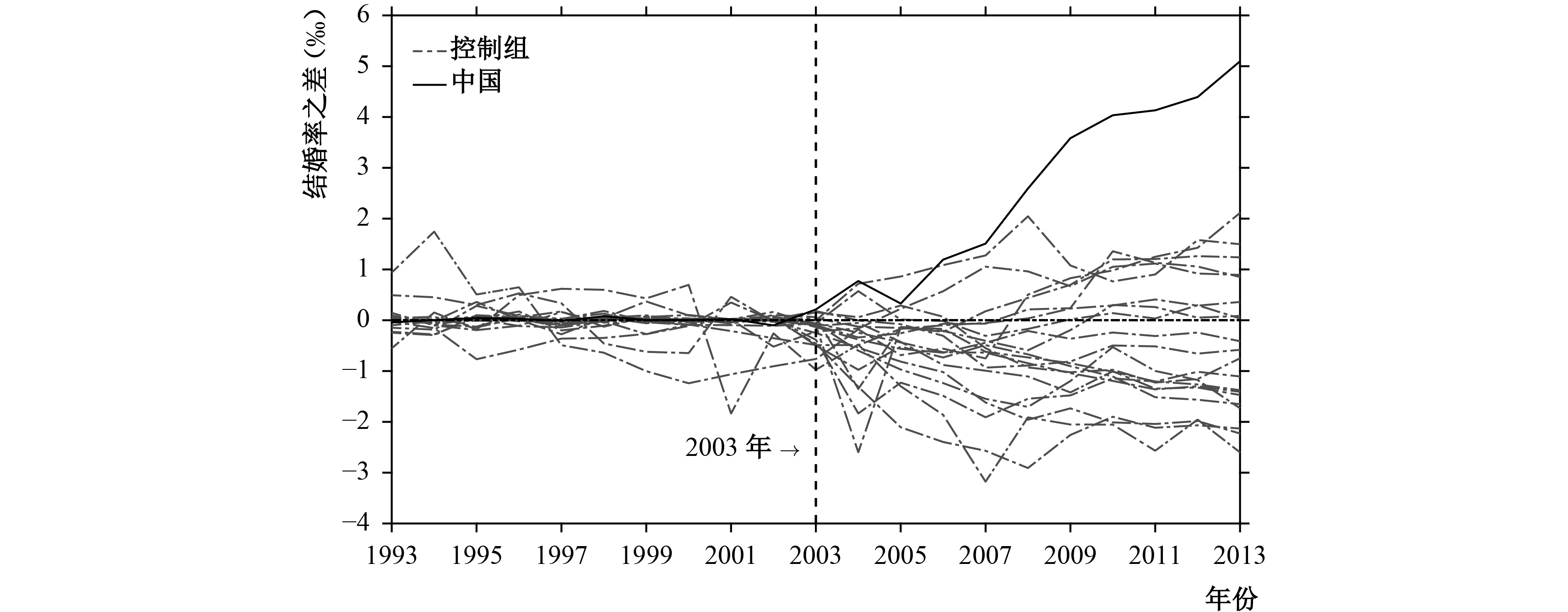
为了避免MSPE过大,本文选取了扩招冲击产生影响前MSPE在1以内的20个国家或地区,并将其安慰剂效应与中国的处理效应进行比较(见图8)。结果显示,扩招冲击对中国结婚率的正向影响(处理效应)要明显大于其他20个国家或地区的安慰剂效应。如果扩招并未对中国结婚率产生正向影响,那么在一共21个国家或地区中,中国的处理效应恰好最大的概率为1/21(≈0.048<5%),即扩招冲击对中国结婚率并未产生正向影响的概率小于5%。因此,我们可以认为这种正向影响在5%的置信水平上显著。
|
| 图 8 中国与控制组国家或地区的真实结婚率与合成结婚率之差的变动趋势 注:图8中深色曲线表示中国的真实结婚率与合成结婚率之差,浅色曲线表示控制组国家或地区的真实结婚率与合成结婚率之差。 |
以上安慰剂检验只是将处理组的处理效应和对照组的安慰剂效应进行了比较,证明处理组的处理效应比安慰剂效应更大。但是,如果在扩招冲击产生影响前处理组的均方差(MSPEpre)就很大,那么合成控制法就无法很好地预测处理组的结果,变量在扩招产生影响后处理组的均方差(MSPEpost)也会很大。鉴于此,我们利用两者的比值来控制MSPEpre的影响。如果扩招确实对中国结婚率有较大的正向影响,且其他国家或地区的安慰剂效应相对较小,那么MSPEpost与MSPEpre之比值应该明显大于其他国家或地区。为此,我们计算了中国以及其他20个国家或地区的MSPEpost/MSPEpre值,具体结果如图9所示。从图9可以看出,中国的MSPEpost大约是MSPEpre的4 600倍,远远大于其他国家或地区的MSPEpost/MSPEpre⑱。同样,如果扩招对中国结婚率没有产生正向影响,中国的处理效应大于其他国家或地区的安慰剂效应的概率只有1/21(≈0.048<5%)。
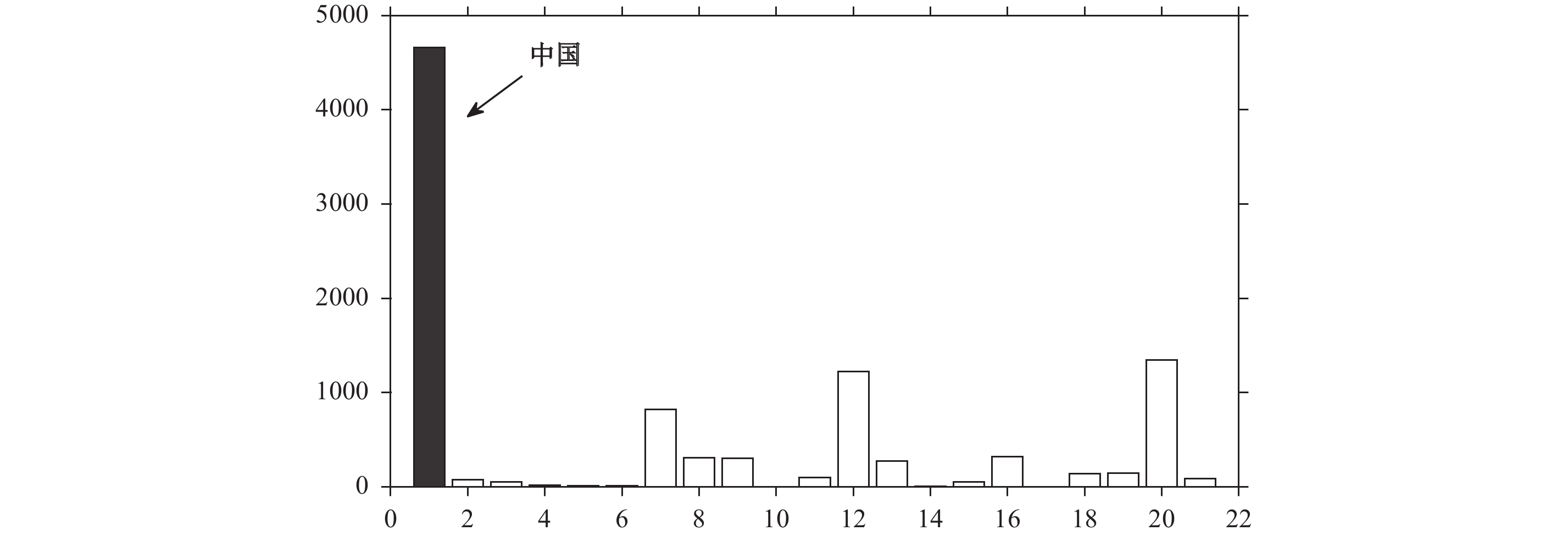
|
| 图 9 处理组与控制组国家或地区的MSPEpost/MSPEpre 注:横轴为每个国家或地区的编号,第一个为中国;竖轴表示MSPEpost/MSPEpre值。 |
2. 基于时间的安慰剂检验
通过地区安慰剂检验可以确定,高校扩招对中国结婚率有显著的正向影响。但是,考虑到扩招冲击时间节点选择的主观性,我们借鉴Abadie等(2015)基于时间的安慰剂检验(in-time placebo test)方法,对扩招冲击的时间节点进行检验。具体而言,假设扩招冲击产生影响的时间节点为2000年,而后再次利用控制合成法对扩招产生的影响进行估计(如图10所示)。结果显示,当扩招冲击节点设为2000年时,对比中国与合成中国结婚率的走势不难发现,2003年仍旧是二者之间产生明显差异的节点。
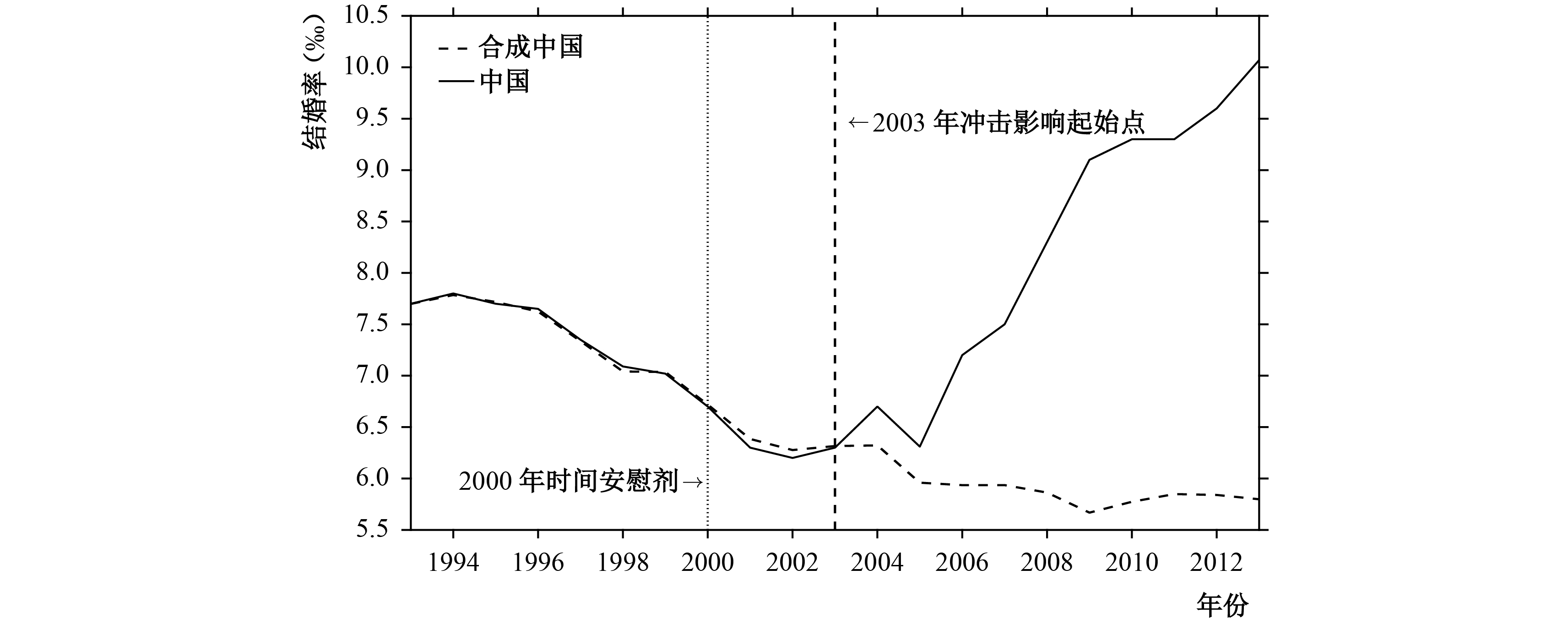
|
| 图 10 基于时间的安慰剂检验 注:假设扩招冲击的影响起始于2000年。 |
同样,为了更加直观地分析以2000年为冲击点时高校扩招对中国结婚率的影响,我们计算了该情形下中国结婚率与合成中国结婚率之间的差值,并据此画出了变化趋势(见图11)。从图11可以看出,以2000年为扩招冲击点时,2000年至2003年中国与合成中国结婚率的差值不大,而在2003年以后两者的差值才逐渐显现。这意味着,假想的2000年为冲击点是无效的,高校扩招真正开始对结婚率造成影响的时间点应为2003年。
为了更好地说明这一点,我们计算出了两个不同时间冲击点下,历年的中国与合成中国的结婚率差值,并据此画出了走势图(如图12所示)。通过比较分析可以看出,无论是以2000年还是以2003年为时间冲击点,中国与合成中国的结婚率之间差值的具体走势基本一致:在2003年以前走势较为平稳,但是2003年以后开始急剧上升。这再次说明,扩招冲击真正开始影响结婚率的时间节点是2003年。

|
| 图 11 中国与合成中国的结婚率差值变动趋势图 |
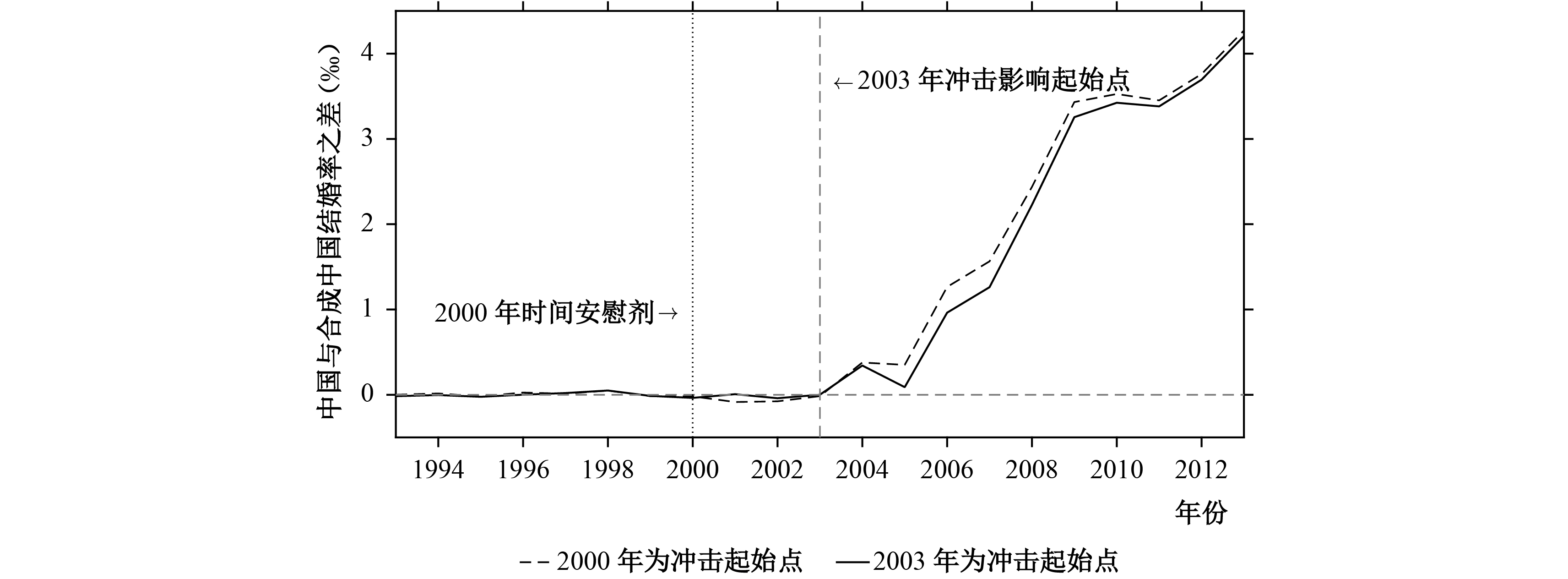
|
| 图 12 不同时间冲击点中国与合成中国的结婚率差值走势 |
近年来,随着“单身潮”、“剩男剩女”、“晚婚晚育”现象的凸显,高校扩招对中国婚姻市场的冲击受到了越来越多的关注与讨论。但是,从中国粗结婚率的变动趋势来看,2002年开始中国整体结婚率呈上升趋势,且人口年龄结构因素也无法完全解释这种现象。鉴于2003年是中国第一批大规模扩招学生开始步入社会的时间,我们推测中国结婚率的上升有可能受到了扩招政策的影响。于是,本文利用合成控制法,通过将中国与选取具有代表性的35个国家和地区构造出合成中国的结婚率对比分析发现:2003年以前,二者之间相差无几;而在2003年以后,中国的结婚率开始显著高于合成中国的结婚率,且这种差距随着时间的推移越来越大。这意味着扩招政策对中国结婚率产生了正向影响。考虑到教育对不同性别影响的差异性,本文通过合成控制法分别研究了扩招对女性和男性结婚率的影响,发现扩招对女性和男性的结婚率都具有正向促进作用,且对女性结婚率的影响要大于男性。我们认为,扩招以来高等教育女性占比的迅速提升、婚姻市场的同质性匹配和女大男小的婚龄差趋势以及双收入的家庭模式等都可解释扩招对中国女性结婚率的正向影响要大于男性的原因。为了排除其他因素以及冲击点主观性的影响,我们分别进行了两种安慰剂检验,第一种通过假设扩招冲击影响其他地区,第二种假设扩招冲击产生的时间节点提前,进一步验证了扩招对中国结婚率有显著的正向影响。
从人们的惯常认知来看,扩招带来的受教育时间的延长以及女性社会经济地位的提升,将会导致人口平均初婚年龄的推迟,但据此推断社会整体结婚率下降是不对的。事实上,从图1可以看出,初婚年龄上升和结婚率提高是可以同时出现的。本文认为,推迟初婚年龄并不意味着不婚,高等教育推迟人们进入婚姻时间的同时,往往还提升了人们的经济潜力,提高了他们进入婚姻的优势(於嘉和谢宇,2013)。特别在中国这种普婚且家庭性别分工不那么明显的国家,个人教育在婚姻匹配中的优势将更为明显。也许有人会质疑:当前中国社会存在着大量的“空巢青年”,有近两亿适龄青年仍然保持单身,这便是婚姻市场整体结婚率下降的证明。对此,我们并不否认当今中国存在着大量未婚青年男女,但这与结婚率上升的现象之间也并不存在必然的矛盾。随着中国经济社会的发展,结婚所要面临的经济压力越来越大,年轻人往往一时无法具备相应的经济条件;加之,人们婚姻观的不断变化,也使得以过往观念定义的“适婚”青年不再认同自身已经达到“适婚年龄”,所以这部分年轻人群推迟婚姻年龄会引起结婚率的下降。但与此同时,比这些人年龄更大一些的人群,他们认为自身已达到了“适婚年龄”,于是便陆续进入婚姻市场,而这部分人的婚姻匹配效率可能非常高,以至于可以弥补之前的年轻人群推迟初婚年龄对结婚率所带来的负面影响。也就是说,正是由于这部分人群结婚率的大幅上升,才导致了中国同时出现“单身潮”和结婚率上升的现象⑲。
当然,本文的研究结论并非否认当前中国婚姻市场中存在的晚婚、不婚等现象,以及其可能产生的不利社会影响,但这些现象产生的原因复杂,相应的解决途径也需要更具有针对性的研究。
① 该数据来源于《论联合政府》(毛泽东,1945)。
② 即每千人的结婚数。本文所用结婚率均为粗结婚率数据。
③ 相对于1950的《婚姻法》。
④ 这个“合成中国”与“真实中国”在扩招政策冲击前的结婚率拟合度最高。
⑤ 如住房改革带来的房价上涨等。
⑥ 自身人力资本和丈夫的收入。
⑦ 作者利用CGSS2013数据计算得到,我国80后群体中60%以上的家庭由夫妻双方共担家庭支出。
⑧ 2002年是扩招之后第一批大专生毕业的年份,而2003年是扩招之后第一批本科生毕业的年份。
⑨ 由于中国现行法律并不认可同性结婚等情况,因此这里不考虑同性恋等少数群体。
⑩ 即平性趋势假设(parallel trend assumption)。
⑪ 版面所限条件略,详见Abadie等(2010)。
⑫ 如果所选择的预测变量与结果变量没有关系,那么所得到的矩阵便无法很好地完成“合成”任务。
⑬ 感谢审稿人对预测变量提出的建议,当然文责自负。
⑭ 由于数据限制,我们只能使用粗结婚率数据(即每千人结婚数),虽然这一数据包含了再婚的数据,但考虑到再婚数据相对而言非常小,所产生的影响不大。
⑮ 此处及后文的详细结果可向作者索取。
⑯ 其中,2003年以前的差值代表二者结婚率的差距,其绝对值越小,说明利用合成控制法得到的合成中国对真实中国的婚姻市场特征复制越成功,反之则说明合成控制法不适用;2003年以后的差值则代表扩招冲击对中国结婚率造成的影响,即为处理效应。
⑰ 2013年CGSS的数据显示,我国1980年以后出生的人口所组成的双收入家庭占63.72%,1950年以后出生的人口所组成的双收入家庭占56.03%。
⑱ 最大值不超过1500。
⑲ 由于数据限制,目前我们无法证明扩招政策提升中国结婚率的具体作用机制,有待进一步的探究。
| [1] | 李煜. 婚姻的教育匹配: 50年来的变迁[J].中国人口科学,2008(3). |
| [2] | 刘甲炎, 范子英. 中国房产税试点的效果评估: 基于合成控制法的研究[J].世界经济,2013(11). |
| [3] | 刘爽, 高华. 我国人口初婚风险影响因素及其变迁——基于CGSS2010的研究[J].南方人口,2015(1). |
| [4] | 刘爽, 梁海艳. 90年代以来中国夫妇年龄差变动趋势及其原因分析[J].南方人口,2014(3). |
| [5] | 刘昊. 高校扩招对我国初婚年龄的影响——基于普查数据的分析[J].人口与经济,2016(1). |
| [6] | 潘丽群, 李静, 踪家峰. 教育同质性婚配与家庭收入不平等[J].中国工业经济,2015(8). |
| [7] | 苏治, 胡迪. 通货膨胀目标制是否有效?——来自合成控制法的新证据[J].经济研究,2015(6). |
| [8] | 王鹏, 吴愈晓. 初婚年龄的影响因素分析——基于CGSS2006的研究[J].社会,2013(3). |
| [9] | 王贤彬, 聂海峰. 行政区划调整与经济增长[J].管理世界,2010(4). |
| [10] | 王忠. 广东家庭户规模与家庭生命周期变化特点[J].人口与经济,2003(2). |
| [11] | 吴要武, 刘倩. 高校扩招对婚姻市场的影响: 剩女?剩男?[J].经济学(季刊),2015(1). |
| [12] | 於嘉, 谢宇. 社会变迁与初婚影响因素的变化[J].社会学研究,2013(4). |
| [13] | Abadie A, Gardeazabal J. The economic costs of conflict: A case study of the basque country[J].American Economic Review,2003,93(1):113–132. |
| [14] | Abadie A, Diamond A, Hainmueller J. Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program[J].Journal of the American Statistical Association,2010,105(490):493–505. |
| [15] | Abadie A, Diamond A, Hainmueller J. Comparative politics and the synthetic control method[J].American Journal of Political Science,2015,59(2):495–510. |
| [16] | Blossfeld H P, Huinink J. Human capital investments or norms of role transition? How women's schooling and career affect the process of family formation[J].American Journal of Sociology,1991,97(1):143–168. |
| [17] | Cready C M, Fossett M A, Kiecolt K J. Mate availability and African American family structure in the U.S. nonmetropolitan South, 1960-1990[J]. Journal of Marriage & Family,1997,59(1):192–203. |
| [18] | Currie J, Moretti E. Mother’s education and the intergenerational transmission of human capital: Evidence from college openings[J].The Quarterly Journal of Economics,2003,118(4):1495–1532. |
| [19] | Goldin C, Katz L F, Kuziemko I. The homecoming of American college women: The reversal of the gender gap in college[J].Journal of Economic Perspectives,2006,20(4):133–156. |
| [20] | Goldstein J R, Kenney C T. Marriage delayed or marriage forgone? New cohort forecasts of first marriage for U.S. women[J].American Sociological Review,2001,66(4):506–519. |
| [21] | Isen A, Stevenson B. Women’s education and family behavior: Trends in marriage, divorce and fertility[R]. NBER Working Paper No. 15725, 2010. |
| [22] | Lichter D T, LeClere F B, McLaughlin D K. Local marriage markets and the marital behavior of black and white women[J].American Journal of Sociology,1991,96(4):843–867. |
| [23] | Lichter D T, McLaughlin D K, Kephart G, et al. Race and the retreat from marriage: A shortage of marriageable men?[J].American Sociological Review,1992,57(6):781–799. |
| [24] | Lichter D T, Mclaughlin D K, Ribar D C. Economic restructuring and the retreat from marriage[J].Social Science Research,2002,31(2):230–256. |
| [25] | Liu Q, Nordstrom Skans O. The duration of paid parental leave and children’s scholastic performance[J]. The B.E. Journal of Economic Analysis & Policy,2010,10(1):135. |
| [26] | Ono H. Women’s economic standing, marriage timing, and cross-national contexts of gender[J].Journal of Marriage and Family,2003,65(2):275–286. |
| [27] | Oppenheimer V K. A theory of marriage timing[J].American Journal of Sociology,1988,94(3):563–591. |
| [28] | Raymo J M. Educational attainment and the transition to first marriage among Japanese women[J].Demography,2003,40(1):83–103. |
| [29] | Society T. Panel data models with interactive fixed effects[J].Econometrica,2009,77(4):1229–1279. |
| [30] | Sweeney M M. Two decades of family change: The shifting economic foundations of marriage[J].American Sociological Review,2002,67(1):132–147. |
| [31] | Thornton A, Axinn W G, Teachman J D. The influence of school enrollment and accumulation on cohabitation and marriage in early adulthood[J].American Sociological Review,1995,60(5):762–774. |
| [32] | Thornton A, Axinn W G, Hill D H. Reciprocal effects of religiosity, cohabitation, and marriage[J].American Journal of Sociology,2016,98(3):628–651. |
| [33] | White L K. A note on racial differences in the effect of female economic opportunity on marriage rates[J].Demography,1981,18(3):349–354. |
 2018, Vol. 20
2018, Vol. 20



