文章信息
 | 上海财经大学 2018年20卷第2期 |
- 刘国栋, 苏志伟
- Liu Guodong, Su Zhiwei
- “菜篮子”农产品价格投机泡沫:证据、特征与启示
- Bubbles of Vegetable Basket Prices: Evidence, Characteristics and Enlightenments
- 上海财经大学学报, 2018, 20(2): 100-115.
- Journal of Shanghai University of Finance and Economics, 2018, 20(2): 100-115.
-
文章历史
- 收稿日期:2017-06-09

2018第20卷第2期
“菜篮子”工程是指自1988年开始,我国针对农副产品供给紧张的局面而实施的一项系统性工程。广义概念的“菜篮子”涵盖范围较广,而本文所指的“菜篮子”农产品主要是指狭义角度上的蔬菜类农产品。自从实施“菜篮子”工程以来,我国农副产品供应得到了基本保证,从根本上解决了我国“菜篮子”农产品供应不足的问题。但是,随着我国城镇化进程的加快,作为我国居民消费价格指数核算的基本组成部分,“菜篮子”系列农产品的供求状况也面临着诸多挑战,其价格泡沫问题近些年来更是成为社会关注的热点。对“菜篮子”农产品价格波动的规律和特点进行研究,具有重要的政策和现实意义。首先,近些年来,生产和销售两端的价格差距越来越大,部分“菜篮子”农产品价格呈现出较大的不稳定性。在生产端,由于销售困难,经常出现“菜贱伤农”的情形;而在销售端,消费者却仍然高价买菜。供求两端价格差距较大,影响“菜篮子”农产品的稳定供应。其次,由于“菜篮子”系列农产品与居民日常生活关系密切,其价格波动直接影响居民消费价格指数的稳定。因而,做好“菜篮子”系列农产品的物价稳定工作,对于确保地方生产及生活秩序稳定,具有重要意义。最后,“菜篮子”农产品种植多属于经济作物生产中的劳动密集型行业,能够充分吸纳农村富余劳动力,有助于实现农村过剩劳动力的就地转移(李超民,2005)。由于我国的蔬菜大棚种植技术较为成熟,加上种植业对劳动力文化水平要求不高,工作强度不大,妇女及老人均可参与劳动。因而,“菜篮子”农产品种植业对吸纳农村当地闲散劳动力贡献较大。做好“菜篮子”农产品种植业的风险管理,有助于促进当地社会稳定及经济发展,进而形成种植、仓储、物流等一系列农业规模经济集群,进一步繁荣地方经济。因此,根据“菜篮子”系列农产品的价格波动规律和特点,对相关种植产业适时、适地进行政策调控和引导,可以降低“菜篮子”农产品主产区农民面临的价格风险,抑制投机性泡沫,从而引导农民对价格的理性预期,优化农产品供给侧结构。
本文从“菜篮子”价格总体指数出发,首先利用X-12方法剥离出“菜篮子”价格指数的季节性因子、趋势及周期性因子、非常规因素影响等时间序列数据。然后,根据“菜篮子”农产品价格指数的波动特征,针对价格指数中非常规因素的影响及特点,提出了两点假设,即“菜篮子”农产品价格中存在投机泡沫,且投机泡沫具有周期性特征。利用Phillips等提出的sup ADF系列泡沫检验方法,我们在构成“菜篮子”价格总体指数的九类农产品指数中发现有四类存在投机泡沫现象,从而验证了“菜篮子”农产品价格中存在投机泡沫的假设。为了深入分析投机泡沫的产生过程及周期性特征,我们从存在周期性投机泡沫的姜葱蒜分类指数中选择了具有代表性的“菜篮子”农产品大蒜作为研究对象,结合泡沫发生的时点及背景,进一步归纳分析了投机泡沫的周期性特征。最后,对上述两点设想的实证过程进行总结分析,并给出了政策建议。
二、文献综述关于农产品价格波动,国内研究文献主要从宏观和微观两个不同的角度,具体着眼于供求关系、调控政策变动、价格波动特点、形成机制及成因等方面分别进行了研究。国外研究则主要从价格泡沫本身出发,就其具体特征及机制、传递性等方面进行了研究。
(一) 国内文献农产品价格形成机制中的矛盾历来为我国学者所重视,生产周期性的波动和流通渠道的不完善会对农产品的价格波动具有重要作用(郭世勤,1993),国家经济体制改革也对农产品的价格波动具有重要影响(巫国兴,1997)。中国的农产品价格在不断上升的同时,表现出显著的阶段性和周期性波动特点,并且其波动特征与自身政策、流通、生产成本等环节具有密切关系(康竹君和马红瀚,2007),劳动力供给从无限到短缺的刘易斯供给转折点对农产品价格的波动具有重要作用(魏乐献,2009)。然而,另一种观点认为,农产品价格的形成机制主要遵循“蛛网模型”效应(程瑞芳,2007)。由于农产品的供求弹性较小,任何一端的波动都会引起价格的较大变化。这种观点显然无法对“菜篮子”农产品价格的波动特征提供强有力的解释。于是,有学者从供应链管理角度出发(唐赛,2010;傅阳,2011),认为供应链体系不健全,导致上下游市场参与者地位不平等是造成有关农产品价格波动的内在原因。王孝松和谢申祥(2012)与肖小勇和李崇光(2013)认为,国际农产品价格波动对国内农产品价格具有显著影响。李辉尚(2010)从宏观政策、供求关系及进出口贸易等角度对农产品价格的影响因素进行了讨论,认为投机现象严重、产品供销渠道不通畅、信息不及时是导致部分农产品价格波动的主要原因。具体到个别农产品,国内很多学者对大蒜价格进行了研究。其中,丁超(2010)认为大蒜的种植面积减少、成本增加、国际价格以及物价水平上升等共同促成了大蒜价格的上涨。这为大蒜价格的价值论观点提供了较为有力的支持。然而,有关大蒜价格对外部性冲击反应的研究结果却与此相左。陈攀和章胜勇(2014)对大蒜的出口价格进行了分析,认为大蒜出口价格的波动周期具有不可重复性和非对称性的特征,并且极易受到外部因素冲击的影响。更进一步,另有学者认为大蒜价格波动主要受货币供给量的影响,成本消耗和气象变化也会产生一定的影响,而替代品的价格影响最弱(李京栋和张吉国,2015),且与游资炒作关系不大(张利庠等,2010)。但是,这一观点不断受到新的挑战。姜辉和查伟华(2016)从供给量、价格和货币三个角度对大蒜价格波动的原因进行了实证检验,认为国内大蒜价格对出口蒜价的波动具有显著性影响,进而得出社会游资炒作及小宗商品的易操控性是导致价格波动的主要原因,这与大蒜价格剧烈波动系游资炒作为主因的观点一致(陈楚天和雷娜,2012)。上述有关学者对“菜篮子”部分农产品价格波动的影响因素及特征进行了研究,但是对于有关农产品价格投机泡沫的认定及投机泡沫起始区间的确认等方面,缺乏有力的计量证据和理论说明。
(二) 国际文献国际上产生了较多的关于价格泡沫研究的文献。价格泡沫首先被认为是某种资产或商品因预期而出现超过其内在价值的更高价格的现象(Stiglitz,1990),或者是其他买方因价格预期而持续投资导致价格继续升高(Kindleberger,2005)。其中,脱离自身价值和基本面因素而引起的高价被认为是投机泡沫(Shiller,2000)。在早期的泡沫研究中,马尔科夫模型被应用于价格泡沫的研究(Hall等,1999)。Gürkaynak(2008)认为,价格由实际价值和泡沫两部分组成,且资产价格体现了其未来全部可能的收益。如果价格超过了实际价值,投资者就可以通过低买高卖赚取利润,反之亦然。当资产价格没有泡沫产生时,这种投资方式就会带来损失。
基于资产价格泡沫的定义,Diba和Grossman(1984)运用协整检验的方法进行了泡沫检验,结果在资产价格中没有发现投机泡沫。然而,该结论由于0阶单整和1阶单整之间的转换及相应的单位根检验存在疑问而广受质疑(Evans,1991)。因为这个原因,此后许多研究提出了新方法以解决周期性泡沫检验的有效性(Homm和Breitung,2011)。这方面,比较经典的有马尔科夫ADF检验(Hamilton,1989;Hall等,1999)及本文采用的SADF检验和GSADF(Phillips和Yu,2011;Phillips等,2013)检验等方法。鉴于马尔科夫ADF方法把多种因素纳入资产价格的泡沫计算,扩大了资产价格的基础性价值,因而具有一定的局限性。因此,许多研究者使用SADF和GSADF(Baur和Glover,2012)方法进行泡沫检测,发现检测效果明显,且该方法对于不同频率的数据具有良好的适应性。此外,该方法对泡沫类型也进行了区分,将正向泡沫定义为泡沫期间均价高于泡沫起点价格,负向泡沫定义为泡沫期间均价低于泡沫起点价格(Gomez-Gonzalez,2017)。Arora等(2011)检测了个人消费指数中的有关成分,发现食品和能源价格存在泡沫现象。同时,他们也发现泡沫与非泡沫期间人们的通胀预期不同。Etienne等(2014)对十二种农产品的日度市场价格波动进行了检测,发现了多个泡沫过程。但是,泡沫过程的期间很短,多数泡沫过程只持续10天左右或更少。因而得出结论,认为当前农产品市场的价格泡沫已经远没有20世纪70年代那样剧烈。Alexakis等(2017)对农产品与金融市场之间的泡沫传递进行了研究,认为两者之间存在长期的协整关系。此外,不同商品市场(Zhao等,2015;Zhang和Yao,2016)及不同地区之间的泡沫传递现象也被纳入研究范围。值得一提的是,上述研究中使用的sup ADF系列检验方法与传统的ADF方法有很大的不同。传统的ADF方法采用左侧检验的方式,而sup ADF系列方法使用的则是右侧检验。如果不存在泡沫的零假设被拒绝,就可以得出存在价格泡沫的结论。因而,通过对递归滚动的检测值与模拟的临界值进行比较,我们就可以得出是否存在价格泡沫的结论。这样,相应的价格泡沫起始时间也可以被确定。由于该方法能够跟踪投机泡沫的起始时间,因而对于“菜篮子”农产品种植风险预警及防范、种植面积规划、生产、销售及贸易等经营活动具有一定的参考价值。
本研究的创新点主要表现在以下几个方面:首先,本文首次从计量角度对我国“菜篮子”农产品价格中的周期性投机泡沫问题进行了泡沫检验及归纳分析,丰富了关于农产品价格问题研究的文献。此前国内文献中关于农产品价格波动的研究,诸如“上涨过快”、“异常波动”等表述过于笼统,缺乏明确的概念及计量证据。鉴于此前研究的不足,本文对“菜篮子”农产品价格中投机泡沫的产生及持续时间进行了明确界定。其次,本文研究结果表明,在我国“菜篮子”农产品价格中存在较为严重的周期性投机泡沫现象,与当前国外研究中关于农产品市场中投机泡沫趋弱的结论不同,反映了中国“菜篮子”农产品价格波动具有自身鲜明的特点。最后,本文对于价格投机泡沫产生时点及持续时间的研究,可以为“菜篮子”系列农产品的供给侧改革、适时市场调控、种植风险管理等政策制定提供参考。
三、“菜篮子”农产品价格波动特征及设想 (一) “菜篮子”农产品价格总体指数的波动特征为深入分析我国“菜篮子”农产品价格总体指数波动的特征,我们采用商务部设立的“寿光蔬菜价格指数”月度数据作为研究对象,数据取自2010年10月至2017年12月。寿光作为全国最大的蔬菜批发市场,拥有中国最大的农产品物流园,是全国蔬菜的定价中心和集散中心,被国务院命名为“中国蔬菜之乡”。该指数能够从不同层次反映寿光蔬菜市场行情,具有代表性强、连续性好、精确度高等特点。该价格总体指数由十二种明细分类指数加权计算得出,从而使我们能够对“菜篮子”农产品价格进行深入研究和对比分析。因而,对于“菜篮子”农产品而言,该蔬菜价格指数最具有代表性。
首先,我们针对初始蔬菜价格定基指数数据进行季节性调整,利用X-12方法从中分离出趋势及周期性时间序列(VEGET_TC)、季节性因子序列(VEGET_SF)、非常规因素影响序列(VEGET_IR)及调整后序列(VEGET_SA)(见图1)。X-12方法是在X-11基础上进一步发展而来的,能够按照大蒜价格指数的数据特征进行针对性分解,因而对有关序列组成因子的估算更为精细。从图1中的季节性因子序列(VEGET_SF)中可知,我国“菜篮子”系列农产品价格的波动具有明显的季节性特征,且通常以一年为周期。由图1可知,季节性因子在第一季度表现为快速上涨趋势,第二季度和第三季度则为下跌趋势。这说明,我国“菜篮子”系列农产品价格受农作物本身生产周期的影响明显。此外,由于受到中国传统节假日的影响,第四季度及第一季度季节性因子会出现一个高峰,第二季度的季节性因子则由于市场需求下降而得以回归正常。第三季度的波动,则主要反映了市场供应量增加的情形。
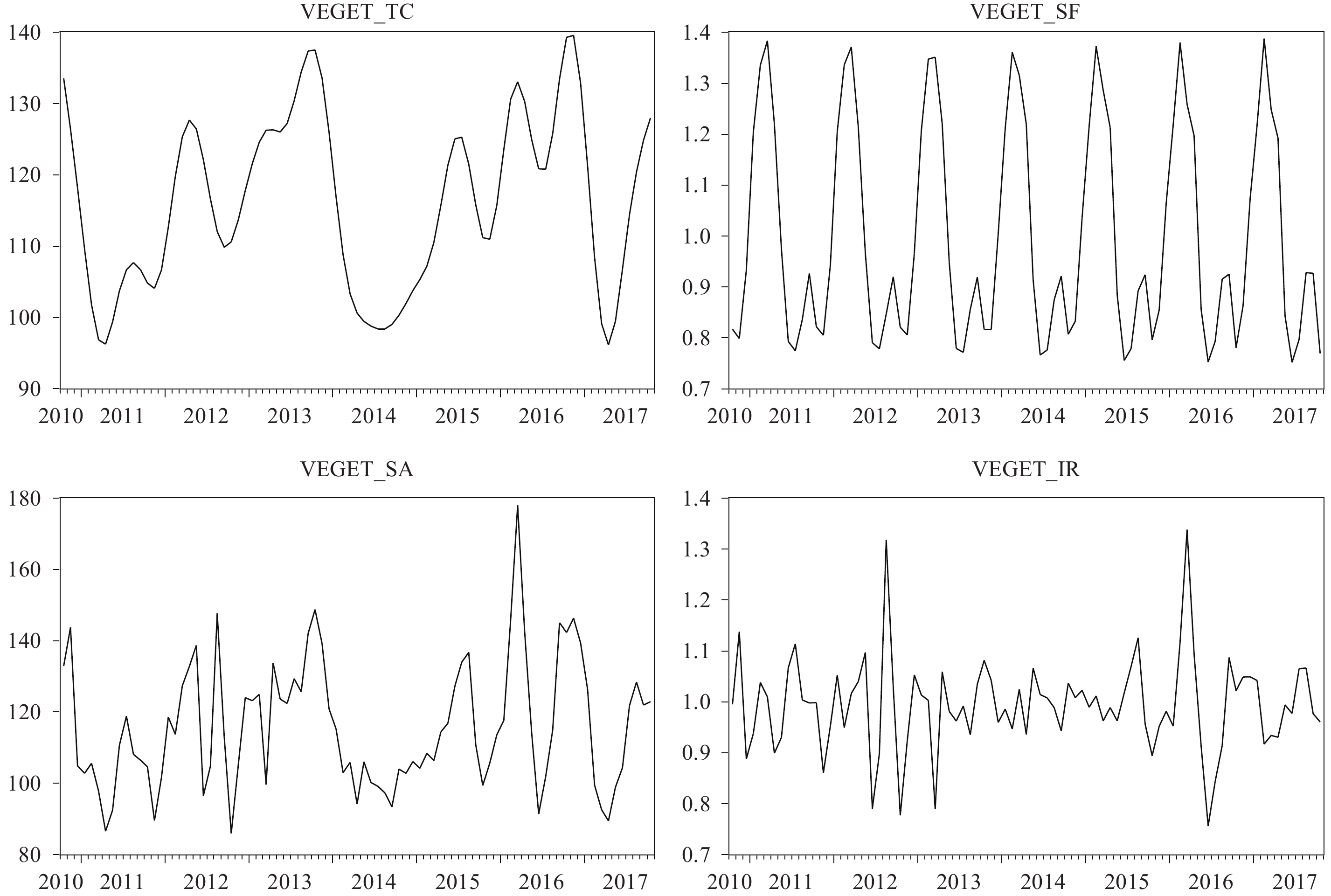
|
| 图 1 “菜篮子”系列农产品指数季节性调整及分解 |
其次,我们注意到非常规因素(VEGET_IR)对“菜篮子”价格指数的影响较为显著,波动幅度较大,且具有一定的周期性特征。由图1中VEGET_IR可知,2010年10月至2013年4月,这段时间的非常规因素影响较为明显。由于季节性影响已经排除,因此该部分影响并非由季节性因素主导。自2013年5月到2015年7月,这段时间的非常规因素对价格指数波动的周期性影响相对较弱。但自2015年8月至今,非常规因素影响又变得较为显著。由此可知,非常规因素对我国“菜篮子”系列农产品价格指数的影响较为明显,且呈现出明显的周期性特征。结合“菜篮子”农产品供求关系的实际状况,考虑到影响价格的常规因素,诸如波动及趋势因素、季节性因素都已经剥离,剩下的非常规因素影响则来自可能的气候突变或投机性因素。更进一步分析发现,非常规因素影响波动的周期性特点显然不支持单一的气候突变假设,因而我们有理由认为非常规因素影响中可能存在周期性的投机因素作用,从而提出我国“菜篮子”农产品价格中存在周期性投机泡沫的假设。
(二) “菜篮子”农产品价格投机泡沫设想根据指数特征分解后非常规因素对价格总体指数的显著影响及其周期性特征,为验证“菜篮子”农产品价格中存在周期性投机泡沫的设想,本文提出以下两点假设:
假设1:我国“菜篮子”农产品价格中存在投机泡沫。
假设2:投机泡沫发生具有周期性特征。
针对上述问题,本文采用广义sup ADF泡沫检验方法及模型,从构成“菜篮子”价格指数的分类指数,到具体“菜篮子”农产品大蒜,逐层进行检验及归纳分析。首先,我们对构成“菜篮子”价格指数的分类指数进行泡沫检验及归纳分析,验证是否存在投机泡沫,并从中筛选出投机泡沫周期性特征比较明显的分类指数。然后,考虑到分类指数的加权化计算方式无法充分反映具体品种的价格波动特征,本文从投机泡沫周期性特征明显的姜葱蒜分类指数中,选择了价格波动具有代表性的“菜篮子”农产品大蒜为例,结合具体背景对投机泡沫现象的特征及成因进行深入分析。最后,针对上述两点假设,总结分析并提出政策建议。
四、泡沫检验理论及模型 (一) 泡沫检验理论模型Gürkaynak(2008)认为,价格由泡沫与实际价值两部分组成。因此,资产价格可以表示如下:
| ${P_t} = \sum\limits_{i = 0}^\infty \left( {\frac{1}{{1 + {r_f}}}}\right)^i{ E_t}({D_{t + i}} + {U_{t + i}}) + {B_t}$ | (1) |
其中,Pt为t时资产价格,rf为无风险利率,Dt为该项资产在t期的收益,Ut为未知因素,Bt表示泡沫现象。Pt–Bt则表示资产价格中的基本价值,而泡沫部分则由Bt表示,并且满足爆炸性泡沫的下鞅性质:
| ${ E_{{t}}}{{(}}{B_{t + 1}}{{)}} = {{(}}1 + {r_f}{{)}}{B_t}$ | (2) |
若Bt=0,则表示资产价格中不存在泡沫。因此,该资产价格是否含有泡沫,主要取决于资产收益Dt及未知因素Ut。根据协整要求,如果Dt为I(1),则Ut必然为I(1)或I(0),所以资产价格最多为I(1)。否则,基于公式(2)的价格泡沫Bt会不断增大。若未知因素Ut是1阶单整或0阶单整,那么Dt在一阶差分后应该平稳。
(二) SADF系列检验根据式(2),泡沫不会破灭且不会重复发生。如果资产价格是一个非负数,可知Bt和残差εt之间的关系应有:
根据最小二乘估计自回归等式:
| ${x_t} = \mu + \rho {x_{t - 1}} + {\varepsilon _t}$ | (3) |
其中,εt服从
| $\mathop {{{sup}}}\limits_{{r_w} \in {{[}}{r_0},1{{]}}} \left\{ \frac{{{r_w}{{[}}\smallint _0^{{r_w}}WdW - \frac{1}{2}{r_w}{{]}} - \smallint _0^{{r_w}}Wdr W{{(}}{r_w}{{)}}}}{{r_w^{1/2}{{{{\{ }}{r_w}\smallint _0^{{r_w}}{W^2}dr - {{{{[}}\smallint _0^{{r_w}}W{{(}}r{{)}}dr{{]}}}^2}{{\} }}}^{1/2}}}} \right\} $ | (4) |
为进一步提高该检测方法的敏感性,Phillips等(2013)将原来的SADF改进为扩展的sup ADF检验(GSADF)。SADF方法的起始点是固定的,而GSADF方法则允许检测起始点r1在0到1–rw之间变动。因此,整个检测过程从r1=0,到r1=1–rw为止。
| $\mathop {{{sup}}}\limits_{{r_w} \in {{[}}{r_0},1{{]}}} \mathop {{{sup}}}\limits_{{r_1} \in {{[}}0,1{{ - }}{{{r}}_w}{{]}}\atop{r_2} = {r_1} + {r_w}} \left\{ \frac{{{r_w}{{[}}\smallint _{{r_1}}^{{r_2}}WdW - \frac{1}{2}{r_w}{{]}} - \smallint _{{r_1}}^{{r_2}}W{{(}}r{{)}}dr {{[}}W{{(}}{r_2}{{)}} - W{{(}}{r_1}{{)]}}}}{{r_w^{1/2}{{{{\{ }}{r_w}\smallint _{{r_1}}^{{r_2}}{W^2}dr - {{{{[}}\smallint _{{r_1}}^{{r_2}}Wdr{{]}}}^2}{{\} }}}^{1/2}}}}\right\} $ | (5) |
Wiener过程具有独立分布增量
Phillips和Yu(2011)提出资产价格的变化过程式:
| ${X_t} = {X_{t - 1}}I\{ t < {\tau _e}\} + {\delta _n}{X_{t - 1}}I\{ {\tau _e} {\text{≤}} t {\text{≤}} {\tau _f}\} + \Biggr(\sum\limits_{k = {\tau _f} + 1}^t {{\varepsilon _k} + X_{{\tau _f}}^*} \Biggr)I\{ t > {\tau _f}\} + {\varepsilon _k}I\{ t {\text{≤}} {\tau _f}\} $ | (6) |
其中,X为资产价格,
| ${\hat r_e} = \mathop {\inf }\limits_{r {\text{≥}} {r_0}} \{ r_:ADF_r^t > cv_{{\beta _n}}^t\} $ | (7) |
| ${\hat r_{f}} = \mathop {\inf }\limits_{r {\text{≥}} {{\hat r}_e} + \log (n)/n} \{ r_:ADF_r^t < cv_{{\beta _n}}^t\} $ | (8) |
其中,
寿光蔬菜价格指数共包含十二个分类指数。为了深入分析“菜篮子”价格指数的波动特征,我们略去与蔬菜属性关系较弱的三个分类指数,保留了九个分类指数:根菜类、姜葱蒜类、白菜类、甘蓝类、叶菜类、瓜菜类、茄果类、菜豆类及菌菇类。这九类指数代表了绝大多数“菜篮子”产品,其价格指数变化也反映了“菜篮子”主要农产品的波动情况。
如图2所示,在泡沫检验结果中,三条时间序列曲线分别为GSADF统计量值、临界值CV及分类价格指数数据,分左右轴列出。根据第四部分内容所述,当GSADF统计量值突破临界值时,可以视为发生了投机泡沫。当GSADF统计量值再次突破临界值时,可以认为该投机泡沫过程结束。因而,只要观察图2中GSADF突破临界值(5%显著性水平)的次数及过程,就可以得出该分类价格指数中是否发生了投机泡沫现象。从以下对九个分类指数泡沫检验结果的直观图示中可以得知:在姜葱蒜类、白菜类、瓜菜类、茄果类四个分类中存在投机泡沫现象;而在其他根菜类、甘蓝类、叶菜类、菜豆类、菌菇类五个分类中,则不存在投机泡沫现象。这五个不存在投机泡沫的分类价格指数走势相对比较平稳,对于稳定“菜篮子”价格总体指数起到了关键作用。上述关于泡沫检验的结果表明,在我国“菜篮子”农产品价格中,存在投机泡沫现象。
通过对图2泡沫检验结果的观察,我们可以发现姜葱蒜类和瓜菜类价格指数具有鲜明的周期性波动特征,而白菜类和茄果类则不明显。同时,我们也发现,投机泡沫多分布在生产供给比较集中(姜葱蒜类)或者对供给保鲜程度要求较高(瓜菜类和茄果类)的分类指数中。对保鲜程度要求稍低(根菜类、甘蓝类)或者可替代产品比较多(叶菜类、菜豆类、菌菇类)的分类指数则不存在投机泡沫。总之,从“菜篮子”分类指数的检验结果可知,“菜篮子”产品投机泡沫的发生具有显著的周期性特征。

|
| 图 2 “菜篮子”九类价格指数泡沫检验结果 |
上述泡沫过程验证了“菜篮子”农产品价格中的投机泡沫现象。但是,由于上述投机泡沫现象仅反映了分类价格指数的变化,没有反映“菜篮子”具体农产品的有关信息,因而上述周期性的投机泡沫现象无法全面反映“菜篮子”具体农产品价格泡沫的特征及发展过程。这些投机泡沫发生的原因是什么?为何投机泡沫具有周期性特征?我们将以大蒜价格为例,结合实际背景,探究投机泡沫发生的原因及其周期性特征。
(二) 大蒜价格投机泡沫实证分析以大蒜为例进行实证研究,主要基于以下五个方面原因:其一,大蒜是“菜篮子”姜葱蒜类农产品中价格波动较为明显的农产品之一,能更好地体现价格波动中非常规因素的影响。对分类价格指数的泡沫检验结果表明,姜葱蒜类“菜篮子”农产品具有明显的周期性投机泡沫现象。因而,对于投机泡沫的检测效果会更加明显,从而更好地暴露种植风险的管理问题。其二,中国大蒜产业规模及国际地位迫切需要开展此类研究。目前,中国已经成为世界主要的大蒜生产国、出口国及消费国,产量及出口规模均占世界大蒜年产量及贸易量的70%以上(陈攀和章胜勇,2014),是中国单项出口创汇最多的农产品。其三,“菜篮子”价格总体指数及分类指数都是由具体品种加权计算得出,这样很难体现具体“菜篮子”农产品价格波动的周期性特征。因而,有必要结合具体“菜篮子”农产品具体分析。其四,大蒜主产地在山东,气候四季分明,更能体现“菜篮子”系列农产品价格波动的生产周期性特征。其五,大蒜产业在山东已经形成了规模性的交易市场,并且从生产、物流到仓储、交易等环节形成了一条产业链,交易数据相比其他品种而言,也更具可得性。因此,我们选择以大蒜价格为例,探究“菜篮子”农产品价格中是否存在周期性投机泡沫问题。
1. 数据及描述性统计
本文采用2006年8月至2017年5月中国国家商务部公布的大蒜批发市场价格(下文简称大蒜价格)数据,共有560个有效周度观察值,反映了中国大蒜市场十多年以来的价格波动情况。由于大蒜的交易种类不同,价格也不相同,商务部采用全国范围内具有代表性的大蒜批发市场的平均交易价格,因而具有较强的代表性和权威性。

|
| 图 3 大蒜批发价格走势图(2006.8–2017.5) |
图3为大蒜批发价格走势图。从图3中可以看出,大蒜价格从2006年8月份开始,整体上呈波动上升趋势,并且在2009年、2010年、2012年、2016年经历了四波价格暴涨的过程。大蒜价格自2006年8月开始不断下降,最低时跌至2元/公斤以下。随后,在2009年下半年快速飙升至12元/公斤以上。这段时间,大蒜因价格暴涨的表现极为抢眼,被舆论称为“蒜你狠”。然而,从2011年开始,价格开始跳崖式下跌,快速跌至4元/公斤附近后企稳。经过大约一年时间的整理,又在2012年下半年上涨至8元/公斤附近。关于2009年、2010年大蒜价格的暴涨,有观点认为,这与前期大蒜种植面积锐减,供给减少等有着密切关系(胡冰川,2010;李国祥,2011)。在供给层面,大蒜价格因前期价格低迷而引致的产量由2008年的1 835.7万吨减少至2009年的1 796.79万吨。但是,由于产量减少幅度仅为2.12%,尚不足以对2009–2010年大蒜价格暴涨的结论构成有效支撑(李京栋和张吉国,2015)。种植成本上涨固然是推动大蒜价格上涨的因素之一,但是不足以推动大蒜价格持续大幅度上涨。大蒜在经历快速上涨后,又快速下跌,对地方农业经济也造成了较大的冲击,舆论称其为“蒜你贱”。从2012年6月开始,大蒜价格又经历了一波快速涨跌的过程。此后,大蒜价格自2013年后又快速下跌,然后逐渐企稳。2016年,大蒜价格又出现了一波加速上涨的行情。所有这些价格变化,都对大蒜种植、物流、仓储等行业造成了较大的影响。
表1给出了我国大蒜批发市场价格数据的描述性统计。从中可以看出,2006年8月至2017年5月间大蒜价格最高升至14.98元/公斤,最低跌至1.31元/公斤,标准差为3.52。由此可见,大蒜批发市场价格波动幅度较大,可能存在投机泡沫问题。因此,有必要对大蒜批发市场价格进行泡沫检验。
2. 价格泡沫检验
考虑到物价因素对我国大蒜价格的影响,我们对大蒜价格数据进行了平减处理。根据大蒜价格的成本构成,我们采用了生产价格指数PPI对大蒜价格进行平减。经与非平减的数据对比分析及泡沫检验(传统ADF与GSADF检验)后确认,因PPI变化而导致的价格偏差已经被有效去除。从中可知,通货膨胀并非是我国大蒜价格投机泡沫产生的主要原因。为了更好地对比分析检验结果,我们首先进行了常规的ADF泡沫检验(Diba和Grossman,1988)。通过对价格进行对数化处理并取一阶差分,然后对对数时间序列及一阶差分序列作平稳性检验。如表2所示,大蒜价格的对数时间序列ADF检验结果说明,其对数序列是不平稳的,但一阶差分序列平稳。因而,按照ADF检验标准,可以认为2006年8月至2017年5月间大蒜价格序列中不存在泡沫现象。
| 检验序列 | 检验模式 | t统计量 | 尾概率 | 结论 |
| 对数序列 | (c,t,0) | –1 | 0.94 | 非平稳 |
| 差分序列 | (c,t,0) | –14.42 | 0.00 | 平稳 |
| 注:检验模式中c代表常数项,t代表趋势项,最后值0代表ADF方程滞后阶数,采用SIC准则确定,结果由Eviews软件计算得到。 | ||||
然后,我们再使用SADF和GSADF泡沫检验方法对大蒜价格序列进行检验。样本数据采用2006年8月至2017年5月间的560个周度观察数据,根据最小有效窗口(Phillips和Yu,2011)的有关说明,我们选择最小窗口为r0=56/560=0.1。
| 检验方法 | SADF | GSADF |
| 统计值 | 4.40*** | 10.14*** |
| 临界水平 | SADF临界值 | GSADF临界值 |
| 90% | 1.157 0 | 1.928 0 |
| 95% | 1.525 8 | 2.137 4 |
| 99% | 1.983 7 | 2.569 4 |
| 注:***表示显著性水平p<0.01。 | ||
表3第二列和第三列列示了大蒜价格的统计量值及SADF和GSADF临界值。其中,不同显著性水平上的临界值结果均由2 000次蒙特卡洛模拟得出。大蒜价格的SADF和GSADF的统计值分别为4.40和10.14,结果均大于95%的临界值(4.40>1.53,10.14>2.14),说明在2006年8月至2017年5月间大蒜价格存在泡沫现象。
至此,通过对传统ADF及SADF和GSADF检验结果的对比,我们发现SADF和GSADF方法能够检测出传统ADF方法难以发现的泡沫过程。同时,这也说明了传统ADF在检测泡沫过程问题上,不如SADF和GSADF有效,且GSADF方法对于周期性价格泡沫的检测更为敏感(Phillips和Yu,2011)。鉴于大蒜价格数据样本已经通过了GSADF检验,下一步我们需要根据GSADF的统计值与临界值,具体确定各个泡沫过程。
3. 实证分析
通过观察图4中CV临界值、GSADF值与大蒜价格(Garlic Price)的走势图发现,从2006年8月到2017年5月,大蒜价格中一共存在五个泡沫过程。这五个泡沫过程分别是2009.6.12–2011.4.15、2011.6.17–2011.9.23、2012.7.6–2012.7.20、2013.6.21–2013.7.12、2015.9.11–2017.5.12五个区间(见图4)。根据泡沫的理论框架,泡沫的发生主要是由于外部冲击或投机性因素导致,而非大蒜本身的价值提升引起。下面结合泡沫发生的起始时间,进行具体分析。

|
| 图 4 大蒜价格的泡沫区间(2006.8–2017.5) |
第一个泡沫出现在2009年6月,到2011年4月结束。在此期间,大蒜价格由最低2.03元/公斤,上涨至12.24元/公斤。首先,我们回顾一下2009年大蒜市场的供求变化情况。每年6月至8月期间正是新蒜上市的时间,然而当年的新蒜供应量却大幅减少。此外,2008年以来,大蒜主产区低温,春季又持续干旱,气候条件不利于大蒜的生长,保鲜入库量持续大幅下滑。所有这些因素共同发生作用,导致市场价格预期发生变化,引起了社会游资的兴趣(丁超,2010)。期间,很多中间流通环节也大量囤货,大量小规模的蒜贩和储藏商等纷纷囤积货源,形成了人为炒作、囤积居奇的局面。这次价格投机泡沫检验结果的起始时间与供求关系实际状况发生改变的时间基本一致。其次,大范围的突发恶劣天气是导致大蒜价格泡沫的重要因素(卞茂启和王翠英,2011)。2007–2008年,西南五省持续干旱,北方大蒜的主产区又接连出现干旱、倒春寒等一系列反常天气,导致北方的大棚蔬菜生产受到严重影响,大蒜的产量和生产周期都受到较大冲击(李辉尚,2010)。同时,由于北方和南方的大规模农产品调剂渠道不通畅,交通运输不足以支撑短时间的供求余缺调剂,区域间流通受到阻碍,引起了一系列农产品的价格上涨,为大蒜价格的后期上涨提供了强力支撑。第三,我国的货币发行量连续递增,社会资金比较充裕(陆前进和朱丽娜,2011),持续上升的居民消费指数也导致社会公众不断提高通胀预期水平。这些因素为大蒜价格的炒作提供了必要条件,加上大蒜供求关系失衡,社会资金在楼市降温、股市低迷的情况下进入大蒜市场,导致大蒜成为社会游资的炒作热点。第四,大蒜生产加工技术经过多年的发展,已经能够对大蒜进行深加工处理并实现了长期储存。这导致大蒜能够长时间囤积,使投机者能够根据市场行情,适时囤积和抛售。大蒜生产加工技术的这一新变化,为游资炒作提供了更便利的条件。不少民间资本从种植环节就开始重金圈地,控制大蒜供给来源,并且蒜商之间极易形成联盟,互相抬高大蒜出货价格。第五,大蒜市场的信息发布渠道不通畅,导致供求两端信息不对称(陈楚天和雷娜,2012),加上新闻媒体宣传及供货商的刻意操纵,导致大蒜价格水平不断被炒高。此外,大蒜交易批发市场已经出现了电子盘交易,允许卖空买空的保证金形式交易。由于缺乏规范性的监管。市场投机力量利用电子盘保证金交易优势,操纵市场价格。所有这些因素,导致了第一个投机泡沫的产生,并得以长时间延续。2010年5月,国家发改委、商务部、工商总局等联合发布通知,强调加强对农产品价格异常波动的市场监管,严厉打击农产品的囤积居奇行为,这次投机泡沫最终宣告结束。这次投机泡沫的持续时间较长且波动幅度较大,与当前国外研究中农产品市场投机泡沫已经趋弱的结论(Etienne等,2014)完全不同,反映出我国“菜篮子”农产品市场价格波动具有自身鲜明的特点。
第二个投机泡沫出现在2011年6月到9月。这次投机泡沫的发生时间点与第一个投机泡沫相同,但持续的时间相对较短。大蒜价格由前期高位急速下跌至3.69元/公斤。这次投机泡沫的出现时间,是在大蒜价格出现连续快速暴跌之后,此时大蒜价格已经大大低于其经济价值。究其原因,主要与以下几个因素有关。首先,此前的农产品价格炒作行为引起了国家各部门对大蒜等农产品市场价格操纵行为的严厉打击,导致很多蒜商集中出货,供求关系进一步失衡,促成大蒜价格跳崖式下跌。其次,大蒜市场价格的崩溃效应传入生产环节,严重损伤了蒜农的生产积极性,同时,也打击了蒜商的收购意愿。虽然大蒜已经丰收,但是却无人问津,蒜农损失较大。所有这些因素共同作用,导致了第二次投机泡沫的产生。由于此次投机泡沫导致大蒜价格远远低于其实际价值,因此,此次投机泡沫属于典型的负向投机泡沫。第二个投机泡沫发生后,大蒜价格跌入谷底,进入了一个底部企稳的阶段。
第三个投机泡沫出现在2012年7月。这次投机泡沫的出现时间点与第一个及第二个相同,充分说明了大蒜价格波动的周期性特征。这次投机泡沫的鲜明特征是时间短,且与前两个投机泡沫的发生时间相同,大蒜价格波动的周期性特征再度得到体现。应当指出,2011年冬天至2012年春天的低温天气对大蒜的产量产生了影响。另外,部分产区4–5月份的高温多雨也影响了大蒜的生长。以大蒜主产区山东金乡为例,期间蒜苗因高温引致的病虫害较为严重,死苗率达2%,且降水量较2011年增加109.1%(陈明均,2012)。大蒜电子交易市场在此期间也充当了推波助澜的角色,交易行为亟待规范,信息及监管机制等有待完善。
第四个投机泡沫出现在2013年6月到7月。这次投机泡沫与第二个、第三个出现的时间点基本相同,其价格波动的周期性特征再次得到验证。由上可知,泡沫持续时间一般维持在2个月左右,发生时间点一般是新蒜上市前后。
第五个投机泡沫出现在2015年9月且持续至今,出现时点与此前泡沫过程基本一致。这次投机性泡沫持续的时间较长,现在已经出现泡沫破灭的信号。这次投机泡沫的发生过程与持续时间,与此前的四个投机泡沫有很大不同,主要表现在持续时间较长、涨幅比较大。值得注意的是,此次价格泡沫的发生与其他农产品价格的上涨联系相对较弱。比如,同期的寿光蔬菜指数从2017年初的153.88下跌至106.56,跌幅高达31%,而大蒜价格却一直居高不下,不断创出新高。值得警惕的是,大蒜泡沫一旦再次破灭,将会再次对蒜农利益造成严重损害,进而对仓储、流通等环节造成破坏,从而损害大蒜主产区的正常生产秩序,危害地方经济发展。
综上所述,我国“菜篮子”部分农产品价格中存在投机泡沫现象,且投机泡沫的产生具有显著的周期性特征。以大蒜为例,在每年的6–8月份期间,适逢新蒜上市,且第二年种植规划尚不确定,市场供求预期变化较大,极易产生投机性泡沫。大蒜价格投机泡沫产生的背后,反映的是我国“菜篮子”系列农产品价格的投机泡沫问题。从中可以看出,上述四类“菜篮子”农产品价格中泡沫发生的时间,与第三部分图1中非常规因素对“菜篮子”总体指数影响突出的两个阶段是一致的。尤其是从2015年8月至今,四类“菜篮子”产品价格中均产生了投机泡沫,而同期非常规因素对“菜篮子”整体指数的影响又较为显著。这充分说明,投机泡沫对“菜篮子”价格指数造成了显著影响,我们对“菜篮子”产品价格中存在投机泡沫及周期性特征的假设是合理的。此外,投机泡沫在“菜篮子”不同农产品之间的传递问题应该引起重视。“菜篮子”农产品价格投机泡沫是否存在跨产品传递现象?传递过程又是如何发生的?这些问题都值得我们继续探究,也是我们下一步的研究方向。
六、结论及建议“菜篮子”农产品是我国居民消费价格指数核算的基本组成部分,其价格波动关系国计民生,影响社会生产及生活秩序稳定。随着我国城镇化进程的加快,“菜篮子”系列农产品供求状况面临着诸多挑战。因而,根据“菜篮子”系列农产品的价格波动规律和特点,对相关种植产业适时、适地地进行政策调控和引导,可以降低“菜篮子”农产品主产区农民面临的价格风险,抑制价格投机泡沫,引导市场价格理性预期,适时调整种植规划,从而真正实现“菜篮子”系列农产品的供给侧改革。本文的研究结果表明,我国“菜篮子”价格总体指数中存在周期性的非常规因素影响,在构成“菜篮子”价格总体指数的四类农产品价格指数中存在周期性投机泡沫现象。以具体“菜篮子”农产品大蒜为例,我们发现,从2006年8月到2017年5月,在大蒜价格中存在五个周期性的投机泡沫。大蒜价格投机泡沫问题的背后,折射的是“菜篮子”系列农产品的投机泡沫问题。同时,对于投机泡沫在“菜篮子”不同农产品之间的传递应当引起重视,这将是我们下一步的研究方向。
鉴于“菜篮子”农产品价格投机泡沫对日常生活和生产秩序的重要影响,政府部门有必要加强市场调控与监管,切实推进“菜篮子”农产品的供给侧改革。本文对于“菜篮子”系列农产品的供给侧改革及市场调控等具有较强的现实意义。首先,政府有关部门应该加强对“菜篮子”系列农产品的投机泡沫监控,进一步加强对“菜篮子”农产品价格非法操控、囤积居奇等行为的打击力度。例如,针对前期“菜篮子”农产品价格波动仅仅通过上涨幅度或速度等描述性监控指标的不足,适当加入关于市场投机力量有关的监控指标,如投机泡沫预警等。结合影响投机泡沫发生及破灭的具体环节,将物流、仓储等有关信息及时纳入监控体系。其次,规范“菜篮子”农产品有关的电子交易市场,尤其是针对电子交易中的保证金交易及资金存管方式等具体环节,进一步加强监督及规范,确保公平、公开、公正交易,避免其为市场投机力量所利用。“菜篮子”农产品价格关系国计民生,其价格波动直接影响居民消费价格指数波动。因此,政府有关部门应该加大对市场操纵行为的监管与处罚力度,并及时对社会公布有关信息。再次,从生产端角度,应该积极引导“菜篮子”农产品种植户的种植规划及理性价格预期,避免因价格信息失真而导致产量大起大落,危害当地生产秩序,损害地方经济生态。因此,政府部门应该进一步引导种植户关注市场价格泡沫风险。当投机泡沫发生时,要注意价格信息失真引致的有关风险;及时调整种植规划和价格预期,避免盲目囤货或恐慌性抛售而导致较大损失。针对此类问题,应积极引导种植户适时购买“菜篮子”农产品有关的种植保险,利用期货、保险等金融工具管理市场风险。当前,虽然有很多学者已经提出了类似建议,但是,从实际情况来看,由于生产端缺乏系统培训,种植户对此了解有限,加之“菜篮子”农产品的金融化进程较慢,尚无法在销售决策、风险管理等方面对“菜篮子”农产品生产端提供足够的支持,因而此类金融产品的推广力度有待进一步加强。最后,从前文中关于投机泡沫的周期性特征来看,仓储、物流等环节也均受到了周期性投机泡沫的影响。因此,从销售端角度政府部门应该加强仓储、物流等中间环节的信息监控,及时发布“菜篮子”农产品市场的供求信息,避免因为突发性事件或者投机力量作用而导致供求关系失衡,引起价格预期剧烈波动,影响地方生产及生活秩序稳定。
| [1] | 卞茂启, 王翠英. 2010年我国大蒜价格与出口情况及2011年形势展望[J].保鲜与加工,2011(3). |
| [2] | 陈楚天, 雷娜. 我国大蒜价格波动特征及对策研究[J].价格理论与实践,2012(6). |
| [3] | 陈明均. 我国大蒜市场形势及稳定大蒜价格的建议[J].中国蔬菜,2012(13). |
| [4] | 陈攀, 章胜勇. 基于小波分析的我国大蒜出口价格波动研究[J].青岛农业大学学报(社会科学版),2014(4). |
| [5] | 程瑞芳. 我国农产品价格形成机制及波动效应分析[J].中国流通经济,2007(3). |
| [6] | 丁超. 浅析大蒜价格暴涨的原因[J].中国蔬菜,2010(15). |
| [7] | 傅阳. 基于供应链视角探究大蒜价格异常波动的原因及对策[D]. 上海: 复旦大学, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D398674 |
| [8] | 郭世勤. 关于转换农产品价格形成机制的几个问题[J].经济研究,1993(12). |
| [9] | 胡冰川. 消费价格指数、农产品价格与货币政策——基于2001~2009年的经验数据[J].中国农村经济,2010(12). |
| [10] | 姜辉, 查伟华. 我国大蒜价格波动成因及政策调控研究[J].价格理论与实践,2016(10). |
| [11] | 康竹君, 马红瀚. 关于中国农产品价格上涨的经济学分析及对策[J].云南社会科学,2007(6). |
| [12] | 李超民. 中国农业现代化进程中的经济政策思想探索[J].上海财经大学学报,2005(2). |
| [13] | 李国祥. 2003年以来中国农产品价格上涨分析[J].中国农村经济,2011(2). |
| [14] | 李辉尚. 大蒜价格快速上涨引发的思考[J].中国食物与营养,2010(7). |
| [15] | 李京栋, 张吉国. 中国小品种农产品价格波动特征及其影响因素——基于2005–2014年大蒜价格数据的实证分析[J].湖南农业大学学报(社会科学版),2015(4). |
| [16] | 陆前进, 朱丽娜. 货币政策工具对基础货币和货币乘数的影响机制研究——基于中国2003–2011年的数据分析[J].上海财经大学学报,2011(5). |
| [17] | 唐赛. 由" 疯狂的大蒜”论失调的供应链[J].中国集体经济,2010(12). |
| [18] | 王孝松, 谢申祥. 国际农产品价格如何影响了中国农产品价格?[J].经济研究,2012(3). |
| [19] | 魏乐献. 2006–2009年处于刘易斯转折点附近的我国农产品价格波动研究[D]. 上海: 华东师范大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10269-2009186806.htm |
| [20] | 巫国兴. 我国农产品价格波动研究[J].农业经济问题,1997(6). |
| [21] | 肖小勇, 李崇光. 我国大蒜出口的" 大国效应”研究[J].国际贸易问题,2013(8). |
| [22] | 张利庠, 张喜才, 陈姝彤. 游资对农产品价格波动有影响吗——基于大蒜价格波动的案例研究[J].农业技术经济,2010(12). |
| [23] | Alexakis C, Bagnarosa G, Dowling M. Do cointegrated commodities bubble together? The case of hog, corn, and soybean[J].Finance Research Letters,2017,23:96–102. |
| [24] | Arora V, Gomis-Porqueras P, Shi S P. Testing for explosive behaviour in relative inflation measures: Implications for monetary policy[R].Monash Economics Working Paper No. 37/11, 2011. |
| [25] | Diba B T, Grossman H I. Rational bubbles in the price of gold[R]. NBER Working Paper No. 1300, 1984. |
| [26] | Diba B T, Grossman H I. Explosive rational bubbles in stock prices?[J]. The American Economic Review,1988,78(3):520–530. |
| [27] | Etienne X L, Irwin S H, Garcia P. Bubbles in food commodity markets: Four decades of evidence[J].Journal of International Money and Finance,2014,42:129–155. |
| [28] | Evans G W. Pitfalls in testing for explosive bubbles in asset prices[J]. The American Economic Review,1991,81(4):922–930. |
| [29] | Gomez-Gonzalez J E, Ojeda-Joya J N, Franco J P. Asset price bubbles: Existence, persistence and migration[J].South African Journal of Economics,2017,85(1):52–67. |
| [30] | Gürkaynak R S. Econometric tests of asset price bubbles: Taking stock[J].Journal of Economic Surveys,2008,22(1):166–186. |
| [31] | Hall S G, Psaradakis Z, Sola M. Detecting periodically collapsing bubbles: A Markov-switching unit root test[J].Journal of Applied Econometrics,1999,14(2):143–154. |
| [32] | Hamilton J D. A new approach to the economic analysis of nonstationary time series and the business cycle[J].Econometrica,1989,57(2):357–384. |
| [33] | Homm U, Breitung J. Testing for speculative bubbles in stock markets: A comparison of alternative methods[J]. Journal of Financial Econometrics,2011,10(1):198–231. |
| [34] | Kindleberger C P. Manias, panics, and crashes: A history of financial crises[M]. 5th ed. Hoboken, New Jersey: John Wiley & Sons, 2005. |
| [35] | Phillips P C B, Shi S P, Yu J. Testing for multiple bubbles: Historical episodes of exuberance and collapse in the S&P 500[R].Cowles Foundation Discussion Paper No. 1914, 2013. |
| [36] | Phillips P C B, Yu J. Dating the timeline of financial bubbles during the subprime crisis[J].Quantitative Economics,2011,2(3):455–491. |
| [37] | Shiller R. Irrational exuberance[M]. Princeton, New Jersey, U.S.: Princeton University Press, 2000. |
| [38] | Stiglitz J E. Symposium on bubbles[J].Journal of Economic Perspectives,1990,4(2):13–18. |
| [39] | Tirole J. On the possibility of speculation under rational expectations[J].Econometrica,1982,50(5):1163–1181. |
| [40] | Zhang Y J, Yao T. Interpreting the movement of oil prices: Driven by fundamentals or bubbles?[J].Economic Modelling,2016,55:226–240. |
| [41] | Zhao Y P, Chang H L, Su C W. Gold bubbles: When are they most likely to occur?[J].Japan and the World Economy,2015,34-35:17–23. |
 2018, Vol. 20
2018, Vol. 20


