文章信息
 | 上海财经大学 2018年20卷第1期 |
- 刘金全, 王俏茹, 刘达禹
- Liu Jinquan, Wang Qiaoru, Liu Dayu
- 中国跨越“中等收入陷阱”的路径突破——基于增长收敛理论的识别及“双轮驱动”检验
- The Path Breakthrough of Escaping the “Middle-income Trap” in China: Based on an Identification Method of Growth Convergence Theory and “Two-wheel Drive” Test
- 上海财经大学学报, 2018, 20(1): 29-42.
- Journal of Shanghai University of Finance and Economics, 2018, 20(1): 29-42.
-
文章历史
- 收稿日期:2017-08-04

2018第20卷第1期
根据世界各国的收入分布,世界范围内绝大多数中等收入国家的收入水平与美国的收入差距基本保持在一个稳定的水平上,即中等收入水平的国家没有表现出明显的向发达国家收敛的迹象,这意味着中等收入国家可能在达到高收入水平之前就在中等收入水平处实现了收敛,达到了一种相对稳定的状态,这一稳定状态即为“中等收入陷阱”。而陷入中等收入陷阱的国家以现有的增长模式难以脱离这一稳定状态,无法缩小与发达国家的收入差距,只有探索新的驱动因素、转变经济增长模式才有机会向更高的收入水平跃升,实现向高收入水平的收敛。现阶段我国正位于国际参考系下的上中等收入阶段,伴随着刘易斯拐点的来临,我国的人口红利日趋减弱,低成本优势逐渐消失;与此同时,投资方面也面临着边际效率递减、高杠杆以及泡沫化的风险,新古典增长理论中的两大生产要素在进一步发展过程中遭遇到了瓶颈,索洛余项的重要作用由此凸显。2012年,党的十八大明确提出实施创新驱动发展战略,将科技创新提高到了战略性的高度,随后《关于促进科技和金融结合 加快实施自主创新战略的若干意见》等措施出台,强调了金融服务实体经济的本质要求,并将科技与金融作为我国发展自主创新道路的两大驱动因素,简称“双轮驱动”。这两大因素将作为我国战略转型关键期对传统经济增长动力的更替,并在跨越中等收入陷阱的过程中发挥不可替代的关键作用。因此,在潜在增长率下降以及经济增长动力转换的关键时期,我国有两大问题亟待解决:一是经济潜在增长率下降是否意味着我国已陷入了中等收入陷阱,二是科技和金融两大因素在现阶段的驱动效果是否使我国具备了向高收入水平收敛的条件。这两大问题的解决能够为引领新常态、实现“追赶—赶超”路线提供重要的借鉴。
二、文献综述关于经济增长收敛理论最早可以追溯到索洛模型(Solow,1956),索洛模型的关键假设在于资本边际收益递减,这一假设的存在使得经济体能够收敛于一个稳定的状态。给定相同的外生因素,所有经济体最终将收敛于同一稳定状态,即“无条件收敛”。无条件收敛的概念可能太过苛刻,不同经济体应存在不同的平衡增长路径并收敛于不同的稳态,即“条件收敛”。随后,学术界开始对人均收入水平与增长率的关系展开了深入的研究,Barro和Salai-Martin(1992)以美国48个州为研究对象,基于边际收益递减的假设,得出了人均收入水平与增长率呈负向关系的结论,并以此证明各经济体的收入水平最终均会趋于收敛;而Lucas(1988)则对此结论进行了反驳,认为经济体只存在增长率收敛而不存在收入水平的收敛,并指出要素流动性的提高能够对收敛起到促进作用。Aghion和Howitt(2008)认为,大多数国家正在向相同的或平行的增长路径收敛,这一结论为从收敛角度研究中等收入陷阱问题提供了思路;Eichengreen等(2012,2013)在Hausmann等(2005)方法的基础上,研究了经济增速持续下降的案例,认为经济体的收入水平在达到10 000–11 000美元与15 000–16 000美元后会出现明显的增速下降趋势,但无法确定这一趋势是向中等收入水平收敛时的自然下降,还是从高收入水平收敛路径脱离的过程。不过,他们的研究结果表明,中等和高等教育水平相对较高的国家和高科技产品占出口比例相对较大的国家经济放缓的几率更小。Aiyar等(2013)比较了亚洲和拉丁美洲新兴市场经济体的时间序列数据,认为中等收入阶段经济增速的放缓是经济剧烈且持续地背离于条件收敛所预期的增长路径的过程,且实证研究结果表明,中等收入经济体经济增速下降的概率明显高于低收入与高收入经济体,由此证明了中等收入陷阱的存在;Ito(2017)将东亚国家按照收入水平进行划分,得出了不同收入组国家存在不同收敛曲线的结论,并认为经济体要想从一个收敛路径转向更高的路径,需要通过经济与政治改革来产生创新,如若不然,经济可能会陷入低收入或中等收入陷阱。国内从收敛的角度研究中等收入陷阱的文章相对较少,林志帆(2014)采取了加入人力资本与物质资本的条件收敛模型,为中等收入陷阱的识别提供了新方法,模型的识别结果也与现实高度相符。闫森(2017)在经济增长收敛理论的基础上,对亚洲经济体不同类别的国家分别进行了“β收敛”的检验,并得出了各组别间收敛曲线存在明显差异的结论,并从收敛的角度对跨越中等收入陷阱的路径问题进行了相应的解释。
陷阱被定义为是一种超稳定的均衡状态(蔡昉,2011),中等收入陷阱问题则被视为一种因缺乏动力而难以保持经济持续增长的长期性问题(Kenichi,2009;马岩,2009;刘伟,2011)。受到来自低收入国家制造业与高收入国家高科技行业双重竞争压力而引致的增速放缓是陷入中等收入陷阱的普遍现象,而从要素驱动向创新驱动转变的增长方式是跨越中等收入陷阱的关键(Kharas和Kohli,2011)。创新作为经济增长的内生动力最早可追溯到约瑟夫•熊彼特(1990)的《经济发展理论》,其中特别强调了金融与技术进步的密切关系;随后,约翰•希克斯(1987)在《经济发展史理论》一书中也进一步强调了金融效率对技术创新的重要作用,认为比技术本身更重要的是将技术推广的金融安排。而Solow(1956)模型中有效资本积累的概念本质上也是技术创新与金融的有机结合,因此,技术进步与金融发展是创新战略实施过程中的两大重要的驱动因素。近年来,越来越多的学者开始关注科技与金融二者相互融合对经济增长的促进作用,Schwartz(2000)从微观的视角强调了科技金融对经济增长的重要性,认为金融安排决定了企业技术发展的快慢,而技术的成败也直接影响了金融系统的盈利能力,最终对宏观经济产生影响;赵昌文等(2009)首次对科技金融进行了理论阐释,认为科技金融是各金融主体向创新主体提供金融支持的系统安排,以深度融合科技链与金融链;段世德和徐璇(2011)认为科技金融的发展是我国战略新兴产业长足发展的重要契机,也是我国进行经济转型的战略性突破口;陈守东等(2017)对我国新常态以来经济增长动力转换问题进行了研究,发现传统的“三驾马车”对经济增长的拉动作用有限,而以科技和金融为主的新兴驱动因素的作用在逐渐增强,但仍不及“三驾马车”的作用,由此说明我国正处于转型阶段,尚未完成阶段增长动力的转换。
中等收入陷阱已成为我国现阶段不得不面临的一大重要问题,而这一问题的本质则是经济增长的收敛问题,即现阶段我国的经济增长是否在向中等收入水平收敛的问题。然而,既有的根据经典理论框架分析经济增长收敛的文献缺乏对“中等收入陷阱”的本质阐释,而专门研究“中等收入陷阱”的文献却仅停留于现象描述层面,从收敛的角度对“中等收入陷阱”的本质进行理论分析的文献实属罕见。当然,仅停留在对是否陷入陷阱的问题进行讨论还远远不够,更重要的是如何顺利跨越这一陷阱而联通“中国梦”的问题。由前文可知,向创新驱动战略转变是跨越中等收入陷阱的必由之路,有必要对科技和金融两大因素在我国现阶段的表现进行检验。作为对传统经济增长动力的更替,“双轮驱动”的表现在新常态时期逐渐得到关注,但相关的研究尚处于初级阶段,缺乏相应的量化分析,对应的机制分析与对策研究也缺乏依据,实践性不强。有鉴于此,本文将利用经济增长收敛理论,对我国经济增长的收敛状况进行系统的分析,并在此基础上对我国是否陷入中等收入陷阱问题进行识别;随后,通过LT-TVP-VAR模型对“双轮驱动”因素的动态机制进行分析,进一步对我国能否成功跨越中等收入陷阱问题进行探讨。
三、理论分析作为经济学中使用最广泛的模型之一,索洛模型的实用性与普适性使得其经常被作为其他模型分析的基础,本文也是在索洛模型的框架下进行相应的扩展,首先考虑索洛模型的基本形式
| $Y\left( t \right) = F\left( {K\left( t \right),A\left( t \right)L\left( t \right)} \right)$ | (1) |
其中Y是产出,F是一次齐次的生产函数,K是资本,A是技术水平,L是劳动。单位有效劳动的资本与单位有效劳动的产出分别为:
| $k\left( t \right) = \frac{{K\left( t \right)}}{{A\left( t \right)L\left( t \right)}},\;f\left( {k\left( t \right)} \right){\rm{ = }}\frac{{Y\left( t \right)}}{{A\left( t \right)L\left( t \right)}} = F\left( {\frac{{K\left( t \right)}}{{A\left( t \right)L\left( t \right)}},1} \right)$ | (2) |
人均产出定义为:
| $y\left( t \right) = \frac{{Y\left( t \right)}}{{L\left( t \right)}}$ | (3) |
其中k的增长率可以表示为:
| $\frac{{\dot k\left( t \right)}}{{k\left( t \right)}} = \frac{{sf\left( {k\left( t \right)} \right)}}{{k\left( t \right)}} - \left( {\delta + a + n} \right)$ | (4) |
也即:
| $\dot k\left( t \right) = sf\left( {k\left( t \right)} \right) - \left( {\delta + a + n} \right)k\left( t \right)$ | (5) |
其中a与n分别为技术进步与劳动的增长率,当生产函数F满足某些条件时,存在唯一的全局稳定的稳态k*>0,满足
| $sf\left( {{k^*}} \right) - \left( {\delta + a + n} \right){k^*} = 0$ | (6) |
将人均收入的稳态值表示为y*,且定义
人均产出增长率g可以表示为:
| $g = \frac{{\dot y\left( t \right)}}{{y\left( t \right)}} = a + \varepsilon \left( k \right)\frac{{\dot k\left( t \right)}}{{k\left( t \right)}}$ | (7) |
其中
借鉴Acemoglu(2008),在等式(4)中关于
| $g \simeq \frac{{\dot y\left( t \right)}}{{y\left( t \right)}} \approx a - \varepsilon \left( {{k^*}} \right)\left( {1 - \varepsilon \left( {{k^*}} \right)} \right)\left( {\delta + a + n} \right)\left( {\ln k\left( t \right) - \ln {k^*}} \right)$ | (8) |
同时,将
| $\ln y\left( t \right) - \ln {y^*}\left( t \right) \simeq \varepsilon \left( {{k^*}} \right)\left( {\ln k\left( t \right) - \ln {k^*}} \right)$ | (9) |
并将其代入等式(8)中即可得到以下收敛方程(Acemoglu, 2008):
| $g = \frac{{\dot y\left( t \right)}}{{y\left( t \right)}} \simeq a - \left( {1 - \varepsilon \left( {{k^*}} \right)} \right)\left( {\delta + a + n} \right)\left( {\ln y\left( t \right) - \ln {y^*}\left( t \right)} \right)$ | (10) |
由方程(10)可以看出,在索洛模型中,人均产出的增长率有两大来源:第一个是技术进步增长率a,第二个是收敛条件。如果
方程(10)中另一个值得注意的特征是,
根据以上理论推导,可以认为,经济体在经济发展过程中可能存在多条收敛线,假设在某一时点
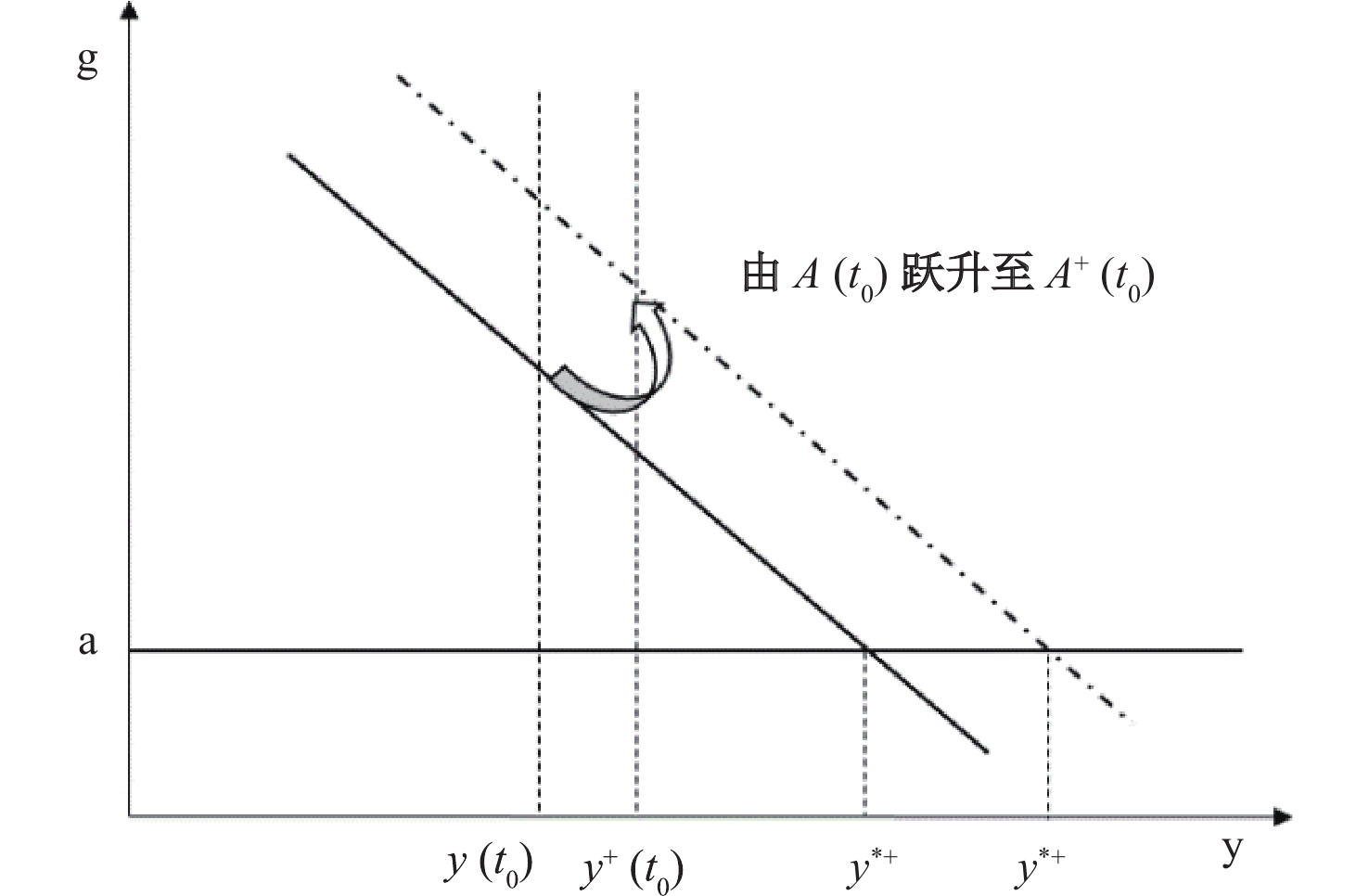
|
| 图 1 收敛路径的转变 |
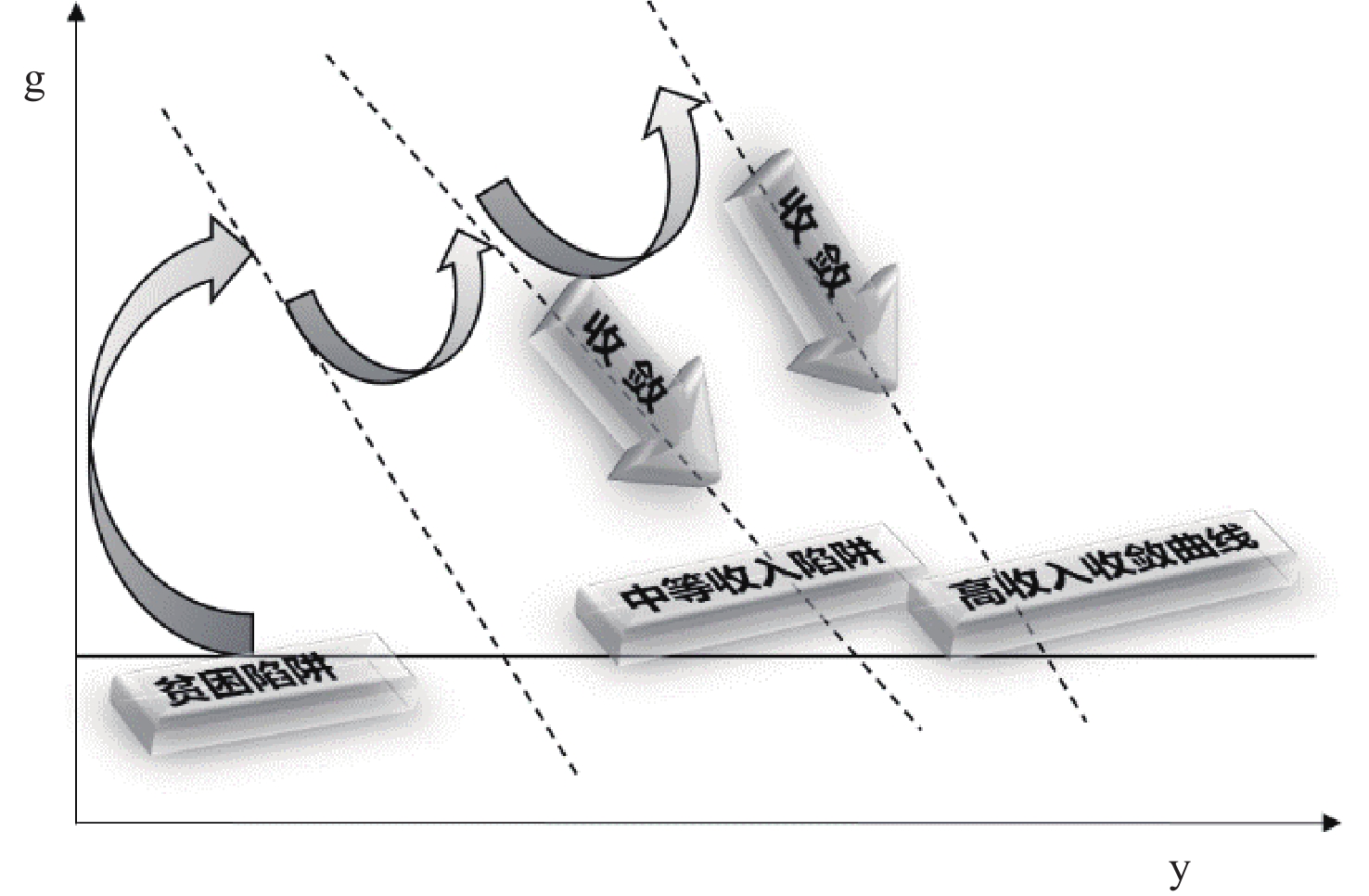
|
| 图 2 经济增长收敛模式 |
与此同时,本文借鉴Ito(2016)对经济增长收敛模式的描述,进一步绘制了典型经济体由低收入水平向高收入水平的发展路径,如图2所示。低收入经济体通过一定的发展实现经济腾飞,摆脱了“贫困陷阱”,随后经济开始收敛,这一阶段的经济体可以进一步借助制度红利、人口红利等实现经济的持续增长,期间收入水平可能出现多次跃升,直到跃升至中等收入水平的收敛曲线。当经济体达到中等收入水平后,先前的红利开始逐渐消失,同时面临来自低收入国家的“追逐效应”与高收入国家的“压制效应”,原有增长模式难以应对集中爆发的矛盾与风险,经济增长陷入停滞,即陷入“中等收入陷阱”。只有少部分国家通过适时转换经济增长动力改变了现有的收敛态势,进而维持了经济增长的持续性,并成功跃升至高收入阶段。根据索洛模型的推导以及图1的分析可知,创新能力的上升才是实现跃升的关键,只有当技术进步积累到一定程度,经济才能扭转当前的经济收敛趋势,跃升至高收入水平的收敛曲线,最终实现向高收入水平收敛。
四、经济增长收敛路径的识别与检验 (一) 门限回归模型的建立与数据处理根据上述理论分析,本文将经济收敛的基本计量模型表示为以下形式:
| ${g_t} = \alpha + \beta \left[ {\ln {y_t} - \ln y_t^*} \right] + {\varepsilon _t}$ | (11) |
式(11)意味着经济的增长率由两部分构成,一部分为稳态时的增长率a,另一部分为赶超部分
| ${g_t} = (\alpha + \beta {\rm{gap}})I\left( {gap {\text{≤}} {\gamma _1}} \right) + (\alpha ' + \beta '{\rm{gap}})I\left( {{\gamma _1} < gap {\text{≤}} {\gamma _2}} \right) + (\alpha '' + \beta ''{\rm{gap}})I\left( {gap > {\gamma _2}} \right) + {\mu _t}$ | (12) |
其中,
在建立门限回归模型前首先要对是否存在门限效应进行相应的检验,由Hansen(1996)提出的相应的检验方法如下:
| $F = T\left( {{{\tilde \sigma }^2} - {{\hat \sigma }^2}} \right)/{\hat \sigma ^2}$ | (13) |
其中,T为样本量,
| $F = \mathop {\sup }\limits_{{{\hat \gamma }_ * } \in \Gamma } \left( {F\left( {{{\hat \gamma }_ * }} \right)} \right)$ | (14) |
| $F\left( {{\gamma _ * }} \right) = T\left( {{{\tilde \sigma }^2} - {{\hat \sigma }^2}\left( \gamma \right)} \right)/{\hat \sigma ^2}\left( \gamma \right)$ | (15) |
若模型不存在异方差,则根据Hansen(1996)所提出的自举法(Bootstrap)可得到上述F统计量的渐近分布,而若模型存在异方差,则需借助Wald统计量予以检验:
| $W\left( {{\gamma _ * }} \right) = {\left[ {R\hat \beta \left( {{\gamma _ * }} \right)} \right]^\prime }{\left[ {R\left( {M{{\left( {{\gamma _ * }} \right)}^{ - 1}}V\left( {{\gamma _ * }} \right)M{{\left( {{\gamma _ * }} \right)}^{ - 1}}} \right)R'} \right]^{ - 1}}R\hat \beta \left( {{\gamma _ * }} \right)$ | (16) |
| $M\left( {{\gamma _ * }} \right) = \sum\nolimits_{t = 1}^T {{x_t}\left( {{\gamma _ * }} \right)} {x_t}^\prime \left( {{\gamma _ * }} \right),\;V\left( {{\gamma _ * }} \right) = \sum\nolimits_{t = 1}^T {{x_t}\left( {{\gamma _ * }} \right)} {x_t}^\prime \left( {{\gamma _ * }} \right)\hat \varepsilon _t^2$ | (17) |
其中,R为相应的约束条件,
| $W = \mathop {\sup }\limits_{{{\hat \gamma }_ * } \in \Gamma } \left( {F\left( {{{\hat \gamma }_ * }} \right)} \right)$ | (18) |
在此基础上,同样借助自举法得到Wald统计量的渐近分布,通过对以上统计量进行计算,能够对模型的门限效应及门限个数进行检验,相应的检验与估计结果如表1所示,出于对比的考虑,本文也同时将线性模型的估计结果列于表1中。
| 线性方程 | 区制1 | 区制2 | 区制3 | ||||||||
| 参数 | 估计值 | 标准差 | 参数 | 估计值 | 标准差 | 参数 | 估计值 | 标准差 | 参数 | 估计值 | 标准差 |
|
|
5.252*** | 0.611 | α | –21.849*** | 0.923 | α' | 37.979*** | 1.500 | α'' | –1.832* | 0.949 |
|
|
–1.237*** | 0.206 | β | –8.168*** | 0.235 | β' | 8.445*** | 0.428 | β'' | –4.466*** | 0.469 |
| R2 | 0.198 | R2 | 0.998 | R2 | 0.965 | R2 | 0.701 | ||||
| 门限 | — | 门限 |
|
门限
|
门限 |
|
|||||
| 门限效应P值:— | 门限效应P值:0.000 | 门限效应P值:0.000 | 门限效应P值:0.000 | ||||||||
| 注:括号内为对应的标准误差,***、**与*分别代表1%、5%与10%的显著性水平。 | |||||||||||
从表1可以看出,就线性方程的估计结果来看,我国的经济从整体趋势上来看确实存在一定的收敛性,但若将其看作一条收敛线太过牵强,因为其拟合优度R2仅为0.198,说明线性方程对数据的拟合并不理想。而从门限回归模型的估计结果来看,模型存在两个门限值,分别为–3.688与–2.793,这两个门限值进一步将模型分成了三个区制,且三个区制均显著通过了门限效应检验,就拟合优度而言,三个区制的R2均明显高于线性模型,说明经济中确实存在结构性变化,构建门限回归模型存在其合理性。从估计系数的符号来看,区制1与区制3的截距项与收敛项均为负,表现出明显的收敛特性,可以认为区制1与区制3分别代表两条显著不同的收敛曲线,而区制2的截距项与收敛项均为正,意味着区制2代表了经济从低收敛线向高收敛线跃升的过程。通过观察具体的估计值可以发现,区制1与区制2的截距项虽然均为负值,但区制2的截距项远高于区制1,由前文的理论分析可知,截距项α代表的是经济达到稳态时所应该达到的增长率,这一水平的高低直接决定着经济的发展水平,说明我国经济在发展的过程中实现过一次由低收敛曲线向更高的收敛曲线跃升的过程,结合我国经济的具体数值可以发现,收入差距在–3.688(γ1)附近,对应着我国1997–1998年间,而根据世界银行公布的人均GNI数据及其收入分组标准,我国是在1997年进入下中等收入阶段的,随后经济增长迅速,经济逐渐脱离原先的收敛曲线,呈现出跃升的态势,经济由区制1进入了区制2,在进入区制2后,经济经历了收入差距缩小与经济增速提高并存的高速增长时期,直到收入差距达到–2.853(γ2),经济再一次发生结构性变化,而这一收入差距对应着我国2007–2008年间。众所周知,受美国次贷危机的影响,我国经济受到了很大的影响,经济增速出现了明显的下滑,紧随其后的刺激政策的出台使经济在短期内迅速回升,我国也于2010年成功进入上中等收入阶段,然而刺激效果的非持续性并未改变经济增速换挡的事实,反而催生了诸如杠杆率过高等现实问题,经济增速呈现逐年下降的趋势,表现出明显的收敛态势,当然,区制3的拟合优度较前两个区制来说相对较小,α''也仅在10%的显著性水平上通过了显著性检验,这可能是由于美国次贷危机这一短期冲击因素,使得经济产生了相对于正常趋势的偏离。通过对比β的估计值可以发现,区制2的收敛速度约为区制1收敛速度的一半,经济表现出明显的平稳化趋势,无需担心经济的“硬着陆”问题,这意味着经济的缓慢下行不会带来猛烈的冲击,也为经济增长动力机制转换预留了大量的空间,以时间换取空间,同时也为宏观经济调控提供了良好的预期,为我国顺利进行供给侧改革创造了条件。这一结果与我国当局在进入新常态以来进行宏观调控时坚持的“适度微调”原则密不可分,再一次证明了将决定权交给市场的正确性。
通过以上的分析可知,我国目前的经济增长正处于收敛态势,且这一收敛曲线的稳态增长率为负值,说明继续沿着这一收敛曲线我国无法保持经济增长的持续性,经济也不能顺利进入高收入阶段,但这并不能为我国经济陷入“中等收入陷阱”提供证据。根据贾康和苏京春(2016)的统计,成功跨越中等收入陷阱的经济体跨越“上中等收入陷阱”的平均时长约为15.9年,且每年的经济增速不能低于5.8%,意味着若在未来9年,我国经济仍沿着目前的收敛曲线发展而没有脱离现有收敛曲线的趋势,且经济增速跌破5.8%,则意味着我国已经陷入了“中等收入陷阱”,如若不然,则无法为“中等收入陷阱”提供证据。当然,这一结论只是通过对已成功跨越陷阱国家的经验总结,属于经验之谈,我国能否跨越“中等收入陷阱”需要深入分析这背后的本质,即经济增长的驱动因素问题。为此,下文将通过LT-TVP-VAR模型的建立深入分析经济增长驱动因素的影响。
五、经济增长驱动因素的时变特征分析根据前文的理论分析可知,经济由低收敛曲线向高收敛曲线跃升的根本动力在于创新,伴随着4.0版工业革命的到来,发达国家正在探索制造业的创新之路,我国在经济增速换挡的新常态时期,更应坚持创新驱动型增长模式。根据发展经济学理论与新古典经济增长等相关理论,创新的关键在于发挥技术进步与资本形成的内生作用,技术进步由于其规模效应、乘数效应等特点在产业结构优化升级、劳动生产率提高等方面均发挥着不可替代的作用,而资本的形成与积累是经济增长的基础,是社会扩大再生产的必然要求,其对经济增长的作用毋庸置疑,而这一过程的本质可视为储蓄转化为投资的内生机制,金融效率的高低则在此起到了关键的作用,因此,技术与金融“双轮驱动”将成为未来我国经济增长最为核心的动力因素,能够为跨越中等收入陷阱提供持久的内生动力。
为了更加深入地分析“双轮驱动”因素对经济增长影响的动态特征,本文建立了含潜在门限变量的时变系数向量自回归(LT-TVP-VAR)模型。该模型在考虑时变特征的基础上进一步考虑了变量之间的结构性与非线性特征,进而对传统的TVP-VAR模型可能带来的拟合偏差问题进行了改进,使估计结果更为可信。
(一) LT-TVP-VAR模型结构设定首先,建立一个S-VAR模型:
| $A{y_t} = {F_1}{y_{t - 1}} + \cdots + {F_s}{y_{t - s}} + {\mu _t},\;\;t = s + 1, \cdots ,n$ | (19) |
其中,A为
| $\Sigma = \left[ {\begin{array}{*{20}{c}}{{\sigma _1}}&0& \cdots &0\\0&{{\sigma _2}}& \ddots &0\\ \vdots & \ddots & \ddots & \vdots \\[4pt]0&0& \cdots &{{\sigma _k}}\end{array}} \right]\;\;\;\;\;\;A = \left[ {\begin{array}{*{20}{c}}1&0& \cdots &0\\{{a_{2,1}}}& \ddots & \ddots &0\\ \vdots & \ddots & \ddots & \vdots \\[4pt]{{a_{k,1}}}& \cdots &{{a_{k,k - 1}}}&1\end{array}} \right]$ |
设
| ${y_t} = {X_t}{\beta _t} + A_t^{ - 1}{\Sigma _t}{\varepsilon _t},\;\;t = s + 1, \cdots ,n$ | (20) |
借鉴Nakajima 和 West(2013)的设定,本文将模型参数的演进过程设定如下:
| $\begin{aligned}\begin{aligned}{\beta _t} = {\mu _\beta } + {\Phi _\beta }\left( {{\beta _{t - 1}} - {\mu _\beta }} \right) + {v_t},t = s + 1, \cdots ,n,\\{\alpha _t} = {\mu _\alpha } + {\Phi _\alpha }\left( {{\alpha _{t - 1}} - {\mu _\alpha }} \right) + {\zeta _t},t = s + 1, \cdots ,n,\\{h_t} = {\mu _h} + {\Phi _h}\left( {{h_{t - 1}} - {\mu _h}} \right) + {\xi _t},t = s + 1, \cdots ,n,\end{aligned}&\;\;\;{V = Var\left( {\begin{aligned}{{\varepsilon _t}}\\{{v_t}}\\{{\zeta _t}}\\{{\xi _t}}\end{aligned}} \right) = \left( {\begin{aligned}& {{I_n}}\;\;\;0\;\;\;\;\;\;\;0\;\;\;\;0\\& 0\;\;\;\;{{\Omega _\beta }}\;\;\;\;0\;\;\;\;0\\& 0\;\;\;\;0\;\;\;\;\;\;{{\Omega _\alpha }}\;\;0\\& 0\;\;\;\;0\;\;\;\;\;\;\;0\;\;\;\;{{\Omega _h}}\end{aligned}} \right)}\end{aligned}$ | (21) |
其中,
| ${b_t} = {\beta _t} \times I\left( {\left| {{\beta _t}} \right| {\text{≥}} {d_b}} \right)$ | (22) |
| ${a_t} = {\alpha _t} \times I\left( {\left| {{\alpha _t}} \right| {\text{≥}} {d_a}} \right)$ | (23) |
其中,
技术进步指标选取高科技产品在制成品出口中的占比作为代理变量,具有高研发强度的产品的出口占比能够较为真实地反映我国的技术水平与技术成果。而金融资源的配置效率则表示为全社会固定资产投资的实际到位资金中的国内贷款与金融机构人民币各项存款余额的比值,以此来表示金融机构将存款转化为投资的效率,该值越大,表明转化效率较高。基于稳健性考虑以及模型的需要,本文将年度数据分解为频率更高的季度数据。
根据滞后阶数设定准则,本文决定构建二阶滞后三变量LT-TVP-VAR模型,并将模拟样本数设定为10 000,其中前1 000次为预模拟。相应的参数后验分布均值、标准差以及无效影响因子如表2所示。观察表2中的无效影响因子可以看出,除了参数
| 参数 | 均值 | 标准差 | 无效影响因子 |
|
|
0.029 2 | 0.017 1 | 34.74 |
|
|
0.808 9 | 0.081 0 | 72.88 |
|
|
0.021 2 | 0.001 9 | 83.53 |
|
|
–0.1764 | 0.157 8 | 59.46 |
|
|
0.914 4 | 0.058 6 | 66.66 |
|
|
0.075 5 | 0.022 4 | 103.32 |
|
|
0.017 0 | 0.017 6 | 90.76 |
|
|
0.878 4 | 0.060 2 | 57.01 |
|
|
1.170 8 | 0.361 2 | 214.54 |
|
|
0.043 6 | 0.039 2 | 163.96 |
|
|
0.187 8 | 0.108 1 | 5.04 |
|
|
0.178 1 | 0.109 7 | 101.74 |
|
|
0.354 7 | 0.354 0 | 170.34 |
| 参数 |
|
|
|
|
| 可接受率 | 43.3 | 24.1 | 89.0 | 48.3 |
在上述模型构建与估计的基础上,本文将通过等间隔脉冲响应函数进一步刻画“双轮驱动”因素对经济增长的动态作用机制,同时,考虑到“双轮驱动”因素之间的相互作用关系,本文还给出了“双轮驱动”因素之间的动态冲击机制,如图3至图6,图中实线、散点及点线分别代表短期(一年)、中长期(两年)及长期(三年)的响应函数曲线。
图3给出了技术进步对经济增长冲击的脉冲响应函数图,从整体趋势来看,三条曲线趋势大致相同,表现出估计结果的稳健性。技术进步对经济增长的影响在1994–1996年间出现下降甚至表现出负效应,在1996–1998年间这一影响逐渐提高,1998–2010年间这一影响在0.13附近上下波动,表现出稳定的正向效应;而在2010年之后又出现了明显的下降,直到2014年这一下降趋势才得以缓解,随后稳步回升。这一冲击曲线走势与前文所述的收敛阶段高度耦合,进一步说明技术进步是经济增长的内生动力,其变动能够影响经济的内生波动。技术进步对经济增长的影响主要表现在:首先,技术进步能够产生规模效应,创新技术一旦被熟练掌握且运用于生产,即可在扩大生产规模的过程中无需支付额外的成本却能使产出成倍增加,获得递增的规模收益;其次,技术进步具有集聚效应,一个产业的技术革新可以带动相关产业提高产品附加值,改进生产方式,最终提升社会整体的生产率;最后,技术进步具有溢出效应,由于知识、信息等具有共享性特征,一个地区技术进步能够带动周边地区技术的发展,周边地区通过学习、模仿等对新技术进行应用,并在实践过程中进一步创新,随后进一步扩散,如此良性循环,技术进步能够使产出成倍甚至指数性增加。可以看出,技术进步对经济增长的影响主要表现为显著的正向影响,但图3中1994–1996年间却出现了短暂的负向影响。纵观历史可知,1992年邓小平南巡,形成了社会主义市场经济体制,但体制基础尚未稳定,依然存在“双轨制”,虽然工业化的发展战略正稳步开展,但生产率较为低下,甚至存在产能过剩现象,即出现了历史上公认的由“短缺经济”向“过剩经济”的转变。因此,1994–1996年间负向效应的产生主要是制度原因,随后我国经济进入了高速增长的黄金发展阶段。与此同时,我国对科技创新的认识不断增强,但总体来说,我国仍位于全球产业链的中低端,对于国际尖端技术的掌握水平较低,技术产业表现出“大而不强”的特点;同时,随着刘易斯拐点的到来,我国的人口红利日趋减弱,低成本优势逐渐消失,出现了中等收入国家所面临的问题。过去粗放型的经济增长方式难以为经济增长提供强有力的支持,导致促进作用趋于减弱。自2012年以来,“创新驱动”的发展战略在党的十八大中被明确提出,并强调营造公平的竞争环境,形成技术创新的市场导向,从制度、法律等多方面为技术创新提供了保障,这一战略的实施为我国供给侧改革提供了突破口,对我国产业结构优化升级、经济质量效益的提升以及经济动能的转换等均发挥了重要的作用。从图3中也可以看出,这一战略的实施卓有成效,科技进步对经济增长的促进作用从2012年起逐年增强,为经济的增长提供了稳定的内生动力。
图4给出了金融效率对经济增长冲击的脉冲响应函数图,与技术进步不同,金融效率对经济增长的冲击响应曲线表现出先上升后下降的趋势,峰值出现在2005年附近,2005年以后开始下降,中间虽有小幅回升,但整体趋势仍趋于下降,直到2013年之后,才出现了明显的上升趋势。金融效率对经济增长的影响包括以下两方面:一方面,作为投融资中介,金融机构担任着聚集闲散资金并将其投入高效益部门的角色,实现资源的优化配置,金融效率高意味着金融部门将储蓄转化为投资的效率较高,进而对经济增长所产生的积极作用就越大;另一方面,金融部门的投资渠道主要分为实体部门投资与虚拟经济部门投资,当虚拟经济部门投资过度挤占实体部门投资时,实体经济会面临融资难等问题,增加了企业的贷款成本,实体部门的市场活力也会随之下降,难以为创新创业营造良好的氛围,同时,虚拟经济部门也会出现资产泡沫化等问题,进而引致一定的金融风险,这一系列后果均不利于经济的平稳健康发展。这两大方面的影响在图4中也得到了充分的体现,自金融体制改革以来,我国的金融市场经历了高速发展阶段,金融体系日趋健全,金融效率不断提升,对经济增长的促进作用也不断攀升,但随着我国金融市场的不断发展壮大,金融市场业务迅速扩大,虚拟经济部门投资也不断增加,对实体经济投资的挤占作用逐渐显现,加之体制、法律不完善以及市场不规范等原因制约了金融效率作用的发挥,使得从2005年开始这一促进作用开始逐渐下降,直到全球金融危机爆发,这一影响作用达到波谷,随后政府推出的救市行为使这一影响有了小幅回升,但依旧没有从根本上解决资产泡沫的问题。直到新常态以来,供给侧改革开始如火如荼地展开,去泡沫、去杠杆的效果逐渐显现,金融效率对经济增长的促进作用也开始逐渐提升。由此观之,新常态时期确实是我国向高收入水平跃升的重要战略机遇期,我国在这一阶段解决了很多问题也取得了诸多成就,当然,我国依然面临着前所未有的困难与挑战,经济新常态下也产生了诸多新的风险,由产能过剩引起的不良贷款率过高、由地方性政府债务增加带来的系统性风险隐患、由住房市场前景不明带来的抵押风险等均在新常态时期逐渐凸显,未来还有很长的路要走,只有把握机遇,全面深化改革,才能成功跃升至更高的收入水平。
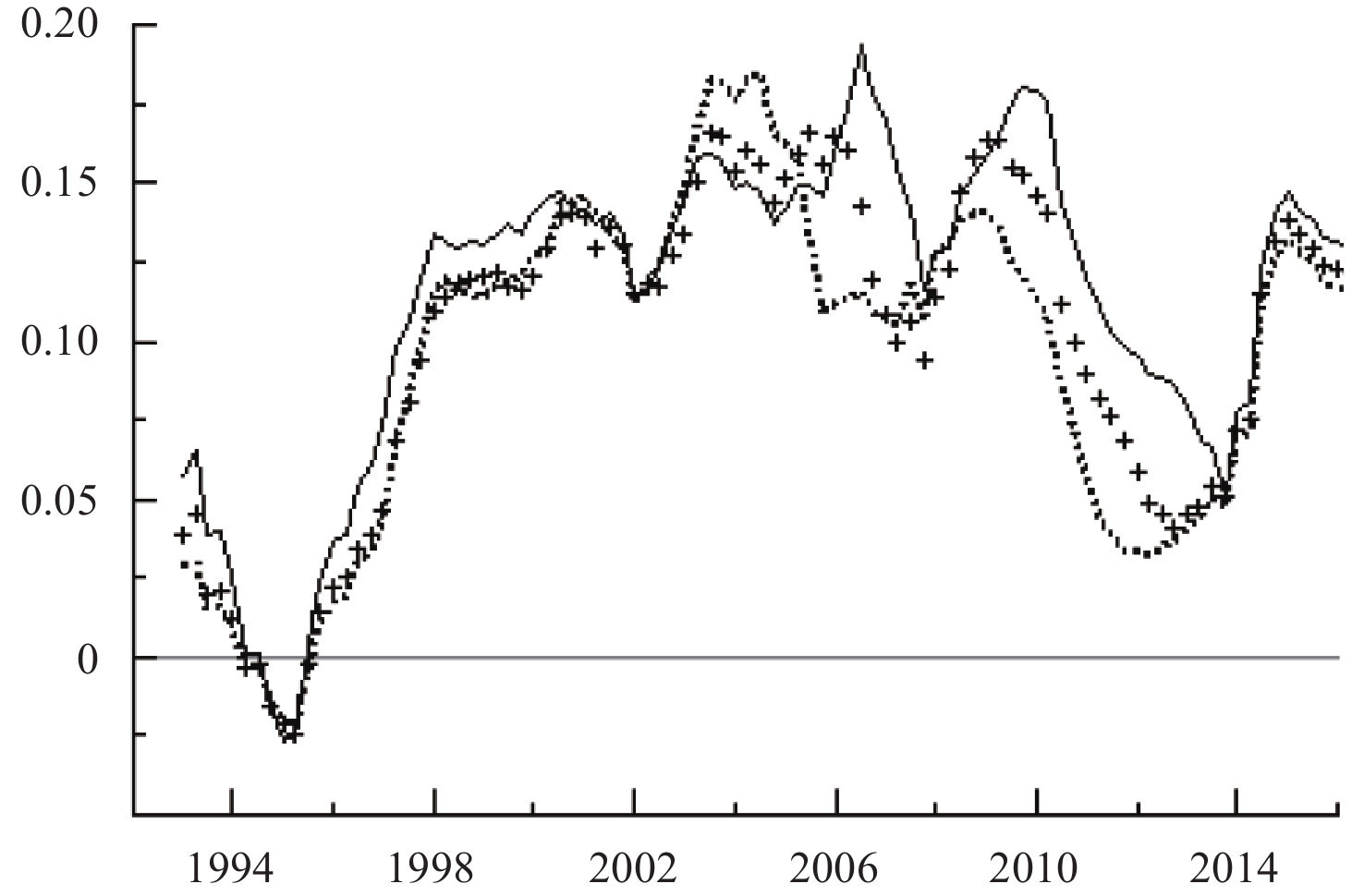
|
| 图 3 技术进步对经济增长冲击的时变响应 |
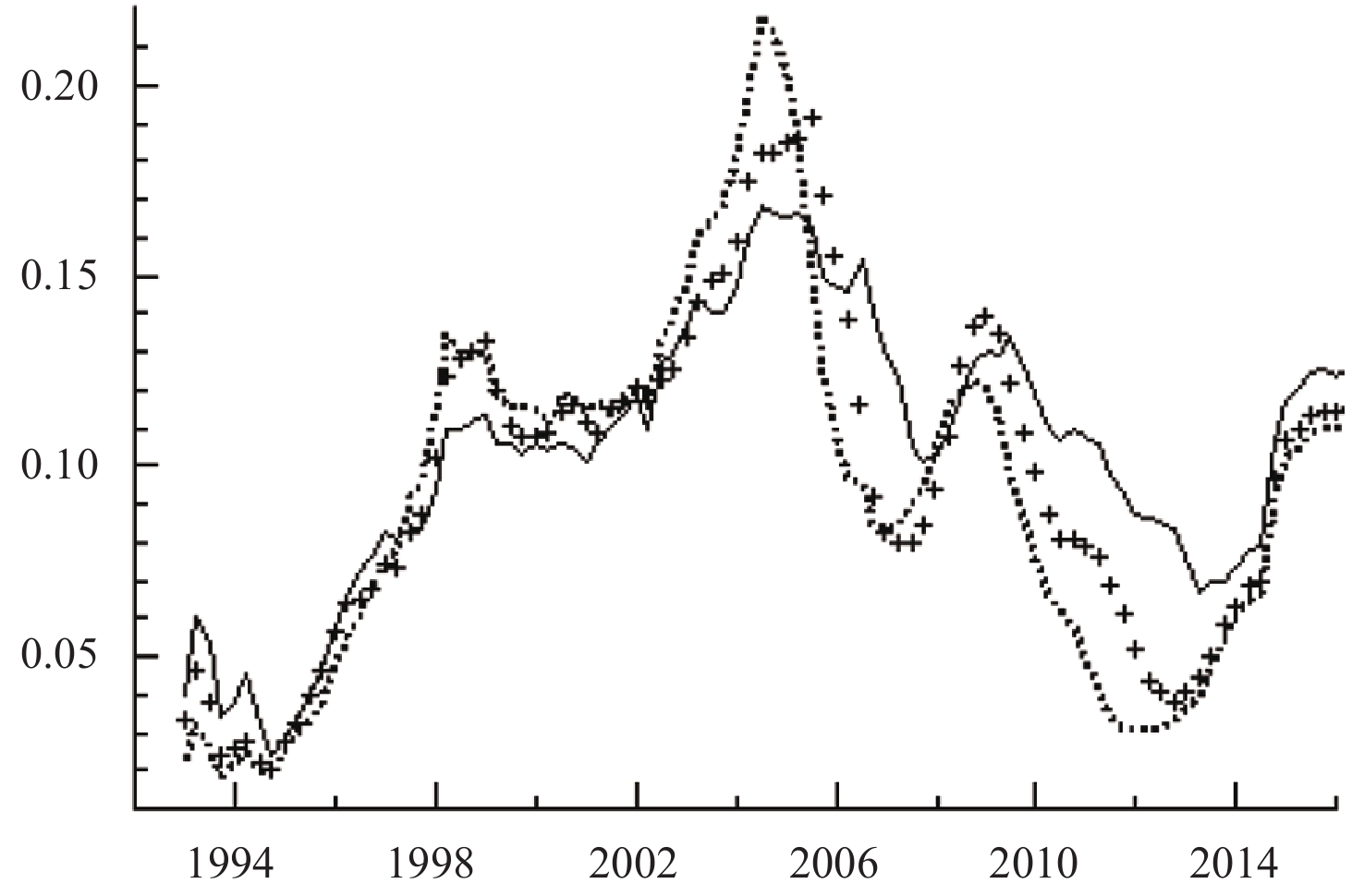
|
| 图 4 金融效率对经济增长冲击的时变响应 |
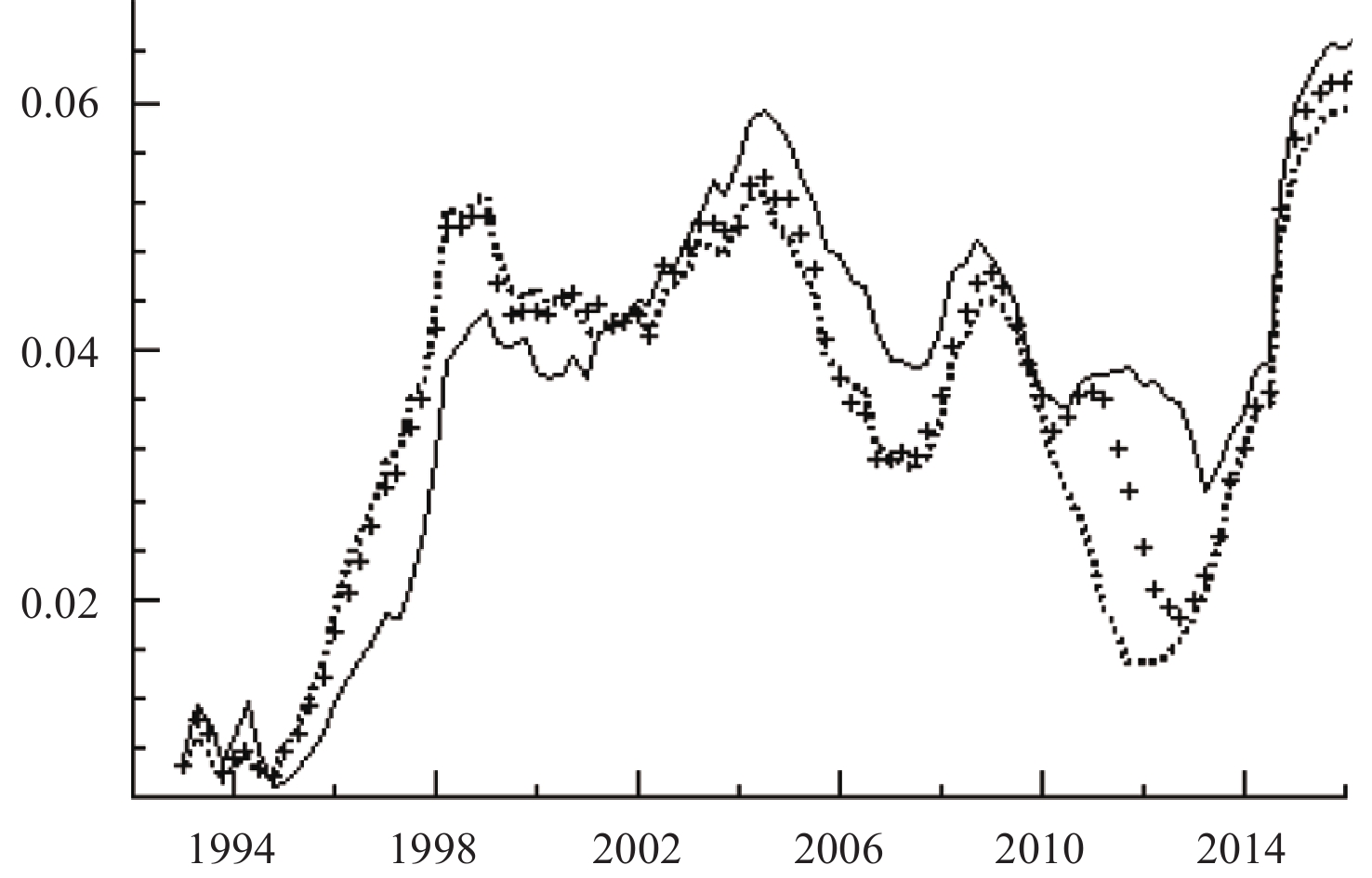
|
| 图 5 金融效率对技术进步冲击的时变响应 |
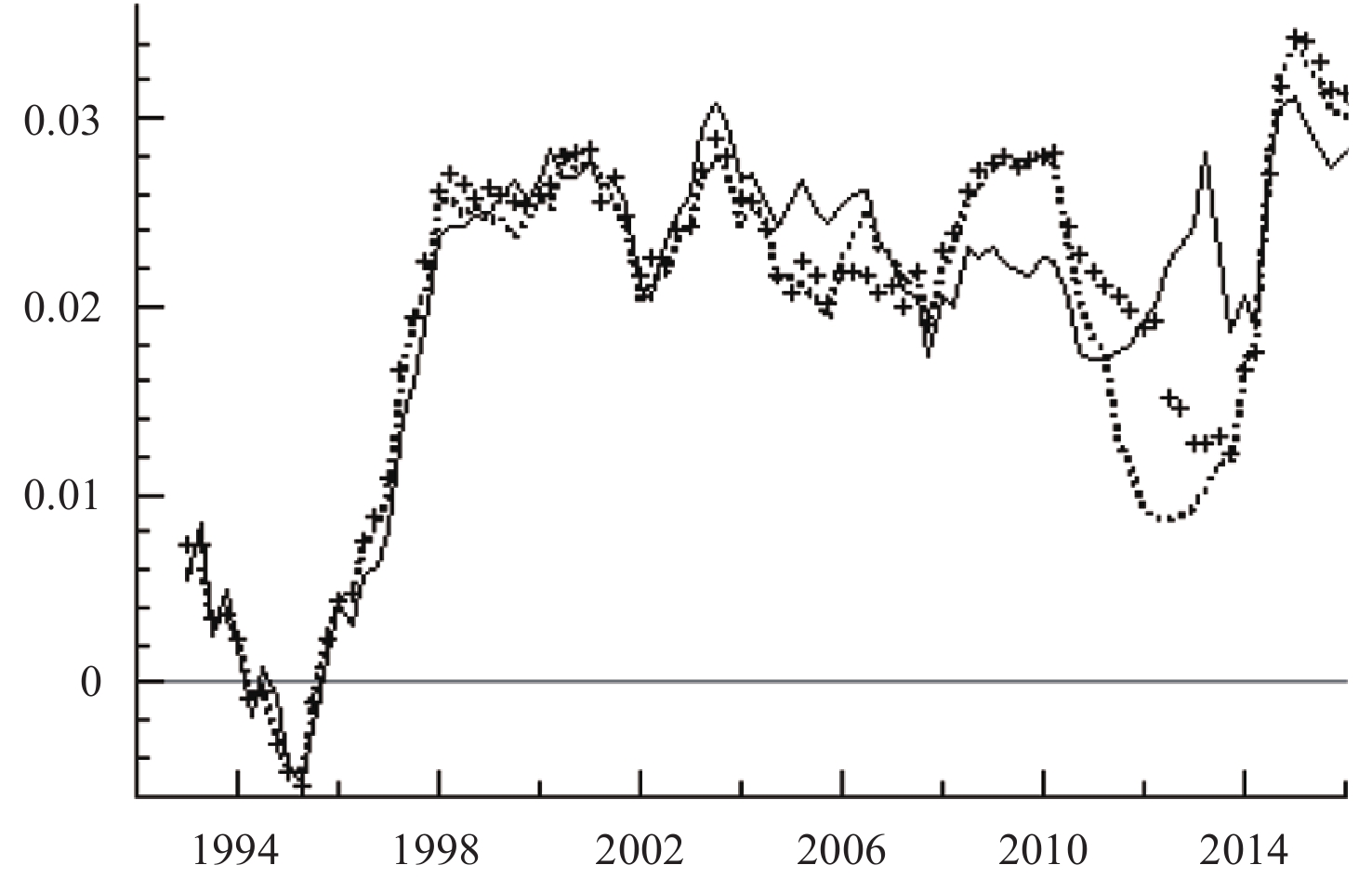
|
| 图 6 技术进步对金融效率冲击的时变响应 |
图5与图6分别给出了金融效率与技术进步相互冲击的脉冲响应函数图。从整体趋势来看,二者之间相互冲击的趋势大体相同,均在1995–1998年间有明显的上升趋势,而在1998–2010年间表现出平稳的正向效应,在2012年间出现小幅下降后又逐渐回升,且回升幅度达到历史新高,说明二者之间的融合达到了前所未有的水平。金融效率对于技术进步的促进作用可以通过金融市场的功能进行讨论:首先,金融市场资金融通和优化资源配置的功能能够保证具有高投入特点的高科技项目获得充足的资金;其次,金融市场价值发现的功能能够将行业的发展现状与前景通过资产价格变动体现出来,进而引导资金流向,寻找最具价值的创新项目;最后,金融市场分散与管理风险的功能能够解决技术创新项目的另一大特点——高风险,投资者能通过套期保值等多元化投资手段在金融市场上进行风险管理,解决投资者的后顾之忧,进而使得高科技投资更加活跃。反过来,技术进步也能对金融效率产生一定的影响:一方面,科技的创新与发展能够打破金融市场的传统经营模式,优化业务流程,使金融体系向快捷化、个性化的方向发展,进而提高金融市场的效率;另一方面,科技的创新能够拓宽金融市场现有的经营范围,使金融部门的经营业务与面向的对象更加多元,为金融市场挖掘到新的增长点,进一步促进金融效率的提高。通过对二者间影响作用进行对比可以发现,金融效率对科技进步的促进作用要强于科技进步对金融效率的促进作用,体现出了非对称性特征,说明科技创新倒逼金融业进行自我改革的过程需要较长的时间,当然,也说明科技创新对金融方面的技术支持有待进一步提升。同时,经济新常态以来这两种促进作用的上升幅度明显提升,说明“双轮驱动”因素间的融合无论从深度上还是广度上均达到了前所未有的水平,经济增长动力转换正在有效进行,新的经济增长动力正在以相互强化的方式发挥其内生作用。若继续保持这样的发展态势,我国陷入中等收入陷阱的可能性较小,因此,除了深度挖掘科技创新驱动与金融效率驱动在经济增长过程中所发挥的作用,探索科技创新与金融效率的融合路径将是我国在跨越中等收入陷阱过程中另一大重要任务。
六、结论与政策建议“中等收入陷阱”问题是我国正在面临的一个顶级真问题,而鲜有文献从收敛性的角度对我国的中等收入陷阱问题进行研究。本文通过门限回归模型的建立,对我国经济增长的收敛路径进行识别与检验,研究发现,我国目前的经济增长正处于收敛态势,且这一收敛曲线的稳态值为负,说明现有收敛曲线无法使我国步入高收入阶段,我国只有转变经济增长的驱动因素,才有可能顺利成为高收入国家。为此,本文借助LT-TVP-VAR模型,研究“双轮驱动”因素对经济增长影响的动态特征,以此对我国是否具备向高收入阶段跃升的动力条件进行判断,通过对脉冲响应函数进行分析,可以得到以下结论:第一,技术进步通过规模效应、集聚效应以及溢出效应对经济增长表现出明显的正向作用,这一作用与前文识别的收敛路径高度耦合,在经济新常态时期,由于创新驱动发展战略的有效实施,这一促进作用较之前有明显的增强;第二,金融机构通过提高其资源配置效率对经济增长产生显著的积极作用,但随着金融市场业务的扩大,其虚拟投资对实体投资的挤占则会引致一定的金融风险,不利于经济的增长,我国金融效率对经济增长的影响整体上表现为正向效应,但这一正向作用从2005年起就逐渐减弱,至金融危机爆发降至最低,而经济新常态以来,随着供给侧改革的开展,我国在优化投资结构,提高资源配置效率等方面取得了相当的进展,金融效率对经济增长的促进作用得到了显著提升;第三,就技术进步与金融效率间的相互作用而言,二者之间以相互强化的方式发挥其内生作用。具备高风险、高投入以及更新速度快特点的创新活动离不开高效率的金融支持,这要求金融市场充分发挥其风险分散、资金配置以及价值发现的功能,以促进科技成果转化为生产力。而技术进步反过来也能推动科技创新,改变传统的运营模式、对象及产品,促进金融效率的提高,进而更好地服务创新活动与实体经济,二者相互推动,缺一不可。但金融效率对科技进步的促进作用要强于科技进步对金融效率的促进作用,表现出非对称性特征。经济新常态以来这两种促进作用的上升幅度明显提升,说明“双轮驱动”因素间正在以前所未有的水平相互融合,经济增长动力转换正在有效进行。
由此观之,以我国目前的收敛曲线来看,向高收入水平跃升面临着重重困难,但从“双轮驱动”因素的表现来看,技术进步与金融效率对经济增长的促进作用以及二者之间的相互作用均在经济新常态时期得到了明显的提升,说明新常态时期我国经济增长的动力转换过程初具成效,为了顺利向高收入水平跃升,需要继续保持现有的发展势头,并进一步挖掘“双轮驱动”因素的潜能,为此,需要促进科技与金融的深度融合。首先,要重视政府的引导与服务的作用。实施创新型政策以激励与保障相应的创新行为,同时进一步加大财政对技术创新的投入力度;更为重要的是,以政府为担保,为科技与金融的合作搭建平台,并通过立法明确具体的合作事宜,使科技与金融的融合过程更加顺畅。其次,充分发挥市场的作用。完善多层次资本市场,丰富融资渠道,为科技创新提供多样化的资金支持。同时完善风险防范措施,通过建立信用担保制度、科技保险制度、风险投资退出制度等分散风险,提高资金运用效率。
| [1] | 蔡昉. " 中等收入陷阱”的理论、经验与针对性[J].经济学动态,2011(12). |
| [2] | 陈守东, 孙彦林, 毛志方. 新常态下中国经济增长动力的阶段转换研究[J].西安交通大学学报(社会科学版),2017(1). |
| [3] | 段世德, 徐璇. 科技金融支撑战略性新兴产业发展研究[J].科技进步与对策,2011(14). |
| [4] | 贾康, 苏京春. 中国的坎: 如何跨越" 中等收入陷阱”[M]. 北京: 中信出版社, 2016. |
| [5] | 林志帆. " 中等收入陷阱”存在吗?——基于增长收敛模型的识别方法[J].世界经济研究,2014(11). |
| [6] | 刘伟. 突破" 中等收入陷阱”的关键在于转变发展方式[J].上海行政学院学报,2011(1). |
| [7] | 马岩. 我国面对中等收入陷阱的挑战及对策[J].经济学动态,2009(7). |
| [8] | [英国]约翰•希克斯. 经济史理论[M].北京: 商务印书馆, 1987. |
| [9] | [美国]约瑟夫•熊彼特. 经济发展理论[M]. 北京: 商务印书馆, 1990. |
| [10] | 闫森. 经济增长收敛与" 中等收入陷阱”——基于亚洲经济体的实证研究[J].亚太经济,2017(1). |
| [11] | 赵昌文, 陈春发, 唐英凯. 科技金融[M]. 北京: 科学出版社, 2009. |
| [12] | Acemoglu D. Introduction to modern economic growth[M]. Princeton: Princeton University Press, 2008. |
| [13] | Aghion P, Howitt P. The economics of growth[M]. Cambridge: MIT Press, 2008. |
| [14] | Aiyar S S, Duval R, Puy D, et al. Growth slowdowns and the middle-income trap[R]. Washington: International Monetary Fund, 2013. |
| [15] | Barro R J, Salai-Martin X. Convergence[J].Journal of Political Economy,1992,100(2):223–251. |
| [16] | Eichengreen B, Park D, Shin K. When Fast-Growing economies slow down: International evidence and implications for China[J].Asian Economic Papers,2012,11(1):42–87. |
| [17] | Eichengreen B, Park D, Shin K. Growth slowdowns redux: New evidence on the middle-income trap[R]. NBER Working Paper No. w18673, 2013. |
| [18] | Hansen B E. Inference when a nuisance parameter is not identified under the null hypothesis[J].Econometrica,1996,64(2):413–430. |
| [19] | Hausmann R, Pritchett L, Rodrik D. Growth accelerations[J].Journal of Economic Growth,2005,10(4):303–329. |
| [20] | Ito T. Growth convergence and the Middle-income trap[J].Asian Development Review,2017,34(1):1–27. |
| [21] | Kharas H, Kohli H. What is the middle income trap, why do countries fall into it, and how can it be avoided?[J].Global Journal of Emerging Market Economies,2011,3(3):281–289. |
| [22] | Lucas R E Jr. On the mechanics of economic development[J].Journal of Monetary Economics,1988,22(1):3–42. |
| [23] | Nakajima J, West M. Bayesian analysis of latent threshold dynamic models[J]. Journal of Business & Economic Statistics,2013,31(2):151–164. |
| [24] | Ohno K. Avoiding the middle-income trap: Renovating industrial policy formulation in Vietnam[J].ASEAN Economic Bulletin,2009,26(1):25–43. |
| [25] | Primiceri G E. Time varying structural vector autoregressions and monetary policy[J].The Review of Economic Studies,2005,72(3):821–852. |
| [26] | Schwartz E S, Moon M. Evaluating research and development investments[A]. Brennan M J, Trigeorgis L. Project flexibility, agency, and competition: New development in the theory and application of real options[M]. New York: Dxford University Press, 2000. |
| [27] | Solow R M. A contribution to the theory of economic growth[J].The Quarterly Journal of Economics,1956,70(1):65–94. |
 2018, Vol. 20
2018, Vol. 20


