文章信息
 | 上海财经大学 2017年19卷第6期 |
- 马红旗
- Ma Hongqi
- 产能利用率、企业性质与经营效益——基于钢铁企业的实证分析
- Capacity Utilization, Enterprise Nature and Operation Benefits: Empirical Study Based on Iron and Steel Industry
- 上海财经大学学报, 2017, 19(6): 31-45.
- Journal of Shanghai University of Finance and Economics, 2017, 19(6): 31-45.
-
文章历史
- 收稿日期:2017-08-15

2017第19卷第6期
无论从哪个角度看,钢铁行业都是通过实证研究来探讨未来供给侧改革路径与方式的理想选择。这不仅是因为钢铁行业本身的标准化特质,也是因为我国钢铁企业的产能过剩问题由来已久,是一个长期性的顽疾,其治理过程中遭遇的问题也提供了当前供给侧改革的重要参考。
实际上,自20世纪90年代末我国告别短缺经济以来,钢铁行业就显现了产能过剩的端倪,而中央政府也最早针对钢铁企业的产能过剩问题出台了有关项目审批、市场准入和行业技术标准等多方面的产业政策措施,这应当属于改革开放以来中央政府实施的第一轮产能过剩治理政策(徐朝阳和周念利,2015)。随后,因为钢铁行业产能过剩问题的愈演愈烈,中央政府先后实施了一系列更加严厉的产能治理政策,如《关于制止钢铁电解铝水泥行业盲目投资若干意见的通知》(2003)、《关于调整部分行业固定资产投资项目资本金比例的通知》(2004)、《钢铁产业发展政策》(2005)等。2008年美国金融危机之后,被快速工业化需求所掩盖的钢铁行业产能过剩矛盾日趋严重,日益凸显的产能过剩矛盾已经成为影响我国钢铁行业持续健康发展的重要因素,“三去一降一补”的产能化解更成为党中央、国务院的重大决策部署。总体而言,改革开放以来政府对于钢铁企业的产能过剩治理进行得最早,累积的经验与教训也最多。而总结钢铁行业产能过剩的历史演变及其结构特征,不仅事关化解钢铁企业产能过剩本身,也事关企业经营效益的提高,对供给侧结构性改革的顺利推进也具有重要的理论和现实意义。
回顾20世纪90年代以来国内钢铁行业产能过剩的演变路径,有几个问题值得重点关注:第一,20世纪90年代末以来我国钢铁企业的产能利用状况在所有制结构方面存在怎样的企业性质差异?第二,这种差异在多大程度上能够解释钢铁企业经营效益的企业性质差异?第三,产能利用状况的企业性质差异主要表现在哪种规模类型的企业上?因为在我国钢铁企业中,相同所有制类型的企业存在很大的规模差异。对于上述几个问题的解答,不仅关系到我们对产能过剩现实成因及其实际经济效益影响的准确解读,而且为破解产能过剩提供了突破口。据此,本文将在测算我国钢铁企业产能利用率的基础上,分析企业产能利用状况的变动趋势、企业性质差异以及与企业经营效益的关系,并通过进一步分析企业性质差异的规模因素为治理钢铁企业产能过剩提供一个明晰的路径。
二、文献综述目前学术界主要用产能利用率指标考察企业产能过剩状况及其实际影响,该指标的测算主要取决于对生产能力的界定准则。Chamberlin(1947)首次提出产能过剩的概念,并以生产成本最小化为逻辑基础,从经济学角度对生产能力进行了界定:认为生产能力是完全竞争均衡下的企业产出水平,也即平均成本最小时的企业产出水平。理论上,该观点以微观企业生产理论为支撑,其对生产能力的界定完全贴近经济学意义,但构建成本函数的复杂性和数据获取的难度却给统计工作带来了较大的阻力。为了统计便利,Smithies(1957)又从工程学意义上提出了新的生产能力界定准则,即现有设备在正常运转和工人运转轮班制情况下的产出水平。根据Smithies(1957)的界定思想,这里隐含两个测算准则:一是设备正常运转,如把机器调试、机器故障以及工人替换衔接等一些因素造成的设备暂时性停工时间排除在外;二是工人上工实行轮班制,需要排除因不同地区、不同行业和不同企业机器运转小时数的不同对产能估算带来的偏差,若两个企业具有完全相同的机器设备,一个企业采取8小时工作制,而另一个企业采取10小时工作制,若不考虑轮班制则会统计出不同的产能水平。当然,Smithies(1957)产能界定准则还存在一个潜在的假设,即每个设备或每条生产线具有核定的产出水平。对此,只需统计每个企业设备和生产线的数量便可核算企业整体的生产能力。基于Smithies(1957)的界定思想,Foss(1963)利用企业最大用电量衡量企业的生产能力,原因是企业设备的核定功率是一定的。工程学意义上的界定方法显然有利于统计部门的实践,在美国早期统计企业生产能力的五家独立机构中,有四家就是从工程意义上展开调查统计工作的,包括麦克希尔经济部、国民工业委员会、财富杂志、美联储研究与统计部(Phillips,1963;Klein等,1973)。然而工程学界定方法仍面临两大缺陷:一是需要耗费大量的人力、物力和财力,这是一般的研究团队难以企及的,因此该方法仅限于政府决策部门和大型的研究机构,很少见之于学术研究;二是工程意义上统计的生产能力无法与经济学意义上统计的生产能力保持一致的波动趋势。因为即使不受需求约束,企业设备在一定的时间内也不可能持续性地运转,而且企业运营的核心不是产量而是利润,这也从客观上造成工程意义上的生产能力与经济学意义上的生产能力无法保持一致。
因此,在随后的拓展和应用中,产能利用率的工程学测算方法并没有太大的改善和推广,而经济学测算方法则得到了不断的修正和推进(Berndt和Morrison,1981)。目前产能利用率的经济学测算方法主要发展了峰值法、前沿面分析法和函数法三大类。(1)峰值法。该方法把企业平均成本函数的最低点的产出水平界定为企业的生产能力,并认为厂商在完全竞争时的均衡产出处于平均成本函数最低点,而在垄断竞争条件下的均衡产出将低于平均成本函数最低点的产出,由此形成了过剩生产能力。具体测算过程中,Klein(1960)及后续研究Klein和Summers(1966)、Klein等(1973)利用了统计学上的“过峰趋势技术”进行了近似替换。具体的做法是,首先假定一定时间内实际产出的峰值年份产能得到了充分利用,而非峰值年份未得到充分利用,进而把相邻两个峰值点拟合成一条平滑线,若第三个峰值点超出这条平滑线之外,则取消这条平滑线并把第一个峰值点和第三个峰值点拟合出一条新的平滑线作为生产能力的评估曲线,依次类推可以得出一条最终修正后的生产能力趋势线,实际值与趋势值之比便是产能利用率。该方法最早被美国宾夕法尼亚大学沃顿商学院测算美国工业产能利用率编制“Wharton Index”时所采用(开创者为Klein(1960)教授),沈利生(1999)、Kirkley等(2000)也沿用了类似的估算方法。这种“过峰趋势技术”是把生产能力趋势线上的点假定为厂商完全竞争条件下的均衡产出,而把生产能力趋势线以下的点则假定为垄断竞争条件下的均衡产出。然而,实际情况很可能是生产能力趋势线上的点并不一定为厂商完全竞争条件下的均衡产出,正如Phillips(1963)、Frank(1968)对峰值法批判时提出的“弱高峰”问题,经济复苏阶段实际产出所表现出的高峰就是在产能未实现充分利用的“弱高峰”,若此时采用峰值法测算产能利用率必定是高估的。(2)前沿面分析法。与峰值法的处理手段一样,为了避开函数设定的复杂性,前沿面分析法并没有完全依照Chamberlin(1947)的生产成本界定准则,而是首先假定企业的最大生产能力等同于一定时期内企业的前沿生产面,用每个决策单元的实际产出与前沿产出的相对效率来衡量产能利用率。目前主要有数据包络分析法(DEA)法(Fare等,1989、2000;Bruno和Kerstens,2000;Kirkley等,2002;Coelli等,2002;Pascoe和Tingley,2006;Lindebo等,2007;Bye等,2009;Karagiannis,2015)和随机生产前沿分析法(SPF)(Kirkley,2002)两类。然而,数据包络分析法(DEA)和随机生产前沿分析法毕竟是学术界测算企业技术效率的惯用统计技术,当我们用这种类似“索洛余值”的形式来衡量企业技术效率时,完全忽视了产能利用率的存在。不可否认的是,生产单元的实际产出与前沿面产出的差距起码糅合和了技术效率和产能利用率两种效应,因此如何分离、应怎样分离是前沿面分析法面临的一个重要现实问题。虽然Fare等(1989)对产能过剩和效率损失的分离做了一定的尝试,却又遭遇更多的质疑,Coelli等(2002)认为技术效率的损失部分实质是“落后产能”,因此技术效率应属于产能利用率的一部分。Pascoe和Tingley(2006)又指出除自然环境等无法消除的因素导致的技术效率损失外,其他情况下产生的效率损失均可以看作为过剩产能。(3)函数法。函数法的具体做法是先设定成本函数(或利润函数)的具体形式,通过完全竞争条件下的均衡条件求出企业的生产能力,最终用实际产出与生产能力之比表示产能利用率。函数法需要预先设定先验性的成本函数,函数构建的不确定性、要素价格数据的难以获取以及参数估计的复杂性是难点,这也是峰值法和前沿面分析法避开函数设定的主要原因。函数法的争议焦点在于均衡条件的设定:其一,Berndt和Morrisom(1981)、Berndt和Hesse(1986)、Nelson(1989)、Garofalo和Malhotra(1997)、Gokcekus(1998)、Lazkano(2008)等从短期角度考察了企业的生产能力,认为企业在保持固定成本不变的条件下,其最大生产能力应该用短期平均成本曲线最低点时的产出水平表示;其二,Paine(1936)、Cassell(1937)、Hickman(1964)、Morrison(1985)则认为企业的最大生产能力应该出现在固定成本和可变成本均可调节的情况下,由此将企业生产能力界定为长期平均成本曲线最低点时的产出水平;其三,Klein(1960)最初在所编制的“Wharton Index”中的论述是赞同从长期角度考虑企业生产能力的,但Klein(1960)又作了进一步补充。他认为长期平均成本曲线在实践中更大程度上表现为L形,以找到曲线的最低点,主张把企业生产能力界定到长期平均成本曲线和短期平均成本曲线的切点的产出水平上。这一建议后来也得到了Segerson和Squires(1990)、Morrison(1985)的采纳。Pascoe等(2003)和Pascoe和Tingley(2006)基于不同的均衡条件测算了企业的产能利用率,发现不同的均衡条件所测算的生产能力是有差异的。Morrison(1985)对不同的均衡条件进行甄别后指出,企业规模报酬是均衡条件选定的重要参考依据,当企业规模报酬不变时宜采用短期成本曲线最低点的产出作为企业生产能力,否则采用长期成本曲线与短期成本曲线的切点的产出作为企业生产能力。可见,尽管函数法操作起来比较棘手,但学界对其论证和改进的研究热度不减,这主要源于函数法的理论基础和统计技术更容易使得产能过剩概念还原为Chamberlin(1947)首次界定的初衷。
国内文献对产能过剩监测方法的研究起步较晚,研究内容主要是基于国外模型的中国应用。工程学意义的测算方面:龚刚和杨琳(2002)、何彬(2008)假定一定时期内的用电量与资本服务使用量成固定比例,然后以用电量乘以该比例代替无法观测的资本服务使用量来求得我国的资本设备利用率;经济学意义测算方面:沈利生(1999)利用了峰值法,董敏杰等(2015)利用了数据包络分析法,孙巍等(2009)、韩国高等(2011)、国务院研究中心“进一步化解产能过剩的政策研究”课题组(2015)利用成本函数法分别测算了我国工业部门的产能利用率。
本文试图基于Morrison(1985)的研究架构,结合钢铁企业的实际运行特征,采用长期成本曲线与短期成本曲线切点的产出测算我国钢铁企业的生产能力,采用成本函数法测算我国钢铁企业的产能利用率,最终来分析其产能过剩状况、所有制格局及对经营效益的影响。
三、我国钢铁企业产能利用率的变动趋势及企业性质差异我们首先在借鉴Klein(1960)、Nelson(1989)和Morrison(1985)研究成果的基础上,基于1998–2007年中国工业企业数据库提供的企业微观数据,测度我国钢铁企业的产能利用率。
(一) 理论模型假定代表性企业在技术水平为T的情况下组织资本K、劳动L和中间投入M进行生产,生产函数设定为:
| $Y = {\rm{f}}(K,L,M,T)$ | (1) |
其中,Y表示总产出,用时间变量来衡量技术水平T。假定资本K为短期分析的固定要素,劳动L和中间投入M为可变要素。若用P1和P2分别表示劳动和中间投入的市场价格,根据Lau(1976)的定义可以把可变成本表述成一个由Y、K、T、P1和P2决定的函数形式:
| $VC = (Y,K,T,{P_1},{P_2})$ | (2) |
把式(2)用超越对数形式表示为:
| $\begin{split}\ln VC = & {a_0} + \sum\limits_f {F{D_f}} + \sum\limits_i {{a_i}} \ln {P_i} + \frac{1}{2}\sum\limits_i {\sum\limits_j {{a_{ij}}} } \ln {P_i}\ln {P_j} + {b_y}\ln Y + \frac{1}{2}{b_{yy}}{(\ln Y)^2} + \sum\limits_i {{b_{yi}}} \ln Y\ln P + {c_k}\ln K\\[-2pt]& + \frac{1}{2}{c_{kk}}{(\ln K)^2} + \sum\limits_i {{c_{ki}}} \ln K\ln {P_i} + {c_{ky}}\ln K\ln Y + {d_t}T + \frac{1}{2}{\delta _{tt}}{T^2} + \sum\limits_i {{d_{ti}}T\ln {P_i}} + {d_{tk}}T\ln K + {d_{ty}}T\ln Y\end{split}$ | (3) |
其中,i和j表示可变要素的种类,f表示企业数量;FDf表示企业的个体特征,用来控制企业的个体效应;ai、aij、by、byy、byi、ck、ckk、cki、cky、dt、dtt、dti、dtk和dty为各要素组合的参数值;a0为常数项,表示企业固有的可变成本。在可变投入要素价格的对称性和线性齐次性条件约束下,式(3)的待估参数满足:
| $\sum\limits_I {{a_i}} = 1,\sum\limits_i {{b_{yi}}} = 0,\sum\limits_i {{c_{ti}} = 0} ,\sum\limits_i {{d_{ki}}} = 0,\sum\limits_i {{a_{ij}}} = \sum\limits_j {{a_{ij}}} = 0$ | (4) |
对式(3)取对数微分得出可变要素投入的份额方程(谢波德引理):
| ${S_i} = \frac{{\partial \ln VC}}{{\partial \ln {P_i}}} = {a_i} + \sum\limits_j {{a_{ij}}\ln {P_j}} + {b_{yi}}\ln Y + {c_{ki}}\ln K + {d_{ti}}T$ | (5) |
假定企业的固定成本方程为资本的市场租赁价格与资本的乘积:
| $TFC = r \times K$ | (6) |
则企业短期总成本函数可表示为:
| $SRTC = VC + r \times K$ | (7) |
进一步可得出企业短期平均成本函数(在式(7)左右两边同除以总产出Y):
| $SRATC = VC/Y + r \times K/Y$ | (8) |
根据Klein(1960)和Morrison(1985)的思想,企业生产能力应是短期平均成本曲线(SRATC)与长期平均成本曲线(LRATC)切点处的产出水平。当长期成本曲线与短期成本曲线相切时,假定企业处于长期均衡时的资本为K*,对式(8)求关于长期均衡资本K*的导数可得:
| $\frac{{\partial SRTC}}{{\partial {K^*}}} = \frac{{\partial VC}}{{\partial {K^*}}} + r = 0$ | (9) |
式(9)表明,在长期均衡状态下,企业增加一单位资本给生产成本带来的增量为资本的要素价格。把式(9)右边第一项再次拓展为:
| $\frac{{\partial VC}}{{\partial {K^*}}} = \frac{{\partial \ln VC}}{{\partial \ln {K^*}}}\frac{{VC}}{{{K^*}}}$ | (10) |
自此,对式(3)关于lnK*求导可得:
| $\frac{{\partial \ln VC}}{{\partial \ln {K^*}}} = {c_k} + {c_{kk}}\ln {K^*} + \sum\limits_i {{c_{ki}}\ln {P_i}} + {c_{ky}}\ln Y + {d_{tk}}T$ | (11) |
将式(11)和式(10)代入式(9)则可求出企业在既定资本存量条件下短期成本曲线和长期平均成本曲线切点处的产出水平,也即企业的生产能力,计算实际产出与生产能力之比便可以得出企业产能利用率。
(二) 数据选取1. 样本提取
样本主要从1998–2007年中国工业企业数据库中提取,范围为所有行业类型属于黑色金属冶炼及压延加工业企业(两位数行业代码为32)的钢铁企业,其中包括了四个四位数行业代码分别为3210、3220、3230和3040的细分行业,依次为炼铁业、炼钢业、钢压延加工业和铁合金冶炼业。其中,“炼铁”是指用高炉、直接还原、熔融还原等方法从矿石等含铁化合物中还原出生铁的生产过程;“炼钢”是指利用不同来源的氧去氧化炉料(主要是生铁)中所含的杂质以达到金属提纯的生产过程;“钢压延加工”是指通过热轧、冷加工、锻压和挤压等塑性加工使连铸坯、钢锭产生塑性变形,制成具有一定形状尺寸的钢材产品的生产活动;“铁合金冶炼”是指把铁与其他一种或一种以上的金属或非金属元素冶炼成合金生产活动。
根据聂辉华等(2012)、谢千里等(2008)和Bai等(2009)的指标剔除标准,剔除了以下样本:工业总产值、固定资产净值、工业销售产值、实收资本缺失或小于0的企业;从业人数小于8的;销售额低于500万元的;总资产小于流动资产、总资产小于固定资产净额或者累计折旧小于当期折旧的企业;利润率低于1%或高于99%的企业①;固定资产净额、工业总产值、从业人数和实收资本前后1%分位的企业。在识别企业性质时,我们采用实收资本中各种资本金的比例来识别企业的所有制类型②:国有资本金比例超过50%为国有企业;集体资本金比例超过50%为集体企业;私人资本金比例超过50%为私有企业;港澳台资本金和外商资本金比例之和超过25%为外资企业①;把无法通过资本金比例识别的企业定义为其他企业。表1报告了最终提取样本信息的情况。
①这里依据Cai和Liu(2009)的会计核算标准来计算,具体公式为:企业利润(利润=工业总产值–中间投入–财务费用–工资–当期折旧–增值税)。
②至少有15%的注册类型为国有企业的企业其实已经不是真正的国有企业,因此工商局登记注册的企业类型并不能确切地识别企业的所有制类型(聂辉华等,2012)。
①按照中国的法律规定,外资企业的投资比例原则上不能低于25%,故借鉴路江涌(2008)的做法,设定外资实收资本金比例超过25%的企业为外资企业。
| 全部企业 | 炼铁 | 炼钢 | 铁合金冶炼 | 钢压延加工 | ||
| 全部企业 | 数量 | 37 789 | 6 880 | 2 107 | 12 885 | 15 917 |
| 比例 | 100% | 18.20% | 5.60% | 34.10% | 42.10% | |
| 国有企业 | 数量 | 2 282 | 605 | 183 | 1 012 | 482 |
| 比例 | 6.00% | 8.80% | 8.70% | 7.90% | 3.00% | |
| 集体企业 | 数量 | 5 941 | 1 210 | 359 | 3 005 | 1 367 |
| 比例 | 15.70% | 17.60% | 17.00% | 23.30% | 8.60% | |
| 私营企业 | 数量 | 22 213 | 3 797 | 1 093 | 6 274 | 11 049 |
| 比例 | 58.80% | 55.20% | 51.90% | 48.70% | 69.40% | |
| 外资企业 | 数量 | 2 622 | 284 | 134 | 736 | 1 468 |
| 比例 | 6.90% | 4.10% | 6.40% | 5.70% | 9.20% | |
| 其他企业 | 数量 | 4 731 | 984 | 338 | 1 858 | 1 551 |
| 比例 | 12.50% | 14.30% | 16.00% | 14.40% | 9.70% | |
2. 指标构建
用“本年应付工资总额”与“中间投入合计”之和表示可变成本VC,用工业增加值表示总产出Y ②,用固定资产净值年平均余额表示资本K,用《中国统计年鉴》中黑色金属冶炼及加工行业劳动力年人均工资表示劳动价格P1,用《中国价格统计年鉴》中黑色金属材料类购进价格指数表示中间投入价格指数P2(P1和P2已换算成以1998年为基期的定比价值指数)。
②由于部分样本缺失工业增加值指标,我们采用刘小玄和李双杰(2008)的估算公式进行了推算:工业增加值=产品销售额–期初存货+期末存货–中间投入合计+增值税。
由于资本租赁价格难以直接获取,我们根据Jorgenson(1963)的理论推导来获得。Jorgenson(1963)假定在竞争性市场条件下,企业持有资本的使用成本等于它未来所有期望租赁收入的折现和,有三部分组成:一是企业放弃利息收入的机会成本;二是折旧费用;三是资本价格的波动带来的资本使用成本,即资本价格下降预示着企业资本的使用成本上升,反之亦然。基于此,可用公式表示资本租赁rit:
| ${r_{it}} = {p_{it}}({r_t}^* + {\delta _{it}} - \frac{{\mathop {{p_{it}}}\limits^. }}{{{p_{it}}}})$ | (12) |
其中,Pit表示i企业t时间在资本市场的真实购置价格,用固定资产投资价格指数表示;rt*表示企业支付的真实利率,用企业当年利息支出与负债合计之比表示;δit为资本的折旧率,用企业本年折旧与固定资产原价合计之比表示;
此时可以由式(3)、式(4)和式(5)获取超越对数成本函数的参数估计值。式(5)是由企业最大化问题推导而来,式(4)是式(3)的参数约束条件,该方程组存在跨方程的参数约束,多方程系统估计会比单一方程OLS法的估计更有效。而且,因式(3)、式(4)和式(5)各变量之间不存在内在联系,而各方程的扰动项存在一定的相关性,本节宜采用似不相关回归法(SUR)对可变成本方程的参数值进行估计。由于所选取的四类细分行业之间的组织结构和运营特征又存在一定的差异,为了避免可变成本构成的差异对估计结果的影响,分别对四种类型企业进行了参数估计。参数估计结果见表2。
| 参数 | 估计值 | 标准误 | 参数 | 估计值 | 标准误 | |
|
|
0.694*** | 0.059 |
|
0.008*** | 0.000 | |
|
|
0.306*** | 0.059 |
|
–0.008*** | 0.000 | |
|
|
–0.017*** | 0.002 |
|
–0.029*** | 0.002 | |
|
|
–0.017*** | 0.002 |
|
–0.063*** | 0.012 | |
|
|
0.017*** | 0.002 |
|
0.003*** | 0.001 | |
|
|
–0.473*** | 0.031 |
|
–0.003*** | 0.001 | |
|
|
0.162*** | 0.004 |
|
–3.25e–07*** | 0.000 | |
|
|
–0.016*** | 0.000 |
|
–2.04e–07 | 0.000 | |
|
|
0.016*** | 0.000 |
|
2.04e–07 | 0.000 | |
|
|
–0.245*** | 0.021 | 常数项 | 9.235 7*** | 0.165 | |
|
|
0.081*** | 0.003 | ||||
| 注:***、**和*分别表示1%、5%和10%的显著水平,下同;观察值个数为37 629;adj. R-sq=0.720。 | ||||||
把估计参数值代入式(9)、式(10)和式(11),利用迭代技术可测算出短期成本曲线和长期平均成本曲线切点处的产出水平便是企业的生产能力,企业实际产出与生产能力之比可得出企业产能利用率。用组内企业实际总产出总和与组内企业生产能力总和之比计算的不同类型企业间产能利用率如表3所示①。与此同时,为了从统计性描述的角度展示钢铁企业产能利用率与利润率的相关性,表3的下半部分又罗列了钢铁企业相应年份的产值利润率和销售利润率(计算方法仍采用组内计算方法),以示对比。由表3的测算结果可知:
| 企业性质 | 1998年 | 1999年 | 2000年 | 2001年 | 2002年 | 2003年 | 2004年 | 2005年 | 2006年 | 2007年 | 平均 | |
| 产能利用率 | 全部企业 | 0.697 0 | 0.717 9 | 0.733 4 | 0.751 6 | 0.757 5 | 0.763 4 | 0.772 2 | 0.766 5 | 0.763 8 | 0.758 4 | 0.759 6 |
| 国有企业 | 0.644 0 | 0.632 7 | 0.652 4 | 0.687 5 | 0.692 2 | 0.703 5 | 0.740 9 | 0.729 6 | 0.728 9 | 0.713 6 | 0.691 4 | |
| 集体企业 | 0.704 2 | 0.726 8 | 0.744 0 | 0.737 7 | 0.745 9 | 0.739 4 | 0.765 3 | 0.759 3 | 0.750 7 | 0.747 3 | 0.747 0 | |
| 私营企业 | 0.730 0 | 0.749 7 | 0.754 2 | 0.764 7 | 0.772 4 | 0.773 9 | 0.788 2 | 0.767 0 | 0.762 3 | 0.760 4 | 0.766 0 | |
| 外资企业 | 0.739 5 | 0.746 7 | 0.772 1 | 0.777 1 | 0.781 9 | 0.786 9 | 0.794 7 | 0.792 9 | 0.789 6 | 0.782 4 | 0.784 5 | |
| 产值利润率 | 全部企业 | 0.000 9 | 0.014 3 | 0.016 2 | 0.020 9 | 0.023 8 | 0.025 9 | 0.028 0 | 0.020 1 | 0.019 4 | 0.018 8 | 0.018 8 |
| 国有企业 | 0.006 6 | |||||||||||
| 集体企业 | 0.025 8 | |||||||||||
| 私营企业 | 0.026 9 | |||||||||||
| 外资企业 | 0.029 0 | |||||||||||
| 销售利润率 | 全部企业 | 0.000 9 | 0.014 9 | 0.016 7 | 0.021 4 | 0.024 3 | 0.026 4 | 0.028 7 | 0.020 7 | 0.020 4 | 0.019 2 | 0.019 4 |
| 国有企业 | 0.006 7 | |||||||||||
| 集体企业 | 0.026 5 | |||||||||||
| 私营企业 | 0.027 6 | |||||||||||
| 外资企业 | 0.029 4 |
①由于所选样本企业规模差异较大,在统计总体企业以及不同类型企业的产能利用率时我们没有采取算术平均法。
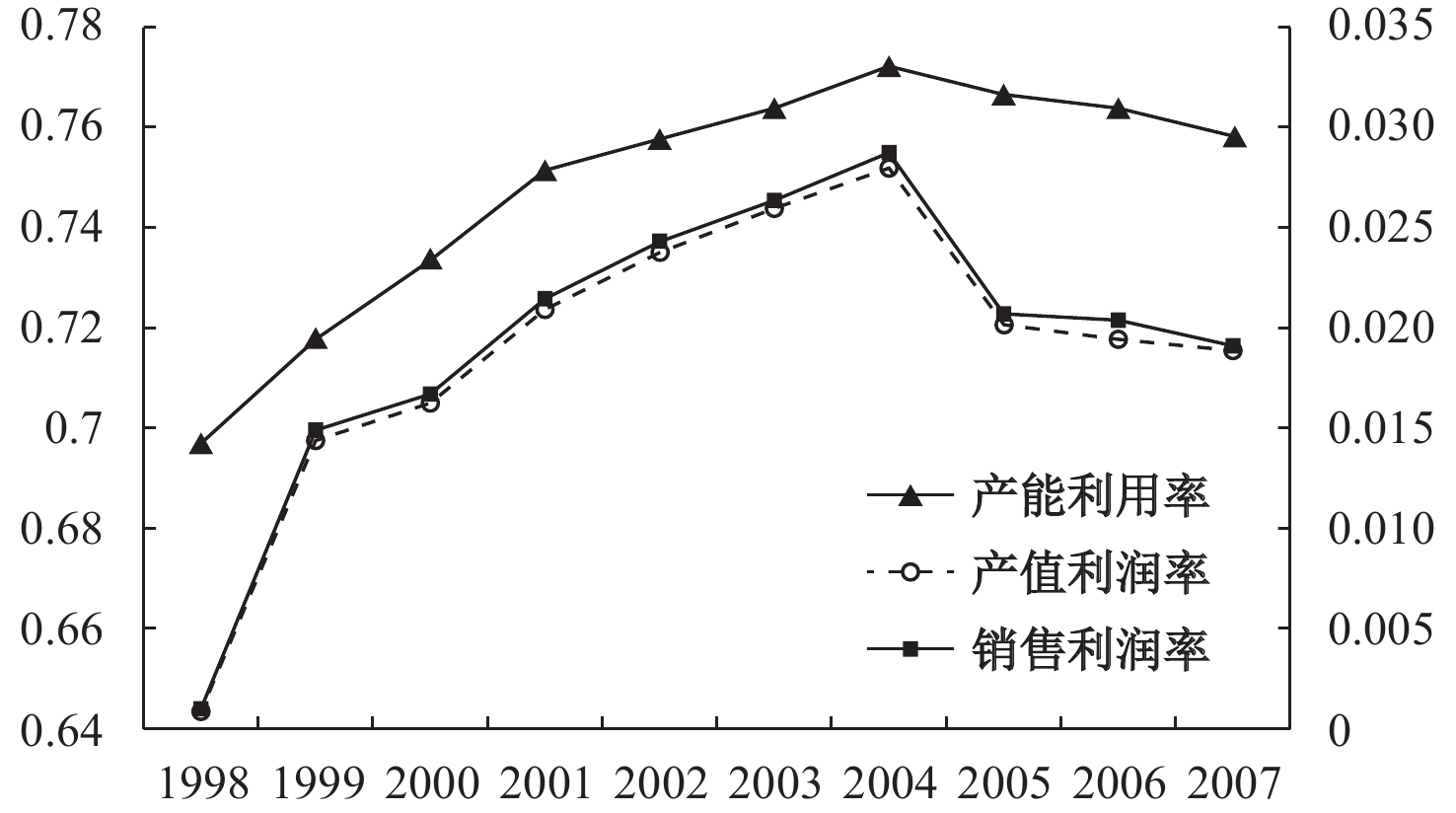
(1)我国钢铁企业的产能利用率与利润率具有相近的变化趋势(见图1)。1998–2004年钢铁企业产能利用率逐步上升,由1998年的0.697上升到2004年的0.772,上升幅度为10.8%,2005年开始出现下降趋势,由2004年的0.772下降到2007年的0.758,下降近2%,整体上呈现一个倒U形趋势。而在相应时间段内,钢铁企业的经营效益也经历了相似的倒U形变化趋势。以产值利润率为例,由1998年的0.001到2004年的0.029,上升了近30倍;2005年之后也开始出现下降趋势,由2004年的0.029下降到2007年的0.019,下降了32.6%,销售利润率在两个时间段内也经历了与产值利润率几乎同步的变化趋势。
|
| 图 1 我国钢铁企业产能利用率和利润率变化趋势 |
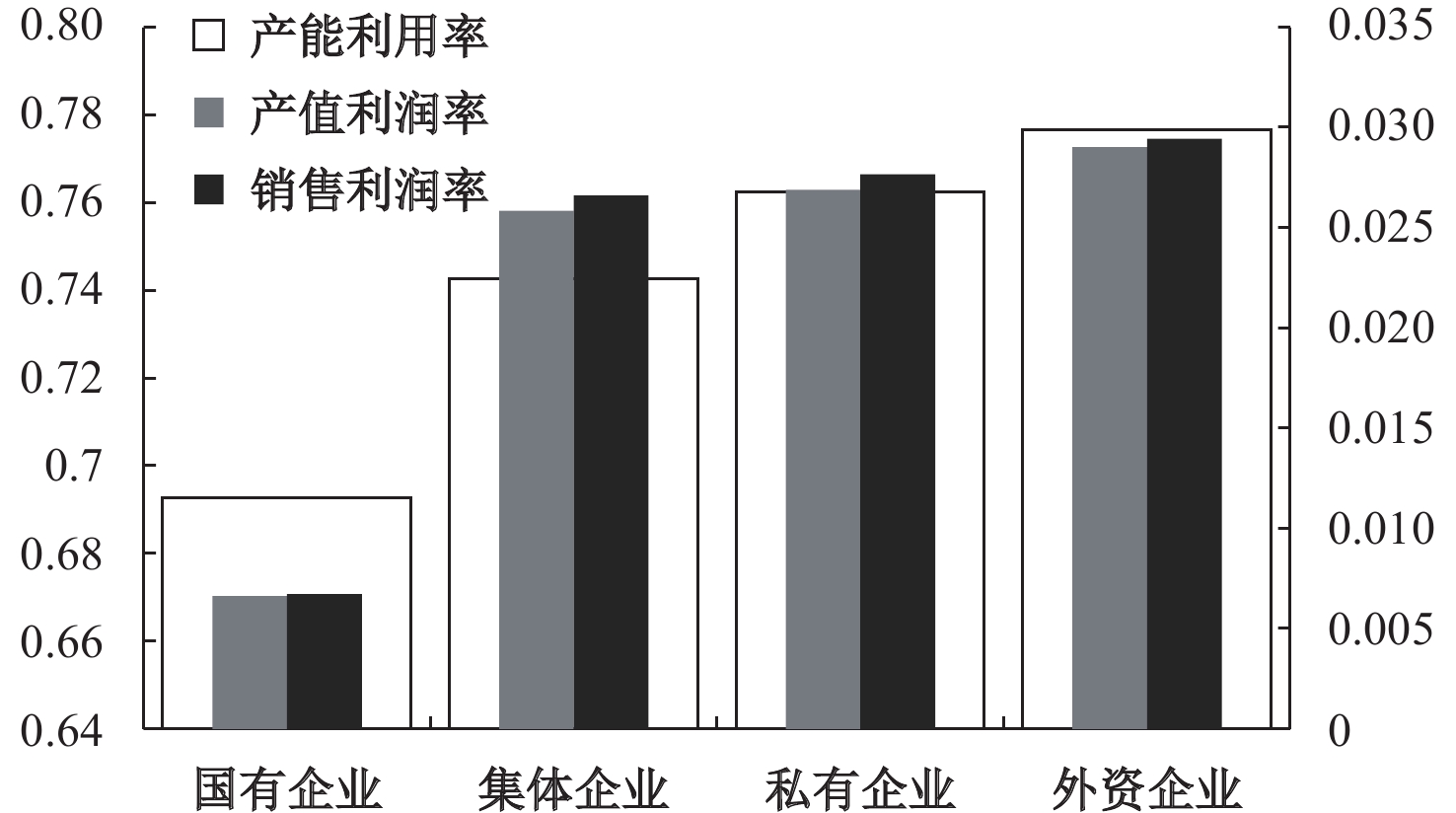
(2)我国钢铁企业的产能利用率存在鲜明的企业性质差异,其经营效益也存在类似的企业性质差异(见图2)。1998–2007年间国有、集体、私营和外资钢铁企业平均产能利用率分别为0.693、0.742、0.762和0.776,后三类企业依次比国有钢铁企业高7.2%、10.1%和12.1%。钢铁企业的经营效益也出现集体、私营和外资逐次大于国有企业的格局,1998–2007年间国有、集体、私营和外资钢铁企业产值利润率分别为0.006、0.026、0.027和0.029,后三类企业依次比国有钢铁企业高2.9倍、3.1倍和3.4倍,相应时间段的企业销售利润率的差异表现出同样的特征。
|
| 图 2 不同所有制钢铁企业产能利用率和利润率对比 |
产能利用率与利润率之间这种相似变化趋势和企业性质差异,说明企业的产能利用状况和所有制属性应是深入分析我国钢铁企业经济效益的重要因素,但简单的数据统计描述尚不能真实地反映企业产能利用状况、性质差异及经营效益的内在关联。下文将在控制其他影响因素的情况下,采用计量分析方法实证分析这些因素之间的量化关系。
四、产能利用率和性质差异对我国钢铁企业利润率的影响 (一) 模型设定和指标构建依据前面的理论描绘和文献综述,设定实证模型如下:
| $P{R_{it}} = {\beta _0} + {\beta _1}C{U_{it}} + {\beta _2}dum\_j{t_{it}} + {\beta _3}dum\_s{y_{it}} + {\beta _4}dum\_w{z_{it}} + {\beta _5}{\Omega _{it}} + {\delta _{it}}$ | (13) |
| $P{R_{it}} = {a_0} + {\alpha _1}dum\_j{t_{it}} + {\alpha _2}dum\_s{y_{it}} + {\alpha _3}dum\_w{z_{it}} + {\alpha _4}{\Omega _{it}} + {\lambda _{it}}$ | (14) |
在模型(13)和模型(14)中,i和t分别表示企业和时间(为了简便,接下来的变量介绍将省去下标i和t)。PR表示利润率,分别用企业利润总额与工业总产值之比(PR_y)和利润总额与销售收入之比(PR_s)表示。dum_jt、dum_sy和dum_wz分别表示所有制类型分别为集体、私营和外资企业虚拟变量,四个虚拟变量的主要参照是国有企业,用来衡量在其他变量得到控制的情况下,集体、私营和外资企业的利润率与国有企业的差距。CU表示产能利用率,这个变量是用来考察产能过剩对我国钢铁企业利润率影响的主要指标。模型(13)与模型(14)的主要差别是,后者剔除了产能利用率变量CU,目的是观察两个模型在产能利用率得到控制的情况下,dum_jt、dum_sy和dum_wz三个虚拟变量系数的变化程度,以此考察产能利用率对国有和非国有钢铁企业利润率差距的贡献程度。贡献度测算公式为(β2-α1)/α1。
Ω表示模型的一系列控制变量,主要包括:(1)资本价格Price_k,由于央行公布的利率具有一定的非市场特征和滞后性,我们用企业利息支出与负债合计之比表示资本价格。资本价格越高则企业单位产出成本越高,进而会降低企业利润率,预期系数为负。(2)劳动价格Price_l,用本年应付工资总额、劳动及待就业保险费和本年应付福利费总额表示,并将其换算成以1998年为基期的定比价值指数。劳动价格体现的是企业所支付的劳动力成本,劳动力成本上升则不利于企业利润率的提升,预期系数为负。(3)技术水平Tech,用新产品产值与工业总产值之比表示。技术水平直接体现着企业的市场竞争力,技术水平越高越有利于企业利润率的提升,预期系数为正。(4)市场化程度Market,用非国有企业总产值与所有企业总产值之比表示,市场化程度越高则表明市场竞争程度越高,且不利于企业利润率的提高,预期系数为负。(5)对外开放度Open,用企业出口交货值与工业总产值之比表示。企业对外开放程度越高,则表明企业的市场开拓能力就越强,是利润率提升的重要影响因素,预期系数为正。(6)企业年龄Age,年龄越大则表明企业技术设备和管理体制更新相对滞后(Braguinsky等,2015),进而影响利润率的提升,预期系数为负。在回归过程中我们同时又加入了企业规模虚拟变量、行业虚拟变量、时间虚拟变量和地区虚拟变量。δit表示残差项。各变量的描述性统计及构建方法见表4。
| 中文名称 | 英文标识 | 观察值 | 平均值 | 标准差 | 最小值 | 最大值 | 测算方法 |
| 产能利用率 | CU | 35 781 | 0.668 2 | 0.058 2 | 0.177 6 | 0.909 1 | 由第三部分测算而得 |
| 产值利润率 | PR_y | 36 217 | 0.127 3 | 0.097 0 | –0.090 8 | 0.397 7 | 利润总额/工业总产值 |
| 销售利润率 | PR_s | 36 212 | 0.132 7 | 0.101 4 | –0.077 5 | 0.386 6 | 利润总额/工业销售产值 |
| 资本价格 | Price_k | 35 949 | 0.021 5 | 0.027 6 | 0.000 0 | 0.149 1 | 利息支出/负债合计 |
| 劳动价格 | Price_l | 36 208 | 1.831 9 | 0.524 9 | 1.000 0 | 3.201 1 | 已换算成以1998年为基期的定比价值指数 |
| 技术水平 | Tech | 30 422 | 0.005 3 | 0.042 1 | 0.000 0 | 0.589 5 | 新产品产值/工业总产值 |
| 市场化程度 | Market | 36 217 | 0.894 8 | 0.066 9 | 0.754 0 | 0.953 2 | 非国有企业总产值/全部企业工业总产值 |
| 开放程度 | Open | 36 217 | 0.009 5 | 0.057 6 | 0.000 0 | 0.613 3 | 出口交货值/工业总产值 |
| 企业年龄(年) | Age | 36 194 | 11.815 7 | 6.953 9 | 3 | 41 | 来自工业企业数据库 |
| 沉没成本 | Sunk | 36 217 | 0.217 | 0.251 | 0.009 1 | 2.112 | 固定资产净值/总产值 |
| 金融支持 | Support_Fin | 36 217 | 0.007 | 0.010 | 0.000 | 0.058 | 利息支持/工业总产值 |
| 政府扶持 | Support_gov | 36 217 | 0.001 | 0.005 | 0.000 | 0.055 | 补贴收入/工业总产值 |
为了能够更好地反映产能利用率和其他控制变量对企业利润率的影响程度,这里对所有数据进行了标准化处理。Driscoll和Kraay(1998)把面板数据存在截面相关、异方差和序列相关的情况称为“Driscoll-Kraay标准误问题”,Daniel Hoechle(2007)指出,若面板数据存在“Driscoll-Kraay标准误问题”,则固定效应和随机效应等传统的估计方法虽然可以得到一致的估计量,但基于标准差的统计推断是非有效的。由此我们采用Daniel Hoechle(2007)的“Driscoll-Kraay标准误”的固定效应模型回归方法来克服面板数据的上述问题,结果见表5。
| Driscoll-Kraay固定效应 | 稳健性估计(2SLS) | Driscoll-Kraay固定效应 | ||||
| 估计(1) | 估计(2) | 估计(3) | 估计(4) | 估计(5) | 估计(6) | |
| PR=PR_y | PR=PR_s | PR=PR_y | PR=PR_s | PR=PR_y | PR=PR_s | |
| CU | 0.134 7*** (0.034 2) |
0.146 9*** (0.037 8) |
0.042 2*** (0.005 7) |
0.048 1*** (0.006 2) |
||
| Price_k | –0.001 8*** (0.000 3) |
–0.002 3*** (0.000 3) |
–0.003 3
(0.017 8) |
–0.004 9
(0.019 5) |
–0.001 7*** (0.000 1) |
–0.002 3*** (0.000 1) |
| Price_l | –0.021 0*** (0.006 0) |
–0.023 6*** (0.005 7) |
0.012 6* (0.007 1) |
0.011 1
(0.007 8) |
0.006 2
(0.005 7) |
0.009 3** (0.004 3) |
| Tech | 0.000 3
(0.001 5) |
0.004 0** (0.002 0) |
0.008 0
(0.006 7) |
0.010 1
(0.007 3) |
0.003 6
(0.003 8) |
0.009 6*** (0.002 0) |
| Market | –0.033 1*** (0.012 6) |
–0.035 4** (0.014 8) |
–0.022 2*** (0.007 9) |
–0.022 6*** (0.008 6) |
–0.004 4
(0.007 3) |
–0.008 2
(0.005 9) |
| Open | –0.000 7*** (0.000 3) |
–0.001 1*** (0.000 4) |
–0.000 0
(0.003 2) |
–0.000 8
(0.003 5) |
–0.001 6*** (0.000 6) |
–0.001 9*** (0.000 7) |
| Age | –0.006 9*** (0.002 0) |
–0.006 6** (0.002 6) |
–0.017 0*** (0.004 4) |
–0.019 1*** (0.004 9) |
–0.006 4** (0.003 1) |
–0.005 8* (0.003 0) |
| dum_jt | 0.017 9** (0.008 2) |
0.017 4* (0.009 5) |
0.086 3*** (0.015 6) |
0.098 6*** (0.017 1) |
0.019 7* (0.010 2) |
0.019 5* (0.010 2) |
| dum_sy | 0.018 9*** (0.006 8) |
0.018 5** (0.007 7) |
0.097 8*** (0.015 4) |
0.108 2*** (0.016 9) |
0.026 4** (0.011 5) |
0.028 2*** (0.010 1) |
| dum_wz | 0.020 3* (0.012 0) |
0.024 6*** (0.012 4) |
0.069 0*** (0.019 0) |
0.076 7*** (0.020 8) |
0.021 2* (0.012 7) |
0.028 2** (0.011 8) |
| Cons | –0.077 0*** (0.010 3) |
–0.095 0*** (0.014 7) |
–0.170 8*** (0.054 9) |
–0.198 8*** (0.060 0) |
0.016 9
(0.049 5) |
–0.013 1
(0.049 2) |
| dum_scale | Yes | Yes | Yes | Yes | Yes | Yes |
| dum_industry | Yes | Yes | Yes | Yes | Yes | Yes |
| dum_year | Yes | Yes | Yes | Yes | Yes | Yes |
| dum_region | Yes | Yes | Yes | Yes | Yes | Yes |
| N | 37 277 | 37 265 | 23 390 | 23 388 | 37 411 | 37 399 |
| adj. R-sq | 0.032 0 | 0.032 0 | 0.024 2 | 0.024 6 | 0.001 1 | 0.001 1 |
| 注:估计(3)和估计(4)报告的Sargan过度识别检验分别为0.521(0.470)和0.283(p=0.595),Cragg Donald弱工具变量检验结果分别为8 684.3(0.000)和8 692.1(0.000)。 | ||||||
估计(1)和估计(2)分别为以产值利润率PR_y和销售利润率PR_s为被解释变量的“Driscoll-Kraay标准误”的固定效应模型回归结果。由估计(1)和估计(2)可知,产能利用率CU的回归系数均在1%水平条件下显著为正,且绝对值要高于其他控制变量。为了排除利润率和产能利用率之间相互影响的内生性问题对估计结果带来的偏误,估计(3)和估计(4)分别以产值利润率PR_y和销售利润率PR_s为被解释变量,进行了两阶段最小二乘(2SLS)回归。在工具变量选取方面,我们采用企业应收账款率(应收账款与工业总产值之比)和滞后一期的产能利用率作为产能利用率的工具变量。应收账款率越高表明企业面临的市场需求将趋于萎缩,所以应收账款很大程度上反映了厂商和客户对未来的市场预期,尚未构成对当期企业利润率的影响,但应收账款率的高企则会对当期产能利用率的提高造成压力。估计(3)和估计(4)报告的Sargan过度识别检验结果分别为0.521 1(0.470 4)和0.283 39(p=0.594 5),Cragg Donald弱工具变量检验结果分别为8 684.34(0.000 0)和8 692.08(0.000 0)①,说明模型所选工具变量是合理的。估计(3)和估计(4)显示,产能利用率CU回归系数依然均在1%水平上显著为正,而且绝对值仍然高于其他控制变量。这说明1998–2007年间我国钢铁企业的产能利用状况在其利润率的变化过程中发挥着主导作用,因此若要解决我国钢铁企业经营效益的低下问题,首先要从治理产能过剩入手。
①Sargan过度识别和Cragg Donald弱工具变量检验的原假设分别为:不存在过度识别和存在弱工具变量。
估计(5)和估计(6)为剔除了产能利用率CU的“Driscoll-Kraay标准误”的固定效应模型回归结果。对比估计(1)与估计(5)中所有制虚拟变量dum_jt、dum_sy和dum_wz回归系数可知,当在模型中加入产能CU时,dum_jt、dum_sy和dum_wz的回归系数分别由0.019 7、0.026 4和0.021 2降低到了0.017 9、0.018 9和0.020 3,依次降低了9.1%、28.4%和4.2%。同样,对比估计(2)与估计(6)中所有制虚拟变量dum_jt、dum_sy和dum_wz回归系数可知,当加入产能CU时,dum_jt、dum_sy和dum_wz的回归系数分别由0.019 5、0.028 2和0.028 2降低到了0.017 4、0.018 5和0.024 6,依次降低了10.8%、34.4%和12.8%。总体来看,产能利用率差异解释了国有与集体企业间利润率差距的10%左右,解释了国有与私营企业利润率差距的30%左右,解释了国有与外资企业间利润率差距的7%左右。上述分析表明,长期以来产能利用率的差异在很大程度上可以解释国有与非国有钢铁企业间的利润率差异,尤其是国有与私营企业之间的利润率差异。因此提高国有钢铁企业经营效益的改革应着重企业所有制改革,通过所有制改革大力缩小国有与非国有钢铁企业之间的产能利用率差距,进而提升国有钢铁企业经营效益。
五、基于企业规模对产能利用率企业性质差异的进一步分析产能利用状况很大程度上决定着我国钢铁企业的经营效益,且钢铁企业的产能利用率又存在较大的企业性质差异,因此解决钢铁企业的经营效益低的问题可以基于所有制改革的角度来治理产能过剩。那么,在产能过剩的治理过程中,除了考虑企业的所有制形式外,是否还要对企业的规模类型进行区分?因为相同所有制类型的企业又存在很大的规模差异,规模差异又或许是产能利用率差异的重要影响因素,若忽略规模差异而仅仅根据企业所有制类型对企业产能过剩进行一刀切式的治理,势必会影响钢铁企业过剩产能的有效化解。对此,我们在分析企业所有制类型的基础上进一步区分企业的规模类型,进而探析我国钢铁企业产能利用率的影响因素。
(一) 模型设定和指标构建设定产能利用率影响因素的实证模型如下:
| $C{U_{it}} = {\gamma _0} + {\gamma _1}dum\_j{t_{it}} + {\gamma _2}dum\_s{y_{it}} + {\gamma _3}dum\_w{z_{it}} + {\gamma _5}{\Omega _{it}} + {\upsilon _{it}}$ | (15) |
| $\begin{split}C{U_{it}} =& {\varphi _0} + {\varphi _1}dum\_j{t_{it}} + {\varphi _2}dum\_s{y_{it}} + {\varphi _3}dum\_w{z_{it}}\\& + {\varphi _4}dum\_middl{e_{it}} + {\varphi _4}dum\_smal{l_{it}} + {\varphi _5}{\Omega _{it}} + {\rho _{it}}\end{split}$ | (16) |
在模型(15)和模型(16)中,dum_middle和dum_small分别表示企业规模为中型和小型企业的虚拟变量,四个虚拟变量主要参照的是大型企业,用来衡量在其他变量得到控制的情况下,中型和小型企业的产能利用率与大型企业的差距。其他的字母标识同模型(13)和模型(14)。相对于模型(15)而言,模型(16)中增加了dum_middle和dum_small虚拟变量,用来考察在控制企业规模类型差异的情况下,产能利用率的所有制差异有何变化。
控制变量Ω主要包括:(1)沉没成本Sunk,用企业固定资产净值年平均余额与工业总产值之比表示。沉没成本越高表明企业前期付出的无法收回的成本较高,在市场需求下降条件下,企业往往无法及时退出过剩产能,最终变现为较低的产能利用率。(2)金融支持Support_Fin,由于我国企业目前的主要融资渠道来自银行系统,我们用企业当年利息支出总额与工业总产值之比来表示企业获得的金融支持力度。企业得到的金融支持越高,则企业的投资冲动就越强,自然也是产能过剩的重要诱因。(3)政府扶持Support_gov,用企业当年获得的政府补贴与工业总产值之比表示。在以GDP为主的政绩考核体制下,地方政府具有较强的动力对当地企业给予大力的扶持以增加当地生产总值和创造更多的就业机会,同时也会加剧产能过剩。(4)对外开放度Open,用企业出口交货值与工业总产值之比表示。企业开放程度越高越有利于提高产能利用程度。此外,在模型中我们还加入了行业、时间和地区虚拟变量,用以控制行业、时间和地区的差异造成的产能利用差异。各变量的描述性统计见上文的表4。
(二) 模型估计由于我们测算的产能利用率处于0到1之间,故我们采用Tobit估计方法对模型(15)和模型(16)进行回归,回归结果如表6所示。表6中的估计(1)和估计(2)分别为模型(15)和模型(16)的估计结果。由估计(1)可知,在没有加入dum_middle和dum_small虚拟变量的情况下,dum_jt、dum_sy和dum_wz虚拟变量的回归系数依次显著为0.095、0.115和0.232。这表明,当不考虑不同所有制企业间存在的规模差异时,集体企业、私营企业和外资企业的产能利用率分别比国有企业高0.095、0.115和0.232。事实上,不同所有制企业间存在很大的规模差异,如国有企业的规模明显大于其他类型企业,若不控制企业规模因素的影响,则会将规模因素带来的产能利用差距融入所有制因素中来。估计(2)在估计(1)的基础上加入了dum_middle和dum_small虚拟变量,结果显示dum_middle和dum_small虚拟变量回归系数显著,分别为–0.040和–0.271,意味着中型企业和小型企业的产能利用率分别比大型企业低–0.040和–0.271。由此可见,我国钢铁企业在产能利用方面发挥了很大的规模优势,钢铁企业的大型化在一定程度上可以提高企业产能利用率。进一步观察可以发现,相对于估计(1)而言,估计(2)中dum_jt、dum_sy和dum_wz的回归系数均得到了显著提高,分别提高0.109、0.134和0.260,提高幅度分别为14.7%、16.5%和12.1%,表明若不考虑规模因素,国有企业与非国有企业的产能利用率差距会进一步扩大15%左右。因此,在治理我国钢铁企业产能过剩问题时,除了考虑企业的所有制形式外,还要区分企业的规模类型,同时坚持企业所有制改革和大型化的发展路径。
| 全部企业 | 大型企业 | 中型企业 | 小型企业 | ||
| 估计(1) | 估计(2) | 估计(3) | 估计(4) | 估计(5) | |
| Sunk | –3.025 9***(1.037) | –3.013 6***(1.037) | –2.100 3***(0.301 8) | –3.010 2***(0.421 94) | –2.798 0***(0.107 1) |
| Support_Fin | –4.895 9***(0.144 9) | –4.974 3***(0.144 8) | –2.366***(0.346 2) | –3.357 9***(0.255 3) | –5.108 8***(0.169 2) |
| Support_gov | –0.000 5(0.011 0) | –0.001 7(0.011 0) | –0.030 6(0.134 4) | –0.021 0(0.025 8) | –0.008 3(0.011 7) |
| Open | 0.010 2**(0.005 2) | 0.008 2(0.005 2) | 0.036 7(0.055 0) | 0.015 3(0.011 0) | 0.008 1(0.005 7) |
| dum_jt | 0.095 0***(0.027 2) | 0.109 2***(0.019 3) | –0.144(0.134 0) | 0.024 6***(0.002 2) | 0.208 1***(0.034 3) |
| dum_sy | 0.115 2***(0.025 9) | 0.134 0***(0.025 9) | 0.050 4(0.149 6) | 0.150 2***(0.039 1) | 0.185 4***(0.032 9) |
| dum_wz | 0.231 5***(0.033 5) | 0.260 3***(0.033 5) | 0.220(0.267 9) | 0.171 7***(0.055 7) | 0.328 5***(0.040 9) |
| dum_middle | –0.039 8***(0.006 5) | ||||
| dum_small | –0.271 0***(0.061 1) | ||||
| dum_industry | Yes | Yes | Yes | Yes | Yes |
| dum_year | Yes | Yes | Yes | Yes | Yes |
| dum_region | Yes | Yes | Yes | Yes | Yes |
| Constant | –0.984 1***(0.094 3) | –0.781 5***(0.109 9) | –6.339 6***(0.564 8) | –1.670 6***(0.208 2) | –1.183 9***(0.101 3) |
| sigma_u | 0.761 0***(0.006 3) | 0.747 9***(0.006 3) | 0.475 6***(0.047 5) | 0.655 1***(0.013 8) | 0.756 0***(0.006 8) |
| sigma_e | 0.589 5***(0.002 7) | 0.590 9***(0.002 7) | 0.371 6***(0.023 4) | 0.487 5***(0.006 0) | 0.589 5***(0.003 0) |
| Rho | 0.625 0 | 0.615 7 | 0.620 9 | 0.643 6 | 0.621 9 |
| N | 37 033 | 37 033 | 257 | 5 566 | 31 210 |
为了进一步寻求化解钢铁企业产能过剩的有效途径,我们进一步把整体样本按企业类型分为大型企业、中型企业和小型企业三个子样本对模型(15)进行回归,估计结果见估计(3)、估计(4)和估计(5)。估计(3)中,dum_jt、dum_sy和dum_wz的回归系数不显著,说明企业的所有制形式并没有带来大型钢铁企业间产能利用率的差异。估计(4)中dum_jt、dum_sy和dum_wz的回归系数显著,依次为0.025、0.150和0.172;估计(5)中dum_jt、dum_sy和dum_wz的回归系数显著,依次为0.208、0.185和0.329。这说明企业的所有制形式给中小型钢铁企业产能利用率带来了显著的差异,其中小型企业最为明显。总体而言,我国钢铁企业产能利用率的企业性质差异主要表现在中小型企业,尤其是小型企业,这一结果为我国钢铁企业的产能过剩理清了更为鲜明的治理路径,治理我国钢铁企业应首先从中小型企业入手,对中小型企业的治理以所有制改革为主,即国有钢铁企业仍应该继续坚持“抓大放小”的改革思路。
六、结论及政策启示本文采用1998–2007年中国工业企业数据库提供的微观数据,首先测度了我国钢铁企业的产能利用率,分析了产能利用率的演变趋势、企业性质差异及其对企业经营效益的影响,并进一步分析了企业性质差异的规模因素。主要结论及政策启示为:(1)我国钢铁企业的产能利用率与利润率具有相近的变化趋势,且具有相似的企业性质差异,即国有企业的产能利用率和利润率明显低于集体、私营和外资等非国有企业。(2)产能利用率是影响我国钢铁企业利润率的诸多因素中的主导因素,它的差异在很大程度上可以解释国有与非国有钢铁企业间的利润率差异。具体表现为,国有与集体企业利润率差异的10%左右、国有与私营企业利润率差异的30%左右以及国有与外资企业利润率差异的7%左右都可以由产能利用率差异来解释。因此,未来国有钢铁企业的改革更应该注重产能过剩的抑制和治理,大力缩小国有钢铁企业与非国有钢铁企业之间的产能利用率差距,才是提升国有钢铁企业经营效益的关键。(3)通过进一步区分企业的规模类型发现,我国钢铁企业产能利用率的企业性质差异主要表现在中小型企业,尤其是小型企业。因国有企业的规模较大,若不考虑规模因素,国有企业与非国有企业的产能利用率差距会进一步扩大15%左右。因此,治理我国钢铁企业产能过剩问题除了考虑企业的所有制形式外,还要区分企业的规模类型,同时坚持企业所有制改革和大型化的发展路径。我们应首先从中小型企业入手,对中小型企业的治理以所有制改革为主,即国有钢铁企业仍应继续坚持“抓大放小”的改革思路。
| [1] | 刘小玄, 李双杰. 制造业企业相对效率的度量和比较及其外生决定因素(2000—2004)[J]. 经济学(季刊), 2008, (3). |
| [2] | 路江涌. 外商直接投资对内资企业效率的影响和渠道[J]. 经济研究, 2008, (6). |
| [3] | 聂辉华, 江艇, 杨汝岱. 中国工业企业数据库的使用现状和潜在问题[J]. 世界经济, 2012, (5). |
| [4] | 沈利生. 我国潜在经济增长率变动趋势估计[J]. 数量经济技术经济研究, 1999, (12). |
| [5] | 徐朝阳, 周念利. 市场结构内生变迁与产能过剩治理[J]. 经济研究, 2015, (2). |
| [6] | Berndt E R, Morrison C J. Capacity utilization measures: underlying economic theory and an alternative approach[J]. American Economic Review, 1981, 71(2): 48-52. |
| [7] | Berndt E R, Hesse D M. Measuring and assessing capacity utilization in the manufacturing sectors of nine oecd countries[J]. European Economic Review, 1986, 30(5): 961-989. |
| [8] | Braguinsky S, Ohyama A, Okazaki T, et al. Acquisitions, productivity, and profitability: Evidence from the Japanese cotton spinning industry[J]. Electronic Journal, 2015, 105(7): 1-63. |
| [9] | Borger B D, Kerstens K. The malmquist productivity index and plant capacity utilization[J]. Scandinavian Journal of Economics, 2000, 102(2): 303-310. |
| [10] | Bye T, Bruvoll A, Larsson J. Capacity utilization in a generalized malmquist index including environmental factors: A decomposition analysis[J]. Land Economics, 2009, 85(3): 529-538. |
| [11] | Cai H B, Liu Q. Competition and corporate tax avoidance: Evidence from Chinese industrial firms[J]. Economic Journal, 2009, 119(537): 764-795. |
| [12] | Cassels J M. Excess capacity and monopolistic competition[J]. The Quarterly Journal of Economics, 1937, 51(3): 426-443. |
| [13] | Chamberlin E H. The theory of monopolistic competition[M]. Cambridge: Harvard University Press, 1947. |
| [14] | Coelli T, Grifell-Tatjé E, Perelman S. Capacity utilization and profitability: A decomposition of short-run profit efficiency[J]. International Journal of Production Economics, 2002, 79(3): 261-278. |
| [15] | Driscoll J C, Kraay A C. Consistent covariance matrix estimation with spatially dependent data[J]. Review of Economics and Statistics, 1998, 80(4): 549-560. |
| [16] | Fare R, Grosskopf S, Kokkelenberg E C. Measuring plant capacity, utilization and technical change: A nonparametric approach[J]. International Economic Review, 1989, 30(3): 655-666. |
| [17] | Fare R, Grosskopf S, Kirkley J. Multi-output capacity measures and their relevance for productivity[J]. Bulletin of Economic Research, 2000, 52(2): 101-112. |
| [18] | Garofalo G A, Malhotra D M. Regional measures of capacity utilization in the 1980s[J]. Review of Economics and Statistics, 1997, 79(3): 415-421. |
| [19] | Gokcekus O. Trade liberalization and capacity utilization: New evidence from the Turkish rubber industry[J]. Empirical Economics, 1998, 23(4): 561-571. |
| [20] | Hickman B G. On a new method of capacity estimation[J]. Journal of the American Statistical Association, 1964, 59(306): 529-549. |
| [21] | Hoechle D. Robust standard errors for panel regressions with cross-sectional dependence[J]. The Stata Journal, 2007, 7(3): 281-312. |
| [22] | Jorgenson D W. Capital theory and investment behavior[J]. The American Economic Review, 1963, 53(2): 247-259. |
| [23] | Karagiannis R. A system-of-equations two-stage DEA approach for explaining capacity utilization and technical efficiency[J]. Annals of Operations Research, 2015, 227(1): 25. |
| [24] | Kirkley J, Paul C J M, Squires D. Capacity and capacity utilization in common-pool resource industries[J]. Environmental and Resource Economics, 2002, 22(1): 71-97. |
| [25] | Kirkley J, Paul C, Squires D. Capacity and capacity utilization in fishing industries[R]. Working Paper, 1999. |
| [26] | Klein L R. Some theoretical issues in the measurement of capacity[J]. Econometrica, 1960, 28(2): 272-286. |
| [27] | Klein L R, Long V, Greenspan A, et al. Capacity utilization: Concept, measurement, and recent estimates[J]. Brookings Papers on Economic Activity, 1973, 4(3): 743-763. |
| [28] | Lazkano I. Cost structure and capacity utilisation in multi-product industries: an application to the basque trawl industry[J]. Environmental and Resource Economics, 2008, 41(2): 189-207. |
| [29] | Lindebo E, Hoff A, Vestergaard N. Revenue-based capacity utilisation measures and decomposition: The case of Danish North Sea trawlers[J]. European Journal of Operational Research, 2007, 180(1): 215-227. |
| [30] | Morrison C J. On the economic interpretation and measurement of optimal capacity utilization with anticipatory expectations[J]. The Review of Economic Studies, 1985, 52(2): 295-309. |
| [31] | Nelson R A. On the measurement of capacity utilization[J]. Journal of Industrial Economics, 1989, 37(3): 273-286. |
| [32] | Paine C L. Rationalisation and the theory of excess capacity[J]. Economica, 1936, 3(9): 46-60. |
| [33] | Pascoe S, Tingley D. Economic capacity estimation in fisheries: A non-parametric ray approach[J]. Resource and Energy Economics, 2006, 28(2): 124-138. |
| [34] | Pascoe S, Tingley D. Capacity and technical efficiency estimation in fisheries: Parametric and non-parametric techniques[A]. Weintraub A, Romero C, Bjørndal T, et al, eds. Handbook of Operations Research in Natural Resources[C]. Boston, MA: Springer, 2007: 273-294. |
| [35] | Phillips A. An appraisal of measures of capacity[J]. The American Economic Review, 1963, 53(2): 275-292. |
| [36] | Smithies A. Economic fluctuations and growth[J]. Econometrica, 1957, 25(1): 1-52. |
 2017, Vol. 19
2017, Vol. 19


