
2021第43卷第6期
2.华东理工大学 商学院,上海 200237;
3.上海对外经贸大学 工商管理学院,上海 201620
2.School of Business, East China University of Science and Technology, Shanghai 200237, China;
3.School of Management, Shanghai University of International Business and Economics, Shanghai 201620, China
金融是现代经济的核心组成部分,资本市场又是金融主要的资源配置场所,它能有效地通过价格发现功能来整合市场资源,并优化资源配置。成熟的资本市场可以对投融资双方进行合理匹配,实现对有限资源的合理配置,从而促进社会经济的平稳发展。我国资本市场自建立以来发展态势迅猛,这与我国经济增长迅速、经济发展潜力巨大有着密切的关系。2018年6月,我国A股按照2.5%的比例被纳入MSCI指数,至2019年底这一比重逐步提升到20%,这标志着A股市场又向国际化迈进了一步。但是作为一个新兴转轨的资本市场,我国资本市场的各种制度、法律法规和相关配套设施仍然不够完善,股票市场也面临着诸多问题与挑战。我国资本市场的稳定性和抗风险性与发达国家资本市场相比均有一定差距。在过去近30年里,我国股市先后经历了8次暴跌,导致投资者损失惨重。2015年3月开始,上证指数在三个月的时间内从3000点左右暴涨到5178点,而后又在两个月多的时间内暴跌回3000点附近。股票市场的暴涨暴跌现象一方面使投资者的相关利益受到了严重损害,另一方面又对市场的资源配置效率产生了极大的影响,这严重损害了金融市场的稳定,损害了实体经济的平稳发展,干扰了经济社会的正常运行。
股价暴跌往往会引发灾难性后果,因此,对股票市场崩盘风险的形成原因进行探究并且施之以策,能够有效地防范金融风险的产生,促进资本市场平稳有序地发展。股价崩盘指的是股票收益率短时间内出现较大的异常负值,通常有两种表现形式,一种是由于负面消息的冲击,股票价格在短时间内急速下跌,另一种是股票存在泡沫,当泡沫积累到一定程度时,由于自身原因或者外界信息刺激,进而导致股票价格快速大幅度下跌(Jin和Myers,2006)。对于股价崩盘风险的研究,刚开始是基于完全信息的理性预期理论,随着行为金融学的产生和发展,非理性因素越来越多地被考虑到,因而股价崩盘风险的理论研究也更多地基于不完全信息理论和行为金融理论来展开。
证券分析师是解决证券市场信息不对称问题的重要角色。相较于一般投资者,分析师们拥有更加准确的信息,更加专业的分析能力,对于提高市场信息透明度,增进市场效率,促进资源分配和保护投资者利益等方面都有着至关重要的作用。然而在现实中,由于各种原因,分析师也会发布一些违背市场预期,并不能与其专业水平相匹配的分析预测和报告,这取决于分析师自身的主观情感和客观条件制约,比如,分析师有可能受到市场的影响,主动迎合市场情绪,并且根据某些因素甚至是利益来改变自己的判断。更为重要的是,正是由于分析师根据市场其他参与者行为来改变自己的预测,进而产生分析师的羊群行为,使得这种偏差的产生具有趋同性。基于信息不对称理论,分析师在市场中充当的角色应该是弥补信息不对称,但分析师的这种趋同行为产生的偏差加剧了信息不对称的危害,严重阻碍了信息的传递和资源分配效率,随着股价过度偏离真实价值,产生泡沫,坏消息的逐步积累终将导致股价崩盘现象的出现。
我国资本市场情况特殊,根据上交所2018年统计年鉴数据显示,截至2017年底,沪市共有1.95亿投资者,其中个人投资者贡献了相当于机构投资者5倍的交易额,近八成交易量却收获总盈利规模的一成不到。相关调查显示,散户投资者依据“股评推荐”“亲友引荐”以及“小道消息”做出投资判断的比重高达51.5%,频繁的交易使得2017年散户交易额占到交易总额的82.01%。可以看出,投资者异质信念较高,一旦有风吹草动,市场立刻不得安宁。
基于以上分析,本文将探究分析师的行为对于股价崩盘的影响,通过研究分析师对A股上市公司的分析预测,以信息不对称理论和行为金融学理论为基石,通过计量模型进行实证检验,最终提出关于防范股价崩盘风险,维护资本市场稳定的建议。首先,本文将从股票市场的信息中介——分析师研究报告入手,探讨分析师预测偏差对个股股价的影响,弄清分析师预测偏差与个股股价崩盘的联动机制。其次,在以上研究基础上,分析投资者异质信念在分析师预测偏差对股价崩盘风险影响过程中的作用,考察分析师预测偏差是否能通过影响投资者异质信念,进而影响股价崩盘风险。
本文的主要贡献有以下两点。首先,本文构建了一个完整的影响路径和传导机制。将分析师、投资者与上市公司股价同时纳入研究框架,该路径以分析师预测偏差为起点,投资者异质信念为中介,个股股价崩盘风险为终点。尽管已经有很多学者(许年行等,2012;肖土盛等,2017)研究了分析师偏差与股价崩盘风险的关系,但并未对详细机制进行进一步分析,他们往往将投资者行为置于研究框架之外。其次,本研究结论具有较为重要的实践价值,本文的研究涵盖了多个市场参与者,因此对于券商行业从业者、投资者、监管部门和政府有效地认识和防范股价崩盘风险具有较好的参考意义。
二、文献综述与假设提出(一)分析师预测偏差与股价崩盘风险
分析师是上市公司与投资者之间信息传递的媒介之一,分析师报告能有效缓解上市公司与投资者之间的信息不对称。分析师不仅限于应用公开的市场信息,还从公司管理层处挖掘私有信息,这样不仅使分析师预测准确度进一步提高,而且还能促进公司治理的完善(Healy和Palepu,2001)。然而,分析师是否能公正客观地做出业绩预测,仍受到广泛的质疑。Dowen(1989)实证结果表明,在多数年份分析师预测偏差显著为正,表明证券分析师会对未来的收益持有乐观的情绪,并且这种情绪具有连续性。Malmendier和Shanthikumar(2007)研究证明,为了获得更高的佣金,分析师更倾向选择性发布盈利预测,并且有意引起个人投资者的追随。周冬华和赵玉洁(2016)发现分析师预测受到利益驱动和认知偏差的影响,这二者相互独立作用于分析师本身,进而导致分析师预测发生偏差。孙淑伟等(2019)证实公司内部人与分析师之间存在“共谋”行为,以帮助彼此增加收益。因此,分析师预测的偏差是普遍存在的,甚至可能是有意为之以获取私利。
股价崩盘的主要原因是公司的代理问题,上市公司管理层掌握了公司的私有信息,可能会由于各种原因,管理层倾向于隐藏坏消息、披露好消息,坏消息的累积可能会在某一时间突然释放,造成股价短时间的剧烈下跌(Jin和Myers,2006)。在有效市场中,所有分析师都能对公开信息与非公开信息进行收集和分析,与股价相关的信息均已反映在价格中,分析师对于公司业绩的预测应该趋于一致,预测偏差较小,较低的预测误差可以缓解股价崩盘风险(肖土盛等,2017)。而分析师偏差越大,一方面,表明有部分分析师利用私有信息或者为了自身利益,而发布了与其他分析师不同的预测,市场中的信息不对称程度较高,因而投资者对于公司的实际经营情况更难了解,公司管理层所隐藏的坏消息更难披露出来,这将导致未来股价崩盘风险越高。另一方面,表明分析师对于公司未来的经营状况有更多的不确定性,这种不确定性可能会通过分析师传递给投资者,进而给股价带来更大的不确定性,这也将导致未来股价崩盘风险增加。
(二)分析师预测偏差与投资者异质信念
投资者异质信念是指不同投资者对于相同持有期下同一股票的期望收益率和期望收益率方差的估计不同。一方面,投资者异质信念的产生有投资者自身的原因。比如,Hirshleifer和Teoh(2003)研究探讨了投资者有限注意的影响,投资者会由于自身关注点的不同而对信息进行选择性吸收。Peng和Xiong(2006)对于投资者有限注意的进一步研究表明,这种特征会导致投资者归类学习行为,最终导致忽略公司特质信息,当面对决策或者选择时,更容易产生过度自信,在信念上引发更严重的分歧。而投资者自身的偏好、禀赋等的不同,造成了对信息有着不同的解读,这就是投资者之间的先验异质性(Harris和Raviv,1993)。钟晨等(2017)认为,投资者在面对公开信息时的心理过程是不同的,不同人的偏好、效用、情感阈值引发了投资者的认知偏差,从而造成投资者间的异质信念。
另一方面,投资者异质信念也可能是受到外界信息的影响。作为市场重要的信息中介,分析师的分析报告在市场上起到至关重要的沟通作用,因此来自分析师的信息也会影响到投资者。甘露润和张淑慧(2013)的研究发现,分析师关注水平的提高增加了分析师们的预测分歧,并导致投资者异质信念的增加。Brown等(2014)进一步研究得出,分析师行为可以影响市场投资者行为,不仅仅是散户投资者,还包括职业基金经理对于分析师行为都有敏感的反应。分析师受到自身私有信息获取的局限和相关利益冲突的影响,可能对上市公司的经营状况没有做出准确客观的判断,从而产生了预测的偏差,而这种有偏的信息传递给投资者后,实际上又加大了投资者与公司管理层之间的信息不对称。此外,由于投资者自身存在认知的差异和对市场信息的有限关注,彼此间对于有偏差的分析师预测报告会产生不同的解读,这又进一步加大了投资者间的异质信念。从这个理论角度分析,可以合理推测,分析师预测偏差越大,投资者间的意见分歧就越严重。基于以上分析,本文提出以下假设:
假设1:分析师预测偏差与投资者异质信念呈正相关关系,即分析师预测偏差越大会导致投资者之间的异质信念越大。
(三)投资者异质信念与股价崩盘风险
投资者之间异质信念的存在会导致在卖空受限的市场上,证券价格被高估。基于金融市场理论,Hong和Stein(2003)认为,由于卖空限制,对市场看空的投资者无法将私有信息融入股价中,造成股价被高估,而一旦市场出现低迷,这些私有信息将集中释放,引起股价震荡下跌。Miller(1977)认为,不确定性和风险意味着意见分歧,投资者之间的意见分歧可能会导致股价被信息不充分的投资者哄抬到过高的水平。在一个有较多卖空限制的市场,负面信息不能很好地反映在股票价格中,投资者异质信念越大,股价越可能被哄抬至较高水平(张维和张永杰,2006),未来个股发生暴跌的可能性越大(陈国进和张贻军,2008),且股票预期收益越低(尹慧和赵国庆,2013)。除了股价被高估外,异质信念还会增加股价波动性。胡昌生和池阳春(2013)的研究显示,资产价格的异常波动性并不是不同类别投资者情绪波动的简单加总,起关键作用的是投资者之间的异质信念。
综上所述,在卖空受限的市场上,股票价格形成实际上是非理性的,因为投资者倾向于高估股价,而负面信息由于卖空受限不能及时反映在股价中,投资者异质信念越大,股价越可能被哄抬至高位。股价高估所形成的价格泡沫,可能在负面信息集中披露时突然破裂,再加上因为异质信念而提高的波动性,都会成为造成股价崩盘的重要原因。基于以上分析,本文提出以下假设:
假设2:投资者异质信念与股价崩盘风险呈正相关关系,投资者异质信念增大会加剧股价崩盘风险。
(四)投资者异质信念的中介作用
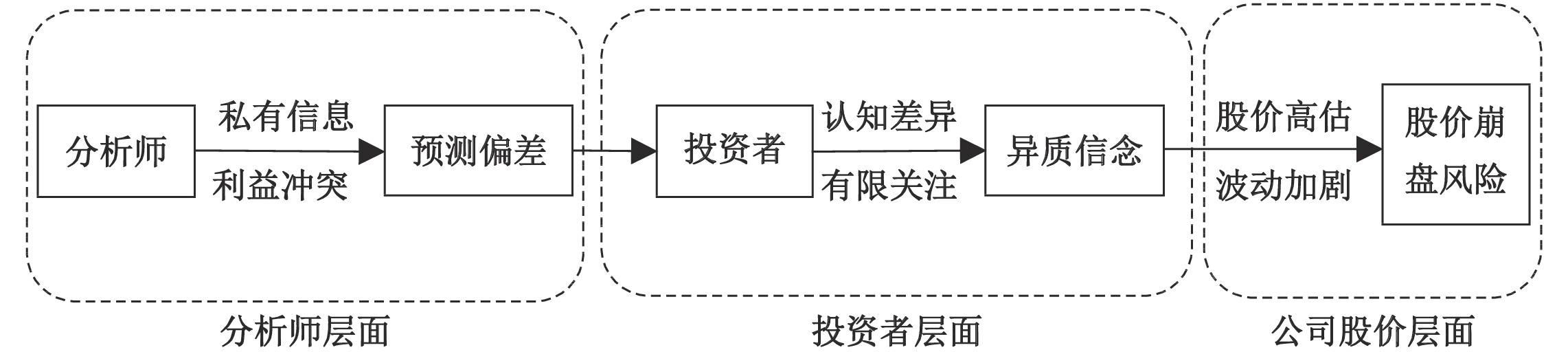
随着行为金融学的兴起,股价崩盘风险研究文献所探讨的范围也逐步扩大,对导致股价崩盘原因的研究越来越多地从公司治理、信息披露、媒体覆盖、分析师关注等角度转移到了投资者自身行为方面。事实上,投资者也是市场上的重要参与者,投资者的异质信念是投资者重要的行为指标,并且如前文所述,已有大量研究证实异质信念也是造成股价崩盘的重要原因,因此,将分析师、投资者与上市公司股价崩盘风险作为一个整体来分析必不可少。前述分析表明,在信息不对称和投资者自身差异的作用下,分析师预测偏差的增大会导致投资者异质信念的增加;而在卖空受限情况下,投资者异质信念越大,股价越可能被哄抬至较高水平,从而加剧股价崩盘风险。因而,分析师预测偏差对股价崩盘风险的影响,很可能是通过投资者异质信念的中介作用来实现的。“分析师预测偏差—投资者异质信念—股价崩盘风险”传导机制如图1所示。
根据文献回顾和理论分析:首先,分析师通过获取上市公司公开信息以及个人的私有信息进行分析预测,发布预测报告,但是由于个人私有信息的局限或是利益冲突,分析师的预测往往是存在偏差的。其后,这样有偏差的预测信息传递给投资者,进一步增大了外部投资者与公司管理层间的信息不对称,势必会影响投资者对公司价值的判断和对公司前景的预期;同时,因为投资者之间存在着个体间禀赋、偏好的差异,对于分析师的预测信息可能有不同的解读,从而在不同投资者间产生异质信念。最后,投资者间的异质信念又会反映在股价上,由于卖空受限,股价对负面信息的反映不足,容易被乐观投资者哄抬至高位,形成价格泡沫。在这样的情况下,一旦负面信息得到披露,股价可能会崩盘,因而崩盘风险加剧。从以上的分析中可以推断,投资者异质信念实际上在分析师预测偏差与个股股价崩盘风险之间起到了中介的作用。因此,本文提出以下假设:
假设3:分析师预测偏差通过影响投资者异质信念,从而引起股价崩盘风险的改变;投资者异质信念在分析师预测偏差对股价崩盘风险的影响中起到中介作用。
|
| 图 1 分析师预测偏差、投资者异质信念与股价崩盘风险传导机制 |
(一)数据来源及选取
本文研究所需的股票和会计数据来自万得数据库(WIND),分析师预测数据来自国泰安数据库(CSMAR)。为保证一定的数据时间范围和数据准确性,相关数据选取范围为2008年第一季度至2019年第四季度。
本文对数据进行了以下的样本预处理:(1)去除ST、*ST等经过特别处理的样本。(2)剔除金融业的样本数据。(3)剔除变量严重缺失的样本数据。(4)为了确保股价崩盘风险指标的可靠性,删除年度市场交易日小于30周的上市公司样本数据。(5)为了确保分析师的差异性,剔除分析师关注人数少于5人的样本公司数据。(6)若一个分析师对同一家公司发布过多篇预测分析,则以当期最后一篇报告为准选取数据。最终筛选得到公司季度样本20028个,按照证监会行业分类标准进行行业分类,并对样本数据进行1%和99%的缩尾处理。
(二)变量定义
1. 分析师预测偏差
本文借鉴游家兴等(2013)关于分析师预测偏差的计算方法,采取分析师对公司股票预测的EPS与当期季报公布的实际EPS计算预测偏差,对于第t期每个被分析师j预测的公司i,分析师预测偏差变量指标Bias定义为:
| $Bia{s_{i,j,t}} = \left( {FEP{S_{i,j,t}} - AEP{S_{i,t}}} \right)/\left| {AEP{S_{i,t}}} \right|$ | (1) |
其中,
2. 股价崩盘风险
参考Kim等(2011)以及许年行等(2012),本文采用以下两种方法计算得到的指标来描述上市公司股价崩盘风险。首先,用股票周收益率和市场收益率模型做回归,得到公司的特有收益率,即残差
| ${R_{i,t}} = {{\rm{\alpha }}_i} + {\beta _1}{R_{m,t - 2}} ++ {\beta _2}{R_{m,t - 1}} + {\beta _3}{R_{m,t}} + {\beta _4}{R_{m,t + 1}} + {\beta _5}{R_{m,t + 2}} + {\varepsilon _{i,t}}$ | (2) |
其中,
| $NCSKE{W_{i,t}} = - \left[ {n{{\left( {n - 1} \right)}^{3/2}}\mathop \sum \nolimits W_{i,t}^3} \right]/\left[ {\left( {n - 1} \right)\left( {n - 2} \right){{\left( {\mathop \sum \nolimits W_{i,t}^2} \right)}^{3/2}}} \right]{\rm{}}$ | (3) |
其中,n代表股票i在t季度上市交易的周数。公式(3)计算了公司个股处理后的特质收益率的偏度,为了便于比较和分析,将偏度值进行了负处理,故当统计指标负收益偏态系数NCSKEW数值越大时,偏态系数的偏度越大,即可代表个股股价暴跌风险越大。第二种是收益率上下波动比率(DUVOL)方法,计算指标如下:
| $ {DUVOL}_{i,t}=\mathrm{log}\frac{({n}_{u}-1)\sum \nolimits_{Down}{W}_{i,t}^{2}}{({n}_{d}-1)\sum \nolimits_{Up}{W}_{i,t}^{2}} $ | (4) |
该方法首先要计算第t季度i公司的平均周特有收益率
3. 投资者异质信念
投资者异质信念描述的是投资者情绪上的一种偏差,无法直接观测发现。由于异质信念与信息不对称等市场概念存在内生性问题,寻找独立指标衡量也有一定的难度,表1表示几种指标的优缺点对比分析(金永红和罗丹,2017)。
| 指标 | 优点 | 缺点 |
| 分析师预测差异指标 | 代表机构预测分歧,易于理解 | 并不能确定存在因果影响 |
| 换手率指标 | 数据易于获取,具有代表性 | 存在股票自身流动性的影响 |
| 收益率波动率指标 | 数据容易获取 | 缺少相关理论 |
参考以往文献以及权衡相关指标优缺点,我国A股市场换手率是衡量异质信念的最合适指标,个股换手率既包含了市场本身所需流动性信息,也包括了个股的特有信息。在变量选取上,本文采取朱宏泉等(2016)文中提到的方法对换手率进行处理,以此来衡量投资者异质信念。首先,根据Fama-French三因子模型拟合个股日收益率:
| $ \left({R}_{i,j}-{R}_{f,j}\right)={\alpha }_{i}+{\beta }_{i}\left({R}_{M,j}-{R}_{f,j}\right)+{s}_{i}{SMB}_{j}+{h}_{i}{HML}_{j}+{\varepsilon }_{i,j} $ | (5) |
其中,
| $ {TO}_{i,j}={\kappa }_{i}+{\gamma }_{1}^+{\left|{R}_{i,j}^{M}\right|}^++{\gamma }_{1}^-{\left|{R}_{i,j}^{M}\right|}^-+{\gamma }_{2}^+{\left|{R}_{i,j}^{F}\right|}^++{\gamma }_{2}^-{\left|{R}_{i,j}^{F}\right|}^-+{\mu }_{i,j} $ | (6) |
其中,
| $ {\widehat{TO}}_{i,j}={\widehat{\kappa }}_{i}+{\widehat{\gamma }}_{1}^+{\left|{R}_{i,j}^{M}\right|}^++{\widehat{\gamma }}_{1}^-{\left|{R}_{i,j}^{M}\right|}^-+{\widehat{\gamma }}_{2}^+{\left|{R}_{i,j}^{F}\right|}^++{\widehat{\gamma }}_{2}^-{\left|{R}_{i,j}^{F}\right|}^- $ | (7) |
| $ {HB}_{i,j}={TO}_{i,j}-{\widehat{TO}}_{i,j} $ | (8) |
实证中用的季度异质信念为每季度三个月份异质信念的平均值。
4. 其他控制变量
根据已有文献加入可以影响股价崩盘风险的重要控制变量,其中包括公司规模(Size)、财务杠杆比率(Lev)、账面市值比(BM)、资产收益率(Roa)、股票回报率(Return)、收益率波动性(Vol)、投资者情绪综合指数(CICSI)。具体变量定义如表2所示。
| 变量性质 | 变量名称 | 变量代码 | 变量指标 |
| 因变量 | 股价崩盘风险 | NCSKEW | 负收益偏态系数 |
| DUVOL | 收益上下波动比率 | ||
| 自变量 | 分析师预测偏差 | Bias | 分析师预测值与实际值偏差 |
| 中介变量 | 投资者异质信念 | HB | 用处理后的换手率表示 |
| 控制变量 | 收益率波动性 | Vol | 周收益率标准差平均值 |
| 股票回报率 | Return | 周收益率平均值 | |
| 公司规模 | Size | 总资产自然对数 | |
| 财务杠杆 | Lev | 总负债/总资产 | |
| 经营业绩 | Roa | 净利润/总资产 | |
| 公司成长能力 | BM | 账面价值/总市值 | |
| 投资者情绪 | CICSI | 投资者情绪综合指数 | |
| 季度虚拟变量 | Quarter | 数据选取季度 | |
| 行业虚拟变量 | Industry | 公司所属行业 |
(三)研究模型
根据前文的分析,分析师预测偏差可以通过投资者异质信念对股价崩盘风险产生影响,并且股票价格同时受到以上控制变量的影响,分别根据三个假设建立相关的检验模型。
1. 分析师预测偏差与投资者异质信念
首先建立分析师预测偏差与投资者异质信念关系的模型如下:
| $ {HB}_{i,t}={a}_{0}+{a}_{1}{Bias}_{i,t-1}+{\gamma }_{1}\times {ControlVariables}_{i,t-1}+{\varepsilon }_{i,t} $ | (9) |
式中,用
2. 投资者异质信念与股价崩盘风险
针对假设2,本文构建如下模型:
| $ {CrashRisk}_{i, t}={b}_{0}+{b}_{1}{HB}_{i,t}+{\gamma }_{2}\times {ControlVariables}_{i,t-1}+{\varepsilon }_{i,t} $ | (10) |
式中,用
3. 投资者异质信念中介效应检验
假设3研究投资者异质信念的中介作用。本文借鉴温忠麟等(2014)所提到的中介效应检验方法,以模型(11)、模型(9)和模型(12)组成一个完整的检验中介效应的模型:
| $ {CrashRisk}_{i, t}={c}_{0}+{c}_{1}{Bias}_{i,t-1}+{\gamma }_{3}\times {Control Variables}_{i,t-1}+{\varepsilon }_{i,t} $ | (11) |
| $ {HB}_{i, t}={a}_{0}+{a}_{1}{Bias}_{i,t-1}+{\gamma }_{1}\times {Control Variables}_{i,t-1}+{\varepsilon }_{i,t} $ | (9) |
| $ {CrashRisk}_{i, t}={{c}^{'}}_{0}+{{c}^{'}}_{1}{Bias}_{i,t-1}+{b}_{1}^{'}{HB}_{i, t}+{\gamma }_{4}{Control Variables}_{i,t-1}+{\varepsilon }_{i,t} $ | (12) |
投资者异质信念可以很快地反映到股价之中,受前期分析师预测偏差影响,又作用于当期股票价格,故采用当期数据,控制变量滞后一期处理。
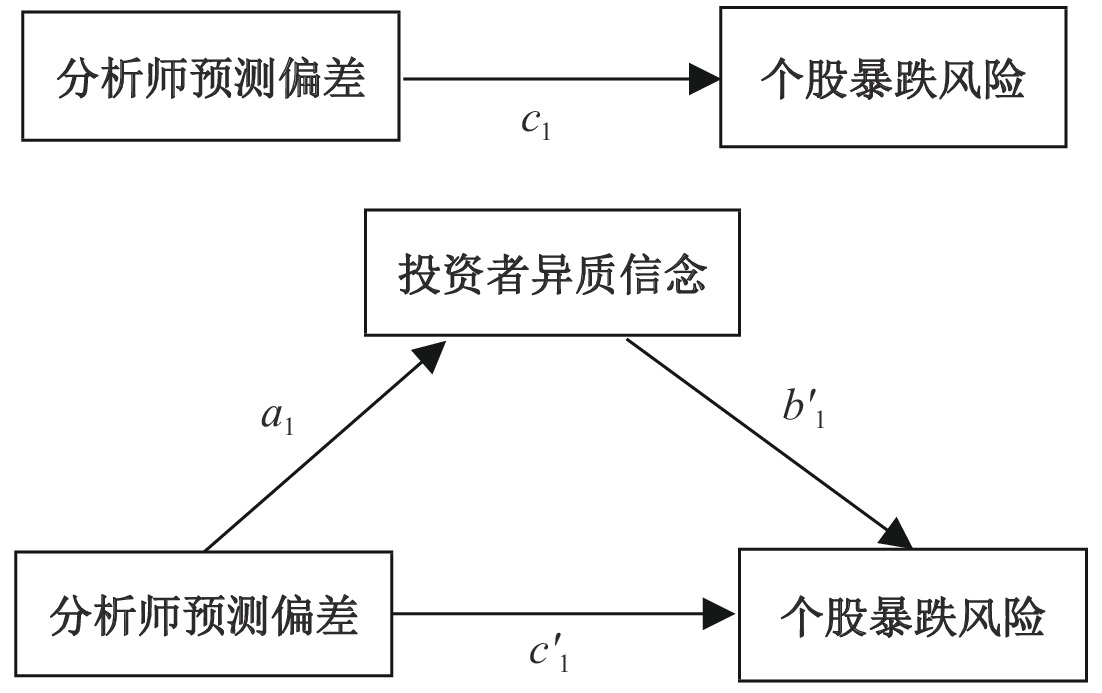
图2是本文用到的中介模型图。在本文中具体验证步骤如下:(1)检验分析师预测偏差是否对股价崩盘风险产生正向影响,也就是看模型(11)系数
|
| 图 2 模型说明 |
(一)描述性统计
表3列出的是本文研究变量的描述性统计结果。从表3的描述性统计分析可以看出,被解释变量股价崩盘风险的衡量指标NCSKEW和DUVOL的平均值分别为0.047和0.035,其标准差分别为1.511和1.664,这表明两个代理变量存在差别,使用二者对股价崩盘风险进行衡量可以使文章结论更有稳健性。分析师预测偏差平均值大于0,可以印证分析师对股票市场存在乐观偏差。
| 变量 | 样本数 | 平均值 | 标准差 | 最小值 | 最大值 |
| NCSKEW | 20028 | 0.047 | 1.511 | −2.793 | 2.796 |
| DUVOL | 20028 | 0.035 | 1.664 | −3.273 | 3.387 |
| HB | 20028 | −0.341 | 1.085 | −3.009 | 2.407 |
| Bias | 20028 | 0.928 | 1.709 | −0.395 | 8.373 |
| Roa | 20028 | 1.518 | 1.379 | −0.946 | 5.397 |
| BM | 20028 | 0.354 | 0.205 | 0.084 | 0.944 |
| Lev | 20028 | 0.427 | 0.201 | 0.076 | 0.808 |
| Size | 20028 | 22.429 | 1.265 | 15.921 | 28.636 |
| Return | 20028 | 0.063 | 0.305 | −0.362 | 1.243 |
| Vol | 20028 | 0.092 | 0.061 | 0.013 | 0.268 |
| CICSI | 20028 | 39.331 | 5.082 | 30.830 | 48.217 |
(二)分析师预测偏差和投资者异质信念
表4给出了分析师预测偏差与投资者异质信念的回归结果。从表4可以看出,在未加入控制变量的模型(1)中,滞后一期的分析师预测偏差的系数为0.020,在1%水平下显著。在加入控制变量后的模型(2)中,系数基本保持不变,为0.019,同样在1%水平下显著。如果公司的透明度较好,信息不对称程度低,那么分析师预测偏差就比较小。反之,如果分析师预测偏差越大,表明市场信息不对称程度越高,带有较大偏差的预测信息传递给投资者,使得投资者更难以分辨公司实际的经营状况,对未来前景抱有更多不确定性,与公司间的信息不对称进一步加重,因而不同投资者间更容易产生意见分歧,异质信念增大。以上结果验证了假设1:分析师预测偏差与投资者异质信念呈正相关关系,即分析师预测偏差越大将会导致投资者之间的异质信念越大。
| 变量 | (1) | (2) |
| HBt | HBt | |
| Biast−1 | 0.020*** | 0.019*** |
| (4.39) | (3.05) | |
| Roat−1 | −0.025*** | |
| (−2.99) | ||
| Sizet−1 | 0.056* | |
| (1.70) | ||
| Levt−1 | −0.184 | |
| (−1.58) | ||
| Returnt−1 | −0.025 | |
| (−0.53) | ||
| BMt−1 | −0.314*** | |
| (−3.89) | ||
| Volt−1 | 0.397** | |
| (2.34) | ||
| CICSIt−1 | 0.137*** | |
| (7.96) | ||
| Company FE | YES | YES |
| Time FE | YES | YES |
| Observations | 20028 | 20028 |
| R2 | 0.238 | 0.233 |
| 注:括号内为系数对应的t值,***、**、*分别表示在1%、5%、10%水平下通过显著性检验,以下同。 | ||
从控制变量的角度来看,Roa和BM的系数在1%水平下显著为负,表明经营状况越好的公司,投资者产生的异质信念越小。该结果也与实际情况吻合,在本文中,异质信念的代理指标与换手率相关,通常对于一家经营状况好、成长能力好的公司,投资者会有比较大的信心持有其股票,因此换手率较低。
(三)投资者异质信念与股价崩盘风险
表5给出了投资者异质信念与股价崩盘风险关系的回归结果。从表5中的模型(1)和(2)来看,在未加入控制变量情况下,以两个衡量股价崩盘风险的指标分别做因变量时,异质信念的系数分别为0.069和0.067,均在1%的水平下显著。从模型(3)和(4)来看,将所有控制变量加入后,系数分别为0.066和0.064,在1%水平下显著,说明投资者异质信念会显著增加股价崩盘风险。投资者异质信念是衡量投资者心理和行为的重要指标,是股价的重要影响因素。投资者由于各人先天禀赋、偏好、教育、资产等诸多因素的影响,呈现出多种多样的市场情绪。投资者异质信念越大,表明乐观投资者和悲观投资者分化越严重,而在卖空受限的市场中,股价会更多地反映市场的乐观情绪,很可能导致股价高估,随着负面信息积累,股价崩盘风险增大。以上的结果基本验证了假设2成立,即投资者异质信念与股价崩盘风险呈正相关关系,投资者异质信念的增大会加剧股价崩盘风险。
| 变量 | (1) | (2) | (3) | (4) |
| NCSKEWt | DUVOLt | NCSKEWt | DUVOLt | |
| HBt | 0.069*** | 0.067*** | 0.066*** | 0.064*** |
| (6.71) | (5.88) | (5.18) | (4.61) | |
| Roat−1 | −0.013 | −0.017 | ||
| (−1.06) | (−1.28) | |||
| Sizet−1 | 0.279*** | 0.233*** | ||
| (6.14) | (4.68) | |||
| Levt−1 | 0.117 | 0.256 | ||
| (0.72) | (1.44) | |||
| Returnt−1 | 0.016 | 0.119 | ||
| (0.24) | (1.62) | |||
| BMt−1 | 1.717*** | 1.893*** | ||
| (14.98) | (15.14) | |||
| Volt−1 | −5.248*** | −5.329*** | ||
| (−21.11) | (−19.64) | |||
| CICSIt−1 | −0.124*** | −0.109*** | ||
| (−5.32) | (−4.34) | |||
| Company FE | YES | YES | YES | YES |
| Time FE | YES | YES | YES | YES |
| Observations | 20028 | 19314 | 20028 | 19314 |
| R2 | 0.010 | 0.009 | 0.057 | 0.055 |
(四)投资者异质信念中介效应
按照中介效应的研究思路,第一步先就分析师预测偏差对股价崩盘风险的影响进行验证。表6列出了分析师预测偏差对股价崩盘风险影响的回归分析结果,未加入控制变量的情况下,两个股价崩盘风险指标NCSKEW、DUVOL对应的分析师预测偏差的系数分别为0.075和0.081,均在1%水平下显著。在控制了部分变量后,分析师预测偏差对于两个崩盘风险指标NCSKEW和DUVOL的回归系数分别提高到0.090和0.097,并且均在1%的水平下显著,可以表明二者之间存在非常显著的正向关系,分析师预测偏差增大会导致股价崩盘风险增加。
| 变量 | (1) | (2) | (3) | (4) |
| NCSKEWt | DUVOLt | NCSKEWt | DUVOLt | |
| Biast−1 | 0.075*** | 0.081*** | 0.090*** | 0.097*** |
| (9.33) | (9.16) | (8.18) | (8.08) | |
| Roat−1 | 0.010 | 0.009 | ||
| (0.67) | (0.51) | |||
| Sizet−1 | 0.335*** | 0.283*** | ||
| (5.53) | (4.27) | |||
| Levt−1 | 0.087 | 0.264 | ||
| (0.41) | (1.14) | |||
| Returnt−1 | 0.185** | 0.347*** | ||
| (2.21) | (3.78) | |||
| BMt−1 | 1.290*** | 1.452*** | ||
| (8.77) | (9.07) | |||
| Volt−1 | −5.252*** | −5.282*** | ||
| (−16.98) | (−15.66) | |||
| CICSIt−1 | −0.118*** | −0.116*** | ||
| (−3.78) | (−3.43) | |||
| Company FE | YES | YES | YES | YES |
| Time FE | YES | YES | YES | YES |
| Observations | 20028 | 19488 | 20028 | 19488 |
| R2 | 0.015 | 0.013 | 0.059 | 0.051 |
一般来说,除了公开信息之外,分析师还能够以专业能力对公司有关的信息进行整合分析,并挖掘私有信息,减小预测偏差。因此,分析师预测的偏差越大,表明公司透明度越低,市场投资者与公司间的信息不对称程度越高,投资者将更难对公司实际经营状况做出判断,因而未来股价崩盘风险越高。
另外,从控制变量的角度来看,公司规模(Size)、账面价值和市值比(BM)、股票回报率(Return)与股价崩盘风险都是显著正相关,表明公司规模越大、前景不佳时,更容易发生股价崩盘风险。同时,公司成长性在股票市场追涨杀跌的特性下被进一步放大,此时通过买卖价差可以获得更高的回报,因而也更容易导致崩盘风险。
第二步,检验模型(9)和(12)的系数
| 变量 | (1) | (2) | (3) | (4) |
| NCSKEWt | DUVOLt | NCSKEWt | DUVOLt | |
| Biast−1 | 0.074*** | 0.079*** | 0.089*** | 0.095*** |
| (9.14) | (8.99) | (8.05) | (7.97) | |
| HBt−1 | 0.082*** | 0.075*** | 0.080*** | 0.073*** |
| (6.14) | (5.10) | (4.74) | (3.95) | |
| Roat−1 | 0.012 | 0.010 | ||
| (0.80) | (0.62) | |||
| Sizet−1 | 0.331*** | 0.279*** | ||
| (5.46) | (4.21) | |||
| Levt−1 | 0.101 | 0.275 | ||
| (0.48) | (1.18) | |||
| Returnt−1 | 0.187** | 0.350*** | ||
| (2.24) | (3.82) | |||
| BMt−1 | 1.315*** | 1.474*** | ||
| (8.94) | (9.20) | |||
| Volt−1 | −5.284*** | −5.303*** | ||
| (−17.09) | (−15.73) | |||
| CICSIt−1 | −0.129*** | −0.126*** | ||
| (−4.12) | (−3.72) | |||
| Company FE | YES | YES | YES | YES |
| Time FE | YES | YES | YES | YES |
| Observations | 20028 | 19488 | 20028 | 19488 |
| R2 | 0.016 | 0.014 | 0.060 | 0.058 |
第三步,检验模型(12)的系数
分析师预测偏差以投资者异质信念为中介,从而引起个股股价崩盘的传导过程也可以这样理解:分析师的预测影响了投资者的预期,而当真实业绩报告发布之后,很可能投资者发现真实业绩与市场预期存在偏差,偏差越大就越容易导致大量抛售。此时投资者异质信念表现为在不同的价位发生频繁买卖,非预期的换手率增高,随之引导股价向下波动,进而造成个股股价崩盘风险提高。由此,假设3得以证实,投资者异质信念在分析师预测偏差对股价崩盘风险的影响中起到中介作用,分析师预测偏差加剧股价崩盘风险的作用有一部分是通过增大投资者异质信念实现的。
在模型(1)的计算中,考虑到乐观偏差与悲观偏差可能会相互抵消,从而对结果造成影响,因此,我们将分析师的预测偏差分为乐观偏差与悲观偏差来进行进一步讨论。表8给出了乐观偏差下的回归结果。从表8的结果来看,第(1)和(2)列中Bias系数显著为正,表明分析师的乐观偏差与股价崩盘风险正相关,第(3)列系数也显著为正,表明乐观偏差与异质信念正相关,分析师乐观偏差越大,投资者异质信念越大。第(4)和(5)列中Bias系数和HB系数均显著为正,可以验证假设3的成立。而在悲观偏差的回归中,三个假设所关注的系数都不显著或者显著性很低,表明在悲观偏差下,三个假设均不能得到有效的验证。因此,主要是分析师的乐观偏差引起投资者异质信念增大,进而加剧股价崩盘风险。
| 变量 | (1) | (2) | (3) | (4) | (5) |
| NCSKEWt | DUVOLt | HBt | NCSKEWt | DUVOLt | |
| Biast-1 | 0.066*** | 0.072*** | 0.023*** | 0.065*** | 0.071*** |
| (5.98) | (5.99) | (3.64) | (5.88) | (5.91) | |
| HBt | 0.048*** | 0.040** | |||
| (2.72) | (2.07) | ||||
| Control Variables | YES | YES | YES | YES | YES |
| Observations | 12113 | 11644 | 12113 | 12113 | 11644 |
| R2 | 0.057 | 0.057 | 0.291 | 0.058 | 0.058 |
| 注:表中省略了控制变量的回归结果。 | |||||
(五)稳健性检验①
1. 选择性偏差
本文的研究可能存在这样的选择性偏差:一般来说,分析师更倾向于关注那些市值较大、业绩较好、成长性较高或是比较有名的公司,而对于另外一些相对较小的公司,关注的分析师数量可能就会比较少,从而产生选择性偏差。从样本数据的整理中,也发现大约有1000家公司缺少分析师预测数据,或是由于发布预测的分析师数量太少而被剔除。因此,本文选用Heckman两阶段模型来做稳健性检验,以期尽可能消除这种选择性偏差。Heckman两阶段回归的结果显示,主要的自变量Bias、中介变量HB的系数略微有所减小,但系数正负性和显著性均不变,这说明原来的结果具有稳健性。此外,逆米尔斯比率(IMR)的系数显著,这表明样本存在选择性偏差,用Heckman两阶段模型是必要的。
2. 更换异质信念指标
本文中所构造的异质信念指标采用了朱宏泉等(2016)提出的方法,其方法第一步运用了Fama-French三因子模型。在稳健性检验时,我们借鉴了Liu等(2019)提出的方法,将三因子中价值因子HML由用BM(权益账面市值比)计算改为用EP(每股收益/股票价格)计算,他们证实这样的计算方法更适用于中国股市。该结果显示,更换三因子模型指标后,分析师预测偏差Bias和异质信念HB的系数依然在1%水平下显著为正,并且投资者异质信念的中介效应检验也通过,这表明以上三个假设依然能够得到验证,前文的研究结果具有稳健性。
3. 剔除特殊年份的数据
本文样本期间包括了2008年全球金融危机和2015年中国A股大跌两次大的金融市场动荡,考虑到市场出现系统性危机和全局性下跌时,投资者异质信念会自然地大幅增加,且股价崩盘风险也会普遍暴增,因此,剔除2008年和2015年的数据来考察结果是否稳健,从回归结果来看,主要系数的正负性和显著性不变,不论股票市场是否出现全局性的危机,投资者异质信念在分析师预测偏差与股价崩盘风险之间的中介作用依然显著,表明本文的结论是稳健的。
五、结论及建议根据文献回顾和理论分析,本文认为,在信息不对称和投资者自身差异的作用下,分析师预测偏差的增大会导致投资者异质信念的增加;而在卖空限制情况下,投资者异质信念越大,股价越可能被哄抬至较高水平,从而加剧股价崩盘风险。因而,分析师预测偏差对股价崩盘风险的影响很可能是通过投资者异质信念的中介作用来实现的。为了验证这样的理论假说是否成立,本文以我国2008—2019年沪深两市上市公司为样本,构建相关模型并进行实证分析,以研究投资者异质信念在分析师预测偏差对股价崩盘风险的影响中起到什么样的作用。研究结果显示:第一,分析师预测偏差对投资者异质信念存在着正向影响,前一期的分析师预测偏差越大,当期的投资者异质信念越大。第二,投资者异质信念对股价崩盘风险有显著的增强作用,投资者异质信念增大会加剧个股股价崩盘风险。第三,分析师预测偏差会加大投资者异质信念,进而加剧股价崩盘风险,即投资者异质信念在分析师预测偏差对股价崩盘风险的影响中起到了部分中介作用。这一结论基本验证了前述理论分析结果。
本文的研究结论对于分析师、政策制定者与投资者都有一定启示。分析师作为公司信息向市场传递过程中的中介之一,扮演着重要的角色,分析师的预测行为对于市场预期有着比较大的影响力。为避免广大投资者因为受到分析师不客观、不公正的,甚至带有明显误导性的预测信息的影响,而产生不理性的投资行为,进而造成股价崩盘风险加剧的情况,分析师自身应当努力提高业务水平和职业道德素养,真实客观地将公司信息传达给投资者,降低投资者间的异质信念,以减少股价崩盘的情况发生。对监管部门来说,要完善相关的法律法规,加强分析师职业道德教育的同时加大对违规分析师的惩处,进一步规范和引导分析师行为,使其在市场中更好地发挥作用。同时,对分析师所处的证券公司而言,要建立完善起分析师考核评价体系,将预测准确度指标纳入其中,从而督促分析师提高预测准确性和真实性。而对投资者而言,应当提高自己的知识水平,清楚地认识分析师在市场中扮演的角色,不能盲目地相信分析师预测信息,要多方面地参考市场中的有关信息,对公司价值做出自己的判断,从而减小由于不准确的预测信息带来的异质信念,降低股价崩盘风险。
① 限于篇幅,稳健性检验的回归结果暂未列出,如有需要可向作者索取。
| [1] | 甘露润, 张淑慧. 公司治理、分析师关注与股票市场信息含量[J]. 财经问题研究, 2013(6): 58–65. |
| [2] | 胡昌生, 池阳春. 异质信念与资产价格异常波动性[J]. 金融评论, 2013, 5(3): 55–71. |
| [3] | 金永红, 罗丹. 异质信念、投资者情绪与资产定价研究综述[J]. 外国经济与管理, 2017, 39(5): 100–114. |
| [4] | 孙淑伟, 梁上坤, 付宇翔, 等. 择机还是共谋——内部人减持前的分析师行为[J]. 管理科学学报, 2019, 22(12): 105–123. |
| [5] | 肖土盛, 宋顺林, 李路. 信息披露质量与股价崩盘风险: 分析师预测的中介作用[J]. 财经研究, 2017, 43(2): 109–120. |
| [6] | 许年行, 江轩宇, 伊志宏, 等. 分析师利益冲突、乐观偏差与股价崩盘风险[J]. 经济研究, 2012, 47(7): 127–140. |
| [7] | 尹慧, 赵国庆. 异质信念、卖空限制与股票收益[J]. 上海经济研究, 2013, 25(12): 85–94. |
| [8] | 游家兴, 邱世远, 刘淳. 证券分析师预测“变脸”行为研究——基于分析师声誉的博弈模型与实证检验[J]. 管理科学学报, 2013, 16(6): 67–84. |
| [9] | 张维, 张永杰. 异质信念、卖空限制与风险资产价格[J]. 管理科学学报, 2006, 9(4): 58–64. |
| [10] | 钟晨, 张晓朴, 吴雄. 公开信息披露会加剧投资者异质信念吗?——以29家房地产上市公司为例[J]. 西南民族大学学报(人文社科版), 2017, 38(3): 146–153. |
| [11] | 周冬华, 赵玉洁. 证券分析师盈余预测乐观倾向: 利益关联还是启发式认知偏差?[J]. 管理评论, 2016, 28(1): 205–218. |
| [12] | 朱宏泉, 余江, 陈林. 异质信念、卖空限制与股票收益——基于中国证券市场的分析[J]. 管理科学学报, 2016, 19(7): 115–126. |
| [13] | Brown N C, Wei K D, Wermers R. Analyst recommendations, mutual fund herding, and overreaction in stock prices[J]. Management Science, 2014, 60(1): 1–20. |
| [14] | Hirshleifer D, Teoh S H. Limited attention, information disclosure, and financial reporting[J]. Journal of Accounting and Economics, 2003, 36(1-3): 337–386. |
| [15] | Hong H, Stein J C. Differences of opinion, short-sales constraints, and market crashes[J]. The Review of Financial Studies, 2003, 16(2): 487–525. |
| [16] | Jin L, Myers S C. R2 around the world: New theory and new tests [J]. Journal of Financial Economics, 2006, 79(2): 257–292. |
| [17] | Kim J B, Li Y H, Zhang L D. Corporate tax avoidance and stock price crash risk: Firm-level analysis[J]. Journal of Financial Economics, 2011, 100(3): 639–662. |
| [18] | Liu J N, Stambaugh R F, Yuan Y. Size and value in China[J]. Journal of Financial Economics, 2019, 134(1): 48–69. |
| [19] | Malmendier U, Shanthikumar D. Are small investors naive about incentives?[J]. Journal of Financial Economics, 2007, 85(2): 457–497. |
| [20] | Peng L, Xiong W. Investor attention, overconfidence and category learning[J]. Journal of Financial Economics, 2006, 80(3): 563–602. |


