
2023第49卷第10期
一、引 言
城市作为现代经济发展中最重要的空间载体,在快速聚集资源、劳动力、资本和技术等生产要素过程中,城市工业及其他产业部门快速发展,中国逐步由工业大国向工业强国转变,但也存在一些高耗能、高排放等环境问题,而城市成为碳排放的主要产生地。截至2020年,中国人均碳排放约为7吨,约有过半城市人均碳排放量超过全国平均水平,如天津、兰州、无锡、银川、西宁和惠州等地的人均碳排放超过13吨。
工业部门作为中国碳排放的主要源头,数字技术在工业部门的运用为解决中国高碳排放问题提供了机遇。工业4.0和人工智能等技术与经济社会活动的融合运用成为推动制造业转型升级的重要引擎(Vinuesa等,2020)。工业机器人作为工业4.0和人工智能的关键技术在中国实现跨越式发展。新能源、新材料与工业机器人的深度融合推动实现产业技术变革,进一步放大工业机器人的环境效益,助力经济低碳转型。智能化过程对劳动力的补充与替代必然会影响资本与劳动之间的要素份额与边际产出(Acemoglu和Restrepo,2019),已有研究重点讨论了工业机器人对劳动力市场的影响(Graetz 和 Michaels,2018;Acemoglu 和 Restrepo,2020;李磊等,2021;王晓娟等,2022)。此外,Kromann 等(2020)、周广肃和丁相元(2022)等人探讨了工业机器人对经济增长和居民收入差距的影响。
中国一直高度重视气候变化问题,如何降低碳排放也成为学术界关注的焦点问题。现有关于中国碳减排因素的研究主要有两类:一类是从服务业集聚(韩峰和谢锐,2017)、高铁开通(孙鹏博和葛力铭,2021)、金融发展(赵军等,2020)等具体因素出发,通过促进技术进步或生产效率的提升(邵帅等,2019;杨莉莎等,2019),从而实现减碳;另一类则从中国环境政策入手,关注碳交易试点政策(黄向岚等,2018)、低碳试点城市建设(张华,2020)和绿色财政政策(薛飞和陈煦,2022)的碳减排效应。随着通用技术的发展,少量国外文献开始关注ICT对碳排放和能源强度的影响(Zhou等,2019;Lange 等,2020;Sun 和 Kim,2021)。Li 等(2022)和Wang 等(2022)利用跨国数据的实证研究发现,工业机器人的碳减排效应具有行业和国别异质性影响。上述研究为本文深入探讨工业机器人的城市碳减排效应提供了理论逻辑基础。通过文献梳理发现,现有研究仍存在以下两方面不足:一是国内外关于工业机器人是否具有环境红利的研究较少,理论研究基础薄弱,实证研究尚处于起步阶段;二是国内以往有关碳排放的实证研究大多集中在省级层面,基于城市层面的研究主要关注各种环保节能政策的实施效果,对城市工业碳排放的实证研究也较少。
为了弥补上述不足,本文构建包含工业机器人和能源投入的理论模型,并利用2007—2019年中国城市面板数据,研究了工业机器人对工业碳排放的影响效应、作用机制与实现路径。研究发现:第一,工业机器人的运用显著降低了城市工业碳排放。第二,机制分析发现,绿色技术创新和人机匹配度是工业机器人降低工业碳排放的重要作用机制。第三,工业机器人能够促进非资源型城市低碳发展,但对资源型城市工业碳排放的影响并不明显。只有在数字化水平较高的城市,工业机器人才能发挥显著的碳减排效应。此外,工业机器人有效降低东部城市和南方城市的工业碳排放,对中西部城市和北方城市的影响不显著。第四,互联网基础设施建设、人力资本水平和政府科技投入是工业机器人降低碳排放的重要实现路径。
本文的研究贡献主要体现在:(1)在“双碳”目标约束条件下,对Acemoglu和 Restrepo(2018)的任务模型进行拓展,构建包含机器人、能源投入和环境因素的内生经济增长模型,考察工业机器人对碳排放的影响,为利用智能技术协调经济增长和环境保护之间的矛盾提供重要的理论模型框架。(2)在基于任务的人工智能模型框架下,本文对工业机器人与工业碳排放的影响机制展开实证研究,从绿色技术创新和人机匹配度两个方面,分析工业机器人实现工业碳减排的影响机制,为工业机器人赋能工业节能减排效应提供必要的经验证据。(3)重点关注城市层面的工业碳排放问题,在工业机器人和工业碳排放的全景式逻辑框架链中嵌入城市区位、资源禀赋和城市特征等因素,识别工业机器人对城市低碳经济的异质性影响,为智能技术促进工业碳减排提供城市差异化政策启示。(4)基于人工智能技术应用角度,识别工业机器人发挥工业碳减排效应的边界条件,从互联网基础设施建设、人力资本水平和科研资金投入三方面探索城市经济低碳转型发展的实现条件,提出在新一代信息技术应用条件下推动城市经济绿色高质量发展的实现路径。
本文剩余的结构安排如下:第二部分为理论模型构建与研究假说;第三部分为研究设计;第四部分为基准估计结果和异质性分析;第五部分为机制检验和实现条件分析;第六部分为研究结论和政策建议。
二、理论模型与研究假说
(一)理论模型
在内生经济增长模型框架下,技术进步是导致中国经济增长与波动的主要来源(黄赜琳和朱保华,2015)。技术进步的一部分就是生产过程的自动化,随着人工智能技术的快速发展与普及应用,Autor等(2003)提出基于任务的人工智能技术模型,这为探讨机器人影响经济增长提供了新的模型框架。然而,现有研究较少将环境因素纳入基于工业机器人的任务模型中。因此,本文率先尝试在“双碳”目标约束条件下,对Acemoglu和 Restrepo(2018)的任务模型进行拓展,构建包含机器人、能源投入和环境因素的任务模型,考察工业机器人对碳排放的影响,为利用人工智能协调经济增长和环境保护之间的矛盾提供重要的理论模型框架。
基于Acemoglu和Restrepo(2018)构造的模型框架,整个经济由各种不同的任务(行业)组成,并且所有任务
| $ \mathrm{ln}Y={\int }_{N-1}^{N}\mathit{\mathrm{ln}}y\left(x\right)dx$ | (1) |
其中,
| $ y\left(x\right)=\left\{\begin{aligned}&{\gamma }_{m}\left(x\right){k\left(x\right)}^{\alpha }{m\left(x\right)}^{\beta }{e\left(x\right)}^{1-\alpha -\beta }\quad {if}\quad x\in [N-1,I]\\& {\gamma }_{L}\left(x\right){k\left(x\right)}^{\alpha }{l\left(x\right)}^{\beta }{e\left(x\right)}^{1-\alpha -\beta }\quad\ {if}\quad x\in [I,N]\end{aligned}\right. $ | (2) |
其中,
在完全竞争市场条件下,投入要素的价格等于其边际产品,由此可以计算得到各种生产要素价格及其所占总产出的份额。均衡条件下资本回报率
| $ R=\frac{\partial y}{\partial k}=\left\{\begin{aligned} & \alpha \dfrac{y\left(x\right)}{k\left(x\right)}\quad {if}\quad x\in [N-1,I]\\ & \alpha \dfrac{y\left(x\right)}{k\left(x\right)}\quad {if}\quad x\in [I,N]\end{aligned}\right.\Rightarrow \frac{RK}{Y}=\alpha $ | (3) |
劳动工资
| $ W=\frac{\partial y}{\partial l}=\left\{\begin{aligned}\text{0}\quad if\;x\in [N-1,I]\\ \beta \dfrac{y\left(x\right)}{l\left(x\right)}\quad if\;x\in [I,N]\end{aligned}\right.\Rightarrow \frac{WL}{Y}=\beta (N-I) $ | (4) |
机器人价格
| $ {P}_{m}=\frac{\partial y}{\partial m}=\left\{\begin{aligned}&\beta \frac{y\left(x\right)}{m\left(x\right)}\quad if\;x\in [N-1,I]\\& 0\quad if\;x\in [I,N]\end{aligned}\right.\Rightarrow \frac{{P}_{m}M}{Y}=\beta (I-N+1) $ | (5) |
能源价格
| $ {P}_{e}=\frac{\partial y}{\partial e}=\left\{\begin{aligned}&(1-\alpha -\beta )\dfrac{y\left(x\right)}{e\left(x\right)}\quad if\;x\in [N-1,I]\\ & (1-\alpha -\beta )\dfrac{y\left(x\right)}{e\left(x\right)}\quad if\;x\in [I,N]\end{aligned}\right.\Rightarrow \frac{{P}_{m}E}{Y}=1-\alpha -\beta $ | (6) |
根据柯布—道格拉斯生产函数及均衡条件下四种要素价格式(3)至式(6),可得出企业使用这两种形式进行生产的成本函数满足如下方程:
| $ c\left(x\right)=\left\{\begin{aligned} & \dfrac{y\left(x\right)}{{\gamma }_{m}\left(x\right)}(\dfrac{R}{\alpha }{)}^{\alpha }(\frac{{P}_{m}}{\beta }{)}^{\beta }\text{(}\frac{{P}_{e}}{1-\alpha -\beta }{)}^{1-\alpha -\beta }\quad if\;x\in [N-1,I]\\ & \dfrac{y\left(x\right)}{{\gamma }_{L}\left(x\right)}(\frac{R}{\alpha }{)}^{\alpha }(\dfrac{W}{\beta }{)}^{\beta }\text{(}\dfrac{{P}_{e}}{1-\alpha -\beta }{)}^{1-\alpha -\beta }\quad if\;x\in [I,N]\end{aligned}\right. $ | (7) |
企业选择使用机器人生产还是劳动生产的关键在于这两种形式对应的成本,企业通常会选择成本较小的生产形式。这也就决定了完全竞争条件下每个任务的价格
| $ p\left(x\right)=\left\{\begin{aligned}& \dfrac{1}{{\gamma }_{m}\left(x\right)}(\dfrac{R}{\alpha }{)}^{\alpha }(\dfrac{{P}_{m}}{\beta }{)}^{\beta }\text{(}\dfrac{{P}_{e}}{1-\alpha -\beta }{)}^{1-\alpha -\beta } if\;x\in [N-1,I]\\ &\dfrac{1}{{\gamma }_{L}\left(x\right)}(\dfrac{R}{\alpha }{)}^{\alpha }(\frac{W}{\beta }{)}^{\beta }\text{(}\dfrac{{P}_{e}}{1-\alpha -\beta }{)}^{1-\alpha -\beta } if\;x\in [I,N]\end{aligned}\right. $ | (8) |
根据Dixit-Stiglitz框架,可以得出:
| $ y(x)=\frac{Y}{p(x)}\Rightarrow p(x)=\frac{Y}{y(x)}\Rightarrow {\rm{ln}}[p(x)]={\rm{ln}}Y-{\rm{ln}}[y(x)]$ | (9) |
对式(9)两边同时积分,可得:
| $ {\int }_{N-1}^{N}\ln p\left(x\right)dx=\ln Y{\int }_{N-1}^{N}dx-{\int }_{N-1}^{N}\ln y\left(x\right)dx=\ln Y-\ln Y=0 $ | (10) |
根据
| $\begin{aligned} & {\int }_{N-1}^{I}[\alpha {\ln}R-\alpha {\ln}\alpha +\beta {\ln}{P}_{m}-\beta {\ln}\beta +(1-\alpha -\beta ){\ln}{P}_{e}-(1-\alpha -\beta ){\ln}(1-\alpha -\beta )-{\ln}{\gamma }_{m}\left(x\right)]dx\\ &+{\int }_{I}^{N}[\alpha {\ln}R-\alpha {\ln}\alpha +\beta {\ln}W-\beta {\ln}\beta +(1-\alpha -\beta ){\ln}{P}_{e}-(1-\alpha -\beta ){\ln}(1-\alpha -\beta )-{\ln}{\gamma }_{L}\left(x\right)]dx=0 \end{aligned} $ | (11) |
接着,将式(3)—式(6)中的四要素价格代入式(11)中,整理可得:
| $ \begin{aligned} & {\int }_{N-1}^{I}[\alpha {\ln}\frac{Y}{K}+\beta {\ln}\frac{(I-N+1)Y}{M}+(1-\alpha -\beta ){\ln}\frac{Y}{E}-{\ln}{\gamma }_{m}(x\left)\right]dx\\ & + {\int }_{I}^{N}[\alpha {\ln}\frac{Y}{K}+\beta {\ln}\frac{(N-I)Y}{L}+(1-\alpha -\beta ){\ln}\frac{Y}{E}-{\ln}{\gamma }_{L}(x\left)\right]dx=0 \end{aligned} $ | (12) |
通过求解式(12),可得整体的生产函数
| $ \begin{aligned} {\ln}Y= & \alpha {\ln}K+\beta (I-N+1){\ln}M+\beta (N-I){\ln}L+(1-\alpha -\beta ){\ln}E-\beta (I-N+1){\ln}(I-N+1)\\ &-\beta (N-I){\ln}(N-I)+{\int }_{N-1}^{I}\left[{\ln}{\gamma }_{m}\right(x\left)\right]dx +{\int }_{I}^{N}\left[{\ln}{\gamma }_{L}\right(x\left)\right]dx \end{aligned} $ | (13) |
根据
| $ Y=A{K}^{\alpha }(\frac{M}{I-N+1}{)}^{\beta (I-N+1)}(\frac{L}{N-I}{)}^{\beta (N-I)}{E}^{1-\alpha -\beta } $ | (14) |
其中,
| $ TFP=A(\frac{1}{I-N+1}{)}^{\beta (I-N+1)}(\frac{1}{N-I}{)}^{\beta (N-I)}$ | (15) |
式(14)表明,在其他要素投入不变的情况下,随着机器人使用量
从产出侧来看,碳排放等污染物可被视为生产过程中伴随能源要素的使用而产生的一种非期望产出(袁晓玲等,2009)。假定生产过程中碳排放按能源使用与期望产出的一定比例产生,即碳排放满足如下运行规律:
| $ indco=E/Y $ | (16) |
其中,我们将
| $ {\ln}indco={\gamma }_{0}-{\ln}A-\beta (I-N+1){\ln}M-\beta (N-I){\ln}L-\alpha {\ln}K+(\alpha +\beta ){\ln}E $ | (17) |
其中,
(二)工业机器人对工业碳排放的影响
1. 影响效应。根据式(17)可知,由于
假说1:工业机器人能够赋能城市工业碳减排。
2. 影响机制分析。作为解决环境问题的重要技术,绿色技术创新能够实现产出增长与环境保护双赢(Lee和Min,2015),助力工业机器人发挥减碳效应。首先,当工业企业尤其是重污染工业企业广泛使用绿色技术时,工业机器人能够助力企业进行清洁生产,实现企业低碳转型升级,从生产端减少能源消耗和污染排放,从而能够抑制城市整体的工业碳排放。其次,绿色技术创新为收集、封存和转换利用二氧化碳提供技术支撑,降低脱碳成本,助力工业部门享受技术红利,从环境治理端助力工业碳减排(邵帅等,2022)。城市绿色技术创新水平较高说明此城市绿色技术的吸收能力高,研发资金和高技术人才较多。这为推进以工业机器人为代表的工业智能化建设提供了必要的软件和硬件支持,有助于促进企业内、企业间和区域间互相学习智能化技术和绿色技术,将绿色技术运用到智能生产的每一个环节,进一步强化工业机器人的绿色技术溢出效应,充分发挥工业机器人对工业碳排放的抑制作用。而城市绿色技术水平较低表明该城市自动化、人工智能等新技术研发较慢,绿色技术在智能化生产过程中使用效率较低,这也弱化了工业机器人的减碳作用。故本文提出如下假说:
假说2:绿色技术创新是工业机器人降低城市工业碳排放的重要影响机制。
根据
假说3:人机匹配度是工业机器人降低城市工业碳排放的重要影响机制。
三、研究设计
(一)模型设定
为了检验工业机器人对工业碳排放的影响,根据前文的理论模型,本文构建如下计量模型以验证假说1:
| $ {\mathrm{ln}indco}_{it}={\beta }_{0}{+\beta }_{1}{robot}_{it}+\gamma {X}_{it}+{\mu }_{t}+{\delta }_{i}+{\varepsilon }_{it} $ | (18) |
其中,
(二)变量选取与数据来源
1. 城市工业碳排放强度(lnindco)。参照孙鹏博和葛力铭(2021)的研究,采用单位工业增加值碳排放量的自然对数值衡量。我们利用夜间灯光数据推导出城市工业碳排放。具体步骤如下:一是提取夜间灯光数据。参照Chen等(2019)的研究,灯光数据来自DMSP和VIIRS这两组卫星影像提取所得,并对数据进行校准和统一处理,从而获得连续的中国省级和城市2007—2019年的夜间灯光数据。二是测算省级工业碳排放。在CEADs数据库获取利用17种能源数据测算到的省级碳排放数据(Shan等,2018),本文将工业部门的碳排放数据加总得到省级工业碳排放总量。三是估算省级碳排放与省级夜间灯光数据之间的弹性。构建如下计量模型:
| $ {CO}_{kt}=a{light}_{kt}+{prov}_{k}+{v}_{t}+{\varepsilon }_{it} $ | (19) |
其中,
| $ {CO}_{it}={CO}_{kt} \times \left[\right(a{light}_{it}+{city}_{i}+{v}_{t}+{\varepsilon }_{it})/(a{light}_{kt}+{prov}_{k}+{v}_{t}+{\varepsilon }_{it} )] $ | (20) |
其中,
2. 城市工业机器人渗透度(robot)。参照Acemoglu 和 Restrepo(2020)、魏下海等(2020)的方法进行测度。具体而言,先将IFR提供的行业分类与《国民经济行业分类》(GB/T4754-2002)进行匹配,得到我国分行业的工业机器人安装数量,再选定2004年作为基准年份,根据Bartik工具变量法的思想,采用基准年份各城市分行业的就业份额与行业机器人渗透度计算每个城市的工业机器人渗透度,计算公式如下:
| $ {Robot}_{it}=\sum _{j=1}^{J}\frac{{labor}_{i,j,t=2004}}{{labor}_{i,t=2004}}\times \frac{{Robot}_{jt}}{{labor}_{j,t=2004}} $ | (21) |
其中,
3. 控制变量。基于理论模型和余壮雄等(2020)的研究,选取如下控制变量:政府科技支出(edu),以财政科技支出占财政总支出的比值衡量;城镇化率(urban),用城镇常住人口占总人口比重表示;人口密度(lnpop),采用取对数的每平方公里人口数量表示;经济发展水平(lnpgdp),用实际人均GDP的对数值衡量;工业能耗强度(energ),使用工业用电总量占工业增加值的比重衡量;对外开放程度(open)和金融发展程度(fin)用来反映工业发展过程中资本积累情况,分别用实际利用外商投资总额和金融机构贷款余额与GDP的占比来衡量。
由于IFR从2006年才开始提供中国分行业的工业机器人数据,同时剔除上述变量连续缺失4年及以上的城市样本后,本文采用2007—2019年262个地级以上城市的面板数据作为实证样本。数据主要来源于CNRDS数据库、EPS数据、同花顺数据库、《中国城市统计年鉴》和各城市的《统计年鉴》与统计公报。主要变量的描述性统计如表1所示。
| 变量类型 | 变量名 | 英文名 | N | 均值 | 标准差 | 最大值 | 最小值 |
| 被解释变量 | 工业碳排放强度 | lnindco | 3406 | 1.412 | 0.524 | 3.682 | 0.187 |
| 解释变量 | 工业机器人渗透度 | robot | 3406 | 3.278 | 4.004 | 27.00 | 0.0073 |
| 控制变量 | 政府科技支出 | edu | 3406 | 0.016 | 0.015 | 0.207 | 0.0006 |
| 城镇化率 | urban | 3406 | 0.523 | 0.151 | 0.998 | 0.175 | |
| 人口密度 | lnpop | 3406 | 5.806 | 0.886 | 7.882 | 1.573 | |
| 经济发展水平 | lnpgdp | 3406 | 10.20 | 0.631 | 12.80 | 4.358 | |
| 工业能耗强度 | energ | 3406 | 0.093 | 0.092 | 1.117 | 0.001 | |
| 金融发展程度 | fin | 3406 | 0.883 | 0.540 | 7.450 | 0.112 | |
| 对外开放程度 | open | 3406 | 0.019 | 0.018 | 0.198 | 1.34e-06 |
(三)特征事实
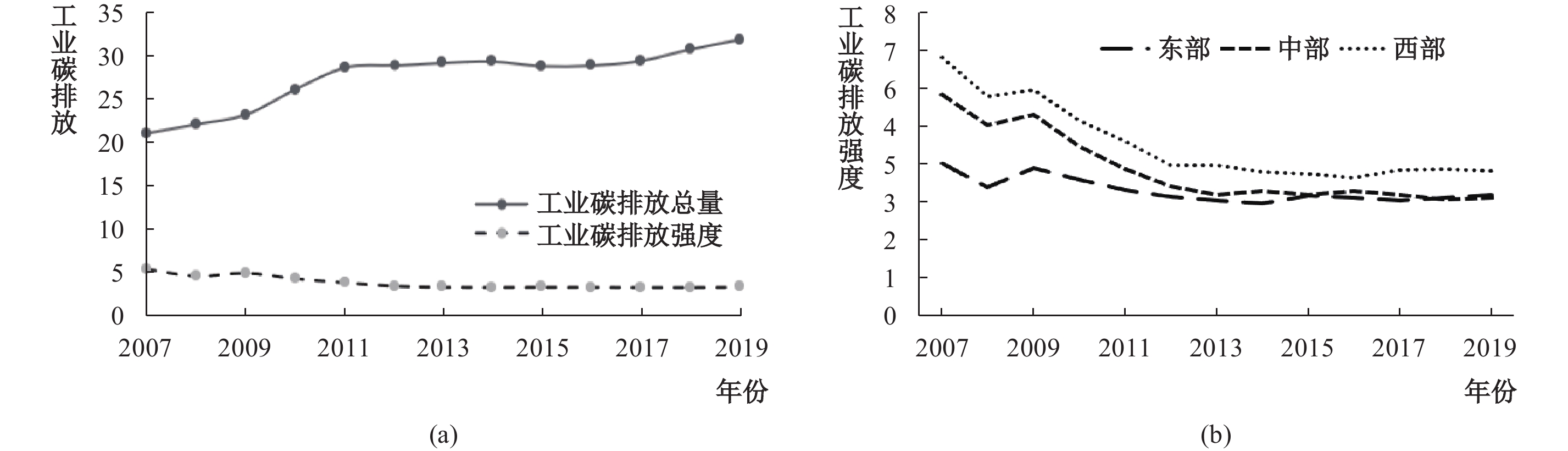
根据图1,可以看出工业碳排放总量呈现上升态势,这与邵帅等(2022)、Xu等(2022)计算的城市全口径碳排放总量的演化趋势相一致。工业碳排放强度在2008—2009年间低位回升,自2009年以后一直呈现下降态势。长期以来,中国工业发展形成以煤炭为主的能源消费结构,尤其是2009年我国成为全世界最大的能源消费国,造成总体的工业碳排放量逐年增加。随着各项环境政策的持续推进和数字赋能工业的深化发展,工业碳排放总量在2011年以后上升趋势有所放缓。结合我国工业智能化发展的历程看,2012年国务院颁布《“十二五”国家战略性新兴产业发展规划》,推动了工业化和信息化的深度融合。此后,工业和信息化部分别在2015—2018年间陆续开展智能制造试点示范项目试点工作。可以看出,工业碳排放强度下降与我国大力推进工业智能化发展的历程是重合的。综合图1工业碳排放总量和工业碳排放强度的演变趋势,可以发现工业碳排放强度下降,总量保持缓慢持续增长的态势。一个可能的原因在于,相比工业部门,以ICT为代表的通信技术部门和服务业行业虽然表面上是环境友好型部门,但是生产活动需要电力、化学品、金属等材料等产业链上游的工业部门提供碳密集型中间投入品,导致工业部门的碳排放总量持续居高不下。随着工业智能化的深化发展,工业技术进步促进单位工业产值的能耗下降,因而工业碳排放强度呈现下降趋势(邵帅等,2022)。
|
| 图 1 城市工业碳排放趋势图(均值) |
图1还展示了中国三大区域的工业碳排放强度演变趋势。从区域来看,东部、中部和西部地区的工业碳排放强度均呈明显的下降趋势,且具有收敛性,但中西部地区碳排放水平明显高于东部地区。其原因可能在于:一是“十一五”和“十二五”时期中西部地区减碳目标较低,特别是青海、四川、重庆等城市能源使用效率较低,而重化工业占比较高,造成工业碳排放高于东部地区(汤维祺等,2016);二是随着全国范围内环境政策和工业智能化发展,产业转移带来的技术进步也在一定程度上推动中西部工业碳减排,2012年以后呈低位震荡状态,与东部的差距在缩小。
四、实证结果分析
(一)基准结果分析
运用式(18)估计工业机器人渗透度对城市工业碳排放强度的影响,结果如表2所示。表2列(1)、列(2)分别为不加控制变量和加入所有控制变量的估计结果,工业机器人的估计系数始终显著为负。这意味着当城市使用更多的工业机器人从事生产活动时,地区的工业碳排放强度会显著下降。列(2)的结果表明工业机器人渗透度每提升1个单位,城市工业碳排放强度下降1.3%,假说1得证。借鉴唐松等(2020)的研究,将工业机器人渗透度滞后1—5期,并替换当期变量,列(3)—列(7)的结果表明,工业机器人滞后1—5期的系数在1%的显著性水平下显著为负,且随着滞后期增加,负向效应更强。上述结论表明工业机器人在较长的时间中都能够抑制工业碳排放强度,显示出机器人的工业碳减排效应存在显著的动态叠加特性。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| robot | −0.013*** | −0.013*** | −0.013*** | −0.013*** | −0.020*** | −0.021*** | −0.023*** |
| (0.005) | (0.004) | (0.004) | (0.004) | (0.006) | (0.007) | (0.008) | |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | |
| Constant | 1.454*** | 4.408*** | 4.226*** | 4.230*** | 4.199*** | 4.675*** | 4.431*** |
| (0.015) | (0.811) | (0.852) | (0.949) | (1.613) | (1.538) | (1.227) | |
| 观测值 | 3406 | 3406 | 3144 | 2882 | 2620 | 2358 | 2096 |
| R2 | 0.854 | 0.878 | 0.883 | 0.893 | 0.907 | 0.918 | 0.928 |
| 注:*、**和***分别为10%、5%和1%的显著性水平,括号内报告了城市层面的聚类稳健标准误,所有模型均控制了时间和城市固定效应,下表同。 | |||||||
(二)内生性处理
1. 工具变量法。本文选择如下四种工具变量进行重新估计:一是借鉴孙早和侯玉琳(2021)的研究,使用去除本市的其他同省份城市的工业机器人渗透度的均值作为工具变量;二是参照易行健和周利(2018)的研究,采用地级市工业机器人渗透度的滞后一期与工业机器人渗透度时间上的一阶差分的乘积构造工具变量;三是参照王晓娟等(2022)的研究,使用美国制造业工业机器人渗透度作为工具变量;四是采用Lewbel(2012)提出的异方差工具变量法进行内生性处理。Kleibergen-Paap rk LM检验结果均显著拒绝工具变量识别不足的原假设,Cragg-Donald Wald F统计值均大于10%的临界值,表明工具变量不存在弱识别问题。根据估计结果,工业机器人的估计系数显著为负,即工业机器人能够抑制城市工业碳排放,这与基准结论保持一致,说明在缓解潜在的内生性问题之后,假说1仍然成立。
2. 外生政策冲击。除了采用IV-2SLS估计之外,我们寻找外生政策冲击作为准自然实验,并采用双重差分(DID)模型进一步处理内生性问题。党的十七大首次提出了“两化融合”这一概念,即推动工业化与信息化的深度融合。工信部于2008年开启国家级“两化融合试验区”。根据各地区的建设方案,可以发现“两化融合”主要是利用信息技术赋能,全力推动信息技术在工业领域的渗透和深度运用(李磊等,2022)。因此,我们认为国家级“两化融合试验区”推动了工业智能化发展,可以被视为城市工业机器人应用的外生冲击政策。
工信部分别在2008年、2009年和2011年开启了两个批次共16个国家级“两化融合试验区”。我们构建多时点双重差分模型检验工业智能化的碳减排效应。如果城市被批复成为试验区,则当年及其之后设定为1,否则为0。由于“呼、包、鄂”三个城市在2008年10月才被批复成为试验区,故和李磊等(2022)研究一致,将上述三个城市的政策起始年份设定为2009年。根据估计结果,发现无论是否添加控制变量,国家级“两化融合试验区”政策的估计系数均显著为负。这表明在采用外生政策冲击解决内生性问题后,工业智能化依旧具有显著的碳减排效应,进一步佐证了前文的结论。
(三)稳健性检验
为了确保基准回归结果可靠,本文还从替换被解释变量、更换解释变量、剔除直辖市等方面进行稳健性检验。具体来说,将被解释变量替换为碳排放总量的对数值(lnco)。借鉴韩峰和谢锐(2017)的研究,计算城市工业碳排放强度(lnindco1)。在样本期内,中国陆续推出众多以减低碳排放为目标的环境政策,以及推动工业信息化发展的试点政策,我们控制了低碳试点城市政策、工业化和信息化两业融合政策以尽可能排除政策干扰。回归结果表明,工业机器人的估计系数显著为负,说明工业机器人的确能够显著抑制城市工业碳排放强度,证明假说1成立,这也进一步佐证了理论模型与基准回归的分析结论。
(四)异质性分析
1. 城市规模。工业机器人的环境效应在不同规模城市中具有不确定性。为了加以验证,本文按《关于调整城市规模划分标准的通知(2014)》的划分标准,分为大城市和中小城市进行分组估计。根据回归结果,工业机器人的估计系数均显著为负,组间差异系数的检验结果表明,工业机器人的碳减排效应在中小城市更大。这就意味着工业机器人能够更好地推动中小城市绿色低碳转型。
2. 资源禀赋。本文根据2013年颁布的《全国资源型城市可持续发展规划(2013−2020年)》将样本划分为资源型城市和非资源型城市两组进行估计。根据回归结果,工业机器人的估计系数在非资源型城市显著为负,而在资源型城市的影响不显著,且通过了组间差异系数检验,表明现阶段工业机器人仍难以突破资源型城市依靠煤炭资源开采和加工的产业“路径依赖”发展模式。
3. 数字化水平。本文借鉴赵涛等(2020)的指标体系,运用主成分分析方法测算2011—2019年各个城市的数字化水平,并按中位值将样本划分为两组进行估计。根据回归结果,只有在数字化水平较高的城市,工业机器人才能发挥减碳作用,而在数字化水平较低的城市,工业机器人的估计系数不显著。因此,数字化进程为实现工业智能制造提供了技术、资本和人才等生产要素支撑,更有利于城市低碳发展。
4. 城市区位。本文按东部和中西部分组的回归结果证实了上述结论。根据回归结果,工业机器人的估计系数在东部城市显著为负,而在中西部城市则不显著,表明工业机器人的使用能够有效降低东部城市的工业碳排放。此外,我国北方城市传统重工业比重较高,不利于减碳。为了加以验证,我们将城市样本划分为南方和北方两组进行检验。回归结果表明,工业机器人显著抑制南方城市的工业碳排放,而对北方城市的影响不显著。
五、作用机制与实现条件
(一)影响机制检验
人工智能影响城市经济低碳化发展的影响机制仍然有待进一步验证。本文构建交互项模型进行机制检验,以验证假设2和假设3:
| $ {\mathrm{ln}indco}_{it}={\beta }_{0}{+\beta }_{1}{robot}_{it}{+\beta }_{2}{M}_{it}{+\beta }_{3}{M}_{it}\times {robot}_{it}+\gamma {X}_{it}+{\mu }_{it}+{\delta }_{it}+{\varepsilon }_{it} $ | (22) |
其中,
| $ hmatch= \sqrt{U\times V} $ | (23) |
其中,U=
| (1) | (2) | (3) | (4) | (5) | |
| robot | 0.013 | 0.010 | |||
| (0.013) | (0.011) | ||||
| M | 0.015 | 0.147 | |||
| (0.016) | (0.253) | ||||
| M×robot | −0.004** | −0.036** | |||
| (0.002) | (0.015) | ||||
| robot(
|
−0.009** | −0.006 | 0.0005 | ||
| (0.004) | (0.005) | (0.005) | |||
| robot
|
−0.019*** | −0.018*** | −0.015*** | ||
| (0.004) | (0.004) | (0.004) | |||
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 观测值 | 3406 | 3406 | 3406 | 3406 | 3406 |
| R2 | 0.879 | 0.879 | 0.428 | 0.431 | 0.431 |
在表3列(1)中,交互项的估计系数显著为负,说明绿色技术创新是工业机器人实现工业碳减排的重要影响机制。随着城市绿色技术创新水平提升,城市工业具有先进的低碳生产体系,并且能够激活生产和优化管理机器人的活力,进一步激发工业机器人的工业碳减排效应。列(2)中,交互项的估计系数为−0.036,且在5%的显著性水平下显著,表明人机匹配度强化工业机器人对工业碳排放的抑制作用。当人机匹配程度较低时,工业机器人和劳动者之间并不能实现充分协作,导致生产率的损失,即存在“索洛悖论”,制约工业机器人发挥工业碳减排效应。随着人力资本水平的不断提升,高技能劳动者与工业机器人之间的配合程度越来越高,熟练地将工业机器人运用到工业生产、管理、运输和销售等各个环节,有效强化了工业机器人对工业碳排放的抑制作用。综上所述,随着城市绿色技术创新水平和人机匹配度的提升,工业机器人的工业碳减排效应得以进一步强化,从而假设2和假设3也成立。
(二)实现条件
为了进一步考察工业机器人发挥工业碳减排效应的实现条件,本文构建如下门槛模型进行估计:
| $ {\mathrm{ln}indco}_{it}={\beta }_{0}{+\beta }_{1}{robot}_{it}\cdot I\left({T}_{it}\le \phi \right){+\beta }_{1}{robot}_{it}\cdot I\left({T}_{it} > \phi \right)+\gamma {X}_{it}+{\mu }_{it}+{\delta }_{it}+{\varepsilon }_{it} $ | (24) |
其中,T为门槛变量,I(ˑ)为根据不同门槛值进行分段的指示函数;
门槛模型的回归估计结果见表3。首先,根据表3列(3)的估计结果可知,互联网普及率越高,工业机器人的工业碳减排效应也就越大,工业机器人的工业碳减排效应呈现边际递增的趋势。其次,工业机器人的使用对劳动者的技能水平提出了较高要求,要充分激活以工业机器人为代表的城市工业智能化建设,就需要依靠人力资本。表3列(4)的估计结果表明,只有当人力资本水平越过门槛时,工业机器人才能显著抑制工业碳排放,目前有30%的城市跨过了门槛值。最后,在推进工业智能化转型过程中,技术创新不仅要依靠市场的力量,也离不开政府的引导和支持。政府科技支出反映了政府部门对城市技术创新的支持力度。表3列(5)的结果表明,只有当科技财政支出占比大于门槛值时,工业机器人才能充分发挥工业碳减排效应。
六、结论与政策建议
在我国将智能制造提升至国家发展战略的时代背景下,工业机器人作为智能制造的重要表现形式,为降低工业碳排放提供了强大的动力。本文将能源和环境因素纳入任务模型,构建包含机器人、能源要素投入和环境因素的理论模型,并利用2007—2019年的中国城市面板数据实证检验工业机器人对工业碳排放的影响效应与作用机制,探索工业机器人减碳效应的实现条件。理论模型和实证研究均表明工业机器人有效降低了城市工业碳排放强度。异质性分析表明,工业机器人对非资源型城市、数字化水平较高城市、东部及南方城市的工业碳排放强度产生抑制作用,但对资源型城市、数字化水平较低城市、中西部及北方城市的碳减排作用不显著。影响机制检验发现,绿色技术创新和人机匹配度是工业机器人抑制城市工业碳排放强度的重要影响机制。工业机器人的碳减排效应随着互联网普及率、人力资本水平和政府科技投入的提升呈现边际效应递增态势。
上述研究结论为推动我国完善工业机器人的运用、降低城市工业碳排放提供了重要的政策启示。第一,大力推广应用工业机器人,提升工业智能化水平。为了充分发挥工业机器人的碳减排效应,应加大对国内机器人的技术研发投入,通过自主研发减少对国外操作系统等核心零部件和集成系统的依赖,以此大幅降低国产工业机器人的使用成本。另外,鼓励企业推动就业结构优化,引进机器操作人才,同时加大企业内部人才教育培训的投入,完善职工技术培训体系,实现企业内部的知识溢出,通过设备和人才的双重作用,加速工业智能技术的使用和扩散实现碳减排。第二,因地制宜实施差别化的环境政策。对于中西部地区、北方城市和小城市,应加快淘汰高耗能落后产业,加强城市工业互联网建设,并为企业使用机器人生产提供资金、技术和人才等方面的支持。对于东部、南方和大型城市,应拓宽工业机器人的运用场景,注重工业机器人的升级换代和智能制造的技术突破,为释放环境红利提供条件。非资源型城市通过知识和技术扩散效应实现工业及其他部门的智能化转型发展,拓宽工业机器人的减碳空间。第三,加强绿色技术创新,提高人机协作能力。通过减税、财政补贴等财税、金融政策支持,激发市场创新创业活力,尤其是鼓励企业积极开展绿色技术创新。由于较低的人机协调能力制约工业机器人发挥碳减排效应,政府部门应当通过人才政策吸引高端自动化技术等方面的人才以匹配工业机器人的研发、生产和操作。企业则应注重数智化技术人才的职业培训,提升整体的人机匹配度。此外,应继续加强城市宽带建设,通过建立数智化人才集聚的制度设计,增强城市对人才的吸引力。同时加大科技研发的支持力度,为激活社会创新活力提供重要的人才和资金保障,推动城市经济社会绿色低碳运行和高质量发展。
| [1] | 韩峰, 谢锐. 生产性服务业集聚降低碳排放了吗?——对我国地级及以上城市面板数据的空间计量分析[J]. 数量经济技术经济研究, 2017(3): 40–58. |
| [2] | 胡晟明, 王林辉, 赵贺. 人工智能应用、人机协作与劳动生产率[J]. 中国人口科学, 2021(5): 48–62. |
| [3] | 黄向岚, 张训常, 刘晔. 我国碳交易政策实现环境红利了吗?[J]. 经济评论, 2018(6): 86–99. |
| [4] | 黄赜琳, 朱保华. 中国的实际经济周期与税收政策效应[J]. 经济研究, 2015(3): 4–17,114. |
| [5] | 李磊, 刘常青, 韩民春. 信息化建设能够提升企业创新能力吗?——来自“两化融合试验区”的证据[J]. 经济学(季刊), 2022(3): 1079–1100. |
| [6] | 李磊, 王小霞, 包群. 机器人的就业效应: 机制与中国经验[J]. 管理世界, 2021(9): 104–118. |
| [7] | 邵帅, 范美婷, 杨莉莉. 经济结构调整、绿色技术进步与中国低碳转型发展——基于总体技术前沿和空间溢出效应视角的经验考察[J]. 管理世界, 2022(2): 46–69. |
| [8] | 邵帅, 张可, 豆建民. 经济集聚的节能减排效应: 理论与中国经验[J]. 管理世界, 2019(1): 36–60. |
| [9] | 孙鹏博, 葛力铭. 通向低碳之路: 高铁开通对工业碳排放的影响[J]. 世界经济, 2021(10): 201–224. |
| [10] | 孙早, 侯玉琳. 工业智能化与产业梯度转移: 对“雁阵理论”的再检验[J]. 世界经济, 2021(7): 29–54. |
| [11] | 唐松, 伍旭川, 祝佳. 数字金融与企业技术创新——结构特征、机制识别与金融监管下的效应差异[J]. 管理世界, 2020(5): 52–66. |
| [12] | 汤维祺, 吴力波, 钱浩祺. 从“污染天堂”到绿色增长——区域间高耗能产业转移的调控机制研究[J]. 经济研究, 2016(6): 58–70. |
| [13] | 唐晓华, 迟子茗. 工业智能化提升工业绿色发展效率的实证研究[J]. 经济学家, 2022(2): 43–52. |
| [14] | 王晓娟, 朱喜安, 王颖. 工业机器人应用对制造业就业的影响效应研究[J]. 数量经济技术经济研究, 2022(4): 88–106. |
| [15] | 魏下海, 张沛康, 杜宇洪. 机器人如何重塑城市劳动力市场: 移民工作任务的视角[J]. 经济学动态, 2020(10): 92–109. |
| [16] | 薛飞, 陈煦. 绿色财政政策的碳减排效应——来自“节能减排财政政策综合示范城市”的证据[J]. 财经研究, 2022(7): 79–93. |
| [17] | 杨莉莎, 朱俊鹏, 贾智杰. 中国碳减排实现的影响因素和当前挑战——基于技术进步的视角[J]. 经济研究, 2019(11): 118–132. |
| [18] | 易行健, 周利. 数字普惠金融发展是否显著影响了居民消费——来自中国家庭的微观证据[J]. 金融研究, 2018(11): 47–67. |
| [19] | 余壮雄, 陈婕, 董洁妙. 通往低碳经济之路: 产业规划的视角[J]. 经济研究, 2020(5): 116–132. |
| [20] | 袁晓玲, 张宝山, 杨万平. 基于环境污染的中国全要素能源效率研究[J]. 中国工业经济, 2009(2): 76–86. |
| [21] | 张华. 低碳城市试点政策能够降低碳排放吗?——来自准自然实验的证据[J]. 经济管理, 2020(6): 25–41. |
| [22] | 张万里, 宣旸. 智能化如何提高地区能源效率?——基于中国省级面板数据的实证检验[J]. 经济管理, 2022(1): 27–46. |
| [23] | 赵军, 刘春艳, 李琛. 金融发展对碳排放的影响: “促进效应”还是“抑制效应”?——基于技术进步异质性的中介效应模型[J]. 新疆大学学报(哲学·人文社会科学版), 2020(4): 1–10. |
| [24] | 赵涛, 张智, 梁上坤. 数字经济、创业活跃度与高质量发展——来自中国城市的经验证据[J]. 管理世界, 2020(10): 65–75. |
| [25] | 周广肃, 丁相元. 工业机器人应用对城镇居民收入差距的影响[J]. 数量经济技术经济研究, 2022(1): 115–131. |
| [26] | Acemoglu D, Restrepo P. Modeling automation[J]. AEA Papers and Proceedings, 2018, 108: 48–53. DOI:10.1257/pandp.20181020 |
| [27] | Acemoglu D, Restrepo P. Automation and new tasks: How technology displaces and reinstates labor[J]. Journal of Economic Perspectives, 2019, 33(2): 3–30. DOI:10.1257/jep.33.2.3 |
| [28] | Acemoglu D, Restrepo P. Robots and jobs: Evidence from US labor markets[J]. Journal of Political Economy, 2020, 128(6): 2188–2244. DOI:10.1086/705716 |
| [29] | Autor D H, Levy F, Murnane R J. The skill content of recent technological change: An empirical exploration[J]. The Quarterly Journal of Economics, 2003, 118(4): 1279–1333. DOI:10.1162/003355303322552801 |
| [30] | Chen X H, Gong X M, Li D Y, et al. Can information and communication technology reduce CO2 emission? A quantile regression analysis [J]. Environmental Science and Pollution Research, 2019, 26(32): 32977–32992. DOI:10.1007/s11356-019-06380-8 |
| [31] | Ghobakhloo M, Fathi M. Industry 4.0 and opportunities for energy sustainability[J]. Journal of Cleaner Production, 2021, 295: 126427. DOI:10.1016/j.jclepro.2021.126427 |
| [32] | Graetz G, Michaels G. Robots at work[J]. The Review of Economics and Statistics, 2018, 100(5): 753–768. DOI:10.1162/rest_a_00754 |
| [33] | Kromann L, Malchow-Møller N, Skaksen J R, et al. Automation and productivity—a cross-country, cross-industry comparison[J]. Industrial and Corporate Change, 2020, 29(2): 265–287. |
| [34] | Lange S, Pohl J, Santarius T. Digitalization and energy consumption. Does ICT reduce energy demand?[J]. Ecological Economics, 2020, 176: 106760. DOI:10.1016/j.ecolecon.2020.106760 |
| [35] | Lee K H, Min B. Green R&D for eco-innovation and its impact on carbon emissions and firm performance[J]. Journal of Cleaner Production, 2015, 108: 534–542. DOI:10.1016/j.jclepro.2015.05.114 |
| [36] | Lewbel A. Using heteroscedasticity to identify and estimate mismeasured and endogenous regressor models[J]. Journal of Business & Economic Statistics, 2012, 30(1): 67–80. |
| [37] | Li M J, Tao W Q. Review of methodologies and polices for evaluation of energy efficiency in high energy-consuming industry[J]. Applied Energy, 2017, 187: 203–215. DOI:10.1016/j.apenergy.2016.11.039 |
| [38] | Li Y Y, Zhang Y R, Pan A, et al. Carbon emission reduction effects of industrial robot applications: Heterogeneity characteristics and influencing mechanisms[J]. Technology in Society, 2022, 70: 102034. DOI:10.1016/j.techsoc.2022.102034 |
| [39] | Remes J, Mischke J, Krishnan M. Solving the productivity puzzle: The role of demand and the promise of digitization[J]. International Productivity Monitor, 2018, 34: 28–51. |
| [40] | Shan Y L, Guan D B, Zheng H R, et al. China CO2 emission accounts 1997-2015 [J]. Scientific Data, 2018, 5(1): 170201. DOI:10.1038/sdata.2017.201 |
| [41] | Sun H Y, Kim G. The composite impact of ICT industry on lowering carbon intensity: From the perspective of regional heterogeneity[J]. Technology in Society, 2021, 66: 101661. DOI:10.1016/j.techsoc.2021.101661 |
| [42] | Vinuesa R, Azizpour H, Leite I, et al. The role of artificial intelligence in achieving the Sustainable Development Goals[J]. Nature Communications, 2020, 11(1): 233. DOI:10.1038/s41467-019-14108-y |
| [43] | Wang E Z, Lee C C, Li Y Y. Assessing the impact of industrial robots on manufacturing energy intensity in 38 countries[J]. Energy Economics, 2022, 105: 105748. DOI:10.1016/j.eneco.2021.105748 |
| [44] | Xu T T, Kang C Y, Zhang H. China's efforts towards carbon neutrality: Does energy-saving and emission-reduction policy mitigate carbon emissions?[J]. Journal of Environmental Management, 2022, 316: 115286. DOI:10.1016/j.jenvman.2022.115286 |
| [45] | Zhou X Y, Zhou D Q, Wang Q W, et al. How information and communication technology drives carbon emissions: A sector-level analysis for China[J]. Energy Economics, 2019, 81: 380–392. DOI:10.1016/j.eneco.2019.04.014 |

