
2023第49卷第3期
一、引 言
党的二十大明确指出,要建立健全覆盖全民、统筹城乡、公平统一、安全规范、可持续的多层次社会保障体系,坚持“可持续”的基本方针,首次提出“安全规范”的新要求。然而,我国企业职工基本养老保险基金的可持续性正在逐年减弱,财政部发布的《社会保险基金收支决算报告》显示,2018年企业职工基本养老保险基金征缴收入和基本养老金支出分别为29507.15亿元和30279.84亿元,当期收支缺口为772.69亿元,2019年增至3181.33亿元,2020年当期收支缺口上升到15155.92亿元,两年时间增加近19倍。若缺乏有效政策干预,这一缺口还将继续扩大(吕有吉等,2021)。
新冠疫情对经济社会产生了显著影响,也对基本养老保险基金的可持续性提出了新的挑战。在疫情之下,企业生产经营受到限制,用工需求降低,缴费基数、缴费人数下降,这加剧了养老保险基金收支矛盾(席恒,2022)。基金可持续风险已然显现,需要建立可持续风险预警机制,通过动态监测及时发布预报,切实采取防范措施,确保基金安全和规范运行。
现有文献对城镇职工基本养老保险基金的收支预测研究有很多,主要基于基金收支缺口研究养老保险基金的可持续性。一方面,若无政策干预,基金可持续性将逐渐恶化。刘学良(2014)认为,城镇职工基本养老保险基金于2023年开始当期收入将不能弥补当期支出,累计结余将于2029年耗尽,2050年当期赤字为当年GDP的8.70%。王翠琴等(2021)测算发现,自2019年起,城镇职工基本养老保险基金已收不抵支,累计滚存结余下降明显,2023年首次出现负值,2035年将会达到−82.75万亿元。另一方面,若实行非财政补贴等外部融资的政策干预,基金可持续性则会有所改善,但在未来年份仍会面临风险。比如,征收体制改革有利于提升征缴率(Enoff和Mckinnon,2011),但即使征缴率提升至100%,基金于2036年就会不可持续,基金累计赤字耗尽时点仅向后延迟1至11年,2050年累计赤字将超141万亿元(曾益等,2019)。延迟退休能够增加养老金总额(杨钒,2020),男性与女性职工每年延退6个月后,累计赤字时点延后21年至2057年(曾益等,2021)。提高基金统筹层次显著降低基金收入,但不影响基金支出(朱恒鹏等,2020),全国统筹后首次出现累计赤字时间为2023年,2050年累计赤字将达1567.17万亿元(曾益和杨悦,2021)。尽管学者们运用不同的模型、方法和参数,测算基金累计结余耗尽时间和赤字规模有所差异,但对未来年份我国城镇职工基本养老保险基金可持续性不容乐观的结论达成一致。
上述文献从不同政策背景展开研究,但仍存在以下几点不足:第一,未考虑疫情的影响。较少文献考虑新冠疫情对基金收支的影响,并且对疫情影响进行直接假设,赵亮和李灯强(2020)将疫情期间缴费基数增长率直接设定为比无疫情时低0.5%。第二,未区分灵活就业人员与企业职工的参保差异。灵活就业人员参保享受“低缴费、同待遇”的政策优惠,即缴费率低于企业职工总缴费比例4%,缴费档次自主选择,但养老金计发调整与企业职工相同,大多研究忽略了这一政策安排。第三,基金可持续风险覆盖面过窄。当前对基金可持续的研究仅局限于财务可持续上,忽略了基金可持续应当是筹资可持续、财务可持续和待遇可持续的有机结合。
为及时监测养老保险基金可持续风险,需要建立预警机制。一方面,在预警理论研究上,集中探讨预警系统的建立。王柱和方彬(2014)提出养老保险基金收支预测预警系统的设计框架与实现步骤。何文炯等(2002)基于基金支付能力、赡养率、成本率、养老金率四个预警指标,建立预警模型,设计预警系统。王翠琴和薛惠元(2011)从制度设计风险、筹资风险、基金保值增值风险、给付风险、管理风险和制度环境风险六大方面选择指标,建立了新农保风险预警指标体系。另一方面,在预警实证分析上,主要监测单一的可持续风险。朱衡(2015)预测了2013—2018年养老保险基金的财务风险警情。汪泓(2008)运用系统动力学模型与计算机仿真技术模拟了上海市养老保险基金运营状况,建立GARCH模型划分警区,对基金积存量的警情做出预警预报。然而,以上研究主要强调预警系统的构建原则,预警指标设计全面但针对性不强,神经网络等预警技术复杂导致可推广性受限,对预警过程的描述过于模糊。因此,养老保险基金可持续风险预警研究有待补充完善。
在此背景下,本文基于新冠疫情这一外生冲击影响程度,划分三种疫情风险情景:疫情低风险情景、疫情中风险情景和疫情高风险情景。本文以无疫情情景为对照,测算在不同情景下,2022—2051年企业职工基本养老保险基金的收支结余状况,并构建基金可持续风险监测预警系统。结果表明:疫情影响每提高一个风险等级,测算期间的基金收入累计现值平均降低23.45%,基金支出累计现值平均降低7%,而基金累计结余现值之和平均降低59.76%。在疫情冲击下,如果不采取有效的应对措施,企业职工基本养老保险基金累计结余将于2030—2032年耗尽,并且赤字规模逐年增大。因此,需要建立基金可持续风险预警机制。在可持续风险预警系统下,基金筹资风险权重最大,基金给付风险次之,基金积累风险最小,该系统警示与无疫情情景相比,疫情提高了基金可持续风险警级。不同疫情风险情景下,可持续风险警级在测算前期均为轻警,持续年限有所差异,之后提升至中警。通过对关键警源进行敏感性监测,发现不同警源对三类风险指标影响程度和方向不同,影响程度较大的是退休年龄和工资增长率,征缴率、基金保值增值率影响居中,而总和生育率与就业率影响较小。
相比现有研究,本文的边际贡献在于:第一,合理评估了疫情对基金收支的影响。本文运用双重差分方法评估疫情冲击,并通过情景分析技术研究疫情影响的不确定性。不仅考虑了疫情对人口、经济和政策等多类参数的影响,还考虑了疫情影响程度的差异。第二,构建了“筹资、积累和给付”三位一体的养老保险基金可持续风险监测预警系统。从学术价值上,本文对预警系统进行了理论构建,详细描述预警的基本要件,并对可持续风险预警系统进行实证分析。从实践意义上,本文建立了一个通用预警系统,设计了预警全流程。各地社保部门只需载入当地数据即可得到预警结果,也为建立自定义的基金风险预警系统提供了参考。第三,建立“预测、预警和预控”的风险防控体系。本文基于养老保险基金收支预测结果,进行基金可持续风险预警分析,并从警源调整角度明确预控对策,不仅完善了养老保险基金风险防控体系,也为有效应对和防范化解重大风险提供参考。
余下内容的安排如下:第二节构建精算模型,第三节进行参数设置,第四节报告在疫情冲击下基金收支预测结果,第五节构建可持续风险预警系统,最后总结结论和提出建议。
二、精算模型
根据就业模式将企业职工基本养老保险的参保者分为企业职工(或称为“企业正规就业者”)和灵活就业人员两个群体,分别测算基金收支。基于《国务院关于建立统一的企业职工基本养老保险制度的决定》(国发〔1997〕26号)划分企业职工“参保身份”:1997年及之前退休为“老人”,1997年之前就业但未退休为“中人”,而1997年及之后就业为“新人”。《国务院关于完善企业职工基本养老保险制度的决定》(国发〔2005〕38号)为灵活就业人员参保提供了法律依据,据此划分灵活就业人员“参保身份”:2005年及之前退休为“老人”,2005年之前就业但未退休为“中人”,而2005年及之后就业为“新人”。基于政策文件和实践安排,灵活就业“老人”无职工养老金,灵活就业“中人”无过渡养老金。精算模型的构建参考石晨曦(2018)、杨再贵和陈肖华(2021)的研究和相关政策规定,测算期为2022—2051年。
(一)基金收入模型
基金收入由参保人数、缴费基数、缴费率、征缴率和连续缴费概率决定,公式如下:
| AIt=[(∑3i=1∑ri−1x=aiNit,x)−wtd1(R1i,t+R2i,t)+(∑2j=1∑rj−1x=ajNjt,x)−wtd2(R1j,t+R2j,t)]⋅αt⋅∂t | (1) |
其中,
(二)基金支出模型
由于不同“参保身份”群体的养老金计发办法存在差异,基金支出
| AEt=AELt+AEZt+AEXt+AEIDt | (2) |
1. “老人”养老金支出
如果测算区间
| AELt=∑ωx=r+t−zNLt,xPt,x=∑ωx=r+t−zNLt,x(1+b)x−rRtSt−1,r−1=∑ωx=r+t−zNLt,x(1+b)x−rRt(1+s)r−1−eSt,e/(1+g) | (3) |
2. “中人”养老金支出
如果测算区间
| AEZt=ω∑x=r+t−zNZt,xBzt,x+ω∑x=r+t−zNZt,xTzt,x+ω∑x=r+t−zNZt,xIzt,x=ω∑x=r+t−zNZt,x{−St−(x−r)−12[1+∂tdt−(x−r)−zt−(x−r)−z∑k=1St−(x−r)−k−1,r−k−1−St−(x−r)−k−1][t−(x−r)−z]%∏th=t−(x−r)1+ρh1+ρt}+ω∑x=r+t−zNZt,x{−St−(x−r)−1∂tdt−(x−r)−z[t−(x−r)−z∑k=1St−(x−r)−k−1,r−k−1−St−(x−r)−k−1]ε{r−e−[t−(x−r)−z]}%∏th=t−(x−r)1+ρh1+ρt}+ω∑x=r+t−zNZt,x{12m∂tdR1Sz−1,x−[t−(z−1)]1+gz−2t−(x−r)−z−1∑n=0[n∏k=0(1+gz−2+k)t−(x−r)−z−1∏h=n(1+vz+h)]} | (4) |
3. “新人”养老金支出
如果测算区间
| AEXt=ω∑x=r+t−zNXt,xBxt,x+ω∑x=r+t−zNXt,xIxt,x=ω∑x=r+t−zNXt,x{−St−(x−r)−12[1+∂tdr−er−e∑k=1St−(x−r)−k−1,r−k−1−St−(x−r)−k−1](r−e)%∏th=t−(x−r)1+ρh1+ρt}+ω∑x=r+t−zNXt,x{12m∂tdR1St−(r−e)−1,e−11+gt−(r−e)−2r−e−1∑n=0[n∏k=0(1+gt−(r−e)−2+k)r−e−1∏h=n(1+vt−(r−e)+h)]} | (5) |
4. 个人账户余额返还性支出
在退休前死亡需返还其所有个人账户养老金,在计发月数内死亡需返还其剩余个人账户养老金,因此这两部分支出需计入基金支出,则t年个人账户余额返还性支出
| AEIDt=∂tdR1∑r−1x=eSt−1,x−1∑x−e+1k=1(1+gt−11+vt∏kn=11+vt−n+11+gt−n)Dt,x+∑r−[m/12]−1x=r(m/12−x+r−1)It,xDt,x | (6) |
(三)当期结余模型
当期结余
| CSt=AIt−AEt | (7) |
(四)累计结余模型
当年累计结余
| ASt={ASt−1(1+τt−1)+CSt,ASt−1>0ASt−1+CSt,ASt−1⩽0 | (8) |
其中,
三、参数设置
(一)人口预测
1. 城镇人口结构
以2020年第七次全国人口普查为基准数据,采用队列要素法,上一年分年龄、性别人口结构乘以生存概率和城镇化率,再考虑分年龄、性别乡城迁移人口,得到下一年城镇人数,最后乘以分年龄、性别就业率,得到各年城镇就业人口结构。其中,分年龄、性别的生存概率由第七次全国人口普查数据得到。根据“十四五”规划纲要,城镇化率预计在“十四五”期间年均提高0.8%至80%,之后保持不变(王金营和戈艳霞,2016)。初始就业和参保年龄为最低劳动年龄16岁,极限年龄为100岁。
新生儿人数为15—49岁育龄妇女人数与对应年龄平均生育率的乘积之和,各年龄平均生育率为分年龄生育率标准化系数与总和生育率的乘积,分年龄生育率标准化系数取2005—2020年平均值,总和生育率(以下简称“生育率”)采用1960—2019年历史数据运用AR-LSTM组合模型预测。其中,AR(2)模型预测时间序列的线性趋势,LSTM长短期记忆算法预测AR模型残差序列的非线性趋势,再将两部分相加(Khashei和Bijari,2011)。其中,AR模型形式和阶数由ADF检验、相关图、偏相关图、模型和系数显著性以及AIC、BIC、HQ信息准则综合判断。出生人口性别比从2020年的111.3线性降至2030年的107,之后保持不变。①
2. 灵活就业人员和企业职工的参保人口结构
灵活就业人数测定采用综合法,以最大值和最小值的均值测算(黄彬云,2014)。从就业部门来看,若城镇单位就业以外均为灵活就业,灵活就业人数最大值为城镇就业人数减去城镇单位就业人数。从参保情况来看,若没有参加企业职工基本养老保险的人员是灵活就业人员,灵活就业人数最小值为城镇就业人数减去在职职工参加养老保险人数。通过求均值得到2000—2020年灵活就业人数,建立ARIMA-LSTM模型预测未来人数,线性部分预测模型为ARIMA(1,1,0)。非私营企业就业人数与私营企业就业人数之和为企业职工就业人数,再乘以在岗率得到2001—2019年企业在岗职工人数,④建立ARIMA-LSTM模型预测未来企业在岗职工人数,线性部分预测模型为ARIMA(1,2,0),女工人和女干部人数之比为4(杨再贵和陈肖华,2021)。
灵活就业参保人数参考郑秉文(2019)的测算,得到2020年灵活就业人员参保率为40%,比上年提高3个百分点。由于大多数灵活就业人员参加城乡居民基本养老保险,在全民参保的全覆盖目标要求下,假定灵活就业人员参保率每年提高3%至45%,之后保持不变。企业职工基本养老保险在职参保人数减去灵活就业参保人数为企业在岗职工参保人数,那么2019年企业职工参保率为80%。参考“十四五”规划纲要目标,假定参保率在2025年匀速提高到95%,之后保持不变。未来企业职工参保人数和灵活就业参保人数为对应就业人数与参保率的乘积。假设在岗职工参保人口结构和城镇就业人口结构一致,得到企业职工和灵活就业在岗职工参保人口结构。参保离退休总人数采用1989—2020年数据建立ARIMA-LSTM模型预测,线性部分预测模型为ARIMA(1,1,1),企业职工和灵活就业离退休人数根据两者当年参保在岗职工人数比例确定,假设离退休人口结构和城镇人口结构一致,从而得到2022—2051年企业职工和灵活就业离退休人口结构。
(二)经济参数
《2021全国毕业生起薪点薪酬报告》中专科毕业生月起薪点为4560元,将此作为2021年全国企业职工新入职人员月平均工资,而正规就业者收入是灵活就业者的1.56倍(薛进军和高文书,2012;张晓昕,2021),那么灵活就业人员新入职月平均工资为2923元。基金保值增值率参考2019年一年期定期存款基准利率与各银行实际存款利率,本文设为2%。工龄工资增长率设为1.58%,高龄养老金增长率设为1.03%(杨再贵和陈肖华,2021),折现率取一年期Shibor同业拆借利率3%。
(三)政策参数
以全口径城镇单位就业人员平均工资为社会平均缴费基数,缴费基数变化通常与经济增速挂钩,在经济新常态背景下,2014—2019年GDP平均增速为8.87%,假定缴费基数增长率在此基础上每十年下降0.5%,直至2%。基础养老金平均增速为缴费基数平均增速的75%。⑤个人账户记账利率取2016—2019年公布的记账利率平均值7.83%。⑥企业职工基本养老保险基金实缴收入来源于《2018—2019年全国社会保险基金收入决算表》,将实缴收入除以应征缴收入得到平均征缴率约为65%。由2001—2020年企业职工基本养老保险基金支出与离退休人数之比得到人均养老金,除以缴费基数得到历年养老金替代率,取均值52%作为“老人”养老金替代率。过渡系数取各省均值1.2%。企业职工按照社会平均缴费基数缴费,设
四、疫情冲击下企业职工基本养老保险基金收支预测
(一)疫情冲击的情景设置
美国联邦社会保险信托委员会(Board of Trustees,2019)在预测养老保险基金收支状况时,通常采用情景分析技术描述未来的不确定性。参考这一方法,测算疫情影响不确定性下养老保险基金的收支结余状况,将参数的可能变化分为疫情低风险情景、中风险情景和高风险情景,三种情景下疫情风险逐渐提升,疫情影响程度逐渐增加。另外,以无疫情情景为对照组,该情景下的基金参数对应第三部分的参数设置。
1. 经济参数
(1)经济增长率
新冠疫情作为一项外生冲击,可构建双重差分模型,评估疫情对经济的影响。由于我国各省份均遭受不同程度的疫情冲击,采取传统双重差分方法将缺少对照组。因此,以疫情影响程度差异为第一重差分,以疫情前后时间差异为第二重差分,通过评估疫情冲击程度的差异,间接测算不同疫情风险情景下的经济增长率,模型如下:
| Yit=β0+β1treati×postt+Z′itβ2+ui+vt+ξit,i=1,⋯,N;t=1,⋯,T | (9) |
其中,i为个体,共有30个省份中234个城市;⑦t为年份,从2014年至2020年;Yit为城市i在t年的经济增长率,用地区生产总值增长率衡量。postt在疫情前为0,疫情后为1。treati表示较低的疫情冲击组时为0,表示较高的疫情冲击组时为1。借鉴分位数回归思想,按照省级维度每百万人口平均累计确诊病例数升序排列,1/3分位数及以下省份对应的城市归为疫情低风险组,1/3分位数以上到2/3分位数归入疫情中风险组,超过2/3分位数为疫情高风险组,分别对应疫情低风险情景、中风险情景和高风险情景。
回归结果如表1,列(1)、列(2)为中风险组与低风险组差分结果,前者为处理组,结果表明疫情导致中风险组的经济增长率比低风险组低1.096%。表1列(3)、列(4)为高风险组与低风险组差分结果,前者为处理组,结果表明疫情导致高风险组的经济增长率比低风险组低3.758%。列(3)、列(4)的回归系数小于列(1)、列(2)的回归系数,说明疫情冲击越大,经济增长率下降幅度越大。褚福灵和司絮(2022)研究了不同疫情情景的经济增长率,在乐观情景下疫情风险较低,2022年经济增长率为7.5%,以此作为疫情低风险情景下的经济增长率。结合双重差分结果,在疫情中风险情景下经济增长率为6.404%,在疫情高风险情景下经济增长率为3.742%。随着不断优化完善疫情防控措施和持续提升疫苗注射率,在三种疫情情景下经济增长率每十年上升0.5%,但不高于无疫情情景。
| (1) | (2) | (3) | (4) | |
| Y | Y | Y | Y | |
| treat×post | −1.510*** | −1.096*** | −3.884*** | −3.758*** |
| (0.383) | (0.358) | (0.742) | (0.704) | |
| Secondind | 0.041** | 0.087*** | ||
| (0.018) | (0.029) | |||
| Socialconsum | −0.273 | −0.245 | ||
| (0.229) | (0.284) | |||
| Budgetexp | 0.171 | 0.648 | ||
| (0.379) | (0.554) | |||
| Deposit | 2.809*** | 3.127** | ||
| (0.836) | (1.236) | |||
| Loan | −0.532 | −1.811 | ||
| (0.609) | (1.136) | |||
| Getechno | −0.144 | −0.433** | ||
| (0.131) | (0.215) | |||
| Indprofit | 0.546*** | 0.468*** | ||
| (0.124) | (0.173) | |||
| Pop | −0.330 | 0.818 | ||
| (0.557) | (0.689) | |||
| 常数项 | 7.047*** | −31.130*** | 6.678*** | −36.960** |
| (0.065) | (11.630) | (0.089) | (16.250) | |
| 城市效应 | 控制 | 控制 | 控制 | 控制 |
| 时间效应 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 1344 | 1344 | 833 | 833 |
| 注:括号内为稳健标准误;*、**和***分别表示10%、5%和1%的显著性水平下显著;列(1)、列(3)为不加控制变量的回归结果,列(2)、列(4)为加上控制变量的回归结果,并且双重差分模型通过了平行趋势检验的建模条件。 | ||||
(2)就业率
关于“失业与工资”的菲利普斯曲线和奥肯定律从理论层面说明了经济增长能促进就业增加,经济下滑导致就业下降。实证研究中通常采用经济增长的就业弹性衡量就业率,即经济变动1个百分点带来的就业变动百分比。Li和Zhao(2010)研究发现中国经济增长的就业弹性在不同发展阶段呈现下降趋势,长期为0.103241(Slimane,2015)。因此,根据三种疫情情景经济增长率的下降幅度,得到疫情低、中、高风险情景下就业率分别降低0.14%、0.25%和0.53%。⑧为稳定就业形势,政府会促进就业,增加岗位。因此,假定就业率下降幅度每五年减小0.05%,直至0。
(3)基金保值增值率
基金增值保值率受宏观经济的影响。因此,在疫情低风险、中风险和高风险情景下,基金保值增值率参考2022年不同疫情风险情景下经济增速之比,但不低于一年期存款基准利率。
2. 人口参数
新冠疫情对总和生育率主要体现为负向影响(Aassve等,2021)。Wang等(2022)运用世界流行病不确定性指数模拟了流行病的不确定性,从防疫措施、经济周期等方面解释了疫情期间生育率下降的原因。Berrington等(2022)结合生育率五年趋势外推及调整因子,预测不同疫情风险情景下的生育率变化。参考该研究得到疫情低、中、高风险情景下生育率调整因子分别为0.89、0.85和0.67。为鼓励生育,我国相继实施“二孩政策”和“三孩政策”,完善相关配套支持措施,故假设生育率调整因子每五年提高5个百分点,但不超过1。
3. 政策参数
(1)基础养老金增长率
基础养老金增长率仍为对应情景下经济增速的75%,保持同步变化。
(2)个人账户记账利率
疫情低、中、高风险情景下个人账户记账利率参考2022年不同疫情风险情景下经济增速之比,得到个人账户记账利率分别为6.62%、5.65%和3.30%。
(3)灵活就业人员缓缴比例
《人力资源社会保障部办公厅、国家税务总局办公厅关于特困行业阶段性实施缓缴企业社会保险费政策的通知》(人社厅发〔2022〕16号)指出,以个人身份参加企业职工基本养老保险的个体工商户和各类灵活就业人员可自愿暂缓缴费至2023年底前补缴。由于缺乏缓缴数据,考虑到我国统筹疫情防控和经济社会发展,假设在低、中、高风险情景下2022年灵活就业人员缓缴比例分别为15%、25%和35%,2023年、2024年连续下降5%,2025年恢复正常缴费。
(二)疫情冲击下的基金收支预测
将四种情景对应的参数分别代入精算模型得到基金收支,如图1所示。一方面,基金收入在不同疫情风险情景下均呈上升趋势,但随疫情风险等级的提升而降低。无疫情情景下基金收入最高,低风险情景次之,中风险和高风险情景下基金收入依次减小,2022—2051年的基金收入折现到2022年的累计现值分别为383.29万亿元、322.52万亿元、268.65万亿元和167.12万亿元。平均来讲,疫情影响每提高一个风险等级,测算期间的基金收入累计现值平均降低23.45%。另一方面,不同疫情风险情景下的基金支出稳步上升,对比来说,疫情风险等级越高,基金支出越低。无疫情、疫情低风险、中风险和高风险情景下的基金支出依次走低,2022—2051年的基金支出折现到2022年的累计现值分别为439.97万亿元、426.01万亿元、405.24万亿元和352.69万亿元。平均来说,疫情影响每提高一个风险等级,测算期间的基金支出累计现值平均降低7%。综上所述,疫情对企业职工基本养老保险基金的收入和支出产生了不同程度的负向作用,并且疫情对基金收入的负向影响大于对基金支出的负向影响。
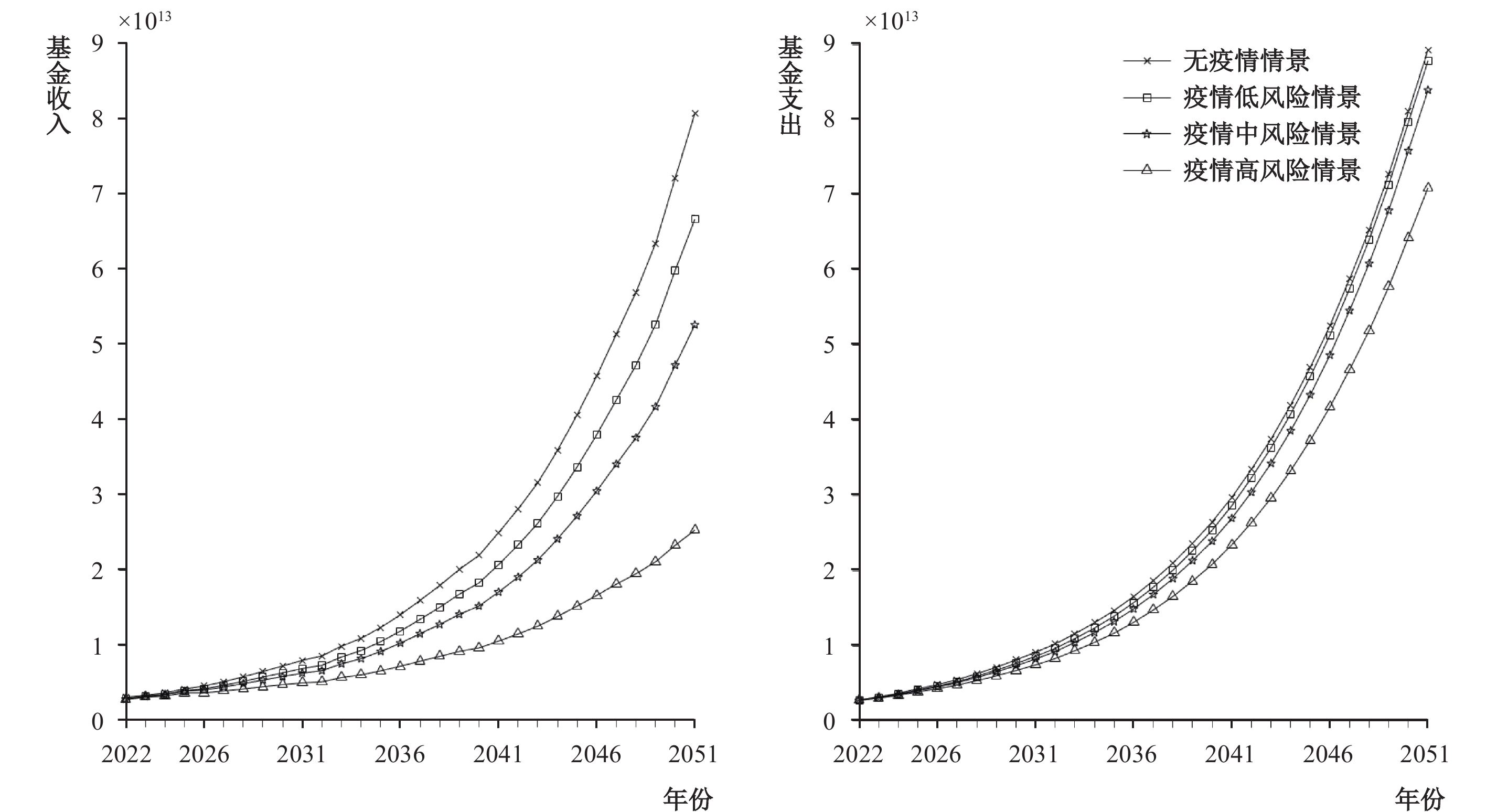
|
| 图 1 2022—2051年企业职工基本养老保险基金收入和基金支出 |
(三)疫情冲击下的基金结余预测
截至2021年底,企业职工基本养老保险基金累计结余约5.1万亿元,未来年份不同疫情风险情景下的基金结余测算结果如图2所示。在无疫情情景下,2021年累计结余由1989—2019年基金累计结余趋势外推得到,约为6.03万亿元。无疫情情景的当期结余和累计结余最大,大于疫情低风险情景,中风险情景次之,高风险情景最小。平均来讲,疫情影响每提高一个风险等级,测算期间的基金累计结余现值之和平均降低59.76%。主要原因是疫情对基金收入的负向影响大于基金支出。疫情风险提高导致当期基金收入的减少值高于当期基金支出的减少值,从而使得基金收入累计现值降幅大于基金支出累计现值降幅。因此,疫情愈严峻,基金结余也越少。
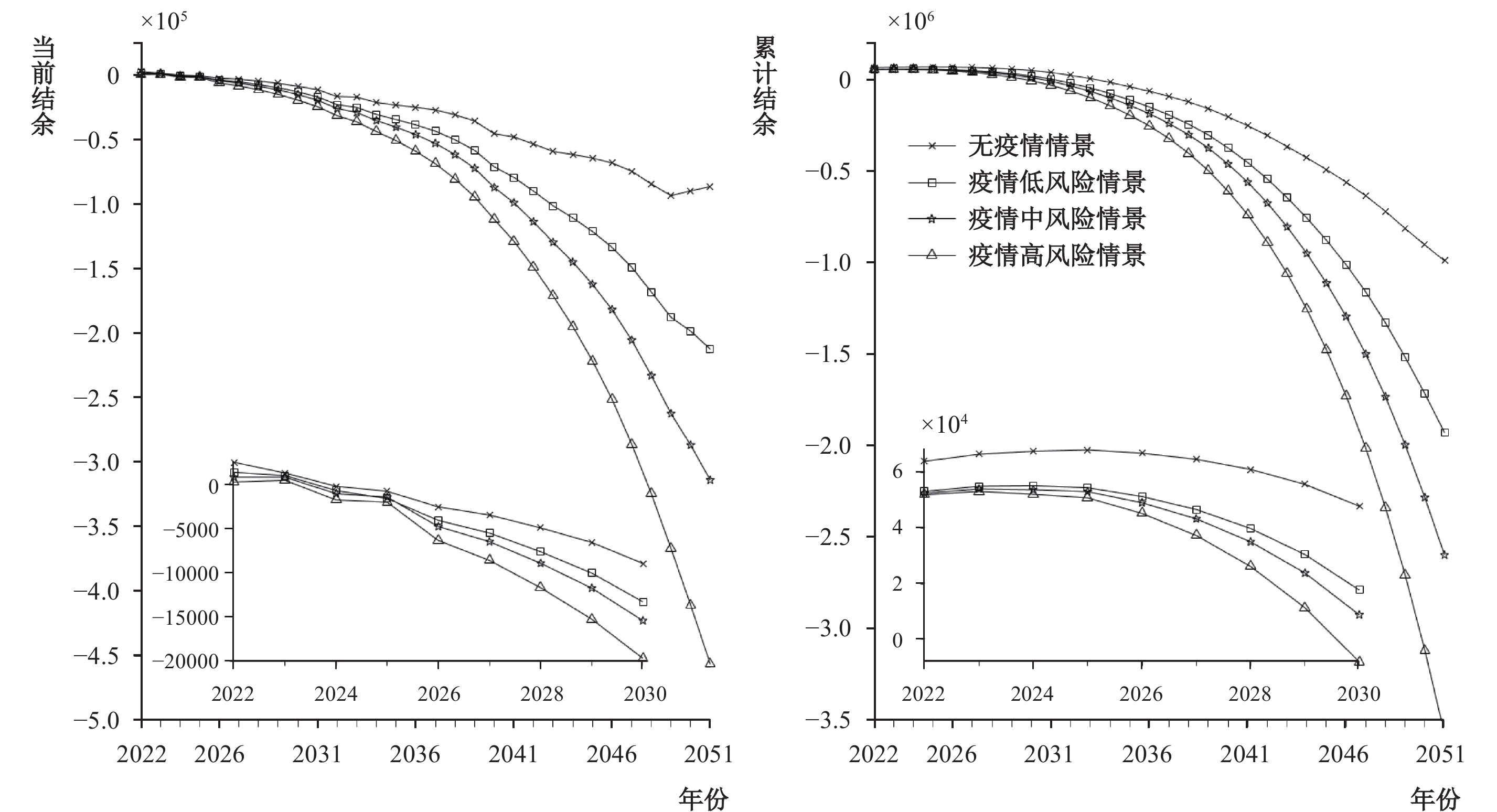
|
| 图 2 2022—2051年企业职工基本养老保险基金当期结余和累计结余 |
疫情风险由低到高的四种情景下,当期收不抵支时点均为2024年,并且收支缺口逐年扩大,累计结余耗尽时点分别为2034年、2032年、2031年和2030年。在疫情冲击下,企业职工基本养老保险基金累计结余可持续时间仅维持8—10年至2029—2031年。因此,需要建立基金可持续风险预警机制,监测警源,防范化解基金风险。
五、疫情冲击下企业职工基本养老保险基金可持续风险预警
(一)可持续风险预警系统的理论构建
养老保险基金可持续风险预警系统是基于一定的预测方法,由各类反映养老保险基金可持续风险的预警指标及其警情、警级的未来演化趋势构成的有机整体,其度量基金状态偏离预警线的强弱程度,发出预警信号,并适时调整警源制定防控措施。
企业职工基本养老保险基金可持续风险预警系统包括预警数据输入端口、预警过程、预警结果输出端口和预控对策,构建“筹资、积累和给付”三位一体的可持续风险监测预警系统:(1)预警数据输入端口为预警基础,主要包括预警所需要的指标数据,也包括引发养老保险可持续风险的因素,即警源,而输入参数由可持续风险预警指标决定;(2)预警系统的预警过程由子风险识别、子风险预警、子风险评价和综合风险预警四个部分构成;(3)预警结果输出端口不仅包括不同类别可持续风险的警级,还包括综合可持续风险警级,多方面反馈可持续风险预警结果;(4)预警系统的预控对策,明确警源对可持续风险的影响程度和方向,以便根据警情制定预防措施,及时有效调整警源降低风险,具体如图3所示。
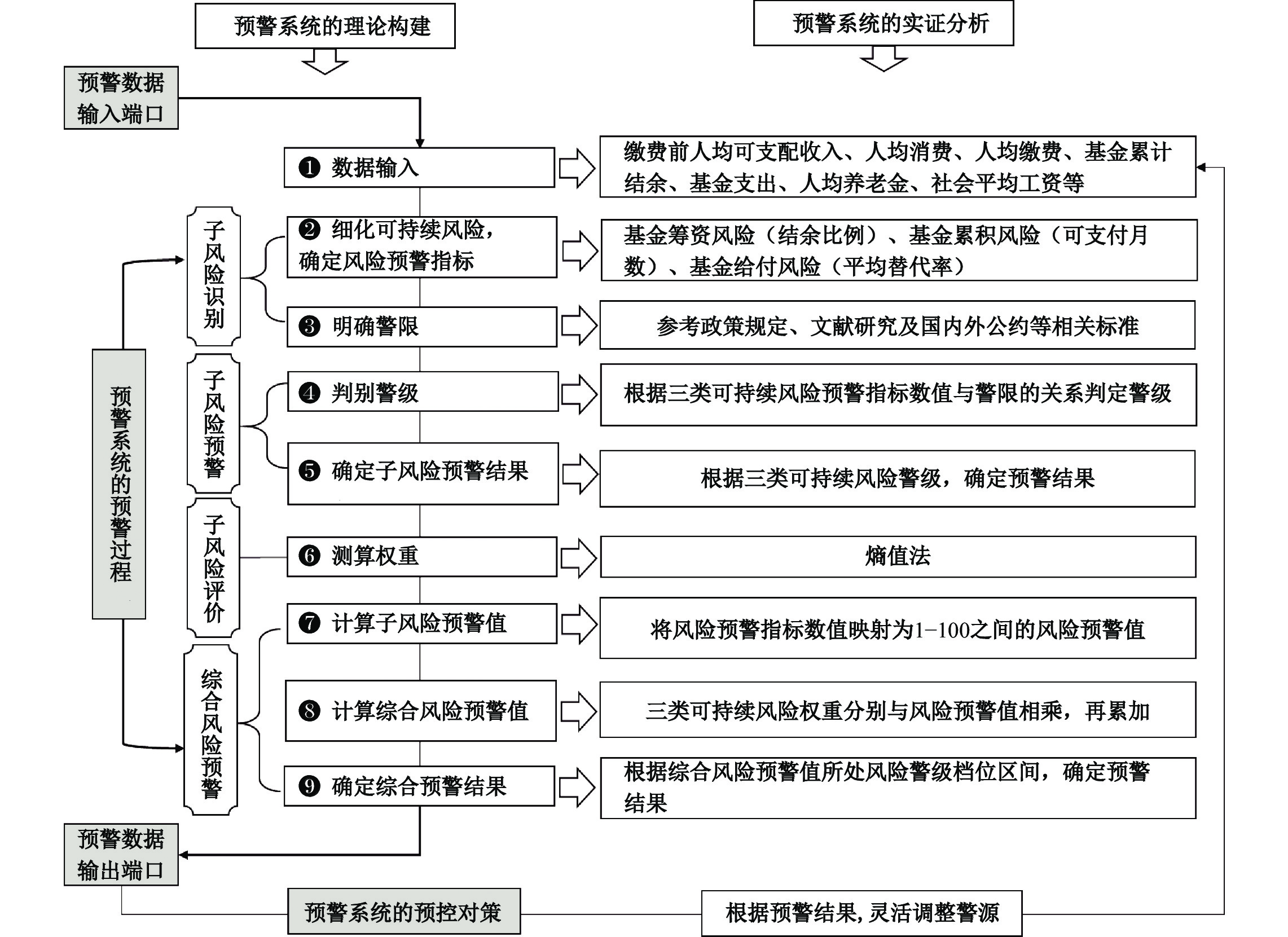
|
| 图 3 企业职工基本养老保险基金可持续风险监测预警系统 |
(二)可持续风险预警系统的实证分析
1. 预警数据输入端口
预警系统输入数据用于计算基金可持续风险预警指标和权重。输入指标包括基金收入、基金支出、累计结余、在岗职工参保人数、离退休人数、全口径社会平均工资、缴费前人均可支配收入⑨和人均消费。除了最后两项,前文均有所测算,在无疫情情景下,2022—2051年缴费前人均可支配收入和人均消费根据2000—2019年历史数据趋势外推得到。在三种疫情风险情景下,这两项数据分别按照2000—2020年平均增长率与经济增长率比值保持同步变化。相关数据来自历年《中国住户调查统计年鉴》《中国劳动统计年鉴》和《中国统计年鉴》。
2. 预警系统的预警过程
(1)子风险识别:三类可持续风险预警指标及警限
子风险识别在于细化可持续风险、量化风险指标。养老保险基金可持续性受众多因素的影响,根据不同标准可进行不同的分类。其中,按照基金运作流程划分基金可持续风险最为直观贴切,本文选择了基金运作流程中三个最为关键的环节,筹资端的筹资可持续性、积累运营中的财务可持续性以及发放端的待遇可持续性。基金筹资不足、基金积累过少、发放的养老金不足以满足退休生活需要,均会损害基金长期可持续性,故联动基金筹资风险、基金积累风险和基金给付风险,共同描绘基金可持续风险。
第一,基金筹资风险。基金筹资的不确定性会制约可持续发展(卢成会和吴丽丽,2016)。保险费收入是基金收入主要来源,包括企业缴费和个人缴费。企业缴费通常转移给个人(Hamaaki和Iwamoto,2010),故个人缴费能力关系到养老保险资金来源的稳定性。基金筹资风险的关键在于参保者的缴费能力要与养老保险缴费要求相适应。用结余比例衡量养老保险缴费后的剩余,结余比例=(缴费前城镇居民人均可支配收入−人均消费支出−养老保险人均缴费)/缴费前城镇居民人均可支配收入。根据经验法则,结余比例一般不低于25%,可适当降低,但最低不能低于10%(汪连新,2019)。以此作为预警指标临界值,即警限,从而划分基金筹资风险预警区间,如表2所示。
| 可持续风险类别 | 风险预警区间 | ||||
| 基金筹资风险 | 筹资状态 | 筹资能力不足 | 筹资能力较低 | 筹资能力适中 | 筹资能力充足 |
| 警限 | (−∞,0) | [0,10%) | [10%,25%] | (25%,+∞) | |
| 警级 | 重警 | 中警 | 轻警 | 无警 | |
| 基金积累风险 | 结余状态 | 结余过少 | 结余较低 | 结余适中 | 结余充足 |
| 警限 | (−∞,2) | [2,9] | (9,15] | (15,+∞) | |
| 警级 | 重警 | 中警 | 轻警 | 无警 | |
| 基金给付风险 | 给付状态 | 待遇水平过低 | 待遇水平偏低 | 待遇水平适中 | 待遇水平较高 |
| 警限 | (−∞,39%) | [39%,55%) | [55%,70%] | (70%,+∞) | |
| 警级 | 重警 | 中警 | 轻警 | 无警 | |
第二,基金积累风险。基金积累风险衡量基金运营过程中的累积能否满足养老金支出,具备持续支付能力是基金积累风险的直接体现。《劳动和社会保障部关于加快实行养老金社会化发放的通知》(劳社部发〔2000〕9号)指出,要建立基金支付风险预警制度,一般以支付两个月养老金的基金积累水平作为预警线。养老保险基金支付能力不足时,采取相应措施需要一定时间。因此,参考《人力资源和社会保障部、财政部关于进一步加强基本医疗保险基金管理的指导意见》(人社部发〔2009〕67号),累计结余为6至9个月平均支付水平能够满足短期支出需要,超过15个月为结余较充足。据此划分基金积累风险预警区间,可支付月数=基金累计结余/下年基金支出×12。
第三,基金给付风险。基金给付端的可持续风险体现为待遇可持续,反映养老金能否保障退休生活。郝勇(2012)测算国内保障老年基本生活的养老金替代率适度水平为39%至56%,而国际劳工组织制定的《社会保障最低标准公约》(102号)提出,养老金替代率最低目标为55%。结合国内外标准,以社会平均替代率作为基金给付风险预警指标,划分基金给付风险预警区间。其中,社会平均替代率=人均养老金/全口径社会平均工资。
(2)子风险预警:三类可持续风险的预警结果
不同疫情风险情景在同一类别可持续风险下风险警级不同,如图4所示。原因是在不同疫情风险情景下,经济系统的“市场”作用与基本养老保险体系的“政府”作用存在差异。第一,基金筹资风险。无疫情情景于2038年由无警转入轻警,基金筹资风险最低,其次是疫情高风险情景,2029年进入轻警,又于2048年提升至中警,疫情中风险情景和疫情低风险情景在预测后期提高到重警,疫情低风险情景下的基金筹资风险最高。基金筹资风险由结余比例衡量,不同疫情风险情景下个人缴费能力与缴费要求变化的相对幅度不同,从而导致风险警级的差异。个人缴费能力为经济体系指标,以市场机制作用为主,疫情风险越大,缴费能力随之下降。养老保险缴费要求为养老保险体系指标,属于公共政策范畴,以政府干预为主。疫情越严峻,降低和减免社保费等政策越宽松,人均缴费要求越低。第二,基金积累风险。在不同疫情风险情景下,测算前期均为无警,随后依次转入轻警、中警,甚至重警,疫情风险越高出现重警时间越早,并且重警持续时间随疫情风险的提升而增加,出现非重警的年数略有差异,无疫情情景为11年,疫情低风险情景为9年,其他情景均为8年。第三,基金给付风险。在疫情高风险情景下,基金给付风险最小,2036年由重警转为中警,2042年转为轻警,2048年及之后均为无警,而中风险、低风险、无疫情情景的基金给付风险依次增大。

|
| 图 4 三类可持续风险预警图 |
(3)子风险评价:三类可持续风险预警指标权重测算②
子风险评价的关键在于子风险的重要性排序,并且以其作为一级指标,以一级风险预警指标计算公式中的各参数为二级指标。根据二级指标2015—2020年实际数据,采用熵值法(Maïsseu和Voss,1995)测算二级指标权重,累加得到一级指标权重(任海军等,2014)。熵值法通过指标间信息量的变异程度进行客观赋权,变异程度越小,权重也越小。③根据图表分析结果,筹资风险对基金可持续影响最大,为46.40%,而给付风险次之,为27.22%,积累风险权重最小,为26.38%。
(4)综合风险预警:综合可持续风险预警
根据风险预警区间将风险预警指标的实际数值映射为1—100之间的风险预警值。数值越大,警情愈严峻,根据本文预警区间与吴成颂(2011)的研究,定义四个档位区间:[0,20)表示无警,[20,50)表示轻警,[50,80)表示中警,[80,100]表示重警。再将风险预警值与三类可持续风险预警指标的权重相乘,得到综合风险预警值,以该值所处区间作为综合可持续风险预警结果。
3. 预警结果输出端口
预警系统输出端口输出预警结果。测算前期不同疫情风险情景下综合可持续风险警级均为轻警,持续年限有所差异,之后均提升至中警:第一,在无疫情情景下,轻警持续时间最长,达11年,2033年提升至中警之后保持该警级,这一情景下基金综合可持续风险最小;第二,在疫情高风险情景下,轻警持续年数比中风险情景多2年,比低风险情景多3年。
4. 预警系统的预控对策:警源调整
预控对策是根据警情适时调整警源,确定预防方案,以避免养老保险基金可持续问题,这就需要对关键警源进行敏感性监测。以疫情中风险情景为基准,退休年龄采取渐进式延迟退休年龄的办法,其他警源敏感性采取提高1%的方法测算。不同警源对三类风险预警指标影响程度和方向不同,影响较大的是退休年龄和工资增长率,征缴率、基金保值增值率居中,总和生育率与就业率影响较小。
六、结论与建议
全球新冠疫情带来诸多不确定性,为养老保险可持续性带来新挑战。本文运用计量模型和精算模型,测算四种不同疫情风险情景下企业职工基本养老保险基金的收支结余状况,构建“筹资、积累和给付”三位一体的可持续风险监测预警系统,建立“预测、预警和预控”的风险防控体系,为防范化解重大风险提供借鉴。研究发现:首先,疫情影响每提高一个风险等级,测算期间的基金收入累计现值平均降低23.45%,基金支出累计现值平均降低7%,而基金累计结余现值之和平均降低59.76%。其次,本文联动基金筹资风险、基金积累风险和基金给付风险构建可持续风险预警系统。通过该系统研究表明,与无疫情情景相比,疫情提高了基金可持续风险警级。在不同疫情风险情景下,可持续风险警级在测算前期均为轻警,持续年限有所差异,之后提升至中警。最后,对退休年龄、征缴率等关键警源进行敏感性监测,发现不同警源对三类可持续风险影响程度和方向不同,可通过调整警源制定预控对策。
本文提出以下建议:第一,多措并举可以缓解疫情对养老保险基金的冲击。与无疫情情景相比,疫情风险降低了基金结余,提高了基金综合可持续风险警级,基金收支测算理应考虑疫情因素。在实践中,除了持续优化调整疫情防控工作,完善公共卫生应急管理体系,还应降低疫情的负外部性,增强企业抗风险韧性以及多渠道支持灵活就业等,从而降低疫情对经济体系和养老保险体系的影响。第二,建立综合可持续风险预警系统。可持续风险已然显现,需多方面监测可持续风险,如缴费融资端的筹资风险、积累运营中的积累风险、待遇发放端的给付风险等,从预警数据输入、预警过程、预警结果输出和预控对策等方面,建立完备的可持续风险预警系统。第三,持续监测关键警源对基金可持续风险的影响。不同警源指标对基金可持续风险的影响程度和方向均不同,要想尽快提升基金可持续性,应优先改革退休政策、调整工资增长率,并且建立投资管理机制。
① 文件来源:《国务院关于印发国家人口发展规划(2016—2030年)的通知》(国发〔2016〕87号)。
② 限于篇幅,下文的图表分析省略,读者若是感兴趣可向作者索取。
③ 限于篇幅,基本原理省略,读者若是感兴趣可向作者索取。
④ 数据来源:2018—2020年《中国人力资源和社会保障年鉴》,因缺乏私营企业在岗职工人数,在岗率=非私营企业在岗职工人数/非私营企业就业人数,取2017—2019年平均值92.68%。
⑤ 由《中国统计年鉴》计算1997—2019年缴费基数和企业职工人均养老金平均增速分别为12.16%和9.09%,则9.09%/12.16%=75%。
⑥ 人社部办公厅公布2016—2019年职工基本养老保险个人账户记账利率依次为8.31%、7.12%、8.29%和7.61%,均值为7.83%。
⑦ 基于数据可得性,不包括西藏自治区、中国香港特别行政区、中国澳门特别行政区和中国台湾省,也不包括其他省份中部分数据缺失的城市。
⑧ 在疫情低风险情景下,经济增长率比无疫情情景下降1.37%(8.87%−7.5%=1.37%),故就业率下降0.14%(1.37%×0.103241=0.14%),其他情景类似。
⑨ 缴费前城镇居民人均可支配收入为人均可支配收入与企业职工基本养老保险人均缴费之和。
| [1] | 褚福灵, 司絮. 突发疫情与城镇职工基本医疗保险基金支付风险预警——基于COVID-19干预下的情景分析[J]. 经济社会体制比较, 2022(2): 85–98. DOI:10.3969/j.issn.1003-3947.2022.02.009 |
| [2] | 何文炯, 张奕, 徐林荣, 等. 企业职工基本养老保险预警系统初探[J]. 浙江社会科学, 2002(4): 179–181. DOI:10.3969/j.issn.1004-2253.2002.04.036 |
| [3] | 黄彬云. 城镇非正规服务就业规模的估计[J]. 统计与决策, 2014(23): 37–40. |
| [4] | 刘学良. 中国养老保险的收支缺口和可持续性研究[J]. 中国工业经济, 2014(9): 25–37. |
| [5] | 卢成会, 吴丽丽. 社会养老保险基金筹资风险的规避研究[J]. 江汉论坛, 2016(3): 17–22. DOI:10.3969/j.issn.1003-854X.2016.03.003 |
| [6] | 吕有吉, 景鹏, 郑伟. 人口老龄化、养老保险基金缺口弥补与经济增长[J]. 金融研究, 2021(1): 51–70. |
| [7] | 任海军, 曹盘龙, 张爽. 基于熵值法的生态社会评价指标体系研究——以我国西部地区为例[J]. 华东经济管理, 2014(5): 71–76. |
| [8] | 石晨曦. 企业职工统筹账户自平衡性与财政负担[J]. 求实, 2018(3): 45–57. DOI:10.3969/j.issn.1007-8487.2018.03.004 |
| [9] | 万磊, 石玉建, 魏栋鸿, 等. 灵活就业人员参保缴费政策评估[J]. 中国社会保障, 2014(6): 36–37. DOI:10.3969/j.issn.1008-4304.2014.06.011 |
| [10] | 王翠琴, 薛惠元. 新型农村社会养老保险风险预警指标体系的构建[J]. 统计与决策, 2011(16): 28–31. |
| [11] | 王翠琴, 岳晓, 薛惠元. 城镇职工基本养老保险基金可持续性仿真测算[J]. 统计与决策, 2021(12): 131–135. |
| [12] | 王金营, 戈艳霞. 全面二孩政策实施下的中国人口发展态势[J]. 人口研究, 2016(6): 3–21. |
| [13] | 汪泓. 社会保险基金的良性运营: 系统动力学模型、方法、应用[M]. 北京: 北京大学出版社, 2008. |
| [14] | 吴成颂. 我国金融风险预警指标体系研究[J]. 技术经济与管理研究, 2011(1): 19–24. |
| [15] | 席恒. 全球新冠肺炎疫情、超级老龄化、新型就业三重挑战下的中国社会保障[J]. 社会保障评论, 2022(1): 35–46. |
| [16] | 杨钒. 延迟退休对养老金可持续性影响研究[J]. 宏观经济研究, 2020(5): 91–101. |
| [17] | 杨再贵, 陈肖华. 降费综合方案下企业职工基本养老保险财政风险预警[J]. 保险研究, 2021(1): 91–106. DOI:10.13497/j.cnki.is.2021.01.006 |
| [18] | 曾益, 魏晨雪, 李晓琳, 等. 征收体制改革、延迟退休年龄与养老保险基金可持续性——基于“减税降费”背景的实证研究[J]. 公共管理学报, 2019(4): 108–118. |
| [19] | 曾益, 杨悦. 从中央调剂走向统收统支——全国统筹能降低养老保险财政负担吗?[J]. 财经研究, 2021(12): 34–48. |
| [20] | 张晓昕. 教育、非正规就业与劳动者工资收入——基于CFPS数据的实证分析[J]. 云南财经大学学报, 2021(9): 31–45. |
| [21] | 朱恒鹏, 岳阳, 林振翮. 统筹层次提高如何影响社保基金收支——委托-代理视角下的经验证据[J]. 经济研究, 2020(11): 101–120. |
| [22] | Enoff L D, McKinnon R. Social security contribution collection and compliance: Improving governance to extend social protection[J]. International Social Security Review, 2011, 64(4): 99–119. DOI:10.1111/j.1468-246X.2011.01413.x |
| [23] | Hamaaki J, Iwamoto Y. A reappraisal of the incidence of employer contributions to social security in Japan[J]. The Japanese Economic Review, 2010, 61(3): 427–441. DOI:10.1111/j.1468-5876.2009.00494.x |
| [24] | Maïsseu A, Voss A. Energy, entropy and sustainable development[J]. International Journal of Global Energy Issues, 1995, 8(1-3): 201–220. |

