
2022第48卷第12期
2. 上海交通大学 安泰经济与管理学院,上海 200030
2. Antai College of Economics & Management, Shanghai Jiao Tong University, Shanghai 200030, China
一、引 言
在最低工资上涨和机器人广泛使用的背景下,社会劳动者能否公平地分享技术红利引起了学界的热议。据IFR数据显示,中国于2016年成为全球工业机器人数量最多的国家,机器人兴起推动了经济快速增长。党的十九大报告指出,中国要坚持经济与居民收入同步增长,劳动生产率与劳动报酬同步提高。现有关于劳动者权益保护的法律法规不断加强其保护力度,其中包括上调最低工资标准。尽管如此,中国劳动收入份额在国民收入中的占比却长期处于较低水平。为深入剖析内在原因,文章从企业层面入手,探究最低工资对劳动收入份额的冲击以及机器人应用在收入分配中扮演何种角色,以及最低工资的作用是否因机器人应用而发生了改变。回答这一系列问题,有利于预判劳动保护法律法规在智能化技术冲击下的作用效果,并据此提出合理的政策建议。
在经济不断向好态势下,世界上许多国家出现了劳动收入份额下滑的现象(Karabarbounis和Neiman,2014)。劳动者不能公平享受经济发展成果,长此以往会引发劳资冲突,不利于社会和谐稳定发展。已有大量学者意识到这点,并对劳动收入份额影响因素进行研究,发现如政治制度(Acemoglu和Robinson,2015)、技术进步(王林辉和袁礼,2018)、产业结构(Cacciatore和Fiori,2016)和资本要素(Bentolila和Saint-Paul,2003)等均会改变劳动收入份额的大小,其中不乏对最低工资和劳动收入份额关系的研究(万江滔和魏下海,2020)。最低工资具有两面性,一方面能增加低技能劳动者工资,对其产生保护作用;另一方面会使劳动力成本不断上升,使企业用机器替代劳动,造成人员失业(Acemoglu和Restrepo,2020)。目前,中国企业对机器人应用较为普遍,“机器换人”现象已蔚然成风(余玲铮等,2021),然而少有文献结合这一特征事实,综合考虑最低工资、机器人使用和劳动收入份额三者间的关系。
在多项政策扶持下,中国工业机器人得以迅速发展。国务院颁布的《中国制造2025》指出,智能制造是国家全力打造制造强国的重要抓手。党的二十大报告进一步将“推进新型工业化,加快建设制造强国”作为发展目标。工业机器人运用于企业生产已成为制造业发展趋势,无法避免其对劳动力市场带来的影响(Cheng等,2019)。而相关研究主要发生在欧美等发达国家,国内此类研究开始较晚,只有少数学者从微观企业层面探讨机器人使用对中国劳动力市场的影响(王永钦和董雯,2020;孔高文等,2020)。中国工业机器人数量保持高增长率,无疑会对企业内部就业结构和收入分配带来巨大冲击。那么,机器人应用究竟在多大程度上提升了企业的营业收入?企业是否愿意与员工共享技术发展的经济成果呢?又会怎样调整企业收入分配呢?文章试图对此进行解答。
首先,本文构建最低工资与企业机器人应用的理论模型,利用IFR数据,基于“巴蒂克工具变量”思想,构造中国企业层面机器人渗透度指标,从理论和实证两个方面分析与检验机器人应用如何影响最低工资对企业劳动收入份额的补偿效应。并从企业规模、工资率高低、要素密集度、城市规模等视角作异质性讨论。研究发现:第一,最低工资上涨显著提升了企业劳动收入份额,而机器人应用削弱了这种作用,高机器人渗透行业中的企业对最低工资补偿效应的破坏性更强。第二,大规模、低工资企业中机器人应用显著降低了最低工资对企业劳动收入份额的补偿效应,在资本密集型行业中机器人对企业劳动收入份额的抑制效应更大。在中小城市和大城市中机器人应用抑制了最低工资对企业劳动收入份额补偿效应,而在超大城市则相反。第三,企业工资率是机器人应用降低最低工资对企业劳动收入份额补偿效应的渠道,且机器人应用增加了高学历对低学历人员的替代,这一发现是对企业工资率影响渠道的一种补充与验证。
本文的边际贡献在于:①从机器人应用视角探讨最低工资对企业劳动收入份额的影响,补充了收入分配的现有研究。②构建了最低工资和机器人应用影响企业劳动收入份额的理论模型,实证检验了机器人应用如何影响最低工资对企业劳动收入份额的补偿效应,从微观层面提供了机器人应用效应的直接证据。③验证了企业工资率是机器人应用降低最低工资对企业劳动收入份额补偿效应的渠道,为理解企业劳动收入份额演变提供了有益启示。
二、文献回顾
(一)最低工资对劳动收入份额影响。最低工资影响效应可归纳为最低工资通过补偿和替代效应的直接影响,以及通过生产率和工资率效应的间接影响。首先,补偿效应是指最低工资的设立提高了那些实际工资低于最低工资的劳动者的收入,产生补偿性收入,使企业收入分配更多向劳动者转移,企业劳动收入份额增加。如翁杰和徐圣(2005)从理论层面分析了补偿效应对劳动收入份额的促进作用。最低工资的替代效应又可分为正向替代和负向替代,正向替代是指用高技能劳动者替代低技能劳动者(Pischke,2005),进一步提高了高技能劳动者的工资,对该群体产生的溢出效应提高了企业劳动收入份额。负向替代是指企业用相对便宜的资本对低技能劳动者进行替代,这种替代效应会减少对劳动力的需求(Acemoglu和Restrepo,2018)。
劳动收入份额可以表示为劳动生产率和工资率的比值,最低工资通过影响生产率和工资率间接影响企业劳动收入份额。一方面,最低工资促使企业提高劳动生产率,原因在于员工工作积极性得到提升(Hirsh等,2015)和企业选择劳动节约型技术进步进行生产(Acemoglu和Autor,2011)。另一方面,最低工资提高企业平均工资水平,马双等(2012)研究发现,最低工资每上涨10%,制造业企业的平均工资将上涨0.4%至0.5%。最低工资对企业劳动收入份额的最终影响取决于工资率效应和生产率效应的大小,万江滔和魏下海(2020)发现,最低工资使企业工资率和劳动生产率同时上升,但是前者上升幅度小于后者,因此企业劳动收入份额将下降。
(二)机器人使用对劳动收入份额的影响。现有研究对于机器人如何影响企业劳动收入份额尚未达成一致。DeCanio(2016)认为企业劳动收入份额由资本所有者决定,投入机器人后,企业为获得更大利润,将减少劳动者收入,从而降低企业劳动收入份额。但也有学者持相反观点,如Acemoglu和Restrepo(2018)研究发现,机器人为劳动者创造新的工作岗位,在长期来看,机器人的使用会提高劳动收入份额。同样,韩民春和韩青江(2020)研究发现,机器人应用对工资有促进作用,因此提高了企业劳动收入份额。
机器人使用对企业劳动收入份额的影响可从工资率和劳动生产率两方面探究。大多观点认为机器人使用提高了企业生产率(Acemoglu和Restrepo,2018),Graetz和Michaels(2017)利用17个发达国家数据发现,机器人应用使制造业企业劳动生产率提高0.36%;李磊和徐大策(2020)利用中国工业企业数据分析得出,使用机器人的制造业企业比不使用企业的劳动生产率高出7.45%。但对于机器人如何影响企业工资率,有两种相反观点,有学者认为机器人应用促进工资率提升(Caselli和Manning,2019),还有学者认为机器人应用对工资率产生抑制效应(Acemoglu和Restrepo,2018)。此外,这种影响在不同技能劳动者间存在差异,机器人与高技能者互补,提高了该群体工资,而与低技能者相替代,降低其工资水平(Berg等,2016)。由于机器人应用如何影响工资率和劳动生产率的研究尚未达成一致,对于劳动收入份额的影响结论也具有多样性。
有关机器人应用的研究主要关注的是发达国家,对发展中国家机器人应用的研究较少。自机器人在中国得到广泛应用,国内学者对机器人展开了系列研究。但鲜有文献考虑到机器人应用对已有经济活动的调节作用,如机器人应用是否会扩大或削弱某一经济关系等,此类研究需要更加细腻的手段和更丰富的内容。综上,本文在现有研究的基础上将重点关注最低工资对劳动收入份额的影响机制以及机器人应用对最低工资影响效果的调节效应。
三、理论模型
(一)模型设定。参考文雁兵和陆雪琴(2018),构建了最低工资和机器人应用影响企业劳动收入份额的综合框架。并将资本分为传统资本KiM(如厂房等)和机器人资本KiR(如喷涂机器人等),Li为劳动力。构建包含三要素的嵌套型生产函数:
| $ {Y_i} = AK_{iM}^\alpha {[\gamma K_{iR}^\varepsilon + (1 - \gamma ){L_i}^\varepsilon ]^{(1 - \alpha )/\varepsilon }} $ | (1) |
其中,效益系数
| $ \max {\pi _i} = {Y_i} - {w_i}{L_i} - {p_i}{K_{iR}} - {r_i}{K_{iM}} $ | (2) |
其中,ri为资本的租金,pi为购买机器人的费用,wi为企业工资率。
(二)企业最优化。根据利润最大化的一阶条件,分别对Li、KiR和KiM求偏导,求得要素价格wi、pi和ri。根据欧拉定理,生产的产品被要素完全分配,可将劳动收入份额表示为:①
| $ l{s_i} = \frac{{{w_i}{L_i}}}{{{Y_i}}} = {w_i}^{\varepsilon /(\varepsilon - 1)}{[(1 - \alpha )(1 - \gamma )]^{1/(1 - \varepsilon )}}{[A{(\alpha /{r_i})^\alpha }]^{\varepsilon /(1 - \alpha )(1 - \varepsilon )}} $ | (3) |
为探究工业自动化对收入分配的影响,得到包含机器人资本的劳动收入份额表达式:②
| $ l{s_i} = {w_i}^{\varepsilon /(\varepsilon - 1)}{[(1 - \alpha )(1 - \gamma )]^{1/(1 - \varepsilon )}}A{Z^\alpha }^{\frac{{\varepsilon (1 - \varepsilon - {\alpha ^2})}}{{(1 - \alpha )(1 - \varepsilon )(1 - \alpha - \varepsilon )}}}{[(1 - \alpha )\frac{{{r_i}}}{{{p_i}}}]^{\alpha \varepsilon /(1 - \varepsilon )(1 - \alpha - \varepsilon )}}K_{iR}^{\frac{{{\alpha ^2}\varepsilon }}{{(1 - \alpha )(1 - \varepsilon )}}} $ | (4) |
(三)最低工资与企业劳动收入份额分析。最低工资存在“灯塔效应”(Bosch和Manacorda,2010),且《劳动法》规定企业工资不得低于当地最低工资,最低工资标准作为重要参考纳入企业基本工资制定中。假定
首先,我们分析最低工资对企业劳动收入份额的直接影响,将式(3)对
| $ \frac{{\partial l{s_i}}}{{\partial {\tau _i}}} = \frac{{\partial l{s_i}}}{{\partial w({\tau _i})}} \times \frac{{\partial w({\tau _i})}}{{\partial {\tau _i}}} $ |
| $ \frac{{\partial l{s_i}}}{{\partial {w_i}}} = \frac{\varepsilon }{{\varepsilon - 1}}{w_i}{({\tau _i})^{1/(\varepsilon - 1)}}{[(1 - \alpha )(1 - \gamma )]^{1/(1 - \varepsilon )}}{[A{(\alpha /{r_i})^\alpha }]^{\varepsilon /(1 - \alpha )(1 - \varepsilon )}} $ | (5) |
已知
现有研究认为企业生产中资本和劳动相互替代(Berkowitz等,2015;陈登科和陈诗一,2018),即要素替代弹性大于1。本研究认为机器人资本与劳动之间为互补关系。理由如下:①诸多文献研究发现机器人应用可提升就业,两者为互补关系(Akerman等,2015;Hjort和Poulsen,2019;李磊等,2021;王晓娟等,2022);②相比工业企业,上市公司在企业人员构成方面存在显著优势,尤其是高技能劳动更多,与机器人之间形成互补关系。此外,本文对此进行了实证检验,回归结果进一步佐证两者为互补关系。在此情况下
本文关注的焦点在于机器人应用后最低工资对企业劳动收入份额的影响效应,根据式(4)对最低工资
| $ \frac{{\partial l{s_i}}}{{\partial {\tau _i}}} = \frac{{\partial l{s_i}}}{{\partial {w_i}({\tau _i})}} \times \frac{{\partial {w_i}({\tau _i})}}{{\partial {\tau _i}}} $ |
| $ \frac{{\partial l{s_i}}}{{\partial {w_i}}} = \frac{\varepsilon }{{\varepsilon - 1}}{w_i}{({\tau _i})^{1/(\varepsilon - 1)}}{[(1 - \alpha )(1 - \gamma )]^{1/(1 - \varepsilon )}}{(A{Z^\alpha })^{\frac{{\varepsilon (1 - \varepsilon - {\alpha ^2})}}{{(1 - \alpha )(1 - \varepsilon )(1 - \alpha - \varepsilon )}}}}{[(1 - \alpha )\frac{{{r_i}}}{{{p_i}}}]^{\alpha \varepsilon /(1 - \varepsilon )(1 - \alpha - \varepsilon )}}K_{iR}^{\frac{{{\alpha ^2}\varepsilon }}{{(1 - \alpha )(1 - \varepsilon )}}} $ | (6) |
其中,机器人资本KiR的指数为
此外,本文还需要探究两者内在影响机制。前文认为最低工资通过提高企业工资率进而影响企业劳动收入份额。现有研究也验证了最低工资标准具有成本效应,能够提高企业平均工资和社会劳动力成本(Malloy,2020;许明和李逸飞,2020)。尤其是,最低工资显著提升企业工资率这一结论得到了经验验证(Dube等,2010;马双等,2012)。鉴于此,提出第三个命题H3:最低工资通过促进企业工资率提高进而提升企业劳动收入份额。
四、研究设计
(一)计量模型设定与变量说明。
1. 计量模型设定。
| $ \begin{aligned} L{S_{it}} = &{\beta _0} + {\beta _1}M{W_{ct}} + {\beta _2}Robo{t_{ist}} + {\beta _3}M{W_{ct}} \times Robo{t_{ist}} \\ &{ + \gamma {Z_{isct}} + {\delta _i} + {\delta _s} + {\delta _c} + {\delta _t} + {\varepsilon _{isct}}} \end{aligned} $ | (7) |
其中,下标i、s、c和t分别表示企业、行业、城市和年份。LSit为企业劳动收入份额,MWct为城市最低工资、Robotist为企业机器人应用。
2. 核心变量测度。企业劳动收入份额(LSit)。借鉴王雄元和黄玉菁(2017)及施新政等(2019)的做法,采用上市公司年报中的“支付给职工以及为职工支付的现金”除以“营业总收入”来衡量,且取对数。并利用其他计算方法进行稳健性检验。
机器人应用(Robotist)。参考Acemoglu和Restrepo(2020)的方法计算企业层面工业机器人渗透度指标,即“巴蒂克工具变量”思想(Bartik,1991)。测算方法如下:
第一步,计算行业层面工业机器人渗透度指标:
| $ Index_{st}^{CN} = \frac{{MR_{st}^{CN}}}{{L_{s,t = 2012}^{CN}}} $ | (8) |
其中,
第二步,构造企业层面工业机器人渗透度指标:
| $ Robo{t_{ist}} = \frac{{labo{r_{it = 2012}}}}{{allabo{r_{t = 2012}}}} \times Index_{st}^{CN} $ | (9) |
其中,laborit=2012表示制造业
选用OP和LP方法计算得到的企业全要素生产率(Tfp)。采用价格平减后企业应付职工薪酬与企业员工数之比衡量企业工资率( wage_rate)。
(二)数据来源。最低工资数据来源于各省市政府发布的官方文件,共得到405个市级层面最低工资标准。工业机器人数据来源于IFR,国际机器人联合会是目前最为权威的机器人统计组织。劳动收入份额由制造业上市公司数据计算得到,职工薪酬等企业层面数据来自CSMAR上市公司数据库。平减指数采用上一年平减指数×本年价格指数(上年价格=100)计算,基期为2012年。GDP平减指数数据来源于《中国统计年鉴》,固定资产投资价格指数、工业生产者购进价格指数、工业生产者出厂价格指数来源于《中国工业统计年鉴》与《中国区域统计年鉴》。
本文选用2012—2019年制造业上市公司数据,因应用机器人生产的中国企业大多来自制造业行业,机器人应用从2010年才有明显的上升趋势。国家统计局于2011年对《国民经济行业分类》做出调整,将交通运输设备制造业细分为汽车制造业和铁路、船舶、航空航天和其他运输设备制造业两个行业,2011年交通运输设备制造业还未被细分,2012年制造业各分行业的就业人数数据尚未公布。据统计数据显示:铁路、船舶、航空航天和其他运输设备制造业从业人员年均人数在2013—2016年间未发生较大变动,因此本文采用2013年数据作为2012年基期数据。
(三)描述性统计。整体样本中,中国制造业上市公司的企业劳动收入份额在24%左右,标准差为0.13,表明企业劳动收入份额在不同企业间存有差异;企业对机器人的使用情况用企业层面机器人渗透指标表示,最小为0、最大为938.11台/万名员工,差异性较大。④样本的组间差异比较分析结果显示:大企业的劳动收入份额高于小企业,高工资率企业的劳动收入份额和机器人渗透度均高于低工资率企业,超大城市中企业的劳动收入份额和机器人渗透度同样较高。⑤
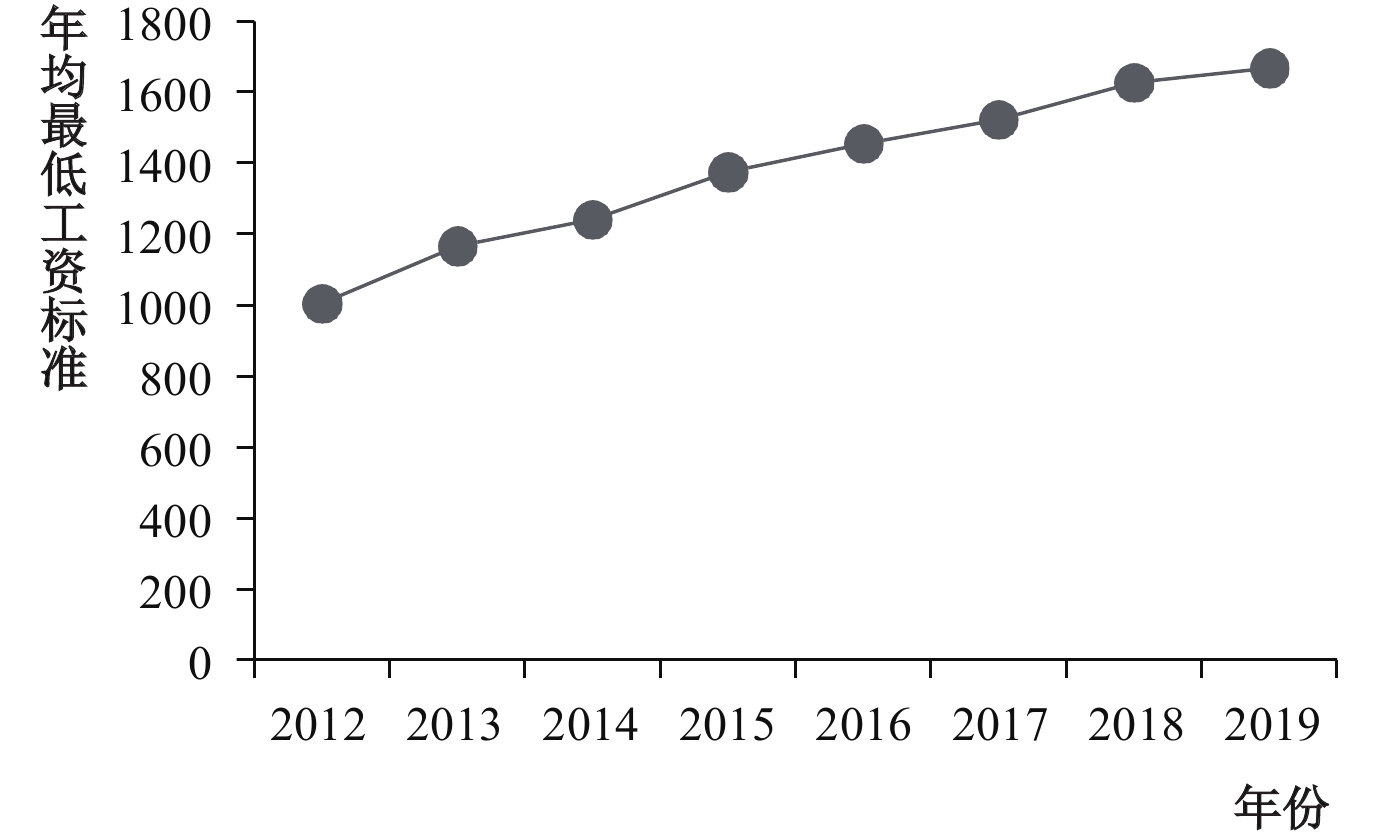
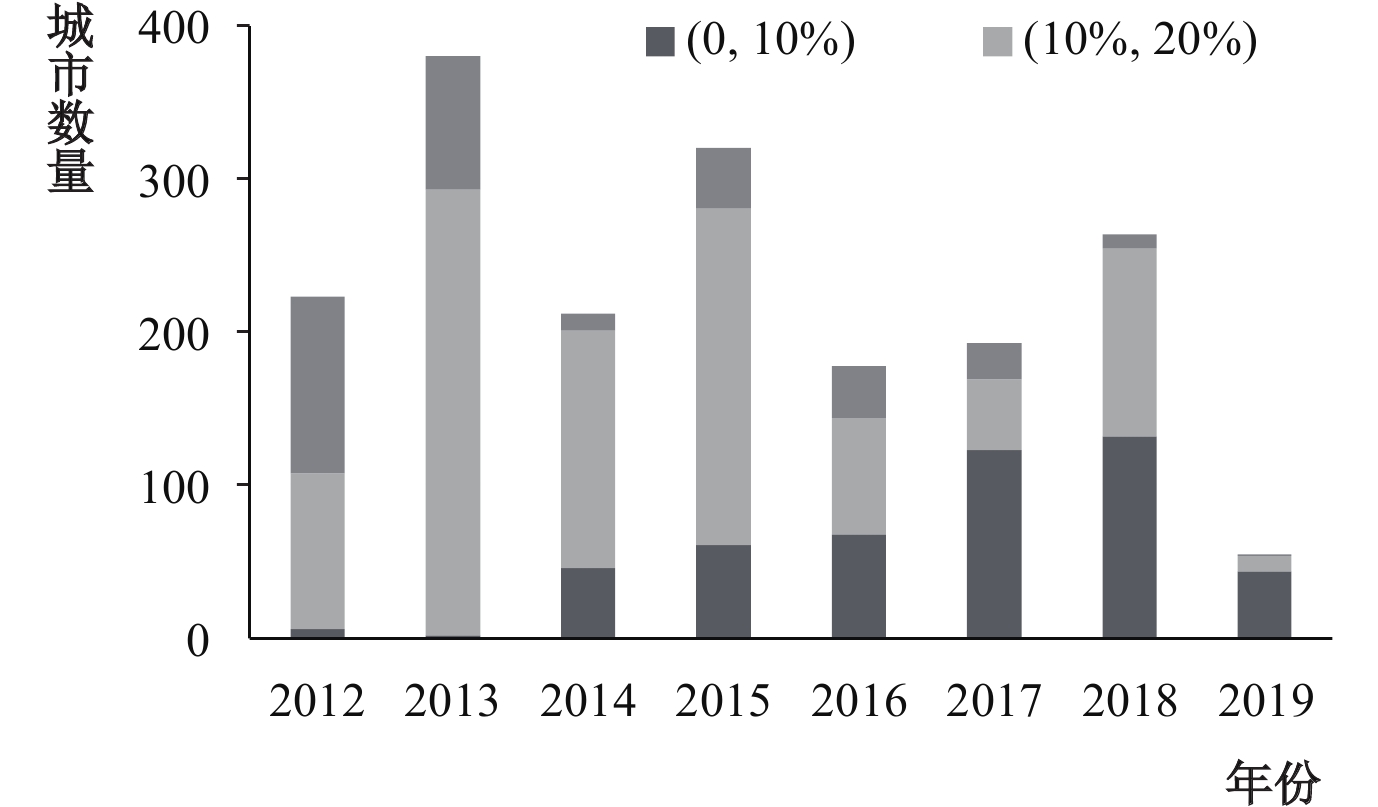
图1显示我国年均最低工资标准逐年上调,涨幅稳定。图2是我国最低工资标准按上升幅度分组后各组的城市个数,除了2017年和2019年外,城市最低工资标准的提升比例在10%—20%的居多。2013年有近400座城市对当地最低工资进行了调整,并且调整的幅度均在10%以上,而2019年仅有50多座城市调整了最低工资,调整幅度较少。
|
| 图 1 2012—2019年均最低工资标准趋势图 |
|
| 图 2 2012—2019年最低工资标准提升数量图 |
通过绘制2012—2019年中国和美国细分行业工业机器人渗透度增长率随时间变动的趋势图可以看出,各行业机器人渗透度增长率均在逐年上升,表明我国制造业各行业的机器人数量和增量逐年增加,制造业对机器人的需求越来越大。其中,纺织业、造纸及印刷业和木材加工业等行业的机器人渗透度均处于较低水平,而塑料和化学制品业、电力光学制品业及汽车制造业等技术密集型行业的机器人渗透度均处于较高水平。从细分行业整体走势看,中国工业细分行业机器人渗透度增长趋势与同时期美国机器人渗透度增长趋势基本相同。⑥
五、实证结果分析
(一)基准回归结果。为有效消除测量误差和遗漏变量等问题,列(1)采用企业个体固定效应,列(2)采用个体—时间双向固定效应,同时控制了行业、地区层面固定效应。列(3)采用企业个体固定效应、列(4)采用企业个体和时间的双向固定效应,列(5)进一步采用年份—行业、年份—地区、行业—地区高维固定效应。
表1列(1)结果显示,最低工资的估计系数显著为正。列(2)在控制一系列不可观测因素后,该系数依然显著为正。由此得出最低工资上涨显著提升了企业劳动收入份额,验证了命题1。为进一步分析最低工资与机器人应用对企业劳动收入份额的影响,在列(3)—列(5)中加入交互项(MW×Robot)。结果表明,交互项系数均显著为负,尤其在控制高维固定效应后仍显著为负,说明机器人应用存在调节效应,机器人应用削弱了最低工资对企业劳动收入份额的促进作用,高机器人渗透行业企业相比低渗透行业企业对最低工资补偿效应的破坏性更强。原因可能在于,一方面最低工资制度实施为低收入者提供了一定的工资补偿,通过溢出效应间接提升高收入者的工资水平,另一方面不断上升的用工成本逼迫企业选择“机器换人”的生产决策,进而提高企业生产率,降低了企业的劳动收入份额。最低工资对企业劳动收入份额的促进效应会随着机器人应用的不断增加而降低,验证了命题2。
| (1) | (2) | (3) | (4) | (5) | |
| MW | 0.031***(0.004) | 0.024***(0.005) | 0.062***(0.006) | 0.011(0.008) | 0.022(0.015) |
| MW×Robot | −0.011***(0.002) | −0.004**(0.002) | −0.010***(0.003) | ||
| Robot | 0.013***(0.003) | −0.000(0.003) | 0.002(0.005) | ||
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 14 299 | 14 299 | 14 299 | 14 299 | 14 235 |
| 拟合优度 | 0.832 | 0.833 | 0.833 | 0.835 | 0.839 |
| 注:括号内数值表示企业固定效应的稳健标准误,***、**和*分别表示1%、5%和10%的显著性水平。其中,行业固定是以二分类行业划分,年度虚拟变量是以2012年为基期,地区固定以企业所在省份测度,下表统同。 | |||||
(二)稳健性检验。为验证本文结果的稳健性,进行如下的稳健性检验。一是匹配海关机器人数据。本文参照李磊等(2021)的做法,采用中国海关数据库中的进口机器人数据作为企业机器人应用的代理变量进行稳健性分析。按照HS6位产品编码,在2012—2016年间,识别出42家企业存在进口机器人。结果见表2列(1)。二是更换被解释变量测算方式。借鉴杜鹏程等(2021)的做法,用劳动收入份额=职工薪酬/(营业收入−营业成本+职工薪酬+固定资产折旧)计算企业劳动收入份额,结果见表2列(2);借鉴胡奕明和买买提依明·祖农(2013)的做法,采用劳动者报酬占企业期末总资产数的比重计算企业劳动收入份额,结果见表2列(3);借鉴魏下海等(2013)的做法进行Logistic转换处理,结果见表2列(4)。三是将最低工资滞后一期。考虑到部分城市年末才对最低工资标准进行调整,且企业改变生产决策需要时间,因此选用最低工资滞后一期进行回归,结果见表2列(5)。四是将制造业行业重新分组。按照2011年之前的行业分类方法,将汽车制造业和铁路、船舶、航空航天和其他运输设备制造业的数据合并为交通运输设备制造业,结果见表2列(6)。五是区分城市最低工资当年是否变动。《最低工资规定》指出各省市地区应当至少每两年对最低工资标准进行调整,但部分城市在某些年份未进行调整。因此,根据企业所属城市当年是否调整,划分为两组进行回归,结果见表2列(7)和列(8)。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| 海关机器
识别 |
更换企业劳动收
入份额测度变量 |
滞后效应 | 合并交通运输
设备制造业 |
最低工资
调整地区 |
最低工资未
调整地区 |
|||
| MW | −0.019 | 0.038*** | 0.099*** | 0.146*** | 0.039** | 0.009 | −0.003 | 0.063** |
| (0.047) | (0.005) | (0.033) | (0.019) | (0.018) | (0.015) | (0.023) | (0.031) | |
| MW×Robot | −0.029** | −0.006*** | −0.021** | −0.030*** | −0.014*** | −0.006** | −0.011** | −0.012** |
| (0.015) | (0.002) | (0.010) | (0.006) | (0.003) | (0.003) | (0.004) | (0.006) | |
| Robot | 0.043* | 0.005* | −0.035** | 0.038*** | 0.003 | −0.004 | 0.008 | −0.002 |
| (0.022) | (0.003) | (0.016) | (0.009) | (0.005) | (0.005) | (0.007) | (0.009) | |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 125 | 13 856 | 13 856 | 13 856 | 11 210 | 13 796 | 8 135 | 4 839 |
| 拟合优度 | 0.901 | 0.870 | 0.790 | 0.803 | 0.882 | 0.872 | 0.887 | 0.891 |
| 注:选用包括企业、年份、行业、地区固定的双向固定效应模型进行估计,下表统同。 | ||||||||
上述稳健性结果均与基准回归结果保持一致,增强了文章结论的可靠性。
(三)内生性检验。
1. 构建机器人工具变量。本文借鉴王永钦和董雯(2020)的方法,利用美国行业层面的工业机器人数据构造企业层面机器人渗透度指标作为工具变量。计算公式如下:
| $ Robot\_I{V_{ist}} = {{(labo{r_{it=2012}}} \mathord{\left/ {\vphantom {{(labo{r_{it}}} {allabor}}} \right. } {allabor_{t=2012}}}) \times Index_{st}^{US} $ |
其中,
两阶段最小二乘法结果显示:表3列(1)中的工具变量系数显著为正,列(2)中机器人应用的估计系数显著为负,表明机器人应用降低了企业劳动收入份额;列(3)中工具变量、交互项系数均显著为正,列(4)中交互项系数显著为负,表明机器人应用抑制了最低工资对企业劳动收入份额的补偿效应,结果与基准回归一致。第一阶段F值超过10,验证了本文所构建的工具变量具有合理性。
| (1)第一阶段 | (2)第二阶段 | (3)第一阶段 | (4)第二阶段 | |
| Robot | LS | Robot | LS | |
| Robot_IV | 0.958***(0.016) | 0.918***(0.031) | ||
| MW×Robot_IV | 0.026*(0.015) | |||
| MW | 0.105***(0.024) | 0.035***(0.005) | 0.050(0.040) | 0.064***(0.008) |
| MW×Robot | −0.011***(0.003) | |||
| Robot | −0.011***(0.003) | 0.006(0.005) | ||
| 控制变量 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 13 856 | 13 856 | 13 856 | 13 856 |
| 第一阶段F值 | 3 780.23 | 2 059.60 | ||
| 拟合优度 | 0.174 | 0.177 |
2. 构建最低工资工具变量。本文借鉴赵瑞丽等(2018)的做法,以城市平均工资预测值的40%作为最低工资的工具变量。计算公式如下:
| $ Wage_{t + 2}^c = ({{Wag{e_{china/c,t}}} \mathord{\left/ {\vphantom {{Wag{e_{china/c,t}}} {Wag{e_{china/c,t - 2}}}}} \right. } {Wag{e_{china/c,t - 2}}}}) \times wag{e_{c,t}} $ |
其中,
表4列(1)和列(3)中最低工资的工具变量的系数显著为正,列(4)中工具变量及其交互项系数均显著为正;列(2)和列(5)中最低工资系数显著为正,交互项系数显著为负,这说明同时构建最低工资和机器人应用工具变量也是合理有效的,且结果与基准回归结果相一致。
| (1) | (2) | (3) | (4) | (5) | |
| 第一阶段 | 第二阶段 | 第一阶段 | 第二阶段 | ||
| MW | LS | MW | Robot | LS | |
| MW_IV | 0.298***(0.036) | 0.284***(0.041) | 0.073*(0.043) | ||
| Robot_IV | −0.016(0.063) | 0.761***(0.085) | |||
| MW_IV×Robot_IV | 0.007(0.008) | 0.027**(0.010) | |||
| MW | 0.099***(0.020) | 0.145***(0.021) | |||
| MW×Robot | −0.020***(0.005) | ||||
| Robot | 0.024***(0.003) | −0.005**(0.002) | 0.019**(0.008) | ||
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 12 724 | 12 724 | 12 724 | 12 724 | 12 724 |
| 第一阶段F值 | 70.32 | 67.69 | 642.05 | ||
| 拟合优度 | 0.175 | 0.178 | |||
(四)异质性研究。
1. 企业异质性。根据《中小企业划分标准》,从业人员数超过1000人为大企业。表5列(1)和列(2)汇报了不同规模企业的估计结果,交互项系数在大企业中显著为负,在小企业中为正且不显著,这说明在大规模企业中机器人应用抑制了最低工资对企业劳动收入份额的补偿效应。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| 大规模 | 小规模 | 高工资 | 低工资 | 中小城市 | 大城市 | 特大城市 | 超大城市 | |
| MW | 0.021** | −0.002 | 0.029 | 0.006 | 0.047* | 0.033*** | −0.044 | −0.050*** |
| (0.008) | (0.023) | (0.019) | (0.009) | (0.025) | (0.012) | (0.033) | (0.019) | |
| MW×Robot | −0.006*** | 0.001 | −0.003 | −0.005** | −0.020*** | −0.007** | 0.001 | 0.009** |
| (0.002) | (0.006) | (0.005) | (0.002) | (0.007) | (0.003) | (0.009) | (0.004) | |
| Robot | 0.003 | −0.004 | 0.004 | 0.003 | 0.018* | 0.002 | −0.004 | −0.016** |
| (0.004) | (0.010) | (0.008) | (0.004) | (0.010) | (0.005) | (0.014) | (0.007) | |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 10 250 | 3 366 | 4 952 | 8 398 | 1 268 | 6 486 | 1 864 | 3 981 |
| 拟合优度 | 0.887 | 0.870 | 0.880 | 0.898 | 0.890 | 0.865 | 0.851 | 0.872 |
将样本划分为高、低平均工资企业,平均工资高于所有企业平均工资均值的视作高平均工资企业。表5列(3)和列(4)结果显示,低工资企业中交互项系数显著为负,说明低工资企业中机器人应用显著降低了最低工资对企业劳动收入份额的补偿效应。原因可能在于最低工资上涨主要是为了保护低薪员工的权益,对于高薪员工的工资只起到参考作用。此外,高平均工资企业资金雄厚、盈利状况更佳,企业较少为了节省劳动力成本而选择应用机器人生产。
2. 城市异质性。2014年国务院印发的《关于调整城市规模划分标准的通知》将城市规模划分为五类七档。⑧本文根据研究需要将小城市和中等城市合并为中小城市,将城市规模分为四类。表6列(1)和列(2)中,交互项系数显著为负,列(4)中交互项显著为正,表明在中小城市和大城市中机器人应用抑制了最低工资对企业劳动收入份额补偿效应,超大城市中强化了补偿效应。原因可能是超大城市中企业人员构成多以高技能、高学历为主,企业增加机器人应用同时增加了高级人才投入,最低工资对这些高级人才的溢出效应显著,导致企业在劳动者报酬上支付较多,促进了企业劳动收入份额提升。
| (1)高渗透 | (2)中渗透 | (3)低渗透 | (4)技术密集 | (5)资本密集 | (6)劳动密集 | |
| MW | 0.093**(0.043) | 0.081***(0.016) | 0.085***(0.011) | 0.064***(0.015) | 0.088***(0.009) | 0.060***(0.015) |
| MW×Robot | −0.022***(0.008) | −0.020***(0.005) | −0.019***(0.006) | −0.010***(0.003) | −0.020***(0.003) | −0.014*(0.008) |
| Robot | 0.025*(0.014) | 0.023***(0.009) | 0.032***(0.011) | 0.005(0.006) | 0.025***(0.005) | 0.027*(0.015) |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 2966 | 6677 | 3144 | 4365 | 7438 | 1917 |
| 拟合优度 | 0.904 | 0.899 | 0.906 | 0.857 | 0.870 | 0.853 |
3. 行业异质性。本文将企业按照其所处行业的机器人渗透度指标划分为三类,渗透度指标高于所有行业渗透度指标75分位数的行业为高渗透度行业,低于所有行业渗透度指标25分位数的行业为低渗透度行业。表6中列(1)—(3)结果显示,在高、中和低机器人渗透度行业中最低工资与机器人应用交互项的系数分别在1%的统计水平上显著为−0.022、−0.020、−0.019,显然高机器人渗透度行业中机器人应用的抑制作用更大。
参考李苏苏等(2022)的行业分类标准,将行业分为技术、资本和劳动密集型行业。⑨表6列(4)—(6)结果显示,三类行业中最低工资与机器人应用交互项的系数显著为−0.010、−0.020、−0.014,说明机器人应用在资本密集型行业中对企业劳动收入份额的抑制效应更大。原因可能在于该行业工业机器人渗透度较高,如汽车制造业、机械设备制造等,而纺织服装等传统劳动密集型行业的机器人应用不明显(王永钦和董雯,2020)。资本密集型行业企业更加依赖机器生产,企业生产决策偏向选择工业自动化,进而企业劳动收入份额较低。
六、进一步分析
(一)机制分析。在理论分析中,本文提出最低工资通过企业工资率渠道影响劳动收入份额。表7列(1)和列(2)验证了上述结论。列(3)和列(4)中交互项系数显著为正,说明最低工资上涨增加了企业工资率,尤其在高机器人渗透度的企业中促进程度更大。主要因为,最低工资标准为低收入者提供工资补偿,同时对高收入者工资可能存在溢出效应,整体表现为工资率的上升;在工业机器人应用多的企业,需要雇佣与之相匹配的操作、编程、技术研发等高技能劳动力,而高技能劳动力的劳动报酬相对较高,由此表现为在机器人应用高的企业中最低工资标准对企业工资率的促进效应更大。由此,验证了企业工资率是最低工资提升企业劳动收入份额的机制渠道,而且在机器人应用多的企业提升更加明显,验证了命题3。
| (1) | (2) | (3) | (4) | |
| MW | 2.048***(0.215) | 1.171**(0.510) | 1.309***(0.339) | 0.709(0.580) |
| MW×Robot | 0.211**(0.082) | 0.172*(0.092) | ||
| Robot | −0.713***(0.140) | −0.649***(0.154) | ||
| 控制变量 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 14 299 | 14 299 | 14 299 | 14 299 |
| 拟合优度 | 0.799 | 0.805 | 0.799 | 0.805 |
| 注:列(2)和列(4)进一步控制年份−地区、行业−地区的高维固定效应模型。 | ||||
(二)拓展性讨论。企业劳动收入份额的分解中包含了企业产出和劳动投入两个因素,考虑到企业生产率对企业产出具有决定性作用,并且企业劳动结构对进一步认识工资率渠道至关重要,为此本文进行拓展性分析。分别采用OP法和LP法测算企业全要素生产率,结果如表8所示,最低工资和交互项对企业全要素生产率的估计结果不显著,机器人应用的系数显著为正,说明最低工资标准上升并未显著影响企业生产率,而随着机器人的不断应用,全要素生产率显著提高,从而促进企业产出。这使得我们对命题2有了新的认识,即最低工资对企业劳动收入份额的促进效应会随着机器人应用的增加而降低,原因在于企业机器人应用后显著提升了企业生产率,产量的增加降低了企业劳动收入份额。
| (1) | (2) | (3) | (4) | (5) | (6) | |
| TFP_OP | TFP_LP | |||||
| MW | −0.020(0.026) | −0.016(0.026) | −0.031(0.041) | −0.033(0.027) | −0.027(0.027) | −0.027(0.042) |
| MW×Robot | 0.005(0.010) | 0.000(0.010) | ||||
| Robot | 0.018***(0.007) | 0.011(0.017) | 0.034***(0.007) | 0.033*(0.017) | ||
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 12 629 | 12 629 | 12 629 | 12 629 | 12 629 | 12 629 |
| 拟合优度 | 0.913 | 0.913 | 0.913 | 0.934 | 0.934 | 0.934 |
本文发现最低工资通过工资率提升企业劳动收入份额,且在机器人应用多的企业更明显。考虑教育异质性,需要分学历讨论员工的需求效应以判断企业劳动收入份额的变化。按照员工学历分为研究生、本科、专科和高中及以下学历。表9列(1)和列(2)结果显示最低工资上涨显著降低了企业员工总量,而机器人应用显著增加了员工总量,可能是因为最低工资上升导致企业成本激增从而企业减少了低技能人员,增加与机器人应用相匹配的高技能人员。最低工资与机器人应用交互项系数在列(3)中显著为正,在列(4)和列(5)中不显著,在列(6)中显著为负。这说明随着最低工资上涨,机器人应用多的企业增加了对研究生的需求、降低了高中及以下学历需求,而对本科与专科学历需求不显著。该结论也验证了前文分析结论,最低工资和机器人应用促进了高学历员工需求而替代了低学历人员,高学历人员工资率上升后,又促使了企业劳动收入份额的提升,这一发现是对企业工资率影响渠道的一种补充与验证。
| (1) | (2) | (3) | (4) | (5) | (6) | |
| 企业员工 | 研究生 | 本科 | 专科 | 高中及以下 | ||
| MW | −0.082***(0.025) | −0.207***(0.040) | −0.169(0.185) | −0.112(0.553) | −0.075(0.658) | −1.402(2.292) |
| MW×Robot | 0.039***(0.010) | 0.112**(0.044) | 0.032(0.134) | 0.044(0.161) | −1.213**(0.568) | |
| Robot | 0.024***(0.007) | −0.037**(0.016) | −0.310***(0.076) | −0.891***(0.230) | −0.212(0.276) | 3.975***(0.969) |
| 控制变量 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 14 299 | 14 299 | 9 927 | 12 926 | 12 893 | 8 124 |
| 拟合优度 | 0.953 | 0.953 | 0.920 | 0.956 | 0.948 | 0.945 |
七、结论与政策建议
最低工资对劳动收入份额的影响备受关注,但是近些年机器人应用对其影响有待拓展。本研究发现:第一,最低工资上涨显著提升了企业劳动收入份额,而机器人应用削弱了其促进作用。第二,大规模企业、低工资企业及中小城市和大城市中机器人应用显著降低了最低工资对企业劳动收入份额的补偿效应,而超大城市中机器人应用则强化了这种补偿效应。第三,最低工资上涨显著增加了企业工资率,验证了企业工资率是最低工资影响企业劳动收入份额的渠道。进一步,最低工资对企业劳动收入份额的促进效应随着机器人应用的增加而降低,是由于企业机器人应用后显著提升了企业生产率,产量的增加降低了企业劳动收入份额。此外,机器人应用促进了高学历员工需求,并替代了低学历人员,这一发现是对企业工资率渠道的一种补充与验证。
本研究为中国劳动保护和机器人产业发展提供了新的思路和借鉴。首先,最低工资上升能够提升企业劳动收入份额,这与最低工资保护劳动权益的目的相符合,但随着机器人使用量的增加,最低工资对企业劳动收入份额的促进作用不断被弱化。因此劳动保护部门不能局限于最低工资初始设立阶段的经济环境,需结合劳动力市场新变化形势,如区分行业划分最低工资标准,综合考虑机器人应用的负面冲击,合理制定最低工资标准。其次,机器人应用对最低工资的负向调节效应在大规模、低工资率的企业、机器人渗透度高、资本密集型行业中表现更为明显,政府部门应针对此类企业制定专项政策,重点关注资本密集型行业中工资率较低的企业,机器人应用对其劳动力的破坏冲击最大,可以考虑出台具有针对性的劳动保护政策,如为职工提供操作机器人的技能培训、规定企业平均工资和机器人占有率比值等,避免高自动化低工资企业的出现。此外,在人口规模较小的城市中机器人的作用效应更显著,这类城市政府应加大对劳动力的保护力度,如规定企业最低平均工资。最后,机器人应用对高中及以下学历人员替代效应较为明显,政府应积极引导企业加强对低技能员工的培训,引导其向高技能工作岗位转移,也可以为其提供新岗位,提供岗前培训助力岗位转型。同时,政府应呼吁企业向“人机协助”方向发展,适当对应用机器人生产的企业提供财政支持。
* 感谢南京审计大学高教研究课题(2022JG003)的支持,同时也感谢审稿专家和编辑提出的宝贵意见。
① 限于篇幅,具体推导过程参见工作论文。
② 限于篇幅,具体推导过程参见工作论文。
③ 限于篇幅,控制变量的具体测算方法参见工作论文。
④ 限于篇幅,主要变量的描述统计结果并未展示,详见本文的工作论文。
⑤ 限于篇幅,具体分类见异质性分析部分,组间差异的统计结果并未展示,详见本文的工作论文。
⑥ 限于篇幅,该趋势图并未展示,详见本文的工作论文。
⑦ 见工作论文图3。
⑧ 国务院关于调整城市规模划分标准的通知:http://www.gov.cn/zhengce/content/2014-11/20/content_9225.htm。
⑨ 根据《国民经济行业分类》(GB/T4754-2011)技术密集型行业代码有:26−28、35−37、39−41;资本密集型行业代码有:22−23、25、31−34;劳动密集型行业代码有:13−21、24、29−30、42−43。
| [1] | 陈登科, 陈诗一. 资本劳动相对价格、替代弹性与劳动收入份额[J]. 世界经济, 2018(12): 73–97. |
| [2] | 杜鹏程, 王姝勋, 徐舒. 税收征管、企业避税与劳动收入份额——来自所得税征管范围改革的证据[J]. 管理世界, 2021(7): 105–118. DOI:10.3969/j.issn.1002-5502.2021.07.008 |
| [3] | 韩民春, 韩青江. 机器人技术进步对劳动力市场的冲击——基于动态随机一般均衡模型的分析[J]. 当代财经, 2020(4): 3–16. DOI:10.13676/j.cnki.cn36-1030/f.2020.04.002 |
| [4] | 胡奕明, 买买提依明·祖农. 关于税、资本收益与劳动所得的收入分配实证研究[J]. 经济研究, 2013(8): 29–41. DOI:10.3969/j.issn.1673-291X.2013.08.013 |
| [5] | 孔高文, 刘莎莎, 孔东民. 机器人与就业——基于行业与地区异质性的探索性分析[J]. 中国工业经济, 2020(8): 80–98. DOI:10.3969/j.issn.1006-480X.2020.08.006 |
| [6] | 李磊, 王小霞, 包群. 机器人的就业效应: 机制与中国经验[J]. 管理世界, 2021(9): 104–118. DOI:10.3969/j.issn.1002-5502.2021.09.023 |
| [7] | 李磊, 徐大策. 机器人能否提升企业劳动生产率? ——机制与事实[J]. 产业经济研究, 2020(3): 127–142. DOI:10.13269/j.cnki.ier.2020.03.010 |
| [8] | 李苏苏, 段军山, 叶祥松. 中国工业行业间的资源错配与效率损失研究[J]. 南方经济, 2022(5): 78–100. DOI:10.19592/j.cnki.scje.391651 |
| [9] | 马双, 张劼, 朱喜. 最低工资对中国就业和工资水平的影响[J]. 经济研究, 2012(5): 132–146. |
| [10] | 施新政, 高文静, 陆瑶, 等. 资本市场配置效率与劳动收入份额——来自股权分置改革的证据[J]. 经济研究, 2019(12): 21–37. |
| [11] | 万江滔, 魏下海. 最低工资规制对企业劳动收入份额的影响——理论分析与微观证据[J]. 财经研究, 2020(7): 64–78. DOI:10.16538/j.cnki.jfe.2020.07.005 |
| [12] | 王林辉, 袁礼. 有偏型技术进步、产业结构变迁和中国要素收入分配格局[J]. 经济研究, 2018(11): 115–131. |
| [13] | 王晓娟, 朱喜安, 王颖. 工业机器人应用对制造业就业的影响效应研究[J]. 数量经济技术经济研究, 2022(4): 88–106. DOI:10.13653/j.cnki.jqte.2022.04.002 |
| [14] | 王雄元, 黄玉菁. 外商直接投资与上市公司职工劳动收入份额: 趁火打劫抑或锦上添花[J]. 中国工业经济, 2017(4): 135–154. |
| [15] | 王永钦, 董雯. 机器人的兴起如何影响中国劳动力市场? ——来自制造业上市公司的证据[J]. 经济研究, 2020(10): 159–175. |
| [16] | 魏下海, 董志强, 刘愿. 政治关系、制度环境与劳动收入份额——基于全国民营企业调查数据的实证研究[J]. 管理世界, 2013(5): 35–46. |
| [17] | 文雁兵, 陆雪琴. 中国劳动收入份额变动的决定机制分析——市场竞争和制度质量的双重视角[J]. 经济研究, 2018(9): 83–98. |
| [18] | 翁杰, 徐圣. 最低工资制度的收入分配效应研究——以中国工业部门为例[J]. 中国人口科学, 2015(3): 17–31. |
| [19] | 许明, 李逸飞. 最低工资政策、成本不完全传递与多产品加成率调整[J]. 经济研究, 2020(4): 167–183. |
| [20] | 余玲铮, 魏下海, 孙中伟, 等. 工业机器人、工作任务与非常规能力溢价——来自制造业“企业—工人”匹配调查的证据[J]. 管理世界, 2021(1): 47–59. DOI:10.3969/j.issn.1002-5502.2021.01.004 |
| [21] | 赵瑞丽, 孙楚仁, 陈勇兵. 最低工资与企业价格加成[J]. 世界经济, 2018(2): 121–144. |
| [22] | Acemoglu D, Autor D. Skills, Tasks and technologies: Implications for employment and earnings[J]. Handbook of Labor Economics, 2011, 4: 1043–1171. |
| [23] | Acemoglu D, Restrepo P. The race between man and machine: Implications of technology for growth, factor Shares, and employment[J]. American Economic Review, 2018, 108(6): 1488–1542. DOI:10.1257/aer.20160696 |
| [24] | Acemoglu D, Restrepo P. Robots and jobs: Evidence from US labor markets[J]. Journal of Political Economy, 2020, 128(6): 2188–2244. DOI:10.1086/705716 |
| [25] | Acemoglu D, Robinson J A. The rise and decline of general laws of capitalism[J]. Journal of Economic Perspectives, 2015, 29(1): 3–28. DOI:10.1257/jep.29.1.3 |
| [26] | Akerman A, Gaarder I, Mogstad M. The skill complementarity of broadband internet[J]. The Quarterly Journal of Economics, 2015, 130(4): 1781–1824. DOI:10.1093/qje/qjv028 |
| [27] | Bartik T J. Who benefits from state and local economic development policies?[M]. Kalamazoo: W. E. Upjohn Institute, 1991. |
| [28] | Berg A, Buffie E F, Zanna L F. Robots, growth, and inequality: The robot revolution could have profound negative implications for equality[J]. Finance & Development, 2016, 53(3): 10–13. |
| [29] | Berkowitz D, Ma H, Nishioka S. Declining labor shares and heterogeneous firms[R]. Working Paper No.552, 2015. |
| [30] | Bosch M, Manacorda M. Minimum wages and earnings inequality in urban Mexico[J]. American Economic Journal: Applied Economics, 2010, 2(4): 128–149. DOI:10.1257/app.2.4.128 |
| [31] | Cacciatore M, Fiori G. The macroeconomic effects of goods and labor markets deregulation[J]. Review of Economic Dynamics, 2016, 20: 1–24. DOI:10.1016/j.red.2015.10.002 |
| [32] | Caselli F, Manning A. Robot arithmetic: New technology and wages[J]. American Economic Review: Insights, 2019, 1(1): 1–12. DOI:10.1257/aeri.20170036 |
| [33] | Cheng H, Jia R X, Li D D, et al. The rise of robots in China[J]. Journal of Economic Perspectives, 2019, 33(3): 71–88. DOI:10.1257/jep.33.2.71 |
| [34] | DeCanio S J. Robots and humans-complements or substitutes?[J]. Journal of Macroeconomics, 2016, 49: 280–291. DOI:10.1016/j.jmacro.2016.08.003 |
| [35] | Dube A, Lester T W, Reich M. Minimum wage effects across state borders: Estimates using contiguous counties[J]. The Review of Economics and Statistics, 2010, 92(4): 945–964. DOI:10.1162/REST_a_00039 |
| [36] | Graetz G, Michaels G. Is modern technology responsible for jobless recoveries?[J]. American Economic Review, 2017, 107(5): 168–173. DOI:10.1257/aer.p20171100 |
| [37] | Hjort J, Poulsen J. The arrival of fast internet and employment in Africa[J]. American Economic Review, 2019, 109(3): 1032–1079. DOI:10.1257/aer.20161385 |
| [38] | Karabarbounis L, Neiman B. The global decline of the labor share[J]. The Quarterly Journal of Economics, 2014, 129(1): 61–103. DOI:10.1093/qje/qjt032 |
| [39] | Malloy L C. The minimum wage, bargaining power, and the top income share[J]. Forum for Social Economics, 2020, 49(1): 75–98. DOI:10.1080/07360932.2016.1155468 |
| [40] | Pischke J S. Labor market institutions, wages, and investment: Review and implications[J]. CESifo Economic Studies, 2005, 51(1): 47–75. DOI:10.1093/cesifo/51.1.47 |

