
2022第48卷第9期
2. 北京大学 经济研究所, 北京 100871;
3. 中央民族大学 经济学院, 北京 100081;
4. 北京大学 经济学院, 北京 100871
2. Institute of Economics, Peking University, Beijing 100871, China;
3. School of Economics, Minzu University of China, Beijing 100081, China;
4. School of Economics, Peking University, Beijing 100871, China
一、引 言
近年来,随着5G时代的到来,5G、人工智能、区块链、大数据和云计算等新技术、新业态及新模式迎来“井喷式”发展,世界各国纷纷开启数字化革命,主动迎接数字浪潮。截至2020年,超过30个OECD成员国制定了数字经济相关发展战略。美国更是早在2011年和2012年便推出了“联邦云计算战略”和“大数据研究和发展倡议”。得益于完备的工业体系和雄厚的技术积累,中国成功抓住了数字化革命中的发展机遇。《中国数字经济发展白皮书(2021)》显示,2020年中国数字经济发展规模扩张至39.2万亿元,数字经济占GDP比重高达38.6%。
目前,中国经济发展已经由高速增长步入高质量发展阶段,突破国内“卡脖子”技术成为中国经济发展亟待解决的关键问题。发展数字经济已然成为中国突破技术难题,实现自主性创新的战略选择。数字经济的发展可分为两个方向:一是数字产业化,具体是指电子信息制造业、电信业、软件及信息技术服务业和互联网行业等数字技术产业的发展与壮大;二是产业数字化,具体是指传统农业、工业和服务业对数字技术的引进和使用。其中,产业数字化是数字经济发展的主阵地,成为数字经济赋能经济高质量发展的重要抓手。那么,产业数字化是否会促进企业创新?对于这一问题的回答,目前只有少数学者从互联网应用、数字金融和智慧城市等数字经济相关领域或企业绿色创新视角进行了相关探讨(韩先锋等,2019;唐松等,2020;温湖炜和王圣云,2021;宋德勇等,2022)。总体来看,相关研究依然存在以下不足:一是,目前学者多从总体层面研究数字技术普及或数字化对技术创新的影响,忽略了数字技术产业和传统产业在数字化过程中的差异性问题;二是,既有研究在一定程度上忽视了对数字化影响技术创新的内在机制和经济后果的探讨,特别是缺乏相关的数理分析;三是,关于企业数字化指数的测算,目前学界的主流做法是利用企业年报中的数字化词频解释企业的数字化水平,但既有文献多以“个性化”词汇构建数字化词库,没有充分考虑数字化词汇的“共性”特征。
有鉴于此,本文将研究聚焦于传统产业数字化过程对企业创新的影响。一方面,本文将数字化过程和企业创新的选择行为引入异质性企业技术选择模型,数理分析产业数字化对企业创新的影响效应及作用机理;另一方面,依托机器学习和文本分析构建起2008–2020年中国传统产业上市公司的数字化指数,并利用双向固定效应模型展开实证考察。研究发现,产业数字化显著地促进了企业的技术创新。机制检验显示,产业数字化提高了企业研发资金的供给效率和使用效率,这成为产业数字化促进企业创新的重要路径。为了进一步强化理论机制,还从异质性视角展开考察,发现产业数字化对企业创新的促进效应会受到外部环境和内部因素的多重影响。一方面,企业所在地区的数字经济发展水平越高,产业数字化越能促进企业创新;另一方面,相较于非资本密集型企业,产业数字化对资本密集型企业的创新效应更强。最后,经济后果检验表明,产业数字化可以通过促进企业创新扩大企业的内需市场并提高企业的产品出口质量,这为产业数字化依托技术创新推动构建“双循环”新发展格局提供了证据。
本文的边际贡献主要体现在:①具体研究传统产业数字化的创新效应,将数字化过程和企业创新行为引入异质性企业技术选择模型,通过数理分析揭示了产业数字化对企业创新的影响效应及作用机理,补充解释了产业数字化影响企业创新的理论框架;②综合既有研究的优点和不足,从词汇共性视角重新构建了上市公司数字化词库,对企业数字化指标体系的建设具有一定的补充贡献;③从研发资金的供给效率和使用效率视角理清了产业数字化促进企业创新的传导路径,揭开了数字化背景下企业资金配置及其影响企业创新的“黑箱”;④利用企业所在地区到数字技术起源地的距离作为工具变量解决了内生性问题,为后续研究提供了可行思路;⑤从企业内需市场扩增和产品出口质量提升视角检验了产业数字化促进企业创新的经济后果,为产业数字化推动构建“双循环”新发展格局提供了学理支持。
二、理论分析
产业数字化实则是传统产业内部的企业不断引进和运用数字技术的过程。因此,研究产业数字化的问题可以下沉至企业层面进行探讨。基于此,本文沿用Bustos(2011)的异质性企业技术选择模型构建产业数字化影响企业创新的理论模型,并作出如下改进:(1)将数字化过程引入模型,并根据已有研究和既定事实做出如下假设:一方面数字化存在一定门槛,需要企业前期投入较高的资本和劳动成本(固定成本)(荆文君和孙宝文,2019);另一方面数字化可以从搜寻、复制、追踪和验证等多个方面降低企业的边际成本(Goldfarb和Tucker,2019),从而提高企业的生产效率(Bloom等,2012;Wang和McElheran,2017)。(2)Bustos(2011)只考虑了企业技术选择对生产效率的直接影响,没有考虑间接影响机制。本文认为,企业的数字技术选择行为(即数字化过程)一方面可以直接改变企业的生产率水平,另一方面也可以通过改变企业的创新选择行为而间接地对生产效率产生影响。因此,本文在Bustos(2011)的基础上进一步引入了企业的创新选择行为,以探讨数字化过程对企业创新的影响。
(一)消费者。沿用Bustos(2011)的设置,假设消费者对异质性产品的需求偏好满足不变替代弹性(CES)函数形式,替代弹性
| $ q\left(\omega \right)=E{P}^{\sigma -1}{\left[p\right(\omega \left)\right]}^{-\sigma } $ | (1) |
其中,q(ω)和p(ω)分别表示产品ω的消费数量和价格;E表示消费者总支出。P表示价格指数,具体为:
| $ P={\left[{\int }_{0}^{\Omega }{p\left(\omega \right)}^{1-\sigma }d\omega \right]}^{\frac{1}{1-\sigma }} \text{,} \omega \in \Omega $ | (2) |
(二)厂商。本文简化了Bustos(2011)的市场设置,只考虑封闭经济情形下数字化对企业创新的影响。假设市场是垄断竞争的,每种异质性产品对应不同的异质性企业,企业的总成本由一次性固定成本f和边际成本组成。边际成本的高低取决于生产效率ϕ,姑且以1/ϕ表示。企业可以自由选择引进数字技术的力度。这样,在市场中会自然形成两类企业:一类是数字化水平较高的企业,另一类是数字化水平较低或不进行数字化的企业。为简化分析,假设市场上存在两个异质性企业:企业l处于低数字化水平,企业h处于高数字化水平。对于低数字化水平的企业l 而言,其总成本可由以下函数表示:
| $ {TC}_{l}\left(q,\phi \right)=f+\frac{q}{\phi } $ | (3) |
对于高数字化水平的企业h而言,其固定成本虽然更高,但同时具有更高的生产效率。因此分别引入两个影响因子η和γ,其总成本函数具体表示为:
| $ {TC}_{h}\left(q,\phi \right)=\eta f+\frac{q}{\gamma \phi } $ | (4) |
式(3)和式(4)中,q表示企业产品产量;η为固定成本影响因子,γ为生产效率影响因子,η和γ均大于1。
在CES偏好下,企业为追求利润最大化而制定的产品价格是边际成本之上的恒定价格。因此,参考Bustos(2011)的做法,将企业l和企业h的产品定价分别表示为pl=1/ρϕ和ph=1/ργϕ。结合式(1)至式(4)可得到企业l和企业h的利润函数:
| $ {\pi }_{l}=\frac{1}{\sigma }E{\left(P\rho \phi \right)}^{\sigma -1}-f $ | (5) |
| $ {\pi }_{h}=\frac{1}{\sigma }E{\left(P\rho \gamma \phi \right)}^{\sigma -1}-\eta f $ | (6) |
(三)引入企业创新行为。假设成功的创新可以分别将企业l和企业h的生产效率提升至δlϕ和δhϕ(δl,δl>1),此时企业l和企业h的利润函数可表示为:
| $ {\pi }_{l}=\frac{1}{\sigma }E{\left(P\rho {\delta }_{l}\phi \right)}^{\sigma -1}-f-{R}_{l} $ | (7) |
| $ {\pi }_{h}=\frac{1}{\sigma }E{\left(P\rho {\delta }_{h}\gamma \phi \right)}^{\sigma -1}-\eta f-{R}_{h} $ | (8) |
其中,Rl和Rh分别表示企业l和企业h的研发成本。不妨设δσ-1=θI,表示创新对企业利润的贡献。其中,I表示企业的创新产出;θ表示外生给定的创新转化效率,即每单位创新对生产效率的促进幅度。此时,企业l和企业h的利润函数可进一步表示为:
| $ {\pi }_{l}=\frac{1}{\sigma }E{\left(P\rho \phi \right)}^{\sigma -1}\theta {I}_{l}-f-{R}_{l} $ | (9) |
| $ {\pi }_{h}=\frac{1}{\sigma }E{\left(P\rho \gamma \phi \right)}^{\sigma -1}\theta {I}_{h}-\eta f-{R}_{h} $ | (10) |
进一步地,结合Rivera-Batiz和Romer(1991)、Jones和Williams(2000)及Akcigit 等(2018)的研究,设定企业的创新产出函数为:
| $ {I}_{i}={\chi }_{i}{R}_{i}^{{\kappa }_{i}}{L}_{i}^{{\lambda }_{i}}{A}_{i}^{{\tau }_{i}} $ | (11) |
其中,i∈{l,h};I表示企业的创新产出;R表示企业的研发成本;L和A分别表示研发人员数量和创新知识存量,在这里假设外生恒定,均简化为1。由此可以得到企业的创新成本:
| $ {\pi }_{l}=\frac{1}{\sigma }E{\left(P\rho \phi \right)}^{\sigma -1}\theta {I}_{l}-f-{\left({I}_{l}/{\chi }_{l}\right)}^{\frac{1}{{\kappa }_{l}}} $ | (12) |
| $ {\pi }_{h}=\frac{1}{\sigma }E{\left(P\rho \gamma \phi \right)}^{\sigma -1}\theta {I}_{h}-\eta f-{\left({I}_{h}/{\chi }_{h}\right)}^{\frac{1}{{\kappa }_{h}}} $ | (13) |
对简化后的式(11)两边取自然对数可得:
| $ {\rm{ln}}{I}_{i}={\rm{ln}}{\chi }_{i}+{\kappa }_{i}{\rm{ln}}{R}_{i} $ | (14) |
由式(14)可不失一般性地认为,χ是对企业创新生产能力的综合评价,可看作是企业研发资金的供给效率。也即,企业是否将有限的资金更多地配置给研发创新;κ是研发投入的弹性系数(0<κ<1),可以看作是研发资金的使用效率,也即研发投入转化为创新产出的能力。
讨论:企业创新不能脱离外部环境在真空中独自运行,同外界交换信息的频率和学习外界知识与经验的能力可以显著影响企业的创新效率(Akcigit等,2018)。因此,信息可得性被认为是企业创新成功与否的决定性因素(Kong等,2022)。在传统工业经济时代,企业与外界的信息交换不仅受时间和空间的束缚,而且还会掣肘于信息搜集工具和交流手段的低效性,企业往往会因此付出高昂的信息搜寻和追踪成本,这显然会挤占研发资金投入,降低企业的研发资金供给效率。而在数字经济时代,数字化使得企业与外界的信息交换可以依托5G技术、大数据、云计算等新模式和新技术进行。这不仅可以显著降低信息搜寻与学习的人工成本,而且可以依托数字技术高效精准的信息匹配能力有效减少超额的信息搜寻和追踪成本。由此可见,数字化可以有效降低企业研发创新的附加成本,使企业能将更多的盈余资金投向研发创新,从而提高企业的研发资金供给效率。此外,数字技术的运用还会提高企业的研发资金使用效率。因为人工智能等核心数字技术可以通过复杂技术代替人脑进行甄别、预测和决策,弥补人类脑力的不足,从而可以重塑企业的创新模式和知识获取方式,提高知识创造的效率和精准度(Duan等,2019),进而提高企业的研发资金使用效率。基于上述分析可得命题1:数字化水平越高,企业研发资金的供给效率和使用效率也会越高。也即,χ h> χl,且 κ h> κl。
(四)利润最大化与企业创新决策。根据企业利润函数式(12)和式(13),企业l和企业h的利润最大化形式可分别表示为:
| $ \underset{{I}_{l},{\theta }_{l},{\chi }_{l},{\kappa }_{l}}{\mathrm{max}}{\pi }_{l}=\frac{1}{\sigma }E{\left(P\rho \phi \right)}^{\sigma -1}\theta {I}_{l}-f-{\left({I}_{l}/{\chi }_{l}\right)}^{\frac{1}{{\kappa }_{l}}} $ | (15) |
| $ \underset{{I}_{h},{\theta }_{h},{\chi }_{h},{\kappa }_{h}}{\mathrm{max}}{\pi }_{h}=\frac{1}{\sigma }E{\left(P\rho \gamma \phi \right)}^{\sigma -1}\theta {I}_{h}-\eta f-{\left({I}_{h}/{\chi }_{h}\right)}^{\frac{1}{{\kappa }_{h}}} $ | (16) |
企业要实现利润最大化,一阶条件需满足
| $ {I}_{l}^{*}={\chi }_{l}^{\frac{1}{1-{\kappa }_{l}}}{\left[\frac{{\kappa }_{l}}{\sigma }E{\left(P\rho \phi \right)}^{\sigma -1}\theta \right]}^{\frac{{\kappa }_{l}}{1-{\kappa }_{l}}} $ | (17) |
| $ {I}_{h}^{*}={\chi }_{h}^{\frac{1}{1-{\kappa }_{h}}}{\left[\frac{{\kappa }_{h}}{\sigma }E{\left(P\rho \gamma \phi \right)}^{\sigma -1}\theta \right]}^{\frac{{\kappa }_{h}}{1-{\kappa }_{h}}} $ | (18) |
综上,企业l和企业h要想实现利润最大化,则需分别具备
三、研究设计
(一)数字化的测算。目前学界通常在构建数字化词库的基础上,利用Python技术对年报进行文本分析以测算企业的数字化水平(吴非等,2021;赵宸宇等,2021;袁淳等,2021),这为本文企业数字化指数的测算提供了思路。然而,上述文献均使用“个性化”词汇构建词库,没有充分考虑数字化词汇的“共性”特征。现实中,某个数字技术的表达往往会有不同的名称,特别是在行业之间会存在显著差异。比如,人工智能在电力行业通常被表达为“智能电网”,而在交通行业则会被表达为“智能交通”,类似的还有“智能物流”“智能家居”等,这些个性化词汇甚至会在企业间出现表达上的差异,很难通过人工手段搜集完整。如果仅使用主观上选择的个性化词汇构建词库极有可能会造成企业数字化水平的低估。更重要的是,还有可能导致数字化指数在企业之间出现较为严重的横向偏差。而如果充分考虑数字技术的共性词汇,则可有效避免上述问题。如使用人工智能的共性词汇−“智能”,而不是“智能电网”“智能交通”等个性化词汇。
有鉴于此,本文在既有词库构建思路的基础上,首先,从数字化词汇的共性特征出发构建数字化词库,然后利用Python技术爬取企业年报中的数字化共性词,以此作为数字化指数的初始代理变量。但需要注意的是,使用共性词汇对企业年报进行词频抓取会将与数字化不太相关的词汇一并纳入其中。因此,要想使用数字技术共性词汇精准地测算企业的数字化指数,还需进行降频处理,将共性词汇包含的非数字化信息剔除。对此,本文利用机器学习的方法,在抓取共性词汇时,同时抓取共性词汇的4位词进行分析,以确定4位词中非数字化含义词汇的词频,然后以共性词汇词频和非数字化含义4位词词频的差值作为最后的数字化指数刻画指标(digital)。为了缓解可能存在的非正态分布问题,本文在后续回归中进行了对数处理。①
(二)计量模型的选择。具体构建如下双向固定效应模型检验产业数字化对企业创新的影响效应:
| $ {innov}_{i,t}={\alpha }_{0}+{\alpha }_{1}{digital}_{i,t-1}+{\mathit{\alpha }}_{2}{\mathit{x}}_{i,t-1}+{\mu }_{i}+{\upsilon }_{t}+{\varepsilon }_{i,t} $ | (19) |
其中,i表示企业;t表示年份。innov表示企业的创新产出,参考黎文靖和郑曼妮(2016)的做法,具体以专利申请数量刻画。需要指出的是,我国的专利法将专利分为发明、实用新型和外观设计三种类型。相较于实用新型和外观设计,发明型专利具有更强的创新性。因此,将创新性最强的发明专利申请数量视作企业的创新产出,并以三类专利申请之和用作稳健性检验,在具体回归中本文对专利申请数量加1并取自然对数以缓解可能存在的非正态分布问题。digital表示企业的数字化指数,具体测算方法如上文所述。鉴于企业将数字技术融入生产和研发创新过程的滞后性问题,同时考虑到逆向因果关系对估计结果造成的干扰,本文具体将数字化指数滞后一期纳入计量模型。矩阵向量x表示可能影响企业创新的特征变量,具体包括企业规模(企业总资产的自然对数)、企业年龄(企业成立年限+1的自然对数)、资本结构(企业资产负债率)、董事会规模(企业董事会人数的自然对数)、政府补助(政府补贴与营业收入之比)、行业竞争程度(基于营业收入与三位行业代码计算的赫芬达尔–赫希曼指数)、前十大股东持股比例和机构持股比例等。对于以上控制变量,本文同样进行滞后一期的处理。μi表示企业固定效应;υt表示年份固定效应;ε为随机干扰项。
(三)样本选择与数据来源。依据主题,具体选取2008–2020年传统产业的沪深A股上市公司数据作为初始样本。专利数据整理于国家知识产权局专利检索网;公司年报及其他财务数据均整理于万得(WIND)数据库,个别缺失数据通过国泰安(CSMAR)数据库补齐。参考多数文献的做法,本文对数据样本进行如下处理:(1)剔除银行、证券、保险等金融行业上市公司,原因在于金融类企业的创新存在特殊性,不能以专利产出来衡量(Mukherjee等,2017);(2)剔除主要变量存在缺失的企业样本;(3)对所有连续型变量进行1%的双端缩尾处理,以规避极端值对估计结果的干扰。最终,得到2008–2020年间3 237家上市公司的28 401条观测值。②
四、实证结果分析与稳健性检验
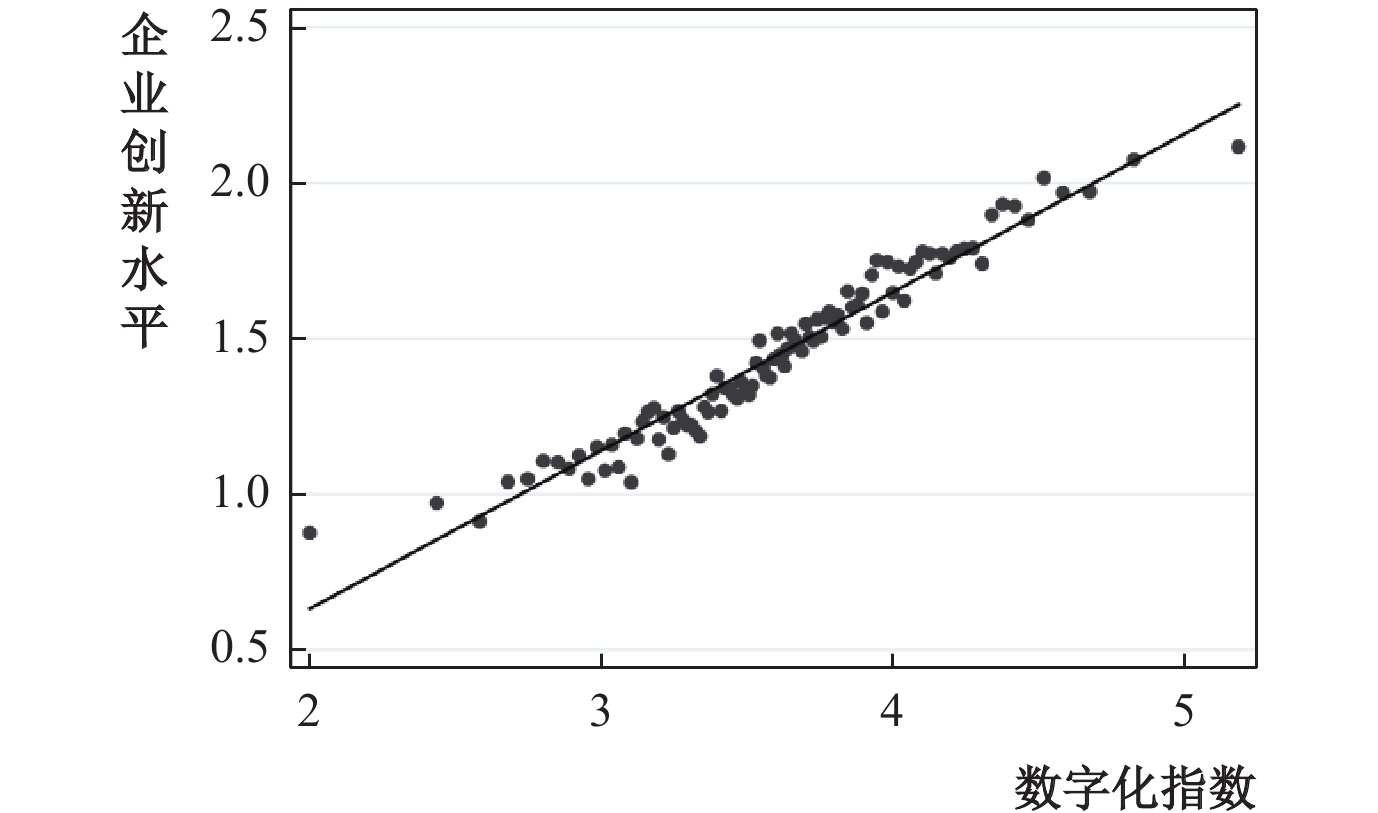
(一)基准结果。在利用模型(19)回归前,首先通过绘制数字化指数与企业创新的分仓散点图进行非参数估计,如图1所示。从图中可以看出,数字化指数与企业创新之间存在明显的正向关系。这初步表明,产业数字化很有可能会促进企业创新。然而,基于散点图的非参数估计并不能从统计上验证这一正向关系的显著性。因此,将利用更加严谨的计量方法加以证明。
|
| 图 1 数字化指数与企业创新的分仓散点图 |
表1进一步基于模型(19)汇报了产业数字化是否影响企业创新的估计结果。其中,列(1)是没有加入其他特征变量的回归结果,不难发现,在控制年份和企业固定效应之后,数字化指数digital的系数为正,且在1%的水平上高度显著。列(2)进一步加入了可能影响企业创新的特征变量,可以看出,数字化指数digital的系数依然在1%的水平上高度显著为正。上述结果表明,企业数字技术的引进和运用确实可以显著地促进企业创新。即,产业数字化可以有效地促进企业创新,命题2成立。
| 企业技术创新水平(innov) | ||
| (1) | (2) | |
| L.digital | 0.0551***(0.0087)
|
0.0533***(0.0087)
|
| L.控制变量 | 否 | 是 |
| 年份/企业固定效应 | 是 | 是 |
| 样本量 | 25 139 | 25 139 |
| Adj-R2 | 0.1569 | 0.1602 |
| 注:L.表示使用滞后一期的解释变量进行回归;*、**和***分别表示10%、5%和1%的显著性水平;括号内为标准误;为了节约篇幅,回归结果略去了对常数项和控制变量估计系数的汇报;因为使用滞后一期的解释变量进行回归,所以实际参与回归的样本小于28 401。下表统同。 | ||
(二)内生性问题。根据固定效应模型的估计原理,表1结果的可信性取决于模型(19)中数字化指数digital的外生性。但这一情形很可能会因为以下两种情况而无法满足:一是“双向因果”问题,一方面数字化会促进企业进行创新,另一方面创新水平高的企业也可能会更容易实现数字化;二是“遗漏变量”问题,虽然本文尽可能地控制了可能影响企业创新的其他因素,但这仍不能保证可以将所有影响企业创新的因素囊括其中。“双向因果”和“遗漏变量”均会使解释变量数字化指数digital出现内生性问题,从而对估计结果的一致无偏性造成干扰。对此,本文利用工具变量法进行解决。
工具变量的选择需满足相关性和排他性约束两个条件。数字经济的运行虽然摆脱了空间上的束缚,但数字技术的扩散仍然遵循通用目的技术的扩散规律,在一定程度上会受地理位置的限制。比如,郭峰等(2017)的研究表明,地理空间因素是影响数字金融发展的关键变量,与杭州相距越远的地区,数字金融推广难度越大。基于这一事实,本文认为,各地区到数字技术起源地的空间距离将是一个不错的工具变量。一方面,各地区到数字技术起源地的空间距离越近,该地区的企业将越容易引进数字技术,从而可以实现更快的产业数字化进程,满足相关性要求;另一方面,空间距离是严格的外生变量,不会因时间的变化和经济的发展而改变,满足排他性约束要求。接下来的问题是如何确定中国的数字技术起源地。1998–2000年期间,腾讯、搜狐、阿里巴巴和百度等数字型企业相继在北京、深圳和杭州成立,这直接将中国的数字化推向了快速发展时期(张辉和石琳,2018)。此后,中国的数字产业蓬勃发展,中国数字经济也逐渐形成了北京、深圳和杭州等城市领跑全局的多极发展模式。因此,北京、深圳和杭州当属中国数字经济的起源地。但需要注意的是,北京作为中国的政治中心,很有可能会通过除数字化之外的其他途径影响各地区企业的创新水平。因此,最终选择企业所在地级市到深圳和杭州的距离作为数字化指数digital的工具变量(iv_sz和iv_hz)。另外,在工具变量较难寻找的情况下,部分学者习惯利用行业层面核心解释变量的均值作为工具变量解决内生性问题(Heutel,2014;杨洋等,2015)。这种方法也存在其合理性,这是因为,行业层面解释变量的均值肯定会与企业层面的解释变量存在相关性,同时,行业层面的指标又不会对微观层面的企业行为产生系统性影响。基于此,本文利用行业层面数字化指数的均值构建了第三个工具变量(iv_ind)。
表2汇报了工具变量法的估计结果。因为到深圳和杭州的距离实则为企业不随时间而改变的固有特征,在以工具变量iv_sz和iv_hz进行回归时,如果控制企业个体固定效应,则会因为多重共线性问题而无法得到内生变量digital的估计系数。因此,在以空间距离(iv_sz和iv_hz)为工具变量的回归中本文利用只控制年份固定效应的两阶段最小二乘法估计(ivreg2),而在以行业层面均值为工具变量的回归中本文利用双向固定效应的面板工具变量法进行估计(xtivreg2)。
| (1)工具变量:地级市到
深圳距离 (iv_sz) |
(2)工具变量:地级市到
杭州距离 (iv_hz) |
(3)工具变量:数字化
指数行业均值(iv_ind) |
||
| 数字化指数(L.digital) | ||||
| 第一阶段回归结果 | iv_sz | −0.0402***(0.0028)
|
||
| iv_hz | −0.0244***(0.0034)
|
|||
| iv_ind | 0.8938***(0.0138) | |||
| 企业技术创新水平(innov) | ||||
| 第二阶段回归结果 | L.digital | 0.6555***(0.1170) | 1.7019***(0.3001)
|
0.1684**(0.0801)
|
| L.控制变量 | 是 | 是 | 是 | |
| 年份固定效应 | 是 | 是 | 是 | |
| 企业固定效应 | 否 | 否 | 是 | |
| 不可识别检验(Anderson LM 统计量) | 207.633***{0.000} | 52.666***{0.000} | 264.295***{0.000} | |
| 弱识别检验(Cragg−Donald Wald F 统计量) | 209.187[16.38] | 52.732[16.38] | 267.238[16.38] | |
| 样本量 | 25 139 | 25 139 | 25 139 | |
| 注:中括号内为Cragg-Donald Wald F 统计量10%显著性水平上的Stock-Yogo临界值;大括号内为Anderson LM 统计量对应的p值。 | ||||
首先,从三个工具变量的有效性来看,在第一阶段回归中工具变量iv_sz和iv_hz的系数均在1%的水平上显著为负,这说明,到深圳或杭州的距离越远,企业数字化难度越大,数字化水平相对更低。这一结果符合上文的理论预期。进一步发现,工具变量iv_ind的系数在1%的水平上显著为正,说明行业层面的数字化水平与企业数字化指数高度正相关。综上结果,再结合弱识别检验的Cragg-Donald Wald F 统计量均远大于10%显著性水平上的临界值16.38可知,本文选择的三个工具变量均不存在弱工具变量问题。同时,由不可识别检验的Anderson LM 统计量均在1%的水平上显著可知,工具变量也不存在不可识别问题。以上结果充分说明,本文选择的工具变量是合理有效的。其次,从工具变量法第二阶段的回归结果来看,在列(1)和列(2)以空间距离为工具变量的回归中,数字化指数digital的系数均在1%的水平上显著为正,在列(3)以行业层面数字化均值为工具变量的回归中,数字化指数digital的系数在5%的水平上显著为正。这些结果充分说明,即使利用工具变量法规避了可能存在的内生性问题,本文的结论依然成立。
(三)稳健性检验。③为保证研究结论的严谨性,本文还从多个视角进行了稳健性检验:①置换代理变量。企业创新层面,将发明型专利置换为三类专利之和;数字化指数层面,将本文测算的数字化指数置换为吴非等(2021)、赵宸宇等(2021)和袁淳等(2021)测算的数字化指数。②改变计量方法。鉴于专利申请数量的计数特征,改用泊松回归(Poisson)、负二项回归(Negative Binomial)和归并回归(Tobit)进行估计。③规避企业的“策略性”行为。鉴于数字化指数的测算可能会受企业“策略性”信息披露行为的干扰,需进一步规避企业的“策略性”行为进行估计。上述稳健性检验结果均一致地表明,产业数字化可以显著地促进企业创新。
五、作用机制检验与异质性分析
(一)作用机制检验。
1.理论机制的实证含义。在理论模型中,高数字化企业最优创新产出大于低数字化企业最优创新产出的条件在于,高数字化企业具有更高的研发资金供给效率和使用效率。由此来看,本文理论机制的实证含义在于以下两个方面:一是要验证数字化是否可以显著提高企业的研发资金供给效率;二是要考察数字化是否会显著提高企业的研发资金使用效率。
对于实证含义的第一个方面,前文认为数字化之所以能够提高企业的研发资金供给效率,关键在于数字化可以节省创新过程中信息的搜寻和追踪成本,从而使得更多的盈余资金流向研发创新。因此,检验数字化是否会促进企业的研发资金供给效率实则是考察企业盈余资金的配置和流向。对于企业而言,将获得的盈余资金用于不同的“投资”项目④实则是该项目的资金投入水平是否与企业的资金获得机会相匹配,可视为“投资”项目资金投入对企业资金获得机会的敏感程度。因此,可以借鉴“投资—投资机会”敏感性模型进行考察。参考靳庆鲁等(2012)的做法,本文构建如下敏感性模型考察数字化是否以及如何影响企业资金的配置和流向:
| $ \begin{aligned} \;\\ {y}_{i,t}= &{\beta }_{0}+{\beta }_{1}{digital}_{i,t-1}\times {roa}_{i,t-1}+{\beta }_{2}{digital}_{i,t-1}+{\beta }_{3}{roa}_{i,t-1}\\ &+{\mathit{\beta }}_{4}{\mathit{x}}_{i,t-1}+{\mu }_{i}+{\upsilon }_{t}+{\varepsilon }_{i,t} \end{aligned} $ | (20) |
模型(20)旨在考察数字化转型下企业盈余资金在信息搜寻、追踪成本和研发活动之间的配置,因此被解释变量y具体表示企业信息搜寻、追踪成本和研发支出。roa为企业的资产收益率,用以刻画企业盈余资金的获得机会。这里只选取企业内源资金的获得机会进行回归的原因在于:企业的创新行为是一个周期长、风险大且收益极不确定的复杂过程,很难得到外源融资的支持(Aboody和Lev,2000)。其他变量定义与模型(19)相同。模型(20)中,交乘项digital×roa的系数β1需重点关注。其反映了数字化对企业盈余资金配置去向的影响。根据理论预期,当y表示信息搜寻、追踪成本时,β1应该显著为负,表示数字化会降低企业信息搜寻、追踪成本对盈余资金的敏感程度,也即数字化会抑制企业盈余资金向信息搜寻、追踪成本的流动,降低信息搜寻和追踪成本的资金供给效率;当y表示研发支出时,β1应该显著为正,表示数字化会提高企业研发支出对盈余资金的敏感程度,也即数字化将使得更多的盈余资金流向研发支出,提高企业的研发资金供给效率。需要注意的是,鉴于数字技术从引进到运用再到生产需要一定的时间,在模型(20)中本文同样利用数字化指数滞后一期的数据进行回归,而资金的获得与分配过程一般不存在太长的滞后时间,因此利用刻画盈余资金获得机会的资产收益率当期数据进行回归。
在企业信息搜寻追踪成本和研发支出的刻画上,参考既有文献(张杰等,2015;虞义华等,2018)的做法,研发支出以企业研发投入与营业收入的比值表示。由于上市公司年报中并不单独披露信息搜寻和追踪成本,因此只能间接进行估计。通常,企业对外界信息的搜寻和追踪是企业与外界“打交道”的过程,这类活动产生的支出一般计入管理费用,比如业务招待费、差旅费和咨询费等。但因为企业的管理费用中包含了大量的常规性支出,如果直接检验数字化对管理费用资金配置的影响有可能会造成估计偏误。因此,本文通过考察企业超额管理费用对盈余资金的敏感性来间接检验数字化中企业的盈余资金与信息搜寻和追踪成本的匹配程度。其中,超额管理费用(emc)利用Richardson(2006)、申宇等(2015)提供的方法测算。
对于实证含义的第二个方面,企业研发资金的使用效率实则为单位研发投入对应的创新产出。因此,本文具体利用发明型专利申请数量与滞后一期的研发投入比值刻画企业的研发资金使用效率(rd_p),并利用模型(21)展开考察:
| $ {rd\_p}_{i,t}={\varphi }_{0}+{\varphi }_{1}{digital}_{i,t-1}+{\mathit{\varphi }}_{2}{\mathit{x}}_{i,t-1}+{\mu }_{i}+{\upsilon }_{t}+{\varepsilon }_{i,t} $ | (21) |
2.理论机制的检验结果。表3汇报了理论机制实证含义第一个方面的结果。所有回归均同时控制了年份固定效应、企业个体固定效应和其他特征变量。列(1)展示了数字化是否影响企业研发支出对盈余资金的敏感性,交乘项digital×roa的系数为正且在1%的水平上高度显著。这说明,数字化显著地提高了企业研发支出对盈余资金的敏感程度,使得更多的盈余资金流向了研发创新活动。列(2)展示了数字化是否影响企业超额管理费用对盈余资金的敏感性,交乘项digital×roa的系数在1%的水平上显著为负。这意味着,数字化显著降低了企业超额管理费用对盈余资金的敏感程度,减少了盈余资金向超额管理费用的流动。这从侧面表明,数字化使得企业减少了对信息搜寻和追踪支出的资金供给。综上可知,数字化显著地改变了企业盈余资金的配置和流向,使得更多的盈余资金流向了研发创新活动而非信息搜寻和追踪支出,从而显著地提高了企业的研发资金供给效率。
| (1)研发支出(rd) | (2)超额管理费用(emc) | |
| L.digital×roa | 0.1481***(0.0391)
|
−0.7141***(0.1433)
|
| L.digital | 0.0828***(0.0101)
|
0.0414(0.1367)
|
| roa | −0.2029*(0.1147)
|
0.0296(0.2214)
|
| L.控制变量 | 是 | 是 |
| 年份/企业固定效应 | 是 | 是 |
| 样本量
Adj−R2 |
19 202
0.3672 |
25 139
0.0032 |
进一步地,表4汇报了理论机制实证含义第二个方面的回归结果。所有回归中均同时控制了年份固定效应和企业个体固定效应。可以看出,在没有加入其他特征变量的回归中,数字化指数digital的系数在1%的水平上显著为正,当加入其他特征变量之后,系数值虽然有所下降,但依然为正且在1%的水平上显著。这说明,数字化也显著提高了企业的研发资金使用效率。
| 研发资金使用效率(rd_p) | ||
| (1) | (2) | |
| L.digital | 0.0032***(0.0006)
|
0.0030***(0.0006)
|
| L.控制变量 | 否 | 是 |
| 年份/企业固定效应 | 是 | 是 |
| 样本量 | 19 202 | 19 202 |
| Adj−R2 | 0.1207 | 0.1231 |
综上,不管是实证含义第一方面数字化是否可以提高企业研发资金供给效率,还是实证含义第二方面数字化是否可以改善企业研发资金使用效率,均得到了充分的证明。因此,理论分析的命题1成立。这意味着,产业数字化可以通过提高企业研发资金的供给效率和使用效率来促进企业的技术创新。
(二)异质性分析。上文的一系列检验证实了产业数字化对企业创新的促进效应及其内在的作用机制。值得注意的是,在不同的外部环境和企业属性下,产业数字化对企业创新的影响效应可能存在异质性。江艇(2022)认为,异质性分析应围绕核心因果关系展开,目的在于强化因果关系及其内在机制的论证高度。对于本文而言,核心的因果链条是产业数字化可以通过提高企业研发资金的供给效率和使用效率促进企业创新,而这其中最本质的机制在于两个方面:一是产业数字化强化了企业与外界的信息交换效率;二是数字技术的使用提高了企业的知识创造效率。这两个机制都有可能会受企业自身特征及其所处环境的影响。因此,十分有必要在基准回归和机制检验之后进一步进行必要的异质性分析,这不仅有利于强化本文的因果关系和内在机制,而且可以为政府后续数字经济发展战略的优化与调整提供更加详细的学理支持。
在识别方法上,本文利用调节效应模型通过考察异质性分类变量影响产业数字化促进企业创新的幅度识别不同维度下产业数字化影响企业创新的异质性。这与分组回归的方法相比,可以利用同一个样本更好地识别出组间差异。具体模型设计如下:
| $\begin{aligned} {innov}_{i,t}=&{\psi }_{0}+{\psi }_{1}{digital}_{i,t-1}\times {hetero}_{i,t}+{\psi }_{2}{digital}_{i,t-1}+{\psi }_{3}{hetero}_{i,t}\\ &+{\mathit{\psi }}_{4}{\mathit{x}}_{i,t-1}+{\mu }_{i}+{\upsilon }_{t}+{\varepsilon }_{i,t} \end{aligned}$ | (22) |
其中,hetero表示0—1型异质性分类变量,其他变量定义与模型(19)相同。
1.基于企业所在地区数字经济发展水平的异质性分析。企业创新并不能在真空中独自进行,创新的成功率依赖于企业与外界的信息交换效率。因此,有理由相信,企业所在地区的数字经济发展水平越高,产业数字化将越能促进企业创新。这是因为,更高的数字经济发展水平匹配了更完善的数字基础设施和更浓郁的数字生产氛围。在这样的环境中,企业与外界的信息交换以及对创新所需信息的搜寻和追踪也将会更有效率。为了验证上述假设,本文定义异质性分类变量area,area等于1表示数字经济发展高水平地区,等于0表示数字经济发展低水平地区。对于地区数字经济发展水平的划分,本文结合中国信通院公布的《中国数字经济发展白皮书(2020)》,将数字经济增加值占GDP比重超过40%的省份归为数字经济发展高水平地区,其他省份归为数字经济发展低水平地区。具体回归结果如表5列(1)所示,可以看出,交乘项digital×area的系数在1%的水平上显著为正。这说明,企业所在地区的数字经济发展水平越高,产业数字化越能促进企业创新,上述假设得以验证。
| 企业技术创新水平(innov) | |||
| 区域异质性 | 资本密集度异质性 | ||
| (1) | (2) | (3) | |
| L.digital×area | 0.0646*** (0.0140) |
||
| L.digital×kl | 0.0983*** (0.0149) |
0.0503*** (0.0126) |
|
| L.控制变量 | 是 | 是 | 是 |
| 企业/年份固定效应 | 是 | 是 | 是 |
| 样本量 | 25 139 | 25 139 | 25 139 |
| Adj−R2 | 0.1610 | 0.1619 | 0.1615 |
| 注:表中略去了对一次项的汇报。 | |||
2.基于企业资本密集度的异质性分析。除了与外界的信息交换,企业自身的资本存量、技术积淀和人力资本积累也是影响创新的重要因素。资本密集型企业不仅拥有雄厚的技术积累,而且具有更高的高技能劳动力占比,从而可以更快地提高知识创造效率。更重要的是,资本密集型企业往往因为拥有强大的资金支持而更愿意进行高水平的技术创新(Sahaym等,2010)。因此,相较于非资本密集型企业,产业数字化可能更容易促进资本密集型企业的技术创新。为了验证这一假设,本文定义异质性分类变量kl,kl等于1表示资本密集型企业,等于0表示非资本密集型企业。对于企业资本密集度的划分,本文采用两种方法刻画,一是参考张璇等(2017)的做法,将属于医药制造业、塑料制造业、通用设备制造业和专用设备制造业等高端制造业的企业列为资本密集型企业,将其他企业列为非资本密集型企业;二是以企业总资产与员工人数的比值定义资本密集度,并以资本密集度的样本均值为临界点,大于等于均值的企业列为资本密集型企业,小于均值的企业列为非资本密集型企业。表5列(2)和列(3)汇报了上述异质性讨论的结果,不难发现,不管如何衡量资本密集型企业的分组,交乘项digital×kl的系数均在1%的水平上显著为正。这表明,产业数字化更能促进资本密集型企业的技术创新,上述假设得以验证。
六、经济后果检验:“双循环”新发展格局视角
前文的理论分析和实证检验充分验证了产业数字化对企业创新的促进效应,那么,产业数字化是否可以通过促进企业创新进一步地推动构建“双循环”新发展格局?对这个问题的回答,可以为数字经济通过数字技术与实体经济的深度融合推动构建新发展格局提供学理上的支持。
畅通国内大循环和实现更高水平的国际循环是构建“双循环”新发展格局的核心要义。畅通国内大循环重在打通社会再生产的生产、分配、流通和消费四个环节,充分激发内需市场潜力,实现国内生产端与消费端的有效对接;而更高水平的国际循环则在于贸易质量的不断提升。因此,落实到实证层面是要重点考察产业数字化是否可以通过促进企业创新进一步地促进企业内需扩增和产品出口质量提升。
对于企业层面内需扩增的测算,借鉴Hummels等(2014)和Berman等(2017)的方法,利用公式(23)计算而得。
| $ {demand}_{i,t}={\sum }_{p}{w}_{i,p,{t}_{0}}\left(\frac{{\sum }_{p,t}{sale}_{p,j,t}-{\sum }_{p,t}{sale}_{p,j,t-1}}{{\sum }_{p,t}{sale}_{p,j,t}+{\sum }_{p,t}{sale}_{p,j,t-1}/2}\right) $ | (23) |
其中,i、j和p分别表示企业、行业和地区;t表示时间;
对于企业产品出口质量的测算,参考Khandelwal等(2013)的做法,选择被广泛使用的需求信息推断法。该方法将产品质量定义为除价格之外其他任何可以提高消费者需求的属性。因此,消费者在最大化自身效应时,若两种产品价格相等,则产品的需求量越大,产品质量越高。关键公式如下所示:
| $ {q}_{i,c,g,t}={p}_{i,c,g,t}^{-\sigma }{\lambda }_{i,c,g,t}^{\sigma -1}{P}_{c,t}^{\sigma -1}{E}_{c,t} $ | (24) |
其中,qi,c,g,t表示企业i在第t年出口到国家c的产品g的数量;pi,c,g,t表示产品的到岸价格;λi,c,g,t表示产品出口质量;σ为产品的替代弹性,具体使用Broda等(2017)给出的替代弹性;Ec,t表示出口目的国c在第t期的总支出,Pc,t为出口目的国c在第t年的价格指数。对式(24)两边取对数并进行固定效应回归便可估算出企业的产品质量。计算产品出口质量所需数据来自中国海关数据库、CSMAR数据库和RESSET数据库,计算获得企业的产品出口质量后,利用公司名称与上市公司数据匹配,便可形成本文考察所需的研究样本。⑤
参考多数文献的做法(张璇等,2017;袁淳等,2021;靳卫东等,2022),具体设计逐步法中介效应模型进行检验。需注意的是,逐步法中介效应模型虽然可以在理论上满足识别经济机制的要求,但现实操作中会不可避免地出现内生性问题,从而造成估计偏误(江艇,2022)。因此,在具体回归中本文直接利用工具变量法进行估计以规避上述内生性问题。⑥模型设计如下:
| $ {demand}_{i,t}\left({quality}_{i,c,g,t}\right)={a}_{0}+{a}_{1}{digital}_{i,t-1}+{\mathit{a}}_{2}{\mathit{x}}_{i,t-1} +{\mu }_{i}\left({\mu }_{i,c,g}\right)+{\upsilon }_{t}+{\varepsilon }_{i,t} $ | (25) |
| $ {innov}_{i,t}={b}_{0}+{b}_{1}{digital}_{i,t-1}+{\mathit{b}}_{2}{\mathit{x}}_{i,t-1}+{\mu }_{i}\left({\mu }_{i,c,g}\right)+{\upsilon }_{t}+{\varepsilon }_{i,t} $ | (26) |
| $ {demand}_{i,t}\left({quality}_{i,c,g,t}\right)={c}_{0}+{c}_{1}{digital}_{i,t-1}+{c}_{2}{innov}_{i,t-1}+{\mathit{c}}_{3}{\mathit{x}}_{i,t-1}+{\mu }_{i}\left({\mu }_{i,c,g}\right)+{\upsilon }_{t}+{\varepsilon }_{i,t} $ | (27) |
其中,企业内需扩增变量为企业层面数据,因此在以企业内需扩增(demand)为被解释变量的回归中,本文对企业的个体固定效应进行了控制;企业产品出口质量为“出口目的国—行业—企业”层面数据,因此在以企业产品出口质量(quality)为被解释变量的回归中,本文对“出口目的国—行业—企业”的个体固定效应进行了控制。另外,在所有模型中均同时控制了年份固定效应。与前文一致,考虑到数字技术和创新成果在运用上的时滞性,将滞后一期的数字化指数和企业创新水平纳入模型进行回归。模型(25)至(27)中,重点关注系数a1、b1、c1和c2的显著性,以判断产业数字化是否可以通过促进企业创新进一步提高企业产品的国内市场需求和出口质量。
表6汇报了逐步法中介效应模型的回归结果。从工具变量的有效性来看,Cragg-Donald Wald F 统计量均远大于10%显著性水平上的临界值16.38,且Anderson LM 统计量均在1%的水平显著。这说明,本文选择的工具变量不存在弱识别或不可识别问题。进一步地,从产业数字化是否可以通过促进企业创新提高企业国内市场需求的估计结果来看,列(1)中数字化指数digital的系数在5%的水平上显著为正,这表明,产业数字化显著地促进了国内市场对企业产品的需求;列(2)与前文表2列(3)的回归结果一致,表明产业数字化可以显著地促进企业创新;列(3)中企业创新innov的系数在1%的水平上显著为正,同时数字化指数digital的系数依然在5%的水平上显著为正,但系数值明显下降。这表明,企业创新在产业数字化促进国内市场对企业产品的需求中发挥了部分中介效应。列(4)—列(6)关于产业数字化是否可以通过促进企业创新提高企业产品出口质量的估计结果也显示,企业创新在产业数字化提高企业产品出口质量中同样发挥了部分中介效应。综上表明,产业数字化通过提高企业创新不仅显著地促进了国内市场对企业产品的需求,而且显著地提高了企业的产品出口质量。这意味着,产业数字化依托促进企业创新成为畅通国内大循环和实现更高水平国际循环的重要推动力量,这从实证层面验证了数字经济对构建“双循环”新发展格局的重要作用。
| 内需扩增(demand) | 企业技术创新
水平(innov) |
内需扩增(demand) | 产品出口质量(quality) | 企业技术创新
水平(innov) |
产品出口质量(quality) | |
| (1) | (2) | (3) | (4) | (5) | (6) | |
| L.digital | 0.0282** (0.0113) |
0.1684** (0.0801) |
0.0232** (0.0093) |
0.4280*** (0.1568) |
0.2567*** (0.0493) |
0.3615*** (0.1197) |
| L.innov | 0.0056*** (0.0010) |
0.3352*** (0.1041) |
||||
| L.控制变量 | 是 | 是 | 是 | 是 | 是 | 是 |
| 年份固定效应 | 是 | 是 | 是 | 是 | 是 | 是 |
| 企业固定效应 | 是 | 是 | 是 | 否 | 否 | 否 |
| 出口目的国−行业−企业固定效应 | 否 | 否 | 否 | 是 | 是 | 是 |
| 不可识别检验
(Anderson LM 统计量) |
87.087*** {0.000} |
264.295*** {0.000} |
87.251*** {0.000} |
31.676*** {0.000} |
31.497*** {0.000} |
24.810*** {0.000} |
| 弱识别检验
(Cragg−Donald Wald F 统计量) |
87.710
[16.38] |
267.238
[16.38] |
87.867
[16.38] |
31.681
[16.38] |
31.500
[16.38] |
24.812
[16.38] |
| 样本量 | 25 139 | 25 139 | 25 139 | 110 559 | 110 559 | 110 559 |
七、结 论
数字技术赋能传统产业升级已然成为新时代推动构建“双循环”新发展格局,促进经济高质量发展的重要力量。“十四五”规划着重强调要“加快数字化发展,建设数字中国”,数字技术与传统产业的深度融合将是未来中长期的重要战略目标之一。在此背景下,进一步从学理上阐释产业数字化的一系列经济效应具有重大的理论意义和现实价值。鉴于此,本文从微观企业层面出发,利用数理建模和实证考察相结合的方式系统考察了产业数字化对企业创新的影响效应、作用机理及经济后果。研究发现,产业数字化可以有效地促进企业创新,这其中的机制在于,产业数字化同时提高了企业研发资金的供给效率和使用效率。进一步的异质性分析表明,产业数字化对企业创新的促进效应会受外部环境和内部因素的多重影响。一方面,企业所在地区的数字经济发展水平越高,产业数字化越能促进企业创新;另一方面,与非资本密集型企业相比,产业数字化对资本密集型企业的创新促进效应更强。最后的经济后果检验发现,产业数字化可以通过促进企业创新进一步提高企业产品的国内市场需求和产品出口质量,对构建“双循环”新发展格局起到了显著的推动作用。
本文的一系列研究不仅丰富并补充了产业数字化影响企业创新的数理分析和实证研究。而且具有鲜明的政策含义,可为政府后续优化与调整数字经济发展战略提供必要的政策启示:第一,本文充分证明了产业数字化对企业创新和构建“双循环”新发展格局的重要性,因此政府应继续大力推进数字化基础层和技术层的建设,聚焦高端芯片和操作系统的自主化研发,强化并保持移动通信技术的国际领先地位,推进人工智能、云计算、区块链、大数据等新模式、新业态、新平台的培育和搭建,打造数字化赋能研发创新,研发创新反哺数字化的良性循环。第二,区域发展不协调仍然是中国经济发展的长期问题,虽然数字经济可以依托新技术优势打破区域间的经济壁垒,但这要以区域之间数字经济发展水平为支撑。因此,后续国家数字经济发展战略的制定与调整应更加关注数字经济发展在区域间的协调与平衡。一方面,中央政府应积极搭建贯通上下、分工明确的专门负责数字经济发展战略制定与执行的职能机关,在加快数字经济顶层发展战略制定的同时,基于各地区数字经济发展现状,编制具有地区差异性的数字经济发展战略实施方案,引导各地区错位竞争、互补合作,营造全国范围内数字经济协调发展的新热潮。另一方面,地方政府也应积极响应中央政府关于数字经济发展的战略决策,在加强5G基站、大数据中心、工业互联网等新型基础设施建设的同时,依托区域内的资源禀赋和比较优势有选择性地打造个性化数字经济发展平台,形成区域间的有效互补,以实现数字经济共赢发展。
① 相关数字化指数的描述性事实详见本文的工作论文版本。
② 限于篇幅,主要变量的描述性统计结果不再展示,详见本文的工作论文版本。
③ 限于篇幅,稳健性检验结果不再展示,详见本文的工作论文版本。
④ 这里的“投资”是指企业搜寻、追踪信息的支出和研发活动支出。
⑤ 囿于中国海关数据的可得性,本部分的样本区间为2008–2015年。
⑥ 具体利用行业层面内生变量的均值作为工具变量。
| [1] | 韩先锋, 宋文飞, 李勃昕. 互联网能成为中国区域创新效率提升的新动能吗[J]. 中国工业经济, 2019(7): 119–136. |
| [2] | 江艇. 因果推断经验研究中的中介效应与调节效应[J]. 中国工业经济, 2022(5): 100–120. DOI:10.3969/j.issn.1006-480X.2022.05.007 |
| [3] | 靳庆鲁, 孔祥, 侯青川. 货币政策、民营企业投资效率与公司期权价值[J]. 经济研究, 2012(5): 96–106. DOI:10.3969/j.issn.1005-913X.2012.05.054 |
| [4] | 靳卫东, 李淑玥, 何丽. “慢就业”的职业损失: 工资收入和工作职位[J]. 财经研究, 2022(7): 33–47. |
| [5] | 宋德勇, 朱文博, 丁海. 企业数字化能否促进绿色技术创新?——基于重污染行业上市公司的考察[J]. 财经研究, 2022(4): 34–48. DOI:10.16538/j.cnki.jfe.20211218.304 |
| [6] | 唐松, 伍旭川, 祝佳. 数字金融与企业技术创新——结构特征、机制识别与金融监管下的效应差异[J]. 管理世界, 2020(5): 52–66. DOI:10.3969/j.issn.1002-5502.2020.05.005 |
| [7] | 吴非, 胡慧芷, 林慧妍, 等. 企业数字化转型与资本市场表现——来自股票流动性的经验证据[J]. 管理世界, 2021(7): 130–144. DOI:10.3969/j.issn.1002-5502.2021.07.010 |
| [8] | 袁淳, 肖土盛, 耿春晓, 等. 数字化转型与企业分工: 专业化还是纵向一体化[J]. 中国工业经济, 2021(9): 137–155. DOI:10.3969/j.issn.1006-480X.2021.09.008 |
| [9] | 张辉, 石琳. 数字经济: 新时代的新动力[J]. 北京交通大学学报(社会科学版), 2019(2): 10–22. |
| [10] | 赵宸宇, 王文春, 李雪松. 数字化转型如何影响企业全要素生产率[J]. 财贸经济, 2021(7): 114–129. DOI:10.3969/j.issn.1002-8102.2021.07.008 |
| [11] | Akcigit U, Caicedo S, Miguelez E, et al. Dancing with the stars: Innovation through interactions[R]. NBER Working Paper, 2018, 24466. |
| [12] | Berman N, Couttenier M, Rohner D, et al. This mine is mine! How minerals fuel conflicts in Africa[J]. American Economic Review, 2017, 107(6): 1564–1610. DOI:10.1257/aer.20150774 |
| [13] | Bloom N, Sadun R, Van Reenen J. Americans do IT better: US multinationals and the productivity miracle[J]. American Economic Review, 2012, 102(1): 167–201. DOI:10.1257/aer.102.1.167 |
| [14] | Broda C, Greenfield J, Weinstein D E. From groundnuts to globalization: A structural estimate of trade and growth[J]. Research in Economics, 2017, 71(4): 759–783. DOI:10.1016/j.rie.2017.10.001 |
| [15] | Bustos P. Trade liberalization, exports, and technology upgrading: Evidence on the impact of MERCOSUR on Argentinian firms[J]. American Economic Review, 2011, 101(1): 304–340. DOI:10.1257/aer.101.1.304 |
| [16] | Duan Y Q, Edwards J S, Dwivedi Y K. Artificial intelligence for decision making in the era of big data-evolution, challenges and research agenda[J]. International Journal of Information Management, 2019, 48: 63–71. DOI:10.1016/j.ijinfomgt.2019.01.021 |
| [17] | Goldfarb A, Tucker C. Digital economics[J]. Journal of Economic Literature, 2019, 57(1): 3–43. DOI:10.1257/jel.20171452 |
| [18] | Khandelwal A K, Schott P K, Wei S J. Trade liberalization and embedded institutional reform: Evidence from Chinese exporters[J]. American Economic Review, 2013, 103(6): 2169–2195. DOI:10.1257/aer.103.6.2169 |
| [19] | Kong D M, Lin C, Wei L, et al. Information accessibility and corporate innovation[J]. Management Science, 2022: online. |
| [20] | Rivera-Batiz L A, Romer P M. Economic integration and endogenous growth[J]. The Quarterly Journal of Economics, 1991, 106(2): 531–555. DOI:10.2307/2937946 |

