
2022第48卷第8期
一、引 言
贫困一直是世界各国政府高度关注的问题。在现行标准下,我国绝大多数农村贫困人口已经成功摆脱贫困,脱贫攻坚工作取得了决定性进展和阶段性胜利。扶贫投入的持续增长是中国取得巨大减贫成就的重要原因之一。在2013年至2020年期间,中央财政专项扶贫资金从381亿元增长至1465亿元,①然而大规模中央扶贫投入的可持续状况存在不确定性(陈志钢等,2019),可持续的减贫策略面临新的困难和挑战。不仅如此,部分脱贫人口存在返贫风险,一些边缘人口存在致贫风险,必须把防止返贫摆到更加重要的位置。2020年后,我国正式步入全面建成小康社会的发展阶段,反贫困战略将主要围绕巩固脱贫成果和减少长期贫困展开(黄征学等,2019;张楠等,2020;郑晓冬等,2020)。因此,有必要针对贫困问题的新特征,探讨减贫政策对防止返贫、降低长期贫困率以及减少贫困深度的影响,并进一步分析减贫政策所需的长期减贫成本,优化现有减贫政策和高效配置扶贫资源。
医疗保险是减贫的重要政策工具之一。直观来讲,一旦家庭遭受疾病风险冲击,在保障范围内,医疗保险会补偿其经济损失,即“保险的损失补偿效应”,从而降低了家庭陷入贫困的可能性。但是,该结论是建立在保费支出不影响家庭资产积累的前提假设下,实际上在基本生活消费和投资不变的情况下,保费支出会降低家庭资产积累规模,即“保费的资产侵蚀效应”,从而可能提高家庭陷入贫困的可能性(景鹏等,2019)。这两种效应都是家庭购买医疗保险的事后效应。那么,医疗保险是否存在事前效应呢?也就是说,即使家庭未购买医疗保险,医疗保险机制的存在也可能改变家庭对未来消费和投资的预期,从而具有事前的投资激励效应,但目前尚未有文献研究医疗保险的这种事前效应。发展是解决贫困问题的“总钥匙”,要从根源上解决贫困问题,关键还是要提升贫困家庭和脱贫家庭的自主发展能力。因此,研究医疗保险对于家庭投资决策的影响具有较强的现实意义。考虑到我国大部分贫困人口位于农村,贫困地区也多以农业生产为主,金融资产投资较少,因此我们通过构建生产函数建立家庭资产随机增长模型,分析医疗保险的事前投资激励效应,丰富了医疗保险减贫作用机制的相关研究。
医疗保险对不同贫困状态家庭的影响可能存在异质性。Kovacevic和Pflug(2011)基于破产理论构建了非贫困家庭(包括脱贫家庭和从未陷入贫困的家庭)的资产随机损失模型,研究发现保险只能降低资产相对较多家庭的陷贫概率。孙武军和祁晶(2016)拓展了Kovacevic和Pflug(2011)的研究,理论研究了临界资本对保险费率的敏感性及对家庭“贫困陷阱”的影响,发现资本较多家庭购买保险后陷贫概率显著下降,但资本较少家庭购买保险后陷贫概率变化不确定,其取决于家庭对保费的敏感程度。在我国精准扶贫战略实施的过程中,我国通过多重保障制度和倾斜性医保报销政策,降低看病门槛,提高补偿比例,显著降低了贫困人口发生家庭灾难性医疗支出的风险,但同时扶贫政策也存在各种不足。例如,扶贫政策难以精确关注贫困群体,贫困家庭可能会陷入“福利陷阱”,边缘非贫家庭可能面临“悬崖效应”等,这些不足使得当前的扶贫政策可能较难从根源上解决贫困问题。简单的“一刀切”的医保扶贫政策无法满足不同家庭的医疗保险需求,相较于贫困家庭,贫困边缘家庭同样值得关注,这些家庭享受不到扶贫优惠政策,“因病致贫”风险依旧较高。因此,在探讨医疗保险减贫的作用机制时,需要针对不同贫困状态的家庭分别进行分析。
现有文献对医疗保险的扶贫效果还存在争议。一些研究认为,医疗保险不仅可以减少贫困(Hamid等,2011;卢盛峰和卢洪友,2013),还可以帮助家庭有效地应对健康风险和平滑消费,实现资产的平稳积累,进而使得家庭摆脱贫困并维持福利效应的增加(Akotey和Adjasi,2014),并且其减贫作用随时间延续有进一步增强的趋势(黄薇,2017)。“新农合”政策是农村地区减贫的重要手段之一,许多学者分析了“新农合”政策的减贫效果,齐良书(2011)、赵思诚等(2019)研究发现,“新农合”政策显著提高了农户收入,减贫效果明显。此外,“新农合”政策还可以显著提高参加者的健康水平(程令国和张晔,2012;王翌秋和刘蕾,2016),减轻农民医疗负担(黄晓宁和李勇,2016)。另一些证据表明,医疗保险的扶贫效果微小或不显著(解垩,2008)。现有研究存在争议的原因,一方面可能是因为医疗保险扶贫效果具有收入异质性(黄薇,2017;于新亮等,2020)、健康异质性(刘子宁等,2019)。另一方面,这些文献大多实证研究医疗保险对当期贫困的影响,较少关注医疗保险对贫困的长期影响,忽视了医疗保险对贫困动态长期作用机制的研究。医疗保险在长期减贫方面能够发挥何种作用?特别是其对于长期贫困有何影响?这些都值得进一步深入研究。
我国政府通过向贫困群体提供现金转移支付或者现金补助来减少当期贫困,最低生活保障以及其他现金补贴(如五保户补助、特困户补贴等)已经成为贫困人群基本生活保障的“社会保护网”。作为当前国际上广泛运用的长期多维减贫方案之一,有条件的现金转移支付项目通过将现金转移支付和儿童人力资本积累、劳动收入奖励、妇幼保健服务等主题相结合,实现长期减贫和包容性均衡发展,郑晓冬等(2020)综合分析了国内外有条件的现金转移支付政策的长期减贫成效,但目前文献较少关注现金转移支付与保险相结合对减贫成本的影响。
鲜有文献从长期视角来研究减贫成本问题。Ikegami等(2019)理论分析表明,从长期来看,相较于政府把现金优先转移给贫困家庭,优先转移给非贫脆弱家庭能减少长期减贫成本。Janzen等(2021)研究表明,相较于单一的公共转移支付政策,引入财产保险后,家庭的贫困动态发生变化,从而减少了长期减贫成本。上述研究表明,减贫政策需要兼顾长期减贫成本和减贫收益,在强调减贫收益的同时,也要关注反贫困成本大幅攀升的问题。因此,将现金转移支付和医疗保险政策相结合,研究其对长期减贫成本的影响,是具有实际意义的。
基于上述原因,本文从长期减贫视角出发,针对我国贫困人口大多从事农业生产的特点,建立了包含医疗保险、消费及投资的家庭资产随机增长模型,在无医疗保险、有医疗保险无保费补贴和有医疗保险有保费补贴三种情形下,数值模拟分析不同资产水平家庭的贫困脆弱性及投资决策变化,考察了这种效应在不同群体之间的异质性,并进一步对比分析了“政府现金补助”“医疗保险+政府现金补助”和“定向保费补贴+政府现金补助”三种政策对长期贫困发生率、贫困深度的影响以及不同政策所需的长期减贫成本,从理论上丰富了医疗保险和政府现金补助政策在长期减贫效果上的研究,为存在分歧的现有实证结果提供了一种新的理论上的解释,有助于学术界和政府对医疗保险的长期减贫作用有一个清晰认识和系统把握,对扶贫机制的完善和扶贫资源配置的优化具有重要价值。
本文通过构建家庭资产随机增长模型,研究发现:(1)医疗保险具有事后的贫困脆弱性降低效应,这种效应对于非贫脆弱家庭尤为显著。(2)医疗保险对贫困家庭和非贫脆弱家庭具有生产投资的事前激励效应。(3)相较于单一的现金补助扶贫模式,“现金补助+保费补贴”的扶贫模式显著降低了长期贫困率和贫困深度,有效减少了长期减贫成本。与仅使用现金补助政策相比,“医疗保险+政府现金补助”使得长期减贫成本下降了
相较于现有文献,本文主要贡献在于:(1)将医疗保险机制纳入包含消费和投资的家庭资产随机增长模型中,分析了在无医疗保险和有医疗保险两种情形下家庭的贫困脆弱性和投资决策的动态变化,揭示了医疗保险对贫困家庭和非贫脆弱家庭生产投资的事前激励效应,丰富了医疗保险减贫和抑制返贫的作用机制的理论研究。(2)从长期减贫视角出发,探讨了医疗保险对不同群体贫困动态的作用机制,特别是医疗保险对非贫脆弱家庭的跨期资本动态的影响,深化了对医疗保险“抑制返贫”功能的认识。(3)在政府现金补助的扶贫政策基础上,加入医疗保险机制,并进一步探讨了二者对长期减贫的协同作用。
本文的结构如下:第二部分为模型构建;第三部分利用数值模拟分析方法探讨了医疗保险减贫的作用机制;第四部分分析医疗保险对长期贫困率、贫困深度和长期减贫成本的影响;第五部分是结论与政策建议。
二、模型构建
本文借鉴Ikegami等(2019)、Janzen等(2021)的多重均衡理论框架,建立家庭资产随机增长模型,引入医疗保险机制,比较分析在无医疗保险、有医疗保险无保费补贴和有医疗保险有保费补贴三种情形下,不同资产水平的家庭受到外生疾病冲击后的贫困脆弱性及投资决策变化。
(一)生产函数
基于我国贫困地区以农业为主的经济特征,本文参考经济学中经典的自给自足的经济模型,假设经济中只有农业生产一种生产活动,只产出一种产品,经济中的个体是具有代表性的理性个体,而本文的个体均指家庭。不同资产水平的个体可能会采用不同效率的生产技术,为了简化模型,本文仅考虑两种生产技术水平,假设贫困地区的农业生产活动的生产函数为:
| $ f\left({k}_{t}\right)=\left\{\begin{array}{c}{f}^{H}={\alpha }^{H}{k}_{t}^{{\gamma }_{H}}+ \underline{f}^{H},{k}_{t} > \tilde{k}\\ {f}^{L}={\alpha }^{L}{k}_{t}^{{\gamma }_{L}}+{\underline{f}}^{L},{k}_{t}\leqslant \tilde{k}\end{array}\right. $ | (1) |
其中,
(二)基准模型
我们考虑无限时域下的家庭资产随机增长模型。假设经济中仅存在一种商品,个体的投入、产出和消费均以此衡量,且不存在农业生产以外的其他投资方式,个体的效用完全源自消费,并且按照追求终身效用最大化的原则进行决策。同时,由于本文关注的是医疗保险,因此并未考虑产出的随机性。在初始时期,个体拥有生产资产
| $ \begin{gathered} \mathop {max}\limits_{\left\{ {{c_t}} \right\}_{t = 0}^\infty } E\left[ {\sum\limits_{t = 0}^\infty {{\beta ^t}u\left( {{c_t}} \right)} } \right] \end{gathered}$ |
| $ s.t.\; \left\{\begin{array}{c}{c}_{t}+{i}_{t}=f\left({k}_{t}\right)+(1-\delta ){k}_{t},\forall t=\mathrm{0,1},2,\dots \\ {k}_{t+1}=\left(1-{\varepsilon }_{t}\right){i}_{t}\end{array}\right. $ | (2) |
其中,
式(2)的含义为在第
| $ {V}_{N}\left({k}_{t}\right)=\underset{{c}_{t}}{max}\left\{u\left({c}_{t}\right)+\beta {E}_{t}\left[{V}_{N}\left({k}_{t+1}\right)\right]\right\} $ | (3) |
| $ {p}_{T}\left({k}_{0}\right)=\mathit{Pr}[{U}_{t=1}^{t=T}({k}_{t} < \mathrm{临}\mathrm{界}\mathrm{资}\mathrm{产}\mathrm{水}\mathrm{平})] $ | (4) |
由式(3)可得一阶条件如下:
| $ {u}'\left({c}_{t}\right)=\beta {E}_{t}\left[{V}_{N}'\left({k}_{t+1}\right)\left(1-{\varepsilon }_{t}\right)\right] $ | (5) |
式(5)等号右侧为
(三)引入医疗保险机制的家庭资产随机增长模型
在基准模型的基础上,我们在经济中引入医疗保险机制,假定在任意时期的期末,个体都可以选择以费率
| $ d\left({\varepsilon }_{t}\right)=\eta \cdot \mathit{max}\left\{{\varepsilon }_{t}-s,0\right\} $ | (6) |
引入医疗保险机制后,个体面临的效用最大化问题可以表示为:
| $\underset{{\left\{{c}_{t}\right\}}_{t=0}^{\infty },{\left\{{I}_{t}\right\}}_{t=0}^{\infty }}{max}E\left[{\sum }_{t=0}^{\infty }{\beta }^{t}u\left({c}_{t}\right)\right] $ |
| $ s.t.\; \left\{ \begin{aligned} &{c}_{t}+{i}_{t}+p{I}_{t}= f\left({k}_{t}\right)+(1-\delta ){k}_{t} \\ &{k}_{t+1}=\left(1-{\varepsilon }_{t}\right){i}_{t}+d\left({\varepsilon }_{t}\right){I}_{t} \\ &{c}_{t}\geqslant 0,\;0\leqslant {I}_{t}\leqslant {k}_{t} \end{aligned} \right.$ | (7) |
上述约束条件的含义为个体根据当期的生产收入
| $ {V}_{I}\left({k}_{t}\right)=\underset{{c}_{t},{I}_{t}}{max}\left\{u\left({c}_{t}\right)+\beta {E}_{t}\left[{V}_{I}\left({k}_{t+1}\right)\right]\right\} $ | (8) |
根据一阶条件
| $ {u}'\left({c}_{t}\right)=\beta {E}_{t}\left[{V}_{I}'\left({k}_{t+1}\right)\left(1-{\varepsilon }_{t}\right)\right]={\lambda }_{I}\left({k}_{t+1}\right) $ | (9) |
| $ \text{}p{\lambda }_{I}\left({k}_{t+1}\right)=\beta {E}_{t}\left[{V}_{I}'\left({k}_{t+1}\right)d\left({\varepsilon }_{t}\right)\right] $ | (10) |
值得注意的是,在式(10)中等号两侧都存在
(四)模型求解
本文使用值函数迭代的方法对上文中第(二)和第(三)部分的模型进行求解,得到无保险、有保险无保费补贴和有保险有保费补贴三种情况下的动态资产路径和政策函数,进一步求得不同情况下个体的流动性成本、贫困脆弱性以及投资函数,深入分析医疗保险对家庭资产路径的影响。函数设定和参数假设主要分为四部分,表1给出了本文所用的函数形式和参数假设。
| 函数形式 | 符号 | 参数值 | 参数含义 | 参数来源 |
|
|
|
|
高技术水平边际生产弹性 | 参考Janzen等(2021)、 Barrett等(2008)、 Barrett和Carter(2013) |
|
|
|
高技术水平最低产出 | ||
|
|
|
高技术水平生产率 | ||
|
|
|
|
低技术水平边际生产弹性 | |
|
|
|
低技术水平最低产出 | ||
|
|
|
低技术水平生产率 | ||
|
|
|
|
相对风险厌恶系数 | Janzen等(2021) |
|
|
|
资产折旧因子 | Liao等(2020) | |
|
|
|
效用折现因子 | Janzen等(2021) | |
|
|
|
|
赔付率 | 政府相关文件 |
|
|
|
免赔率 | ||
|
|
|
|
保费费率 | 根据公式计算 |
| 外生疾病冲击 |
|
|||
|
|
||||
1. 生产函数及参数设定。本文采用形如式(1)的生产函数来描绘生产活动,参考Janzen等(2021),以上标H、L分别代表高技术水平和低技术水平,边际产出弹性分别设定为
2. 效用函数及基础参数设定。参照Janzen等(2021),本文采用CRRA效用函数
3. 医疗保险参数设定。参考《山西省人民政府关于进一步完善城乡居民医疗保险政策的通知》(晋政发[2017]36号)和《贵州省整合城乡居民基本医疗保险制度实施方案》(黔府办发[2016]52号)中的有关规定,设定赔付比例
三、医疗保险对贫困脆弱性的作用机制
(一)医疗保险的贫困脆弱性降低效应
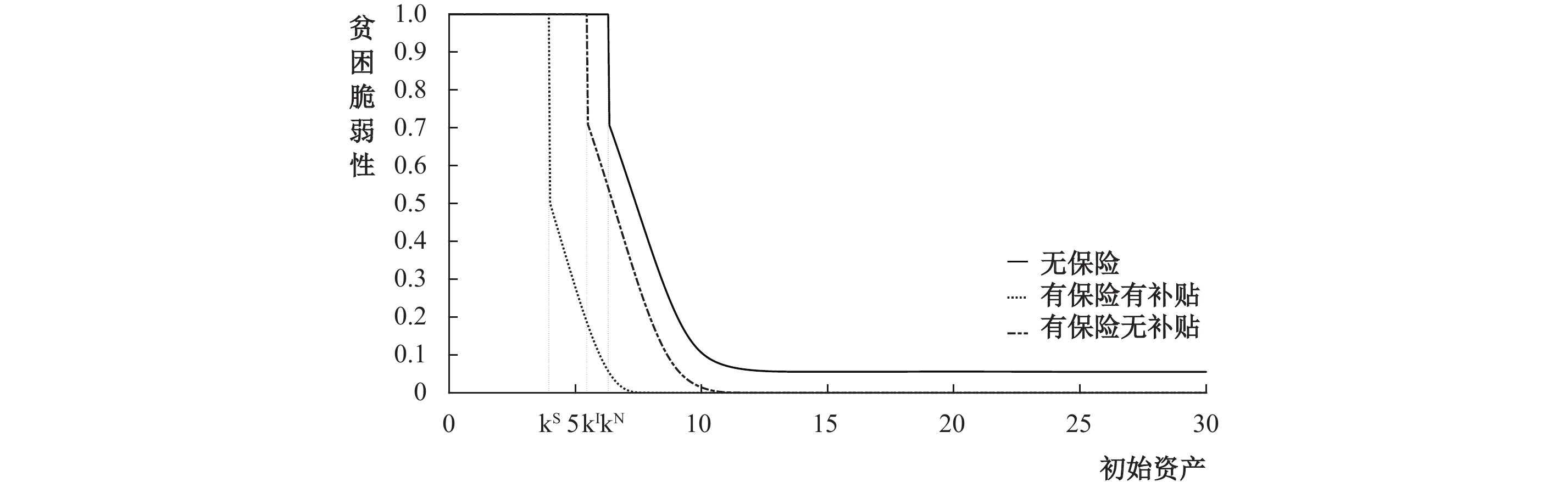
本文构建基于基准模型和引入医疗保险机制的家庭资产随机增长模型,采用表1中的函数形式和参数假设,利用值函数迭代法求解贝尔曼方程,得到无医疗保险、有医疗保险无保费补贴和有医疗保险有保费补贴,三种情形下不同资产水平的个体的贫困脆弱性,分别以实线、点划线和虚点线表示,结果如图1所示。
|
| 图 1 不同情形下的贫困脆弱性大小 |
当经济中不存在医疗保险机制时,若个体的初始资产水平低于
引入医疗保险机制后,Micawber阈值会降低,即
综上所述,医疗保险具有贫困脆弱性降低效应,这是购买医疗保险后所产生的事后效应,无论对贫困脆弱个体还是非贫脆弱个体,保险均通过损失补偿降低了贫困脆弱性。当政府进行医疗保险保费补贴后,该效应更为显著。
(二)医疗保险的投资激励效应
前文讨论了医疗保险的事后脆弱性降低效应,这种事后效应仅对购买了保险的个体有效,与这些个体相比,缺乏充足资产购买医疗保险的个体的贫困脆弱性更值得关注。有鉴于此,下文中我们将讨论医疗保险对个体的事前效应。事前效应在医疗保险机制引入后即会生效,与个体是否购买医疗保险无关,我们将其称为投资激励效应,研究这种事前效应,对于识别医疗保险减贫的内在机制,精准激励个体主动脱贫和防止返贫具有重要意义。
生产函数中的技术转换水平
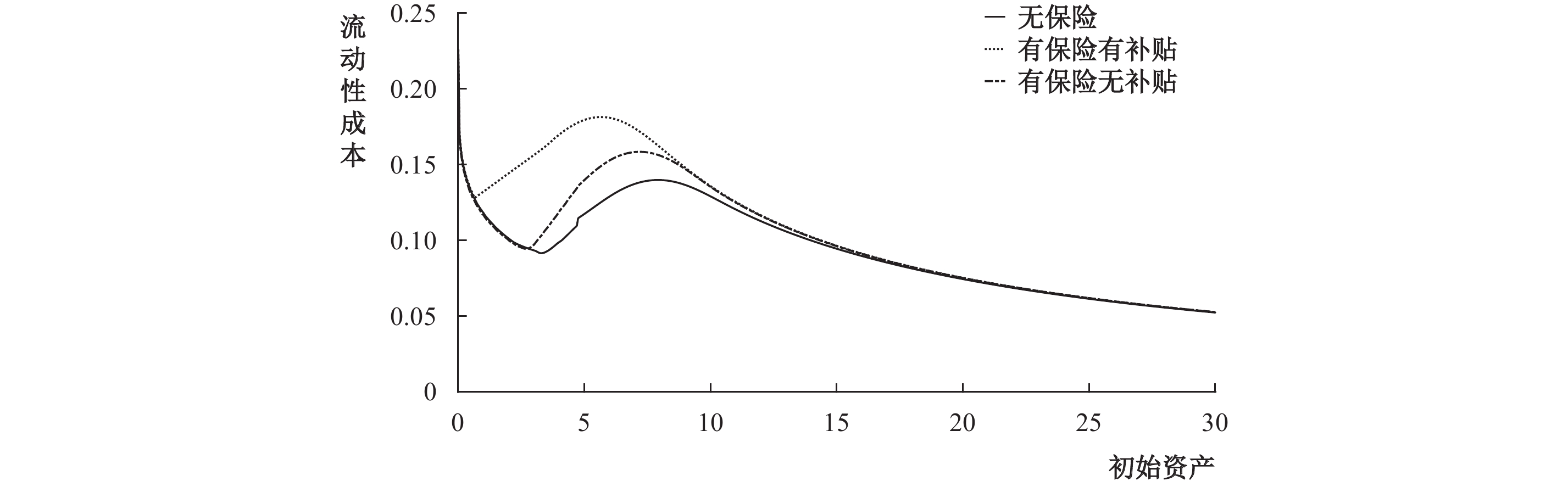
|
| 图 2 不同情形下的流动性成本大小 |
引入医疗保险机制后,由于医疗保险的损失补偿功能,外生疾病冲击的影响会降低,投资的边际期望收益将会提高,这也推高了个体的流动性成本,即
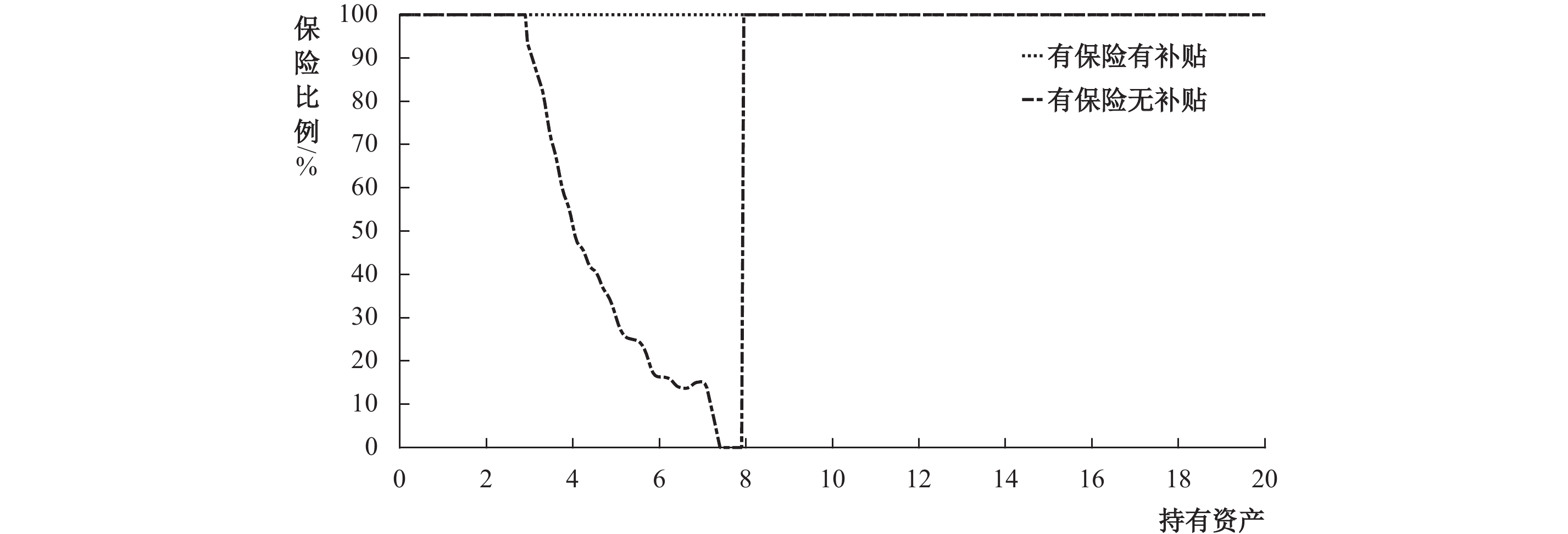
|
| 图 3 不同情形下的保险需求函数 |
在无政府保费补贴的情况下,由于流动性约束,非贫脆弱个体并不会主动选择购买保险,这意味着事后的脆弱性降低效应不存在。然而从图1可以看出,
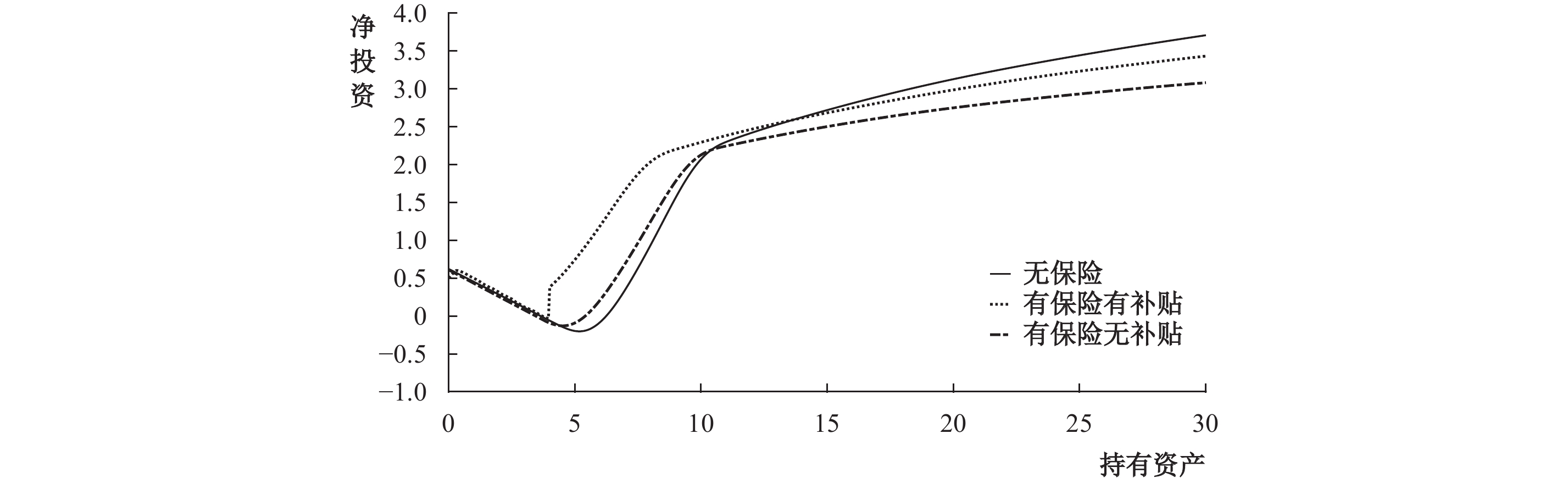
|
| 图 4 不同情形下的净投资大小 |
从图4可以看出,相较于无医疗保险机制的情形,引入医疗保险机制后,资产水平在
从长期来看,图1中位于
综上所述,医疗保险的事前投资激励效应主要作用于资产水平在阈值附近的非贫脆弱个体,无论是否购买医疗保险,这部分个体都会自愿降低当期消费,将更多资产投入生产活动,使得资产累积更快,从而降低了自身的贫困脆弱性。引入医疗保险机制后,相较于无保险的情况,资产水平较高的个体几乎不可能陷入“贫困陷阱”,其贫困脆弱性接近0。在知道这个事实后,这部分个体才会自愿降低当期消费扩大投资,以期未来能永久脱离贫困。在政府对医疗保险进行价格补贴后,医疗保险的投资激励效应会使受益的人群进一步扩大。对于资产水平较低的个体而言,保险机制的引入只能在一定程度上改善其效用,而不足以改变其长期贫困的趋势。对于比较富裕的家庭而言,De Nicola(2015)和McPeak(2004)证实了保险可能会对比较富裕家庭的投资产生负面影响,这与图4的结果相符。
四、医疗保险与长期减贫成本
接下来我们将通过一个数值模拟案例,对比分析无医疗保险、有医疗保险无保费补贴和有医疗保险有保费补贴三种情形对经济中总体长期贫困发生率、贫困深度及长期减贫成本的影响。
(一)经济中长期贫困的动态模拟
为了分析医疗保险对经济中总体贫困的动态影响,首先需要考虑家庭的初始资产分布。本文使用中国家庭追踪调查(CFPS)2018年农村家庭人均年收入数据进行估计,初始样本量为6744户,在剔除缺失值和异常值后,样本量为6204户。表2列出了2018年农村家庭人均年收入的描述性统计结果。数据表明,家庭人均年收入均值为12253.27元,最小值为100元,最大值为40000元。为了便于处理,将原始数据转化为
| 变量名 | 观测值 | 均值 | 标准差 | 最小值 | 25%分位数 | 中位数 | 75%分位数 | 最大值 |
| 家庭人均年收入(单位:元) | 6204 | 12253.27 | 9009.16 | 100 | 5196.67 | 10000 | 16731.67 | 40000 |
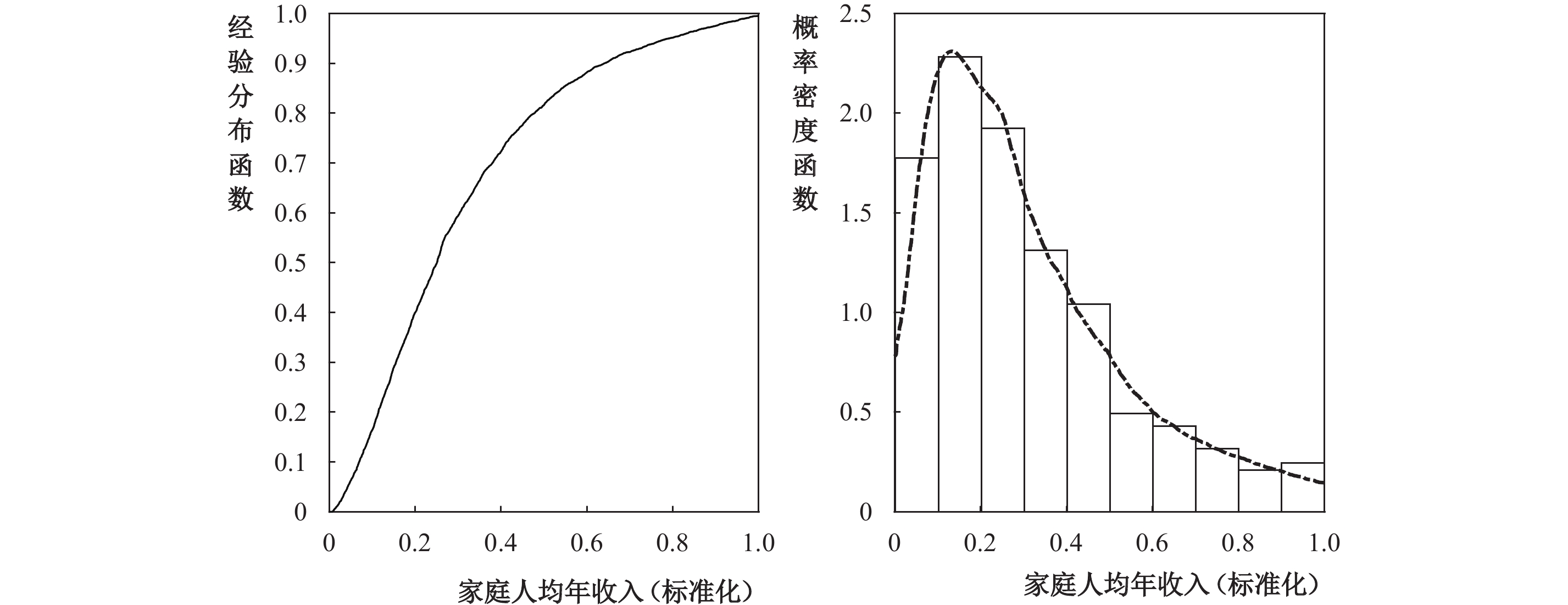
|
| 图 5 农村家庭人均年收入情况 |
我们假设经济中存在200户家庭,⑦其初始资产分布服从上述经验分布,使用数值方法随机生成家庭未来30年可能面临的外生疾病冲击,进而模拟出200户家庭未来30年的资产路径。模拟结果很大程度上取决于生成的初始资产与随机冲击,两次不同的模拟结果可能会有较大差异,为了减小随机性,尽可能地避免极端结果,我们进行了1000次模拟,以1000次模拟路径的均值作为最终的模拟结果,所有家庭第30年的资产分布如图6所示。
图6中,p25、p50、p75分别代表1000次模拟的25分位、50分位和75分位分布。从50分位分布的曲线可以看出,约有30%的家庭资产水平在
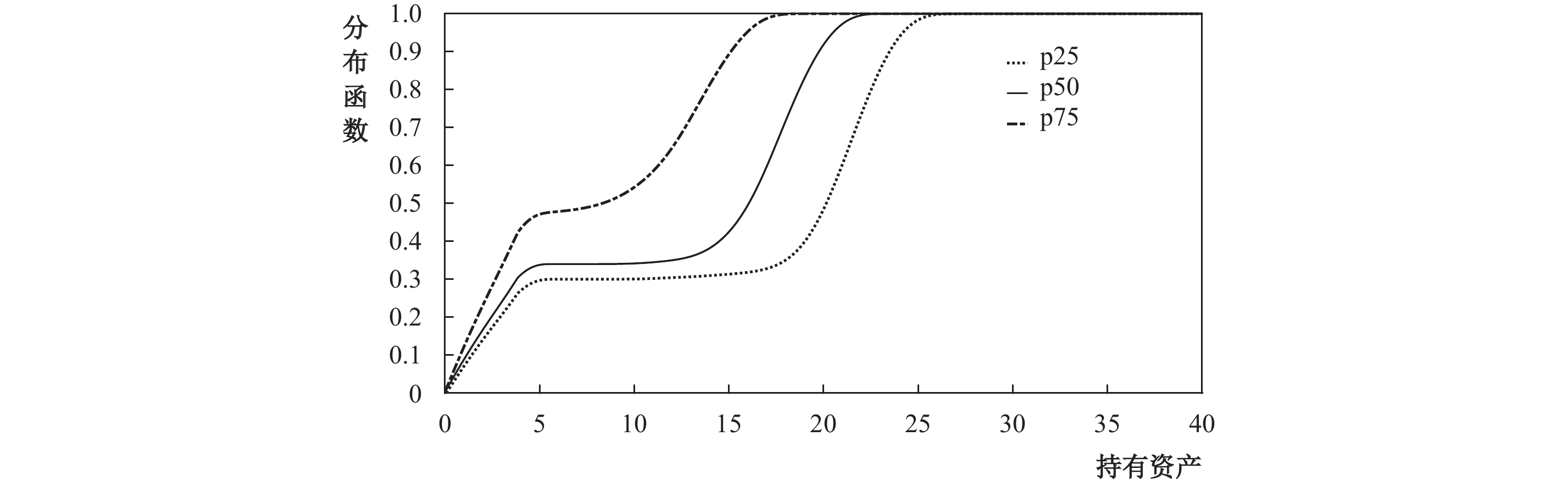
|
| 图 6 模拟分布结果 |
(二)医疗保险对长期贫困动态的影响
为了更好地利用上述模拟结果分析医疗保险对长期贫困动态的影响,我们定义如下三个指标,分别衡量长期贫困率、贫困深度和长期减贫成本。
首先,我们将资产水平低于
其次,借鉴Foster等(1984)的研究,用FGT(Foster-Greer-Thorbecke)贫困指数来衡量贫困深度,以
| $ FGT=\frac{1}{n}{\sum }_{i=1}^{n}\left(\frac{{k}^{N}-{k}_{\left(i\right)}}{{k}^{N}}\cdot {1}_{\left\{{k}_{\left(i\right)} < {k}^{N}\right\}}\right)\times 100\% $ | (11) |
最后,本文用社会保护成本来衡量长期减贫成本,首先对社会保护成本进行定义。在经济中无医疗保险机制时,政府为扶贫所投入的社会保护成本全部为现金补助,即为资产水平低于
由图3可知,政府进行保费补贴仅对资产水平在
图7表明,无医疗保险的情况下,初始时刻贫困家庭占比约为27%,但随着时间的推移,贫困家庭占比持续上升,在第30年已高达43%,相较于初始时刻增加了16%。引入医疗保险机制后,贫困家庭占比在略微上升后达到稳定,30年间贫困家庭比例稳定在27%。而在政府对医疗保险进行保费补贴后,贫困家庭占比迅速下降至20%以下并保持稳定,长期贫困率显著降低。
图8表明,医疗保险的引入不仅有效降低了长期贫困率,同时减小了贫困家庭的贫困深度。无医疗保险的情况下,随时间推移,贫困深度由2%增加至5.7%,涨幅为185%,这意味着贫困家庭的资产在逐渐减少。引入医疗保险后,贫困深度由2%增加至2.7%并保持稳定,第30年的贫困深度相较无医疗保险情形下降了3%。在政府对医疗保险进行保费补贴后,贫困深度进一步降低至1.8%并保持稳定。以初始时刻无保险机制情形下的社会保护成本为基准值100,对社会保护成本进行标准化处理可得图9。
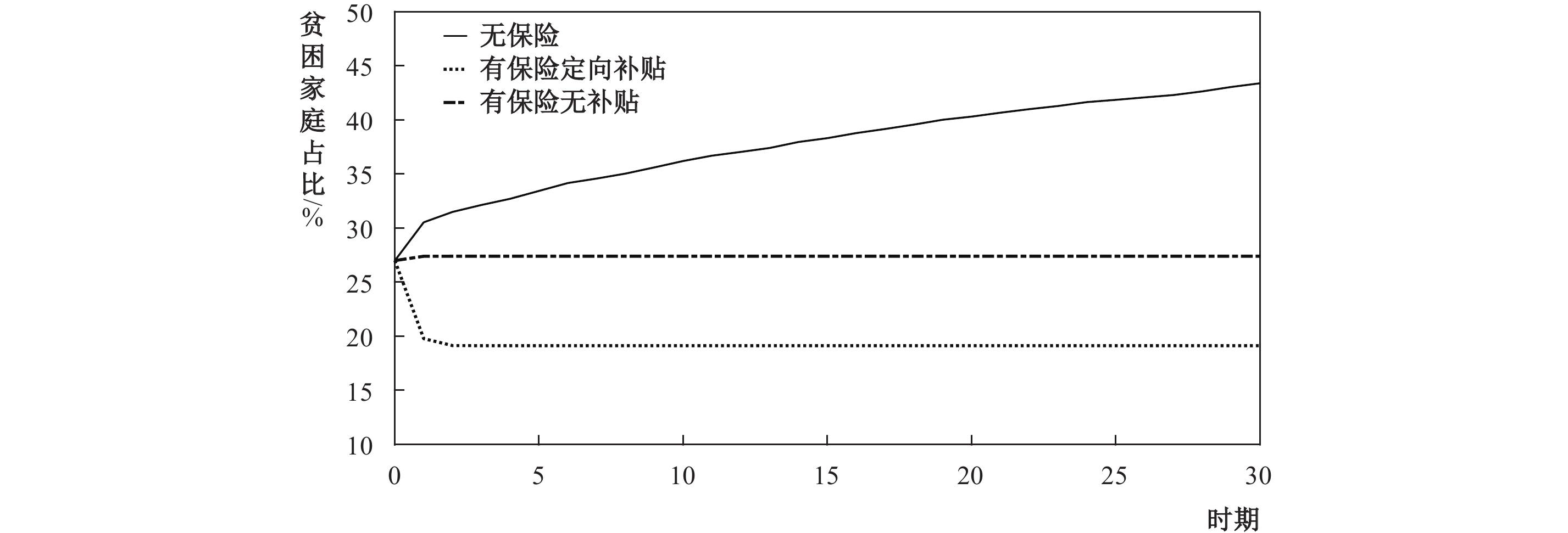
|
| 图 7 贫困家庭占比随时间变化情况 |
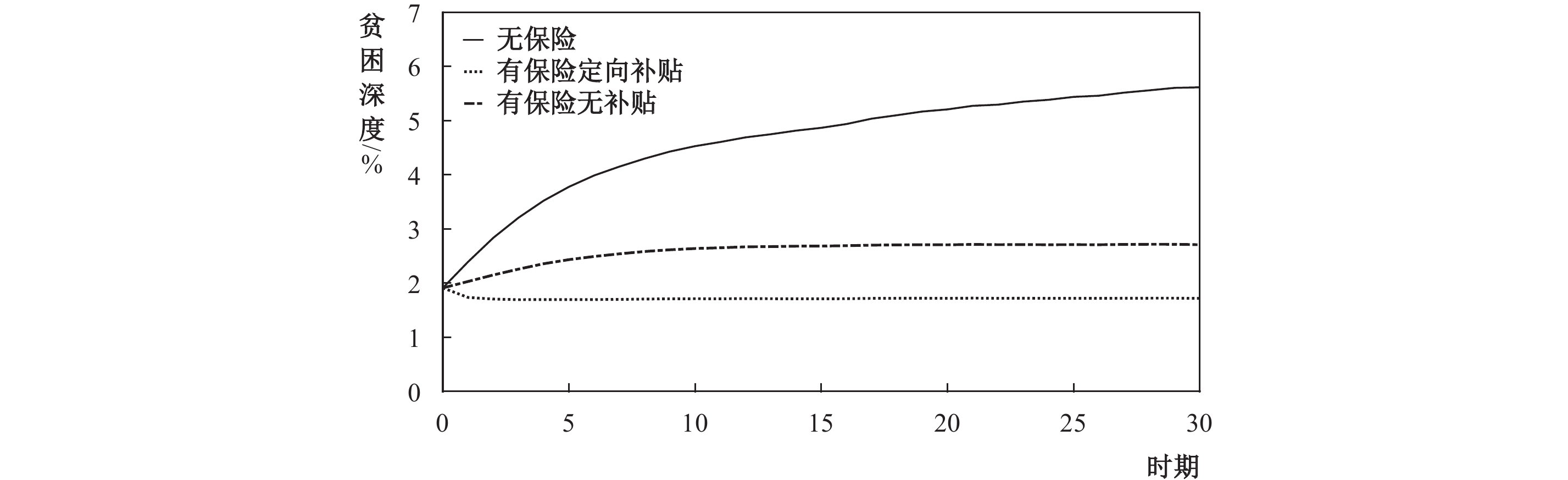
|
| 图 8 贫困深度随时间变化情况 |
|
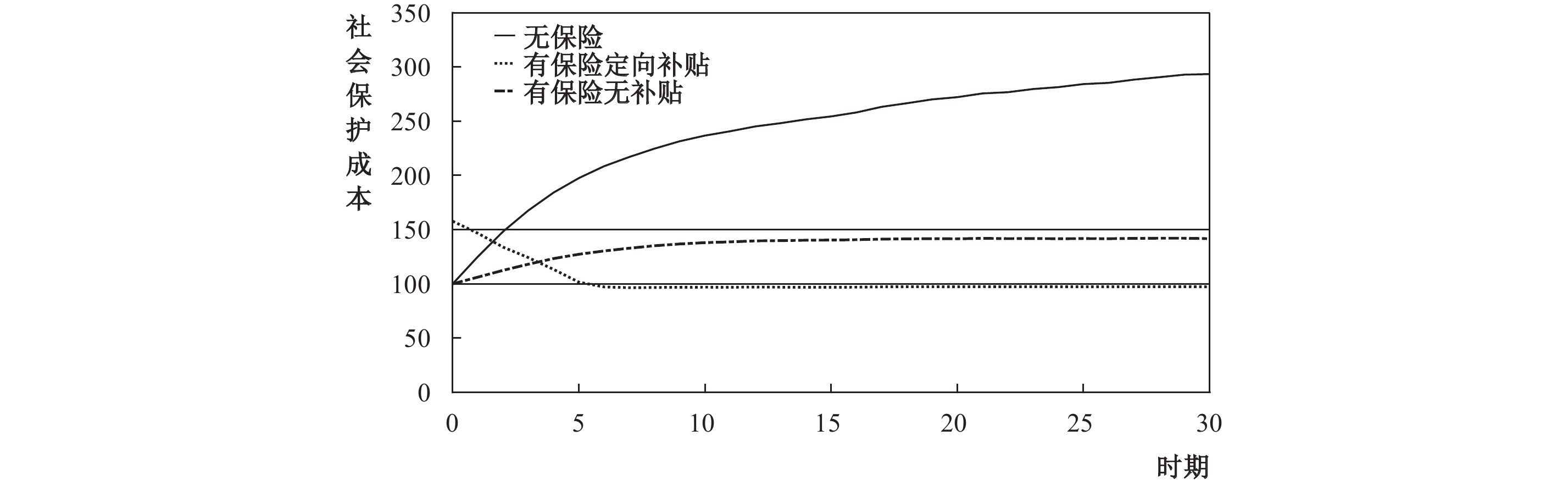
| 图 9 社会保护成本随时间变化情况 |
图9表明,初始时刻,在没有保费补贴的情况下,医疗保险机制对社会保护成本并无影响,都只有现金补助成本,而政府对医疗保险进行保费补贴则会大幅提高社会保护成本,由100上升至150以上。但是其会在短期内迅速下降,5年以内就会低于另外两种情形下的社会保护成本。从长期来看,有保费补贴情形下的社会保护成本会逐渐减小直至稳定。在第30年,相较于单一的现金补助政策,“医疗保险+现金补助”的政策组合会使得社会保护成本下降
综上所述,从长期来看,有政府保费补贴的医疗保险不仅能有效降低长期贫困发生率和贫困深度,巩固脱贫攻坚成果,还能减少长期减贫成本。在无保险情形下,若采用现金补助的扶贫方式,随时间推移,长期减贫成本将持续增加,这是因为现金补助政策只有事后的补偿效应,贫困家庭可能自身不仅缺乏主动努力脱贫的意识,而且对政府的扶贫工作产生福利依赖。而在引入医疗保险保费补贴政策后,由于医疗保险的事前投资激励效应,部分贫困家庭会主动降低消费,充分利用政府的帮扶政策扩大生产,加快资产积累,同时通过医疗保险降低外生疾病冲击的影响,从而脱离“贫困陷阱”。
五、结论与政策建议
发展是解决贫困问题的“总钥匙”,要从根源上解决贫困问题,关键还是要提升贫困家庭和脱贫家庭的自主发展能力,而医疗保险是解决此问题的重要政策工具。本文构建了包含医疗保险、消费和投资的家庭资产随机增长模型,分析了拥有不同资产水平的家庭受到外生疾病冲击后的贫困脆弱性及投资决策的动态变化,厘清了医疗保险对贫困脆弱性的作用机制。本文还分析了无医疗保险、有医疗保险无保费补贴和有医疗保险有保费补贴三种扶贫模式对长期贫困率、贫困深度及长期减贫成本的影响。数值模拟结果表明:(1)医疗保险具有事后的贫困脆弱性降低效应,这种效应对于非贫脆弱家庭效果尤为显著。政府可以通过医疗保险保费补贴政策,缓解贫困个体和贫困边缘个体的流动性压力,激励该类个体通过医疗保险来应对疾病风险,更有效地降低贫困脆弱性。(2)医疗保险具有事前的投资激励效应。医疗保险机制的引入改变了部分贫困家庭和贫困边缘家庭的跨期资本动态,激励部分贫困家庭和非贫脆弱家庭主动降低消费和增加净投资,为了摆脱贫困而努力,从而降低了这类家庭的贫困脆弱性。(3)相较于单一的现金补助扶贫模式,“现金补助+保费补贴”的扶贫模式显著降低了长期贫困率和贫困深度,有效减少了长期减贫成本。与仅使用现金补助政策相比,“医疗保险+政府现金补助”使得长期减贫成本下降了
本文结论具有重要的政策含义。第一,从长期来看,相较于单一的现金补助政策,“医疗保险+政府现金补助”政策的长期减贫效果更显著,所需的成本也更少。因此,在扶贫资源有限的约束下,本文建议政府应当将部分资源投向医疗保险市场,发展普惠型医疗保险,提高扶贫资金使用效率,提升减贫质量,缓解财政压力。第二,医疗保险保障是一项能够预防非贫困人口陷入贫困的良好措施。政府可以通过医疗保险为贫困和贫困边缘人群建立保障机制,也可以建立分段医疗保险保费补贴模式,把保费补贴和家庭资产挂钩,提高医疗保险补贴的精准性。政府可以对需求弹性高的非贫脆弱个体进行定向保费补贴,扩大保险需求,守住脱贫成果。第三,对于贫困家庭,政府在对其提供医疗保险保费补贴的同时,应当建立和实施激励相容的有条件现金转移支付制度,与乡村振兴有效进行衔接,形成贫困农户的内生发展能力,实现农村长效脱贫。第四,需在资源分配过程中兼顾贫困人群与非贫脆弱人群,更加注重贫困人口自身发展能力与抵御风险能力的提升。因此,政府需要建立动态贫困监测系统,动态监测评估贫困个体的行为,避免其产生对现金补助政策的福利依赖,同时也要建立动态系统识别非贫脆弱个体,避免这部分个体因疾病冲击而返贫。
本文的不足之处在于,模型设定中选择了简单的现金补助形式,未能考虑较为复杂的有条件现金转移支付政策在长期减贫实践中的激励相容效应,因此无法对有条件现金转移支付和医疗保险政策的长期减贫效果进行直接比较,这也是未来需要进一步研究的内容。
① 具体请参考《人类减贫的中国实践》白皮书,国务院新闻办公室,2021。
② Micawber阈值最早由Skiba(1978)提出,用以区分个体是否能够进行储蓄和资产良性积累。Zimmerman和Carter(2003)首次将其运用于“贫困陷阱”模型中,用以区分个体是否会陷入“贫困陷阱”。在无保险情形下,资产水平低于Micawber阈值的个体必然会陷入“贫困陷阱”。
③ 由于疾病种类的多样性和治疗费用的差异化,在模型测试过程中,我们加入了随机因素,令疾病冲击和发生概率随机变动(上下变动20%),模型结果依旧稳健,因此本文仅遵循疾病产生的负面冲击和疾病发生概率呈负相关的原则设定了一种可能的分布。
④ 目前,政府对城乡居民基本医疗保险进行了66%左右的保费补贴。本文选取50%的价格补贴进行研究是为了分析在采用略低于现有补贴标准的情况下,医疗保险的长期减贫效果,探讨能否通过降低医疗保险保费补贴来减少长期减贫成本。
⑤ 由式(5)和式(9)可知,均衡状态下个体的流动性成本即为投资的边际收益,投资的边际收益越高,个体的流动性成本也就相应地更高。相较于无保险情形,在有保险无补贴情形下,医疗保险机制的引入会弱化外生疾病冲击的影响,使得投资的边际收益更高,即
⑥ 净投资表示家庭在折旧后的上期投资
⑦ 稳健性检验表明,模拟结果对家庭户数(大于100)的选择不敏感,改变家庭户数,模型结果无显著变化。
| [1] | 陈志钢, 毕洁颖, 吴国宝, 等. 中国扶贫现状与演进以及2020年后的扶贫愿景和战略重点[J]. 中国农村经济, 2019(1): 2–16. |
| [2] | 程令国, 张晔. “新农合”: 经济绩效还是健康绩效?[J]. 经济研究, 2012(1): 120–133. |
| [3] | 黄晓宁, 李勇. 新农合对农民医疗负担和健康水平影响的实证分析[J]. 农业技术经济, 2016(4): 51–58. DOI:10.13246/j.cnki.jae.2016.04.005 |
| [4] | 黄征学, 高国力, 滕飞, 等. 中国长期减贫, 路在何方? ——2020年脱贫攻坚完成后的减贫战略前瞻[J]. 中国农村经济, 2019(9): 2–14. |
| [5] | 黄薇. 医保政策精准扶贫效果研究——基于URBMI试点评估入户调查数据[J]. 经济研究, 2017(9): 117–132. |
| [6] | 景鹏, 郑伟, 贾若, 等. 保险机制能否助推脱贫并守住脱贫成果? ——基于资产积累模型的分析[J]. 经济科学, 2019(2): 104–116. |
| [7] | 刘子宁, 郑伟, 贾若, 等. 医疗保险、健康异质性与精准脱贫——基于贫困脆弱性的分析[J]. 金融研究, 2019(5): 56–75. |
| [8] | 卢盛峰, 卢洪友. 政府救助能够帮助低收入群体走出贫困吗? ——基于1989—2009年CHNS数据的实证研究[J]. 财经研究, 2013(1): 4–16. DOI:10.16538/j.cnki.jfe.2013.01.001 |
| [9] | 齐良书. 新型农村合作医疗的减贫、增收和再分配效果研究[J]. 数量经济技术经济研究, 2011(8): 35–52. DOI:10.13653/j.cnki.jqte.2011.08.001 |
| [10] | 孙武军, 祁晶. 保险保障、家庭资本增长与贫困陷阱[J]. 管理科学学报, 2016(12): 71–82. DOI:10.3969/j.issn.1007-9807.2016.12.007 |
| [11] | 王翌秋, 刘蕾. 新型农村合作医疗保险、健康人力资本对农村居民劳动参与的影响[J]. 中国农村经济, 2016(11): 68–81. |
| [12] | 解垩. 医疗保险与城乡反贫困: 1989—2006[J]. 财经研究, 2008(12): 68–83. DOI:10.3969/j.issn.1001-9952.2008.12.006 |
| [13] | 张楠, 张栋浩, 李建军, 等. 长期减贫的未雨绸缪——来自扶贫改革试验区的证据[J]. 财贸经济, 2020(3): 20–35. DOI:10.3969/j.issn.1002-8102.2020.03.003 |
| [14] | 赵思诚, 杨青, 许庆. 社会保障、信贷获得与农业生产——来自新型农村合作医疗制度的证据[J]. 财经研究, 2019(11): 45–56. DOI:10.16538/j.cnki.jfe.2019.11.004 |
| [15] | 郑晓冬, 上官霜月, 陈典, 等. 有条件现金转移支付与农村长期减贫: 国际经验与中国实践[J]. 中国农村经济, 2020(9): 124–144. |
| [16] | Akotey J O, Adjasi C. The impact of microinsurance on household asset accumulation in Ghana: An asset index approach[J]. The Geneva Papers on Risk and Insurance-Issues and Practice, 2014, 39(2): 304–321. DOI:10.1057/gpp.2014.6 |
| [17] | Barrett C B, Carter M R. The economics of poverty traps and persistent poverty: Empirical and policy implications[J]. The Journal of Development Studies, 2013, 49(7): 976–990. DOI:10.1080/00220388.2013.785527 |
| [18] | De Nicola F. The impact of weather insurance on consumption, investment, and welfare[J]. Quantitative Economics, 2015, 6(3): 637–661. DOI:10.3982/QE300 |
| [19] | Foster J, Greer J, Thorbecke E. A class of decomposable poverty measures[J]. Econometrica, 1984, 52(3): 761–766. DOI:10.2307/1913475 |
| [20] | Ikegami M, Carter M R, Barrett C B, et al. Poverty traps and the social protection paradox[M]. London: The University of Chicago Press, 2019. |
| [21] | Janzen S A, Carter M R, Ikegami M. Can insurance alter poverty dynamics and reduce the cost of social protection in developing countries?[J]. Journal of Risk and Insurance, 2021, 88(2): 293–324. DOI:10.1111/jori.12322 |
| [22] | McPeak J. Contrasting income shocks with asset shocks: Livestock sales in Northern Kenya[J]. Oxford Economic Papers, 2004, 56(2): 263–284. DOI:10.1093/oep/gpf040 |
| [23] | Skiba A K. Optimal growth with a convex-concave production function[J]. Econometrica, 1978, 46(3): 527–539. DOI:10.2307/1914229 |
| [24] | Zimmerman F J, Carter M R. Asset smoothing, consumption smoothing and the reproduction of inequality under risk and subsistence constraints[J]. Journal of Development Economics, 2003, 71(2): 233–260. DOI:10.1016/S0304-3878(03)00028-2 |

