
2022第48卷第6期
一、引 言
改革开放以来,中国经济快速发展,但是土地、劳动力等生产要素可能存在价格扭曲,这对经济增长会有制约作用(徐朝阳和林毅夫,2010;李言,2020)。中国房价整体上涨可能造成投资结构“脱实向虚”,同时房价上涨的区域间溢出又扭曲了要素市场价格,这不仅对劳动力集聚造成重要影响,导致区域间劳动力技能结构的显著差异(周颖刚等,2019),而且改变了地区间资本和劳动的相对配置效率(刘贯春等,2017;孙巍和徐邵军,2021)。地区间房价差距不仅影响劳动力集聚,而且要素价格扭曲已经成为制约国家实现高质量发展的瓶颈。地区房价上涨对要素相对价格扭曲之间的作用机理是什么?地区间房价差异如何影响异质性劳动力流动的结构性特征?现有研究尚未对这些问题形成统一的结论,需要从理论上对此给出一个答案。
现有研究对地区房价和要素价格扭曲之间关系的讨论,主要从要素价格的相对扭曲程度出发,研究劳动力和资本在地区和行业间的配置规律(陈斌开等,2015;罗知和张川川,2015)以及资本深化程度特征(陆铭等2015;张巍等,2018)。这类研究大多认为房价对劳动集聚存在挤出效应(高波等,2012;李勇刚和罗海艳,2017),高房价一方面造成“简单”劳动力流出,促使企业利用资本替代劳动。在粘性工资和市场利率的前提下,造成要素相对扭曲和总体扭曲程度的变化(许家云和张巍,2020)。另一方面,房地产行业的高利润会吸引资金脱离实体行业(吴海民,2012),尤其是对研发投入存在显著的挤出效应(Miao和Wang,2014;王文春和荣昭,2014),进而造成经济“脱实向虚”以及资本错误配置(郭念枝和村濑英彰,2018;王竹泉等,2019)。根据现有文献的研究,房价无论是通过挤出劳动密集型产业,还是吸引实体行业的利润,都会对地区的资本深化程度产生系统性影响。当地区资本的深化程度超过生产技术决定的最优区间时,可能会造成要素在地区间流动,并形成要素扭曲。
然而,现有大多数的研究所揭示的关于房价、劳动力流动以及要素价格扭曲之间的内在机制,只能在不区分劳动力技能水平的条件下,对劳动力流入地区起到一定的解释能力,而对于整个经济系统而言,尤其是对异质性劳动力流出的地区而言,解释能力较弱(宋弘和吴茂华,2020)。如在揭示房价和要素价格扭曲的研究中,大多数研究默认地区间房价存在显著差异以及低技能劳动力的工资水平难以负担一些地区的高房价。然而区域房价存在差异的原因以及房价与劳动力集聚之间的内在机制,现有研究较少对此进行深入的讨论。对于劳动力集聚和房价关系的研究,学者们将劳动力大规模流动作为分析房价变化的先决条件。这不仅忽视了异质性劳动力在流动过程中会产生不同的集聚效应的机制和临界条件,而且排除了异质性劳动力之间的相互作用关系,从而无法对劳动力流动和要素扭曲的相互作用机制进行深入分析。那么房价是否对异质性劳动力集聚存在不同的影响?异质性劳动力集聚与要素价格扭曲之间存在着怎样的联系?本文试图在完整的理论框架下,基于异质性劳动力流动的视角对房价、异质性劳动力集聚和要素价格扭曲之间的内生机制进行深入剖析。
异质性劳动力流动始终贯穿着“房价变化和要素价格扭曲”这一过程。对于异质性劳动力流动和房价变动之间的关系来说,技能型劳动力的相对议价能力更高(陈宇峰等,2013;谢申祥等,2019),房价对技能型劳动力流动的阻碍作用相对更小,而对低技能劳动力集聚的挤出效应则更大。在技能型劳动力集中并形成高技术产业集聚的过程中,产业相依性决定了发展高端技术产业的同时需要服务业作为支撑(郭卫军和黄繁华,2020),即高技能劳动力集聚对低技能劳动力集聚产生了引致效应,从而在一定程度上抵消房价对低技能劳动力集聚的挤出。在房价的挤出效应和产业相依性的影响下,决定了异质性劳动力集聚的动态平衡。而劳动力集聚带来的住房刚需又决定了房价的动态均衡,最终形成了异质性劳动力集聚和房价变动的内生反馈机制。
对于异质性劳动力流动和要素价格扭曲之间的关系来说,异质性劳动力集聚直接改变了地区间劳动力的技能结构以及要素配置结构,前者导致了技能型劳动和非技能型劳动的替代,后者导致了劳动和资本的替代。在粘性工资前提下,上述两种替代过程直接影响要素价格的相对扭曲程度(袁鹏和朱进金,2019)。要素市场价格扭曲不仅是决定要素流动的直接动因,而且由劳动力集聚导致的房价上涨,会导致资本和劳动价格双重扭曲,从而改变异质性劳动力和资本在行业间和地区间的配置状态和配置效率(张巍等,2018)。
综上所述,本文通过构建理论模型进行数值模拟,并利用省际宏观数据进行实证检验,分析了异质性劳动力流动、房价变动和要素价格扭曲之间的内生机制。通过将异质性劳动力流动纳入两区域一般均衡框架内,本文从理论上揭示了劳动力技能结构是影响地区房价变动的决定因素,而由于要素价格粘性造成要素价格的扭曲,这是决定异质性劳动力集聚、区域劳动力技能结构分化的关键所在。实证检验发现由技能型劳动力集聚导致的资本集聚以及市场工资粘性是造成劳动价格负向扭曲和资本价格正向扭曲的根本原因,而高房价对“简单”劳动力产生挤出效应,并且可能导致资本“脱实向虚”,从而造成了劳动价格的正向扭曲和资本价格的负向扭曲。
本文的贡献在于以下三点:第一,将劳动力划分为技能型劳动力、非技能型劳动力和“简单”劳动力,进而研究在异质性劳动力流动过程中,地区劳动力整体技能结构的改变以及地区资本深化程度的改变,研究了异质性劳动力流动对地区要素配置和地区要素价格扭曲的作用机制。第二,本文提出的理论模型表明房价上涨不仅对非技能型劳动力存在挤出效应,而且产业相依性导致了技能型劳动力的集聚,也会对非技能型劳动力产生引致效应。最终异质性劳动力的相对流动均衡取决于上述挤出效应和引致效应的相对均衡。这一研究发现为流入和流出地区实现均衡发展和制定因地制宜的发展策略提供了理论基础。第三,本文发现了技能型劳动力集聚带来的地区劳动力技能结构的提高和对资本的引致效应是造成房价上涨的关键因素。房价上涨抵消了异质性劳动力之间的集聚规模效应,并诱发了要素间的替代,形成了技能集聚地区的房价上涨,劳动力技能结构提升和资本深化的内生反馈机制。这一结论对理解房价变动、住房泡沫的形成机制提供了新的视角,明确了地区间异质性要素的配置状态和效率对房价的作用机制。
接下来本文内容结构安排如下:第二部分构建包含异质性劳动力流动的两区域一般均衡模型;第三部分在参数校准基础上,对理论模型的关键性质进行数值模拟,并以此阐明要素流动与房价变化的联动机理;第四部分利用实证手段检验房价、异质性劳动力流动与地区间要素价格扭曲的关系;第五部分是文章总结和政策建议。
二、理论模型
如前文所述,揭示异质性劳动力流动、房价变化以及要素价格扭曲的内在机制,关键在于识别异质性劳动力流动的相对均衡以及要素之间替代的相对均衡。一方面,异质性劳动力的相对集聚决定了地区住房总需求。另一方面,要素相对配置决定了要素市场价格的扭曲程度,并反作用于要素流动。因此,本文构建两区制一般均衡模型,期望通过以下两个方面的扩展,对上述问题进行分析。首先,通过细分异质性劳动力群体,分析技能型劳动力集聚对资本集聚以及对“简单”劳动力的替代程度。其次,通过引入产业相依性,刻画了在异质性劳动力流动过程中互相之间的引致效应以及房价对异质性劳动力的挤出效应。通过对上述变量之间动态机制的分析,最终得出对房价长期动态均衡演化的一般性规律。
具体而言,考虑一个包含两地区(地区s和n),并且工业品(CMt)、服务品(CBt)和住房(CHt)共存的经济体。住房和服务品不可跨地区交易,工业品在不同地区可自由交易。工业品厂商雇佣技能型劳动力(Ht)、非技能型劳动力(Lt)和使用可变资本(Kt)进行生产,服务品厂商雇佣“简单”劳动力(Jt)和使用固定资本(F)进行生产。地区间工资差距决定了异质性劳动力的跨区域流动,而地区间利率差距决定了资本的跨区域流动。
(一)居民偏好
假设不同的劳动力群体分别对应着不同的代表性家庭,不同群体的家庭均具有替代弹性跨期不变的消费偏好,而每类代表性家庭均追求终生效用最大化。为了便于分析,设定每个代表性家庭均供给一单位相应劳动力从而获得工资收入,并根据市场价格在储蓄和消费之间进行权衡。因此,异质性家庭群体在相应收支约束条件下的效用函数①可表示为:
| $ U = \max \;\sum\limits_{t = 0}^\infty {{\beta ^t}\left[ {\ln (\frac{{C_{B,t}^\sigma }}{\sigma } + {C_{M,t}}) + \gamma \ln {C_{H,t}}} \right]} $ | (1) |
| $ s.t.\;\;P_{B,t}^d \cdot C_{B,t}^d + P_{M,t}^d \cdot C_{M,t}^d + P_{H,t}^d \cdot \Delta C_{H,t}^d + S_{t + 1}^d = (1 + {r_t})S_t^d + W_t^d\;\;\;\;\;d \in \left( {l,h,j} \right) $ | (2) |
其中,
住房具备耐用品属性,住房存量持续为家庭提供效用,并假设住房的折旧率为0。在收支约束下最大化家庭终身效用,可求得家庭d对相应商品的需求分别为:
| $ C_{B,t}^d = {(\frac{{{P_{B,t}}}}{{{P_{M,t}}}})^{\frac{1}{{\sigma - 1}}}} $ | (3) |
| $ C_{M,t}^d = \frac{1}{{1 + \gamma }}\frac{{w_t^d}}{{{P_{H,t}}}} + \frac{1}{{\gamma + 1}}\frac{{{P_{H,t}}}}{{{P_{M,t}}}}\bar \omega {_{t-1}^d} - \frac{{\gamma + \sigma }}{{\sigma (\gamma + 1)}}{(\frac{{{P_{B,t}}}}{{{P_{M,t}}}})^{\frac{\sigma }{{\sigma - 1}}}} $ | (4) |
| $ \Delta C_{H,t}^d = \frac{\gamma }{{\gamma + 1}}\frac{{w_t^d}}{{{P_{H,t}}}} - \frac{1}{{\gamma + 1}}\bar \omega {_{t-1}^d -1} + \frac{{\gamma (1 - \sigma )}}{{\sigma (1 + \gamma )}}\frac{{{P_{M,t}}}}{{{P_{H,t}}}}{(\frac{{{P_{B,t}}}}{{{P_{M,t}}}})^{\frac{\sigma }{{\sigma - 1}}}} $ | (5) |
其中,
| $ {P_{H,t}} = \frac{{\gamma \cdot {{\bar w}_t} \cdot {O_t}}}{{(1 + \gamma )Y_{Ht}^s + {{\bar \varpi }_t} \cdot {O_t}}}\left[ {1 + \frac{{(1 - \sigma ){P_{M,t}} \cdot {O_t}}}{\sigma }{{(\frac{{{P_{B,t}}}}{{{P_{M,t}}}})}^{\frac{\sigma }{{\sigma - 1}}}}} \right] $ | (6) |
其中,Ot表示地区所有劳动力总量,即Ot=Ht+Lt+Jt。
(二)服务品厂商
由于假设服务品在地区间不可贸易,因此地区间服务品的价格差异是决定居民生活成本的关键。这样的假设蕴含的重要信息是当居民需要消费相应的服务品时,则必须通过跨地区流动来实现对特定服务品的消费。这个条件所蕴含的现实意义在于当居民对相应的城市交通、社保、户籍、教育等公共服务产生需求时,必须到相应地区才有可能实现此类公共服务的消费。
根据传统D-S框架,假设服务品的生产表现出显著的规模报酬递增特点,且满足垄断竞争条件。服务品厂商雇佣可流动的普通劳动力Jit以及使用相应的固定投资Fi来提供不同种类的服务品。除此之外,设定每个地区的市场存在qt个服务品厂商,②每个厂商生产存在一定差异的服务品。假设每个服务品厂商利用固定资本Fi(假设不存在资本折旧)和可变劳动力Jit来生产服务品xit的技术为Jit=Fi+aTxit。其中aT为产品转化效率。
设定地区存在qt个差异性服务品厂商。根据D-S条件,每个服务品厂商生产的服务品数量cit以及居民消费的“打包”服务品数量CBt之间关系满足:
| $ {C_{B,t}} = {(\int_0^q {c_{i,t}^\rho di} )^{\frac{1}{\rho }}} $ | (7) |
其中ρ为每种服务品之间的替代弹性。根据居民支出的约束条件,得到居民购买“打包”服务品支付的价格PB,t和每个服务品厂商制定的出厂价格pi,t之间关系为:
| $ {P_{B,t}} = {(\int_0^q {p_{i,t}^{\frac{\rho }{{\rho - 1}}}di} )^{\frac{{\rho - 1}}{\rho }}} $ | (8) |
均衡条件下地区异质性家庭群体对服务品的总需求等于地区服务品总供给。结合服务品出厂价格方程(8),可求得服务品厂商i的供给xit为:
| $ {x_{i,t}} = {O_t}{(\int_0^q {p_{i,t}^{\frac{\rho }{{\rho - 1}}}di} )^{\frac{{\rho - 1}}{{\rho (\sigma - 1)}}}} \cdot P_{M,t}^{\frac{1}{{1 - \sigma }}} \cdot q_t^{ - 1} $ | (9) |
当商品完全同质的情况下,pi=p,xi=x。同时,由于M商品可自由贸易,则工业品价格满足一价定律。出于计算简便考虑,假设同一市场内部不存在商品运输成本,设定工业品价格作为价格基准,即PM=1。那么地区单个服务品厂商的产出可进一步化简为:
| $ {x_t} = {O_t}q_t^{\frac{{\rho - 1}}{{\rho (\sigma - 1)}}}{p_t}^{\frac{1}{{\sigma - 1}}} $ | (10) |
根据厂商零利润条件,可求出服务品厂商制定的出厂价格和支付劳动的工资率:厂商的全部利润用于支付普通劳动工人的工资,即
| $ W_t^J = {(\frac{{{O_t}}}{{{J_t}}})^{1{\text{ - }}\sigma }}q_t^{\frac{{1 - \rho }}{\rho }}{(\frac{{2\sigma - 1}}{{{a_T}\sigma }})^\sigma } $ | (11) |
每个服务品厂商生产服务品的数量关于支付工资和价格之间的关系为:
| $ {x_t} = \frac{{W_t^JF}}{{{p_t} - {a_T}W_t^J}}\; $ | (12) |
方程(11)中Ot/Jt表示地区普通劳动力的供养系数或者理解为地区劳动力技能水平结构。
而利用服务品厂商的利润函数在产出约束条件下构造利润最大化函数:
| $ {\pi _{i,t}} = {p_{i,t}}{x_{i,t}} - W_{i,t}^J({F_i} + {a_T}{x_{i,t}}) $ | (13) |
| $ s.t.\;\;\;{x_t} = {O_t}q_t^{\frac{{\rho - 1}}{{\rho (\sigma - 1)}}}{p_t}^{\frac{1}{{\sigma - 1}}} $ | (14) |
由上式能够推出服务品出厂价格关于厂商支付的普通劳动力工资的表达式为:
| $ {p_t} = \frac{{{a_T} \cdot \sigma \cdot W_t^J}}{{2\sigma - 1}} $ | (15) |
将方程(12)和方程(15)同时代入服务品厂商生产技术方程,得到每个服务品厂商雇佣普通劳动力的均衡数量为:
| $ {J_t} = (F + {a_T}{x_t}) = F + \frac{{2\sigma - 1}}{{1 - \sigma }}F = \frac{\sigma }{{1 - \sigma }}F $ | (16) |
若地区普通劳动力禀赋为
| $ {q_t} = \frac{{\overline J }}{{{J_i}}} = \frac{{\overline J (1 - \sigma )}}{{\sigma F}} $ | (17) |
式(17)表明,地区服务业规模和单个厂商生产的固定资本投入呈反向关系,即在短时期内,当地区总资本禀赋固定的情况下,地区工业和传统服务业之间的产业结构存在最优区间。结合方程(12)中的普通劳动力供养系数,发现异质性劳动力之间的相依性以及异质性劳动力所代表的产业规模和结构决定了地区劳动力技能结构的最优区间。
(三)工业品厂商
设定每个地区只存在一个典型加总的工业品厂商。工业生产技术满足C-D生产函数形式,用资本和劳动份额参数之间的差别来描述区域要素密集程度的差异:
| $ M_t^s = A_t^s \cdot K_{s,t}^{{a_s}} \cdot H_{s,t}^{{b_s}} \cdot L_{s,t}^{1 - {a_s} - {b_s}} $ | (18) |
其中,
对工业品厂商的生产函数关于生产要素求一阶导数,得到相应要素的边际产出,即厂商使用资本所付出的名义利率和雇用异质性劳动力付出的名义工资。同时排除市场价格因素,得到异质性劳动力的实际工资以及资本回报率为:
| $ w_{s,t}^d = {{W_{s,t}^d} \mathord{\left/ {\vphantom {{W_{s,t}^d} {\left( {P_{M,t}^s \cdot P_{B,t}^s \cdot P_{G,t}^s} \right)}}} \right. } {\left( {P_{M,t}^s \cdot P_{B,t}^s \cdot P_{G,t}^s} \right)}}\;\;\;\;\;d \in (h,l,j) $ | (19) |
| $ r_t^s = {a_s}K_{s,t}^{{a_s} - 1}H_{s,t}^{{b_s}}L_{s,t}^{1 - {a_s} - {b_s}} $ | (20) |
其中,
(四)房地产厂商
本文重点关注的问题在于住房价格对市场要素配置的影响以及住房价格形成的内生机制。由于住房供给在很多情况下受非系统因素的决定和制约(韩立彬和陆铭,2018;汪勇和李雪松,2019)。因此出于计算简便的考虑,本文设定住房的生产是线性增长的,具体满足如下形式:
| $ {Y_{H,t}} = z{G_t} $ | (21) |
其中Gt为外生变量,z为相应的政策调控参数。住房市场的均衡条件满足市场对住房的总需求等于总供给:
| $ {H_t} \cdot \Delta C_{H,t}^h + {L_t} \cdot \Delta C_{H,t}^l + {J_t} \cdot \Delta C_{H,t}^j = z \cdot {G_{H,t}} $ | (22) |
而劳动力分为原住民和流动居民。因此上式关于住房的总需求,本质上是不同性质的居民关于住房的异质性需求的加总。
(五)异质性要素流动
在实际要素流动过程中,要素的流动规模取决于地区间收入差距以及生活成本差距,即地区实际工资水平差异是决定异质性劳动力跨区域流动的关键。标记 s 地区为流入地区,则流入地区的异质性劳动力的动态积累方程为:
| $ H_{t + 1}^s = (1 + h)H_t^s + {\psi _h} \cdot H_t^n \cdot {{(w_{s,t}^h - w_{n,t}^h)} \mathord{\left/ {\vphantom {{(w_{s,t}^h - w_{n,t}^h)} {w_{s,t}^h}}} \right. } {w_{s,t}^h}} $ | (23) |
| $ L_{t + 1}^s = (1 + n)L_t^s + {\psi _l} \cdot L_t^n \cdot {{(w_{s,t}^l - w_{n,t}^l)} \mathord{\left/ {\vphantom {{(w_{s,t}^l - w_{n,t}^l)} {w_{s,t}^l}}} \right. } {w_{s,t}^l}} $ | (24) |
| $ J_{t + 1}^s = (1 + n)J_t^s + {\psi _j} \cdot J_t^n \cdot {{(w_{s,t}^j - w_{n,t}^j)} \mathord{\left/ {\vphantom {{(w_{s,t}^j - w_{n,t}^j)} {w_{s,t}^j}}} \right. } {w_{s,t}^j}} $ | (25) |
其中,h为技能型劳动力的自然增长率;n为非技能劳动力和“简单”劳动力的自然增长率;
而资本的转移取决于地区间的利率差异。由于利率本身代表货币的价格,因此资本是否转移取决于地区间名义利率。资本动态方程的化简形式为:
| $ K_{t + 1}^s = (1 + {g_k})K_t^s + {\psi _k} \cdot K_t^n \cdot {{({r_{s,t}} - {r_{n,t}})} \mathord{\left/ {\vphantom {{({r_{s,t}} - {r_{n,t}})} {{r_{s,t}}}}} \right. } {{r_{s,t}}}} $ | (26) |
其中gk为稳态下资本积累速度;
三、理论模型的数值模拟
为揭示异质性劳动力流动与房价之间的关系以及房价影响要素配置的内在机理,本文对理论模型的均衡条件及关键性质进行数值模拟。由于本文研究重点并未涉及国外部门以及金融摩擦,同时对政府关于住房的调控进行了简化,因此在采用中国实际数据进行校准和数值模拟过程中,主要目的在于揭示异质性劳动力流动与房价上涨之间的内在联系。
(一)参数校准③
为了使本文构建的理论模型的性质结果与中国经济发展现实相契合,本文对理论模型中的参数和状态变量进行赋值模拟,相应的赋值规则见表1。
| 参数及取值 | 经济含义 | 理论依据 |
| as=0.43 | 流入地的资本产出弹性 | 投入产出表的要素收入份额占GDP比重; 孙巍和徐邵军(2021) |
| bs=0.24 | 流入地的技能型劳动力产出弹性 | |
| (1-as-bs)=0.35 | 流入地的非技能型劳动力产出弹性 | |
| an=0.41 | 流出地的资本产出弹性 | |
| bn=0.21 | 流出地的技能型劳动力产出弹性 | |
| (1-an-bn)=0.32 | 流出地的非技能型劳动力产出弹性 | |
| Fs=Fn=300 | 地区服务业的固定资产使用总额 | Mori(2012);何雄浪和毕佳丽(2014) |
| aTs=aTn=0.3 | 产品转化效率 | |
| ρ=4 | 异质性服务品替代参数 | |
| gs=0.12 | 流入地区的房地产年平均增长率 | 国信房地产信息网 |
| gn=0.17 | 流出地区的房地产年平均增长率 | |
| β=0.99 | 主观贴现因子 | 李尚骜和龚六堂(2012) |
| gk=0.15 | 资本的稳态增长率(储蓄率) | |
| σ=0.55 | 风险规避系数 | 主观贴现率测算 |
| γ=0.3 | 住房偏好参数 | 郭念枝和村濑英彰(2018) |
| ψh=0.05 | 技能型劳动力的流动敏感系数 | 误差最小化原则测算 |
| ψj=ψl=0.03 | 普通劳动力、非技能型劳动力的流动敏感系数 | |
| ψk=0.05 | 资本的流动敏感系数 | |
| h=0.02 | 技能型劳动力的平均增长率 | 《劳动与就业统计年鉴》 |
| n=0.01 | 非技能型劳动力平均增长率 |
(二)数值模拟
在完成参数校准和赋值后,本文对异质性劳动力与资本的相对流动速度及其是否造成了资本和劳动力配置状态的改变进行数值模拟。通过模拟地区间不同要素的流动规模、地区房价、地区劳均资本存量、地区劳动力技能结构等变量的时间演化趋势,对异质性要素集聚、房价和要素配置之间的内在机制进行验证。
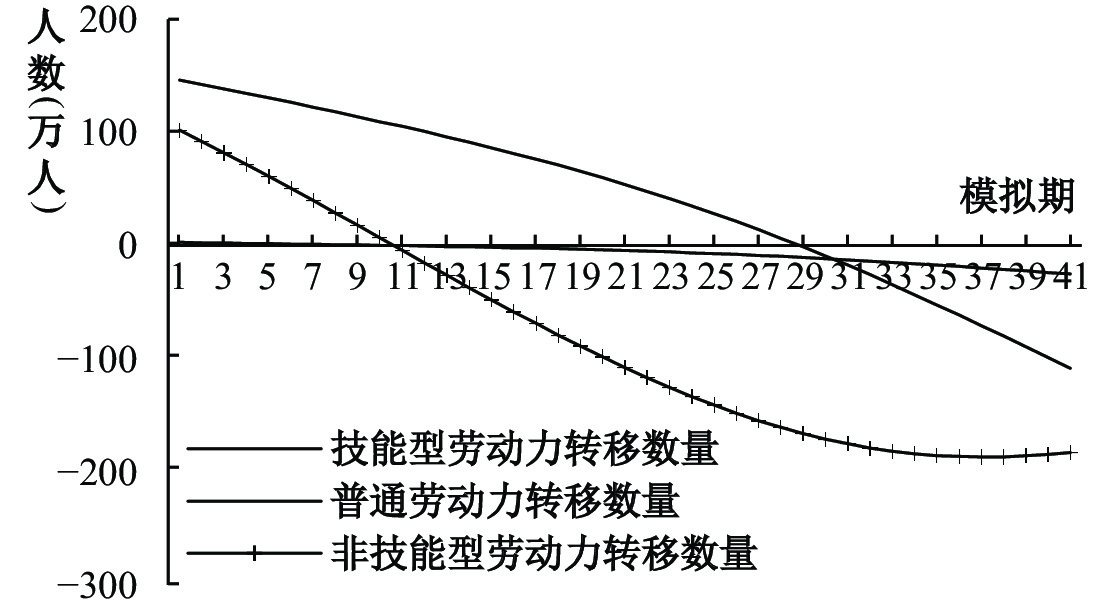
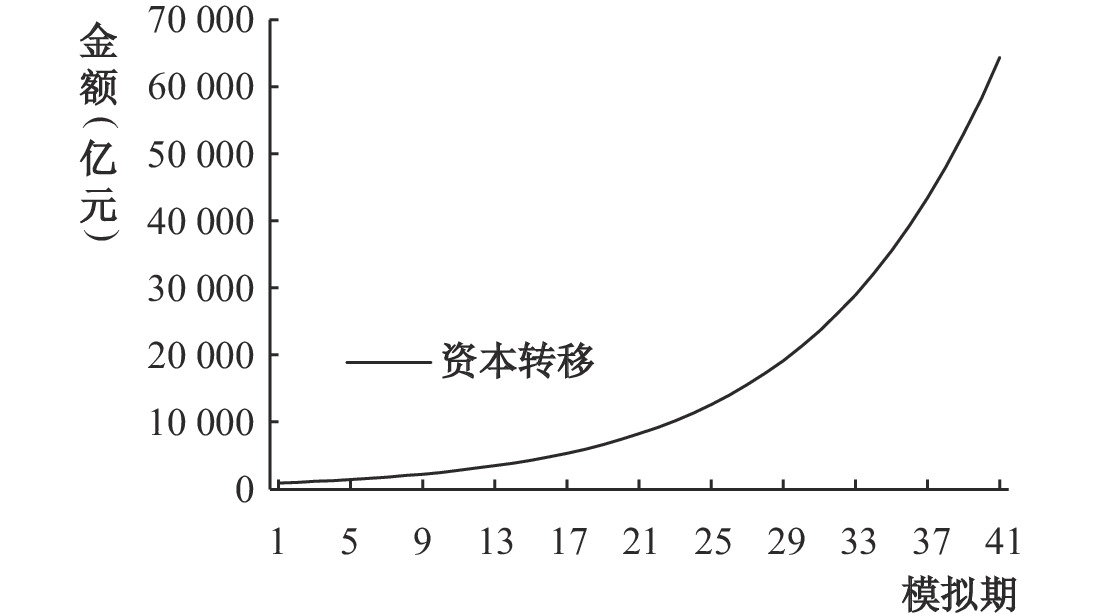
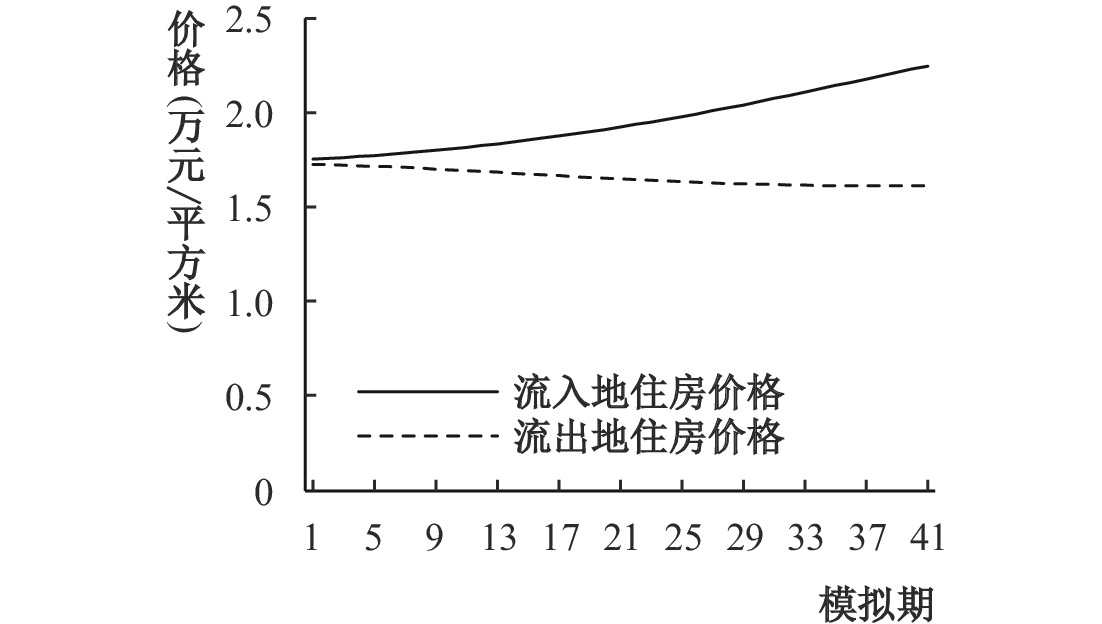
从图1和图2可以看出,在要素追逐技术的理论机制作用下(孙巍和徐邵军,2021),生产要素和研发要素会向着技术优势地区集聚。人口规模扩张显著提高了集聚地的住房需求,造成集聚地区房价显著上升,地区间房价产生显著分化,具体如图3所示。此外高房价对异质性劳动力也产生了不同程度的挤出效应。可以看出,要素集聚造成的房价上涨对工业部门的非技能型劳动力的挤出效应最为明显。而产业相依性又使得技能型劳动力集聚阻滞了房价对普通劳动力的挤出,因此高房价促使非技能型劳动力回流比普通劳动力回流更早发生。如图2所示,技能型劳动力集聚会导致资本流入,进而诱发资本对非技能型劳动力的替代。最终,技能型劳动力集聚造成了对非技能型劳动力的大规模替代,说明高房价可能会排斥低技能型劳动力。
|
| 图 1 地区异质性劳动力流动 |
|
| 图 2 地区资本流动 |
|
| 图 3 地区住房价格分化 |
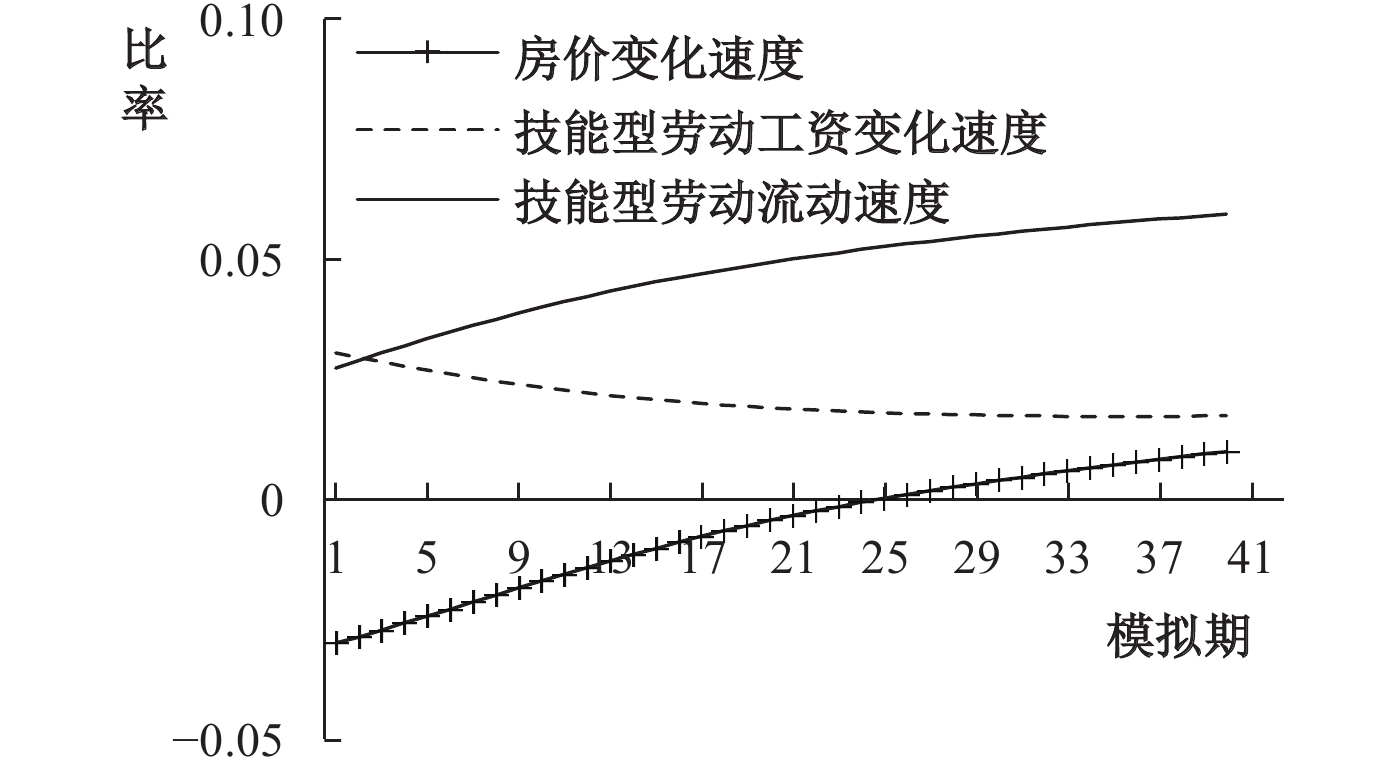
本文的模拟结果发现,技能型劳动力集聚并不受限于房价上涨,而取决于地区间的工资差距。④从图4、图5看出,流入地的技能型劳动力集聚规模并没有随着房价上涨趋势减缓而扩大,反而因为粘性工资的微弱下降而显著缩小。对比流出地区的演化规律,同样能够确定工资水平下降是造成技能型劳动力流失的主要原因,房价变动仅是对于技能型劳动力规模变动的自发反应,具体如公式(6)所示。

|
| 图 4 流入地技能型劳动力 |
|
| 图 5 流出地技能型劳动力 |
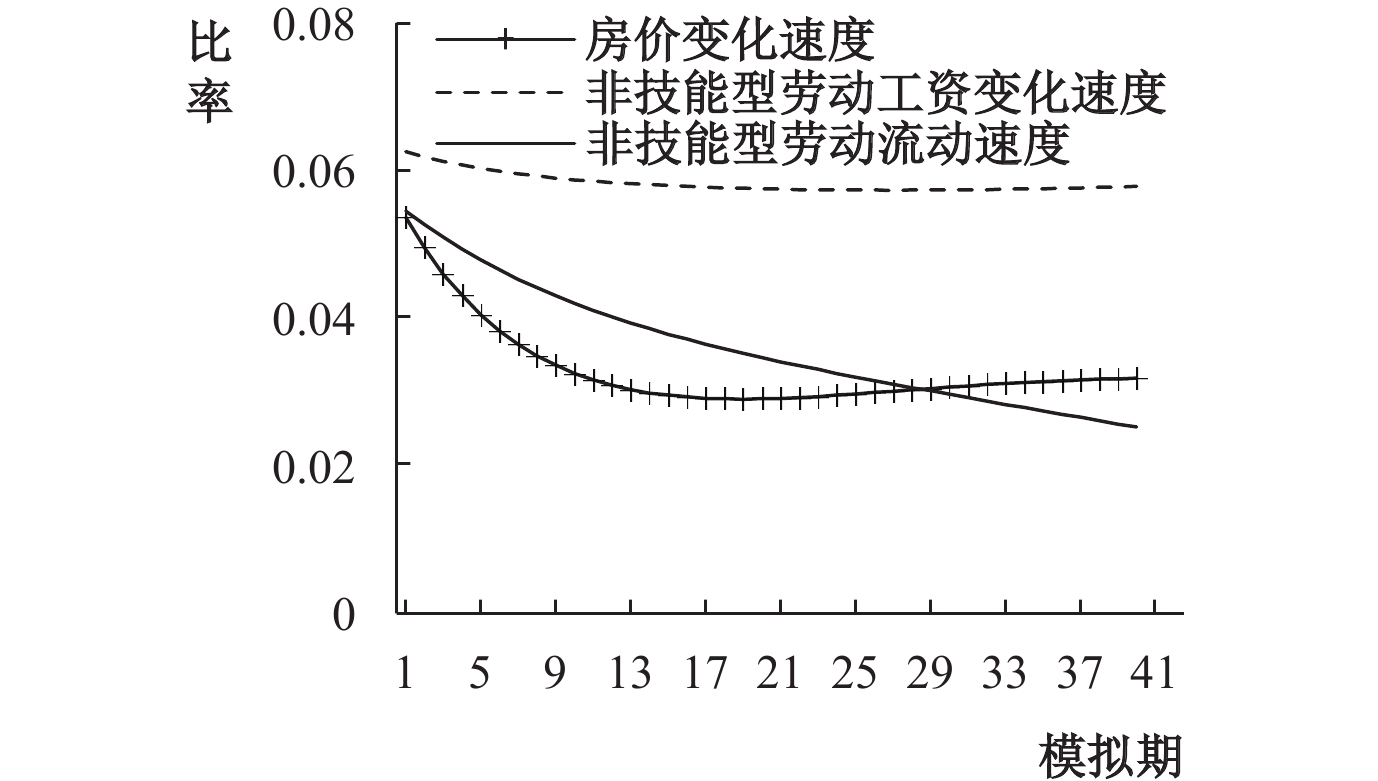
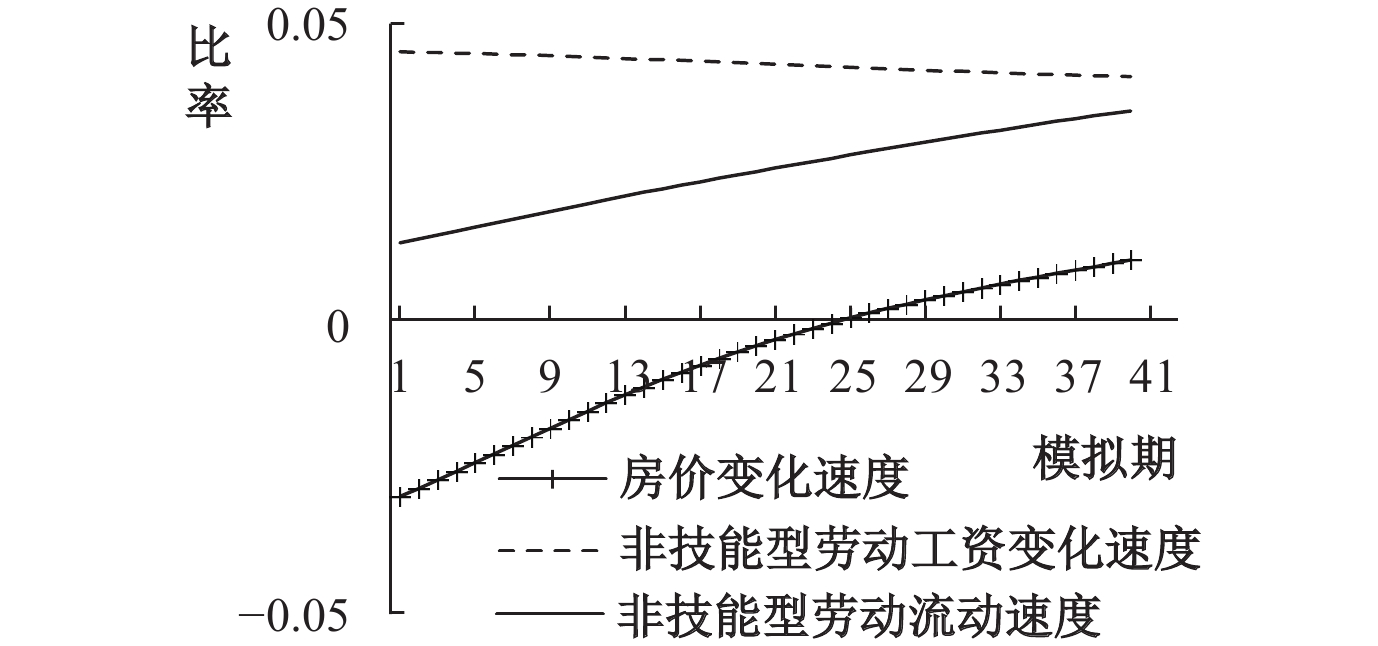
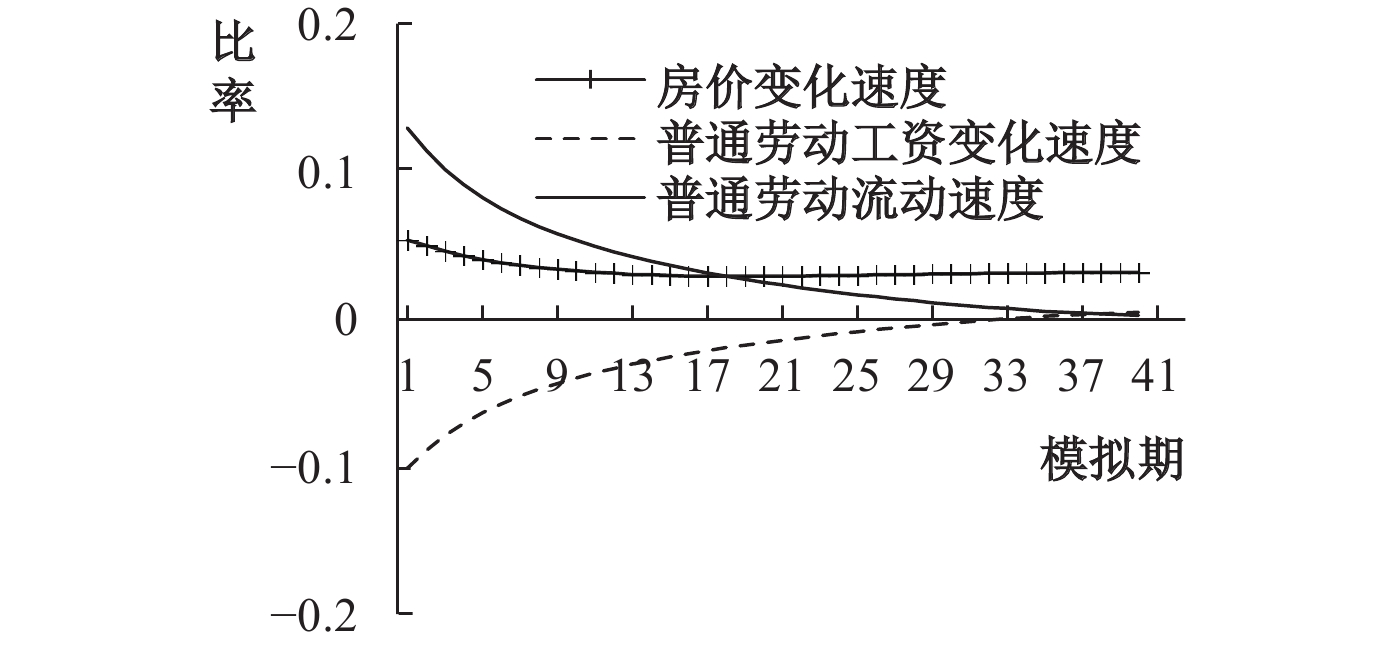
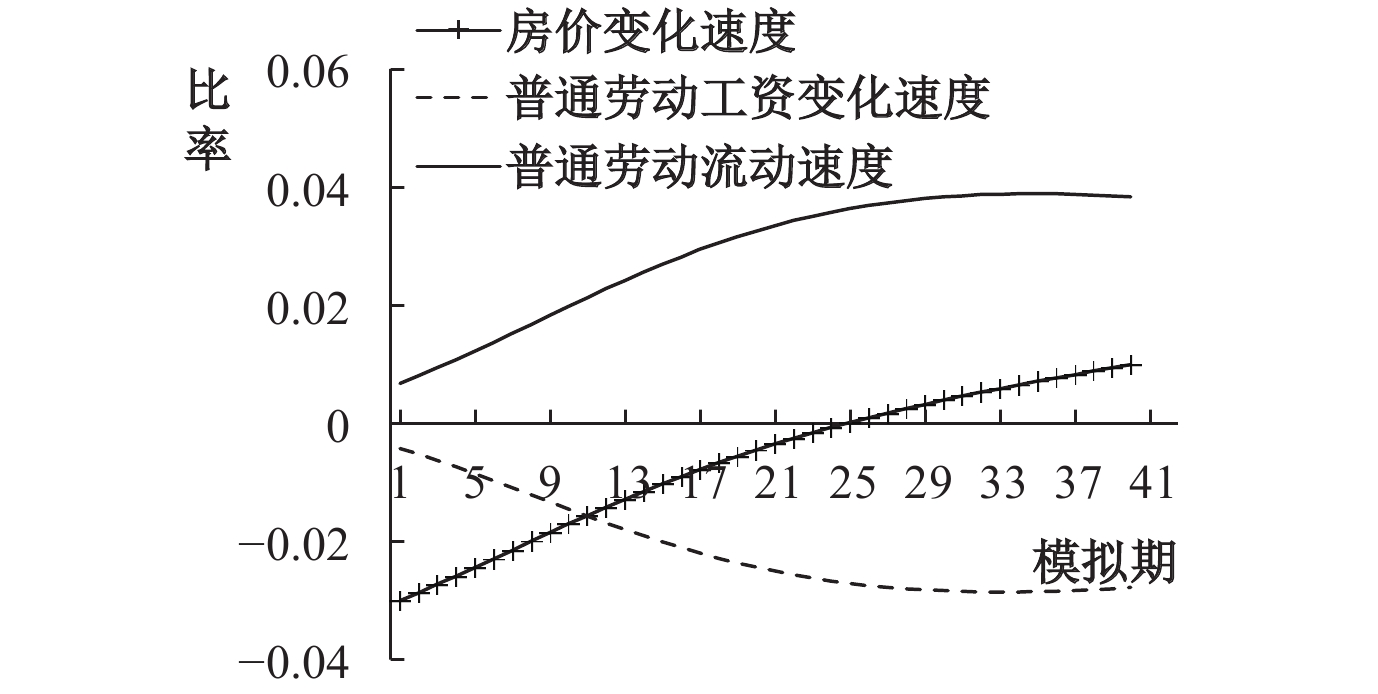
本文数值模拟结果的一个新发现是对于非技能型劳动力而言,若工资不存在显著上升趋势,即使房价下降速度快于工资下降速度,也不会吸引非技能型劳动力的流动,具体如图6、图7所示。对于技能水平较低、市场价格粘性较强和可替代性较高的非技能型劳动力,可观测的名义收入水平上涨是决定其流动的根本原因。上述规律同样体现在普通劳动力的流动过程中。如图8所示,随着普通劳动力的工资水平逐渐上升,普通劳动力的地区间流动规模也会逐渐降低。流出地区则刚好相反:工资水平逐渐降低,普通劳动力流失规模则逐渐扩大,如图9所示。
|
| 图 6 流入地非技能型劳动力 |
|
| 图 7 流出地非技能型劳动力 |
|
| 图 8 流入地普通劳动力 |
|
| 图 9 流出地普通劳动力 |
数值模拟结果的另一个新发现在于,市场中工资粘性是普遍存在的,且劳动力价格扭曲的微小变动会引发劳动力流动规模显著变化。结合技能型劳动力、非技能型劳动力和普通劳动力的工资水平模拟结果发现,技能水平越低、越容易被资本替代的劳动力,其工资粘性越强。而异质性劳动力流动规模却并未表现出与房价变动显著的反向特征,粘性工资的微弱变动反而诱发了劳动力流动规模的明显改变。
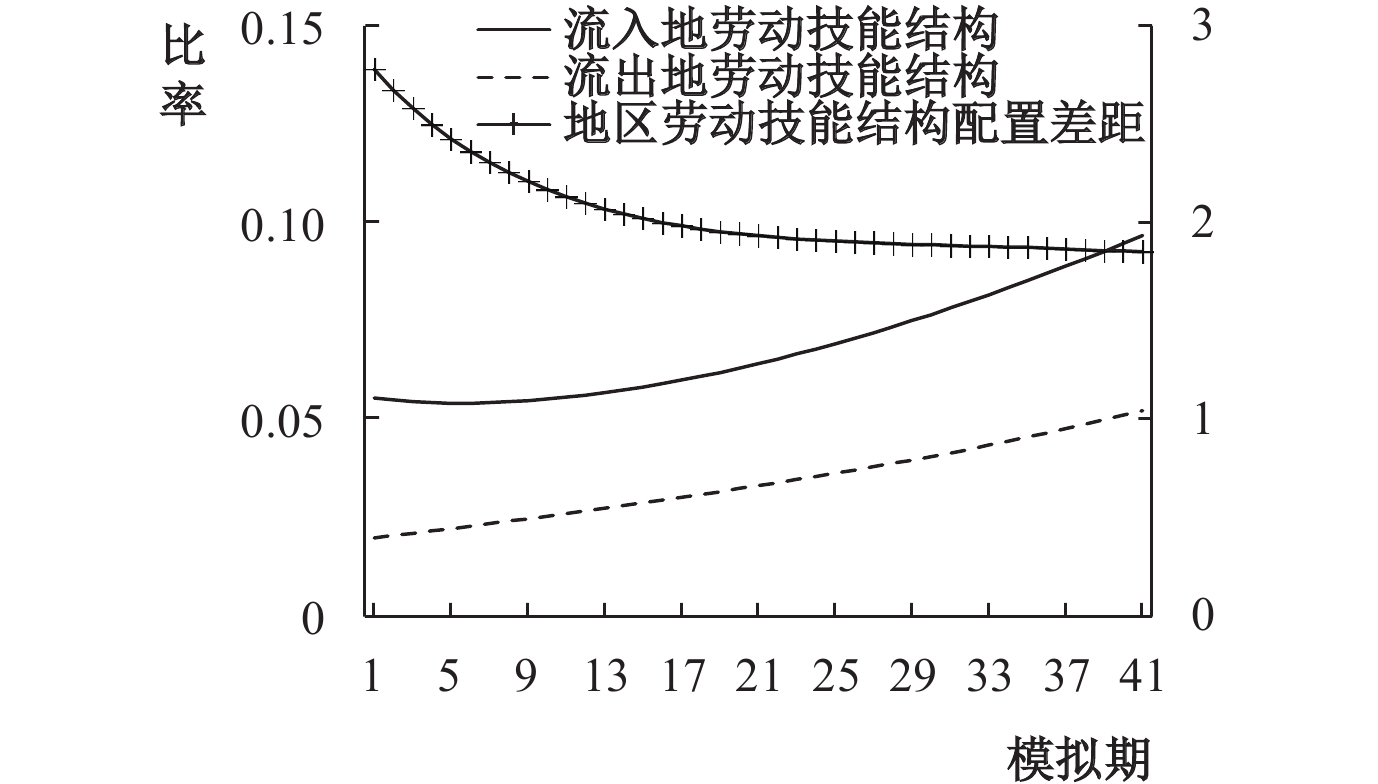
如图10和图11所示,关于房价变化对地区要素配置问题,通过模拟地区劳均资本存量和地区劳动力技能结构发现,由于技能型劳动力和资本对非技能型劳动力存在显著的替代,那么在集聚地住房价格持续走高和劳动力价格扭曲导致工资上涨缓慢的背景下,普通劳动力受到的挤出效应要高于产业相依性对普通劳动力的引致效应,进而造成流入地的要素配置逐渐向资本深化调整。同时,在要素追逐技术的作用下,技能型劳动力会向技术优势地区集聚,进而提高集聚地区的劳动力技能结构。

|
| 图 10 劳均资本存量 注:地区间劳均资本配置差距为比值,将其作次坐标轴显示。本文将所有涉及比值的变量均以次坐标轴反映,下图同。 |
|
| 图 11 劳动力技能结构 |
结合本文模拟结果,异质性劳动力流动与房价变化之间的内在机制可归纳为,当不同地区的技术密集程度存在差异时,地区间技术差距决定的要素报酬差距必然诱发劳动力流动,而集聚规模决定了对住房的刚需。对于劳动力而言,技能水平的高低决定了其在生产过程中的工资水平及其满足自身住房需求所需的时间周期。因此,工资是决定劳动力集聚和房价上涨的关键因素。不同技能结构的劳动力工资水平不同,达到自身住房需求餍足点的周期存在差异,即房价动量趋势的周期取决于劳动力技能结构的分布状态,地区劳动力平均技能水平越高,房价上涨越快,上涨周期越短。地区劳动力平均技能水平越低,房价上涨越慢,上涨周期则越长。而现实中较难发生极端的劳动力技能极化现象,原因在于产业相依性对普通劳动力的引致效应,在一定程度上抵消了高房价的挤出效应。最终,房价取决于异质性劳动力的平均技能结构以及社会平均工资水平。正如模拟结果揭示的那样,粘性工资的微小变动均容易造成异质性劳动力集聚的显著变化。
四、异质性劳动力集聚、房价与要素扭曲的实证检验
(一)变量构造及数据选取
根据上文理论模型的构建以及数值模拟的结果可以看出,地区劳动力技能结构是影响房价变动的关键因素,而房价变动和要素价格粘性又决定了异质性劳动力的集聚。因此,本节利用空间计量的方法,对异质性劳动力流动、房价和要素扭曲之间的关系进行实证检验。
本文选取要素价格扭曲作为核心被解释变量。参照Hsieh和Klenow(2009)、蒲艳萍和顾冉(2019)等学者的测算方式,定义要素价格扭曲为要素边际报酬和市场价格的比值(distLit=MPLit/wit,distKit=MPKit/rit)。其中资本和劳动对产出的贡献份额(
| $ total\_dis{t_{i,t}} = distK_{i,t}^{\frac{\alpha }{{\alpha + \beta }}}distL_{i,t}^{\frac{\beta }{{\alpha + \beta }}} $ | (27) |
| $ relative\_dis{t_{i,t}} = {{dist{L_{i,t}}} \mathord{\left/ {\vphantom {{dist{L_{i,t}}} {dist{K_{i,t}}}}} \right. } {dist{K_{i,t}}}} $ | (28) |
本文选取各地区商品房平均销售价格(元/平方米)作为衡量房价的指标;选取各地区本科及以上学历的劳动力数量作为衡量技能型劳动力的指标,同时为了检验模型稳健性,以各地区研发人员总量(万人)作为技能型劳动力的替代指标;选取各地区城镇单位就业人员总量、私营企业就业人员和个体就业人员总量(万人),并扣除技能型劳动力作为衡量普通劳动力数量的指标;采用永续盘存法对地区资本存量进行计算;以“地区年末常住人口”与“地区年末户籍人口”之差和“地区年末户籍人口”的比值作为劳动力净迁入比率。考虑到数据完整性,剔除了西藏地区的相关指标。本文所采用的样本时间为2004—2019年,相应数据源于《中经网统计数据库》《中国科技统计年鉴》和《中国人口和就业统计年鉴》。详细的指标含义和处理过程见表2。
| 变量名称 | 符号 | 测度方式 |
| 要素相对价格扭曲 | relative_dist | relative_distit=distLit/distKit |
| 要素整体价格扭曲 | total_dist |
|
| 房价 | ph | 地区商品房平均售价的对数 |
| 技能型劳动力 | skill | 地区本科及以上学历劳动力的对数 |
| 非技能型劳动力 | lab | 地区劳动总量的对数 |
| 流动比率 | mig | (常住人口−户籍人口)/户籍人口 |
| 资本 | cap | 永续盘存法计算资本存量的对数 |
(二)空间溢出效应分析
在进行空间计量分析之前,首先需要检验各个地区是否存在空间溢出效应。采用经典的空间相关Moran指数对地区间可能存在的空间相关性进行检验:
| $ I = \frac{{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{w_{i,j}}\left( {{x_i} - \overline x } \right)\left( {{x_j} - \overline x } \right)} } }}{{{S^2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{w_{i,j}}} } }} $ | (29) |
其中,xi分别代表地区i的要素价格的相对扭曲和要素价格整体扭曲;n为地区总数;wij为空间权重矩阵W中的元素。本文采用经济距离阵来构建莫兰指数。从表3中可以看出,在2004—2019年间,中国各省份之间的要素价格扭曲存在正向显著的空间集聚效应。
| 时间 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| 相对扭曲 | 0.229
(1.585) |
0.337*** (2.876) |
0.464*** (6.324) |
0.480*** (5.168) |
0.440*** (3.795) |
0.340*** (3.001) |
0.305** (2.239) |
0.309** (2.267) |
| 整体扭曲 | 0.252** (2.081) |
0.265*** (2.854) |
0.285*** (4.523) |
0.264*** (3.857) |
0.374*** (3.763) |
0.365*** (3.048) |
0.353** (2.012) |
0.447** (2.064) |
| 时间 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| 相对扭曲 | 0.271* (1.643) |
0.244
(1.377) |
0.264** (2.088) |
0.271** (2.181) |
0.242* (1.701) |
0.198** (2.133) |
0.215* (1.801) |
0.207* (1.795) |
| 整体扭曲 | 0.428** (2.063) |
0.442* (1.759) |
0.421** (2.136) |
0.395*** (2.703) |
0.342** (2.050) |
0.414
(1.638) |
0.403** (2.132) |
0.417** (2.112) |
| 注:小括号内为z值。***、**和*分别表示在 1%、5% 和 10% 的显著性水平下显著。 | ||||||||
(三)要素扭曲的实证检验
通过数值模拟结果可以发现,若技能型劳动力集聚引发劳动偏向型技术进步并提高劳动生产效率时,粘性工资的存在会使得劳动价格发生负向扭曲,而房价对劳动力的挤出则会造成劳动价格的正向扭曲。若当技能型劳动力集聚引发了资本偏向性技术进步并提高资本生产效率时,应当引发资本价格的正向扭曲,而房价导致资本“脱实向虚”,从而造成资本价格的负向扭曲。为验证理论模型的结论,本文首先进行LM检验,结果表明SEM模型、SAR模型均适用。其次,LR检验拒绝了原假设,说明SDM模型不会简化为SEM模型或SAR模型。再次,Hausman检验结果支持固定效应。最后,联合显著性检验拒绝了原假设,说明选用时间和个体双重效应的SDM模型较为合适。本文构建如下空间杜宾面板模型(SDM)对此进行检验:
| $ {z_{i,t}} = \tau {z_{i,t - 1}} + \rho {w'_i}{z_t} + {x'_{i,t}}\beta + {d'_i}{X_t}\delta + {\mu _i} + {\gamma _t} + {\varepsilon _{i,t}} $ | (30) |
其中,
| 要素整体价格扭曲 | 要素相对价格扭曲 | |||||
| 经济距离阵 | 空间权重阵 | 替代变量 | 经济距离阵 | 空间权重阵 | 替代变量 | |
| skill | 0.172** (0.0815) |
0.0721** (0.0344) |
0.406*** (0.0764) |
0.0129*** (0.00389) |
0.0696* (0.0392) |
0.106** (0.0499) |
| ph | −0.0560** (0.0252) |
−0.562*** (0.0889) |
−0.0831** (0.0359) |
−0.164*** (0.0495) |
−0.204*** (0.0618) |
−0.108*** (0.0342) |
| mig | 1.266** (0.642) |
1.027*** (0.391) |
1.133*** (0.325) |
−0.520** (0.214) |
−0.608*** (0.213) |
−0.513** (0.208) |
| cap | −0.346*** (0.113) |
−0.397*** (0.0787) |
−0.323*** (0.0725) |
0.0224
(0.0309) |
0.0313
(0.0340) |
0.0407
(0.0265) |
| lab | 0.665*** (0.250) |
0.173
(0.122) |
0.585*** (0.0972) |
−0.189* (0.102) |
−0.271*** (0.0758) |
−0.0436
(0.140) |
| W×skill | −24.18
(14.93) |
−1.173
(10.47) |
−3.745
(2.856) |
−7.018*** (1.169) |
−3.389
(6.748) |
−10.28*** (1.350) |
| W×ph | 17.59* (10.40) |
−8.029
(11.05) |
−13.63
(9.525) |
14.01*** (4.854) |
10.10** (4.522) |
10.40** (4.682) |
| W×mig | 61.33
(91.80) |
28.46
(27.57) |
37.04
(23.96) |
25.72
(28.59) |
42.90* (24.17) |
33.80
(27.86) |
| W×cap | 4.007
(11.14) |
3.254
(6.371) |
−0.210
(4.956) |
7.789*** (3.007) |
6.626** (3.084) |
8.114*** (2.841) |
| W×lab | −11.93
(20.21) |
6.002
(11.36) |
19.63* (10.20) |
−12.92** (6.486) |
−24.57*** (5.783) |
−4.291
(7.008) |
|
|
−2.071** (1.0497) |
−0.366** (0.163) |
−1.922*** (0.576) |
−0.658*** (0.182) |
−1.068** (0.481) |
−1.317** (0.601) |
| sigma2 | 0.253*** (0.0125) |
0.296*** (0.0197) |
0.291*** (0.0190) |
0.0413*** (0.00631) |
0.0425*** (0.00266) |
0.0409*** (0.00613) |
| 时间固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 空间固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| N | 480 | 480 | 480 | 480 | 480 | 480 |
| R2 | 0.4783 | 0.4278 | 0.4357 | 0.3895 | 0.3710 | 0.3953 |
| 注:小括号内数值为经稳健标准误调整后的t值。***、**和*分别表示在 1%、5% 和 10% 的显著性水平下显著,下表同。 | ||||||
结果表明,技能型劳动力集聚与要素整体价格扭曲、相对价格扭曲之间均存在显著的正向关系,而房价与要素整体价格扭曲、相对价格扭曲之间均存在显著的负向关系。具体而言,在技能型劳动力集聚造成社会劳动生产率提高的过程中,普遍存在的工资粘性阻碍了市场的价格发现功能,使得当期市场工资无法迅速反映劳动边际产出的提高。而资本的市场价格调整较为灵活。因此,在劳动价格被负向扭曲和资本价格未被负向扭曲的同时,要素整体价格和相对价格均产生负向扭曲。而房价的提高则挤出了议价能力相对较低的“简单”劳动力,促进了市场工资向劳动边际报酬收敛。同时房价上涨诱发了资本“脱实向虚”,而房地产比重扩大提高了社会平均资本边际回报率。因此,在房价造成劳动价格正向扭曲和资本价格负向扭曲双重叠加下,要素整体价格和相对价格均产生正向扭曲。
为更细致地揭示技能型劳动力集聚、房价变动对要素扭曲的主要作用主体和作用机制,本文进一步对技能型劳动力集聚、房价变动与资本和劳动价格扭曲之间的内在机制进行实证检验。⑤除了上文所采用的核心变量,本文同样选取地区产业结构(struit)以及要素市场化程度(factit)作为控制变量构建固定效应面板模型(许家云和张巍,2020;王小鲁等,2021)。实证结果表明,技能型劳动力集聚会显著造成劳动价格的负向扭曲以及资本价格的正向扭曲,即技能型劳动力的集聚在促使生产率提高的同时,因工资粘性的缘故,市场工资水平调整存在滞后,这使得市场工资水平低于劳动边际产出水平。此外,技能型劳动力集聚会导致资本集聚,而由于边际报酬递减,人均资本深化会造成资本边际报酬率下降,同时也会造成资本价格的正向扭曲,促使资本市场价格向真实回报率收敛。
而房价上涨对“简单”劳动力存在显著的挤出效应,而对技能型劳动力的流动的影响并不大。结合住房定价方程(6)以及数值模拟结果,高房价在造成技能型劳动力集聚的同时,也提高了市场平均工资水平和劳动力平均技能结构,促使市场工资向劳动真实回报率收敛,即劳动价格发生正向扭曲。同时,劳动力集聚造成的刚需提高不仅巩固了房价的动量效应,使得社会资本的平均边际报酬水平提高,而实体经济市场回报率下降,最终造成资本价格负向扭曲。
五、结 论
本文通过构建包含房地产部门的一般均衡模型,在刻画异质性劳动力的相对流动和要素配置演化规律的基础上,揭示出现代工业部门、传统服务部门与房地产部门之间的相互依存关系,并以此阐明异质性要素集聚、要素价格扭曲与房价变化的联动机理。在机制验证方面,本文在对理论模型的性质和关键结论进行数值模拟的同时,利用中国省际宏观年度数据进行空间计量的实证检验,并得到如下结论和启示:
本文的理论模型揭示出,第一,地区房价变动的根本原因可能是异质性劳动力集聚造成的地区劳动力结构的变化。技能型劳动力集聚对资本和“简单”劳动力的引致效应,均会诱发房价上涨。第二,针对理论模型的数值模拟结果发现,劳动市场的粘性工资是普遍存在的,劳动力价格扭曲的微小变动会显著改变劳动力流动的特征,即对于劳动力而言,可观测的名义工资是决定其跨区域流动的重要原因,高房价并不是阻滞劳动力流动的决定原因。第三,劳动力的技能特征是决定其工资粘性程度和集聚程度的关键。由于资本和技能型劳动力容易对在制造业中的非技能型劳动力产生替代,而在服务业中的劳动力则与技能型劳动力存在相互依存关系,因此产业相依性在一定程度上阻滞了高房价对“简单”劳动力的挤出,使得高房价造成的在制造业中的非技能型劳动力回流比在服务业中的普通劳动力的回流更早发生。
本文利用空间计量模型验证了理论模型的核心机制。从要素整体价格扭曲和相对价格扭曲的视角来看,技能型劳动力集聚会造成要素整体价格负向扭曲以及要素相对价格负向扭曲,而房价上涨会造成要素整体价格正向扭曲以及要素相对价格正向扭曲。进一步的实证验证表明由技能型劳动力集聚带来的生产效率的提高以及工资粘性导致市场工资水平调整滞后是造成劳动价格负向扭曲的根本原因。在资本市场价格灵活性和资本边际报酬递减规律的作用下,技能型劳动力集聚对资本集聚的引致效应会造成资本价格的正向扭曲。房价上涨诱发的社会资本“脱实向虚”,使得边际报酬较高的房地产业资本产生了扩张,而实体经济市场回报率下降,最终造成资本价格的负向扭曲。
本文研究对优化区域要素配置和实现区域经济协调发展具有较强的政策启示。异质性劳动力流动、房价变动以及要素价格扭曲之间的内生机制,决定了需要加强政策实施的系统性、整体性。为实现地区间协调发展,提出以下建议:第一,引导要素市场回报率有效回归边际报酬水平。由于资本对在制造业中的非技能型劳动的替代程度要高于对在服务业中的“简单”劳动力的替代程度,因此若不能有效提高相应行业的最低工资标准,容易造成非技能型劳动力大量涌入服务业,从而造成技能型劳动力流失。第二,防止资本无序扩张。新兴行业在发展初期,因资本相对稀缺而使得边际报酬高于社会平均水平,需要政府对此实施前瞻性的产业政策,有效引导资本配置和产业布局,使资本回归实体经济。第三,各地区需加强对异质性劳动力流动的引导。对于技术密集地区而言,在人才吸引的同时需注意产业之间的相关性,避免由高技能劳动力流动产生住房泡沫。对于生产技术较为落后的流出地而言,留住人力资本和形成知识集聚是避免地区产业空心化和缓解地区经济分化等问题的关键。
① 除了要素流动方程外,流入地和流出地的其他所有方程形式完全一致。本文所建立的模型,除需特殊备注说明,所有方程只写出流入地相应方程的表达形式,各变量略去表示地区的下标。
② 同地区厂商数量可能不同,这也是模型求解的关键结论之一。
③ 由于篇幅限制,更为详细的参数校准过程可向作者索取。
④ 数值模拟过程中计算的“工资”指的是相应劳动的边际产出。
⑤ 限于篇幅,分析表格省略,读者若是感兴趣可向作者索取。
⑥ 本文首先进行LM检验,结果表明SEM模型、SAR模型均适用。其次,LR检验拒绝了原假设,说明SDM模型不会简化为SEM模型或SAR模型。再次,Hausman检验结果支持固定效应。最后,联合显著性检验拒绝了原假设,说明选用时间和个体双重效应的SDM模型较为合适。
| [1] | 陈斌开, 金箫, 欧阳涤非. 住房价格、资源错配与中国工业企业生产率[J]. 世界经济, 2015(4): 77–98. |
| [2] | 陈宇峰, 贵斌威, 陈启清. 技术偏向与中国劳动收入份额的再考察[J]. 经济研究, 2013(6): 113–126. |
| [3] | 高波, 陈健, 邹琳华. 区域房价差异、劳动力流动与产业升级[J]. 经济研究, 2012(1): 66–79. |
| [4] | 郭念枝, 村濑英彰. 劳动力成本上升、资产泡沫与中国经济波动[J]. 经济学(季刊), 2018(3): 949–968. |
| [5] | 郭卫军, 黄繁华. 高技术产业与生产性服务业协同集聚如何影响经济增长质量?[J]. 产业经济研究, 2020(6): 128–142. |
| [6] | 韩立彬, 陆铭. 供需错配: 解开中国房价分化之谜[J]. 世界经济, 2018(10): 126–149. |
| [7] | 何雄浪, 毕佳丽. 技术溢出、要素流动与经济地理均衡[J]. 中央财经大学学报, 2014(4): 80–86. |
| [8] | 李尚骜, 龚六堂. 非一致性偏好、内生偏好结构与经济结构变迁[J]. 经济研究, 2012(7): 35–47. |
| [9] | 李言. 中国生产要素价格扭曲的变迁: 2000-2016年[J]. 经济学动态, 2020(1): 34–51. |
| [10] | 李勇刚, 罗海艳. 土地资源错配阻碍了产业结构升级吗?——来自中国35个大中城市的经验证据[J]. 财经研究, 2017(9): 110–121. |
| [11] | 刘贯春, 张晓云, 邓光耀. 要素重置、经济增长与区域非平衡发展[J]. 数量经济技术经济研究, 2017(7): 35–56. |
| [12] | 陆铭, 张航, 梁文泉. 偏向中西部的土地供应如何推升了东部的工资[J]. 中国社会科学, 2015(5): 59–83. |
| [13] | 罗知, 张川川. 信贷扩张、房地产投资与制造业部门的资源配置效率[J]. 金融研究, 2015(7): 60–75. |
| [14] | 蒲艳萍, 顾冉. 劳动力工资扭曲如何影响企业创新[J]. 中国工业经济, 2019(7): 137–154. |
| [15] | 宋弘, 吴茂华. 高房价是否导致了区域高技能人力资本流出?[J]. 金融研究, 2020(3): 77–95. |
| [16] | 孙巍, 徐邵军. 技术进步路径转换、异质性劳动力流动与地区经济差距演化[J]. 经济评论, 2021(5): 65–85. |
| [17] | 王宁, 史晋川. 中国要素价格扭曲程度的测度[J]. 数量经济技术经济研究, 2015(9): 149–161. |
| [18] | 王小鲁, 胡李鹏, 樊纲. 中国分省份市场化指数报告(2021)[M]. 北京: 社会科学文献出版社, 2021. |
| [19] | 汪勇, 李雪松. 外生冲击、房地产价格与企业投资[J]. 财经研究, 2019(3): 60–72. |
| [20] | 王竹泉, 王苑琢, 王舒慧. 中国实体经济资金效率与财务风险真实水平透析——金融服务实体经济效率和水平不高的症结何在?[J]. 管理世界, 2019(2): 58–73. DOI:10.3969/j.issn.1002-5502.2019.02.005 |
| [21] | 吴海民. 资产价格波动、通货膨胀与产业“空心化”——基于我国沿海地区民营工业面板数据的实证研究[J]. 中国工业经济, 2012(1): 46–56. |
| [22] | 谢申祥, 陆毅, 蔡熙乾. 开放经济体系中劳动者的工资议价能力[J]. 中国社会科学, 2019(5): 40–59. |
| [23] | 徐朝阳, 林毅夫. 发展战略与经济增长[J]. 中国社会科学, 2010(3): 94–108. |
| [24] | 张巍, 许家云, 杨竺松. 房价、工资与资源配置效率——基于微观家庭数据的实证分析[J]. 金融研究, 2018(8): 69–84. |
| [25] | 周颖刚, 蒙莉娜, 卢琪. 高房价挤出了谁?——基于中国流动人口的微观视角[J]. 经济研究, 2019(9): 106–122. |
| [26] | Hsieh C T, Klenow P J. Misallocation and manufacturing TFP in China and India[J]. The Quarterly Journal of Economics, 2009, 124(4): 1403–1448. DOI:10.1162/qjec.2009.124.4.1403 |
| [27] | Levinsohn J, Petrin A. Estimating production functions using inputs to control for unobservables[J]. The Review of Economic Studies, 2003, 70(2): 317–341. DOI:10.1111/1467-937X.00246 |
| [28] | Miao J J, Wang P F. Sectoral bubbles, misallocation, and endogenous growth[J]. Journal of Mathematical Economics, 2014, 53: 153–163. DOI:10.1016/j.jmateco.2013.12.003 |
| [29] | Mori T. Increasing returns in transportation and the formation of hubs[J]. Journal of Economic Geography, 2012, 12(4): 877–897. DOI:10.1093/jeg/lbr028 |
| [30] | Rong Z, Wang W C, Gong Q. Housing price appreciation, investment opportunity, and firm innovation: evidence from China[J]. Journal of Housing Economics, 2016, 33: 34–58. DOI:10.1016/j.jhe.2016.04.002 |

