
2022第48卷第5期
一、引 言
新冠肺炎疫情暴发后,全球经济陷入衰退,各国失业率大幅攀升。与此同时,自2020年2月起,在需求不足的情况下,中国通胀在短期内却出现了上升趋势。为了缓解新冠肺炎疫情对经济的负面影响,在2021年4月8日国务院金融稳定发展委员会第五十次会议强调:“就业是最大的民生,宏观政策的首要目标是保就业和保市场主体。要保持物价基本稳定,特别是关注大宗商品价格走势。”当前中国疫情已经基本得到有效控制,但是海外疫情依旧严峻,新冠病毒变异速度较快,疫苗的有效性和有效期都较为有限,未来中国经济依旧面临较大的不确定性。如何减轻极端事件所导致的不确定性对中国宏观经济的影响,推动中国经济在不确定性条件下稳步复苏,逐渐成为各界人士关注的焦点。
Altig等(2020)以及Baker等(2020)从多个角度测度了新冠肺炎疫情所引起的不确定性,发现COVID-19所引起的不确定性将对经济造成极大的负面影响。在此之前,已有较多文献探讨了不确定性对宏观经济的影响及其机制。在不确定性会引起产出下降方面,现有文献已经达成共识,但对于不确定性的影响具体是通缩还是滞胀,却没有形成一致的结论。Leduc和Liu(2016)、Basu和Bundick(2017)以及许志伟和王文甫(2018)的研究表明,由于存在价格黏性,不确定性会导致市场不能及时出清,经济陷入通缩状态。而Mumtaz和Theodoridis(2015) 的跨国研究则表明,在遭遇不确定性冲击后,企业和工人为了抑制Calvo定价所带来的负面影响,会要求提高价格和工资,进而导致经济在短期内陷入滞胀状态。朱军和蔡恬恬(2018)研究发现,政策不确定性冲击会导致经济在短期内呈现滞胀状态,长期则呈现通缩状态。他们认为这主要是因为在短期内实物期权效应占据了主导,而长期则是预防性储蓄动机占据了主导。此外,Carriero等(2018)以及Katayama和Kim(2018)则认为,不确定性虽然对产出和就业具有显著的负向影响,但对通货膨胀率的影响却不显著。
而在遭遇不确定性冲击时,还有一个值得关注的问题,即失业风险。在劳动力市场上,居民并不是完全同质的。这就会导致一部分居民失业风险高,另一部分失业风险低,从而进一步加剧宏观经济波动。对于失业风险,Challe等(2017)在搜寻匹配摩擦的基础上引入异质性居民,发现不同居民所面临的失业风险并不相同,高收入、有失业保险且拥有较多资产的居民不存在失业风险,因为他们持有的资产和失业保险足够帮助其在失业期间平滑个人消费;但对于低收入群体,失业会导致其收入陡降,对生活产生较大影响。Ravn和Sterk(2017)建立包含劳动力市场摩擦的DSGE模型,发现劳动力市场的恶化会增强居民的预防性储蓄动机,导致整个经济的总需求不足;而总需求不足又会进一步恶化劳动力市场,使得经济陷入大衰退。Oh和Picco(2020)研究了不确定性、失业风险与居民消费之间的关系,发现不确定性所引致的失业风险会导致异质性居民之间出现消费分化,即有失业保险的居民消费下滑幅度较小,而没有失业保险的居民消费下滑幅度则较大。
现有文献对不确定性的价格效应尚未达成共识,对失业风险的影响效应也没有进行深入探讨。鉴于此,本文首先实证分析了不确定性对中国宏观经济的影响,然后构建包含企业预防性定价和居民失业风险的DSGE模型,深入分析了不确定性的价格效应以及失业风险的作用,并探讨了货币政策和财政政策在应对不确定性冲击时的有效性。研究发现:第一,在不确定性冲击下,企业预防性定价会使中国经济在短期内陷入滞胀状态,而居民失业风险则会使中国经济长期逐步转向通缩状态;第二,在遭遇不确定性冲击后,存在失业风险的居民的预防性储蓄动机会增强,消费大幅下滑,这部分居民的消费复苏相对较慢;第三,宽松的货币政策能更有效地减缓不确定性对经济的负面影响,但财政政策能够更加精准有效地缓解异质性居民之间的福利损失。
本文的研究贡献主要体现在:第一,现有研究认为,在出现不确定性冲击后,经济会立即进入通缩状态。但本文研究却发现,经济会先短暂进入滞胀状态,然后转入通缩状态。本文建立理论模型对这一现象进行了很好的解释。第二,现有文献没有明确企业定价决策在不确定性影响中国宏观经济中的作用。本文从模型角度出发,厘清了企业定价决策的作用,并分析了企业定价机制。第三,本文构建了一个包含失业风险的理论模型,能较好地解释不确定性对中国宏观经济的影响,并在此模型基础上进行了政策分析。
二、典型事实
本文首先测度中国经济的不确定性。参照王博等(2019)的研究,本文采用Jurado等(2015)基于大量宏观经济指标构建SVAR模型进行识别和估计的方法。这种方法从不确定性的定义出发,构建的不确定性指数能够很好地契合中国经济运行的现实情况。本文根据Jurado等(2015)的方法计算得到的中国经济不确定性指数如图1所示。①在完成对中国经济不确定性的测度后,本文通过构建一个四变量TVP-SV-VAR模型,②分析经济不确定性冲击对宏观经济变量的总量影响与时变效应,从而更好地理解不确定性影响宏观经济的传导机制。
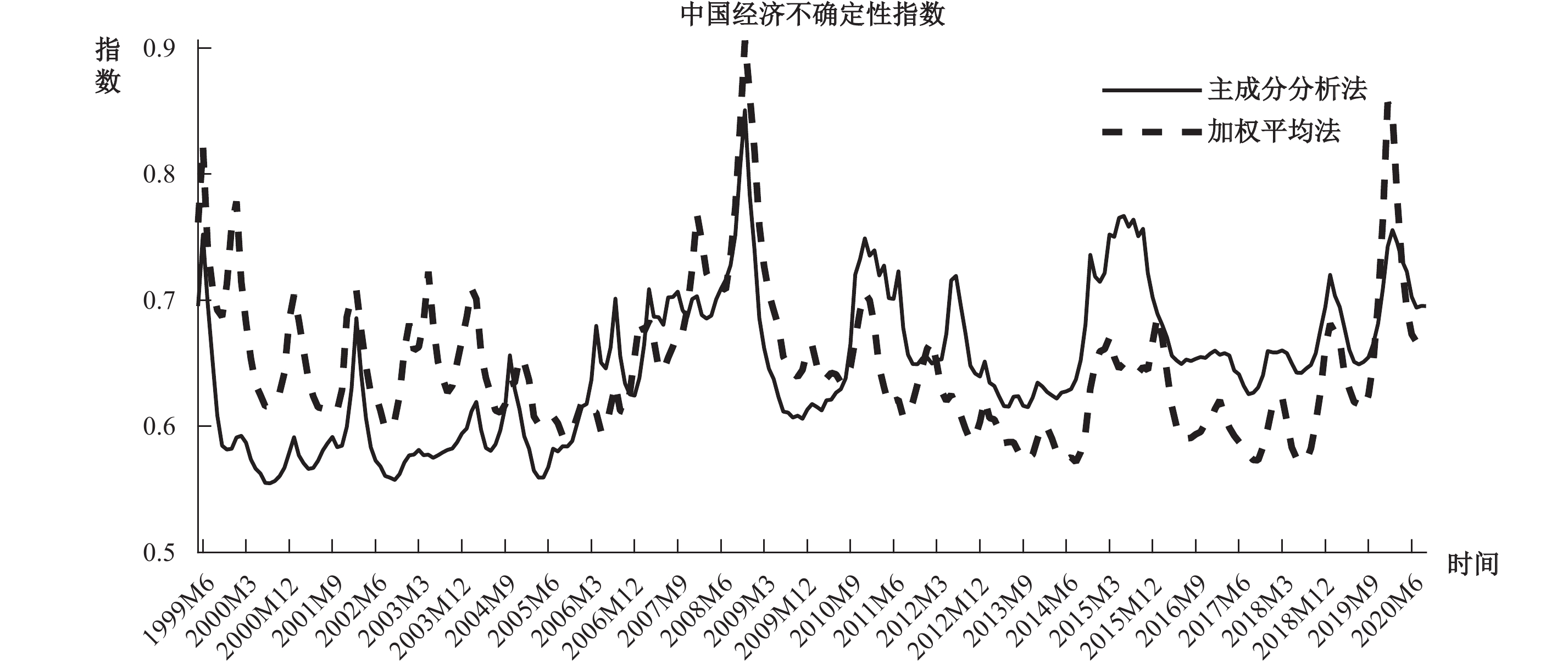
|
| 图 1 中国经济不确定性指数 |
本文选取了中国经济不确定性指数、求人倍率、通货膨胀率以及Fernald等(2014)构建的衡量中国经济波动的CCAT(China Cyclical Activity Tracker)指数。其中,通货膨胀率采用的是以2015年为基期定基处理后的CPI指数,对其进行对数一阶差分处理以使其平稳。对于求人倍率,本文同样采用一阶差分的方式使其平稳。经单位根检验后,CCAT指数和中国经济不确定性指数均为平稳序列。通货膨胀率和求人倍率的数据来源于Wind数据库,时间区间为2001年第一季度至2020年第三季度。图2为TVP-SV-VAR模型的脉冲响应图。从中可以看出,当经济不确定性上升时,产出下降,求人倍率下降,即失业率上升,通货膨胀率下降,经济面临通缩风险,这与现有相关研究结论基本一致。此外,在遭遇不确定性冲击后,经济并没有直接进入通缩状态,而是先会进入短暂的滞胀状态,然后进入通缩状态。这与朱军和蔡恬恬(2018)的结论相同,且与我国经济现实相符。2020年,在新冠肺炎疫情的冲击下,许多服务业企业开工后并没有通过降低价格来吸引大量的消费者,反而通过提高价格来弥补企业损失。因此,本文总结出的典型事实是:不确定性冲击会导致经济先进入滞胀状态,然后转向通缩状态。
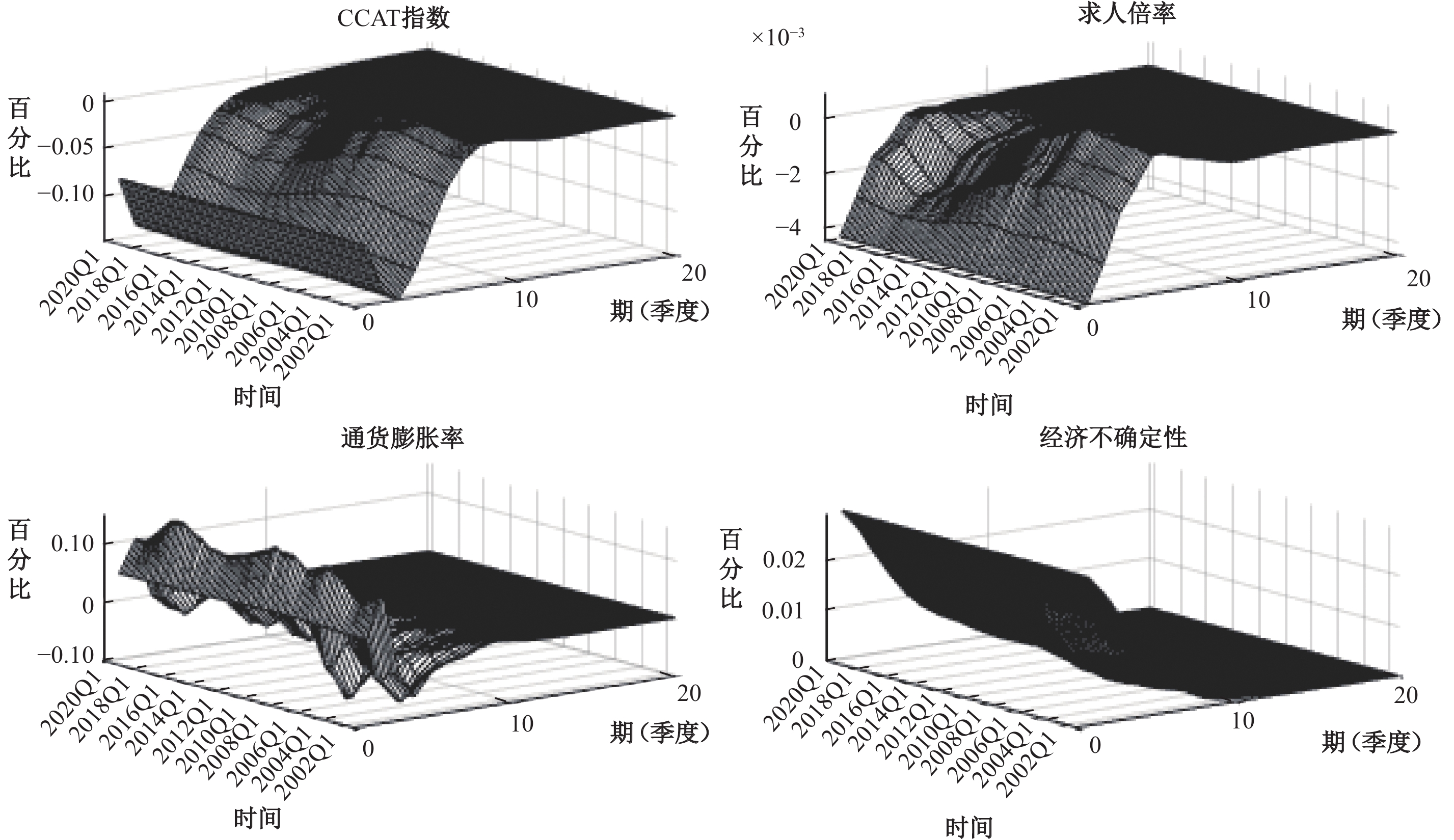
|
| 图 2 经济不确定性对宏观经济的影响 |
三、理论模型
(一)居民部门
考虑一个包含大量无限生命期居民的经济体,每个居民都有一单位的劳动禀赋。如果居民在期初被雇用,那么将无弹性地提供这一单位的劳动禀赋。每一期失业工人中会有
1. 工人。假设所有存在失业风险的工人在区间[0,1]上均匀分布,通过调整消费和储蓄来最大化总效用。工人家庭的目标函数为:
| VI,t=max{aI,t+1(N),cI,t(N)}N∈Z+[∑N≥0nI,t(N)uI,t(N)+βIE(VI,t+1)] | (1) |
其中,
为了引入借贷限制,假设工人在资本市场上为储蓄方,将根据每一期的收入进行储蓄决策。参照Challe等(2017),假设工人处于失业状态时,即
| (1+τcI)cI,t(0)+aI,t(0)⩽(1−τI,w)wt+AtRt−1/[nt(0)πt] | (2) |
其中,
| At=(1−st)nI,t−1(0)aI,t−1(0)+ft∑N⩾1aI,t−1(N)nI,t−1(N) | (3) |
其中,
| (1+τcI)cI,t(N)+aI,t(N)⩽bu+aI,t−1(N−1)Rt−1/πt | (4) |
其中,
| MI,t,t+1(0)=βIEt[(1−st+1)u'c,I,t+1(0)+st+1u'c,I,t+1(1)]/uc,I,t(0) | (5) |
处于失业状态的工人(
| MI,t,t+1(N)=βIEt[(1−ft+1)u'c,I,t+1(N+1)+ft+1u'c,I,t+1(0)]/uc,I,t(N) | (6) |
其中,
2. 企业家。假设所有企业家在区间[0,1]上均匀分布,通过调整消费和储蓄来最大化总效用。企业家的目标函数为:
| VP,t=max{aP,t+1,cP,t}N∈Z+[uP,t+βPE(VP,t+1)] | (7) |
企业家的预算约束为:
| (1+τcp)cP,t+aP,t+1⩽(1−τP,w)wP,tnP,t+aP,tRt−1/πt+Πt | (8) |
其中,
| MP,t,t+1=βPEt(u'c,P,t+1/u'c,P,t) | (9) |
(二)企业
参照Gertler和Trigari(2009),假设经济体中有四种企业类型:最终产品生产商、零售商、中间产品生产商和就业中介。
1. 最终产品生产商。最终产品生产商主要负责对零售商生产的零售品
| yt=[∫10yt(j)ε−1εdj]εε−1 | (10) |
其中,
| yt(j)=[Pt(j)/Pt]−εyt | (11) |
其中,
| Pt=[∫10Pt(j)1−εdj]11−ε | (12) |
2. 零售商。参照Calvo(1983),假定每一期零售商有
| maxEt∑∞k=0θkMP,t,t+k[P∗t(j)Pt+k−Pm,t+kPt+k]yt+k(j) | (13) |
价格分散指数为
| Δt=(1−θ)(P∗t/Pt)−ε+θ(Pt/Pt−1)εΔt−1 | (14) |
3. 中间产品生产商。假设所有中间产品生产商在区间[0,1]上均匀分布,处于完全竞争市场,他们通过雇佣劳动来生产中间产品。中间产品的生产函数为:
| ym,t=zt nt | (15) |
假定全要素生产率
4. 就业中介。就业中介同时雇用工人和企业家,将其打包后为中间产品生产商提供劳动服务。假设每一期都有一个外生的概率
| JI,t=(1−τF)pm,tzt−wt+Et[(1−ρ)MP,t,t+1JI,t+1] | (16) |
同时,假设企业家的劳动技能高于普通工人,每提供一单位劳动力可以产生
| JP,t=ψ(1−τF)pm,tzt−ψwt+Et[(1−ρ)MP,t,t+1JP,t+1] | (17) |
假定每个空缺岗位招到合意员工的概率为
| mt=μuχtυ1−χt | (18) |
其中,
| wt=wγwt−1[w(nt/n)φw]1−γw | (19) |
其中,
(三)政府部门
政府部门需要根据经济运行状况来制定财政政策和货币政策。对于财政政策,政府部门主要通过税收和发债的方式筹集资金,然后进行财政支出,本文假设财政支出只包含政府消费、失业救助和偿还原有借款。政府部门的财政预算约束为:
| cG,t+Ωbu(1−nt)+aG,tRt−1/πt⩽aG,t+1+Tt | (20) |
其中,
| \begin{array}{c}{c}_{G,t}={c}_{G}{({a}_{G,t}/{a}_{G})}^{{\varphi }_{Gb}}{({y}_{t}/y)}^{{\varphi }_{Gy}}\end{array} | (21) |
其中,
| \begin{array}{c}{R}_{t}=R{({\pi }_{t}/\pi )}^{{\varphi }_{\pi }}{({y}_{t}/y)}^{{\varphi }_{y}}{\xi }_{R,t}\end{array} | (22) |
其中,
(四)市场出清
由于所有居民面临同样的找到合意工作的概率
| {\stackrel{~}{n}}_{t}=\mathrm{\Omega }{n}_{I,t}+(1-\mathrm{\Omega })\psi {n}_{P,t} |
其中,
| \begin{array}{c}\Omega {A}_{t}+(1-\mathrm{\Omega }){a}_{P,t}+{a}_{G,t}=0\end{array} | (23) |
中间产品市场出清满足:
| \begin{array}{c}{\mathrm{\Delta }}_{t}{y}_{t}={y}_{m,t}-{\kappa }_{y}\end{array} | (24) |
最终产品市场出清满足:
| \begin{array}{c}{c}_{t}+\kappa {\upsilon }_{t}={y}_{t}\end{array} | (25) |
其中,总消费
| \begin{array}{c}{c}_{t}=\Omega [{n}_{I,t}(0){c}_{I,t}(0)+{n}_{I,t}(1){c}_{I,t}(1)+{n}_{I,t}(N){c}_{I,t}(N)]+(1-\mathrm{\Omega }){c}_{P,t}\end{array} | (26) |
四、参数校准与估计
(一)居民部门的参数校准
本文将稳态时的通货膨胀率
(二)企业部门的参数校准
本文将中间产品之间的替代弹性
(三) 政府部门的参数校准
对于财政政策,参照黄志刚和许伟(2017),我们将政府支出对政府债务的反应系数
(四)其他参数校准
对于全要素生产率和不确定性冲击的一阶自相关系数和方差,我们则选取产出、通货膨胀率和求人倍率数据,采用Born和Pfeifer(2014)矩匹配的方法,对其进行估计,使得模型所产生的方差与实际数据的方差的距离最小,数据区间为2001年第一季度至2020年第四季度。估计可得全要素生产率和不确定性冲击的一阶自相关系数分别为0.974和0.8592,全要素生产率的一阶矩冲击和不确定性冲击的方差分别为0.0022和0.7436。
五、数值模拟与机制分析
为了更好地理解不确定性影响宏观经济的传导机制,我们在上述模型的基础上,还通过舍弃工人部门构建了一个同质性居民模型,即假设经济体中只存在一种同质性的居民,其提供劳动且均为企业的所有者。③图3对比了在同质性居民模型和异质性居民模型下的不确定性对宏观经济影响的脉冲响应图。从图中可以看出,相比异质性居民模型,同质性居民模型中的产出下滑程度要更小。这主要是因为,企业家失业时不会面临借贷约束,即不存在失业风险,而不确定性冲击对这部分居民消费的影响较小,当经济体中只存在企业家这一种居民类型时,遭遇不确定性冲击后,经济体的有效需求并不会有太大的波动,这使得在同质性居民模型中,不确定性对经济的负面影响较小。从图中还可以看出,在同质性居民模型中,遭遇不确定冲击后,通货膨胀率会上升然后逐渐回归稳态,而在异质性居民模型中,通货膨胀率会先上升再下降,经济体在短期内会先面临滞胀,然后逐步进入通缩状态,异质性居民模型中的通胀反应与我们的典型事实相一致。根据这一模拟结果,我们认为短期内的滞胀主要是由企业价格调整所导致的,而长期转向通缩则是由失业风险所引发的异质性居民消费分化和有效需求下降所导致的。接下来我们将从企业价格调整和居民失业风险这两个方面来论述不确定性对宏观经济的影响机制。
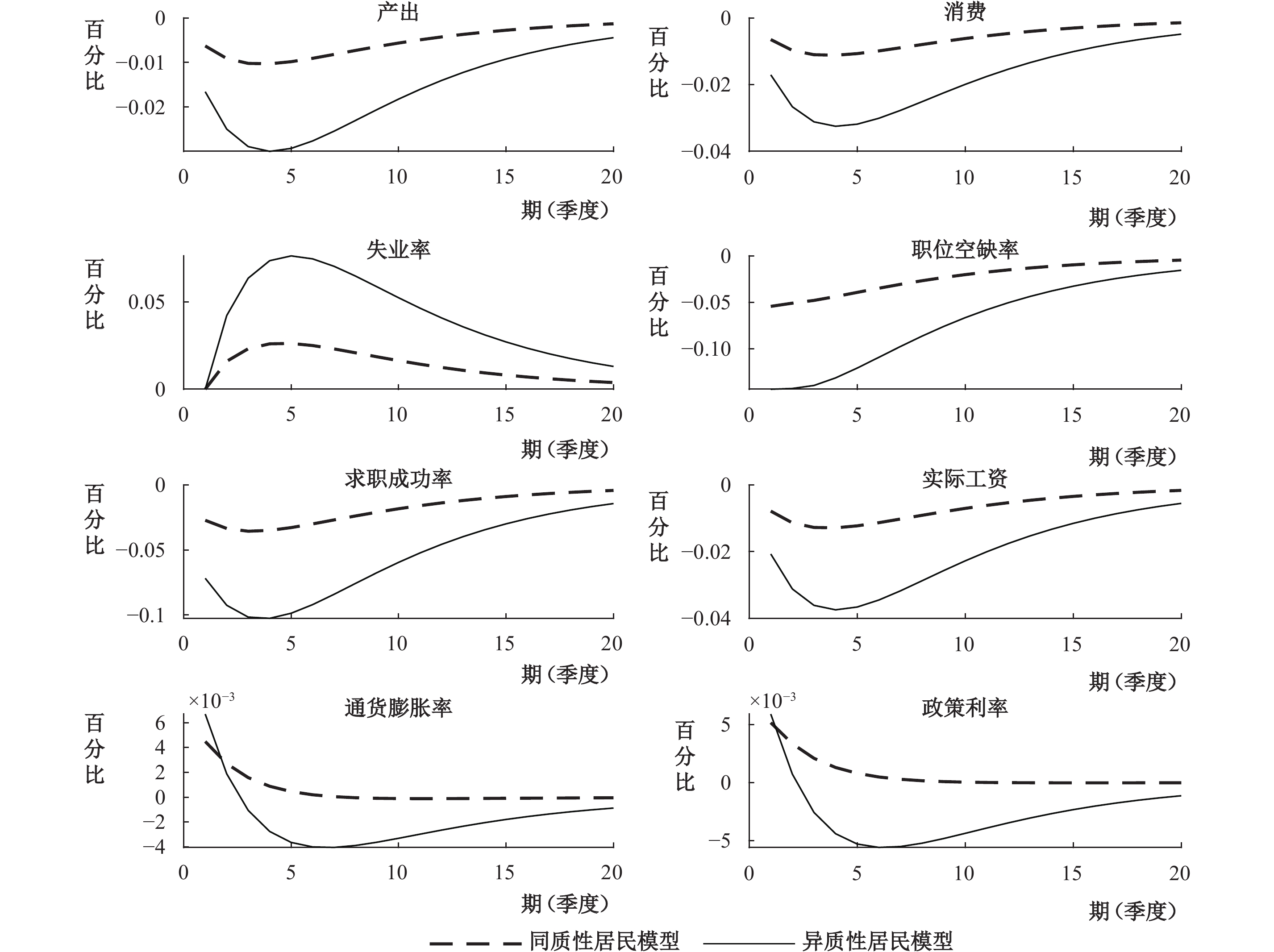
|
| 图 3 同质性居民模型和异质性居民模型下的不确定性冲击 |
(一)企业预防性定价
参考Born和Pfeifer(2021),我们利用企业在稳态时的边际利润函数来解释企业的定价决策。当企业处于确定性稳态时,根据零售商利润最大化条件,企业每一期的边际利润为:
| \begin{array}{c}{mp}_{certainty}=[(1-\varepsilon ){({P}_{certainty}^{\mathrm{*}}/P)}^{1-\varepsilon }+\varepsilon {({P}_{certainty}^{\mathrm{*}}/P)}^{-\varepsilon }{P}_{m}/P]{y}_{m}\end{array} | (27) |
而当企业处于不确定稳态时,即总价格指数存在不确定性时,企业每一期的边际利润则为:
| \begin{array}{c}{mp}_{uncertainty}=q[(1-\varepsilon ){({P}_{uncertainty}^{\mathrm{*}}/{P}^{l})}^{1-\varepsilon }+\varepsilon {({P}_{uncertainty}^{\mathrm{*}}/{P}^{l})}^{-\varepsilon }{P}_{m}/P]{y}_{m}\\ +(1-q)[(1-\varepsilon ){({P}_{uncertainty}^{\mathrm{*}}/{P}^{h})}^{1-\varepsilon }+\varepsilon {({P}_{uncertainty}^{\mathrm{*}}/{P}^{h})}^{-\varepsilon }{P}_{m}/P]{y}_{m}\end{array} | (28) |
假设在不确定状态下,价格总指数为
根据(27)式和(28)式,我们画出了在不同状态下,企业的边际利润与最优价格的关系图。从图4可以看出,企业的边际利润是最优价格的凸函数,这意味着企业在调整价格时像居民部门一样,为风险厌恶型,企业存在预防性定价动机。从企业边际利润与最优价格的关系可以发现,不确定状态下的最优价格

|
| 图 4 确定性稳态和不确定性稳态下企业边际利润与最优价格的关系图 |
为了进一步验证企业预防性定价在不确定性对宏观经济影响中所起的作用,我们模拟了在不同价格黏性系数和价格加成率下不确定性对宏观经济的影响,如图5所示。其中,
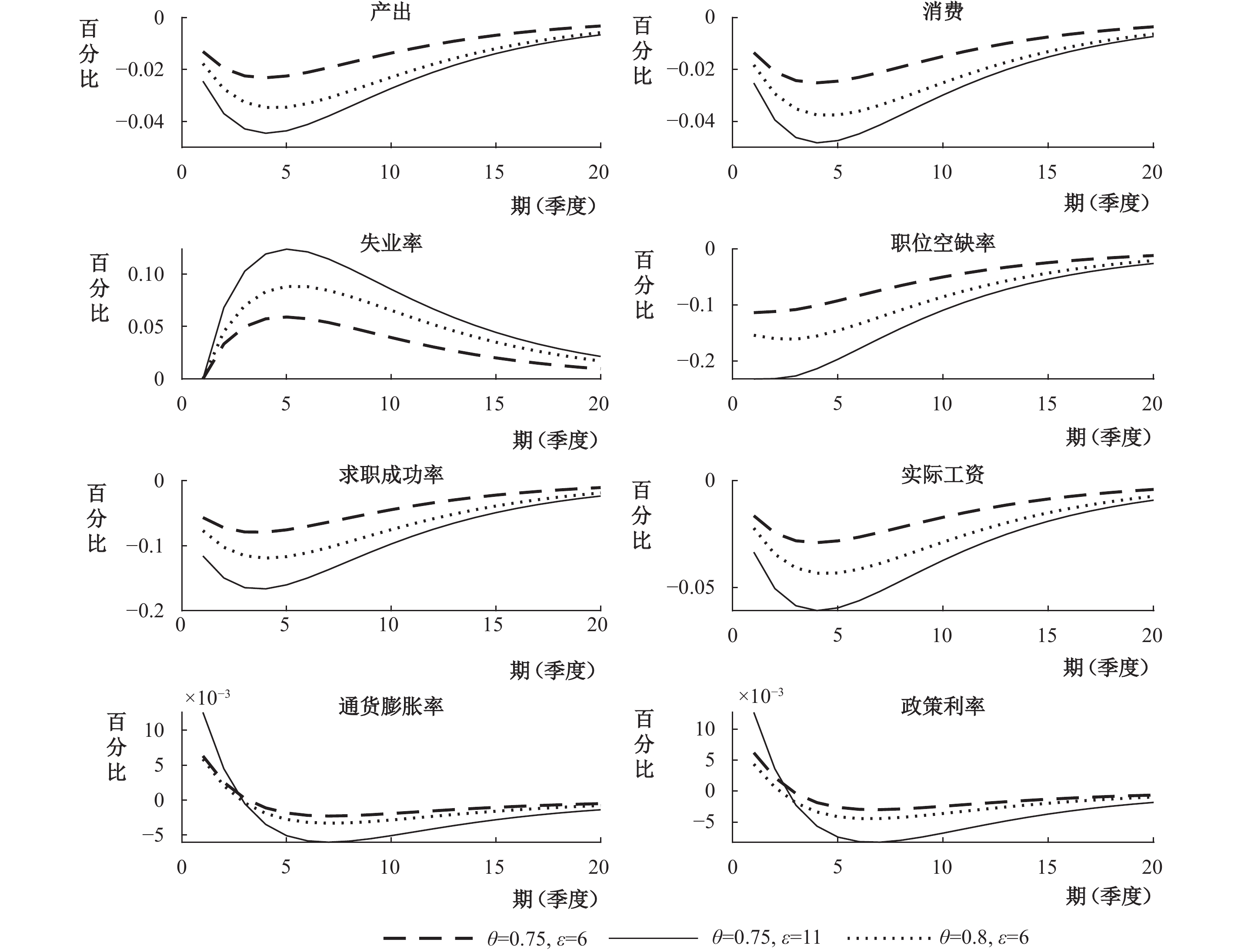
|
| 图 5 不同的价格黏性和价格加成下不确定性对宏观经济的影响 |
(二)工人失业风险
Basu和Bundick(2017)的研究表明失业率上升,会导致居民的预防性储蓄动机增强,这一点与中国遭遇新冠疫情冲击后,居民储蓄率上升相一致。但新冠疫情之后中国也出现了一些不一样的情况,根据贝恩对中国市场奢侈品的调查报告可以看出,疫情之后,中国市场对奢侈品的需求很快恢复,同时在全球奢侈品销售额下降的情况下,中国市场的奢侈品销售额实现了大幅上涨,而中国社会消费品零售总额复苏缓慢。表明中国在遭遇不确定性冲击后,居民的消费出现了一定的分化,以往的同质性居民模型在解释这一点上存在缺陷。故接下来我们将在异质性居民模型中讨论居民的失业风险。
在异质性居民模型中,处于就业状态的工人
| \begin{array}{c}{M}_{I,t,t+1}(0)={\beta }_{I}{E}_{t}\left\{(1-{s}_{t+1}){u}_{c,I,t+1}^{\mathrm{\text{'}}}[{c}_{I,t+1}(0)]+{s}_{t+1}{u}_{c,I,t+1}^{\mathrm{\text{'}}}[{c}_{I,t+1}(1)]\right\}/{u}_{c,I,t}[{c}_{I,t+1}(0)]\end{array} | (29) |
由于
| \begin{array}{c}{M}_{P,t,t+1}={\beta }_{P}{E}_{t}({u}_{c,P,t+1}^{\text{'}}/{u}_{c,P,t}^{\text{'}})\end{array} | (30) |
从(30)式可以看出,企业家的随机折现因子则与
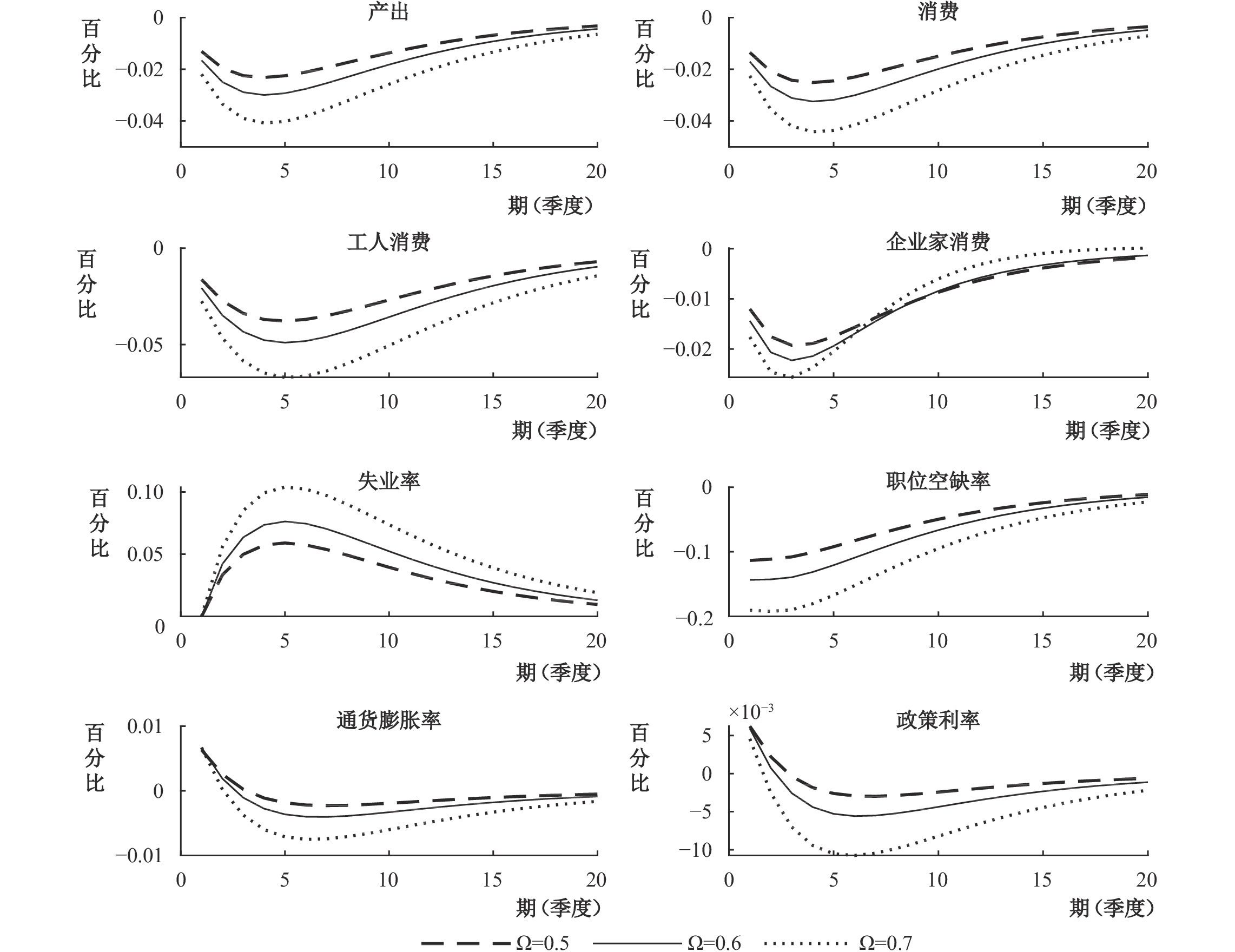
|
| 图 6 不同工人占比下不确定性对宏观经济的影响 |
六、政策及福利分析④
在弄清不确定性对宏观经济的影响机制的基础上,我们将进一步在模型中讨论货币政策和财政政策对不确定冲击的有效性。图7即为在不同的财政政策反应系数、税率和货币政策反应函数下,不确定性冲击对宏观经济影响的对比图。如图7所示,在应对不确定性冲击时,货币政策比财政政策更加有效,能够更加有效地抑制衰退,其对不同类型的居民的影响也都相似。相比之下,财政政策对不同居民则表现出一定的差异性,当财政政策反应系数
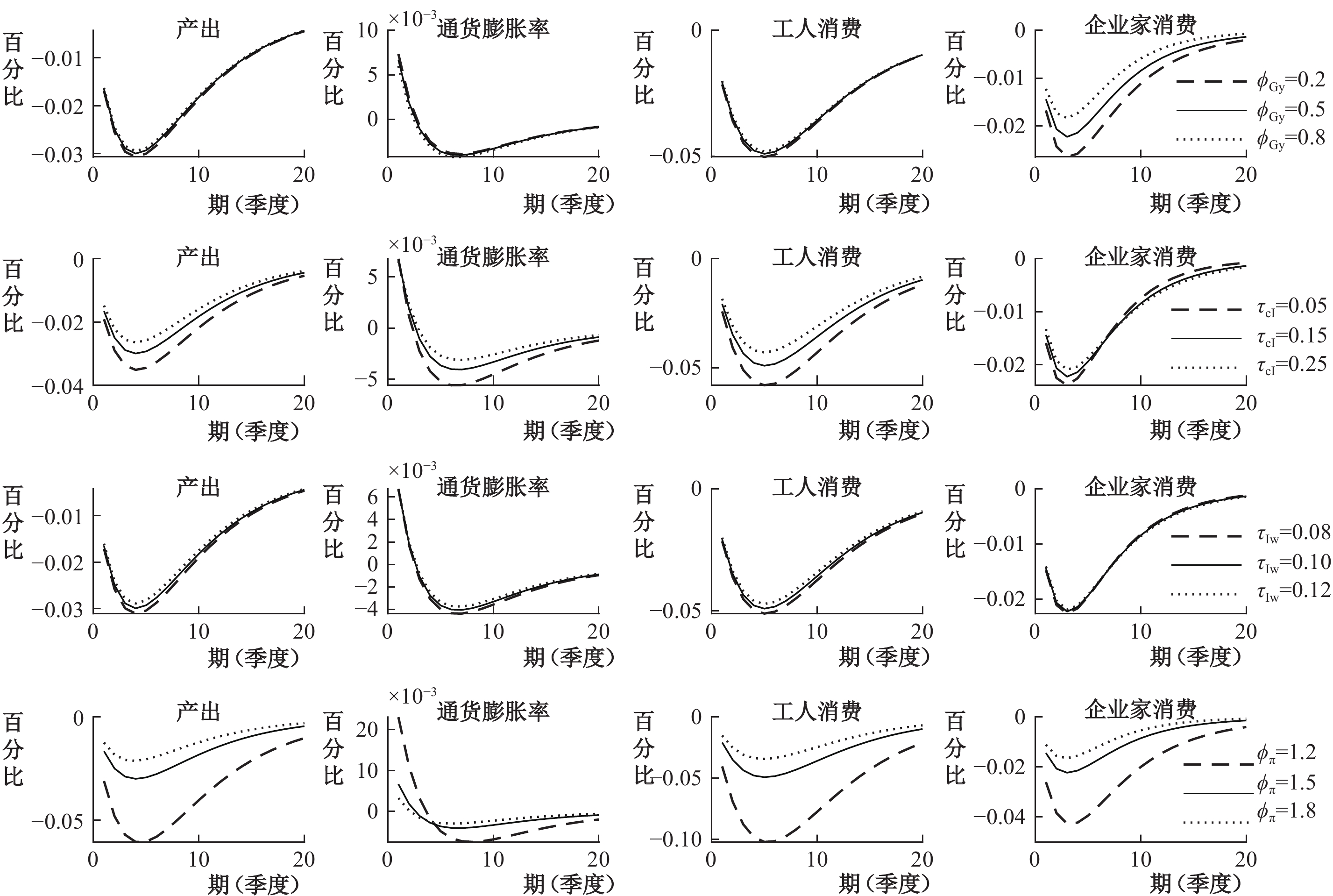
|
| 图 7 不同的财政及货币政策下不确定性对宏观经济的影响 |
在上述脉冲响应分析的基础上,我们进一步从福利分析的角度出发,分析不同政策在稳定经济和应对不确定性上所起的作用。由于调整部分税率后,模型的稳态值会发生变化,故我们根据Elekdağ和Tchakarov(2007),用无条件消费补偿变化来衡量不同类型居民福利的变化,工人和企业家的无条件消费补偿的决定方程如下:
| \begin{array}{c}E\left[{u}_{I}({c}_{I,t})\right]={u}_{I}[(1+{\mathrm{\Delta }}_{I}){c}_{I}];E\left[{u}_{P}({c}_{P,t})\right]={u}_{P}[(1+{\mathrm{\Delta }}_{P}){c}_{P}]\end{array} | (31) |
其中,
| \begin{array}{c}{L}_{wel}={E}_{0}\sum _{t=0}^{n}{\beta }_{p}^{t}\left({\widehat{\pi }}_{t}^{2}+{\lambda }_{wel}{\widehat{y}}_{t}^{2}\right)\end{array} | (32) |
其中,
根据分析结果,在遭遇不确定性冲击后,工人的福利损失要明显大于企业家的福利损失,同时在提高政府支出时,企业家的福利损失下降程度要大于工人福利损失的下降程度,这主要是因为当政府支出增加时,虽然工人可以通过就业和工资上涨来获取政策收益,但其所获得收益要远小于企业家通过企业利润获取的收益。从工人消费税的调整可以看出,当降低消费税税率后,面对不确定性冲击,社会总福利、企业家福利和工人福利下降的幅度都更大了,但是从工人和企业家在稳态时的福利来看,降低消费税后,这两者在稳态时的福利都有所提高,可见降低消费税虽然会增加经济的波动性,但也可以用于减少不确定性所导致社会福利的下降。工人所得税调整的影响机制与工人消费税的影响机制大体一致,但是所得税调整的影响力度要明显弱于消费税的影响力度,这主要是因为工人具有预防性储蓄动机,与消费税相比,调整所得税的财政支出乘数较小。与财政政策相比,货币政策对不同居民的影响则相同,能同时提高两种居民及整个社会的福利,但从数据中也可以看出,货币政策具有边际效用递减的特性,且并不能定向对某一类居民的福利进行补贴。
七、结论及政策建议
本文从企业预防性定价和居民失业风险两个方面探讨了不确定性对宏观经济的影响,研究结果表明:(1)企业的预防性定价使得经济在遭遇不确定性冲击后,在短期会陷入滞胀状态。(2)由于经济体中存在一部分居民,他们的消费支出与工资性收入息息相关,当失业风险加大时,他们的预防性储蓄动机会加大,进而会导致整个经济体的总需求不足,经济由滞胀转向通缩。(3)货币政策能够有效地缓解不确定性对经济的负面影响,财政政策能够有效缓解异质性居民之间的福利损失。
依据本文的研究结论,提出如下政策建议:第一,政府部门在应对新冠疫情等直接冲击时也需要考虑到疫情所引发的不确定性冲击,要坚持积极、稳健的货币政策,加大央行沟通,稳定市场主体信心,进而减少疫情等所带来的不确定性冲击对宏观经济的影响。第二,在不确定性冲击下,因企业预防性定价所引起的短期滞胀现象,货币政策应及时通过降准降息来减缓企业成本和稳定企业收益,进而减缓企业预防性定价的动机,从而稳定通胀。第三,在应对不确定性冲击时,财政政策可以通过定向发放消费券的方式来缓解中低收入群体的预算约束,刺激消费需求,缓解不确定冲击下的消费两极分化。第四,政府部门还需进一步加强劳动力市场建设,完善就业服务体系和建立合理的失业保险制度,进而缩短居民找工作的时间,减少未来收入的不确定性对居民消费的影响。
① 受篇幅限制,文中没有阐述具体的构建方法,可参考Jurado等(2015)。
② 受篇幅限制,与TVP-SV-VAR模型相关的设定可参考Nakajima(2011)。
③ 鉴于篇幅原因,同质性居民模型的具体设定不在文章中展示,读者可向作者索取。
④ 限于篇幅,表格分析省略,感兴趣的读者可向作者索取。
| [1] | 黄志刚, 许伟. 住房市场波动与宏观经济政策的有效性[J]. 经济研究, 2017(5): 103–116. DOI:10.3969/j.issn.1005-913X.2017.05.047 |
| [2] | 刘海波, 邵飞飞, 钟学超. 我国结构性减税政策及其收入分配效应——基于异质性家庭NK-DSGE的模拟分析[J]. 财政研究, 2019(3): 30–46. |
| [3] | 马文涛. 货币政策的数量型工具与价格型工具的调控绩效比较——来自动态随机一般均衡模型的证据[J]. 数量经济技术经济研究, 2011(10): 92–110. |
| [4] | 王博, 李力, 郝大鹏. 货币政策不确定性、违约风险与宏观经济波动[J]. 经济研究, 2019(3): 119–134. |
| [5] | 汪勇, 马新彬, 周俊仰. 货币政策与异质性企业杠杆率——基于纵向产业结构的视角[J]. 金融研究, 2018(5): 47–64. DOI:10.3969/j.issn.1009-3109.2018.05.009 |
| [6] | 许志伟, 王文甫. 经济政策不确定性对宏观经济的影响——基于实证与理论的动态分析[J]. 经济学(季刊), 2018(1): 23–50. |
| [7] | 朱军, 蔡恬恬. 中国财政、货币政策的不确定性与通货膨胀预期——基于中国财政−货币政策不确定性指数的实证分析[J]. 财政研究, 2018(1): 53–64. |
| [8] | Altig D, Baker S, Barrero J M, et al. Economic uncertainty before and during the covid-19 pandemic[J]. Journal of Public Economics, 2020, 191: 104274. DOI:10.1016/j.jpubeco.2020.104274 |
| [9] | Baker S R, Bloom N, Davis S J, et al. Covid-induced economic uncertainty[R]. Working Paper, 2020. |
| [10] | Basu S, Bundick B. Uncertainty shocks in a model of effective demand[J]. Econometrica, 2017, 85(3): 937–958. DOI:10.3982/ECTA13960 |
| [11] | Born B, Pfeifer J. Risk matters: The real effects of volatility shocks: Comment[J]. American Economic Review, 2014, 104(12): 4231–4239. DOI:10.1257/aer.104.12.4231 |
| [12] | Born B, Pfeifer J. Uncertainty-driven business cycles: Assessing the markup channel[J]. Quantitative Economics, 2021, 12(2): 587–623. DOI:10.3982/QE1297 |
| [13] | Calvo G A. Staggered prices in a utility-maximizing framework[J]. Journal of Monetary Economics, 1983, 12(3): 383–398. DOI:10.1016/0304-3932(83)90060-0 |
| [14] | Carriero A, Clark T E, Marcellino M. Measuring uncertainty and its impact on the economy[J]. The Review of Economics and Statistics, 2018, 100(5): 799–815. DOI:10.1162/rest_a_00693 |
| [15] | Challe E, Matheron J, Ragot X, et al. Precautionary saving and aggregate demand[J]. Quantitative Economics, 2017, 8(2): 435–478. DOI:10.3982/QE714 |
| [16] | Elekdağ S, Tchakarov I. Balance sheets, exchange rate policy, and welfare[J]. Journal of Economic Dynamics and Control, 2007, 31(12): 3986–4015. DOI:10.1016/j.jedc.2007.01.030 |
| [17] | Fernald J G, Spiegel M M, Swanson E T. Monetary policy effectiveness in China: Evidence from a favar model[J]. Journal of International Money and Finance, 2014, 49: 83–103. DOI:10.1016/j.jimonfin.2014.05.007 |
| [18] | Gertler M, Trigari A. Unemployment fluctuations with staggered nash wage bargaining[J]. Journal of Political Economy, 2009, 117(1): 38–86. DOI:10.1086/597302 |
| [19] | Jurado K, Ludvigson S C, Ng S. Measuring uncertainty[J]. American Economic Review, 2015, 105(3): 1177–1216. DOI:10.1257/aer.20131193 |
| [20] | Katayama M, Kim K H. Uncertainty shocks and the relative price of investment goods[J]. Review of Economic Dynamics, 2018, 30: 163–178. DOI:10.1016/j.red.2018.05.003 |
| [21] | Mumtaz H, Theodoridis K. The international transmission of volatility shocks: An empirical analysis[J]. Journal of the European Economic Association, 2015, 13(3): 512–533. DOI:10.1111/jeea.12120 |
| [22] | Oh J, Picco A R. Macro uncertainty and unemployment risk[R]. Working Paper, 2020. |
| [23] | Petrongolo B, Pissarides C A. Looking into the black box: A survey of the matching function[J]. Journal of Economic Literature, 2001, 39(2): 390–431. DOI:10.1257/jel.39.2.390 |
| [24] | Ravn M O, Sterk V. Job uncertainty and deep recessions[J]. Journal of Monetary Economics, 2017, 90: 125–141. DOI:10.1016/j.jmoneco.2017.07.003 |


