一、引 言
近几十年来,中国的经济总量显著增长,经济体制改革不断推进。20世纪90年代前后,中国政府确立“抓大放小”政策,在维持重要产业国家资本支配地位的同时,整合和兼并上游产业中的国企,在下游产业中对民营企业敞开大门,逐渐形成了上游产业内国有企业为主导、下游产业内民营企业为主的“垂直结构”(刘瑞明和石磊,2011;Li等,2015;王勇,2017;陈小亮和陈伟泽,2017;钱学锋等,2019)。中国上下游产业的垂直结构有几个特征:第一,占比不同,从比重来看,中国国有企业主要集中在上游产业,而下游产业以民营企业为主;第二,市场结构不对称,上游产业的行政垄断现象更突出,下游产业的进入壁垒则更低,竞争性更强,从行业集中度来看,上游产业的行业集中度明显高于下游产业(陈小亮和陈伟泽,2017);第三,出口占产出比重不对称,上游产业出口比例低于下游产业。
2021年1月27日,国务院国有企业改革领导小组第五次会议对本年度国企改革进行了部署,继续做强做优做大国有资本和国有企业。做强做优做大国有企业,必须考虑其在垂直结构中所起的作用和与其关系密切的民营企业,避免加剧垂直结构下政策实施所带来的市场扭曲。在垂直结构下,下游民营企业对中间品及服务的蓬勃需求将不断巩固上游国有企业在所处产业中的主导地位,下游民企和上游国企可以说是一荣俱荣的关系。但这种生产关系的存在会导致上游国有企业凭借垄断定价抬高中间品价格,加大下游民营企业生产成本,抑制民营企业数量的扩张,最终扭曲市场,降低社会福利。从长远来看,随着经济形势的变化,对下游民营企业异质性产品的内外需若减少,上游国企利用垄断地位从下游民企生产中获得的利润也将逐步减少,这一模式将难以为继。为深入推进国企改革进程,有必要积极开展垂直结构的相关研究,寻求提升垂直结构下提高社会福利的针对性措施,为当今国企改革贡献思路和方向。
在Melitz(2003)的基础上,本文建立了一个上游国企垄断、下游异质性民企垄断竞争的垂直结构模型,之后在模型中分别嵌入上游“竞争自由化”和“上游征税、下游补贴”政策,并比较不同产业政策下的社会福利。研究发现:垂直结构的存在会导致上游国有企业垄断定价和下游民营企业进入不足,降低总体社会福利;进一步通过数值模拟的方法,定量分析了两种产业政策对垂直结构下社会福利的影响。数值结果表明,上游“竞争自由化”政策和“上游征税、下游补贴”政策都可以提高下游民营企业数量和社会福利,而“上游征税、下游补贴”政策下,上游国企的利润也会因为下游企业数量和中间品需求的增加而提高。因此,两种产业政策都具备有效性,但“上游征税、下游补贴”政策更具有现实可行性,并且一定的征税率和补贴率的组合可以提高上游“竞争自由化”政策下的社会福利水平。
本文的研究与产业政策及其对垂直结构的影响相关。作为一国经济发展过程中促进产业发展的重要手段,产业政策越来越受到广泛关注。关于产业政策的必要性,学界持续存在着一定的争议,主要分为支持与反对两派学者。一方面,支持实施产业政策的学者认为,虽然产业政策实施可能会伴随激励机制不通畅、信息不对称、政府间利益博弈等问题,但产业政策能为促进企业创新、增加企业投资、提高融资效率、加快产业升级调整等起到不可或缺的作用(陈冬华等,2010;余明桂等,2010;张纯和潘亮,2012;宋凌云和王贤彬,2013;黎文靖和李耀淘,2014)。另一方面,反对派的学者认为产业政策对产业乃至整个经济的发展并无益处,政府干预甚至会造成资源错配现象,降低经济运行效率(Krugman,1983;程俊杰,2015;王克敏等,2017)。除了对产业政策必要性的研究,学者们还对中国产业政策的有效性进行了充分研究,中国的产业政策逐渐非本意地演变成一种国有偏向型政策,即由于在政策推行过程中出现信息不对称、激励不相容等问题,国有企业实际上比民营企业获得了更多政策优惠,带来资源分配扭曲和企业生产率降低,阻碍了民营企业的进一步发展(Bergoeing等,2002;Hsieh和Klenow,2009;Brandt和Zhu,2010;余明桂等,2010;邵敏和包群,2011;罗德明等,2012;刘瑞明,2012;孔东民等,2013;钱学锋等,2016)。
目前,对垂直结构下产业政策进行研究的文献较为稀缺,钱学锋等(2019)的研究是这一领域的代表性文章之一。他们发现“上游征税、下游补贴”政策才是垂直结构下的良策,而不是现阶段的“交互补贴”政策。总的来看,现有文献对产业政策的必要性和有效性进行了一定的研究,但对垂直结构以及这一结构下实施的产业政策关注不多,相关研究领域较为空白,有待进一步丰富和拓展。
此外,为研究垂直结构对社会福利的影响,学者们分别构建了“上游国企垄断、下游民企自由竞争”(Li等,2015;陈小亮和陈伟泽,2017)、“上游国企寡头竞争、下游民企自由竞争”(刘瑞明和石磊,2011)、“上游国企寡头竞争、下游民企垄断竞争”(钱学锋等,2019)三种模型,模拟垂直结构下的生产者和消费者决策。研究发现,垂直结构会导致上游中间品价格过高和下游民企进入不足,引致社会福利损失。目前的理论文章中,下游民企都是同质的,尚未有研究将下游企业异质性特征引入垂直结构模型进行定量分析,而下游异质性企业的假设更符合中国的现实,也能更好模拟现实情况。
针对垂直结构下产业政策对社会福利影响的研究主要聚焦在上游“竞争自由化”和“上游征税,下游补贴”两种产业政策上。上游“竞争自由化”政策,即引入上游市场竞争有助于削弱上游国企垄断地位,增加下游民企数量,降低中间品价格,最终增进社会福利(刘瑞明和石磊,2011)。同时,相较于中国现行的“交互补贴”政策,“上游征税,下游补贴”政策也能够一定程度上减缓资源错配,促进上游国有企业的利润再分配,提高社会福利水平(钱学锋等,2019)。虽然现有文献已经得出上述结论,但未有学者将两种产业政策及对社会福利的提升效果进行比较。本文在这些文献的基础上将深入研究垂直结构及相关的产业政策对社会福利的影响,通过基于中国数据的参数校准,量化分析产业政策的有效性,根据现实考虑产业政策的可行性,为未来中国在垂直结构下制定合理的产业政策和促进社会福利水平提升提供了理论支撑和思考方向。
本文通过构建垂直结构的理论模型,定量分析垂直结构下各类企业的生产行为以及总体社会福利,并将上游“竞争自由化”和“上游征税、下游补贴”政策分别嵌入模型,讨论两种产业政策对垂直结构下各类企业的生产行为以及总体社会福利产生的影响。本文可能的创新之处体现在以下几个方面:第一,通过构建模型对垂直结构进行了理论补充,并将两种不同的产业政策引入模型,定量研究了垂直结构本身以及相关的产业政策的影响;第二,在下游市场引入了异质性企业特征,采用Melitz(2003)提出的异质性企业模型,假设下游市场由异质性民营企业构成并进行垄断竞争,更好地模拟了中国现实;第三,在模型基础上利用中国现实数据进行了参数校准,通过数值模拟和一系列稳健性检验,定量分析了垂直结构下的社会福利,并对两种产业政策的政策效应进行了定量比较,丰富了垂直结构在产业政策方面的理论研究。本文的研究对于在垂直结构下促进形成合理的生产结构,积极发挥产业政策助力国有企业和民营企业发展,提高总体社会福利,赋予新时代国企改革新内涵具有重要的现实意义。
本文余下的结构安排如下:第二部分构建垂直结构下的基准模型;第三部分分别引入两种产业政策进行理论模型的拓展;第四部分在参数校准的基础上,利用数值模拟方法,定量研究垂直结构下的社会福利和产业政策的政策效应;第五部分总结全文,得到研究结论与政策建议。
二、垂直结构下的基准模型
(一)模型设定
基于中国上下游产业的垂直结构特征,本文借鉴Melitz(2003)提出的异质性企业垄断竞争模型,构建了一个上游国有企业垄断、下游异质性民营企业进行垄断竞争的基准模型。假设总体经济分为农业部门和非农业部门。其中,农业部门生产同质农产品
$C_n $
;非农业部门包括上游国有企业和下游异质性民营企业,其中上游国有企业生产中间品
${X_u}$
,下游由连续的异质性民营企业组成,通过从上游国有企业购买中间品以生产非农品
${C_d}\left( \varphi \right)$
,并复合成最终品
${C_d}$
。下游民营企业进入市场生产异质性产品,将承担一个固定生产成本
$f$
和进入成本
${f_e}$
,并依据自身的生产率
$\varphi $
及可能实现的利润进行生产决策。
代表性消费者通过购买同质农产品和下游异质性产品复合生成的最终品获得效用,且效用函数为:
|
$ U\left( {{C_n},{C_d}} \right) = {C_n} + \frac{\varepsilon }{{\varepsilon - 1}}{C_d}^{\frac{{\varepsilon - 1}}{\varepsilon }},\;\; \varepsilon > 1 $
|
(1) |
其中,
${C_n}$
和
${C_d}$
分别是农产品和下游异质性产品的消费量,假设是非负的,
$\varepsilon $
是对下游异质性产品的需求价格弹性,且
$\varepsilon > 1$
。
${C_d}$
由下游不同异质性产品
${C_d}\left( \varphi \right)$
复合而成,即:
|
$ {C_d} = {\left( {\int_1^\infty {{C_d}^{\frac{{\sigma - 1}}{\sigma }}\left( \varphi \right)d\varphi } } \right)^{\frac{\sigma }{{\sigma - 1}}}},\;\; \sigma > 1 $
|
(2) |
其中,
${C_d}\left( \varphi \right)$
代表每个异质性企业的产出,对应的每一下游异质性产品价格为
$P_d^{}\left( \varphi \right)$
;
$\varphi $
为下游异质性企业进入市场后随机获得的企业生产率,服从Pareto分布,分布函数为
$G\left( \varphi \right) = 1 - {\varphi ^{ - \gamma }}$
,
$\varphi \in \left[ {1,\infty } \right]$
,
$\gamma > \sigma - 1$
,
$\sigma $
为不同异质性产品之间的替代弹性,假设
$\sigma > 1$
。
再根据消费者效用最大化,求出每一个异质性产品的需求函数
${C_d}\left( \varphi \right)$
满足下式:
|
$ {C_d}\left( \varphi \right) = {\left( {\frac{{{P_d}\left( \varphi \right)}}{{{P_d}}}} \right)^{ - \sigma }}{\left( {\frac{1}{{{P_d}}}} \right)^\varepsilon } $
|
(3) |
作为生产者,上游国企在生产过程中每投入1单位的劳动力就能生产
$\eta $
单位的中间品,将该中间品的产量记为
${X_u}$
,对应中间品价格为
${P_u}$
;下游民企在生产时投入劳动力
$l$
和中间品
${X_u}$
,生产出异质性产品
${C_d}\left( \varphi \right)$
,再经复合构成最终品
${C_d}$
。
这一封闭经济体中,农业部门和上游国有企业仅利用劳动力
$l$
进行生产,而下游生产的投入要素既包括劳动力
$l$
,还包括上游生产的中间品
${X_u}$
。因此,将每一个下游异质性企业的生产函数设定为:
|
$ {C_d}\left( \varphi \right) = \varphi {X_u^\alpha} \left( \varphi \right){l^{1 - \alpha }}\left( \varphi \right) $
|
(4) |
其中,
$\alpha $
为中间品成本占下游企业收入的份额,
$1 - \alpha $
为劳动力成本占下游企业收入的份额。根据下游异质性产品的复合形式,可得下游异质性产品部门的价格总指数为:
|
$ {P_d} = {\left( {\int_1^\infty {{P_d^{1 - \sigma }}\left( \varphi \right)d\varphi } } \right)^{\frac{1}{{1 - \sigma }}}},\quad \varphi \in \left[ {1,\infty } \right] $
|
(5) |
其中,
${P_d}\left( \varphi \right)$
代表每一异质性产品的价格。
(二)基准模型的社会福利
首先,对下游民营企业的生产行为进行讨论。类似Romalis(2004)和Bernard等(2007)的做法,我们假设固定生产成本
$f$
是用劳动力和中间品来支付的,且要素密集度与下游异质性产品的生产函数相同,劳动力工资水平为
$w$
,因此每一下游民营企业成本函数
$\tau \left( \varphi \right)$
为:
|
$ \tau \left( \varphi \right) = \left( {f + \frac{{{C_d}\left( \varphi \right)}}{\varphi }} \right)\frac{{{P_u^\alpha} {w^{1 - \alpha }}}}{B} $
|
(6) |
其中,
$B = {\alpha ^\alpha }{\left( {1 - \alpha } \right)^{\left( {1 - \alpha } \right)}}$
,由此可计算得出厂商利润最大化条件下的加成定价
$P_d^{}\left( \varphi \right)$
和每一个下游民营企业的利润函数
${{\text π} _d}\left( \varphi \right)$
。下游企业利润最大化的定价和利润为:
|
$ {P_d}\left( \varphi \right) = \left( {\frac{\sigma }{{\sigma - 1}}} \right)\left( {\frac{{{P_u^\alpha }{w^{1 - \alpha }}}}{{\varphi B}}} \right) $
|
(7) |
|
$ {{\text π} _d}\left( \varphi \right) = \frac{1}{\sigma }{P_d}\left( \varphi \right){C_d}\left( \varphi \right) - \frac{{{P_u^\alpha} {w^{1 - \alpha }}f}}{B} $
|
(8) |
异质性企业进入市场需要支付一定的进入成本
${f_e}$
,同样地,假设该进入成本是用劳动力和中间品来支付的,因此企业市场进入成本为
${P_u^\alpha} {w^{1 - \alpha }}{f_e}/B$
。
对垄断竞争市场中的零利润条件进行讨论。下游市场中,企业进入市场时的自身生产率
$\varphi $
与企业的利润成正比,而当企业实现的利润小于0时企业会决定退出市场,因此可知存在一个生产率临界值
$\bar \varphi $
,此时
${\text π}\left( {\bar \varphi } \right) = 0$
,企业的生产率一旦低于该值就会选择退出市场。将
$\bar \varphi $
代入下游企业利润函数可得,这一最低生产率
$\bar \varphi $
应满足以下条件:
|
$ {\text π} \left( {\bar \varphi } \right) = \frac{1}{\sigma }{P_d}\left( {\bar \varphi } \right){C_d}\left( {\bar \varphi } \right) - \frac{{{P_u}^\alpha {w^{1 - \alpha }}f}}{B} = 0 $
|
(9) |
根据垄断竞争市场中的自由进入条件,进入市场的企业所获得的期望利润应等于企业进入市场的成本
${P_u}^\alpha {w^{1 - \alpha }}{f_e}/B$
,意味着下列等式成立:
|
$ \left[ {1 - G\left( {\bar \varphi } \right)} \right]{\text π} \left( {\tilde \varphi } \right) = \frac{{{P_u}^\alpha {w^{1 - \alpha }}{f_e}}}{B} $
|
(10) |
其中,
$G\left( \varphi \right)$
是生产率的分布函数,
$\left[ {1 - G\left( {\bar \varphi } \right)} \right]$
为企业生产率大于最低生产率
$\bar \varphi $
的概率,也是企业成功进入市场的概率;
$\tilde \varphi $
、
${\text π} \left( {\tilde \varphi } \right)$
分别是下游市场中异质性产品生产企业的平均生产率和平均利润,且企业平均生产率
$\tilde \varphi $
满足以下等式:
|
$ \tilde \varphi = {\left[ {\int_{\bar \varphi }^\infty {{\varphi ^{\sigma - 1}}\frac{{g\left( \varphi \right)}}{{1 - G\left( {\bar \varphi } \right)}}d\varphi } } \right]^{\frac{1}{{\sigma - 1}}}} = {\left( {\frac{\gamma }{{\gamma - \sigma + 1}}} \right)^{\frac{1}{{\sigma - 1}}}}{\left[ {\left( {\frac{{\sigma - 1}}{{\gamma - \sigma + 1}}} \right)\frac{f}{{{f_e}}}} \right]^{\frac{1}{\gamma }}} $
|
此时下游异质性非农产品价格指数为:
|
$ {P_d} = {\left[ {\int_{\bar \varphi }^\infty {M{P_d}^{1 - \sigma }\left( \varphi \right)\frac{{g\left( \varphi \right)}}{{1 - G\left( {\bar \varphi } \right)}}d\varphi } } \right]^{\frac{1}{{1 - \sigma }}}} $
|
(11) |
其中,
$M$
为内生决定的下游异质性企业数量,
$g\left( \varphi \right)$
为概率密度函数。上式可简化成下面关于下游企业数量
$M$
和平均生产率
$\tilde \varphi $
的等式:
|
$ {P_d} = {M^{\frac{1}{{1 - \sigma }}}}{P_d}\left( {\tilde \varphi } \right) $
|
(12) |
把上述公式代入式(9),可以得到企业数量
$M$
的表达式:
|
$ M = {\left[ {\frac{{\sigma f}}{\Omega }{{\left( {\frac{{{P_u}^\alpha {w^{1 - \alpha }}}}{B}} \right)}^\varepsilon }} \right]^{\frac{{1 - \sigma }}{{\sigma - \varepsilon }}}} $
|
(13) |
其中,
$\Omega = {\left( {\dfrac{\sigma }{{\sigma - 1}}} \right)^{1 - \varepsilon }}{\left( {\dfrac{\gamma }{{\gamma - \sigma + 1}}} \right)^{\frac{{\varepsilon - \sigma }}{{\sigma - 1}}}}{\left[ {\dfrac{{\left( {\sigma - 1} \right)f}}{{\left( {\gamma - \sigma + 1} \right){f_e}}}} \right]^{\frac{{\varepsilon - 1}}{\gamma }}}$
,假设
$\sigma > \varepsilon $
。
由上式可知,中间品价格
${P_u}$
和劳动力工资
$w$
实际上与下游企业数量M都成反比关系。从直觉上看,
${P_u}$
或
$w$
越高,下游异质性产品的生产成本就越高,企业获得的利润就越少,最终会导致进入市场的下游企业数量M减少。
再对上游国有企业的生产行为进行讨论。此时,上游国有企业的中间品总需求
${D_u}$
为:
|
$ {D_u} = \int_{\bar \varphi }^\infty {M{X_u}} \left( \varphi \right)\frac{{g\left( \varphi \right)}}{{1 - G\left( {\bar \varphi } \right)}}d\varphi $
|
(14) |
将每一异质性企业的中间品需求
${X_u}\left( \varphi \right)$
代入上述等式,得出下式:
|
$ {D_u} = {P_u}^{\left[ {\frac{{\alpha \sigma \left( {1 - \varepsilon } \right)}}{{\sigma - \varepsilon }} - 1} \right]}\Lambda $
|
(15) |
其中,
$\Lambda = {\left[ {\dfrac{{\sigma f}}{\Omega }{{\left( {\dfrac{{{w^{1 - \alpha }}}}{B}} \right)}^\varepsilon }} \right]^{\frac{{1 - \sigma }}{{\sigma - \varepsilon }}}}{\left( {\dfrac{{\alpha w}}{{1 - \alpha }}} \right)^{1 - \alpha }}\left( {\sigma - 1} \right)f\left( {\dfrac{\gamma }{{\gamma - \sigma + 1}}} \right)$
。
上游国有企业仅投入劳动力进行中间品生产活动,且1单位的劳动力可以生产
$\eta $
单位的中间品,所以平均生产成本为
$w/\eta $
,由此,国有企业的利润函数为:
|
$ {{\text π}_u} = \left( {{P_u} - \frac{w}{\eta }} \right){D_u} $
|
根据上游国有企业利润最大化条件,得出中间品价格
${P_u}$
和利润
${{\text π} _u}$
分别为:
|
$ {P}_{u}=\left[\frac{\alpha \sigma \left(\epsilon -1\right)+\sigma -\epsilon }{\alpha \sigma \left(\epsilon -1\right)}\right]\frac{w}{\eta }\text{,}\;\;{{\text π} }_{u}=\left[\frac{\sigma -\epsilon }{\alpha \sigma \left(\epsilon -1\right)}\right]\frac{w}{\eta }{D}_{u} $
|
(16) |
此时,中间品价格
${P_u}$
为上游垄断国企的定价,加成因子
$\left[ {\alpha \sigma \left( {\varepsilon - 1} \right) + \sigma - \varepsilon } \right]/\left[ {\alpha \sigma \left( {\varepsilon - 1} \right)} \right]$
大于1,与中间品成本占下游企业收入份额
$\alpha $
、异质企业替代弹性
$\sigma $
和异质性产品需求价格弹性
$\varepsilon $
相关,具体为加成因子与
$\alpha $
、
$\sigma $
正相关,与
$\varepsilon $
负相关。
据前文得出的垂直结构均衡状态下的上下游定价及上游国企垄断利润
${{\text π} _u}$
,可以计算出此时的社会福利
$W$
,即生产者剩余
$PS$
与消费者剩余
$CS$
的加总。其中,生产者剩余
$PS$
仅包括上游国企的垄断利润(下游异质性企业利润为零),即
$W = CS + {{\text π}_u}$
。
通过推导得出:
|
$ \begin{gathered} {C_d} = {\left[ {\int_{\bar \varphi }^\infty {M{C_d}^{\frac{{\sigma - 1}}{\sigma }}\left( \varphi \right)\frac{{g\left( \varphi \right)}}{{1 - G\left( {\bar \varphi } \right)}}d\varphi } } \right]^{\frac{\sigma }{{\sigma - 1}}}} = {M^{\frac{{ - \varepsilon }}{{1 - \sigma }}}}{P_d}^{ - \varepsilon }\left( {\tilde \varphi } \right) \hfill \\ \;\quad = \sigma {f^{\frac{{ - \varepsilon }}{{\sigma - \varepsilon }}}}{\left( {\frac{\sigma }{{\sigma - 1}}} \right)^{\frac{{\varepsilon (1 - \sigma )}}{{\sigma - \varepsilon }}}}{\left( {\frac{{{P_u}^\alpha {w^{1 - \alpha }}}}{B}} \right)^{\frac{{ - \sigma \varepsilon }}{{\sigma - \varepsilon }}}}{\left[ {\left( {\frac{{\sigma - 1}}{{\gamma - \sigma + 1}}} \right)\frac{f}{{{f_e}}}} \right]^{\frac{{\varepsilon (1 - \sigma )}}{{\gamma \left( {\sigma - \varepsilon } \right)}}}} \hfill \\ \end{gathered} $
|
(17) |
|
$ CS = I - {P_d}{C_d} + \frac{\varepsilon }{{\varepsilon - 1}}{C_d}^{\frac{{\varepsilon - 1}}{\varepsilon }} = I + \frac{1}{{\varepsilon - 1}}{M^{\frac{{1 - \varepsilon }}{{1 - \sigma }}}}{P_d}^{1 - \varepsilon }\left( {\tilde \varphi } \right) $
|
(18) |
因此,可以得出均衡状态下的社会福利
$W$
为:
|
$ W = CS + {{\text π} _u} = I + \frac{1}{{\varepsilon - 1}}{M^{\frac{{1 - \varepsilon }}{{1 - \sigma }}}}{P_d}^{1 - \varepsilon }\left( {\tilde \varphi } \right) + \left[ {\frac{{\sigma - \varepsilon }}{{\alpha \sigma (\varepsilon - 1)}}} \right]\frac{w}{\eta }{P_u}^{\left[ {\frac{{\alpha \sigma (1 - \varepsilon )}}{{\sigma - \varepsilon }} - 1} \right]}\Lambda $
|
(19) |
此时,对社会福利进行比较静态分析,可以得到
$\dfrac{{\partial W}}{{\partial M}} = \dfrac{{\partial CS}}{{\partial M}} + \dfrac{{\partial {{\text π} _u}}}{{\partial M}} > 0$
。这意味着随着下游产业民营企业数量M的增加,消费者剩余
$CS$
以及社会福利
$W$
也会增加。这是由于垂直结构下,上游国有企业凭借垄断地位抬高了中间品定价,从下游民营企业攫取了一部分利润,使得下游出现民营企业进入不足的现象,造成了社会福利损失。综上所述,得到以下结论:
结论1:在垂直结构的基准模型下,随着下游民营企业数量的增加,消费者剩余和社会福利水平也会增加,此时存在下游民营企业进入不足的现象。
三、垂直结构下的产业政策
(一)上游“竞争自由化”政策
首先,本文考虑在模型中引入一种放开上游市场进入门槛、消除国企在上游垄断地位的产业政策,即上游“竞争自由化”政策,研究在上游市场自由竞争的理想化情况下的社会福利改善情况。上游“竞争自由化”,也就是使上游国企的中间品定价等于中间品的平均生产成本
$w/\eta $
,并求出相应的社会福利
${W_1}$
。此时下游企业数量
${M_1}$
满足下式:
|
$ {M_1} = {\left[ {\frac{{\sigma f}}{\Omega }{{\left( {\frac{w}{{{\eta ^\alpha }B}}} \right)}^\varepsilon }} \right]^{\frac{{1 - \sigma }}{{\sigma - \varepsilon }}}} $
|
(20) |
由于基准模型下的中间品价格高于平均成本,可以得出
${P_{u1}} < {P_u}$
;进一步地,可以得到
${M_1} > M$
,下游民营企业数量在上游自由化政策实施后有所增加,一定程度上缓解了垂直结构导致的下游民营企业进入不足。经过模型推导,最终得到垂直结构下实施上游“竞争自由化”政策的社会福利
${W_1}$
满足:
${W_1} = C{S_1} = I + \dfrac{1}{{\varepsilon - 1}}{M_1}^{\frac{{1 - \varepsilon }}{{1 - \sigma }}}{P_d}{_1^{^{1 - \varepsilon }}}\left( {\tilde \varphi } \right) = I + \dfrac{1}{{\varepsilon - 1}}{\left( {\sigma f} \right)^{\frac{{1 - \varepsilon }}{{\sigma - \varepsilon }}}}{\left( {\dfrac{w}{{{\eta ^\alpha }B}}} \right)^{\frac{{\sigma \left( {1 - \varepsilon } \right)}}{{\sigma - \varepsilon }}}}\left( {\frac{\gamma }{{\gamma - \sigma + 1}}} \right){\Omega ^{\frac{{\sigma - 1}}{{\sigma - \varepsilon }}}}$
(二)“上游征税、下游补贴”政策
下面考虑将“上游征税、下游补贴”政策引入垂直结构模型的情况。政府对上游国企征税率为
$t$
,
$t \in \left( {0,1} \right)$
;对下游每个异质性民营企业的补贴率为
$s$
,
$s \in \left( {0,1} \right)$
。根据政府预算收支平衡,令对上游国有企业的总征税额恒等于对下游民营企业的总补贴额,有:
|
$ \begin{gathered} t{P_{u2}}{D_{u2}} = s{P_{d2}}{C_{d2}} \hfill \\ t{P_{u2}}^{\left[ {\frac{{\alpha \varepsilon \left( {1 - \sigma } \right)}}{{\sigma - \varepsilon }} + \alpha } \right]}{\Lambda _2} = s{\left( {1 + s} \right)^{\sigma - \varepsilon + 1}}{M_2}^{\frac{{1 - \varepsilon }}{{1 - \sigma }}}{P_{d2}}^{1 - \varepsilon }\left( {\tilde \varphi } \right) \hfill \\ \end{gathered} $
|
(21) |
此时,征税率
$t$
和补贴率
$s$
仅有一个为内生变量,任意给定
$t$
或
$s$
,就能通过上式求出另外一个变量。对下游最终产品定价补贴率为s时,根据成本最小化条件,可以求出下游每个异质性企业的中间品需求
${X_{u2}}\left( \varphi \right)$
和劳动力需求
${l_2}\left( \varphi \right)$
,同时得到每个异质性企业的成本函数
${\tau _2}(\varphi )$
,再根据利润最大化条件,可求出下游产品定价
${P_d}_2\left( \varphi \right)$
和利润函数
${{\text π} _d}_2\left( \varphi \right)$
。①因此,由零利润条件可以得到等式:
|
$ {\pi _d}_2\left( {\bar \varphi } \right) = \frac{{\left( {1 + s} \right)}}{\sigma }{P_d}_2\left( {\bar \varphi } \right){C_d}_2\left( {\bar \varphi } \right) - \frac{{{{\left( {1 - t} \right)}^\alpha }{P_{u2}}^\alpha {w^{1 - \alpha }}}}{B}f{\text{ = }}0 $
|
(22) |
此时,由自由进入条件可得到等式:
|
$ \left[ {1 - G\left( {\bar \varphi } \right)} \right]{{\text π} _{d2}}\left( {\tilde \varphi } \right) = \frac{{{{\left( {1 - t} \right)}^\alpha }{P_{u2}}^\alpha {w^{1 - \alpha }}}}{B}{f_e} $
|
(23) |
结合零利润条件和自由进入条件可以计算出,此时下游异质性非农产品的价格指数
${P_d}_2$
和下游民营企业数量
${M_2}$
满足:
|
$ {P_d}_2 = {\left[ {\int_{\bar \varphi }^\infty {{M_2}{{(1 + s)}^{1 - \sigma }}{P_{d2}}^{1 - \sigma }\left( \varphi \right)\frac{{g\left( \varphi \right)}}{{1 - G\left( {\bar \varphi } \right)}}d\varphi } } \right]^{\frac{1}{{1 - \sigma }}}} = \left( {1 + s} \right){M_2}^{\frac{1}{{1 - \sigma }}}{P_{d2}}\left( {\tilde \varphi } \right) $
|
(24) |
|
$ {M_2} = {\left\{ {\frac{{\sigma f}}{\Omega }{{\left[ {\frac{{{{\left( {1 - t} \right)}^\alpha }{P_{u2}}^\alpha {w^{1 - \alpha }}}}{B}} \right]}^\varepsilon }} \right\}^{\frac{{1 - \sigma }}{{\sigma - \varepsilon }}}}{\left( {1 + s} \right)^{\frac{{\sigma \left( {\sigma - 1} \right)}}{{\sigma - \varepsilon }}}} $
|
(25) |
可以看出,
$\dfrac{{\partial {M_2}}}{{\partial s}} > 0$
,即随着对下游民营企业补贴率
$s$
的增加,下游企业数量
${M_2}$
也将得到一定程度的增加,这将有利于提高市场竞争程度。此时上游国有企业中间品总需求
${D_u}_2$
为:
|
$ {D_u}_2 = \int_{\bar \varphi }^\infty {{M_2}} {X_{u2}}(\varphi )\frac{{g\left( \varphi \right)}}{{1 - G\left( {\bar \varphi } \right)}}d\varphi $
|
将每一异质性企业的中间品需求
${X_u}_2\left( \varphi \right)$
代入上述等式,得出下式:
|
$ {D_u}_2 = {P_{u2}}^{\left[ {\frac{{\alpha \sigma \left( {1 - \varepsilon } \right)}}{{\sigma - \varepsilon }} - 1} \right]}{\Lambda _2} $
|
(26) |
其中,
${\Lambda _2} = {\left\{ {\dfrac{{\sigma f}}{\Omega }{{\left[ {\dfrac{{{{\left( {1 - t} \right)}^\alpha }{w^{1 - \alpha }}}}{B}} \right]}^\varepsilon }} \right\}^{\frac{{1 - \sigma }}{{\sigma - \varepsilon }}}}{\left[ {\dfrac{{\alpha w}}{{\left( {1 - t} \right)\left( {1 - \alpha } \right)}}} \right]^{1 - \alpha }}\left( {\sigma - 1} \right)f\left( {\dfrac{\gamma }{{\gamma - \sigma + 1}}} \right){\left( {1 + s} \right)^{\frac{{\sigma \left( {\sigma - 1} \right)}}{{\sigma - \varepsilon }}}}$
此时上游国有企业的利润函数
${\pi_u}_2$
满足:
|
$ {\pi_u}_2 = \left[ {\left( {1 - t} \right){P_{u2}} - \frac{w}{\eta }} \right]{D_{u2}} $
|
根据上游国有企业利润最大化条件,得出中间品价格
${P_u}_2$
和利润
${{\text π} _u}_2$
分别为:
|
$ {P}_{u}{}_{2}=\left[\frac{\alpha \sigma \left(\epsilon -1\right)+\sigma -\epsilon }{\alpha \sigma \left(\epsilon -1\right)\left(1-t\right)}\right]\frac{w}{\eta },\;{{\text π} }_{u}{}_{2}=\left[\frac{\left(\sigma -\epsilon \right)}{\alpha \sigma \left(\epsilon -1\right)}\right]\frac{w}{\eta }{D}_{u2} $
|
(27) |
最后,求解垂直结构下实施“上游征税、下游补贴”政策的社会福利水平,通过推导可以进一步得出:
|
$ {C_{d2}} = {\left[ {\int_{\bar \varphi }^\infty {{M_2}{C_{d2}}^{\frac{{\sigma - 1}}{\sigma }}\left( \varphi \right)\frac{{g\left( \varphi \right)}}{{1 - G\left( {\bar \varphi } \right)}}d\varphi } } \right]^{\frac{\sigma }{{\sigma - 1}}}}\, = {\left( {1 + s} \right)^{\sigma - \varepsilon }}{M_2}^{\frac{{ - \varepsilon }}{{1 - \sigma }}}{P_{d2}}^{ - \varepsilon }\left( {\tilde \varphi } \right) $
|
(28) |
将上式代入
$C{S_2}$
公式并进行计算,可得到:
|
$ \begin{gathered} C{S_2} = I - {P_{d2}}{C_{d2}} + \frac{\varepsilon }{{\varepsilon - 1}}{C_{d2}}^{\frac{{\varepsilon - 1}}{\varepsilon }} = I + \left[ {\left( {\frac{\varepsilon }{{\varepsilon - 1}}} \right){{\left( {1 + s} \right)}^{\frac{{\left( {\sigma - \varepsilon } \right)\left( {\varepsilon - 1} \right)}}{\varepsilon }}} - {{\left( {1 + s} \right)}^{\sigma - \varepsilon + 1}}} \right]{M_2}^{\frac{{\varepsilon - 1}}{{\sigma - 1}}}{P_d}{_2^{1 - \varepsilon }}\left( {\tilde \varphi } \right) \end{gathered} $
|
(29) |
可以得到“上游征税、下游补贴”政策下的社会福利
${W_2}$
由消费者剩余
$C{S_2}$
和生产者利润
${\pi _{u2}}$
构成,并满足:
|
$ \begin{aligned} {W_2} & = C{S_2} + {{\text π} _{u2}}\\ & = I + \left[ {\left( {\frac{\varepsilon }{{\varepsilon - 1}}} \right){{\left( {1 + s} \right)}^{\frac{{\left( {\sigma - \varepsilon } \right)\left( {\varepsilon - 1} \right)}}{\varepsilon }}} - {{\left( {1 + s} \right)}^{\sigma - \varepsilon + 1}}} \right]{M_2}^{\frac{{\varepsilon - 1}}{{\sigma - 1}}}{P_d}{_2^{1 - \varepsilon }}\left( {\tilde \varphi } \right) + \left[ {\frac{{\left( {\sigma - \varepsilon } \right)}}{{\alpha \sigma \left( {\varepsilon - 1} \right)}}} \right]\frac{w}{\eta }{D_{u2}} \end{aligned} $
|
四、数值分析
为了定量分析两种产业政策对垂直结构下社会福利损失的改善效果,下文将进行数值模拟,通过严谨的参数校准和一系列稳健性检验,定量给出垂直结构下两种产业政策对社会福利的影响。
(一)参数校准
首先,对模型参数进行校准,校准的约束条件满足
$\varepsilon > 1$
,
$\sigma > 1$
,
$\gamma > \sigma - 1$
,
$\sigma > \varepsilon $
,
$0 < \alpha < 1$
。Defever和Riaño(2012)在Melitz(2003)模型框架基础上,利用中国工业企业数据对中国企业的生产参数进行了估算,与本文数据源相同。因此,在满足上述约束条件的基础上,本文采用Defever和Riaño(2012)的取值,假定
$\gamma = 2.76$
,
$\sigma = 3$
。同时,为了简化分析,将劳动力工资
$w$
和单位劳动力的中间品产出
$\eta $
都标准化为1。此外,本文参考Bernard等(2007)的研究,将下游民营企业进入成本
${f_e}$
设定为2,将下游异质性产品固定生产成本
$f$
设定为
${f_e}$
的5%,即
$f = 0.1$
。
其次,本文利用1998年到2007年的中国工业企业数据,对中间品成本占下游企业收入的份额
$\alpha $
进行估算。本文对照Li等(2015)计算的上下游指数及对上下游产业的界定,筛选出下游产业的工业企业,并且剔除国有资本占实收资本50%以上的企业,得到下游民营企业初步的估算数据。在工业企业的各项指标中,本文选取工业中间投入合计指标来对应中间品成本,选取产品销售收入指标来对应企业收入。此外,本文还删除了就业人员数小于8,工业增加值、中间投入、工业总产值、实收资本、资产合计、固定资产和本年折旧小于0、固定资产大于资产合计等异常记录,以提高估计的可靠性。经过计算,可以得到中间投入合计占下游企业产品销售收入份额,即中间品成本占下游企业收入份额
$\alpha $
的均值为0.8左右。
此时,已知
$\sigma $
、
$\alpha $
的取值,若能求出国有企业的成本加成率(即加成因子),就可以根据前文在基准模型中推导出的中间品价格
${P_u}$
公式中的加成因子
$\left[ {\alpha \sigma \left( {\varepsilon - 1} \right) + \sigma - \varepsilon } \right]/\left[ {\alpha \sigma \left( {\varepsilon - 1} \right)} \right]$
,推算出异质性产品的需求价格弹性
$\varepsilon $
。
我们利用工业企业数据测算出上游国有企业的中间投入占产出份额
$\alpha _{it}^m$
,并使用DLW方法估算出中间投入的产出弹性
$\theta _{it}^m$
后,可根据DLW方法的企业成本加成率公式
${\mu _{it}} = \theta _{it}^m/\alpha _{it}^m$
,得到上游国有企业成本加成率估计值。在剔除加成率为负值的估计值后,本文得到62 738个有效的成本加成率估计值,保留小数点后两位,取其均值为1.21。②
在得到成本加成率的估计值之后,令其与模型推导出的均衡状态下中间品加成定价
${P_u}$
公式中的加成因子
$\left[ {\alpha \sigma \left( {\varepsilon - 1} \right) + \sigma - \varepsilon } \right]/\left[ {\alpha \sigma \left( {\varepsilon - 1} \right)} \right]$
相等,并将已确定的异质性企业替代弹性
$\sigma $
和利用工业企业数据测算的下游民营企业中间品成本占下游企业收入的份额
$\alpha $
代入,可以计算得出异质性产品需求价格弹性
$\varepsilon $
的数值为2.33。这一数值是大于1的,表明下游异质性产品之间是替代性的。
经过上述的参数校准,数值分析中对各个模型参数的最终取值如表1所示。
表 1 模型参数校准
| 参数 |
描述 |
取值 |
来源 |
|
$\varepsilon $
|
异质性产品需求价格弹性 |
2.33 |
由DLW方法测算的成本加成率和模型公式计算得出
|
|
$\sigma $
|
异质产品间替代弹性 |
3 |
参考Defever和Riao(2012) |
|
$\gamma $
|
Pareto分布参数
|
2.76 |
参考Defever和Riao(2012) |
|
$\alpha $
|
中间品成本
占下游企业收入的份额
|
0.8 |
利用工业企业数据测算 |
|
$w$
|
单位劳动力工资 |
1 |
标准化 |
|
$f$
|
下游异质性产品
固定生产成本
|
0.1 |
参考Bernard等(2007) |
|
${f_e}$
|
下游民营企业进入成本 |
2 |
参考Bernard等(2007) |
|
$\eta $
|
单位劳动力的中间品产出 |
1 |
标准化 |
(二)数值模拟
经过参数校准得到各参数取值后,本文对基准模型及嵌入产业政策后的模型进行数值模拟,可以得到基准模型的上游中间品价格
${P_u}$
、下游企业数量
$M$
、消费者剩余
$CS$
、生产者剩余
$PS$
(上游国企利润
${\pi _u}$
)和社会福利
$W$
等变量的绝对值,并进一步得出上游“竞争自由化”和“上游征税、下游补贴”两种政策实施后对应指标的变化幅度(本文指变化率),分析两种产业政策的政策效应。
首先,经过数值模拟,得到上游“竞争自由化”的政策效应如表2所示。
表 2 上游“竞争自由化”政策效应
| 变量 |
${P_{u1}}$
|
${M_1}$
|
$C{S_1}$
|
$P{S_1}$
|
${W_1}$
|
| 变化幅度 |
−17.35% |
188.70% |
147.88% |
−100% |
120.71% |
对数值模拟结果进行分析可以发现,在实施上游“竞争自由化”政策之后,垂直结构下的中间品价格
${P_{u1}}$
将下降17.35%,下游企业数量将增加188.70%,消费者剩余
$C{S_1}$
获得147.88%的显著提升,生产者剩余降为0,整体社会福利增加了120.71%。这一结果证明,垂直结构下实施上游“竞争自由化”政策将对社会福利产生显著的正向效应。由此,可以得到垂直结构下实施上游“竞争自由化”政策的相关结论。
结论2:在垂直结构下实施上游“竞争自由化”政策后,下游民营企业数量将大幅增加,社会福利水平也将获得显著提升。
从实际的政策效果来看,当上游放开市场准入,国有企业之间实现自由竞争时,中间品价格将恒等于中间品的平均生产成本,进入下游产业的民营企业数量大幅增加,竞争更为激烈,但竞争的加剧使得消费者从中获益,消费者剩余大量增加且增加量超过生产者剩余的减少量,促进了市场扭曲的改善,总体上显著增加了社会福利。此时,在这一理想化的生产结构下,垂直结构导致的垄断问题将得到有效缓解,更多的国有企业进入上游市场,上游市场中的国有企业由垄断回归市场竞争,更多异质性民营企业进入下游产业,“看不见的手”充分发挥其调节经济的作用,经济社会处于高效运行状态。
这样来看,这一政策无疑是应对垂直结构及其导致的经济损失的良策,政策有效性强。但从现实角度看,目前这一政策缺乏可行性。若强制执行该政策必定导致社会性负担的陡然增加,经济社会难以承担其后果。而想要全方位减少实施这一政策的损失,又必然会加剧政策制定和实施的难度。
下面,通过数值模拟定量研究“上游征税、下游补贴”政策效应。在满足上游征税额和下游补贴额等式的条件下,每个征税率
$t$
对应一个确定的补贴率
$s$
,可以得到相应各指标的具体取值。本文选取从0.01至0.2的征税率
$t$
,每次数值模拟将增加0.05的征税率,此时每个征税率
$t$
都对应一个确定的补贴率
$s$
。经过数值模拟后的结果如表3所示。
表 3 “上游征税、下游补贴”政策效应
|
$t$
|
$s$
|
${P_{u2}}$
变化幅度
|
${M_2}$
变化幅度
|
$C{S_2}$
变化幅度
|
$P{S_2}$
变化幅度
|
${W_2}$
变化幅度
|
| 0.01 |
0.0054 |
1.01% |
4.93% |
3.24% |
4.93% |
3.43% |
| 0.05 |
0.0281 |
5.26% |
28.13% |
17.68% |
28.13% |
18.83% |
| 0.10 |
0.0593 |
11.11% |
67.46% |
39.58% |
67.46% |
42.64% |
| 0.15 |
0.0941 |
17.65% |
123.78% |
66.76% |
123.78% |
73.01% |
| 0.20 |
0.1333 |
25% |
206.75% |
100.37% |
206.75% |
112.03% |
| 0.25 |
0.1778 |
33.33% |
332.90% |
141.29% |
332.90% |
162.28% |
随着征税率
$t$
的逐渐增加,补贴率
$s$
也持续增加,但均小于征税率
$t$
;随着征税率
$t$
的增加,中间品价格
${P_{u2}}$
也不断增加,变化幅度从1.01%增加到33.33%,但上游国企的实际税后价格
$(1 - t){P_{u2}}$
与基准模型中的中间品价格数值相差不大;实施“上游征税,下游补贴”政策后,下游民营企业数量
${M_2}$
会增加,且随着补贴率
$s$
的增加,
${M_2}$
的变化幅度也逐渐由4.93%增加到332.90%;同样地,消费者剩余
$C{S_2}$
也随着征税率
$t$
和补贴率
$s$
的增加而迅速增长,变化幅度由3.24%增加至141.29%;由于下游企业的扩张,中间品需求增加,生产者剩余
$P{S_2}$
(上游国企利润)也会增加,因此实施“上游征税,下游补贴”政策后,国企利润非但没有因为征税而降低,反而会因为下游企业数量和中间品需求的增加而提高,是一个上下游企业“双赢”的结果。此时社会福利水平的提升在3.43%—162.28%,社会福利提升效果显著。
这一结果表明,政府仅需分别对上下游开展低税率的征税和低补贴率的补贴就能在一定程度上提高下游企业数量
${M_2}$
,大大提升消费者剩余
$C{S_2}$
和生产者剩余
$P{S_2}$
,获得社会福利
${W_2}$
的显著提升。因此,可以得到垂直结构下实施“上游征税、下游补贴”政策的相关结论。
结论3:在垂直结构下实施“上游征税、下游补贴”政策后,同样可以在一定程度上促进下游民营企业进入市场,提高总体社会福利,并且上游国有企业利润也会因下游企业数量增加而提高。
我们可以从数值模拟的结果推断,政府仅需分别对上下游开展低税率的征税和低补贴率的补贴就能在一定程度上提高下游企业数量、提高上游国企利润以及总体社会福利。比较表2和表3,对国企征收20%的税率就可以提高“竞争自由化”政策下社会福利的改善程度,因此,“上游征税、下游补贴”的政策有效性较高,对社会福利水平同样有显著提升效果。
在确定政策有效性存在的情况下,应结合现实考虑政策的可行性。首先,基于中国的经济现实,对产业内进行鼓励性的补贴政策和限制性的征税政策已经拥有了多年的历史,现有文献也都对这两种政策类型及两者结合的政策效应进行了大量的研究,肯定了两种产业政策对企业创新、融资和贸易等经济行为产生的正向影响。其次,由于中国政府与中央和地方国企国有资本存在内在的联系,在实施国企改革过程中考虑对上游产业内国有企业开展小税率征税难度显然低于开展竞争自由化。总体上看,“上游征税、下游补贴”政策的可行性高于上游“竞争自由化”政策。
(三)稳健性检验
为了验证本文数值模拟结果的稳健性,下文将每次改变表1中一个参数的取值,包括异质性产品的需求价格弹性
$\varepsilon $
和中间品成本占下游企业收入的份额
$\alpha $
等③并计算参数改变后的变化情况。④
首先,在保持其他参数取值不变的情况下,使异质性产品需求价格弹性
$\varepsilon $
改变,分别取2.2、2.3和2.4,进行数值模拟后的上游“竞争自由化”政策效应如表4所示。
表 4 改变
$\varepsilon $
后上游“竞争自由化”政策效应
|
$\varepsilon $
|
${P_{u1}}$
|
${M_1}$
|
$C{S_1}$
|
$P{S_1}$
|
${W_1}$
|
| 2.2 |
−21.74% |
194.04% |
141.68% |
−100% |
112.16% |
| 2.3 |
−18.32% |
189.83% |
146.50% |
−100% |
118.71% |
| 2.4 |
−15.15% |
186.21% |
150.95% |
−100% |
125.45% |
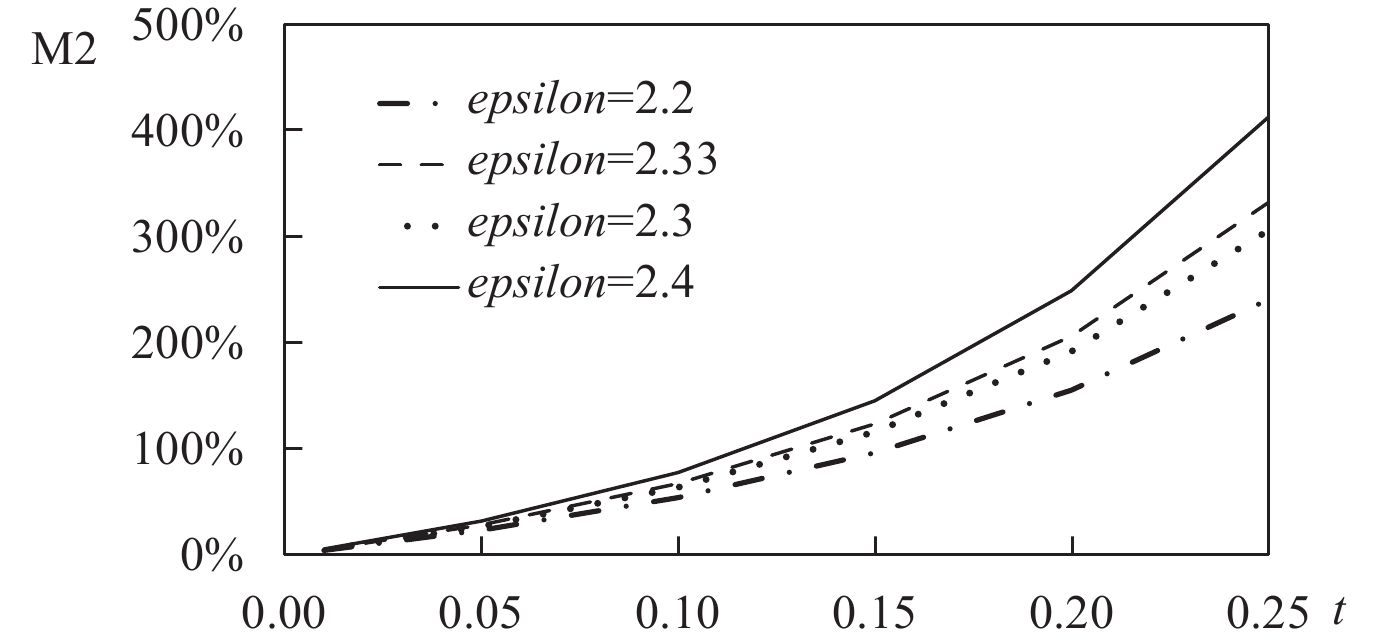
实施“上游征税、下游补贴”政策后,民营企业数量和社会福利的变化率如图1和图2所示。
可以看到,当异质性产品需求价格弹性
$\varepsilon $
取值分别为2.2、2.3和2.4时,数值模拟结果与基准模型类似,两种产业政策对社会福利的提升效果依然显著,且变化处于合理范围内。同样地,当征税率在15%—25%时,“上游征税、下游补贴”政策可以达到上游“竞争自由化”政策下的社会福利改善的目标。
下面,我们再改变中间品成本占下游企业收入的份额
$\alpha $
,分别取0.7、0.75和0.85,进行数值模拟后的政策效应如表5所示。
表 5 改变
$\alpha $
后上游“竞争自由化”政策效应
|
$\alpha $
|
${P_{u1}}$
|
${M_1}$
|
$C{S_1}$
|
$P{S_1}$
|
${W_1}$
|
| 0.7 |
−19.35% |
184.87% |
145.06% |
−100% |
118.79% |
| 0.75 |
−18.29% |
186.88% |
146.55% |
−100% |
119.81% |
| 0.85 |
−16.50% |
190.32% |
149.07% |
−100% |
121.53% |
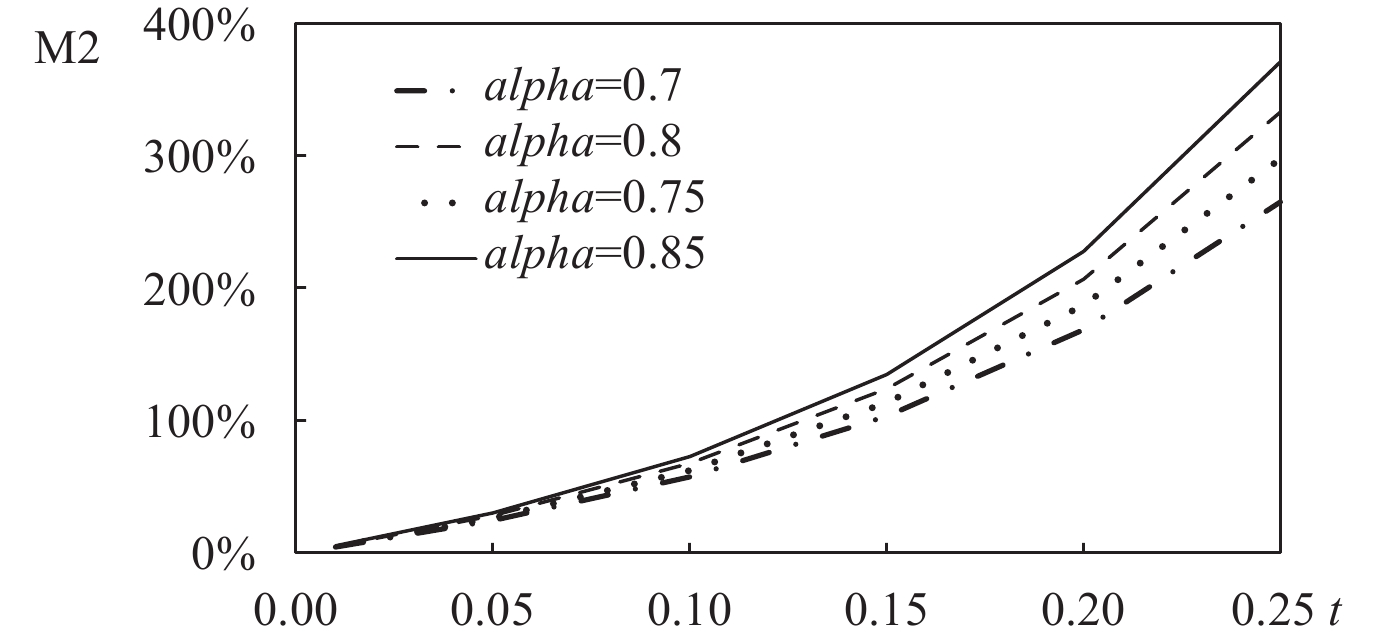
实施“上游征税、下游补贴”政策后,民营企业数量和社会福利的变化率如图3和图4所示。
类似地,可以看到当中间品成本占下游企业收入的份额
$\alpha $
取0.70、0.75和0.85时,数值模拟结果差异不大,两种产业政策对下游企业数量以及社会福利的改善均十分显著,并且20%—25%左右征税率下的“上游征税、下游补贴”的政策效应与上游“竞争自由化”的政策效应基本相同。
综上可以看出,不同参数的取值会改变某个变量具体的数值结果,但是本文得到的基本结论是不变的,即不同的产业政策均具备有效性,采用上游“竞争自由化”的政策可以极大增加下游企业的数量,提高总体社会福利;采用“上游征税、下游补贴”的政策,同样可以提高下游企业的数量,扩大下游企业对于上游中间品的需求,从而提高上游国企的利润,增加总体社会福利,实现上下游企业的“双赢”。并且,一定征税率和补贴率组合下的“上游征税、下游补贴”政策基本可以达到上游“竞争自由化”政策改善社会福利的目标。因此,本文数值模拟的结论具备稳健性,参数取值的调整并不会改变模型主要结论。
五、结 论
本文通过建立一个“上游国企垄断,下游民企垄断竞争”的垂直结构模型,研究这一生产结构如何通过影响上下游国有企业和民营企业的生产经营决策,进而影响社会福利。进一步地,本文将上游“竞争自由化”和“上游征税、下游补贴”这两种不同的产业政策嵌入模型,利用数值模拟的方法,对垂直结构下产业政策的影响进行定量研究,最终得到相应政策建议。
研究结果表明:第一,国有企业在上游凭借垄断地位进行加成定价,垂直结构的存在会使得中间品定价过高,导致下游民营企业出现进入不足的现象,造成社会福利损失;第二,在垂直结构下实施上游“竞争自由化”政策会同时带来上下游竞争程度的提高,促进下游民营企业进入市场,提高总体社会福利水平,政策有效性强。虽然上游“竞争自由化”对垂直结构下社会福利提升效果显著,但在现实中可行性较低,难以在全部行业开展,需要循序渐进地进行引导;第三,在垂直结构下的“上游征税、下游补贴”政策可以有效增加下游企业数量,提高下游民企对中间品的需求,进而提高上游国企的利润,是一个“双赢”的结果,这一政策有助于形成合理的生产结构。同时,这一政策仅需选取少量的征税率和补贴率组合就可以达到社会福利明显提升的效果,兼顾有效性和可行性,应在未来得到科学地运用。
基于以上的研究结论,本文提出的政策建议如下:第一,未来政府应重新界定有必要继续维持垄断地位的战略性上游产业,对于新材料、新能源、新医药、高科技等战略性新兴产业,要充分利用国有企业资本实力雄厚、人才储备丰富的优势,鼓励其进入,努力抢占未来经济发展的制高点;对垄断势力高的非战略性产业进行市场化改革,降低行业准入门槛,给予新进入企业政策支持与补贴,促进国企之间充分竞争,降低上游市场的垄断程度,循序渐进地引导部分上游产业实现“竞争自由化”。第二,为了进一步减少垂直结构带来的社会福利损失,政府应实施“上游征税、下游补贴”的产业政策,通过对上游产业垄断的国有企业进行适当征税和对下游产业内的民营企业提供一定补贴的形式,将传统的税收、补贴政策与垂直结构生产关系相结合。对于上游垄断性国有企业征收资源税、补偿税等税,对于非国有企业,降低企业所得税率,适当提高劳动者收入和政府财政补贴。第三,产业政策的实施不是一刀切,应对不同行业的国有企业配置不同改革方针。在少数涉及国防安全、航空航天等部门,维持一定数量国企的存在是非常必要的。在研发周期长、投资大和风险大的核心技术研发上,国有企业要充分发挥其人才储备、技术积累和成本压力较小的比较优势,更多地主导和参与技术研发,更好地服务国家与社会的发展需要。对于处于自然垄断的行业,如石油、天然气、铁路、电力等,应探索放开竞争性业务的路径,允许国有企业吸收更多民间资本,形成混合所有制经济,推进公共资源配置的市场化,以提高企业经营效益与效率。
* 本文还得到了暨南大学产业大数据实验室与基地自设项目的支持。
① 篇幅所限,推导过程省略,感兴趣的读者可向作者索要。
② 篇幅所限,成本加成率的估算方法未详细展开,感兴趣的读者可向作者索要。
③ 下游民营企业的固定生产成本和市场进入成本两个参数只改变模型变量的绝对值,并不改变每个变量的变化率。
④ 篇幅所限,下图只呈现了“上游征税、下游补贴”政策下企业数量和社会福利的变化,本文还计算了价格、消费者剩余、生产者剩余等变量的变化,与基准模型相比差异在合理范围内,感兴趣的读者可向作者索要。