一、引　言

2020年9月，中国医保局会同财政部印发了《关于扩大长期护理保险制度试点的指导意见》（医保发〔2020〕37号，以下简称《意见》）。《意见》指出，参保对象从职工基本医疗保险参保人群起步，探索建立以互助共济的方式筹资资金的社会保险制度。筹资模式是社会保险制度中的一个重要部分，是社会保险基金稳定性和可持续性的重要影响因素。社会保险基金的筹资模式主要包括现收现付制、完全基金制和混合制（又称部分基金制）三种。在现收现付制下，长期护理保险（下文简称“长护险”）基金需满足年度内的收支平衡，即某一年度内年轻个体的缴费应该等于当年老年个体长期护理的补偿支出。在完全基金制下，长护险基金需实现参保者个人权利与义务的平衡，即参保个人或集体在所有年度内的缴费现值等于未来长期护理支出的现值。混合制是介于现收现付制和完全基金制之间的模式，是两者的结合，具体又包含阶梯平衡制、准备金保费制和长期平衡制三种（王晓军，2011）。显然，不同筹资模式均需满足长护险基金的收支平衡，满足收支平衡时的费率称为均衡费率。均衡费率的高低直接影响长护险筹资主体的缴费负担及基金可持续性。

长护险筹资模式的实证研究主要基于现收现付制和完全基金制。对于现收现付制下均衡费率，陈璐（2013）分城镇和农村测算了40岁以上人群长护险的均衡费率，发现个体的均衡费率大致处于0.052%和0.344%之间。林宝（2016）预测2014—2050年长护险均衡费率呈现上升的趋势，但整体水平并不高，到2050年也保持在1%以下。张盈华（2020）发现，均衡费率到2055年要上升至1.5%，才能维持长护险基金的收支平衡。随着老龄化程度的加深，现收现付制下的保险缴费率必须要增加（Rothgang，2010），且每年调整缴费率增加了社会保险的“菜单成本”，因而缴费水平应该事先进行科学测算，避免频繁的费率调整。完全基金制的研究分为两类：一种是针对个人，一般应用在长期护理商业保险的定价中，如胡晓宁等（2016）、张琳和汤薇（2020）等；另一种是针对群体，常用于社会保险不同年龄参保群体均衡费率的测算，如医疗保险（何文炯等，2010）和长护险（黄枫和吴纯杰，2018）。

从中国目前的社会保障实践来看，养老保险和医疗保险采取的是现收现付制和完全基金制的混合模式。其中，社会统筹账户采取的是现收现付制，个人账户采取的是完全基金制。对于工伤保险、失业保险和生育保险，一般采用现收现付制或混合制，很少采用完全基金制。根据《意见》，长护险基金遵循“收支平衡，略有结余”的原则，使长护险试点地区的筹资模式更符合混合制。在混合制下，一部分资金用于满足当年的长期护理支出需求，另一部分沉淀形成资金储备，用于满足未来因人口老龄化和失能化而增加的长护险支付需要。目前仅有混合制在医保中的实证研究，如李亚青（2015，2017）、徐伟等（2017）等。另外，不同筹资模式的优劣尚无定论。Eling和Ghavibazoo（2019）指出，目前尚不清楚长护险的最佳筹资组合形式，也可能没有一个最佳模式，最佳模式可能取决于经济、社会、文化和人口因素。那么，作为“社保第六险”的长护险究竟该采用何种筹资模式？中国目前各试点地区的筹资标准偏高还是偏低？本文从均衡费率的视角出发，对比了现收现付制和三种混合制中哪种更适合中国当前实际情况，并分别讨论了城镇职工和城乡居民两种参保群体。

均衡费率的测算依赖于对中国未来失能人口规模的预测。从中国长护险制度试点来看，目标人群界定和待遇标准有较大差异，各地区间“碎片化”特征明显。而目标人群的界定和失能水平的不同必然影响长护险制度所覆盖的人口总量和结构（廖少宏和王广州，2021）。未来失能人口规模取决于初始人口分布和失能率。直接运用全国人口规模和失能率数据预测失能人口的方法称为宏观模拟法（景跃军等，2017），通过构建老年个体在不同健康状态之间转换的方法称为微观模拟法。微观模拟法的理论基础是老年个体健康状态演变规律的Markov转移概率矩阵。其优点是允许老年人的身体状况在各种健康状态之间动态转换，且便于对不同参保群体的健康状况分别进行建模（黄枫和吴纯杰，2012）。

健康转移概率的估计方法主要有直接估计法和间接估计法两种。直接估计法就是直接对健康转移概率进行建模，如采用logit模型和Markov过程（胡宏伟等，2015），但回归模型中变量选取具有主观性和多样性。国外数据库中包含个体在不同状态中持续的时间，所以可采用semi-Markov过程进行建模（Biessy，2015；Fuino和Wagner，2018）。国内外学者对商业长期护理保险进行精算定价时一般采用间接估计法，即将转移强度矩阵作为中间变量计算转移概率的方法。而转移强度矩阵的估计一般采用风险暴露法（Hanewald等，2019；胡晓宁等，2016；张琳和汤薇，2020）。这种方法的实施前提是需有个体的跟踪调查数据，包括个体的出生日期、调查日期、死亡日期和状态转移日期，另外还需有关健康状态定义的ADL和IADL问卷。目前，中国满足要求的数据库有中国老年健康影响因素跟踪调查（CLHLS）和中国健康与养老追踪调查（CHARLS）。相比之下，CLHLS对高龄老人健康分布的描述更加精确（陈秉正和范宸，2020）。

当前，关于中国失能率的研究尚存在争议，主要存在三种观点。第一种观点认为老年失能水平呈下降趋势（顾大男和曾毅，2006），第二种观点认为老年失能水平呈上升趋势（丁华和严洁，2018），第三种观点认为老年失能水平在不同时期有不同变化趋势（王金营和李天然，2020）。这种差异可能是三方面原因导致的：一是仅采用截面数据来测算老年失能率，可能会面临样本量不足所导致的估计偏差；二是采用不同的数据来源或失能测量标准；三是对未来老年人口规模的预测不够准确，导致对失能人口的预测存在偏差。基于此，本文运用多期微观跟踪调查数据，采用国际通用的日常行为能力ADL标准，结合2020年第七次人口普查数据，对中国未来老年失能人口规模进行预测。

现有研究存在以下不足：（1）对失能老年人口规模以及相应的长期护理需求的预测不够精准，特别是对老年人失能率、未来人口结构和规模的测算不够科学，应区分不同老年个体，提高预测科学性和精度。（2）现有文献通常限于筹资水平的粗略估算，缺乏对城乡人口迁移、人口结构转变等因素的考虑，从而损失了未来参保人口和均衡费率的预测精度。（3）现有研究集中于现收现付制下长护险均衡费率的测算，缺乏混合制筹资模式的研究，从而无法判断哪种筹资模式更适合。鉴于此，本文利用2008年、2011年、2014年和2018年四期CLHLS数据，基于Markov理论和GLM模型估计了不同性别、不同城乡和不同年龄的健康转移概率矩阵，并结合微观模拟法预测了未来失能人口规模。进一步地，本文区分城镇职工和城乡居民两种参保主体的情形，模拟测算了2020−2040年现收现付制和三种混合制下的均衡费率和缴费额。

二、模型与方法

（一）不同筹资模式下的均衡费率模型

1. 长期护理保险基金收入模型。考虑建立职工长期护理保险（简称“职工长护险”）和居民长期护理保险（简称“居民长护险”）两种制度。理论上，长护险的基金收入主要受到缴费人数和历年均衡费率的影响，令 $ {CI}_{t}^{k} $ 表示长期护理保险基金收入，则有：

其中， $ k\in [z,j] $ ， $ z $ 表示职工长护险， $ j $ 表示居民长护险， $ {ER}_{t}^{k} $ 表示均衡费率， $ {W}_{{t}_{0}}^{k} $ 表示工资收入或人均可支配收入， $ {M}_{t}^{k} $ 表示缴费人口规模， $ g $ 表示工资收入或人均可支配收入增长率， $ {t}_{0} $ 表示测算开始年。

2. 长期护理保险基金支出模型。理论上，基金支出主要受到长期护理费用支出和实际补偿比的影响，前者取决于失能人口规模、护理偏好以及不同护理方式的费用情况，后者取决于目标保障水平。令 $ {CE}_{t}^{k} $ 表示长期护理保险基金支出，则有：

其中， $ {N}_{x,t}^{3,k} $ 表示在t年 $ x $ 岁群体中的健康状态为失能（上标为3）的老年人口数量， $ w $ 表示极限年龄，假定为100岁， $ {\tau }^{m} $ 表示政府对护理方式 $ m $ 的实际补偿比，反映平均保障水平，即不考虑起付线、基金支付比例和最高支付限额，只考虑反映上述因素的实际补偿比。 $ {f}^{m} $ 表示对护理方式 $ m $ 的偏好， $ {cost}_{{t}_{0}}^{m} $ 表示失能老人在护理方式 $ m $ 下的年度总费用， $ b $ 表示长期护理费用增长率。

3. 不同筹资模式下的基金平衡关系。

（1）现收现付制：需满足当期的收支平衡，是一种代际再分配机制。收支平衡关系为：

（2）混合制：包括阶梯平衡制、准备金保费制和长期平衡制三种不同的筹资模式。

①阶梯平衡制。首先预测一段时间内长护险基金支出，然后求得这段时间内基金收支平衡的缴费率，保持年度缴费率不变；在下一个缴费年度，将缴费率提高到一个更高的水平，以保证下一测算时间段内的收支平衡。中国长护险试点有效期大多为2年，并力争在“十四五”期间基本形成适应经济发展水平和老龄化发展趋势的长护险制度框架。因此，假设每两年调整一次，2026年之后的缴费率不变，即2020—2021年、2022—2023年、2024—2025年、2026年及以后存在四种费率水平。

其中， ${T}_{i}$ 分别取2020—2021年、2022—2023年、2024—2025年、2026—2040年这四个时间段。

②准备金保费制：在一定时期内保持准备金比率不变的筹资模式。准备金比率是年末准备金数额与下一年度支出的比率，衡量年末准备金积累满足下一年度支付的程度。准备金比率为1表明不考虑当年的缴费和投资收入，年末积累的准备金恰好满足下一年度的支出。在准备金保费制下，长护险基金每年都计提一定的风险储备金，形成适度的基金累计结余率。假设每年的结余率都相等，根据职工医保的相关规定，^②统筹基金累计结余额应控制在6—9个月的平均支付水平。参考徐伟等（2017）的研究，把基金结余率控制在20%左右，具体公式为：

其中，M表示合理的累计结余率。

③长期平衡制：在测算期内保持均衡费率恒定不变的筹资模式。以 $ {t}_{0} $ 为测算起点，T为测算结束时点，在综合考虑生育率、死亡率、迁移率和失能率（健康状态转移概率矩阵）后，根据相关假定，可以测算出 $ T-{t}_{0} $ 年以后的参保人口状况和失能人口规模， $ T-{t}_{0} $ 年以后基金收入和基金支出的精算现值相等，即实现长期平衡，具体公式为：

（二）参保人口的计算

运用人口学中的队列要素法来计算缴费人口规模 $ {M}_{t}^{k} $ 。即当年区分城乡、性别和年龄的人数等于上一年度相应的人数乘以生存概率，新生儿数由育龄妇女人数乘以生育率得到。考虑到城镇化带来的农村人口向城镇迁移，不同年龄的迁移率基于陈沁和宋铮（2013）的研究得到。具体公式为：

其中， $ \tau \in [u,r] $ ，u代表城镇，r代表农村。 $ s\in [m,f] $ ，m代表男性，f代表女性。 $ {b}_{x,t} $ 表示女性人口的生育率，育龄妇女的年龄为15—49岁。 $ {q}_{x,t}^{s,\tau } $ 表示个体死亡率， $ {r}_{x,t}^{s,\tau } $ 表示个体从农村迁移到城镇的概率。职工长护险参保人口主要包括参保在职职工和参保退休人员。其中，参保退休人员不参与缴费。缴费群体为20—59岁男性、20—49岁女性。而参保在职职工数可由劳动适龄人口数、劳动参与率（假定为100%）、城镇人口就业率和参保率计算得到。 $ t $ 年参保在职职工人口总数 $ {M}_{t}^{z} $ 表示为：

其中， $ {e}_{t} $ 表示就业率， $ {\gamma }_{t} $ 表示社会长期护理保险制度覆盖面（参保率）。参保退休人员结构可由年龄移算法得到，即当年的参保退休人员数等于上一年的参保退休人员数乘以对应年龄的生存概率，则2020—2050年参保退休人员数表示为：

居民长护险的参保人口主要是城镇居民和农村居民。居民长护险的缴费群体为所有城乡居民。城镇居民和城镇职工共同构成了城镇人口，将未来城镇人口数减去参加职工长护险的人数，即得到参加城镇居民长期护理保险的人数。t年居民长护险的参保人数 $ {M}_{t}^{j} $ 表示为：

（三）健康转移概率矩阵的估计

1. 健康状态的划分。在设计长期护理保险的具体规则时，失能状态和失能等级的划分直接影响老人获得给付的资格和水平。不同学者对失能状态的划分略有不同，主要包括三状态（健康、失能和死亡），如Hanewald等（2019）；四状态（健康、健康受损、功能障碍和死亡），如张琳和汤薇（2020）；五状态（健康、轻度失能、中度失能、重度失能和死亡）。显然，失能状态的分类过多过细，会导致每个状态下的样本量过少，健康转移概率的估计精度下降。但如果失能状态的分类过少，则难以刻画老人健康状态转移过程中的重要特征。因此，本文采用四状态的分类：健康 $ h $ （health）表示无任何功能障碍；受损 $ m $ （mild）表示具有器质性日常活动障碍或1—2项日常活动障碍；失能 $ s $ （severe）表示具有3项及以上日常活动障碍；死亡 $ d $ （death）表示身故。

2. 健康转移概率矩阵的估计。 $ {D}_{x} $ 表示不同年龄 $ x $ 下分性别、分城乡基于年度的健康转移概率矩阵。

其中， $ {P}_{ij}\left(x\right) $ 为x岁时的健康转移概率。假设各年龄下老人健康状态的转移均服从时间齐性的Markov过程，即转移概率 $ {P}_{ij}\left(x\right) $ 只与时间间隔有关，而与所处的时间点无关。 $ h $ 、 $ m $ 和 $ s $ 是过渡态， $ d $ 是吸收态。老人进入到 $ s $ 状态后再恢复到健康状态 $ h $ 的可能性较低，所以本文不考虑这种情况。因此，各状态之间的转移概率与转移强度表示为：

其中， $ S\left(x\right) $ 表示个体在年龄 $ x $ 时的随机健康状态， $ {P}_{ij}\left(x,x+t\right) $ 表示处于状态 $ i $ 的个体经过时间 $ t $ 后转移到状态 $ j $ 的概率， $ {\mu }_{ij} $ 表示从状态 $ i $ 转移到状态 $ j $ 的瞬时转移概率，又称转移强度。假设 $ {\mu }_{ij}\left(x\right) $ 是可积的，且仅依赖于年龄。参考Fong等（2015）以及Hanewald等（2019）的模型设定，运用广义线性模型（GLM）对健康状态转移强度进行建模，主要由对数连接函数、线性预测变量和概率分布三部分组成，表示为：

其中， $ {m}_{ij}\left(x\right) $ 是回归变量的线性预测。假设转移强度 $ {\mu }_{ij} $ 只与年龄、性别和城乡有关，在基于不同样本范围分别估计转移强度 $ {\mu }_{ij} $ 时，线性预测部分表示为关于年龄 $ x $ 的多项式：

其中， $ {\beta }_{ij}^{s} $ 为待估计参数。为了避免模型过度拟合，参考Fong等（2015），假设 $ k $ 不超过3。概率分布选择常用的泊松分布，即假定健康状态的转移次数服从泊松分布。从状态 $ i $ 到状态 $ j $ 的转移数量表示为 $ {n}_{ij}\left(x\right) $ ，则有：

其中， $ {e}_{i}\left(x\right) $ 表示年龄为 $ x $ 的个体在健康状态 $ i $ 的风险暴露数。采用最大似然法估计模型中的最优阶数 $ k $ 和多项式系数 $ {\beta }_{ij}^{s} $ ，对数似然函数表示为：

其中， $ C $ 为常数。根据反映模型拟合程度的贝叶斯信息准则（BIC）在1—3之间选择合适的 $ k $ 。BIC惩罚了维数过大且训练样本数据较少的情况下出现的维数灾难现象，数值越小表明模型的拟合效果越好。根据最优项数 $ k $ 和多项式系数 $ {\beta }_{ij}^{s} $ 的估计结果，可以预测出每个年龄不同健康状态之间的转移强度，进一步可通过Kolmogorov微分方程求解相应的转移概率，具体表达式如下：

根据式（20）和Euler方法，可求出不同性别、不同居住类型的个体在不同年龄下的年度（t=1）健康转移概率矩阵 $ {D}_{x} $ 。

（四）失能人口的计算

$ t $ 年的失能人口主要由两部分构成。一部分是 $ t-1 $ 年已满65岁的老人，按照年龄移算法 $ {N}_{x,\mathrm{t}}={N}_{x-1,t-1}{D}_{x-1} $ ，可以得到 $ x $ 岁的个体在 $ t $ 年的健康状态分布。对所有年龄求和，可以得到失能老人总和 $ {\sum }_{x=65}^{100}{N}_{x,t}^{s} $ 。另一部分是 $ t $ 年刚满65岁的失能老人，数量等于 $ 2019+65-t $ 岁的个体在 $ 2019 $ 年的老年人数乘以对应年龄的生存率 $ {p}_{x} $ 。因此，每年新满65岁的老人数量 $ {n}_{t} $ 表示为：

其中， $ {l}_{x} $ 为 $ x $ 岁个体在2019年的生存人数。将 $ {n}_{t} $ 乘以65岁老人在不同健康状态的分布比例 $ {h}_{65} $ ，即得到 $ t $ 年新满65岁的失能老人数量。将上述两个部分的失能人数加总，最终得到 $ t $ 年城乡的失能老年人口规模 $ {N}_{x,t}^{3,k} $ 。

三、参数与数据

（一）长期护理保险基金收支参数

1. 人口相关参数。

（1）死亡率。使用2010年第六次人口普查中分性别、分城乡的0—64岁个体的死亡率数据，并假定在预测期内死亡率保持不变。一方面，本文的预测时间较短，而死亡率在短期内相对稳定；另一方面，本文重点关注失能老年人的规模，而死亡率数据包含在Markov健康状态转移概率矩阵中，意味着 65岁及以上老年人的死亡率具有时间齐性，所以死亡率在测算期内保持不变。

（2）生育率和出生性别比。生育率和出生性别比的变化相对稳定，假定在测算期内，生育率和出生性别比的变化趋势与2000年第五次人口普查和2010年第六次人口普查期间的年度变化水平相同。

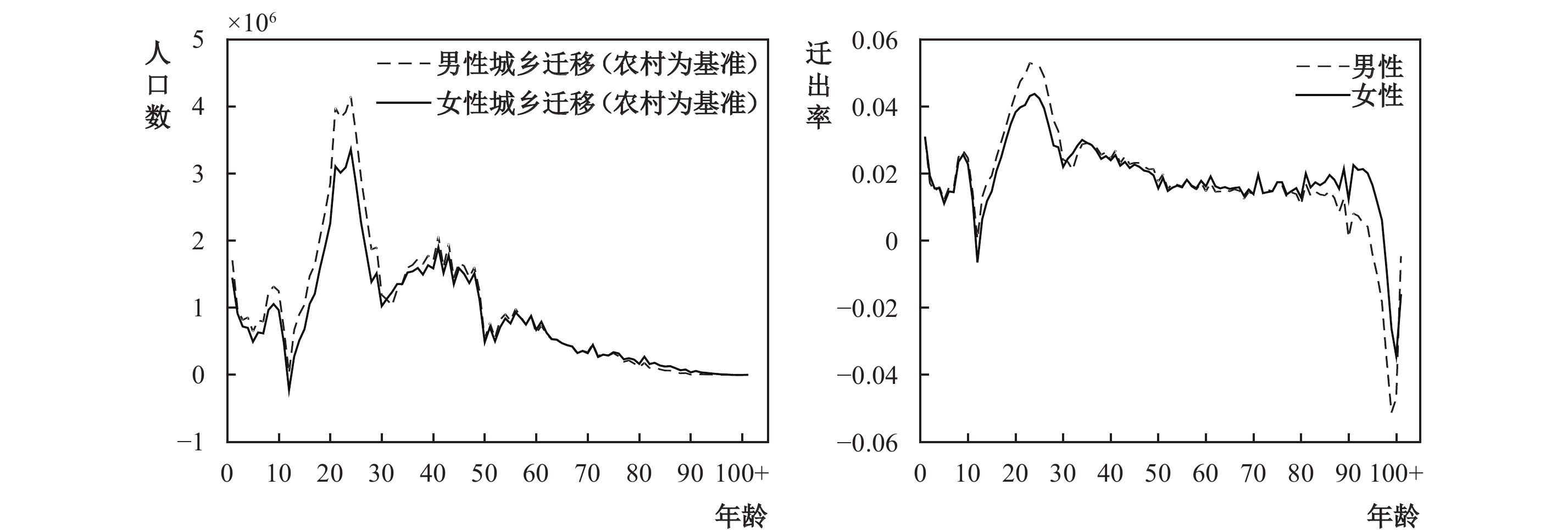
（3）迁移率。根据2000年第五次人口普查和2010年第六次人口普查数据，基于陈沁和宋铮（2013）的计算方法，^③测算结果见图1。从中可以看出，农村人口的迁出率（由农村迁移到城镇）在15—30岁较高，在40—70岁逐渐下降，70岁之后略有上升。总体来看，男性的迁移率高于女性，老年人的迁移率显著低于中青年人（胡宏伟和李延宇，2021）。2000—2010年，乡—城人口迁移总量为1.87亿人，约为2000年城镇人口的38.53%。根据2020年第七次人口普查数据，乡—城流动人口规模达2.49亿人（周皓，2021），约为2010年城镇人口的37.18%。因此，假定迁移率在预测时间段内保持不变具有一定的合理性。

（4）其他人口参数。根据2020年国家医保局公布的统计数据，中国基本医疗保险参保人数达136100万人，占全国总人口的96.4%。可见，中国医疗保险已经基本实现了全覆盖。而中国长期护理保险制度的目标是建成“社保第六险”，假定未来长护险的覆盖率是100%。根据王晓军和米海杰（2013）的研究，将未来城镇就业率设定为80%。根据历年《中国统计年鉴》和《中国人口和就业统计年鉴》，2010—2019年城镇职工参保人数占城镇就业总人口比率的均值为54.75%。在全覆盖的发展目标下，设定职工长护险的在职职工参保率每年增长1%，^④直到实现全覆盖。借鉴吕志勇和王霞（2016）的做法，通过假设退休职工占退休人口（男性为60岁以上，女性为50岁以上）的比例，预测未来退休职工人数。2019年退休人员参保人数为8700.4万人，根据2010—2019年退休参保人员占城镇职工参保人员的比例均值以及2020年职工参保总人数，得到2020年退休人员参保人数为8872.3万人，占2020年退休人口的38.37%，假定未来这一比例也保持不变。

2. 经济相关参数。

（1）城镇职工工资水平、居民人均可支配收入及两者增长率。根据2019年的统计数据，居民人均可支配收入为30733元，城镇单位在岗职工平均工资为93383元。假定在岗职工社会平均工资和城乡居民人均可支配收入增长率均为6%。

（2）失能老人对不同护理方式的偏好、不同护理方式的费用和长期护理费用增长率。目前的护理模式可以分为两大类：居家护理和机构护理（包括养老机构护理和专业护理医疗机构护理）。不同失能等级的老年人对不同护理方式有不同偏好。参考田勇（2020）的研究，轻度失能老人选择居家护理和机构护理的比例分别为77.59%和22.41%，对应的月护理费用分别为962元和1892元；重度失能老人选择居家护理和机构护理的比例分别为56.93%和43.07%，对应的月护理费用分别为1685元和6292元。为了简化参数，实现工资中性的目的，假设长期护理年费用增长率与工资或收入的年增长率相等，均为6%。

（3）目标保障水平。根据《意见》，中国长期护理保险基金的支出不应超过70%。为了充分发挥家庭照料的优势，假定居家护理和机构护理的补偿比分别为75%和70%。各试点地区规定的医疗护理费和照护费综合报销比例普遍达到70%左右，部分地方提高到90%。报销比例过高可能会导致道德风险问题，报销比例过低则不利于发挥社会保险的优势，因而需要在风险分散带来的收益和道德风险引致的损失之间进行权衡（Ellis和Manning，2007）。

（4）利率。本文选取5%，反映对未来宏观经济环境的预测。

（二）估计健康转移概率矩阵所需数据

本文主要利用2008年、2011年、2014年和2018年四期中国老年健康影响因素跟踪调查（CLHLS）数据，构建三次健康状态转移数据，以65岁及以上老人为研究对象。2008—2011年、2011—2014年以及2014—2018年的样本量分别为16954人、9765人和7192人。在界定健康状态时，采用国际上普遍认可的六项日常活动能力（ADLs）和八项器具性日常活动能力（IADLs）进行评估。CLHLS问卷中对每一个问题都进行了询问。如果受访者在没有其他人持续提供帮助的情况下无法完成某项日常活动，则认为失去该项活动能力。有一项即记为1，以老人无法完成的活动数量来衡量失能的严重程度。

本文剔除了健康、性别和居住类型等关键变量缺失的观测值，以及后续跟踪调查中丢失的样本，共得到27275个观测值。根据失能状态进行分类后的描述性统计结果见表1。2008—2011年、2011—2014年以及2014—2018年的样本比例分别为50.51%、30.65%和18.84%。对比分析发现，有10577位老人在后续跟踪调查中去世，占比约38.78%。在剩下的老人中，41.69%为健康状态，无任何功能障碍；13.89%为受损状态；5.64%为失能状态，存在严重的功能障碍且需要护理。数据表明，受损状态的老人有较高的恢复率，占样本的2.11%。而失能状态的老人恢复到健康和受损状态的可能性较低，样本比例仅为0.15%和0.40%。下文不再考虑从失能状态向健康和受损状态的恢复率，但有必要考虑从受损状态向健康状态的恢复率。将男性城镇、女性城镇、男性农村和女性农村四个子样本分别记为mc、fc、mv和fv。子样本描述性统计显示，男性占比44.2%，女性占比55.8%，女性老人多于男性；城镇占比41.0%，农村占比59.0%，农村居民多于城镇。总体上看，子样本数据较为平衡。

四、实证结果分析

（一）健康转移概率矩阵

1. 转移强度。首先根据微观原始数据，计算个体在不同健康状态的风险暴露数，然后利用转移次数除以期初相应健康状态的风险暴露数，得到原始转移强度。风险暴露数可以根据每次调查的调查日期、出生日期和死亡日期来确定，并可以精确到月度数据。如果期末状态为死亡，则状态转移时间为确切的死亡日期；如果期末状态不是死亡但健康状态发生了变化，则假设健康状态的转移时间为两次调查日期的中间点。根据上文分析，不再考虑失能转移到健康和失能转移到受损两种情况，删除相应个体后的风险暴露数见表2。

根据式（16）、式（17）和式（18）对子样本下的7个原始转移强度分别进行GLM拟合，并利用式（19）和BIC准则确定最优的模型形式，参数估计结果见表3。从中可以看出，由受损状态恢复到健康状态（m−h）以及男性群体中受损到失能的转移强度均随着年龄的增长而减小，其他健康状态拟合后的转移强度均随着年龄的增长而增加。另外，健康到受损（h−m）和健康到死亡（h−d）的转移强度是与年龄有关的二次函数，意味着个体年龄越大，健康转移强度的正向变化率越大，即受损和死亡的风险越高。

2. 健康转移概率矩阵。根据表3的参数估计结果，结合式（20），可以求出分性别、分城乡、各年龄（65—105岁）的年度健康转移概率矩阵，共包括164（=2×2×41）个矩阵。受篇幅限制，下文仅列出65岁和75岁的男性城镇、男性农村、女性城镇和女性农村的年度健康转移概率矩阵。

从表4中可以看出：（1）对于不同年龄的老年人，初始健康状态是最显著的失能和死亡风险因素。比如，对于65岁老年个体，初始状态为健康时，下一年失能和死亡的平均概率分别为0.004和0.009；初始状态为受损时，下一年失能和死亡的平均概率为0.044和0.056；初始状态为失能时，下一年死亡的平均概率为0.1433。这表明随着初始健康状态的恶化，老年个体失能和死亡的概率显著增加。（2）老年人失能和死亡的风险随着年龄的增长而显著增加。比如，城镇的65岁男性健康老年人在下一年受损、失能和死亡的概率分别为0.004、0.003和0.016，75岁男性健康个体对应的概率分别为0.017、0.006和0.039。（3）老年人健康状态的变化规律在不同群体间存在差异。女性老人具有明显的生存优势。女性老人在一年内生存（死亡）的概率比相同年龄、相同初始健康状态的男性老人要高（低）。但男性老人具有更明显的健康优势。黄枫和吴纯杰（2012）认为，男性虽然在生存方面具有相对劣势，但是生存男性的健康水平明显高于女性，这与“选择性死亡”的理论推测一致。从居住地来看，城镇老人的死亡率较低，但失能率较高，表现出显著的生存优势和健康劣势。这可能是城乡医疗服务设施差异、生态环境等因素所导致的（Wang和Yu，2016）。

（二）未来失能人口规模

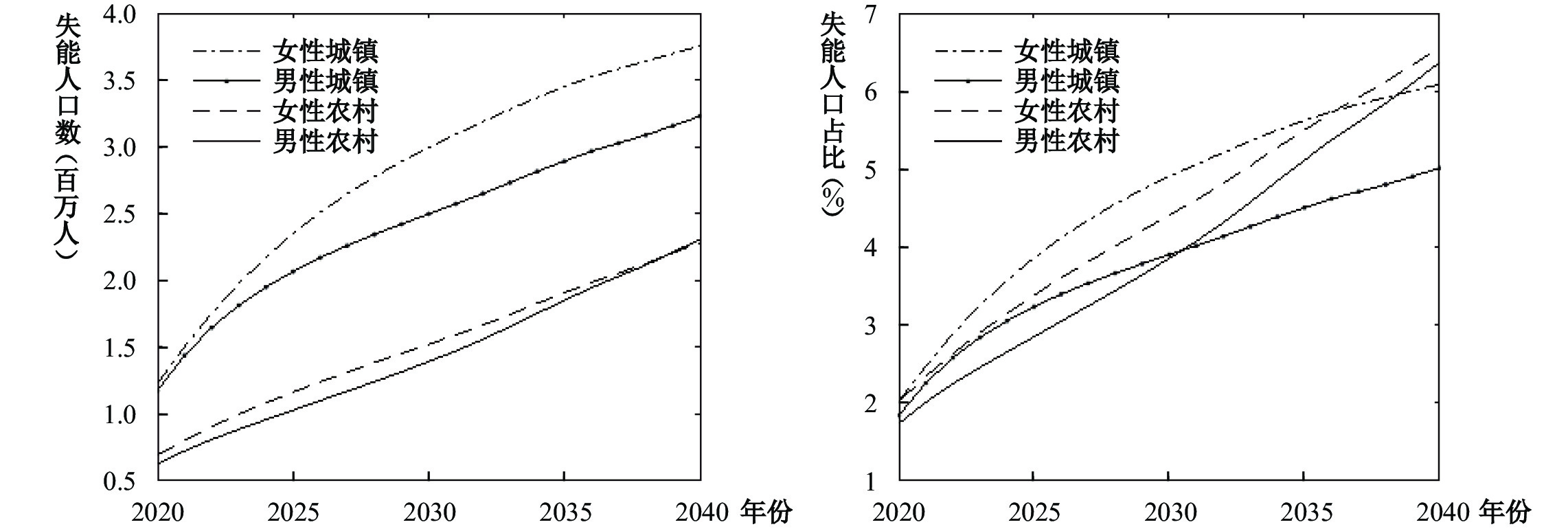
基于人口预测结果，并结合健康转移概率矩阵，预测得到2020—2040年老年失能人口规模，见图2左图。从中可以看出，未来的失能人数持续增加，2020—2040年增长了约3倍；2035年，失能人口更是冲破了1000万人。另外，城镇失能人口显著多于农村，可能是因为城镇失能率高于农村，而且城镇化过程中人口迁移导致城镇老年人口增多。在城镇地区，失能人口规模的性别差异逐渐扩大，女性失能人口增速显著快于男性；而在农村地区，男性失能人口增速与女性逐渐持平。图2右图展示了失能老人占65岁及以上老年人口的比例。可以看出，不同类别下失能老人占比逐步上升，但上升速度存在显著差异。比如，农村男性失能人口占比几乎呈线性增长趋势，城镇女性失能人口的增长最为缓和，呈抛物线趋势。虽然城镇的失能人口规模显著大于农村，但是城镇老年人口总量较大，因而出现失能老人占比相差不大的情况。

（三）参保人口规模

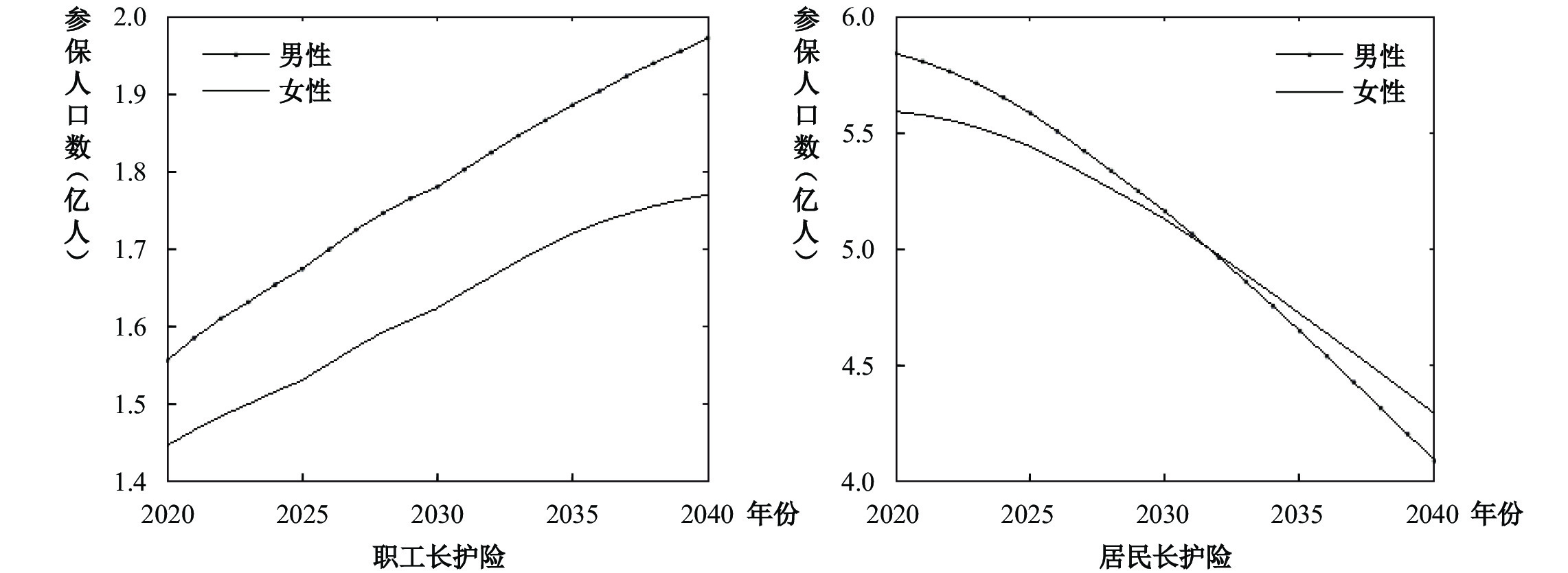
根据式（7）—式（12）可以得到2020—2040年职工长护险和居民长护险参保人数。从图3中可以看出，受人口年老龄化、城乡人口迁移和不同退休年龄等因素的影响，两种制度下未来参保人口总量和结构呈现出明显不同的变动趋势。职工长护险2020年的参保人数约为3.0亿人，而后逐渐上升，到2040年达到峰值约3.8亿人。而居民长护险的参保人数呈持续下降的趋势，这主要是受未来全国人口总量减少和职工长护险参保人口增加的双重影响。居民长护险2020年的参保人数为11.4亿人，到2030年减至11.0亿人，2040年又降至10.1亿人。另外，职工长护险的男性参保人数显著多于女性，且性别差异逐渐增大；而居民长护险的男性参保人数一开始多于女性，但到2032年左右与女性相等，随后少于女性，这与女性的预期寿命长于男性、退休年龄早于男性有关。

（四）不同筹资模式比较

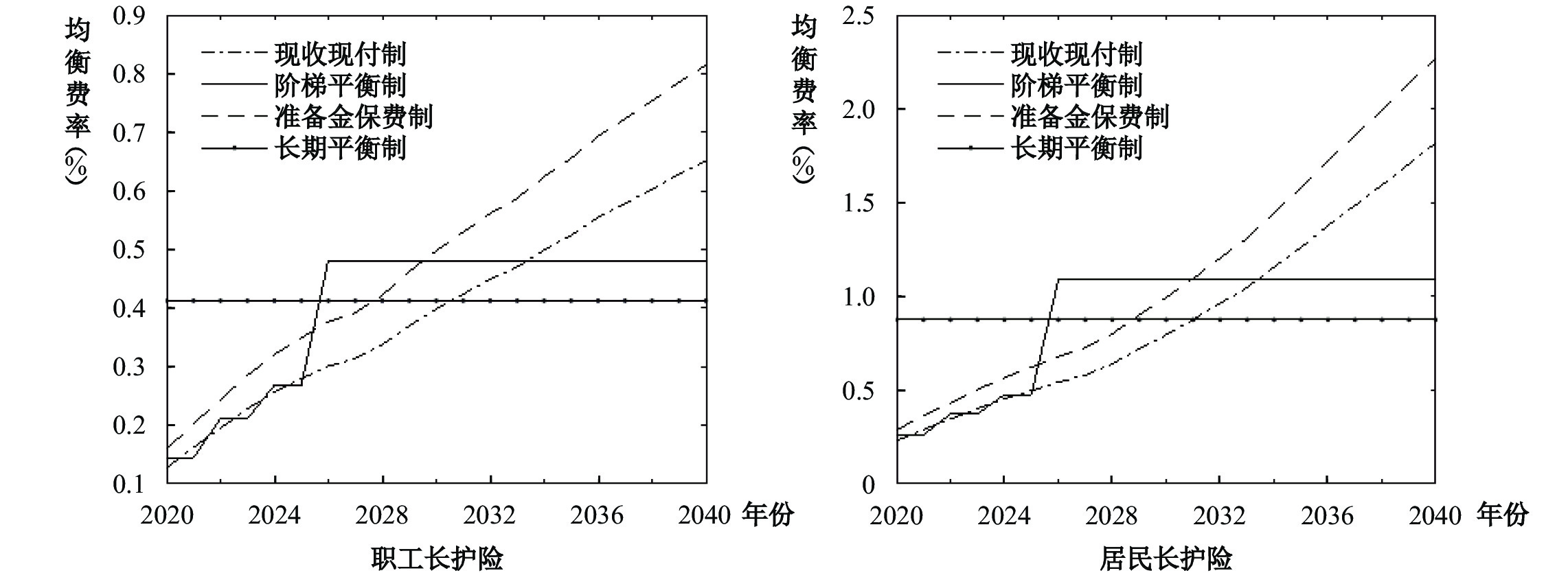
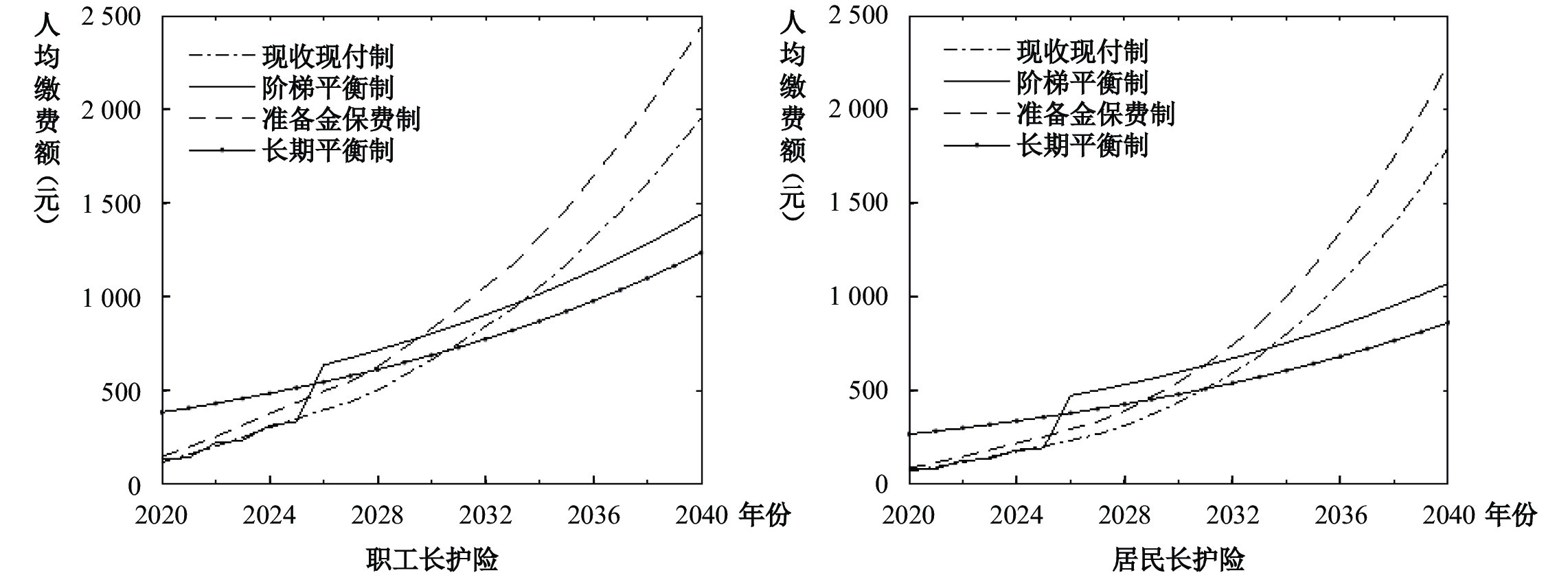
根据式（1）—式（6）可以得到2020—2040年职工长护险和居民长护险在不同筹资模式下的均衡费率（见图4）和缴费额（均衡费率乘以工资或收入，见图5）。无论是职工长护险还是居民长护险，不同筹资模式下均衡费率和缴费额的变化趋势都相同。在现收现付制下，均衡费率逐年递增，准备金保费制与现收现付制的变化趋势相同，但未来基金需要更多的储备收入才能实现结余率不变，所以准备金保费制与现收现付制均衡费率的差距逐渐变大。阶梯平衡制下均衡费率存在四种费率水平和三个变化梯度。长期平衡制下历年的均衡费率均相同。由于历年工资和收入上涨，图5中不同筹资模式下缴费额均逐年递增。另外，无论在何种筹资模式下，职工长护险的相对负担（图4中的均衡费率）均显著低于居民长护险，但绝对负担（图5中的缴费额）略高于居民长护险。这意味着职工长护险的筹资负担较低，《意见》指出“要从覆盖职工长护险起步”具有一定的合理性。将图4和图5的结果与中国长护险试点地区具体的筹资标准进行对比，如表5所示。

⑤职工长护险和居民长护险的筹资方式既包括比例筹资又包括定额筹资，因而需要分别分析均衡费率和缴费额。对于职工长护险，采取比例筹资地区的筹资标准在0.4%—1%之间，与长期平衡制下的均衡费率0.413%接近。这说明按照当前试点地区的筹资标准，职工长护险至少在2020—2040年是可持续的，因此可采取混合制中的任意一种。职工医保采取的也是比例筹资方式。部分长护险试点地区采取的是定额筹资，金额为30—180元/人，此时三种混合制在测算初始年份的缴费额分别为135元、148元和385元。因此，应排除初始缴费额过高的长期平衡制，可选择准备金保费制或阶梯平衡制。对于居民长护险，除了上海和青岛外，其他试点地区均采取定额筹资，年筹资额大致在30—90元之间，远低于本文计算得到的长期平衡制下的缴费额267元。虽然与现收现付制的71元、阶梯平衡制的80元和准备金保费制的89元在2020年的初始缴费额较为接近，但是未来增长较快，居民长护险基金容易陷入入不敷出的财务危机，因此应采取成本最低的现收现付制。

五、结论与启示

本文从老年个体健康状态的演变规律出发，模拟测算了在现收现付制以及阶梯平衡制、准备金保费制和长期平衡制三种混合制筹资模式下，职工长护险和居民长护险的均衡费率和缴费额，为中国长护险试点进程中筹资模式的选择提供了一些启示。

第一，老年失能人口规模快速攀升，失能风险急剧增大，将进一步放大老龄化风险，更加需要长期护理保险来保障失能老年人的基本护理需求。另外，不仅要关注失能老年人的身体健康需求，也要提高其生活质量。这是因为，失能的发生不仅会造成医疗卫生服务和长期护理费用等直接成本的增加，也会让家庭成员面临巨大的护理机会成本，且长期的照料活动还会影响照料者的身心健康。从失能人口的城乡差异来看，由于城镇失能率高于农村，且农村人口的大量迁移导致城镇老年人口增多，城镇失能人口规模显著大于农村。未来城镇人口的长期护理需求不容忽视。从失能人口的性别差异来看，女性失能人口显著多于男性。城镇失能人口的性别差异逐渐扩大，而农村男性失能人数与女性逐渐持平。中国女性高龄老人是失能人口的主体，政府要对高龄、失能且贫困的人口承担“兜底”工作，在养老服务资源供给的制度安排中，也要更多关注女性失能且贫困老年人的需求。

第二，长期护理保险应尽快覆盖城乡居民。在相同的筹资模式下，职工长护险的均衡费率低于居民长护险，但职工长护险的缴费额高于居民长护险。在生育意愿较低、城乡大规模人口迁移以及家庭照护功能减弱的背景下，解决城乡居民中失能老人的照护问题是中国积极应对人口高龄化的重点和难点。《意见》指出要从职工长护险起步，未来要加快将城乡居民医保参保对象纳入居民长护险中。在长护险制度建立初期，可按照护理保险“跟随”基本医疗保险的思路，规定参保人员在参加基本医疗保险的同时自动纳入护理保险制度。对城镇职工和城乡居民的筹资标准进行差异化设置，但未来要逐渐实现两种制度的整合，统一筹资标准，加快形成覆盖全民、保障适度的社会护理保险体系，积极应对人口老龄化和失能化风险。

第三，建议职工长护险采用具有一定积累功能的混合制，筹资压力较大的居民长护险采取成本最低的现收现付制。从中国基本医疗保险的筹资方式来看，职工医保采用比例筹资方式，居民医保采用定额筹资方式。根据本文测算结果，采取比例筹资的职工长护险可采取三种混合制中的任意一种；采取定额筹资的职工长护险建议采用准备金保费制或阶梯平衡制。采用现收现付制的居民长护险在推行初期的群众接受度较高，成本较低，但需要每年调整筹资水平，且基金没有任何结余，在经济环境突然改变时可能面临财务失衡，因此可以考虑建立安全储备机制。中国养老保险有中央财政预算拨款设立的“全国社会保障基金”。居民长护险也可以尝试建立“全国护理保障基金”，便于在护理支出出现资金缺口时进行补偿或调剂，从而增强现收现付制的稳定性。

① 感谢审稿专家的建设性意见。

② 详见《关于进一步加强基本医疗保险基金管理的指导意见》（人社部发〔2009〕67号）。

③ 这里设定极限年龄为100+而不是100，同时在计算不同年龄迁移率时，放宽了10岁以下农村人口迁出率为0的假设，使得迁移率更符合实际。

④ 2010—2019年参保率的年均增长率为0.94%，田勇（2020）等文献将参保率增长率设定为1%，所以这里的假定具有合理性。通过计算，至2045年，职工医保的参保率可达到100%。

⑤ 本文所指的筹资标准即人均筹资额（缴费额），不包括单位缴费、个人缴费、医保基金划拨和财政补贴等来源的具体分摊比例。长护险试点地区筹资标准的数据来源于各试点地区文件。