一、引　言

经济发展与环境污染的平衡问题是世界各国经济增长过程中面临的核心问题，引发了学术界广泛关注。例如，Meadows等（1972）提出了“增长极限说”，认为经济增长在自然资源的约束下不可长期持续；Grossman和Krueger（1991）提出了环境库兹涅茨“倒U形”曲线，认为一国的整体空气污染会随着经济的发展先上升然后再降低；Beckerman（1992）以及Bhagwati（1993）认为，经济发展本身促进了环境资源保护，因此对于空气质量有着正向的提升作用。产业结构变化作为经济发展的重要推动力量，是影响经济发展与环境污染关系的重要因素（王敏和黄滢，2015）。而中国产业结构调整带有明显的经济转型痕迹，如何推动产业结构调整、优化，促进传统粗放式生产方式和消费方式向绿色低碳转变是我国推动经济高质量发展的重要维度，也是实现“碳达峰、碳中和”目标，践行创新、绿色发展理念的重要体现。

研究产业结构与空气污染的文献，可追溯至Grossman和Krueger（1995）分析亚洲国家产业结构与环境污染之间关系的研究，其提出了产业结构与环境污染之间存在着“倒U形”关系，即随着产业结构由一产主导向二、三产主导转变，环境污染呈先上升后下降的过程。但李鹏（2016）的研究发现，环境污染同时受经济增长速度和产业结构调整幅度的影响，当产业结构调整剧烈而经济处于中低增长速度时产业结构与环境污染之间存在“倒U形”关系；但当经济增速变化较大，经济增长效应较高时会导致“倒U形”关系被破坏。李健和周慧（2012）也发现，第二产业虽然相对于第一、三产业对碳排放强度的影响最大，但第二产业并不必然与高碳排放直接挂钩，且第三产业占比的增加对空气质量的提升作用并不明显。可见，产业结构对空气质量影响实际上存在着较为复杂的非线性、结构性特征。产业的转型升级意味着产业间、产业内部结构呈现一定的差异性变化，其对环境的影响也需要更细致的证据。由于影响环境污染的因素较多，如何“干净”地厘清产业结构对环境污染的影响一直是实证研究的难点之一，只有较好地解决遗漏变量以及产业结构与环境污染之间双向因果关系等内生性问题才能准确识别产业结构对环境的效应。始于2019年底的新冠肺炎疫情导致的中国各地“一致”的停工停产为研究这一问题提供了一次“干净”的自然实验。

基于此，本文选取2019与2020年春节前后近三个月中国地级市每周平均空气质量指数（AQI），以2019新冠肺炎疫情（COVID-19）导致的全国范围停工停产为自然实验，采用广义DID方法有效识别了产业结构对空气质量改善的具体影响。研究结果表明：对空气质量的影响主要源于第二产业，在停工环境下，其占GDP比重每上升1%，空气质量指数相较于上年同期下降0.470；第二产业内部细分行业对空气质量影响也呈现较大差异，其中影响最大的是制造业，且制造业中轻工业的影响高于装备制造业与能源化工业；而由于疫情期间的生活需求增加代替了停工减少的工业需求，水电气热生活供应业最终表现出对空气质量改善的影响并不显著。同时，还发现不同产业对空气质量的影响路径存在一定的差异：生产过程对第二产业的污染贡献度高于第三产业；在制造业内部，轻工业受员工通勤因素影响相对更高，而能源化工业受生产过程影响更甚。本文的边际贡献在于：一是创新地以疫情冲击所导致的停工停产作为准自然实验，利用城市样本数据和广义DID等方法比较了强制停工停产下各地空气质量改善的产业结构差异，有效缓解了遗漏变量以及互为因果的内生性问题，为准确识别产业结构对空气污染的影响提供了证据。二是通过对第二产业细分行业的进一步深入研究，有效揭示了产业结构对空气质量改善的结构性影响特征，准确识别出了第二产业不同行业停工对空气质量提升的贡献和具体路径。三是通过上述稳健与精准的识别，本文认为第二产业以及内部的能源化工绿色发展的关键在于生产过程的改造升级，通过技术升级降低对劳动力的依赖是轻工业降碳的主要方向，这为实现“碳达峰、碳中和”的产业结构调整途径提供了实践依据。

二、研究命题与识别策略

（一）研究命题。由于不同区域产业间及产业内部的结构差异较大，简单地从三次产业结构分类来研究无法有效地刻画出产业发展与环境污染关系的真实面貌。为此，众多学者从更为具体的产业入手分析了产业结构对生态环境的影响。曹执令和杨婧（2013）对中国制造业的环境污染水平进行了测算，发现在制造业内部不同细分产业对环境污染存在不同的影响，其中高度污染多为资本密集型行业，而低度污染多为技术密集型行业。陈军和成金华（2015）则发现，在矿产资源中，能源矿产开发利用的环境影响最大、金属矿产次之、非金属矿产的影响相对较低。汪克亮等（2010）以及白俊红和聂亮（2018）则从不同产业的能源消耗量、能源使用效率与环境污染效应间的关系进行了分析，发现能源强度、能源结构和环境污染排放呈正相关，电力、钢铁、有色金属、石油石化、化工、建材等重点耗能产业带来的环境污染最高。可见，准确揭示空气污染的产业结构差异才能厘清二者真实的关系。基于以上分析，本文研究的第一个命题是对环境污染的产业结构效应进行精准识别：城市的空气污染存在产业结构的差异，即使在三次产业结构相同的地区，也会因产业内部结构不同而对空气质量产生异质性影响，只有对三次产业内部尤其是污染效应较大的二产部门进一步细分才能识别孰重孰轻。

识别产业结构差异性对空气污染影响的路径是本文需要进一步探讨的问题。在城市经济生活正常运行下，交通与产业生产常被视作空气污染的重要来源，但不同城市的交通条件、生产结构不同，在经济正常运行时多项经济活动混杂交织，导致政策冲击的效果与经济特征的交互效果被模糊化。如城市的通勤、商业部门运行以及正常的工业生产等（吴力波等，2020）。Viard和Fu（2015）发现限行政策对空气质量有显著改善作用，单双号限行使空气污染指数下降了19%，尾号限行使空气污染指数下降了8%。Fu和Gu（2017）利用双重差分法估计了2012年国庆期间高速公路免收过路费对空气质量的影响，发现汽车出行量的增加使得空气污染程度提升了20%。Davis（2008）与曹静等（2014）分别估计了墨西哥城与北京市的车辆限行政策发现，虽然传统的OLS回归显示出限行政策有很强的效果，当采用断点回归的方法解决其内生性后，限行政策尤其是“尾号限行”对空气质量的影响甚微。此外，Wang等（2019）以及Qian等（2020）通过使用结构分解模型和指数分解模型发现，除产业正常的经济生产活动外，交通通勤和居民的生活消费也是导致中国空气污染的主要因素。而这些因素又往往伴随在居民的日常经济生产活动中，因此本文研究的第二个命题将对以下两种影响路径进行进一步识别：城市空气污染的产业结构性差异主要体现在生产过程以及员工因生产所伴随的通勤与餐饮两种路径，因此隔离这些因素对空气质量的影响，并进一步区分不同产业对空气污染的路径依赖度差异，才能较准确地评估产业生产活动对空气质量的影响。

（二）识别策略。在估计产业结构对环境污染影响的实证过程中，存在着两个重要的内生性问题，一是产业生产活动之外其他影响环境污染的遗漏变量问题；二是环境污染与产业结构调整之间可能存在着反向因果关系。而在产业结构影响空气质量框架下，由于已充分考虑了产业生产活动的影响，因此遗漏变量就主要集中在居民的交通出行与餐饮生活等方面。为了解决非生产性通勤可能出现的遗漏变量内生性影响，借鉴王敏和黄滢（2015）与吴力波等（2020）的做法，将各城市的城内迁徙指数、各城市的路网密度和绿化覆盖率作为代理变量来控制机动车的影响。为了解决餐饮可能带来的内生性问题，将各城市人口密度作为餐饮的代理变量，一定程度上缓解了这一遗漏变量的影响。关于环境污染与产业结构之间的反向因果问题，诸多文献已经论证环境污染与环境规制对产业结构确实存在着一定的倒逼机制。李斌等（2013）认为，加大环境规制力度有利于促进工业发展方式的转变，有效倒逼产业结构朝低碳化方向调整。原毅军和谢荣辉（2014）发现，随着环境规制强度由弱变强，会对产业结构调整产生先抑制、后促进、再抑制的影响。童健等（2016）发现，环境规制对工业行业转型升级的影响呈现“J”形特征，且“J”形曲线的拐点取决于环境规制的资源配置扭曲效应和技术效应在污染密集行业的相对大小。宋建和王静（2018）认为，环境污染通过全要素生产率的“价格效应”机制作用于产业结构，生产性服务业的发展会导致环境污染和行业结构之间存在“U”形关系，而劳动密集型行业的发展使环境污染与产业结构调整之间存在“倒U形”关系。本文构造的准自然实验可以缓解这一内生性问题。

以往研究产业结构和环境污染之间关系的文献，主要基于OLS（于峰等，2006）、联立方程（包群和彭水军，2006）和向量自回归VAR模型（曹慧丰等，2015）等。这些方法在一定程度上解决了内生性问题，但无法完全解决遗漏变量的干扰，也无法有效识别外生政策冲击的影响，对参数的一致性估计会造成偏误。如何有效处理这种内生性所导致的识别偏差一直是实证的难题所在。鉴于此，本文创新地以新冠肺炎疫情导致的全国大面积停工停产为自然实验，以2019年与2020年春节前后近三个月中国地级以上城市每日空气污染物衡量空气质量，采用广义DID方法精准识别了中国产业结构与空气污染的因果关系。其逻辑在于，产业结构是以突变的形式从疫情前的正常状态变为几乎不存在任何生产的停滞状态，时间跨度较短，产业结构能够显著影响空气质量，但空气质量的变化对产业结构变化几乎不会有影响，有效避免了反向因果的内生性问题。疫情带来的冲击是全方位的，所有省市均在这一冲击下受到了强烈影响，传统的DID方法并不适用于这样的数据。而广义DID在处理过程中系统地将所有个体同时受到政策冲击这一特征纳入模型构建过程，并会考虑到政策对每位个体的影响差异，将这些差异的大小作为了冲击的主要变量。本文中，不同产业结构对空气质量的影响正好满足广义DID的适用条件。

为全面深入评估城市产业结构对空气质量的影响，同时提高研究的稳健性，本文将采用两组样本分别进行DID回归检验。第一组样本选取中国279个地级市的三次产业面板数据，以农历的春节为基准，将2020年1月1日—4月7日期间中国279个地级市14个星期的样本作为处理组，并将2019年对应农历时间段的样本作为控制组（2019年1月12日—4月19日），以样本数据的周平均数作为回归的基本单位。第二组样本同样选取相同的农历时间段，且按国民经济统计行业分类标准有公开数据的78个地级市作为样本，将城市第二产业细分为六个子行业，进一步研究了城市细分产业结构对空气质量的影响。首先用“经典DID”模型分析因疫情封城所导致的停工停产对中国城市空气质量的影响，模型设定如下：

代表空气污染指标（下标i代表城市，下标t表示时间序列，单位为星期），选取每座城市每日23点统计的周平均AQI（空气质量指数）作为代理变量；treat_i是虚拟变量，表示研究对象是否为处理组。由于本文选取了中国地级市2019年的样本作为控制组，2020年的样本作为实验组，因此同一城市不同年份数据的下标 是不同的，如2020年的北京与2019年的北京，被看作是同一时间截面上两个不同的城市。这里暗含了一个假设，即产业结构的调整是一个渐进的过程，在短期内某个城市产业构成的变化幅度较小。也就是说，如果没有发生新冠疫情，同一城市主要解释变量产业结构 （下标i代表城市，下标j表示产业）在2020年与2019年的任意时间均保持相对不变。二者除了疫情的冲击外，在产业结构及其他城市固定特征相同，这样就天然地构造出了对照组与实验组。

为处理期虚拟变量，即只有处理组在处理期才会受到政策冲击。2020年1月23日，武汉宣布封城，而1月24日到1月30日为春节假期，且各省市宣布防疫停工的时间均发生在这一时间段内。鉴于中国春节假期及之后几天历年都是普遍停工的，疫情冲击所导致的停工停产效应无法在春节假期表现出来，因此本文认为政策冲击发生在春节结束后，即2020年疫情对企业的影响实际上是从2020年元旦起的第五周才开始。

为其他控制变量，参考现有文献做法（曹静等，2014），选取每周平均风速 和每周雨雪天数 。和 分别为个体固定效应和时间固定效应，为随机误差。由于所选取的研究时间较短（仅春节前后十四周），假设主要解释变量产业结构 在研究时间内均不随时间t变动，因此该变量的影响在模型（1）中会被个体固定效应所吸收从而无法识别其对空气质量的影响。为识别出中国城市产业结构对空气质量的产业结构效应，需要放松模型（1）中对个体固定效应的假设，同时采用一些衡量个体特征的控制变量 替代，参考已有相关文献的控制变量，如李小胜等（2013）及李卫兵和张凯霞（2019）等，在模型中引入组间效应：是否为北方城市 （以秦岭淮河为界），是否为海滨城市 （城市是否有海岸线）。同时为衡量经济发展水平对空气质量的影响，在城市层面控制城市规模 和地区富裕程度（人均 ）。此外，Fu和Gu（2017）认为，机动车尾气和餐饮服务也是影响空气质量的重要因素，由于居民对食物的需求在停工后并不会发生太大变化，餐饮行业停工所减少的空气污染由增加的家庭油烟排放所替代，因此可以通过城市人口密度 来控制餐饮业的影响，而城市人均道路面积 和建成区绿化覆盖率 则作为衡量机动车尾气的控制变量。基于上述考虑，实证模型扩展为如下形式：

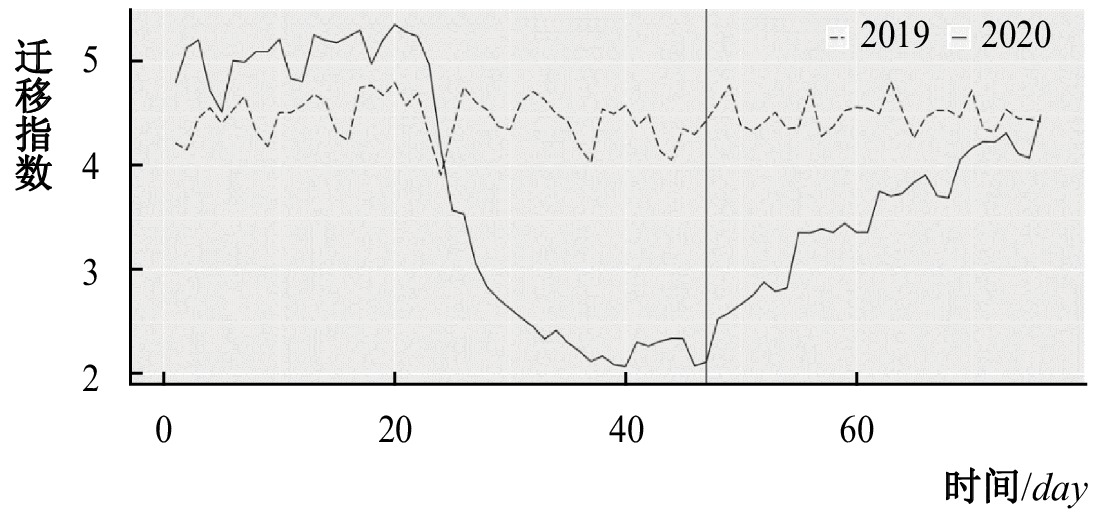
在疫情得到一定的控制后，中央政府随即宣布部分地区逐渐复工，但各类企业不得早于2月9日24时。但事实上，由于疫情的防范措施和防护物品的短缺，部分复工企业并未能在宣布复工后立即恢复原有的产能和生产效率，延迟了大规模恢复生产的实际发生时间。通过查阅2020年城市平均人口迁移指数^①的变动情况（图1），发现在中央政府宣布复工的两周后，城市人口迁移指数才开始提升，这也从侧面进一步证实了复工复产相对于政策的滞后性。鉴于此，选取2020年元旦起的第七周前后作为复工冲击的虚拟变量。另外，虽然每个城市均受到疫情所导致的停工停产冲击，但由于不同城市的产业结构存在着较大差异，因此停工停产的冲击对不同城市空气污染的影响是不同的，由于本文研究疫情冲击下产业结构对环境污染的影响，因此选用产业结构

作为政策冲击的影响力度。在加入复工复产的虚拟变量以及考虑产业结构的差异后，广义DID模型扩展为：

产业结构对空气质量的影响在疫情前为

；当疫情冲击导致停工停产后，产业结构对空气质量的影响为 ；在部分复工之后，影响系数变为 。本文主要考察疫情停工发生后，产业结构影响系数下降的幅度并比较哪个产业停工对空气质量的提升作用较大，即系数 。此外，即使两个城市的三次产业结构相同，其内部细分产业结构对空气质量变化的影响仍然存在个体差异。为准确识别出不同行业影响的差异性，需要进一步对三次产业内部不同细分产业进行分析。通过查找、匹配中国地级市层面的统计年鉴，根据细分行业的数据完整性与行业共性，按照国民经济统计行业分类标准，本文将第二产业内部进一步分成六个子行业类别。^②在对第二产业进行细分之后，第二产业内部产业结构对环境影响的计量模型如下：

其中，产业m在疫情前对空气质量的影响为

，疫情冲击下的影响系数变为 ，而在部分复工之后影响系数变为 。对二产进行细分可以更加精准识别影响空气质量的细分产业特点，干净识别各细分产业对复工之后空气质量的影响。

三、数据说明

（一）数据来源。选取AQI（Air Quality Index，空气质量指数）作为被解释变量，并将其他衡量空气质量的指标如PM2.5、PM10、SO2等作为稳健性检验的替代性指标。通过查阅各城市2019年国民经济和社会发展统计公告获得核心解释变量城市产业结构

，其余控制变量数据来源于各城市统计年鉴。但由于全样本组的279个城市中有许多城市并未公布地方最新的统计年鉴，且部分城市虽然有统计年鉴但却没有公布国民产业统计分类的细分数据，最终收集到有国民统计分类的城市样本共78个（数据来源于各地级市2019年统计年鉴，由于最新数据的缺失，湖南、湖北、河北、辽宁、吉林、黑龙江的城市由2018年统计年鉴作为代替）。

（二）统计性描述。为了避免用日数据得到的结论受意外事件的影响，本文的基准模型采用按星期平均的数据作为基础单位（日数据在后文中用作稳健性检验），得到279个地级市分别在2019年（2019-01-12—2019-04-19）和2020年（2020-01-01—2020-04-07）春节前后14个星期，总计7 812个样本，个体控制变量均以对数形式表示，各变量的统计性描述见表1。从表中可以看出，第二产业与第三产业比重之比大致在40%—50%，正是经济转型与产业结构调整的典型阶段。被解释变量空气质量AQI指数平均处于良好状态，城市之间存在一定的差异，最好的为15.14优的状态，最差的为316.43，处于严重污染状态。对第二产业进一步细分的描述性统计结果和全国样本的趋势基本一致（限于篇幅未列示，具体见本文工作论文）。

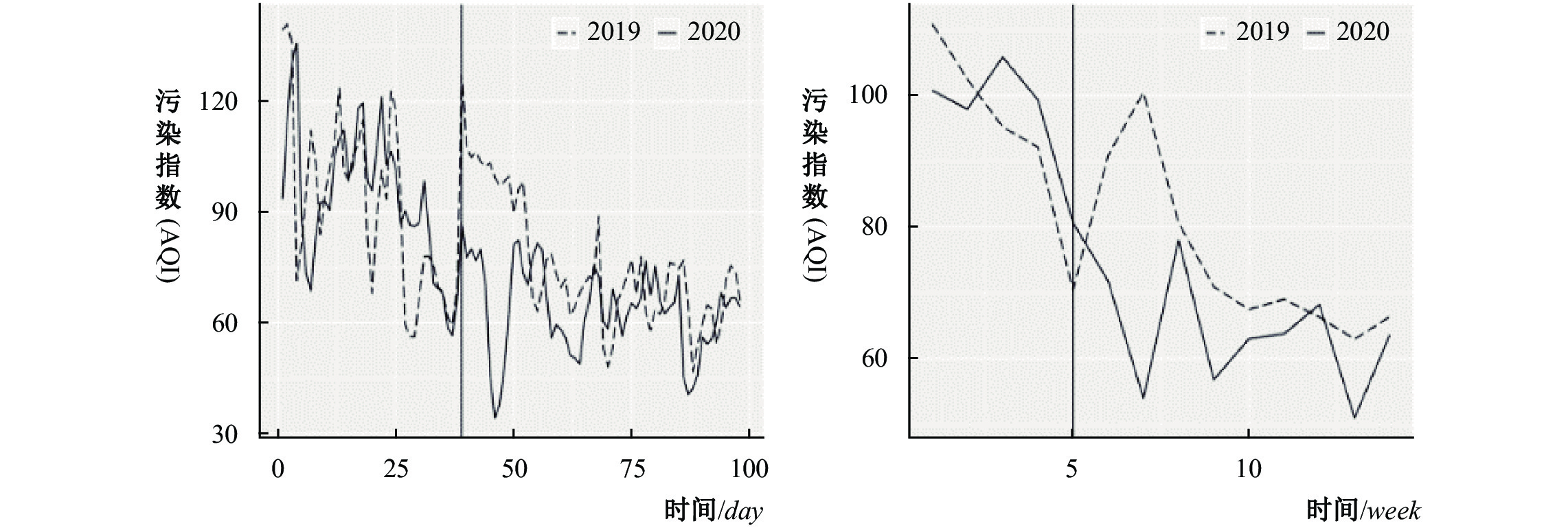
（三）平行趋势检验。双重差分法估计能够有效应用的一个重要前提是要满足平行趋势假设，即不发生疫情所导致停工的情况下，试验组（2020年城市样本）的变化与对照组（2019年城市样本）的趋势变化保持一致，这样得到的平均处理效应才不会因样本自身的周期性变动而存在估计偏误。图2展示了以2019年为对照组，2020年为实验组并以春节为时间基准日期的全国279个地级市日平均污染指数和周污染指数变化趋势图。可以发现，无论以日数据还是周数据为单位，2020年第五、六周（即春节结束后的两周时间）的空气质量指数较2019年都存在显著差异。同时，在2020年的第七到第八周之间，因复工使得各项空气污染指数均有所回升，而在2019年由于没有疫情的冲击与复工影响，这一回升在春节结束后即第五周便开始出现。而在疫情发生的时间之前以及复工之后，实验组与对照组的空气质量指数的变化趋势基本一致，从而可以判定本文所采用的样本数据符合DID双重差分法估计所要求的事前平行趋势假设。

另外，城市的空气污染主要来源于日常生产和通勤，因此空气质量的改善必然意味着居民日常活动的频率降低。本文选取了中国地级市2019-01-12—2019-03-28以及2020-01-01—2020-03-16的城内人口迁移指数（数据来源于百度地图慧眼）作为对比（见图1），发现在2020年春节前夕武汉正式宣布封城后（2020年1月23日），中国城市的平均迁移指数相较2019年同期有明显下滑，直到第七周才出现反弹。这一结果也解释了样本数据符合平行趋势假设的潜在原因。另外，由于城市的空气污染一方面来自于居民的生产活动和以生产为目的的通勤，同时也来源于一些非生产目的的通勤活动，如何剔除因非生产目的通勤活动减少而导致的空气质量改善对本文回归结果的干扰，也是本文实证分析中需要解决的问题。

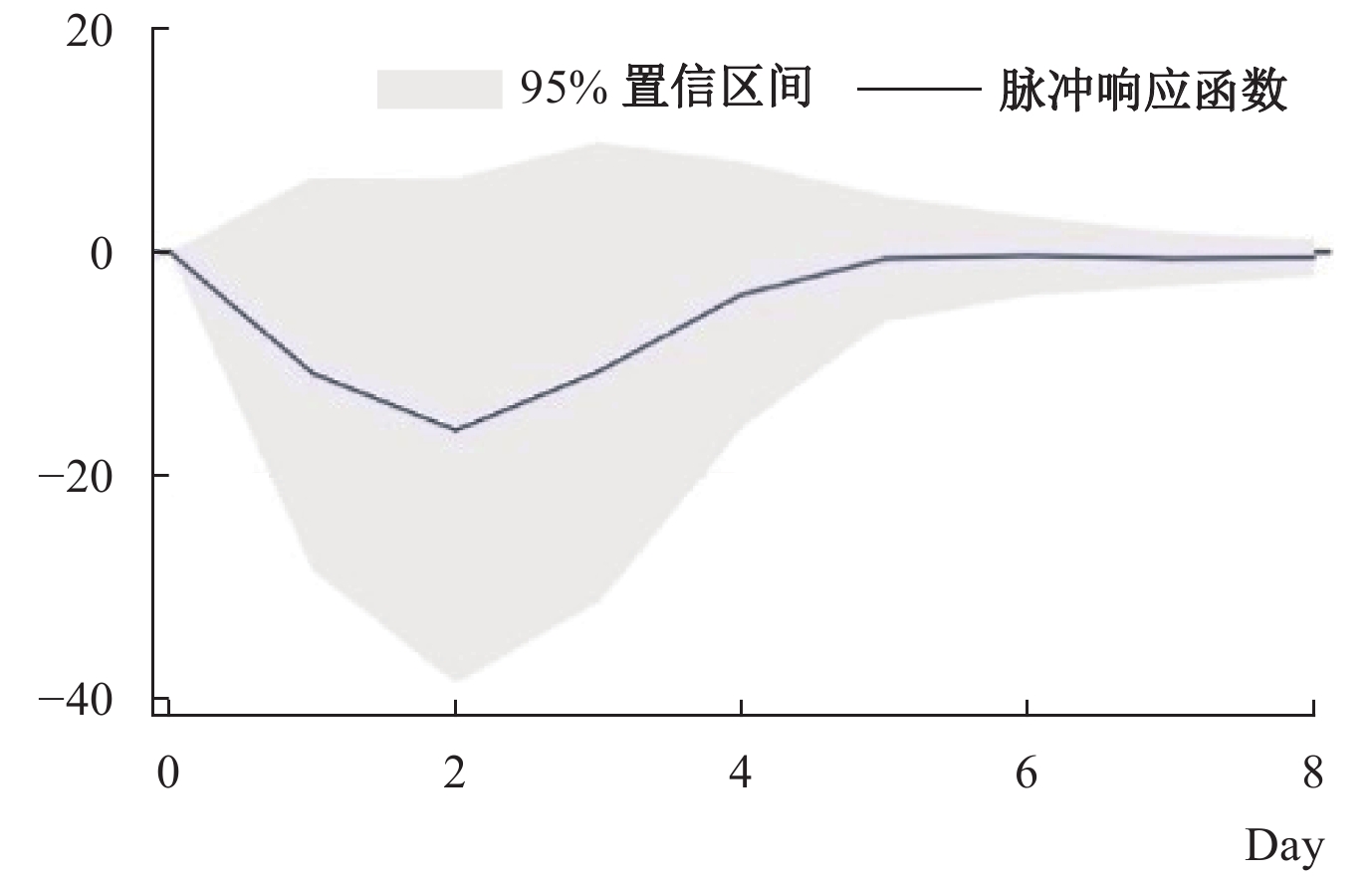
（四）行业间复工程度比较。若不同行业间复工程度存在过大差异，所估计结果不具可比性，因此计算出各行业的复工程度有助于对回归结果进行解读和理解。在2月9日中央政府宣布复工之后，部分企业因劳动力和原材料短缺，实际复工日期可能延后，抑或是企业出于对防疫的考虑，员工日均工作时间低于停工前，都可能导致企业生产效率低于停工前。鉴于城市的人口迁移活动频率可有效衡量城市的复工情况，本文通过对2019年的中国城市日平均AQI指数和中国城市日平均人口迁移指数做VAR向量自回归，^③脉冲响应见图3，发现当人口迁移指数对当期的AQI指数有一短暂的冲击后，在第二日偏离度达到最高水平，五日后AQI指数恢复到原有水平（即如果能在2月9日完全复工，AQI指数2月14日即可恢复原有水平），但观察图2可以发现，在宣布复工之后的两到三周，AQI指数才逐步接近去年同期水平，说明中央政府宣布复工之后，社会整体产能并没有立即恢复到停工前水平。各行业产能效率下降是由于复工延迟，还是日均工作时间的减少，限于数据可得性，本文无法直接识别出来，因此通过查阅中国统计局2018—2020年的各行业第一季季度数据，采用综合复工生产率来衡量复工程度。

利用各行业实际增加值和相应的平减指数计算出各行业2018—2019年和2019—2020年的实际增长率。假设没有发生疫情停工，各行业2018—2019年和2019—2020年的实际增长率应相等，由两项之差即一季度效率损失，进一步可得一季度总生产效率，并基于^④式（5）计算出综合复工生产效率：

表2显示2020年一季度二、三产业的复工程度基本一致，综合复工生产效率分别为91.32%、91.36%。而采矿业及水电气热和金融业的综合复工生产效率超过了100%。说明这些行业在疫情期间很有可能并未停工。第二产业中建筑业复工程度最低，综合复工生产效率为75.39%，第三产业综合复工生产效率为42.84%。对于制造业内部，由于没有各细分行业增加值的数据，因此通过查阅制造业2020年一季度销售额，发现轻工业、能源化工和装备制造2019—2020年的销售增长率分别为−19.98%、−18.86%和−20.37%，可见三个行业的复工程度大致在同一水平。

四、实证结果分析

（一）按三次产业分类的回归结果。

1. 标准DID回归结果。表3报告了标准DID模型估计结果。其中列（1）和列（2）分别为标准DID模型下仅考虑停工冲击和同时考虑停工和复工冲击的结果。结果表明：疫情导致的停工冲击使得空气污染指数明显下降，而复工的冲击使得空气污染指数有了显著上升，但停工和复工冲击的整体净效应对空气污染指数的影响仍为负（列（2）中

与 系数之和）。说明尽管从政府到企业都采取了积极措施复工复产，但由于需求疲软、劳动人口流动限制、供应链受阻以及可能存在的部分企业“虚假复工”，企业实际产能并没有恢复到疫情之前的水平。另外从列（4）可以看出，第二产业停工对空气质量改善有着显著的影响，其占比每上升1%，AQI指数下降0.470。而第三产业停工，每1%占比使AQI指数下降0.307，低于第二产业，说明第三产业的生产经济活动并非影响空气质量的主要产业因素。

主要控制变量的回归结果表明，风速提高可以有效降低空气污染指数，即同一地区风速

越高空气污染相对越轻。而 的系数为负，表明雨雪天气可以有效缓减空气污染。地域发展差异也是我国产业转型的重要特征，和 的回归系数表明相对于滨海城市和南方城市，内陆城市和北方城市空气污染会更加严重，这是因为，自20世纪50年代开始，中国北方（秦岭—淮河以北）就开始集中供暖，而南方地区始终未普及该项政策，因此在同样的居民活动频率下北方地区春节期间所排放的空气污染物会明显高于南方。沿海地区的通风条件和绿色植被等要优于内陆地区。另外，城市经济规模 对空气污染指数有正向的显著作用，即经济总量越高的城市空气污染相对更严重，意味着我国城市经济发展总体而言还比较粗放，而人均 的系数显著为负，由于经济发展水平较高的城市产业升级相对较早，且应对环境治理的综合能力较强，因此对于空气质量有着正向的提升作用（Beckerman，1992；Bhagwati，1993）。建成区绿化覆盖率 的系数为负，表明城市绿化覆盖率的提高有助于提高空气质量。人口密度 和城市人均道路面积 的回归系数显著为正，说明居民活动如餐饮和通勤等对空气质量有着负面的影响。系数并不显著，表明2019年和2020年之间年份个体固定效应的差距不大，即2019–2020年，全国范围内没有发生其他显著影响城市空气质量的遗漏因素，进一步说明了本文将中国城市2019年对应时间的空气质量作为2020年的对照组这一做法是比较合理的。

2. 广义 DID回归结果。由于地区间存在异质性，疫情停工导致的空气质量改善在各地区可能不一样，本文重点关注这种差异性产业结构因素。为此，引入广义DID模型，通过考察第二产业

在冲击前后的系数变化来识别这种差异性。表3列（3）与列（4）即为广义DID回归结果。其中列（4）结果表明，在疫情冲击和复工之后，第二产业 的系数均发生了显著的变化：在疫情发生前 的回归系数为0.433，疫情停工冲击导致系数下降了0.470，部分复工之后系数上升了0.332，但仍低于疫情停工冲击导致的下降数值；第三产业系数变动趋势与第二产业一致，但系数变动幅度均小于第二产业。因此，相较于停工阶段，复工之后第二产业比重越高的城市空气质量指数反弹的幅度就越大，但两次冲击对空气污染的净效应仍然为负，与表3中标准DID回归模型得到的结果一致。同时标准DID与广义DID的控制变量回归系数估计值和显著性均保持高度一致，说明了实证检验的稳健性。上述结果表明，第二产业比重越高的城市，停工停产对空气污染的改善作用越大，且影响系数高于第三产业，即二产的减少能够增进城市空气质量的改善，这说明产业结构由制造经济转向服务经济的过程中，往往会伴随着空气质量的改善与提升。

（二）第二产业细分行业回归结果。以上检验主要基于三次产业分类的估计结果，但实际中由于产业内部的技术特点、生产方式等存在着较大的差异，即使是相同的三次产业结构也会在其各自内部的具体细分构成上存在区别。根据前文估计的结果，第二产业对空气质量影响更大，因此在进一步分析中主要的研究视角聚焦在第二产业。为了准确识别出不同类别的第二产业子行业对空气质量的影响，本文选取具有国民统计细分行业的78个城市作为检验样本，分别进行标准DID（表4中列（1）、列（2））和广义DID（列（3）、列（4））回归。列（1）和列（2）报告了该样本在未细分第二产业的情形下，第二产业在疫情冲击前的影响系数为0.454、冲击后和复工后对空气污染指数影响系数变动幅度为−0.865和0.671，比较这两个系数可知，第二产业对空气的影响在复工之后仍未回到疫情前水平，说明在研究期间，第二产业在复工后仍没有恢复到原有的生产水平。回归结果与表3中大样本得到的结果均保持高度一致。

从表4列（4）可以看出，采矿业占比

的系数无论是疫情冲击前，还是疫情和复工带来的冲击下均不显著，结合前文对行业间复工差异度的比较分析，可能的原因在于疫情对采矿业并没有太大的影响。轻工业 的估计系数在几个模型中均显著，在疫情冲击前估计系数为0.240，疫情冲击之后系数下降了1.464，复工之后上升1.093。除了生产过程带来的空气污染，轻工业本身也是吸纳就业人口较多的制造业部分，所以轻工业造成的污染也包含了一部分以生产为目的的通勤污染和日常能源消耗，因此一旦工厂停产，会极大地减弱对空气的污染影响。同样属于制造业的能源化工业 在疫情冲击前的估计系数为1.009，疫情冲击之后系数下降1.080，复工之后系数上升0.753，但复工冲击的影响系数并不显著，说明能源化工产业在研究期内的复工情况可能并不理想。而装备制造业 在疫情冲击前估计系数为0.727，疫情冲击之后系数下降1.103，复工之后系数上升0.700。能源化工业 和装备制造业 在生产过程中产生了比较大的空气污染，但对人工的依赖相比轻工业低，而自动化程度较高，因此停工之后行业的估计系数下降幅度均小于轻工业。上述三类制造业在复工之后系数的回升幅度均不及停工带来的下降幅度，这说明了制造业在复工之后均没有恢复到原有的生产水平。与前文行业间复工差异度分析结果一致，通过比较停工之后系数的下降幅度可以发现，在隶属于制造业门类的三个子行业中，停工对空气质量改善边际影响最大的是轻工业，装备制造业次之，能源化工业最后。由于疫情发生后，居民隔离在家，对水电燃气的需求上升，正好弥补了工业企业需求下降的缺口，需求弹性较小，产能并未发生太大改变，因此停工和复工冲击对水电气热等生活供应 的估计系数并没有显著影响。建筑业 主要污染在于扬尘，远不如工业制造对空气造成的污染。停工后，系数没有显著变化，由于建筑业是典型的劳动密集型行业，复工之后会造成较大的人员流动，估计系数有小幅回升。综上所述，第二产业的六个子行业中，受疫情停工冲击影响对空气质量改善的边际贡献由高到低依次为轻工业、装备制造业、能源化工、采矿业、建筑业、水电气热。因此，这些行业通过技术创新、结构调整实现绿色发展对于空气质量的改善至关重要，也是实现我国产业高质量发展、实现人与自然和谐发展现代化建设新格局的重要突破口。

（三）异质性分析。产业结构对空气质量的影响一定程度上来自于三产内部的结构差异，经济规模、二产比重差异也会使产业结构对空气污染的影响呈现显著差异。表5反映了按GDP规模和第二产业比重分组的回归结果：停工之后，在GDP规模较大的城市，第二产业比重对空气污染影响系数的变动更大，而疫情冲击和复工带来的系数变化在不同GDP规模城市间差别较小；规模较小的城市，变化幅度相对较大。在不同二产比重城市中，二产比重对空气质量弹性系数变化趋势均保持一致，且二产比重越低的城市系数变化幅度越大。以上结果说明，第二产业对空气污染的影响在城市GDP规模上存在边际效应递增关系，而在二产比重上边际效应递减。即GDP规模越大，第二产业比重越低的城市，第二产业对空气污染的边际作用越大。

五、稳健性分析

（一）稳健性检验。为避免上述结论的偶然性，保证研究结论的可靠性，本文从样本数据替换、异常样本剔除、核心被解释变量替代等方式进行稳健性检验。通过调整样本的时间单位，用日数据替代周数据，得到54 642个新样本并对原模型再次进行回归。另外，由于湖北在此次新冠疫情中的相关防疫政策和其他地区存在着明显的差别，因此本文利用剔除湖北的城市的数据，重新进行回归分析。最后本文将空气污染指数的代理变量AQI替换为PM2.5、CO、NO₂再依次对模型进行回归。以上三种稳健性检验所得到的结论与基准回归基本保持不变（限于篇幅，稳健性检验结果未展示，详见工作论文），从而证明了本文研究的稳健性。

（二）内生性讨论。尽管采用广义DID能够部分避免内生性，但考虑到在疫情期间，由于城市居民通勤频率和交通工具使用次数的下降，尾气排放数量也相应减少，也是城市空气质量改善的原因之一。在之前的回归中，已将人口密度

和人均道路密度 作为控制变量以控制因居民生活消耗和通勤造成的污染。为了进一步增加回归结果的精确度，减少遗漏变量带来的误差，引入“百度迁移指数”这一日变量来控制居民的日通勤频率。^⑤表6显示，的系数显著为正，说明城市居民的通勤增加确实会使空气污染指数提高，符合之前的预期。在控制居民通勤后，其他变量的系数与基准回归结果无显著差异，说明在控制了居民生活活动的内生性之后，回归结果仍然与前文的估计结果一致。

（三）安慰剂检验。安慰剂检验是DID模型中最常用的稳健性检验方法之一，本文为检验空气质量的改善是否真由疫情停工冲击所导致，可以通过虚构疫情冲击发生的时间节点。选取2020年武汉封城前一周和前两周作为虚构冲击时间节点进行回归。表7显示，两种情况下的

的估计系数均不显著，说明在2020年春节之后，中国城市空气质量相较于2019年同期有所改善，确实是由疫情停工所导致的。

六、进一步分析：生产与通勤对空气质量影响的产业间差异

不同产业对空气污染的影响差异除了来源于生产过程的差异，还有一部分是由于对劳动力需求差异所造成的，相比自动化程度高或者可以远程办公的行业，劳动密集型产业在生产过程中会伴随着更多人员通勤和餐饮需求所造成的污染。因此分离出员工通勤和和餐饮需求因素，进而具体比较生产过程中造成的污染，可以更精确地分析出城市空气质量改善的产业结构效应。当劳动力规模固定，产业结构的变化会导致劳动力在行业间的流动，但一个城市劳动力日常的通勤和餐饮需求并不会发生明显变化，而餐饮对于员工属于必需品，需求弹性较小，因此在停工后，只有员工日常的通勤发生变化，而对日常餐饮需求的供给仅是由企业转为家庭内部，对空气质量的影响没有发生显著变化。因此本文拟通过比较行业间劳动力结构来衡量员工通勤所造成污染的差异。

根据表4的回归结果，将所属行业的GDP占比和因停工所导致系数变化的乘积作为该行业的总污染效应（表4）。通过比较二、三产业因通勤造成的污染比率（41.94/58.06）和总污染比率（56.42/43.58）可以发现，已知产业间因通勤造成的污染比率，将第二产业生产过程所造成的空气污染纳入总污染后，对空气污染的贡献度上升14.48个百分点，说明第二产业因生产过程引起的空气污染远高于第三产业。在第二产业内部，表8的回归结果表明因停工所导致的空气质量改善主要源于制造业，进一步对制造业内部细分并计算发现，考虑到生产过程所造成的污染后，轻工业对空气污染的贡献度下降了3.32个百分点，能源化工业上升4.07个百分点，装备制造业下降0.75个百分点。结果说明，在制造业内部由轻工业所引起的污染中，因员工通勤因素所导致的比重相对其他行业更高，而在能源化工业所引起的污染中，因生产过程因素所导致的比重相对其他行业更高。

七、结论与政策含义

本文采用新冠疫情导致的停工停产这一自然实验，采用广义DID方法考察产业结构对空气污染的结构性效应，得到如下结论。首先，第二、三产业占比的影响显著为正，第三产业的影响系数低于第二产业，在疫情冲击与复工前后第二产业的系数发生了显著的变化，且因第二产业生产过程对污染的贡献显著高于第三产业，意味着在目前经济转型过程中产业结构调整是我国实现绿色发展的重要维度，此次疫情冲击为我们识别环境污染的产业结构效应提供了合理的自然实验。其次，即使是相同的三次产业结构下空气质量的改善程度也存在着较大差异：水电气热等行业无显著影响，采矿业与建筑业对空气污染的贡献有限，制造业的影响较为显著，在制造业内部，轻工业的边际贡献为最大、装备制造业次之、能源化工业最弱，且轻工业受员工通勤因素影响相对更高，能源化工业受生产过程因素影响相对更高。二产比重低或GDP规模较大的城市，第二产业对空气污染的边际影响更大，北方与内陆城市的空气污染相对更加严重，说明空气质量不仅与产业结构相关，也与经济总体发展规模与地理环境等因素相关。上述结论也具有较强的政策含义。

第一，从实现“碳达峰、碳中和”的产业结构调整途径来看，需重视第二产业内部结构调整的重要性。第二产业以及内部的能源化工绿色发展的关键在于生产过程的改造升级，通过技术升级降低对劳动力的依赖是轻工业降碳的主要方向，加强对工业尤其是轻工业、能源化工等制造业污染“大户”的防治，能够显著改善空气质量。在制造业中，也有如医药、高分子材料等重点发展的高技术产业，这些产业的重污染意味着其发展方式仍比较粗放，亟需实现结构和技术的双转型、双升级，在产业结构调整中实现高效发展是这些产业未来重要的方向。一方面，向价值链高端、新型集约化业态转型升级能够提升产业整体的发展效率；另一方面，通过数字化、网络化等新经济形式为这些产业赋能，减少生产、销售环节的能耗，亦是践行产业创新、绿色发展理念的重要体现。

第二，产业结构的调整与环境治理需因城而异、实施差异化措施。各地在空气质量的强外部约束下进行产业结构调整时，需充分考虑自身所处经济发展阶段与地理气候条件。特别是正处于工业化大发展阶段的内陆地区，不能重复以往先污染、后治理的发展老路。从本文研究结果来看，这一传统发展模式还比较“流行”。因此，这些地区的产业结构调整更应牢固树立创新、绿色发展理念，充分利用技术的溢出效应，避免落入后发劣势的发展陷阱。

第三，在新形势下，各地都非常重视制造业特别是高端制造业的“回归”。包括一些新兴产业如集成电路、大数据、5G、新能源汽车等的发展，各区域都在一哄而上，实际上这些产业在某些环节具有高消耗、高污染的特征。因此，需要未雨绸缪，始终坚持内部结构优化的理念，在产业发展和环境治理之间平衡时守住高质量发展的底线，避免短视化行为。

① 数据来源于百度地图慧眼。

② 据2017版《国民经济行业分类》大类分类标准，本文定义采矿业（

）包括06-12大类，轻工业（ ）包括13-24大类，能源化工（ ）包括25-29大类，装备制造（ ）包括30-43大类，水电气热（ ）包括44-46大类，建筑业（ ）包括47-50大类。

③ 变量均通过单位根检验，根据AIC信息准则，选择滞后2阶。

④ 因各省市宣布停工时间均在2020年春节（1月24日）假期间，则停工前时长取24天，除湖北省外均于2月9起逐步复工，则复工后时长51天，停工前时长取24天，因历年春节假期，总时长选取84天。

⑤ 鉴于该指数在2019年只公布到年3月28日，本文仅选有相对应对照组的2020年日数据进行回归。