
2021第47卷第1期
2. 华南师范大学 经济与管理学院,广东 广州 510006
2. School of Economics and Management,South China Normal University,Guangzhou 510006,China
一、引 言
在中国,个人所得税(下文简称“个税”)是以人大立法形式确立的少数几个税种之一。①累进性的个人所得税具有比较直接的再分配作用,而且其征收对象涵盖大量的个人与家庭,涉及面广。因此,政策制定者须根据个税与社会、经济之间的关联和影响,采取必要的调整措施来动态地保证个税制度的合理性。2018年8月31日,第十三届全国人民代表大会常务委员会第五次会议通过了《关于修改〈中华人民共和国个人所得税法〉的决定》(2019年1月1日起施行),中国个税制度迎来了1980年开征后的第七次改革。此次改革主要体现在三个方面:(1)再次提高了劳动收入的免征额②(从2011年改革时确定的42 000元/年提高到60 000元/年),并首次增设了重要民生支出的专项附加扣除制度。(2)将工资薪金、劳务报酬、稿酬等合并为“综合所得”,将各类经营性收入合并为“经营所得”,全部按累进税率征税(以往只有工资薪金与各类经营所得适用累进税率)。(3)通过改变税率表中的级次、级距和区间税率,提高税率累进幅度。
第七次个税改革虽然创新点较多,但是仍将免征额与税率表作为主要调整对象,没有偏离2005年以来历次个税改革的基本轨道。在经历2005年及其后的历次渐进式个税改革后,个税负担已相对更多地由高收入人群来承担,低收入者的个税缴纳则基本得到减免(许志伟等,2013)。一个被学界长期关注的问题是,上述税改手段是否能真正有效改善个人所得税的分配效应和缓解不平等问题?对此,学界仍存在大量争论。中国学者结合实际国情,运用各层面的统计调查数据做了大量的量化研究。多数学者选择的量化方法(指数测算等)直接依托截面数据进行计算,适于测度再分配效应,但较难剖析个税改革的初次分配作用(岳希明和徐静,2012;田志伟等;2017),当然,基于考虑行为反馈的微观模拟方法,万相昱(2018)等文献能够在一定程度上克服上述局限,但由于其只考虑局部均衡,仍无法结合整个经济系统来剖析个税改革的初次分配作用。从国内外研究动态来看,克服上述局限的一个可行途径是建立动态化的一般均衡模型,揭示更加复杂的影响机制(初次分配效应、福利损失等),但相关研究同样存在结论分歧。例如,Guvenen等(2014)借助生命周期模型模拟了累进性个税的再分配作用,发现其会动态地缩小税前工资不平等。许志伟等(2013)指出,2011年中国个税改革的确改善了分配,不过其福利代价较大。王韬等(2015)基于CGE模型的研究则表明,个税免征额调整并不是改善个税制度公平性的最合理手段。Heathcote等(2017)发现,累进性个税对税前收入的调节作用很弱,而且会带来市场扭曲和社会福利损失。
一个更值得注意的前沿趋势是,由于金融危机后全球宏观经济波动风险加剧,而且新常态下中国经济的稳定性问题受到更多关注,③因此在短期波动框架下分析个税改革动态效应的研究日益增多,其中最具代表性的是基于动态随机一般均衡(DSGE)分析方法的个税问题研究,如Mattesini和Rossi(2012)、朱军(2015a)、骆永民和翟晓霞(2018)以及张杰等(2018)均在DSGE模型中刻画了累进性的个税。同时,部分学者已开始探索经济波动过程中个税与收入不平等之间的内生关联。例如,骆永民和翟晓霞(2018)指出,打破城乡隔阂、缩小收入差距能够提高个税的自动稳定器作用;而张杰等(2018)发现,缺乏累进性的个税会在波动过程中阻碍工薪阶层的收入与消费扩张、扩大不平等,而且累进性的提升会造成福利损失。
从个人所得税领域的DSGE文献来看,现有研究在方案设计上存在待改进之处。2005年后中国四次个税改革的主要手段之一是调整税率表,提高税率的累进幅度。这确实能够提高个税累进性,减轻中低收入纳税者的实际负担。但同时,改革手段中也包含上调免征额,这很可能会在整体上降低个税累进性,抵消其他改革手段所带来的累进性提升效果,使改革对收入分配的实际影响难以确定(岳希明和徐静,2012)。因此,学者须将不同税改手段的影响分解开来,并尽可能准确地分析不同改革手段的交互与叠加作用。然而,多数DSGE文献的做法是调整某个(或某些)累进税率表达式中的参数,而这只能在有限程度上模拟税率表的调整。当然,骆永民和翟晓霞(2018)等少数研究同时考虑了包括免征额在内的多种税制要素,但遗憾的是,他们的分析方式尚无法实现各税制要素的独立调整与作用分解。因此,在分析中国个税改革的有关问题时,个税的DSGE分析框架依然有较大的改进空间。
本文借鉴Mattesini和Rossi(2012)、朱军(2015a)以及张杰等(2018)等文献,建立了包含累进性税收的新凯恩斯动态随机一般均衡(NK-DSGE)模型,并以文献和微观调查数据等作为依据,灵活地设计了模拟分析方案,使模型能刻画多元化的改革措施,且能分析不同改革措施的叠加与交互作用。此外,本文从权衡效率与公平的角度出发,推导了包含不平等因素的福利损失函数,评价了个税改革的福利效应。本文尝试回答以下两个问题:(1)2005年以来中国历次个税改革的常用手段是否能够带来积极的收入分配效应,改善收入不平等?(2)在调节收入分配的同时,个税改革是否能够在经济波动过程中带来积极的福利效应?换言之,个税改革对收入不平等的调节是否有利于改善经济福利?上述两个问题均从个税改革的分配效应引申而来。第一个问题在现有研究中仍存在分歧与争论,需要进一步加以深入探讨;第二个问题的提出则是基于许志伟等(2013)以及陈利锋(2018)等的福利分析经验,目的是在权衡公平与效率的前提下评价改革效果,使研究内容不仅有利于分配公平,也更能契合稳就业和稳增长等改革发展需要,从而探索未来个税改革方向。
本文接下来的内容安排是:第二部分主要阐述本文动态随机一般均衡模型的基本结构,第三部分主要介绍模型参数的校准与贝叶斯估计过程,第四部分是模型动态分析(含福利损失测算),最后是结论。
二、基本模型
本文借鉴Galí等(2007)、Iwata(2011)、陈利锋(2018)等建立的异质性家庭DSGE模型,以及Mattesini和Rossi(2012)、朱军(2015a)、张杰等(2018)等在分析累进税方面的经验,构建了包含异质性家庭和个税等累进性税种的新凯恩斯动态随机一般均衡(NK-DSGE)模型。④
(一)代表性家庭
假设模型中存在两类家庭:第一类是相对富裕的李嘉图型家庭,其拥有资产且不受流动性约束,可追求跨期的消费平滑;第二类是相对贫困的非李嘉图型家庭,其主要特点是经济决策遵循经验法则(rules of thumb,ROT),无资产且受流动性约束。上述设定能同时体现当前高度集中的财富分布与低收入群体普遍受流动性约束。两类代表性家庭的当期效用函数为:
| $U\left( {C_t^i,N_t^i} \right)=\ln (\tilde C_t^i) - S_t^n{{{{\left( {N_t^i} \right)}^{1 + \varphi }}} / {(1 + \varphi )}}{,}\;\; i \in \left\{ {h,s} \right\}$ | (1) |
其中,李嘉图型家庭(上标为h)和非李嘉图型家庭(上标为s)的消费分别为Cth和Cts,变量
| $ \begin{aligned} & {\max }\;\;{E_h}=\displaystyle\sum\limits_{t=0}^\infty {{\beta ^t}U\left( {C_t^h,N_t^h} \right)} \\ & \;\;{\rm{s}}{\rm{.t}}{{\rm{.}}}{}\;\;(1 + \tau _t^{ch}){P_t}C_t^h + {P_t}I_t^h + R_t^{ - 1}B_{t + 1}^h= {(1 - \tau _t^{wh})W_t^h{P_t}N_t^h + (1 - \tau _t^{kh})R_t^k{P_t}K_t^h + B_t^h + D_t^h} \end{aligned} $ | (2) |
其中,β表示主观贴现率。Pt为第t期物价指数,实际工资为Wth,实际物质资本收益为Rtk,获得的企业红利为Dth,第t期抛售的债券数额(名义值)为Bth,每单位债券的售价为1单位货币。在支出方面,除了消费外,Ith为投资支出,
由上式可知,纳税人须缴纳商品消费税、劳动收入税和资产收入税,税率分别为τtki、τtwi和τtci,均遵循累进税制。⑤一些DSGE研究文献如Iwata(2011)、朱军和许志伟(2018)等均采用了类似税种划分,取得了合意的效果。王蓓和崔治文(2012)的量化测算也证明,上述划分方式能够有效契合中国税收现实情况。⑥参考Mattesini和Rossi(2012),三种税收的税率规则如下:
| $\tau _t^{xi}=1 - (1 - \bar \tau ^x){\left( {{{\bar y} / {{y_t}}}} \right)^{{\omega _x}}}{,} \;\; x \in \{ c,w,k\} {,}\;\; i \in \left\{ {h,s} \right\}$ | (3) |
其中,顶部带横线的变量均表示稳态值(下文同)。
| $K_{t + 1}^h=\left( {1 - \delta } \right)K_t^h + K_t^h\left[ {\phi \left( {\frac{{I_t^h}}{{K_t^h}}} \right)} \right]$ | (4) |
其中,参数δ为物质资本折旧率,函数
结合以上条件,李嘉图型家庭的一阶最优决策条件为:
| $R_t^{}\Lambda _{t,t + 1}^{}\frac{{{P_t}}}{{{P_{t + 1}}}}=1$ | (5) |
| ${Q_t}={E_t}\left\{ {\Lambda _{t,t + 1}^{}(1 - \tilde \tau _{t + 1}^{kh})R_{t + 1}^k + \Lambda _{t,t + 1}^{}{Q_{t + 1}}\left[ {1 - \delta + \phi \left( {\frac{{I_{t + 1}^h}}{{K_{t + 1}^h}}} \right) - \phi '\left( {\frac{{I_{t + 1}^h}}{{K_{t + 1}^h}}} \right)\frac{{I_{t + 1}^h}}{{K_{t + 1}^h}}} \right]} \right\}$ | (6) |
其中,Qt=[
| $\tilde \tau _t^{di}=1 + (1 - {\omega _d})(\tau _t^{di} - 1){,} \;\; d \in \left\{ {c,k,w} \right\}{,} \;\; i \in \left\{ {h,s} \right\} $ | (7) |
非李嘉图型家庭预算紧张且存在流动性约束,设定其实际工资水平为Wts,τtws和τtcs分别为其劳动收入税和商品消费税的累进税率,则消费决定条件可表示为:
| $(1 + \tau _t^{cs})C_t^s=(1 - \tau _t^{ws})W_t^sN_t^s$ | (8) |
参考Iwata(2011)等文献,两类代表性家庭的消费、就业、资本存量、投资额、债券和纳税额等均可以李嘉图型家庭数量占比γnh为权重进行加总。
(二)劳动力市场
两类劳动力的加总方式为:
| $N_t^{}={\left[ {{{(\gamma _n^h)}^{1/\varepsilon _w^{}}}{{(N_t^h)}^{(\varepsilon _w^{} - 1)/\varepsilon _w^{}}} + {{(1 - \gamma _n^h)}^{1/\varepsilon _w^{}}}{{(N_t^s)}^{(\varepsilon _w^{} - 1)/\varepsilon _w^{}}}} \right]^{\varepsilon _w^{}/(\varepsilon _w^{} - 1)}}$ | (9) |
其中,εw表示不同劳动力之间的替代弹性系数,加总后的劳动力Nt将直接进入生产函数中。两类劳动力的当期实际工资分别为Wth和Wts,由于劳动力市场是不完全竞争的且存在工资粘性,名义工资的调整过程服从Calvo规则:
| $W_t^{pi}={\left[ {\theta _w^i{{(W_{t - 1}^{pi})}^{(1 - \varepsilon _w^i)}} + (1 - \theta _w^i){{(W_t^{i*})}^{(1 - \varepsilon _w^i)}}} \right]^{1/(1 - \varepsilon _w^i)}}{,} \;\; i \in \left\{ {h,s} \right\}$ | (10) |
其中,εwi表示第i类劳动力内部的替代弹性系数。按上述规则,每一时期的劳动者在θwi的概率下只能接受与上期一致的名义工资水平
| $ \sum\limits_{k=0}^\infty {{{(\beta \theta _w^i)}^k}{E_t}\left\{ {\left( {\frac{{N_{t + k|t}^i}}{{\tilde C_{t + k}^i}}} \right)\left[ \begin{array}{l} (1 - \tilde \tau _{t + k}^{wi})\left( {\dfrac{{W_t^{i*}}}{{{P_{t + k}}}}} \right) \\ - \mu _w^i(1 + \tilde \tau _{t + k}^{ci})MRS_{t + k|t}^i \\ \end{array} \right]} \right\}} =0{,}\;\;\mu _w^i=\frac{{\varepsilon _w^i}}{{(\varepsilon _w^i - 1)}}{,}\;\; i \in \left\{ {h,s} \right\} $ | (11) |
上式的含义为,若工资水平在t期被重新设定且一直保持至t+k期不变,则t+k期第i类劳动力的就业为
定义Lti为实际工资水平Wti下家庭愿意提供的劳动量,此时家庭成员消费与劳动间的边际替代率
(三)生产部门
模型中同时存在中间产品和最终产品的生产部门,两者形成了产业链条上的衔接关系。中间产品生产部门是由垄断竞争厂商j∈(0,1]构成的连续统,各厂商采用以下的柯布−道格拉斯生产函数进行生产:
| $Y_t^m(j)={K_{t - 1}}{(j)^{(1 - \alpha )}}{\left[ {S_t^aN_t^{}(j)} \right]^\alpha }$ | (12) |
其中,Ytm(j)为第j个中间产品厂商的产量,1−α为资本的产出弹性,Kt−1(j)和Nt(j)分别表示第j个企业的资本投入量和劳动力投入量。Sta是技术(全要素生产率)的冲击项,其自然对数值εta服从平稳的AR(1)过程。根据成本最小化一阶条件可以得出:
| $R_t^k={{(1 - \alpha )M{C_t}Y_t^m(j)} / {{K_t}(j)}}$ | (13) |
| ${W_t}={{\alpha M{C_t}Y_t^m(j)} / {{N_t}(j)}}$ | (14) |
其中,MCt表示厂商的实际边际成本,Rtk和Wt分别表示实际资本收益率和实际劳动要素报酬。中间产品厂商的价格调整过程遵循Calvo规则:
| ${P_t}(j)={\left[ {\theta {P_{t - 1}}(j)^{1 - \varepsilon } + \left( {1 - \theta } \right){{\left( {P_t^*} \right)}^{1 - \varepsilon }}} \right]^{\frac{1}{{(1 - \varepsilon )}}}}$ | (15) |
上述规则的涵义是,中间产品厂商j在向最终产品厂商出售产品时,每一期均能在θ的概率下保持原价格不变(θ即名义价格刚性水平),但也能在1−θ的概率下重新设定一个符合自身利润最大化的最优价格Pt*,其利润最大化一阶条件为:
| $\sum\limits_{k=0}^\infty {{\theta ^k}{E_t}\left\{ {{\Lambda _{t,t + k}}Y_{t + k|t}^m(j)\left[ {\left( {{{P_t^*} / {{P_{t + k}}}}} \right) - \mu M{C_{t + k|t}}} \right]} \right\}} ={0},\;\;\mu ={\varepsilon }/{{(\varepsilon - 1)}}$ | (16) |
其中,ε为各厂商中间产品的替代弹性,μ为稳态下的价格加成。
最终产品厂商则是以Dixit-Stigliz技术采用各中间产品生产Ytm(j),加总得到一揽子的最终消费品Yt,其利润最大化一阶条件为:
(四)宏观经济政策
本文主要从财政和货币这两个方面来描述宏观经济政策。
1. 财政支出。为了简化分析,模型中的财政支出具有与Mattesini和Rossi(2012)以及朱军(2013,2015a)类似的政策规则。财政支出总规模为GtP,其对数偏离值为
2. 税收与财政预算平衡。各类税收的规则见上文中的(3)式和(7)式。若资产收入税、劳动收入税和商品消费税的收入总和为Tt,则财政预算平衡条件为:
| ${P_t}T_t^{} + R_t^{ - 1}{B_{t + 1}}={B_t} + {P_t}G_t^P$ | (17) |
3. 货币政策。模型中的货币政策当局采用带平滑系数的泰勒规则:
| $\frac{{{R_t}}}{{\bar R}}={\left( {\frac{{{R_{t - 1}}}}{{\bar R}}} \right)^{{\rho _m}}}{\left[ {{{\left( {\frac{{{Y_t}}}{{\bar Y}}} \right)}^{{\psi _y}}}{{\left( {\frac{{{\Pi _t}}}{{\bar \Pi }}} \right)}^{{\psi _p}}}} \right]^{(1 - {\rho _m})}}\exp (\varepsilon _t^r)$ | (18) |
其中,ρm为平滑系数,∏t为通胀指标,∏t=Pt/Pt−1,参数ψy和ψp分别表示利率对通胀和产出缺口的反应程度,εtr表示遵循AR(1)过程的外生货币政策冲击。
根据Leeper(1991)、朱军(2015b)以及马勇(2015)的阐述,在本文的模型经济中,政府实施稳健的货币政策和积极的财政政策(由累进税制决定)。这一设定与Mattesini和Rossi(2012)类似,也与中国目前的宏观调控政策导向基本一致。⑧
(五)不平等的衡量
为了分别剖析税收对收入初次分配与再分配的影响,需将收入不平等指标分为税前与税后两类。其中,税前收入不平等的表达式为:
| $GAP_t^{nt}={{W_t^hN_t^h} / {(W_t^sN_t^s)}}$ | (19) |
税后收入不平等的表达式为:
| $GAP_t^l={{(1 - \tau _t^{wh})W_t^hN_t^h} / {\left[ {(1 - \tau _t^{ws})W_t^sN_t^s} \right]}}$ | (20) |
(六)市场出清条件与外生冲击
模型经济的市场出清条件为:
| ${Y_t}={C_t} + {I_t} + G_{_t}^P$ | (21) |
其中,Yt为总产出,Ct为总消费,It为总投资,GtP为财政支出总额。
模型包含外生的劳动供给冲击(εtn)、技术(TFP)冲击(εta)、财政支出冲击(εtgp)和货币政策冲击(εtr),四类外生冲击遵循如下AR(1)过程:
| $\varepsilon _t^k={\rho _k}\varepsilon _{t - 1}^k + e_t^k{,}\;\; e_t^k\sim i{.}i{.}d{.}\; N(0{,}\sigma _k^2){,}\;\; k \in \left\{ {n,a,gp,r} \right\}$ | (22) |
其中,持续性参数ρk的取值在0和1之间,随机扰动项etk服从均值为0、标准差为σk的正态分布。
三、参数校准与估计
在将NK-DSGE模型投入应用之前,首先需要对其做对数线性化转换,⑨然后对模型参数进行校准和估计。
(一)部分参数校准
参考庄子罐等(2018),本文将家庭成员的主观贴现率β校准为0.99。参照Galí和Monacelli(2016)以及陈利锋(2017),本文将物质资本折旧率δ校准为0.04。结合王蓓和崔治文(2012)等文献的测算结果,本文将稳态下资产收入税、劳动收入税和消费税的有效税率
(二)贝叶斯估计
本文采用贝叶斯估计法获得其余22个参数和4个外生冲击标准差的数值。贝叶斯估计的先验分布主要基于国内文献或微观调查数据,如刘斌(2008)、薛鹤翔(2010)、张伟进等(2015)、朱军(2015a)、庄子罐等(2018)⑩以及中国劳动力动态调查(简称CLDS,⑪用于确定李嘉图型家庭占比γnh等参数的先验均值),具体设置见表1。本文以总产出
| 参数 | 先验分布设置 | 后验分布估计结果 | |||
| 先验均值 | 分布类型 | 标准差 | 后验均值 | 95%后验置信区间 | |
| α | 0.400 | beta | 0.050 | 0.4378 | [0.3269,0.5655] |
| θ | 0.750 | beta | 0.050 | 0.7369 | [0.6743,0.7999] |
| h | 0.500 | beta | 0.150 | 0.2906 | [0.1378,0.4481] |
| φ | 6.160 | gamma | 0.500 | 6.1465 | [5.1955,7.1253] |
| ψy | 0.125 | gamma | 0.020 | 0.1362 | [0.0949,0.1821] |
| ψp | 1.500 | gamma | 0.185 | 1.9770 | [1.1630,2.5305] |
| ρa | 0.500 | beta | 0.100 | 0.3648 | [0.2224,0.5184] |
| ρr | 0.500 | beta | 0.100 | 0.6892 | [0.3368,0.8834] |
| ρgp | 0.500 | beta | 0.100 | 0.6853 | [0.5649,0.7970] |
| ρn | 0.500 | beta | 0.100 | 0.5498 | [0.3865,0.7391] |
| θwh | 0.600 | beta | 0.200 | 0.5544 | [0.3151,0.8370] |
| θws | 0.600 | beta | 0.200 | 0.4355 | [0.1730,0.7920] |
| εwh | 1.500 | gamma | 0.200 | 1.4930 | [1.1114,1.8873] |
| εws | 2.500 | gamma | 0.200 | 2.4896 | [2.0982,2.8829] |
| εw | 2.000 | gamma | 0.200 | 2.0050 | [1.6072,2.3984] |
| ε | 1.550 | gamma | 0.200 | 1.5528 | [1.1664,1.9420] |
| ρm | 0.450 | beta | 0.150 | 0.1070 | [0.0165,0.2392] |
| ωc | 0.300 | beta | 0.150 | 0.2845 | [0.0316,0.5673] |
| ωw | 0.300 | beta | 0.150 | 0.4896 | [0.1422,0.8332] |
| ωk | 0.300 | beta | 0.150 | 0.1058 | [0.0046,0.2552] |
| γnh | 0.430 | beta | 0.200 | 0.4840 | [0.3363,0.6390] |
| γch | 0.600 | beta | 0.150 | 0.6025 | [0.3121,0.8852] |
四、个税改革与收入不平等:动态分析
(一)个税改革的模拟方案设计
如前所述,在涉及中国个税改革的DSGE研究中,学者大多通过调节个别参数来改变模型中个税的累进性,不利于分辨不同改革手段的收入分配效应。鉴于此,本文没有完全效仿现有文献中的模拟方法,而是综合调整累进税率参数和征税范围,尝试对2018年个税改革的效应进行近似模拟,具体做法如下:(1)为了模拟2005年以来劳动收入免征额多次提升后税负归宿的改变,调整模型中的征税范围,设定非李嘉图型家庭不缴纳个税,然后观察脉冲响应曲线在征税范围调整前后的变化。征税范围的具体调整方式为:设τtws=0,
| 纳税者占比 | 家庭类型 | ||||||
| 历次个税改革后的免征额(年度值) | 进一步提高后的免征额(模拟)① | ||||||
| 19200元(2005年) | 24000元(2007年) | 42000元(2011年) | 60000元(2018年) | 78000元 | 106000元 | 124000元 | |
| 李嘉图型家庭 | 78.33% | 69.30% | 52.16% | 40.74% | 38.04% | 33.62% | 32.87% |
| 非李嘉图型家庭 | 49.97% | 38.10% | 16.61% | 6.93% | 4.78% | 1.55% | 0.98% |
| 注:若满足以下条件之一,则判定为李嘉图型家庭:(1)有财产性收入;(2)有经营性收入;(3)购置或转卖房产;(4)存在借贷与还贷。根据现行税制,这里剔除了农林牧渔等行业的家庭经营、个体经营收入。 | |||||||
本文首先比较了免征额提高前后的主要经济变量波动性(以劳动供给冲击下的情形为例),并实施了无累进税率(ωw=0)的反事实模拟,主要结果见表3。从中可以看到,如果不提升免征额,原始模型中累进税率的存在会使经济变量的波动性减弱。而免征额的提高削弱了这种“自动稳定器”作用。无论对中国经济的持续健康发展还是深化改革、结构转型和对外开放来说,经济稳定都是重要的先决条件。2019年《政府工作报告》强调要为经济平稳运行创造条件,足见宏观经济稳定的重要意义。从理论角度讲,宏观经济在稳态下是有效率的,过大的经济波动意味着效率下降和福利损失。因此,在分析分配效应的同时,还需通过经济波动幅度的变化情况,考察个税改革所付出的效率代价。这也是下文以福利损失函数进行政策评价的原因。
| 变量波动性(标准差) | |||
| 产出(
${\hat y_t}$
)
|
消费(
$\hat c_t^{}$
)
|
就业(
$\hat n_t^a$
)
|
|
| 原始模型 | 0.0346 | 0.0364 | 0.0675 |
| 原始模型,劳动收入税无累进税率 | 0.0350 | 0.0378 | 0.0687 |
| 免征额提高 | 0.0351 | 0.0378 | 0.0693 |
| 免征额提高,劳动收入税无累进税率 | 0.0350 | 0.0378 | 0.0688 |
现有研究大多认为,个税在经济中的作用传导以劳动供给为起点。为了排除其他因素,直接反映个税改革影响下的DSGE模型动态,这里选取劳动供给冲击下的脉冲响应曲线进行分析。图1反映了1单位标准差的负向劳动供给冲击下免征额提高和税率幅度调整的作用。⑬
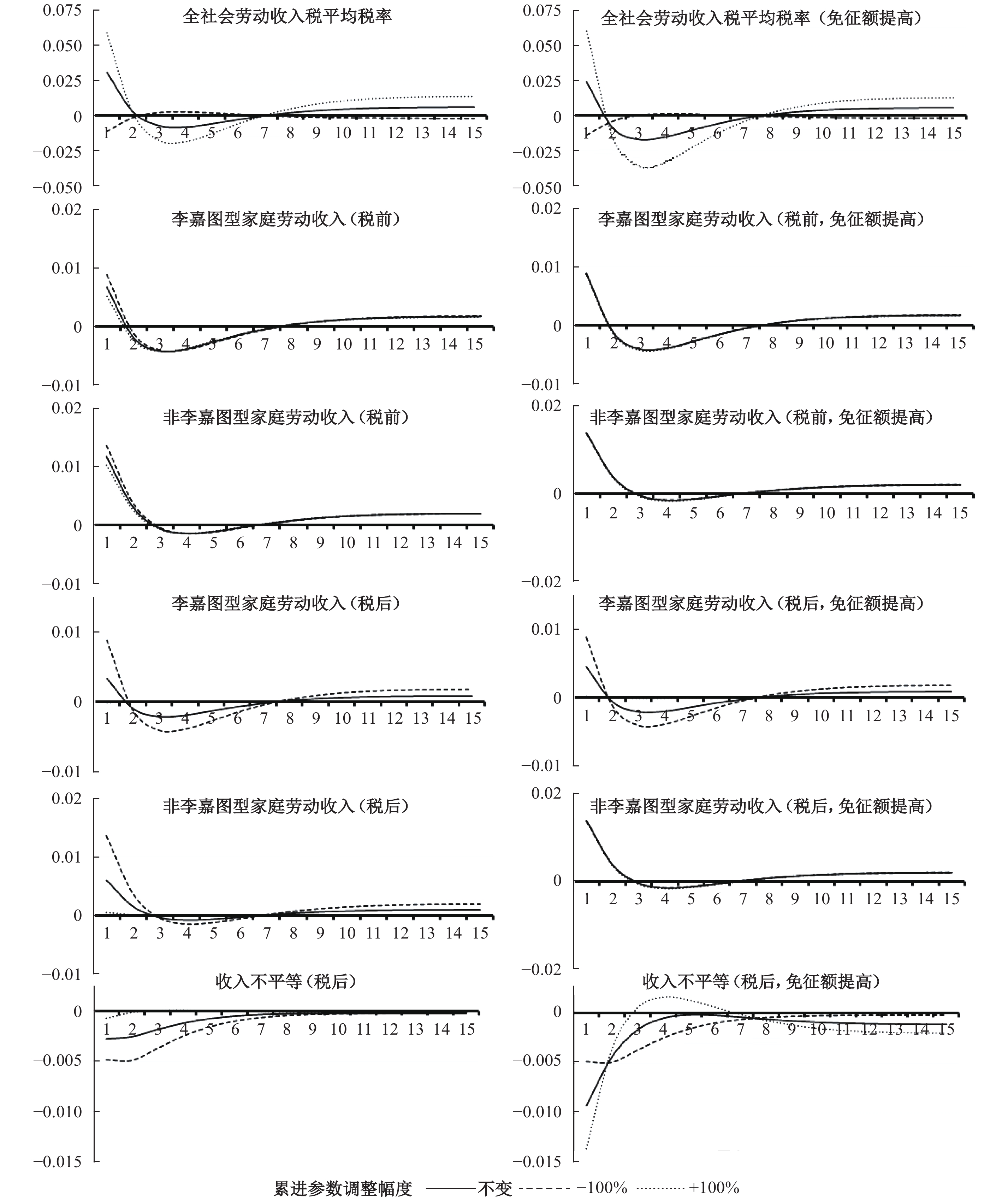
|
| 图 1 个税改革与经济波动过程中的收入不平等 注:左侧为免征额不变时的结果,右侧为免征额提高后的结果。图中“累进参数”是指参数ωw。下图同。 |
从图1中可以看到,提高免征额抑制了劳动收入税平均税率在冲击下的扩张,有利于减轻整个经济系统的个税负担,这与预期相符。在初次分配方面,当外生劳动供给冲击导致经济扩张和就业增加时,提高免征额增大了两类劳动力税前收入的波动幅度,其原因在于:提高免征额能够降低劳动收入税负,增强劳动供给意愿,并提振总需求,促进经济扩张,从而进一步促进就业。此外,与单纯调整税率累进幅度相比,提高免征额会削弱税率累进幅度对初次分配的调节作用。在免征额提高后,累进参数的上升只会使变量的脉冲响应规律受到微弱的影响,说明个税的“自动稳定器”作用被减弱,且无法以原有幅度来调节初次分配,这与岳希明和徐静(2012)、田志伟等(2017)以及万相昱(2018)的发现相近。
在再分配方面,提高免征额改变了税负归宿,使两类家庭税后劳动收入受到了不对称的影响,改善了就业扩张过程中的税后收入不平等。此外,在免征额提高后,不断提升的累进参数能以更大幅度改善税后收入不平等,其原因在于,此时仅有李嘉图型家庭的收入扩张受到累进税率的抑制。上述结果表明,两种改革手段的叠加作用能显著改善再分配,与许志伟等(2013)的观点相似。
当然,由于DSGE模型的脉冲响应规律具有对称性,个税改革的初次分配与再分配效应均具有状态依存特征。如果外生冲击带来的是就业与劳动收入的下降,那么个税改革会导致相反的分配效应,成为“双刃剑”。此外,还有一个需要探究的问题:劳动供给冲击主要作用于供给侧,而其他外生冲击大多作用于需求侧,面对这些冲击时,上述影响规律是否仍成立?下文将进一步展开分析。
(二)个税改革、货币政策与收入不平等
货币政策作用于需求侧,而且是模型经济中唯一的名义冲击,所以这里选取1单位标准差的货币政策冲击进行分析。由图2可见,⑭在初次分配方面,如果模型在提高免征额后面对负向货币政策冲击,税前收入不平等的扩张幅度会加大,带来消极的分配效应。此时,如果进一步调高税率累进参数,税前收入不平等的改善幅度明显比免征额提高前要小,因为提高免征额减弱了累进税对税前收入的调节能力,这与劳动供给冲击下的结论在本质上一致。而在再分配方面,无论是单纯提高免征额,还是在免征额提高后进一步提高税率累进幅度,税后收入不平等均能得到更加显著的改善。上述结果表明,尽管货币政策冲击与劳动供给冲击的具体机制和分配效应不尽相同,但是个税改革的作用效果相似,表明模型分析结果是稳健的。
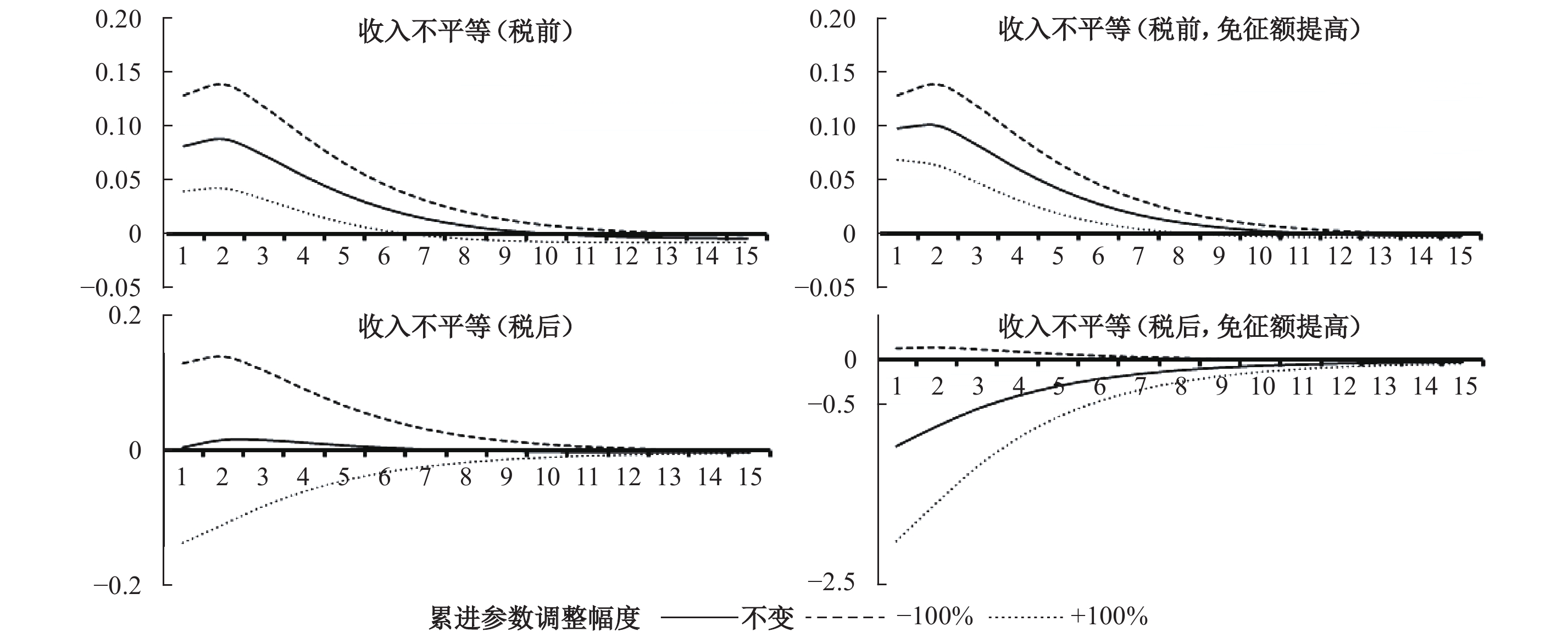
|
| 图 2 个税改革与宽松货币政策冲击下的收入不平等 |
(三)个税改革与社会福利损失
与其他政策类似,个税改革同样需要考虑公平与效率之间的权衡。表3、图1和图2的分析结果显示,个税改革措施(尤其是免征额调整)很可能扩大宏观经济变量的波动幅度,导致效率下降与福利损失,这与稳就业、稳增长等政策目标存在冲突。是否有必要为公平目标而付出上述效率代价?对此,需要进一步引入专门的分析工具,在权衡各类政策目标的前提下进行统一的量化政策评价。借鉴陈利锋(2018)的推导方法,本文对NK-DSGE模型中的家庭效用函数进行线性二次型逼近,可以得到含有不平等的福利损失函数:
| $W{L_t}=0.5\sum\limits_{t=0}^\infty {{\beta ^t}} \left[ \begin{array}{l} {\lambda _p}{(\pi _t^{})^2} + \gamma _n^h\left( {{{\varepsilon _w^h} / {\lambda _w^h}}} \right){(\pi _t^{wh})^2} + (1 - \gamma _n^h)\left( {{{\varepsilon _w^s} / {\lambda _w^s}}} \right){(\pi _t^{ws})^2} \\ + (1 + \varphi ){(\hat c_t^{})^2} + \lambda _{gap}^{}{(\widehat {gap}_t^l)^2} \end{array} \right]$ | (23) |
其中,
| $wl \approx {{\lambda _p}{\rm{var}} (\pi _t^{}) + \frac{{\gamma _n^h\varepsilon _w^h{\rm{var}} (\pi _t^{wh})}}{{\lambda _w^h}} + \frac{{(1 - \gamma _n^h)\varepsilon _w^s{\rm{var}} (\pi _t^{ws})}}{{\lambda _w^s}} + (1 + \varphi ){\rm{var}} (\hat c_t^{}) + \lambda _{gap}^{}{\rm{var}} (\widehat {gap}_t^l)} $ | (24) |
其中,var(·)表示括号内变量的方差。由上式可知,与陈利锋(2018)的推导结果类似,该函数包括产出波动、工资波动、消费波动和分配公平等,能够将个税改革的收入分配效应与当前最受重视的经济稳定问题结合起来,实现各类政策目标之间的兼顾与权衡。根据(24)式得到的外生冲击下社会福利损失值见表4。从中可以看到,单纯调整税率累进参数时,外生冲击下的福利损失能够得到有效抑制,而免征额的提高则会扩大外生冲击下的福利损失,也使其在税率累进幅度(参数ωw)提升的过程中不降反升。这表明提高免征额与税率累进幅度(通过调整税率表)这两类改革手段的叠加运用可能改善收入分配,但同时会带来一定的福利损失。如果未来个税改革不提高免征额而仅增加税率累进幅度,则至少可在一定范围内减少福利损失。
| 税率累进参数(ωw)调整幅度 | 情形1:免征额不调整 | 情形2:免征额提高 | ||
| 劳动供给冲击 | 货币政策冲击 | 劳动供给冲击 | 货币政策冲击 | |
| 不变 | 0.1084 | 91.6502 | 0.1681 | 1.0707×103 |
| +10% | 0.1070 | 90.3785 | 0.1749 | 1.3049×103 |
| +20% | 0.1060 | 89.6531 | 0.1823 | 1.5635×103 |
| +30% | 0.1046 | 89.4735 | 0.1902 | 1.8463×103 |
| +40% | 0.1036 | 89.8387 | 0.1986 | 2.1530×103 |
| +50% | 0.1028 | 90.7474 | 0.2075 | 2.4834×103 |
五、结 论
本文以2005−2018年中国历次个税改革为背景,建立了包含累进性税收的新凯恩斯动态随机一般均衡模型,模拟了各类个税改革措施对收入不平等的调节效果,并分析了包含不平等因素的福利效应,为个税制度的进一步改革优化提供了一些启示。研究结果显示:
第一,个税改革显著影响了收入的初次分配。提高免征额增大了主要经济变量与税前收入不平等的波动幅度,带来了经济波动风险,而且恶化了宽松货币政策等外生冲击下的初次分配。与单纯调整累进参数相比,免征额与税率累进参数的同步提升会削弱累进税率对初次分配的调节作用。上述规律表明,中国个税制度改革重点宜集中在税率表(而非免征额)的优化调整上。分析结果还表明,宽松货币政策等外生冲击会在免征额提高后进一步扩大税前收入不平等。因此,个税改革与货币政策之间的协调应得到足够关注,避免对初次分配产生不利影响。
第二,个税改革改变了收入的再分配结果。在就业扩张过程中,提高免征额带来了税负归宿变化,改善了税后收入不平等;无论是单纯提高免征额还是将其与税率累进幅度一同提高,都能大幅改善税后收入不平等。但由于脉冲响应规律的对称性,上述初次分配与再分配效应均具有状态依存特征,在就业萎缩和劳动收入下降时会导致相反的分配结果,成为一把“双刃剑”。这进一步说明免征额调整在今后的个税改革实践中应当慎用。当然,上述状态依存特征也意味着在今后的个税制度设计中,可考虑加入盯住就业和收入波动的动态免征额规则,使其产生持续的、积极的再分配效应。2018年个税改革方案中的重要民生支出专项抵扣已实现网络申报,这表明上述动态免征额规则在信息化条件下具有一定的可行性。
第三,福利损失分析结果表明,单纯调整税率累进幅度时,各类外生冲击下的福利损失得到了有效抑制;而提高免征额扩大了外生冲击下的福利损失,且削弱了累进税率调整对福利损失的抑制作用。这同样表明,未来的个税改革应在审慎调整免征额的同时提高税率的累进幅度,避免经济波动过程中的福利损失,更好地保障中国经济的高质量发展。
① 到本文完稿时,中国开征的税种共有18个,其中3个税种有对应的实体法律,即《个人所得税法》《企业所得税法》《车船税法》。
② 也称“扣除额”或“费用减除标准”。部分文献将其称作“起征点”,这实际上是不恰当的。起征点是增值税等领域的常用标准,税基数额未达起征点时不用征税,否则须全额征税。而免征额与起征点的主要差异在于,税基数额低于免征额时不征税,若税基数额高于免征额,仅对扣除免征额后的剩余部分征税。
③ 2018年中央经济工作会议提出了“六稳”目标,即稳就业、稳增长、稳外贸、稳外资、稳投资和稳预期。
④ 本文完整的NK-DSGE模型如有需要可向作者索取。
⑤ 需要说明的是,根据王蓓与崔治文(2012)的划分方法,商品消费税中不仅包括现实中的消费税,还纳入了由消费者间接承担的增值税。虽然中国的消费税属于比例税,但是高档商品的适用税率更高,因而实际上也具有累进性(朱军,2015a)。
⑥ 根据王蓓和崔治文(2012),在中国个税的现有结构中,来源为工资薪金、劳务报酬、稿酬、特许权使用费、承包承租经营收入的部分被划入劳动收入税,而来源为利息、股息、红利、财产租赁与转让收入的部分则被划入资产收入税。当然,由于中国个税的税基以劳动收入为主(万相昱,2018),而且劳动收入也是2005年以来四次个税改革的主要涉及对象,因此下文的分析以劳动收入税来表征个税。
⑦ 其计算也可视为累进税征收额的一阶偏导数(以税基为自变量),如
⑧ 2018年中央经济工作会议提出要实施好积极的财政政策和稳健的货币政策。
⑨ 受篇幅限制,文中没有给出对数线性化转换后的模型,如有需要可向作者索取。
⑩ 对于参数的设定依据和完整估计结果,如有需要可向作者索取。
⑪ 本文使用的数据来自中山大学社会科学调查中心的中国劳动力动态调查(CLDS)数据库。本文的观点和内容由作者自负。
⑫ 表中增设了78000元/年、106000元/年和124000元/年这三个更高的免征额标准。需要说明的是,上述三个免征额标准并非完全脱离现实,因为2018年个税改革方案不仅将免征额调至60000元/年,还首次设立了教育、医疗、赡养、住房等重要民生支出的专项附加扣除制度,其效果等同于免征额的进一步提高。
⑬ 受篇幅限制,这里仅展示了家庭劳动收入、收入不平等和劳动收入税平均税率的脉冲响应图,其他图如有需要可向作者索取。
⑭ 受篇幅限制,这里仅展示了收入不平等的脉冲响应图,其他图如有需要可向作者索取。
| [1] | 陈利锋. 劳动力市场结构性改革的宏观经济效应: 一个模拟分析[J]. 财经研究, 2017(10): 4–17. |
| [2] | 陈利锋. 货币政策盯住目标应该考虑不平等吗[J]. 财贸经济, 2018(4): 51–66. DOI:10.3969/j.issn.1002-8102.2018.04.004 |
| [3] | 刘斌. 我国DSGE模型的开发及在货币政策分析中的应用[J]. 金融研究, 2008(10): 1–21. |
| [4] | 骆永民, 翟晓霞. 中国税收自动稳定器功能的双重约束研究[J]. 经济研究, 2018(7): 106–120. |
| [5] | 马勇. 中国的货币财政政策组合范式及其稳定效应研究[J]. 经济学(季刊), 2015(1): 173–196. |
| [6] | 田志伟, 胡怡建, 宫映华. 免征额与个人所得税的收入再分配效应[J]. 经济研究, 2017(10): 113–127. DOI:10.3969/j.issn.1673-291X.2017.10.048 |
| [7] | 万相昱. 中国现行个人所得税制度完善改进的微观模拟研究[J]. 数量经济技术经济研究, 2018(8): 91–107. |
| [8] | 王蓓, 崔治文. 有效税率、投资与经济增长: 来自中国数据的经验实证[J]. 管理评论, 2012(7): 3–12,23. |
| [9] | 王韬, 朱跃序, 鲁元平. 工薪所得免征额还应继续提高吗? ——来自中国个税微观CGE模型的验证[J]. 管理评论, 2015(7): 76–86. |
| [10] | 许志伟, 吴化斌, 周晶. 个人所得税改革的宏观福利分析[J]. 管理世界, 2013(12): 32–42. |
| [11] | 薛鹤翔. 中国的产出持续性——基于刚性价格和刚性工资模型的动态分析[J]. 经济学(季刊), 2010(4): 1359–1384. |
| [12] | 岳希明, 徐静. 我国个人所得税的居民收入分配效应[J]. 经济学动态, 2012(6): 16–25. |
| [13] | 张杰, 庞瑞芝, 邓忠奇. 财政自动稳定器有效性测定: 来自中国的证据[J]. 世界经济, 2018(5): 27–52. |
| [14] | 张伟进, 方振瑞, 黄敬翔. 城乡居民生活水平差距的变化——基于经济周期视角分析[J]. 经济学(季刊), 2015(2): 651–676. |
| [15] | 朱军. 开放经济中的财政政策规则——基于中国宏观经济数据的DSGE模型[J]. 财经研究, 2013(3): 135–144. |
| [16] | 朱军. 中国宏观DSGE模型中的税收模式选择及其实证研究[J]. 数量经济技术经济研究, 2015a(1): 67–81. |
| [17] | 朱军. 现代宏观财政理论研究的脉络与启示——兼谈对财政学基础理论创新的借鉴意义[J]. 财贸经济, 2015b(7): 29–43. |
| [18] | 朱军, 许志伟. 财政分权、地区间竞争与中国经济波动[J]. 经济研究, 2018(1): 21–34. |
| [19] | 庄子罐, 贾红静, 刘鼎铭. 货币政策的宏观经济效应研究: 预期与未预期冲击视角[J]. 中国工业经济, 2018(7): 80–97. |
| [20] | Galí J, López-Salido J D, Vallés J. Understanding the effects of government spending on consumption[J]. Journal of the European Economic Association, 2007, 5(1): 227–270. DOI:10.1162/JEEA.2007.5.1.227 |
| [21] | Galí J, Monacelli T. Understanding the gains from wage flexibility: The exchange rate connection[J]. American Economic Review, 2016, 106(12): 3829–3868. DOI:10.1257/aer.20131658 |
| [22] | Gatzia D E, Woods D. Progressive taxation as a means to equality of condition and poverty alleviation[J]. Economics, Management and Financial Markets, 2014, 9(4): 29. |
| [23] | Guvenen F, Kuruscu B, Ozkan S. Taxation of human capital and wage inequality: A cross-country analysis[J]. The Review of Economic Studies, 2014, 81(2): 818–850. DOI:10.1093/restud/rdt042 |
| [24] | Heathcote J, Storesletten K, Violante G L. Optimal tax progressivity: An analytical framework[J]. The Quarterly Journal of Economics, 2017, 132(4): 1693–1754. DOI:10.1093/qje/qjx018 |
| [25] | Higgins S, Lustig N. Can a poverty-reducing and progressive tax and transfer system hurt the poor?[J]. Journal of Development Economics, 2016, 122: 63–75. DOI:10.1016/j.jdeveco.2016.04.001 |
| [26] | Iwata Y. The government spending multiplier and fiscal financing: Insights from Japan[J]. International Finance, 2011, 14(2): 231–264. DOI:10.1111/j.1468-2362.2011.01285.x |
| [27] | Leeper E M. Equilibria under ‘active’ and ‘passive’ monetary and fiscal policies[J]. Journal of Monetary Economics, 1991, 27(1): 129–147. DOI:10.1016/0304-3932(91)90007-B |
| [28] | Mattesini F, Rossi L. Monetary policy and automatic stabilizers: The role of progressive taxation[J]. Journal of Money, Credit and Banking, 2012, 44(5): 825–862. DOI:10.1111/j.1538-4616.2012.00512.x |



