
2020第46卷第8期
一、引 言
始于政府财力下滑和宏观调控能力弱化背景之下的1994年“分税制”改革,虽然对央地政府之间的收入划分进行了较好的规范,但是中国政府的体制改革把提高中央政府的财力集中度和宏观调控能力作为改革目标,从而解释了“财权上移与事权下放”在中国存在的合理性。然而,收支之间非对称性的逆向运动不仅导致地方政府财力与事权的错配,而且促使地方政府的收支缺口不断扩大,这也就要求中央政府的转移支付在均衡央地政府之间的财政关系时发挥举足轻重的作用。根据现代分权理论,可从两个层面为中央政府转移支付这个关键性角色提供理论注解:一是中央政府需要内化司法管理辖区之间的外溢效应;二是中央政府需要缩小地方政府的财政能力差距,促使地方政府的财力与其履行的事权以及支出责任相适应。由于我国地区经济发展的不平衡和地方政府的财力差异较大,如何有效地发挥中央政府的均衡性转移支付在新型央地政府之间财政关系中的嫁接功能和桥梁作用,不仅有利于构建地方政府公共行政的正向激励机制,而且有助于加快建立现代财政制度。
“营改增”政策的全面推广导致我国地方政府的自有收支缺口不断扩大,并且使得地方政府主体税种出现缺位。因此,后“营改增”时代的地方政府,不仅需要面对税基窄和税源不稳定的多重窘境,还要面对“自上而下”的行政考核压力、“政治晋升锦标赛”“经济锦标赛”等多重制度约束,这在很大程度上解释了地方政府除依赖中央转移支付之外,为何其偏好以经济建设支出为代表的生产性支出。然而,中央政府的现行转移支付制度较少考虑地区经济发展的差异,未能有效地缩小地方政府之间的横向差距,并且可能有失一定的公允性。这是因为,经济发达地区拥有更多的财力进行经济建设和投资,从而不断地推动基础设施和“市容市貌”的改善,虽然这会导致其对财政资金的需求相对较大,但是也推动了地方经济的较快发展。然而,在现行转移支付的制度下,经济发展水平越高和税收努力程度越强的省份,相对会获得更多的转移支付资金,并且这种资金分配的“马太效应”会导致省份之间的贫富差距进一步扩大。
迄今为止,国内外学者围绕中央政府的转移支付对地方政府支出的影响展开了深入研究,但是研究结论迥然各异。Bradford和Oates(1971)认为上级政府的转移支付和本级政府的自有收入之间具有同效性,即自有收入和一次性补助对地方政府支出倾向的影响相同,原因是二者之间存在完全替代性,此现象被称为“面纱假说”。Alesina和La Ferrar(2005)研究发现中央政府转移支付会促使地方政府提高社会保障和医疗卫生等民生性支出比例。Hindriks等(2008)认为科学设计的转移支付会抑制地方政府增加经济性公共品供给,反而增加有利于提升居民福利的民生性公共品的供给。Checherita(2009)发现用于地区再分配的净转移支付阻碍了接受转移支付地区的产出增长,此现象被称为“悲惨性收敛”,因为转移支付减少了受援地区政府增加生产性建设支出的动机。Cyrenne和Pandey(2015)研究发现,中央纵向转移支付降低了接受转移支付的地方政府进行生产性建设支出的动机,与纵向转移支付的非接受省份相比,前者的生产性建设支出占比更低。然而,张军等(2007)认为改善地方政府财力的转移支付会促使地方政府的财政支出行为异化,使其更加偏好生产性支出,从而形成地方政府重建设、轻服务的扭曲的支出结构。范子英和张军(2010)发现地方政府支出规模因中央政府的转移支付的“粘蝇纸效应”而相应增加,并且增量大于同量税收上升而引起的支出增加规模。付文林和沈坤荣(2012)发现中央转移支付不仅对地方政府的支出产生“粘蝇纸效应”,而且地方政府在获得转移支付从而改善财力后,还可能通过调整现有支出结构进而偏离基本公共服务的均等化目标,即存在地方政府支出的可替换效应。徐琰超等(2016)通过实证分析发现,转移支付对地方政府支出结构的影响具有异质性,即转移支付虽然会促使资源禀赋充裕的地方政府增加生产性建设支出,但是对资源禀赋匮乏的地方政府而言,将转移支付资金更多地用于具有福利性质的民生性支出。李永友和张子楠(2017)立足我国社会性公共品供给相对短缺的客观情况,研究转移支付制度对地方政府的社会性公共品供给行为的影响和激励机制发现,我国转移支付制度并不能很好地激励地方政府增加社会性公共品的供给。丁玮蓉和张帆(2018)基于我国321个县2005−2009年的数据,建立面板门槛模型分析了均衡性转移支付对县级政府支出结构的影响,其研究发现中央政府的均衡性转移支付虽然提升了地方政府的福利性公共品的供给水平,但是这种正向激励效应在欠发达区县并不明显。朱光等(2019)利用空间杜宾模型详细分析了一般性转移支付和专项转移支付对地方政府教育与环境保护等五类公共服务支出的影响,其研究发现专项转移支付对每项公共服务支出的影响均显著为正,但是一般性转移支付仅对交通运输与环境保护的影响显著为正。刘贯春和周伟(2019)基于2000−2006年间2859个县级行政单位数据发现,转移支付的不确定性增加了地方政府生产性建设的支出动机,而该效应为非线性,并对中西部区县的生产性建设的支出提升效果最为明显。
随着我国经济从高速增长时期进入高质量发展的新时期,构建激励相容的新型央地政府之间的财政关系,不仅有助于加快建立现代财政制度,而且可以推进国家治理体系的完善与地方政府治理能力的提升。首先,本文尝试在巴罗模型中嵌入中央政府转移支付来构建地方政府支出决策的分析框架,并采取联立效用函数来求解政府支出的决策选择,从理论层面证明了中央政府的转移支付对地方政府的支出结构具有非线性关系。其次,通过建立面板分位数回归模型实证发现,中央政府的均衡性转移支付对地方政府的支出结构的影响,不仅取决于地方政府支出结构的自身变动,还与中央政府的均衡性转移支付占比的变动情况有关:当地方政府生产性支出占比处于相对较低的10%和25%分位时,中央政府的均衡性转移支付的增长会导致地方政府增加生产性支出;然而,当地方政府生产性支出占比达到相对较高的50%分位以上时,中央政府的均衡性转移支付对地方政府支出结构的影响由正转变为负,即地方政府随着中央政府增加均衡性转移支付,其不断降低生产性支出占比而相应增加非生产性支出。最后,本文把中央政府的均衡性转移支付作为门槛变量,建立面板门槛分位数回归模型,进一步研究发现当中央政府均衡性转移支付占比超过门槛值0.4274时,中央政府均衡性转移支付也会促进地方政府加大生产性支出而抑制非生产性的民生公共服务供给。
本文可能的边际贡献为:一是根据中国式分税制改革实践与政策,将中央政府的转移支付分为均衡性转移支付和非均衡性转移支付,尝试在巴罗模型中嵌入中央政府转移支付从而构建地方政府支出决策分析的理论框架,进而采用联立效用函数求解政府的支出决策选择,并用理论证明了中央政府的转移支付与地方政府的支出结构之间具有非线性关系;二是通过采用省级面板数据,建立了面板分位数回归模型,实证发现在地方政府支出结构取值的不同分位点处,中央政府的均衡性转移支付对地方政府的支出结构具有显著的非线性效应;三是进一步选择均衡性转移支付作为门槛变量,建立面板门槛分位数回归模型,研究发现在中央政府均衡性转移支付取值的不同区间,其对地方政府支出结构的影响也具有非线性关系。
二、理论框架
虽然1994年“分税制”改革通过“财权上移与事权下放”的非对称逆向运动提高了中央政府的财力,但是这种非对称性分权也导致了地方政府的财政支出缺口不断扩大。因此,转移支付制度在均衡央地政府之间的财政关系中发挥着至关重要的作用。随着2002年所得税分享制度的改革,国务院明确了中央因所得税分享改革所得的收入全部用于地方,尤其是用于中西部地区的均衡性转移支付,进一步强化了中央政府的转移支付在均衡央地政府之间财政关系的作用。本文通过借鉴Cyrenne和Pandey(2015)的研究,按照转移支付的资金性质和使用方式,将中央政府的转移支付分为均衡性转移支付与非均衡性转移支付,深入考察均衡性转移支付对我国地方政府支出结构的作用机制与影响效应。为简化分析,我们做如下假设。
假设1:中央政府对各地区的均衡性转移支付的资金分配,取决于各地区政府的自有收入和支出之间关系,一般认为自有收入低且收支缺口大的地方政府获得中央政府的均衡性转移支付要大于自有收入高且收支缺口小的地方政府。
假设2:随着地方政府自有收支缺口的降低,中央政府会相应地减少该地区的均衡性转移支付的总量。
本文用
| trbit={ε(ξˉyt−ξyit),ˉyt>yit0,ˉyt⩽yit | (1) |
其中,
假设3:政府公共服务具有可分性,政府可以将公共服务平均分配给每位居民个体。将地方政府财政支出分为生产性支出和非生产性支出,即
在借鉴Cyrenne和Pandey(2015)研究的基础上,本文尝试在巴罗模型的框架中嵌入中央政府的均衡性转移支付,并通过联立居民效用最大化方程来研究其对政府支出结构变化的影响。因为巴罗模型本质上属于
假设4:为满足巴罗模型的前提条件,中央政府下辖各地区的经济初始状态为稳态,即人均资本、人均消费、政府支出和人均产出等所有变量的增速相同。同时地方政府在未获得中央政府的转移支付资金之前,其生产性和非生产性服务的支出仅来源于自有收入,①并且自有收入的最优分配方式如下:
| {guit=θξyitgpit=(1−θ)ξyit | (2) |
其中,
| yit=A1/ωkit((1−θ)ξ)(1−ω)/ω,0<ω<1 | (3) |
其中,
假设5:政府有能力提供生产性和非生产性服务,并且非生产性公共服务是持续定期提供。因此,所有居民均可以持续消费,
| U(cit,guit)=∞∫0e−ρt(lncit+φlnguit)dt | (4) |
其中,折现率
| yit+trit=cit+kit+gpit+guit | (5) |
其中,
| kit=yit+βtrbit−(1−θ)ξyit−θξyit−cit=yit(1−ξ−βεξ)−cit+βεξˉyt | (6) |
在“以人为本”执政理念指引下,辖区居民的满意度也是政府支出选择的重要考虑因素。在获得中央政府转移支付的前提下,地方政府可以通过改变在生产性和非生产性领域的财政支出配比,通过调整支出结构影响辖区居民福利,进而实现整个社会的效用最大化。联立式(4)与(6),构造拉格朗日函数求解地方政府的支出决策:
| L=∞∫0e−ρt(lncit+φlnguit)dt−λit[kit−(1−ξ−βεξ)A1/ωkit((1−θ)ξ)(1−ω)/ω−βεξˉyt+cit]=0 | (7) |
由假设4可推知各变量均处于平衡增长路径,因此通过求解
| ˙citcit=(1−ξ−βεξ)A1/ω((1−θ)ξ)(1−ω)/ω−ρ=γ | (8) |
其中,
| citkit=1−ωωξ(1−ξ−βεξ)A1/ω((1−θ)ξ)(1−2ω)/ωθφ | (9) |
在平衡增长路径上,
| γki0=(1−ξ−βεξ)A1/ωki0((1−θ)ξ)(1−ω)/ω−ci0+εξˉyt | (10) |
联立式(8)和式(10)得到:
| ci0ki0=(1−ξ−βεξ)yi0ki0+εξˉytki0−γ | (11) |
联立式(8)和式(11)得到:
| γ+ρ=(1−ξ−βεξ)yi0ki0 | (12) |
联立式(11)和式(12)可推出:
| ci0ki0=ρ+εξˉytki0 | (13) |
因此,初始
| (1−θ)2ω−1ωθ=1−ωω(1−ξ−βεξ)A1ωξ1−ωωφB | (14) |
| ∂θ∂ε=ξβ1−ξ−βεξ(2ω−1ω(1−θ)+1θ) | (15) |
综上证明,
(1)当
| {当θ<ω1−ω时:∂θ∂ε>0且∂(1−θ)∂ε<0当θ>ω1−ω时:∂θ∂ε<0且∂(1−θ)∂ε>0 | (16) |
当非生产性支出占比
(2)当
| {当θ<ω1−ω时:∂θ∂ε<0且∂(1−θ)∂ε>0当θ>ω1−ω时:∂θ∂ε>0且∂(1−θ)∂ε<0 | (17) |
当非生产性支出占比
综上可知,中央政府的均衡性转移支付不仅会显著地影响地方政府支出结构的变动,而且这种影响在不同取值区间内是不同的,即具有非线性特征。
三、变量选取、数据来源和描述性统计
(一)变量选取
1. 地方政府支出结构。随着我国进入经济高质量发展的新时期,民生福祉成为时代主题与政府的首要任务。因此,政府支出由生产性支出逐渐转向医疗卫生、社会保障和公共安全等非生产性公共服务支出,这不仅体现新时代政府坚持“以人民为中心”和“以民为本”的执政理念,而且也是让全国人民共享改革开放与经济发展成果的根本途径。因此,本文实证部分借鉴理论模型中的做法,将我国政府支出区分为生产性支出和非生产性支出,且用生产性支出占地方政府总支出的比重来测度地方政府支出结构的变化。由于2006年政府收支分类改革导致政府支出科目与统计口径在2007年前后发生较大变化,同时因为国内学者有关生产性支出和非生产性支出的划分方法与计算口径存在一定差异,本文将以2006年为时间界限对地方政府生产性支出进行分段统计。其中,2003−2006年的生产性支出包括农林水利气象事业费、工业交通部门事业费和地质勘探费等。2007年以后的生产性支出口径的计算采用范庆泉等(2015)的划分标准,将基本建设、农林水利、气象、交通运输和工商业等支出归为生产性支出。
2. 中央政府均衡性转移支付占比。中央政府的均衡性转移支付作为分权体制国家均衡央地政府之间财力的政策工具,可以有效地缓解暂时性冲击对地方政府财政收支缺口的压力(Hepp和Von Hagen,2013)。在2002年所得税分享体制改革之前,1994年分税制改革形成了以税收返还为主的转移支付制度,这在较大程度上倾向于增加地方政府的自有收入,并且使得分税制改革顺利进行。然而,随着政府职能的不断调整与优化,中央政府的均衡性转移支付在调整地方政府支出结构中的作用愈加重要。中央政府的均衡性转移支付作为分权体制下校正与弥补地方政府收支缺口的重要政策工具,放松了下级政府的预算约束,并且提高了公共品供给成本的补偿能力。同时,依据辖区竞争理论和“公共池”机制,转移支付可从规模与结构两个层面对地方政府支出行为产生一定影响。虽然,中央政府转移支付包括一般性转移支付、专项转移支付和税收返还等,但是考虑到税收返还作为分税制改革中为增加地方政府财政收入的过渡性措施,且在经济发达省份与欠发达省份之间具有显著的“马太效应”。专项转移支付不仅通常规定特定用途,而且有时需要地方政府提供相关财力配套。因此,本文认为税收返还和专项转移支付都不具有缩小地方政府收支缺口的均衡性作用。而一般性财力转移支付是基于地方政府的标准收支缺口进行测算的,并且此资金由地方政府完全自由支配。所以,本文采用一般性财力转移支付代表中央政府的均衡性转移支付,即中央政府的均衡性转移支付占比为一般性财力转移支付在转移支付总量中的占比。
3. 控制变量。本文引入以下控制变量:一是产业结构(Structure),用第三产业增加值占GDP比重表示;二是城乡居民收入差距(URgap),用城镇居民与农村居民人均收入之比表示;三是平均受教育年限(Education);四是人口老龄化程度(Aging),用65岁以上人口数除以各省份常住人口数表示;五是城市化率(Urban),用各省每年城镇常住人口数除以该省总人口数度量;六是对外开放(Open),用各省份的进出口总额除以GDP表示,由于《中国统计年鉴》中各省份的进出口总额均以美元作为计量单位,因此首先利用各省进出口总额乘以美元平均汇率,然后再除以该省份GDP;七是人均财政收入(Rev),用地方政府一般公共预算收入除以该省份总人口数后取自然对数得到;八是经济发展水平(Econ),用人均GDP的自然对数表示。
(二)数据来源与描述性统计。本文数据均来自《中国统计年鉴2004−2018》《中国国土资源统计年鉴2004−2018》《中国财政年鉴2004−2018》和中经网统计数据库以及各省份的历年统计年鉴,时期跨度为2003−2017年,且相关变量都以2003年为基期(2003年=100)采取相关指数进行价格平减。其中,因为西藏相关数据不全,仅能计算除西藏之外的30个省份。相关变量的描述性统计情况如表1所示。
| 变量名称 | 样本数量 | 最大值 | 最小值 | 平均值 | 标准误 |
| 地方政府支出结构(Govern) | 450 | 0.5272 | 0.2091 | 0.3830 | 0.0662 |
| 中央政府均衡性转移支付(Transfer) | 450 | 0.6570 | 0.0172 | 0.4015 | 0.1676 |
| 产业结构(Structure) | 450 | 0.8056 | 0.2860 | 0.4174 | 0.0879 |
| 城乡居民收入差距(URgap) | 450 | 4.7586 | 1.8452 | 2.8922 | 0.5639 |
| 平均受教育年限(Education) | 450 | 12.3037 | 6.0405 | 8.6852 | 1.0365 |
| 人口老龄化(Aging) | 450 | 0.1638 | 0.0543 | 0.0936 | 0.0192 |
| 城市化率(Urban) | 450 | 0.8960 | 0.2566 | 0.5177 | 0.1444 |
| 对外开放(Open) | 450 | 1.7215 | 0.0169 | 0.3184 | 0.3899 |
| 人均财政收入(Rev) | 450 | 10.2185 | 5.7654 | 7.8346 | 0.9502 |
| 经济发展水平(Econ) | 450 | 11.7675 | 8.2164 | 10.2314 | 0.7227 |
四、实证检验和分析
(一)构建面板分位数回归模型。理论上,分位数回归模型在对被解释变量进行多等分后,可得到自变量对因变量每一分位点处的边际影响。即当对本文的被解释变量地方政府支出结构进行n等分时,分位数回归模型可得到中央政府均衡性转移支付在地方政府支出结构取值的n个分位点上的n个边际影响值。
首先,假设Y为连续型随机变量,累积分布函数为
| q=P(Y⩽yq)=Fy(yq) | (18) |
由公式(18)可知,将总体分布正好分为两部分的总体
| q=P{y⩽yq(x)}=P{x′β+μ⩽yq(x)}=P{μ⩽yq(x)−x′β}=P{x′α⋅ε⩽yq(x)−x′β}=P{ε⩽yq(x)−x′βx′α}=Fε(yq(x)−x′βx′α) | (19) |
其中,
| yq(x)−x′βx′α=F−1ε(q) | (20) |
假设条件分布
| yq(x)=x′iβq | (21) |
其中,
| ∧βq=minn∑i:yi⩾x′iβqq|yi−x′iβq|+n∑i:yi<x′iβq(1−q)|yi−x′iβq| | (22) |
综上所述,一方面,由于地方政府的支出结构存在异质性,因此本文在研究中央政府的均衡性转移支付对地方政府的支出结构影响时不能一概而论。另一方面,本文理论模型部分已经证明中央政府的均衡性转移支付对地方政府的支出结构的影响为分段非线性函数,即随着地方政府支出结构取值范围的不同而发生效应转变。因此,根据地方政府支出结构在不同分位点上的取值,尝试建立以下面板分位数回归模型,实证考察中央政府的均衡性转移支付对地方政府支出结构是否存在非线性影响,具体如下:
| Governit=∂0τ+∂1τ×Transferit+λ1Structureit+λ2URgapit+λ3Educationit+λ4Agingit+λ5Urbanit+λ6Openit+λ7Revit+λ8Econit+uit | (23) |
其中,
(二)实证结果分析
1. 面板分位数回归模型的估计
| 变量名称 | 分位数回归 | ||||
| Q=0.10 | Q=0.25 | Q=0.50 | Q=0.75 | Q=0.90 | |
| 中央政府均衡性转移支付(Transfer) | 0.1218**(0.0500) | 0.0861***(0.0328) | −0.0056(0.0329) | −0.2881***(0.0818) | −0.1218**(0.0528) |
| 产业结构(Structure) | 0.2648***(0.0931) | 0.1026*(0.0740) | 0.0446(0.0560) | 0.6640***(0.1459) | −0.2648***(0.0951) |
| 城乡居民收入差距(URgap) | −0.0126(0.0141) | −0.0232**(0.0098) | −0.0267***(0.0058) | −0.0267**(0.0106) | 0.0126(0.0140) |
| 平均受教育年限(Education |
−0.0155(0.0108) | −0.0111*(0.0067) | −0.0162***(0.0046) | −0.0191*(0.0113) | 0.0155(0.0111) |
| 人口老龄化(Aging) | −0.5837**(0.2495) | −0.7961***(0.1605) | −0.6882***(0.1692) | −0.1516(0.3318) | 0.5837**(0.2287) |
| 城市化率(Urban) | −0.4752***(0.1109) | −0.4682***(0.0593) | −0.4989***(0.0591) | 0.7935***(0.1293) | 0.4752***(0.1125) |
| 对外开放(Open) | 0.0277(0.0223) | 0.0345(0.0808) | 0.0090(0.0216) | −0.0255(0.0676) | −0.0277(0.0227) |
| 人均财政收入(Rev) | 0.0374(0.0297) | 0.0719***(0.0198) | 0.0887***(0.0119) | −0.0472*(0.0306) | −0.0374*(0.0296) |
| 经济发展水平(Econ) | 0.0656*(0.0385) | 0.0284(0.0286) | 0.0145(0.0165) | −0.1267***(0.0458) | −0.0656*(0.0387) |
| 常数项 | −0.3321(0.2110) | −0.0897(0.1558) | 0.0601(0.0953) | 2.0319***(0.2749) | 1.3321***(0.2123) |
| 注:***、**和*分别表示在1%、5%和10%的显著性水平上显著,括号内为系数估计值的稳健标准误。 | |||||
2. 实证结果分析
首先,中央政府的均衡性转移支付对地方政府的支出结构的非线性效应在其取值的任一分位都通过了显著性检验。如表2所示,在地方政府生产性支出占比由低到高的五个分位点处,中央政府均衡性转移支付对地方政府支出结构的影响系数分别为 0.1218、0.0861、−0.0056 、−0.2881和−0.1218。一方面,当地方政府生产性支出占比处于较低的10%和25%分位时,中央政府的均衡性转移支付的增长会导致地方政府生产性支出的增加。另一方面,当地方政府生产性支出占比提高到50%分位及以上时,随着中央政府进一步增加均衡性转移支付,地方政府的生产性支出反而会相应下降,并且会不断提高非生产性支出占比。因为,在中国的政治体制下,地方生产性支出通过直接参与生产建设,不仅能为地方政府带来更多的财政收入,而且还能够刺激地方的经济增长。而地方政府官员在“经济锦标赛”与“政治晋升锦标赛”双重激励下通常会偏好生产性支出。尤其是当地方政府生产性支出占比相对较低时,地方政府都会倾向提高生产性支出占比,并且将中央政府的均衡性转移支付作为相应财政资金的重要补给来源。这样不仅可以有效地缓解地方政府的财政压力,解决政府的“燃眉之急”,而且可以帮助地方政府官员通过推动辖区经济较快发展而赢得两个“锦标赛”。然而,当地方政府的生产性支出占比达到一定程度时,地方政府虽然可从财政投资行为中获得收益,但是一方面受约束于生产性支出的投资边际收益递减规律,另一方面,在当前坚持“以人民为中心”与“以民为本”的新时代主题背景下,辖区居民对民生性公共服务需求不断增长,如何满足人民日益增长的美好生活需求成为了地方政府工作的重中之重。因此,以上两方面的制度约束都会促使地方政府在生产性支出占比较高时,重视民生工程建设,加大政府在医疗、住房与社会保障等方面支出,从而提升辖区居民福祉。
其次,产业结构在地方政府生产性支出占比较低时,二者之间关系表现为显著正相关,当其达到90%分位时,二者之间关系变为显著负相关。这说明在地方政府生产性支出占比相对较低时,第三产业的提高仍然会导致地方政府加大生产性支出,这是因为第三产业的较快发展需要良好的基础设施。然而,当生产性支出占比较高和地方基础设施建设已经有较大发展时,第三产业的发展会要求地方政府增加与之相配套的非生产性的民生公共服务供给。
再次,城乡居民收入差距、平均受教育年限和人口老龄化对地方政府支出结构的影响基本为负,这是因为缩小城乡居民收入差距、提高平均受教育年限和妥善解决人口老龄化问题都需要政府不断增加相应的非生产性民生公共服务。如表2所示,城乡居民收入差距、平均受教育年限和人口老龄化的上升,无论是地方政府支出结构取值处于哪一分位,基本上都会导致地方政府降低生产性支出,而相应增加非生产性的民生公共服务供给。另外,城市化率在地方政府支出结构处于50%分位之前,二者之间为显著负相关,但是在50%分位之后,二者之间关系由显著为负转变显著为正。这说明在城市化水平上升的初期,虽然城市人口的较快增加也会增加对城市基础设施的需求,但是城市居民对子女教育、医疗卫生和住房保障等民生性需求反而更加重视,从而会导致地方政府增加非生产性的民生公共服务供给。然而,当城市化人口扩张后,城市人口规模膨胀带来的聚集效应与扩张效应就会导致其对城市基础设施的需求大幅度增加,进而在短期内促使地方政府生产性支出的较快增加。
最后,人均财政收入和经济发展水平对地方政府支出结构的影响,随着其生产性支出占比的提升由正转变为负。即当地方政府生产性支出占比相对较低时,地方政府增加人均财政收入和提高经济发展水平都会促使地方政府增加生产性支出。但是,当地方政府生产性支出占比达到75%分位时,如果继续增加人均财政收入和提高经济发展水平,地方政府反而会降低生产性支出,从而转向增加非生产性民生支出。这是因为当生产性支出处于较低水平时,地方政府一方面通过“学习效应”和开展“竞好竞争”增加生产性支出,另一方面,经济发展水平的上升和人均财政收入的增加也为地方政府的生产性支出提供了相应的财力来源。虽然对外开放对地方政府支出结构的影响同样由正转负,但是影响效应并不显著,可能的原因有待进一步分析。
五、进一步研究
(一)构建面板门槛分位数回归模型
1. 面板门槛分位数回归模型。中央政府均衡性转移支付占比的提高不仅反映了转移支付结构的变化,而且可能会对地方政府支出结构产生非线性影响。因此,本文为了更加全面与系统地考察中央政府均衡性转移支付对我国地方政府支出结构的非线性效应及其特征,根据Hansen(1999)提出的面板门槛回归模型作进一步研究:首先,对中央政府均衡性转移支付占比的门槛值进行搜索与估算;其次,基于面板分位数回归模型的研究目标,借鉴李金凯和张同斌(2018)的做法,建立面板门槛分位数回归模型(24)。为了简便,本文以单门槛为例,详细阐述面板门槛分位数回归模型(24),具体如下:
| Governit=∂0τ+∂11τ×TransferitI(γ1≺qit)+∂21τ×TransferitI(γ1≻qit)+βXit+εit | (24) |
其中,
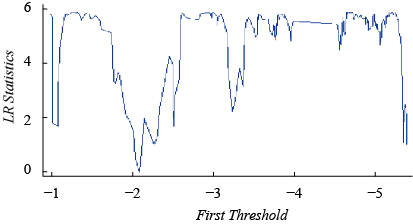
2. 面板门槛分位数回归模型的形式检验。为避免模型的形式设定错误,需要检验面板门槛分位数回归模型(24)是否存在门槛效应,并且还需确定门槛值个数。因此,在对模型(24)估计之前,需要进行门槛效应检验和门槛个数检验。根据表3检验结果,面板门槛分位数回归模型(24)有且只有一个门槛值。因为原假设为无门槛效应的检验统计量,即使是在10%的显著性水平下也拒绝原假设。同时,在是否存在双门槛效应的检验中,估计结果显示接受只存在单一门限效应的原假设。在面板门槛分位数回归模型进行形式检验之后,本文首先采取网格搜索法对门槛变量中央政府的均衡性转移支付的不同取值依次回归,进而通过最小化残差平方和,获得门槛变量中央政府均衡性转移支付的单一估计值
| 门槛类型与检验假设 | 残差平方和 | F统计量 | P值 | 检验结果 |
| 单门槛(原假设:无门槛效应) | 0.7579 | 15.56*** | 0.0780 | 拒绝原假设 |
| 双门槛(原假设:单一门槛效应) | 0.7493 | 6.02 | 0.7210 | 接受原假设 |
(二)实证估计与结果分析
本文进一步对不同区间范围内的中央政府均衡性转移支付和地方政府支出结构进行分位数回归估计,从而考察在中央政府均衡性转移支付不同取值区间内,对地方政府支出结构的非线性影响,回归估计结果如表4所示。
|
| 图 1 中央政府均衡性转移支付的门槛值和90%置信区间 |
| 变量名称 | 面板门槛分位数回归 | |||||
| Q=0.10 | Q=0.25 | Q=0.50 | Q=0.75 | Q=0.90 | ||
| 中央政府
均衡性转 移支付 (Transfer) |
小于
γ1
|
−0.0776
(0.0660) |
−0.0545* (0.0307) |
−0.0793* (0.0466) |
0.0780
(0.0672) |
0.0506
(0.0741) |
| 大于或
等于
γ1
|
0.0938*** (0.0268) |
0.0623** (0.0282) |
0.0408** (0.0205) |
0.0597** (0.0291) |
0.0243
(0.0281) |
|
| 产业结构(Structure) | 0.1995*** (0.0815) |
0.0880
(0.0776) |
0.0290
(0.0560) |
−0.0011
(0.0808) |
−0.0677
(0.1085) |
|
| 城乡收入比(URgap) | −0.0198
(0.0134) |
−0.0276*** (0.0091) |
−0.0246*** (0.0070) |
−0.0154
(0.0109) |
0.0031
(0.0156) |
|
| 平均受教育年限(Education |
−0.0107
(0.0104) |
−0.0139** (0.0063) |
−0.0140*** (0.0051) |
−0.0149* (0.0080) |
−0.0189* (0.0107) |
|
| 人口老龄化(Aging) | −0.6653*** (0.2534) |
−0.6618*** (0.1816) |
−0.6753*** (0.1833) |
−0.5016* (0.2645) |
−0.3242
(0.4794) |
|
| 城市化率(Urban) | −0.5386*** (0.0985) |
−0.4120*** (0.0772) |
−0.4773*** (0.0613) |
−0.4706*** (0.0964) |
−0.0738
(0.1521) |
|
| 对外开放(Open) | −0.0042
(0.0212) |
−0.0111
(0.0221) |
−0.0039
(0.0210) |
0.0213
(0.0301) |
−0.0610
(0.0426) |
|
| 人均财政收入(Rev) | 0.0566** (0.0227) |
0.0839*** (0.0204) |
0.0940*** (0.0127) |
0.0663*** (0.0219) |
0.0699** (0.0276) |
|
| 经济发展水平(Econ) | 0.0491* (0.0385) |
−0.0005
(0.0302) |
0.0056
(0.0189) |
0.0400
(0.0290) |
0.0024
(0.0384) |
|
| 常数项 | −0.2035
(0.1751) |
0.1474
(0.1861) |
0.1003
(0.1104) |
−0.0498
(0.1540) |
0.0770
(0.2385) |
|
| 注:***、**和*分别表示在1%、5%和10%的显著性水平上显著,括号内为系数估计值的稳健标准误。 | ||||||
如表4所示,通过将中央政府均衡性转移支付作为门槛变量,进一步估计面板门槛分位数回归模型发现,中央政府均衡性转移支付在不同取值区间内,对地方政府支出结构的影响存在显著的非线性特征:一是当中央政府均衡性转移支付占比小于门槛值0.4274时,中央政府均衡性转移支付占比对地方政府支出结构的影响在多数情况下都不显著,仅在地方政府支出结构的25%和50%分位时,中央政府均衡性转移支付对地方政府支出结构具有显著负效应,即可以通过改变中央政府均衡性转移支付,达到降低地方政府生产性支出占比的政策效果。二是当中央政府均衡性转移支付占比大于或等于门槛值0.4274时,并且在地方政府生产性支出达到90%分位之前,中央政府均衡性转移支付对地方政府支出结构存在显著正相关关系。这说明如果中央政府提高均衡性转移支付占比,地方政府反而因为均衡性财力规模的较大增加以及“政治晋升锦标赛”和“经济锦标赛”的激励作用等原因,仍然会加大生产性支出从而抑制地方政府增加对非生产性民生公共服务的供给。
综合面板分位数回归与门槛分位数回归模型的实证估计结果,本文认为中央政府均衡性转移支付对地方政府支出结构的影响较为复杂,不仅取决于地方政府支出结构的自身变动,还与中央政府均衡性转移支付占比变动情况有关。因此本文认为,一方面,中央政府需要科学地制定地方政府官员的业绩考评机制,从而使得地方政府不断优化支出结构。另一方面,需要科学设计与不断调整中央政府转移支付结构,充分发挥中央政府的均衡性转移支付对地方政府支出结构的优化效应,促使和激励地方政府在坚持“以人民为中心”的执政理念下,不断增加对医疗、住房、教育、社会保障和生态环境保护等民生性公共服务供给,从而满足新时代人民日益增长的美好生活需求。另外,根据表4估计结果,控制变量对地方政府支出结构影响的变化相对较小,仅少数控制变量回归系数估计值的显著性或符号略有变化。例如,对外开放对地方政府支出结构的影响无论是在哪一个分位上都未通过显著性检验。同时,因为考虑控制变量不是本文的分析重点,在此就不一一赘述。
六、研究结论与政策建议
构建激励相容的新型央地政府之间的财政关系不仅可以加快现代财政制度的建立,也可提升国家的治理能力。首先,本文尝试在巴罗模型中嵌入中央政府转移支付来构建地方政府支出决策的分析框架,并且采取联立效用函数求解政府支出的决策选择,从理论上证明了中央政府转移支付与地方政府支出结构之间存在非线性关系。其次,通过建立面板分位数回归模型,实证发现中央政府均衡性转移支付对地方政府支出结构具有显著的非线性效应。其中,当地方政府生产性支出占比处于相对较低的10%和25%分位时,中央政府均衡性转移支付的增长会导致地方政府增加生产性支出。然而,当地方政府提高生产性支出占比达到相对较高的50%分位以上时,中央政府的均衡性转移支付对地方政府支出结构的影响由正转变为负,即地方政府随着中央政府增加均衡性转移支付的增加,会降低其生产性支出占比,从而相应增加非生产性民生支出。最后,本文通过把中央政府均衡性转移支付作为门槛变量,建立面板门槛分位数回归模型,进一步研究发现中央政府均衡性转移支付对地方政府支出结构的影响在不同区间内具有显著的非线性特征。其中,在中央政府均衡性转移支付占比大于或等于门槛值0.4274的区间内,并且在地方政府生产性支出提高到90%分位之前,中央政府均衡性转移支付对地方政府支出结构存在显著正相关关系。即地方政府反而因均衡性财力规模的较大增加以及在“政治晋升锦标赛”和“经济锦标赛”双重激励下,仍然会加大生产性支出,从而对地方政府优化支出结构产生阻滞作用。以上研究结论不仅对于新时代构建权责清晰、财力协调和区域均衡的新型央地政府间财政关系具有重要的理论与现实意义,同时还有助于加快建立现代财政制度。
综上所述,本文提出以下政策建议:一是从中央政府转移支付与地方政府支出结构两个层面采取“双管齐下”的方法,立足东、中、西部地区各自经济社会发展的差异与目标,最大限度发挥中央政府的均衡性转移支付对地方政府支出结构不断优化的调节职能与引导功效。例如,经济发达地区省份的基础设施建设相对较好,辖区人民的需求不断转向教育、医疗卫生、住房保障等民生性公共服务,当地方政府生产性占比超过50%分位时,中央政府需要缩减对发达省份的专项转移支付,通过对发达省份提高均衡性转移支付占比来增加其地方政府的可支配收入。二是为了更好发挥中央政府均衡性转移支付对地方政府支出结构的影响效应,需要根据门槛效应估计结果,进一步科学地判断与区分中央政府均衡性转移支付占比是否超过门槛经验值。因为,在这两种情况下,中央政府均衡性转移支付对地方政府支出结构取不同分位的影响效应的差异较大。其中,经济欠发达的西部地区为了进一步加大基础设施建设,只要其地方政府生产性支出占比未达到较高分位时,提高中央政府对其均衡性转移支付就会促使西部省份加大基础设施建设,而不需要增加类似的专项转移支付。三是为降低“经济锦标赛”与“晋升锦标赛”对地方政府官员的制度激励,需要通过变革政府官员的业绩考核机制来引导其树立科学的业绩观,使得地方政府官员不断优化地方政府的支出结构,从而发挥中央政府的均衡性转移支付对地方政府支出结构的优化效应,促使地方政府更加重视民生性公共服务的供给。一方面,不断推进地方经济高质量发展,另一方面,不断满足辖区居民不断增长的美好生活需求。最后,还要鼓励地方政府创新发展思路,统筹城乡协调与一体化发展,重视人力资本投入和人口老龄化问题,不断扩大对外开放与注重学习示范效应,并且通过外资流入来弥补地方政府支出的财力不足,从而促使地方政府不断优化支出结构,并更重视民生性公共服务的供给。
① 参考1995年1月1日实施的原《预算法》第28条规定:“地方各级预算按照量入为出、收支平衡原则编制,不列赤字”。
| [1] | 丁玮蓉, 张帆. 均衡性转移支付制度会带来地方政府福利性公共服务支出偏向吗?[J]. 财经论丛, 2018(10): 19–28. |
| [2] | 范庆泉, 周县华, 潘文卿. 从生产性财政支出效率看规模优化: 基于经济增长的视角[J]. 南开经济研究, 2015(5): 24–39. |
| [3] | 范子英, 张军. 财政分权、转移支付与国内市场整合[J]. 经济研究, 2010(3): 53–64. |
| [4] | 付文林, 沈坤荣. 均等化转移支付与地方财政支出结构[J]. 经济研究, 2012(5): 45–57. |
| [5] | 李金凯, 张同斌. 中国城市生产率增长中FDI的分层影响和非对称效应研究[J]. 产业经济研究, 2018(4): 14–25. |
| [6] | 李永友, 张子楠. 转移支付提高了政府社会性公共品供给激励吗?[J]. 经济研究, 2017(1): 119–133. |
| [7] | 刘贯春, 周伟. 转移支付不确定性与地方财政支出偏向[J]. 财经研究, 2019(6): 4–16. |
| [8] | 徐琰超, 柳荻, 杨龙见. 资源禀赋差异与地方政府支出偏向[J]. 金融评论, 2016(4): 31–46. DOI:10.3969/j.issn.1674-7690.2016.04.003 |
| [9] | 张军, 高远, 傅勇, 等. 中国为什么拥有了良好的基础设施?[J]. 经济研究, 2007(3): 4–19. |
| [10] | 朱光, 李平, 姜永华. 专项转移支付、一般性转移支付与地方政府公共服务支出——基于专项转移支付分项数据的空间计量分析[J]. 华东经济管理, 2019(3): 145–151. |
| [11] | Alesina A, La Ferrara E. Ethnic diversity and economic performance[J]. Journal of Economic Literature, 2005, 43(3): 762–800. DOI:10.1257/002205105774431243 |
| [12] | Bradford D F, Oates W E. Towards a predictive theory of intergovernmental grants[J]. American Economic Review, 1971, 61(2): 440–448. |
| [13] | Checherita C D. Variations on economic convergence: The case of the United States[J]. Papers in Regional Science, 2009, 88(2): 259–278. DOI:10.1111/j.1435-5957.2008.00202.x |
| [14] | Cyrenne P, Pandey M. Fiscal equalization, government expenditures and endogenous growth[J]. International Tax and Public Finance, 2015, 22(2): 311–329. DOI:10.1007/s10797-014-9310-7 |
| [15] | Hansen B E. Threshold effects in non-dynamic panels: Estimation, testing and inference[J]. Journal of Econometrics, 1999, 93(2): 345–368. DOI:10.1016/S0304-4076(99)00025-1 |
| [16] | Hepp R, Von Hagen J. Interstate risk sharing in Germany: 1970-2006[J]. Oxford Economic Papers, 2013, 65(1): 1–24. DOI:10.1093/oep/gps018 |
| [17] | Hindriks J, Peralta S, Weber S. Competing in taxes and investment under fiscal equalization[J]. Journal of Public Economics, 2008, 92(12): 2392–2402. DOI:10.1016/j.jpubeco.2007.11.012 |

