2020第46卷第8期
2. 广东外语外贸大学 金融学院,广东 广州 510006
2. School of Finance,Guangdong University of Foreign Studies,Guangzhou 510006,China
一、引 言
防范系统性金融风险是金融工作的永恒主题。在“十九大”期间,中国人民银行原行长周小川指出,对我国来说,防范系统性金融风险的重点是要防止发生“明斯基时刻”,这引起了国内外的广泛关注。自2007—2009年美国次贷危机以来,为了防范经济中可能存在的系统性金融风险,我国做出了许多卓有成效的努力,其中最突出的一点就是推动建立健全宏观审慎政策调节机制。中国人民银行自2009年以来着手推动建设宏观审慎政策体系,在2011年正式实施差别准备金动态调整机制。从2016年开始,中国人民银行将差别准备金动态调整机制“升级”为宏观审慎评估机制,并将外汇流动性和跨境资金流动纳入宏观审慎管理范畴。至此,我国的金融机构已普遍建立起宏观审慎评估体系。党的十九大报告明确指出,健全货币政策和宏观审慎政策双支柱调控框架,深化利率和汇率市场化改革。宏观审慎政策不仅在我国得到充分的认可,在国际社会也得到广泛的肯定。2016年,巴塞尔银行监管委员会(BCBS)发布的报告显示,所有BCBS成员国均已按规定执行巴塞尔协议Ⅲ中关于风险资本和流动性覆盖比率的要求,绝大部分BCBS成员国也发布了对于逆周期资本缓冲的监管要求。
对于宏观审慎政策,早期的研究集中在相关概念的探讨上(IMF,2011;周小川,2011;张健华和贾彦东,2012)。目前的研究主要集中在两个方面:一是面对国内金融冲击,宏观审慎政策和货币政策的协调问题;二是面对国外金融冲击,资本流动宏观审慎政策的协调问题。
关于货币政策和宏观审慎政策的协调问题,国内外学者已经取得了诸多成果。Angeloni和Faia(2013)指出,出于投资者利益最大化的动机,商业银行在经济扩张时期会增加其杠杆比率和风险项目投资比率,在实际数据中表现为银行资本强烈的顺周期特征,这在很大程度上加剧了产出和通货膨胀率的波动。货币政策和宏观审慎政策(逆周期的资本金要求)的组合使用有助于降低银行的挤兑风险,促进银行体系的健康发展。马勇和陈雨露(2013)在一个包含内生性金融体系的DSGE模型框架下,探讨了货币政策、监管政策和信贷政策的搭配协调问题。他们研究认为,宏观审慎下三种政策的合理组合搭配可以提高政策的实施效率。方意(2016)全面探讨了宏观审慎政策工具的分类和有效性,指出宏观审慎政策的有效性在于盯住目标和最终监管对象的一致性。就我国宏观审慎政策实践来说,盯住房屋贷款价值比和存贷比的政策工具都是有效的。Kannan等(2012)将研究重点放在房地产市场上,认为在以抵押贷款约束为核心的借贷关系下,房价的快速上涨会带来信贷的迅速扩张,从而加剧经济中的系统性风险;而宏观审慎政策工具则有助于抵御住房偏好冲击和金融冲击,提高社会整体福利。
过去十多年间,国际资本流动的溢出效应愈发不容忽视,对于新兴市场国家尤其如此。2008年底,美联储开始实施量化宽松政策,大量“热钱”涌入新兴市场国家,加剧了其面临的金融风险;2015年底,美联储开始加息周期,国际资本回流美国,新兴市场国家面临较大的资本外流和货币贬值压力。Rey(2015)指出,在国际金融一体化的趋势下,若想保持货币政策的独立性,必须对国际资本流动进行管制,即使在浮动汇率制度下也是如此。马勇和王芳(2018)认为,金融开放度的提高会加剧一国金融体系的波动,但对产出的冲击并不显著。应对国外经济冲击,以往的研究大多考虑资本管制政策。Aoki等(2015)在一个开放小国DSGE模型的基础上,将银行借款区分为本币借款和国外借款,本国货币贬值会增加银行负债成本,并经由银行资产负债表渠道而影响金融体系的稳定。当国外金融冲击强于国外技术冲击时,资本管制政策能够改善社会福利。Davis和Presno(2017)认为,对新兴市场国家来说,对资本流动加以限制能够提高货币政策的自主性。刘建丰和潘英丽(2019)认为,中美两国的国际货币合作存在诸多困难,因此对我国来说,实施常态化资本管制是必要的。关于资本流动宏观审慎政策的协调机制,国内外学者的研究并不多见。
本文的创新主要体现在:第一,在小国开放经济的DSGE框架下引入包含国内外金融机构的资本流动宏观审慎政策机制,这不仅适用于分析我国的政策选择,也给新兴市场国家提供了一种研究思路。第二,本文不仅考虑了国外金融冲击对国际资本流动的影响机制,还引入了它对国内企业融资成本的影响机制。国外加息冲击会增加国内金融机构的境外融资成本,减弱国内金融机构对企业的资金支持能力。对于国外金融冲击的这种影响机制,国内学者的研究较少。第三,有关我国宏观审慎政策的现有研究通常仅分析国内经济冲击,而金融危机以来国外经济冲击对我国经济的影响愈加显著,本文的分析为我国应对国外经济冲击提供了政策选择依据。
二、模 型
本文建立了一个开放小国的DSGE模型,模型框架借鉴Gertler和Kiyotaki(2015)以及Davis和Presno(2017)的设定。本文在模型中将金融机构区分为国内金融机构和国外金融机构,并在各自的设定中分别引入资本流动的宏观审慎政策,以此来探讨其相互协调机制。与经典小国DSGE模型相比,本文的理论模型具有以下特点:
第一,国内金融机构不仅有国内融资渠道,还可以进行国外融资,国外融资以外币计价。国外金融冲击会直接影响其资产负债表规模,进而影响企业信贷。在国内的研究中,很少有学者在模型设定中引入这种影响机制。
第二,国际金融机构既可以购买我国债券,也可以在我国直接投资,以此引导国际资本流动。以往的研究(Chang等,2015)通常采用家庭对本国资产和外国资产的需求变化来描述国际资本流动。而对我国来说,政府对居民的资本流动管制比较严格,因此使用居民的境内外资产配置变化来反映我国国际资本流动并不恰当。近年来,我国金融领域的开放步伐明显加快,2018年取消银行和金融资产管理公司的外资持股比例限制,并在未来三年内取消证券、基金、期货和寿险公司的外资持股比例上限。本文引入国际金融机构来分析我国的资本流动,具有很强的现实意义。
本文模型中的经济主体包括家庭、厂商、金融机构和中央银行。
(一)家庭
代表性家庭最大化其效用函数:
| $\max {E_0}\sum\nolimits_{t = 0}^\infty {{\beta ^t}} \ln\left( {{C_t} - \frac{{{\varsigma _0}}}{{1 + {\varsigma }}}L_t^{1 + {\varsigma }}} \right)$ | (1) |
其中,
| $ {C}_{t}+{D}_{t}+{Q}_{t}{K}_{t}^{h}-{Q}_{t}{\Delta K}_{t-1}^{h}+\chi \left({K}_{t}^{h}\right)={\omega }_{t}{L}_{t}+{{R}_{t}D}_{t-1}+{Z}_{t}{K}_{t-1}^{h}+\Pi _{t} $ | (2) |
其中,
| $\begin{aligned} {\Pi _t} = & { {\int}}_{0}^{1} \left[ {\left( {\dfrac{{{p_{it}}}}{{{P_t}}} - m_t^C} \right)} {y_{it}} - \dfrac{\kappa }{2}{\left( {\dfrac{{{p_{it}}}}{{{p_{it - 1}}}} - 1} \right)^2}{Y_t} \right] di + \left[ {{Q_t} - 1 - \Phi \left( {\dfrac{{{I_t}}}{I}} \right)} \right]{I_t}\\ & + \left( {1 - \sigma } \right)\left[ {\left( {{Z_t} + \Delta {Q_t}} \right)K_{t - 1}^b - {R_t}{D_{t - 1}} - {\epsilon _t}R_t^fD_{t - 1}^f} \right] - \xi \left( {\Delta {Q_t} + {Z_t}} \right)K_{t - 1}^b \end{aligned}$ | (3) |
其中,第一项为中间厂商的垄断利润,第二项为投资收益,第三项为银行家退休时取得的资产,第四项为银行家的初始资产。代表性家庭的最优化问题对于消费、工作时间、资本、储蓄和投资的一阶条件分别为:
| $ {\lambda }_{t}=\frac{1}{{C}_{t}-{\left[{{\varsigma }_{0}}/{\left({1+\varsigma }\right)}\right]}{L}_{t}^{1+\varsigma }} $ | (4) |
| $ {\omega }_{t}={\varsigma }_{0}{{L}_{t}^\varsigma } $ | (5) |
| $ 1={E}_{t}\left(\Lambda _{t,t+1}\frac{\Delta {Q}_{t+1}+{Z}_{t+1}}{{Q}_{t}+{\chi }_{h}{K}_{t}^{h}}\right) $ | (6) |
| $ 1={E}_{t}\left(\Lambda _{t,t+1}{R}_{t+1}\right) $ | (7) |
| $ \Lambda _{t,t+1}=\beta \frac{{\lambda }_{t+1}}{{\lambda }_{t}} $ | (8) |
| $ {Q}_{t}=1+\mathrm{\Phi }\left(\frac{{I}_{t}}{I}\right)+\left(\frac{{I}_{t}}{I}\right){\mathrm{\Phi }}'\left(\frac{{I}_{t}}{I}\right) $ | (9) |
其中,
(二)厂商
对于厂商的设定,本文参考Bernanke等(1999)的做法,将厂商分为最终厂商和中间厂商。最终厂商在完全竞争的环境中经营;中间厂商在垄断竞争的环境中经营,组成一个测度为1的连续统。
对于任意中间厂商
| $ {y}_{it}={A}_{t}{\left(\frac{{k}_{it}}{{\alpha }_{k}}\right)}^{{\alpha }_{k}}{\left(\frac{{m}_{it}}{{\alpha }_{m}}\right)}^{{\alpha }_{m}}{\left(\frac{{l}_{it}}{{1-\alpha }_{k}-{\alpha }_{m}}\right)}^{{1-\alpha }_{k}-{\alpha }_{m}} $ | (10) |
其中,
| $ {Y}_{t}={\left({\int }_{0}^{1}{{y}_{it}}^{\left({\eta -1}\right)/{\eta }}\right)}^{\frac{\eta }{\eta -1}} $ | (11) |
其中,
| $ {y}_{it}={\left(\frac{{p}_{it}}{{P}_{t}}\right)}^{-\eta }{Y}_{t} $ | (12) |
其中,
| $ {P}_{t}={\left({\int }_{0}^{1}{{p}_{it}}^{1-\eta }di\right)}^{\frac{1}{1-\eta }} $ | (13) |
设定
| $ {m}_{t}^{C}=\frac{1}{{A}_{t}}{Z}_{t}^{{\alpha }_{k}}{\epsilon }_{t}^{{\alpha }_{m}}{\omega }_{t}^{{1-\alpha }_{k}-{\alpha }_{m}} $ | (14) |
对于任意中间厂商
| $ \max {E_0}\left\{ {\sum\nolimits_{t = 0}^\infty {{\Lambda _{0,t}}} \left[ {\left( {\frac{{{p_{it}}}}{{{P_t}}} - m_t^C} \right){y_{it}} - \frac{\kappa }{2}{{\left( {\frac{{{p_{it}}}}{{{p_{it - 1}}}} - 1} \right)}^2}{Y_t}} \right]} \right\}$ | (15) |
其中,
| ${\hat \pi _t} = \frac{{\eta - 1}}{\kappa }\widehat {m_t^C} + \beta {E_t}\left( {{{\hat \pi }_{t + 1}}} \right)$ | (16) |
设定
| $ \frac{{\epsilon }_{t}{M}_{t}}{{Z}_{t}{K}_{t-1}}=\frac{{\alpha }_{m}}{{\alpha }_{k}} $ | (17) |
| $ \frac{{\omega }_{t}{L}_{t}}{{Z}_{t}{K}_{t-1}}=\frac{{1-{\alpha }_{k}-\alpha }_{m}}{{\alpha }_{k}} $ | (18) |
资本
| $ {K}_{t}={I}_{t}+\Delta {K}_{t-1} $ | (19) |
其中,
| $ {EX}_{t}={\left(\frac{{P}_{t}}{{e}_{t}{P}_{t}^{\mathrm{*}}}\right)}^{-\phi }\frac{{Y}_{t}^{\mathrm{*}}}{1+{T}_{t}^{EX}} $ | (20) |
其中,
| $T_t^{EX} = {\bar T^{EX}} + e_t^{EX}$ | (21) |
其中,
(三)金融机构
1. 国内金融机构
国内金融机构的框架参考Gertler和Kiyotaki(2015)的设定。家庭和国内金融机构分别组成一个测度为1的连续统,银行家(国内金融机构的股东)会退休,且职位由家庭成员填补,以此来维持家庭和国内金融机构之间的动态平衡。银行家退休时取得公司的净资产,新进入的银行家会投入初始资产,这排除了国内金融机构仅依靠内部融资来经营的情形。在经营时期,国内金融机构从本国居民或境外居民吸收存款,并以购买资本的形式向企业发放贷款。
在
| $\max {E_{t}}\sum\nolimits_{i = 1}^\infty {{\Lambda _{{\rm{t}},t + 1}}} {\sigma ^{i - 1}}\left( {1 - \sigma } \right){n_{t + i}}$ |
其中,
| $ {n}_{t}=\left({\Delta Q}_{t}+{Z}_{t}\right){k}_{t-1}^{b}-{R}_{t}{d}_{t-1}-{\epsilon }_{t}{R}_{t}^{f}{d}_{t-1}^{f} $ | (22) |
其中,
| $ \left(1+{\tau }_{t}^{k}\right){Q}_{t}{k}_{t}^{b}={n}_{t}+{d}_{t}+\left(1-{\tau }_{t}^{d}\right){\epsilon }_{t}{d}_{t}^{f}+{\tau }_{t}^{n}{n}_{t} $ | (23) |
其中,
| $ {\tau }^{n}{n}_{t}={\tau }_{t}^{k}{Q}_{t}{K}_{t}^{b}+{\tau }_{t}^{d}{\epsilon }_{t}{D}_{t}^{f} $ | (24) |
借鉴Gertler和Kiyotaki(2010)的做法,银行家在
| $ {V}_{t}\geqslant {\theta }_{t}{Q}_{t}{k}_{t}^{b} $ | (25) |
其中,
对于国内金融机构,最优化问题为预算约束和激励约束下最大化现值
| $ {\psi }_{t}\equiv \frac{{V}_{t}}{{n}_{t}}={E}_{t}\left[\beta \left(1-\sigma +\sigma {\psi }_{t+1}\right)\frac{{n}_{t+1}}{{n}_{t}}\right] $ | (26) |
利用(22)式和(23)式,可以得到:
| $\begin{array}{l} \dfrac{{{n_{t + 1}}}}{{{n_t}}} = \left[ {\dfrac{{\Delta {Q_{t + 1}} + {Z_{t + 1}}}}{{{Q_t}}} - \left( {1 + \tau _t^k} \right){R_{t + 1}}} \right]{\phi _t} + \left[ {\left( {1 - \tau _t^d} \right){R_{t + 1}} - \dfrac{{{\epsilon _{t + 1}}R_t^f}}{{{\epsilon _t}}}} \right]{\phi _t}{x_t} + \left( {1 + \tau _t^N} \right){R_{t + 1}} \end{array}$ | (27) |
其中,
| ${\psi _t} = {\max _{{\phi _t},{x_t}}}\left( {{\mu _t}{\phi _t} + {\mu _{dt}}{\phi _t}{x_t} + {v_t}} \right)$ | (28) |
| ${\rm{s}}.{\rm{t}}.\;{\psi _t} = {\theta _t}{\phi _t} = \theta \left( {1 + \frac{\gamma }{2}x_t^2} \right){\phi _t}$ | (29) |
其中:
| $ {\mu }_{t}={E}_{t}\left\{\Omega _{t+1}\left[\frac{{\Delta Q}_{t+1}+{Z}_{t+1}}{{Q}_{t}}-\left(1+{\tau }_{t}^{k}\right){R}_{t+1}\right]\right\} $ | (30) |
| $ {\mu }_{dt}={E}_{t}\left\{\Omega _{t+1}\left[\left(1-{\tau }_{t}^{d}\right){R}_{t+1}-\frac{{\epsilon }_{t+1}{R}_{t}^{f}}{{\epsilon }_{t}}\right]\right\} $ | (31) |
| $ {v}_{t}={E}_{t}\left\{\Omega _{t+1}\left[\left(1+{\tau }_{t}^{n}\right){R}_{t+1}\right]\right\} $ | (32) |
| $ \Omega _{t+1}=\beta \left(1-\sigma +\sigma {\psi }_{t+1}\right) $ |
直观上,
| $ {\phi }_{t}={v}_{t}/\left[{\theta }_{t}-\left({\mu }_{t}+{\mu }_{dt}{x}_{t}\right)\right] $ | (33) |
| $ {x}_{t}=\left[\sqrt{1+\frac{2}{\gamma }{\left({\mu }_{t}^{\mathrm{*}}\right)}^{2}}-1\right]\Bigg{/}{\mu }_{t}^{\mathrm{*}} $ | (34) |
其中,
| $ {\psi }_{t}={\theta }_{t}{\phi }_{t} $ | (35) |
2. 国际金融机构
本文引入国际金融机构来探讨国际资本流动。国际金融机构既可以购买我国债券
| $\max{E_{t}}\sum\nolimits_{t = 1}^\infty {{\Lambda _{{t} - 1,t}}} n_t^f$ | (36) |
预算约束为:
| $\begin{array}{l} {Q_t}k_t^f + b_t^f - {R_t}b_{t - 1}^f + \chi \left( {k_t^f} \right) + \chi \left( {b_t^f} \right) + {\epsilon _t}\left( {{b_t} - R_t^f{b_{t - 1}}} \right) = {\epsilon _t}n_t^f + \left( {{Z_t} + \Delta {Q_t}} \right)k_{t - 1}^f \end{array}$ | (37) |
其中,
最优化问题对于
| $ 1={E}_{t}\left({\lambda }_{t+1}^{\mathrm{*}}{R}_{t+1}^{f}\right) $ | (38) |
| $ 1={E}_{t}\left(\frac{{\lambda }_{t+1}^{\mathrm{*}}{R}_{t+1}}{1+{\tau }_{t}^{f}{b}_{t}^{f}}\frac{{\epsilon }_{t}}{{\epsilon }_{t+1}}\right) $ | (39) |
| $ {1=E}_{t}\left[\frac{{\lambda }_{t+1}^{\mathrm{*}}\left({Z}_{t+1}+{Q}_{t+1}\right)}{{Q}_{t}+{\tau }_{t}^{kf}{K}_{t}^{f}} \frac{{\epsilon }_{t}}{{\epsilon }_{t+1}}\right] $ | (40) |
其中,
(四)中央银行
中央银行不仅是货币政策的制定者,也是宏观审慎政策的制定者。对于我国货币政策的选择,国内外学者存在一些争议(Zhang,2009;Chen等,2017)。而随着我国政策基准利率和市场利率的逐渐统一,基于利率调整的货币政策变得更加有效。②本文的货币政策遵循以下规则:
| $ {\widehat{R}}_{t}=\left(1-{\rho }_{i}\right)\left[{\omega }_{\pi } {\widehat{\pi }}_{t}+{\omega }_{y} \left(\ln{{Y}_{t}}-\ln{{Y}_{t-1}}\right)\right]+{\rho }_{i} {\widehat{R}}_{t-1}+{e}_{t}^{r} $ | (41) |
其中,
本文考虑满足资本充足率要求的宏观审慎政策工具
| $\tau _t^k = {\bar \tau ^k} + {\omega _k}\left( {\ln K_t^b - \ln {K^b}} \right)$ | (42) |
| $\tau _t^d = {\bar \tau ^d} - {\omega _d}\left( {R_t^f - {R^f}} \right)$ | (43) |
| $\tau _t^f = {\bar \tau ^f} - {\omega _f}\left( {{R_t} - R} \right)$ | (44) |
(五)市场均衡条件
产出等于消费、投资、净出口、价格调整成本与家庭持有资本成本之和。
| $ {Y}_{t}={C}_{t}+\left[1+\mathrm{\Phi }\left(\frac{{I}_{t}}{I}\right)\right]{I}_{t}+{EX}_{t}-{{e}_{t}M}_{t}+\frac{\kappa }{2}{\left({\pi }_{t}-1\right)}^{2}{Y}_{t}+\chi \left({K}_{t}^{h}\right) $ | (45) |
对于国内金融机构,资产等于负债与所有者权益之和。
| $ {Q}_{t}{K}_{t}^{b}={N}_{t}+{D}_{t}+{\epsilon }_{t}{D}_{t}^{f} $ | (46) |
| $ {\phi }_{t}={Q}_{t}{K}_{t}^{b}/{N}_{t} $ | (47) |
| $ {X}_{t}={\epsilon }_{t}{D}_{t}^{f}/{Q}_{t}{K}_{t}^{b} $ | (48) |
国内金融机构的净资产等于现存银行家的净资产与新进入银行家所持有的资产之和。
| $ {N}_{t}=\sigma \left[\left({Z}_{t}+\Delta {Q}_{t}\right){K}_{t-1}^{b}-{R}_{t}{D}_{t-1}-{\epsilon }_{t}{R}_{t}^{f}{D}_{t-1}^{f}\right]+\xi \left({\Delta Q}_{t}+{Z}_{t}\right){K}_{t-1}^{b} $ | (49) |
总资产等于家庭持有的资产、国内金融机构持有的资产与国外投资者的直接投资之和。
| $ {K}_{t}={K}_{t}^{h}+{K}_{t}^{b}+{K}_{t}^{f} $ | (50) |
国外净负债的变化等于净进口。
| $ {Q_t}K_t^f - \left( {{Z_t} + \Delta {Q_t}} \right)K_{t - 1}^f + B_t^f - {R_t}B_{t - 1}^f + {\epsilon _t}\left( {D_t^f - {R_t}D_{t - 1}^f} \right) = {\epsilon _t}{M_t} - \left( {1 + {\tau _{EX}}} \right)E{X_t} $ | (51) |
技术
| ${A_t} - \overline {{A_t}} = {\rho _A}{A_{t - 1}} + + e_t^A$ | (52) |
| ${\ln}Y_t^{\rm{*}} - \ln\overline {Y_t^{\rm{*}}} = {\rho _{{Y^{\rm{*}}}}}\ln Y_{t - 1}^{\rm{*}} + e_t^{{Y^{\rm{*}}}}$ | (53) |
| $R_t^f - \overline {R_t^f} = {\rho _{rf}}R_{t - 1}^f + e_t^{rf}$ | (54) |
三、参数校准
本文的部分参数使用我国和美国的宏观经济季度数据来校准,③其他参数借鉴国内外文献。
1. 家庭部门参数
对于折现因子
2. 厂商部门参数
参照国内外文献,厂商折旧率
3. 国内金融机构参数
参考Aoki等(2015)的做法,参数
4. 中央银行部门参数
对于货币政策系数,参考方意(2016)的做法,本文利用我国季度经济数据进行校准。样本区间为1996年第1季度至2018年第4季度。对于政策利率,选择银行间同业拆借利率(一个月加权平均值),产出
5. 外生经济冲击
国外产出
| 参数 | 取值 | 参数 | 取值 | |
|
$ \beta $
|
0.99 |
$ {R}^{\mathrm{*}} $
|
1.005 | |
|
$ \varsigma $
|
0.2 |
$ 1-\Delta $
|
0.025 | |
|
$ {\alpha }_{K} $
|
0.45 |
$ \omega $
|
0.7 | |
|
$ \varphi $
|
0.1 |
$ \gamma $
|
6.67 | |
|
$ \theta $
|
0.37 |
$ \xi $
|
0.007 | |
|
$ \sigma $
|
0.94 |
$ {\omega }_{k} $
|
0.1 | |
|
$ {\rho }_{i} $
|
0.87 |
$ {\omega }_{\pi } $
|
2.28 | |
|
$ {\omega }_{y} $
|
1.00 |
$ {\rho }_{A} $
|
0.8 | |
|
$ {\rho }_{{Y}^{\mathrm{*}}} $
|
0.84 |
$ {\rho }_{rf} $
|
0.77 | |
|
$ {e}_{t}^{r} $
|
0.007 |
$ {e}_{t}^{{Y}^{\mathrm{*}}} $
|
0.01 | |
|
$ {e}_{t}^{rf} $
|
0.004 |
$ {e}_{t}^{EX} $
|
0.01 |
四、模拟分析
本文分析两种宏观经济政策规则的效果。第一种政策规则为基准规则,中央银行不采用资本流动的宏观审慎政策,宏观审慎政策工具均取稳态值。第二种政策规则为资本流动的宏观审慎逆周期调节机制,宏观审慎政策工具
(一)脉冲响应分析
本文重点讨论国外加息冲击对我国宏观经济的影响,结果见图1。在基准规则(规则1)下,国外加息冲击有两种影响途径:第一,当国外利率上升时,国内金融机构的境外融资成本增加,导致其净资产减少,资本负债表收缩。在激励约束(即(25)式)下,国内金融机构减少贷款,企业信贷收紧,导致我国企业的投资减少,社会总资产减少。此外,资产价格下降,产出和消费减少。第二,当国外利率上升时,汇率上升(直接标价法),以外币计价的我国债券收益和投资收益减少,国际资本外流,外债净额下降。资本外流会进一步加剧我国企业的融资困境,拉低投资和产出。
在宏观审慎政策机制(规则2)下,对于资本流动的宏观审慎政策工具
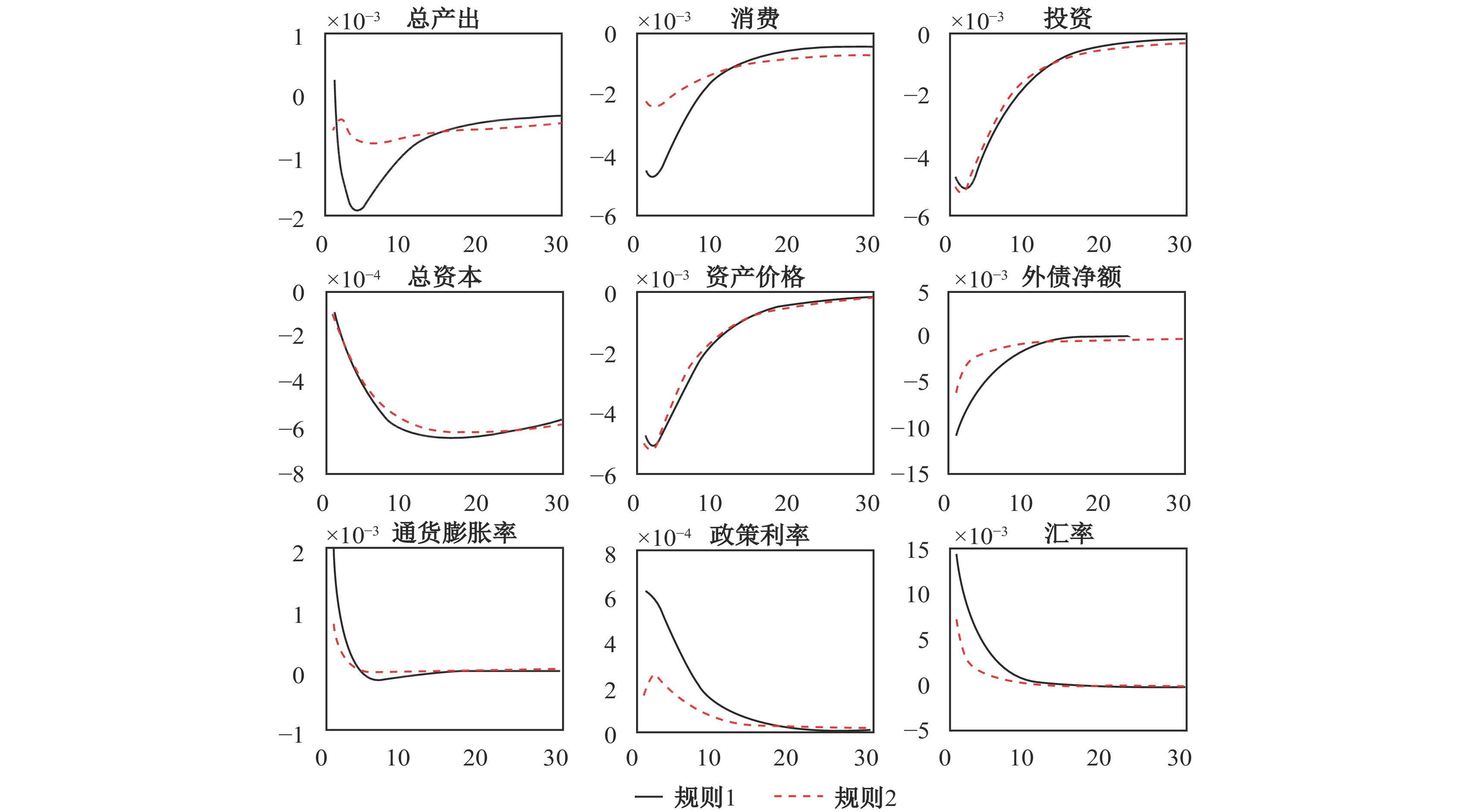
|
| 图 1 国外加息冲击的脉冲响应分析 |
本文还模拟了其他外生经济冲击下主要经济变量的脉冲响应。结果表明,对于基准规则,在正向的技术冲击下,厂商的生产能力增强,投资和产出上升;在紧缩的货币政策冲击下,利率上升,投资和产出下降,同时本国货币升值;在正向的国外产出冲击下,通过国际贸易机制,我国净出口增加,产出上升;在国际贸易摩擦冲击下,出口下降,产出下降。对于以上四种经济冲击,资本流动宏观审慎政策规则下的脉冲响应曲线与基准规则下的结果不存在明显差别,表明资本流动的宏观审慎政策影响并不显著。
(二)资本流动宏观审慎政策的福利分析
本文接下来讨论国外加息冲击下宏观审慎政策系数(
| $ {V}_{t}\equiv {E}_{0}\sum _{t=0}^{\mathrm{\infty }}{\beta }^{t}\ln\left({C}_{t}-\frac{{\varsigma }_{0}}{1+\mathrm{\varsigma }}{L}_{t}^{1+\mathrm{\varsigma }}\right) $ |
递归形式为:
| $ {V}_{t}=\ln\left({C}_{t}-\frac{{\varsigma }_{0}}{1+\mathrm{\varsigma }}{L}_{t}^{1+\mathrm{\varsigma }}\right)+\beta {V}_{t+1} $ |
借鉴Schmitt-Grohé和Uribe(2004)的思路,将效用函数纳入模型方程,对所有方程做二阶泰勒展开。
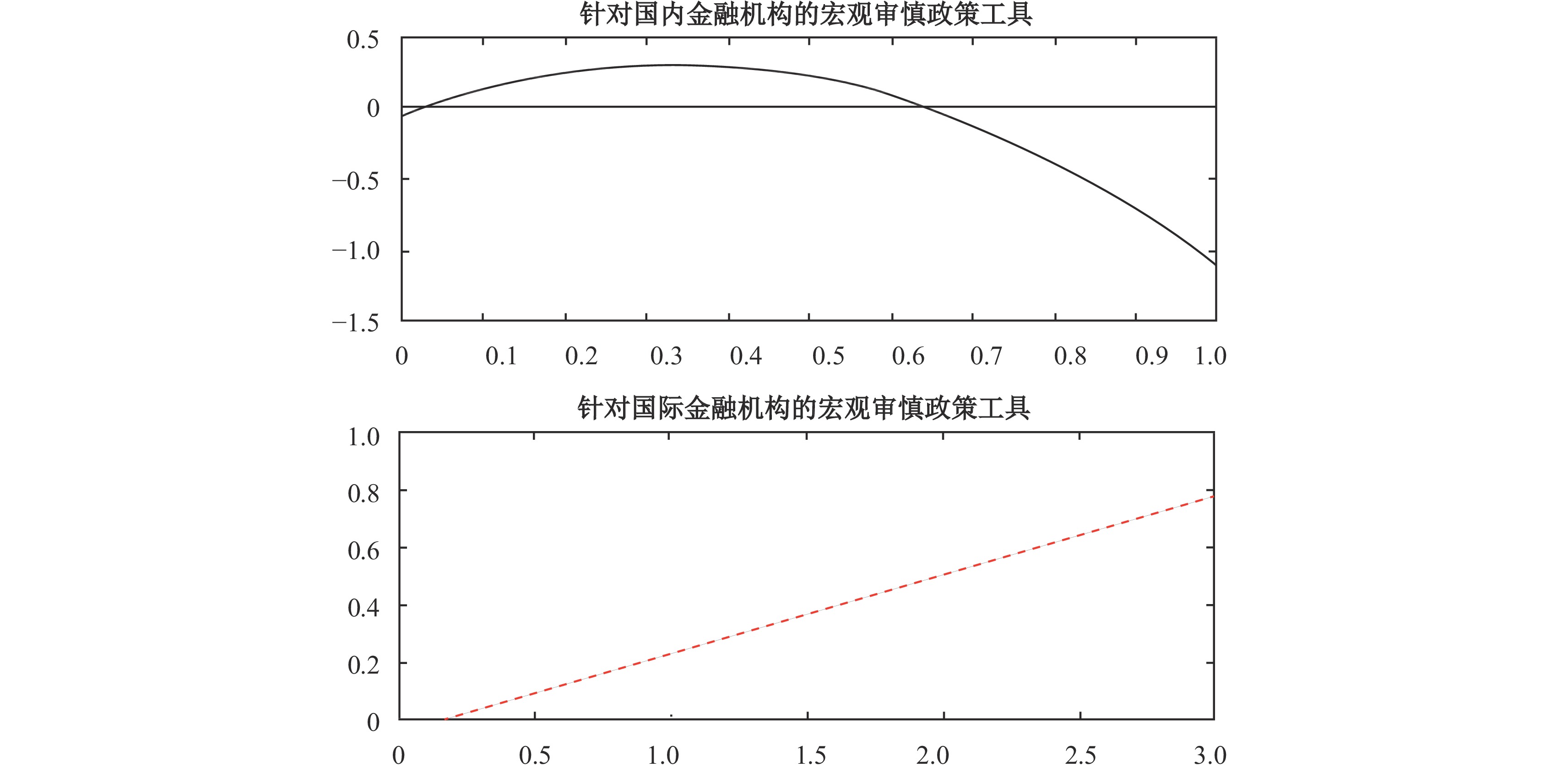
1. 针对国内金融机构的资本流动宏观审慎政策工具
当仅考虑宏观审慎政策工具
2. 针对国际金融机构的资本流动宏观审慎政策工具
当仅考虑宏观审慎政策工具
对比
3. 资本充足率要求的宏观审慎政策工具
当仅考虑宏观审慎政策工具
(三)稳定性分析
对于资本流动的宏观审慎政策,上文的设定如下:
| $\tau _t^d = {\bar \tau ^d} - {\omega _d}\left( {R_t^f - {R^f}} \right),\tau _t^f = {\bar \tau ^f} - {\omega _f}\left( {{R_t} - R} \right)$ |
对于
对于宏观审慎政策规则,直接盯住政策目标的设定也很常见。这里考虑如下形式的资本流动宏观审慎政策工具:
| $\tau _t^d = {\bar \tau ^d} + {\omega _d}\left( {\ln {D_t^f} - \ln {D^f}} \right),\tau _t^f = {\bar \tau ^f} + {\omega _f}\left( {\ln {B_t^f} - \ln{B^f}} \right)$ |
在这种设定下,对于资本流动宏观审慎政策
上文的分析仅考虑了国外加息冲击,当在福利分析中纳入所有外生冲击时,主要结论并不受影响。这再次表明,资本流动的宏观审慎政策能够有效应对国外金融冲击,但对于其他外生经济冲击,影响并不显著。
五、结论与政策建议
党的十九大报告明确指出,要健全金融监管体系,守住不发生系统性金融风险的底线。金融风险具有全球传染性,随着我国金融领域对外开放步伐的加快,国外金融冲击对我国的影响增大。抵御国外金融风险的不利影响,我国需要积极推动建设资本流动宏观审慎政策体系。在此背景下,本文构建一个小国开放经济的DSGE模型,分析了我国资本流动宏观审慎政策的效果。本文在模型中区分了国内金融机构和国际金融机构,前者允许进行境外融资,后者允许购买我国和外国债券,以此将国际资本流动和我国宏观经济波动联系在一起,为考虑资本流动的宏观审慎管理提供了分析框架。本文的模拟分析表明,国外加息冲击会减少国际金融机构对我国的投资,引起国际资本外流;同时;我国金融机构的融资成本上升,资产负债表收缩,资产价格下降。资本流动的宏观审慎政策能够有效应对国外加息冲击,保持我国资本流动和企业信贷的相对稳定,提高社会福利。
本文提出以下政策建议:第一,及时辨别国外金融市场存在的风险,加强防范意识。伴随我国金融业对外开放步伐的加快,国外金融冲击对我国宏观经济的影响不容忽视。2018年美国持续加息导致部分新兴市场国家的金融稳定遭受严重冲击。第二,继续推动建设资本流动的宏观审慎政策协调机制。在我国金融业对外开放的过程中,资本账户开放应当循序渐进,推动建设资本流动的宏观审慎监管机制,能够有效应对国外不利金融冲击对我国的影响。第三,在国外加息冲击下,应当妥善解决企业的融资困境。本文结果表明,外部金融冲击会收紧企业信贷。对此,一方面,应当保持国内金融机构资本金的稳定,增强金融支持实体经济的作用;另一方面,应当减少国际金融机构在我国的投资限制,合理引进外资。
① 国外贷款比例上升时,企业的道德风险增加。
② 中国人民银行行长易纲在2018亚洲博鳌论坛上指出,面对发达经济体逐步收紧货币政策,我国货币政策仍主要考虑国内经济,市场化改革的方向是促进存贷款基准利率和货币市场利率的逐步统一。
③ 我国宏观经济数据来自CEIC经济数据库,美国宏观经济数据来自Federal Reserve Bank of St. Louis。
④ 纵轴为社会福利V相对于稳态的偏离程度(单位为稳态消费)。
| [1] | 方意. 宏观审慎政策有效性研究[J]. 世界经济, 2016(8): 25–49. |
| [2] | 刘建丰, 潘英丽. 常态化资本管制的必要性——基于不同经济发展阶段视角的DSGE模型分析[J]. 财经研究, 2019(1): 135–152. |
| [3] | 马勇, 陈雨露. 宏观审慎政策的协调与搭配: 基于中国的模拟分析[J]. 金融研究, 2013(8): 57–69. DOI:10.3969/j.issn.1009-3109.2013.08.012 |
| [4] | 马勇, 王芳. 金融开放、经济波动与金融波动[J]. 世界经济, 2018(2): 20–44. |
| [5] | 张健华, 贾彦东. 宏观审慎政策的理论与实践进展[J]. 金融研究, 2012(1): 20–35. DOI:10.3969/j.issn.1674-5477.2012.01.005 |
| [6] | 赵胜民, 张瀚文. 我国宏观审慎政策与货币政策的协调问题研究——基于房价波动的非对称性影响[J]. 国际金融研究, 2018(7): 12–21. |
| [7] | 周小川. 金融政策对金融危机的响应——宏观审慎政策框架的形成背景、内在逻辑和主要内容[J]. 金融研究, 2011(1): 1–14. DOI:10.3969/j.issn.1009-3109.2011.01.002 |
| [8] | Angeloni I, Faia E. Capital regulation and monetary policy with fragile banks[J]. Journal of Monetary Economics, 2013, 60(3): 311–324. DOI:10.1016/j.jmoneco.2013.01.003 |
| [9] | Aoki K, Benigno G, Kiyotaki N. Monetary and financial policies in emerging markets[R]. Working Paper, London School of Economics, 2015. |
| [10] | Bernanke B S, Gertler M, Gilchrist S. The financial accelerator in a quantitative business cycle framework[A]. Taylor J B, Woodford M. Handbook of macroeconomics (Vol.1)[M]. Elsevier, 1999: 1341-1393. |
| [11] | Buch C M, Goldberg L. Cross-border regulatory spillovers: How much? How important? Evidence from the international banking research network[R]. Bank of England Working Paper No.595, 2016. |
| [12] | Chang C, Chen K J, Waggoner D F, et al. Trends and cycles in China’s macroeconomy[J]. NBER Macroeconomics Annual, 2015, 30: 1–84. |
| [13] | Chang C, Liu Z, Spiegel M M. Capital controls and optimal Chinese monetary policy[J]. Journal of Monetary Econo- mics, 2015, 74: 1–15. DOI:10.1016/j.jmoneco.2015.04.003 |
| [14] | Christiano L J, Eichenbaum M, Evans C. Nominal rigidities and the dynamic effects of a shock to monetary policy[J]. Journal of Political Economy, 2005, 113(1): 1–45. DOI:10.1086/426038 |
| [15] | Collard F, Dellas H, Diba B, et al. Optimal monetary and prudential policies[J]. American Economic Journal: Macro- economics, 2017, 9(1): 40–87. DOI:10.1257/mac.20140139 |
| [16] | Davis J S, Presno I. Capital controls and monetary policy autonomy in a small open economy[J]. Journal of Monetary Economics, 2017, 85: 114–130. DOI:10.1016/j.jmoneco.2016.11.008 |
| [17] | Gerali A, Neri S, Sessa L, et al. Credit and banking in a DSGE model of the euro area[J]. Journal of Money, Credit and Banking, 2010, 42(S1): 107–141. |
| [18] | Gertler M, Gilchrist S, Natalucci F M. External constraints on monetary policy and the financial accelerator[J]. Journal of Money, Credit and Banking, 2007, 39(2−3): 295–330. DOI:10.1111/j.0022-2879.2007.00027.x |
| [19] | Gertler M, Kiyotaki N. Banking, liquidity, and bank runs in an infinite horizon economy[J]. American Economic Review, 2015, 105(7): 2011–2043. DOI:10.1257/aer.20130665 |
| [20] | Gertler M, Kiyotaki N. Financial intermediation and credit policy in business cycle analysis[A]. Friedman B M, Woodford M. Handbook of monetary economics (Vol.3)[M]. Elsevier, 2010: 547-599. |
| [21] | Justiniano A, Primiceri G E, Tambalotti A. Household leveraging and deleveraging[J]. Review of Economic Dynamics, 2015, 18(1): 3–20. DOI:10.1016/j.red.2014.10.003 |
| [22] | Kannan P, Rabanal P, Scott A M. Monetary and macroprudential policy rules in a model with house price booms[J]. The B.E. Journal of Macroeconomics, 2012, 12(1): 1–44. |
| [23] | Quint D, Rabanal P. Monetary and macroprudential policy in an estimated DSGE model of the euro area[R]. IMF Working Papers, 2013. |
| [24] | Rey H. Dilemma not trilemma: The global financial cycle and monetary policy independence[A]. Proceedings of 2013 Federal Reserve Bank of Kansas City Economic Symposium at Jackson Hole[C]. Jackson Hole, 2015. |
| [25] | Schmitt-Grohé S, Uribe M. Solving dynamic general equilibrium models using a second-order approximation to the policy function[J]. Journal of Economic Dynamics and Control, 2004, 28(4): 755–775. DOI:10.1016/S0165-1889(03)00043-5 |
| [26] | Wang P F, Wen Y, Xu Z W. Two-way capital flows and global imbalances[J]. The Economic Journal, 2017, 127(599): 229–269. DOI:10.1111/ecoj.12290 |