
2020第46卷第5期
2. 上海交通大学 安泰经济与管理学院,上海 200030
2. Antai College of Economics and Management,Shanghai Jiao Tong University,Shanghai 200030,China
一、引 言
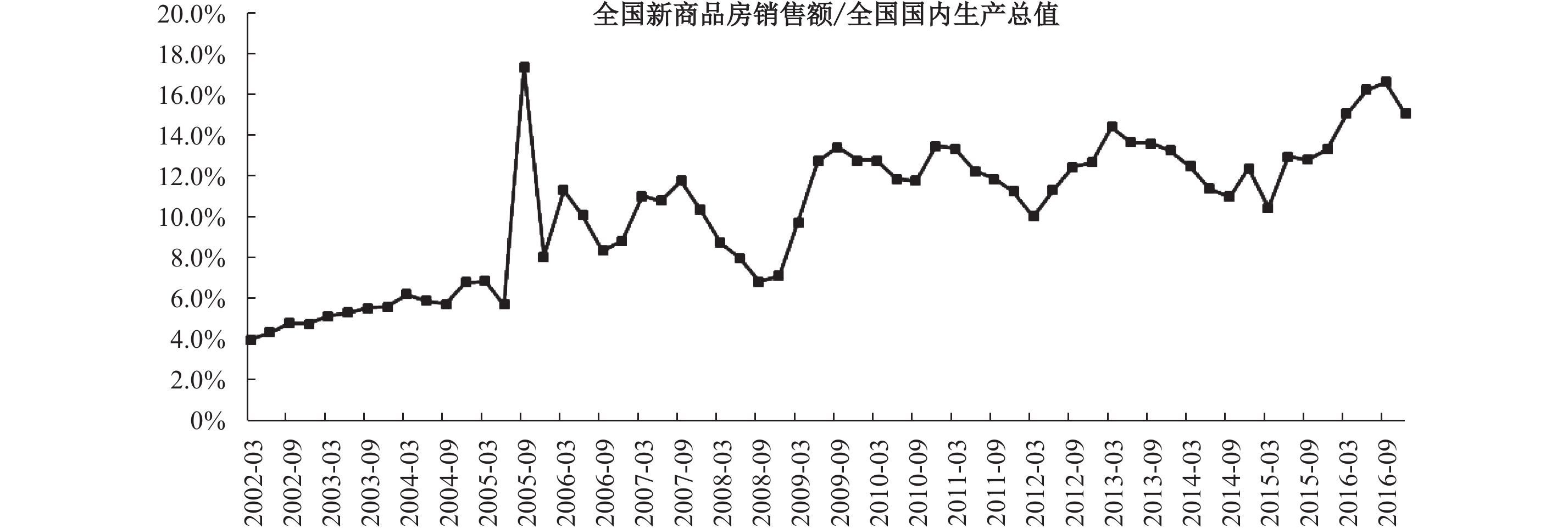
中国房地产部门新商品房销售额占全国GDP的比重在2011—2016年平均已达到13%,2016年更是高达16%(见图1),其对钢铁、水泥和家电等其他生产部门需求的间接拉动作用也很突出。然而,作为中国经济的一个支柱性产业,中国学者还没有得出一个参数比较准确的标准新房总量生产函数。王云清等(2013)等研究一般直接借用外国如美国经济的新房总量生产函数(Iacoviello和Stefano,2010)。①而由《中华人民共和国土地管理法》可知,中国房地产经济中的土地制度和生产结构与欧美国家不同,直接借用其新房生产函数中的参数(如资本、土地和劳动份额分别约为20%、10%和70%),派生的新问题可能较大。事实上,一个准确的新房总量生产函数是从宏观角度研究中国房地产经济的起点。只有基于准确的起点,才有利于研究中国房价与房地产开发投资的增长和波动及在一二线和三四线城市间的分化、房地产市场调控的政策组合、房地产开发投资对其他实体经济投资的间接拉动,以及危机后出现的一二线城市高房价与房地产过度投资对其他实体经济投资、产出和消费可能存在的挤出效应等问题。因此,本文的首要任务是,校准或估计出中国房地产部门的标准新房总量生产函数中更加准确的结构参数。
|
| 图 1 中国房地产部门新商品房销售额占全国GDP的比重 资料来源:Wind资讯。 |
由于各宏观变量之间的相互作用和影响,从局部均衡角度通过传统计量方法来估计新房总量生产函数中的结构参数,一般会因严重的内生性问题而出现较大偏差,因此研究中国的新房总量生产函数,最好放在一般均衡的框架中。
2008年美国房地产业次贷危机所引发的全球金融危机给国内外宏观经济学家建模的一个主要教训是,在研究宏观经济波动时,不能忽视货币信贷金融部门以及在新凯恩斯主义模型中已确认的各种名义摩擦因素。最基本的做法是在异质性新房部门和产品生产部门中,或者在异质性家庭部门中引入货币与信贷等金融约束,考察商业银行或金融市场与这些异质性部门之间的互动关系(Liu等,2013;Piazzesi和Schneider,2016;Chen和Wen,2017;Miao和Wang,2018;高然和龚六堂,2017;赵扶扬等,2017;梅冬州等,2018),从而刻画出货币与信贷等金融因素是怎样在经济繁荣时期因放大效应而导致经济过热,或是怎样在经济萧条时期因收缩效应而导致经济过冷,甚至引发金融或经济危机。
然而,在国外,这些包含金融部门和名义摩擦的研究并没有推翻2008年金融危机前以真实经济周期(RBC)模型为基础而校准或估计出的,以美国宏观经济为背景的一般产品部门生产函数中资本份额和劳动份额分别约为30%和70%(Kydland和Prescott,1982;Hansen,1985),以及以美国房地产经济为背景的新房生产函数中土地份额、资本份额和劳动份额分别约为10%、20%和70%的基本结论。在国内,这些研究也没有推翻以RBC模型为基础而校准或估计出的,以中国宏观经济为背景的一般产品部门生产函数中资本份额和劳动份额分别约为50%和50%(Chow和Li,2002;Song等,2011;郭庆旺和贾俊雪,2005;许志伟和林仁文,2011;许志伟和吴化斌,2012)的基本结论。这主要是因为不管是一般产品部门生产函数还是房地产部门生产函数,其结构参数在长期都比较稳定,并不会随短期的货币与信贷等周期性金融因素而大幅改变。
如前所述,本文并不关注中国宏观经济与房地产经济的短期波动,所以在校准或估计结构参数时,无需建立一个考虑货币信贷金融部门和各种名义摩擦的大型且复杂的动态随机一般均衡(DSGE)模型。为此,本文仍可遵循国内外估计总量生产函数的通行做法,构建一个不考虑金融和名义摩擦因素的基本(Fundamental)模型。本文的小型模型主要包括新房生产、一般产品生产、家庭、投资品厂商、土地转卖商和政府共六个部门。自然地,本文的第二个研究任务是,利用这一模型来分析中国房地产部门的土地供给政策变化效应,以及与宏观经济基本面联系紧密的供给侧结构性改革。
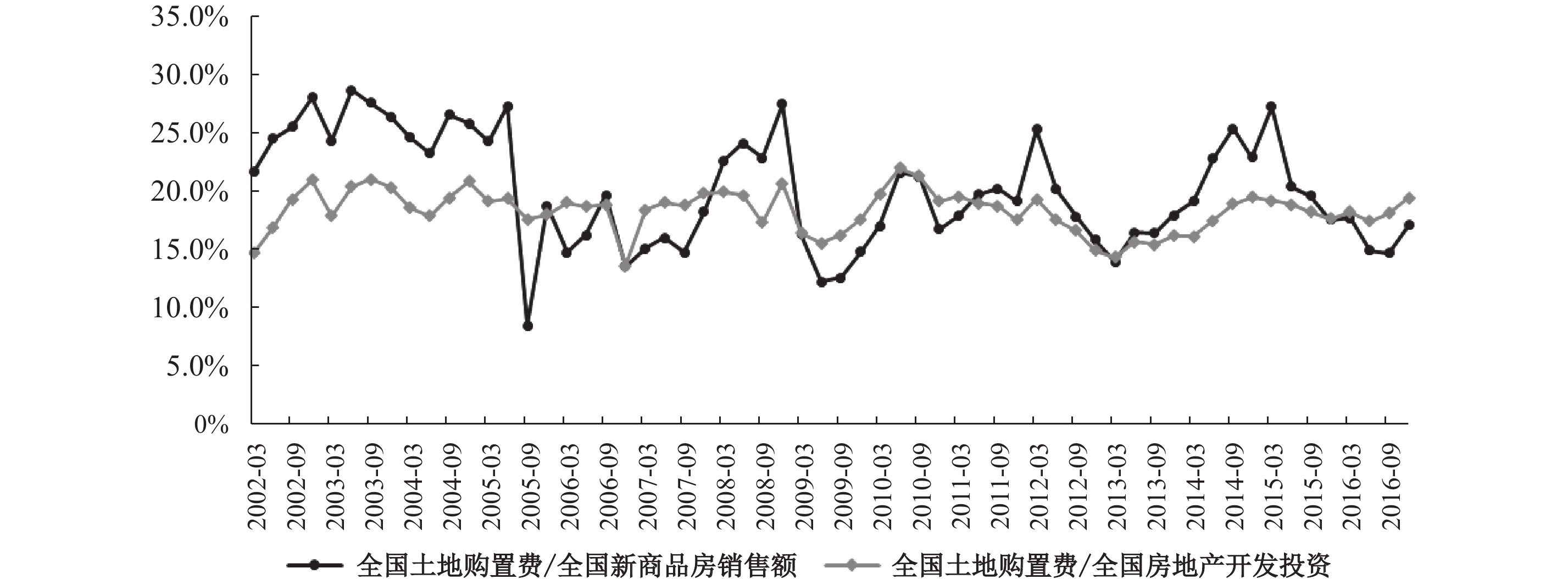
由于缺乏在房地产部门就业的劳动和工资数据,我们无法直接推断新房总量生产函数中的劳动份额;而在2002年第1季度至2016年第4季度,全国房地产业的土地购置费与新商品房销售额和房地产开发投资的平均比率(见图2)与标准的新房总量生产函数理论之间又存在矛盾(详见下文的参数校准部分)。这些统计数据可能存在一定的瞒漏报或虚重报等质量问题,使得新房总量生产函数中的结构参数值难以利用常规的校准或估计方法准确获得。本文通过引入均值可能不为零的系统性偏差和均值为零的测量误差,尝试利用这些“瑕疵数据”和贝叶斯方法来解决参数的估计问题。在正式估计之前,本文引入经济较发达、统计数据质量相对较高的京沪两个城市的数据作为补充信息,采用权重平均法综合利用来自全国和京沪两地的房地产部门信息,对新房总量生产函数的结构参数进行了成功的试校准。贝叶斯方法的特点是能够利用新近信息对先验或原有信息,包括对初始参数值不断进行更新,从而获得更加准确的估计结果。
|
| 图 2 全国土地购置费与新商品房销售额和房地产开发投资的平均比率 资料来源:Wind资讯。 |
本文对基本模型的估计显示,在全国新房生产中,土地份额、资本份额和劳动份额分别为23%、67%和10%。显然,这一结果与Iacoviello和Stefano(2010)对美国新房生产函数的研究发现(资本、土地与劳动份额分别约为20%、10%和70%)差距巨大。因此,我们不能直接借用欧美国家新房生产函数中的结构参数。而在京沪等一线城市的新房生产成本中,土地接近30%,实物资本略超50%,劳动占20%。此外,中国家庭对京沪等一线城市的房产需求偏好参数约为1.09,明显高于全国平均水平0.84。
在模型设定基本正确的假定下,本文对房地产部门统计数据的系统性偏差做了初步估算,结果显示:全国和京沪两地的新商品房销售额分别瞒漏报约8%和3%,土地购置费分别瞒漏报约23%和6%,而房地产开发投资分别虚重报约28%和23%。比较而言,全国的新商品房销售额和土地购置费比京沪两地瞒漏报得更多,全国的房地产开发投资比京沪两城虚重报得更多,这比较符合直觉。当然,受统计数据和理论模型设定的限制,应谨慎对待这些估算结果。
基于模拟分析结果,本文强调对于当前的土地供给应“分城施策”,三四线城市短期内应适当减少土地供给以稳定地价和房价,而一二线城市长期应尽量增加土地供给以降低地价和房价。2020年3月12日,国务院印发《关于授权和委托用地审批权的决定》,进一步深化“放管服”改革,赋予省级人民政府更大的用地自主权,这更加有利于地方政府实施本文所提出的“分城施策”建议。
对于中国房地产部门的土地供给政策变化,本文通过建立理论结构模型进行仿真模拟,进而分析产品和房地产经济的基本面如何相互作用和影响。这与现有文献中研究土地和房地产经济的理论结构模型一般都引入货币金融摩擦与采用新凯恩斯框架来研究经济波动不同。例如,高然和龚六堂(2017)、赵扶扬等(2017)以及梅冬州等(2018)采用类似于如下的传导机制:需求冲击→土地价格上升(金融加速器机制)→地方财政支出增加(土地财政机制)→基础设施建设增多→刺激宏观经济,探讨了中国宏观经济波动。显然,这类文献的核心是增加了土地财政的放大机制。国内研究土地财政的实证文献还有很多。例如,周彬和周彩(2019)研究发现,地方政府对土地财政依存度的上升会提高企业的过度负债概率,增加未来的偿债压力,降低过度负债企业的盈利与持续发展能力。
本文的主要贡献是通过构建一个基本模型进行参数校准和贝叶斯估计,尝试获得中国标准新房总量生产函数中比较准确的结构参数,从而为从宏观经济视角研究中国房地产经济提供了一个比较可靠的起点。此外,本文提供了一种在统计数据可能存在系统性偏差的情况下DSGE模型的参数校准和贝叶斯估计方法,填补了国内外相关文献的空白。
本文余下内容的结构安排为:第二部分为理论模型。第三部门为数据描述与参数校准,包括房地产部门结构参数初次校准的失败和引入新信息后的试校准等。第四部分为房地产部门结构参数的贝叶斯估计,重点是数据可能存在系统性偏差时的处理和冲击的重要性。第五部分为土地供给增减的宏观经济效应与不同城市的土地供给政策变化。第六部分为基本结论与政策建议。
二、理论模型
本节将给出一个包含房地产和一般产品两个生产部门的动态随机一般均衡模型。模型主要包括新房生产、一般产品生产、家庭、实物性投资品厂商、土地转卖商和政府共六个部门。正如上文所述,由于本文的首要目的是校准或估计房地产部门新房生产函数中的结构参数,而且这些参数在较长期内具有稳定性,我们并不需要考虑货币信贷机制所导致的短期经济波动问题。按照国内外估计总量生产函数的通行做法,本文无需加入货币信贷金融部门,也不必采用新凯恩斯主义框架。因此,本文将采用包含两个生产部门的RBC框架。
(一)新房生产部门
代表性新房生产部门的利润最大化问题为:
新房生产部门标准的新房生产函数为:
| Hnewt=[(Kht)αh(Nht)1−αh]1−γLγt | (1) |
其中,
| rht/wt=[αh/(1−αh)]Nht/Kht | (2) |
| qlt/wt=[γ/(1−αh)(1−γ)]Nht/Lt | (3) |
代表性新房生产部门的新房总价值等于其成本:
| qhtHnewt=rhtKht+wtNht+qltLt | (4) |
设
| Hnewt=Ht+1−(1−δh)Ht | (5) |
(二)一般产品生产部门
一般产品的生产企业通过雇用劳动
| Ypt=At(Kpt)α(Npt)1−α | (6) |
其中,
| log(At/Ass)=ρAlog(At−1/Ass)−εAt,εAt∼N(0,σ2A) | (7) |
其中,
代表性企业的利润最大化问题为:
| wt=(1−α)Ypt/Npt | (8) |
| rt=αYpt/Kpt | (9) |
式(8)为一般产品生产部门的劳动需求方程,式(9)为资本需求方程。
(三)家庭部门
代表性家庭关于消费
| log(aht/ah)=ρahlog(aht−1/ah)+εaht,εaht∼N(0,σ2ah) | (10) |
其中,
家庭面临的资源约束为:
| Ct+qhtHnewt+QptIpt+QhtIht=wtNt+rtKpt+rhtKht+Gt | (11) |
其中,
设
| Ipt=Kpt+1−(1−δ)Kpt | (12) |
| Iht=Kht+1−(1−δ)Kht | (13) |
家庭的当期支出是消费
记资源约束式(11)的拉格朗日乘子为
| an=wtλt | (14) |
| Qptλt=βEt[rt+1λt+1+(1−δ)Qpt+1λt+1] | (15) |
| Qhtλt=βEt[rht+1λt+1+(1−δ)Qht+1λt+1] | (16) |
| 1/Ct=λt | (17) |
| qhtλt−β(1−δh)Et(qht+1λt+1)=aht/Ht+1 | (18) |
式(14)为劳动供给方程,式(15)为一般产品生产部门实物性资产的跨期决策方程,式(16)为新房生产部门实物性资产的跨期决策方程,式(17)为消费的最优条件,式(18)为房产需求方程。
(四)实物性投资品厂商
根据Bernanke等(1999)的研究,本文引入代表性投资品厂商。该厂商分别以价格
| \log ({{{Z_t}} / {{Z_{ss}}}}) = {\rho _Z}\log ({{{Z_{t - 1}}} / {{Z_{ss}}}}) - {\varepsilon _{Zt}},{\rm{ }}{\varepsilon _{Zt}} \sim {N(0,\sigma _Z^2)} | (19) |
其中,
| Q_t^p = 1 + \frac{{{\omega _p}}}{2}{(\frac{{I_t^p}}{{I_{t - 1}^p}} - 1)^2}\frac{1}{{{Z_t}}} + {\omega _p}(\frac{{I_t^p}}{{I_{t - 1}^p}} - 1)\frac{{I_t^p}}{{I_{t - 1}^p}}\frac{1}{{{Z_t}}} - \beta {\omega _p}{{\rm{E}}_{\rm{t}}}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}(\frac{{I_{t + 1}^p}}{{I_t^p}} - 1){(\frac{{I_{t + 1}^p}}{{I_t^p}})^2}\frac{1}{{{Z_{t + 1}}}} | (20) |
| Q_t^h = 1 + \frac{{{\omega _h}}}{2}{(\frac{{I_t^h}}{{I_{t - 1}^h}} - 1)^2} + {\omega _h}(\frac{{I_t^h}}{{I_{t - 1}^h}} - 1)\frac{{I_t^h}}{{I_{t - 1}^h}} - \beta {\omega _h}{{\rm{E}}_{\rm{t}}}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}(\frac{{I_{t + 1}^h}}{{I_t^h}} - 1){(\frac{{I_{t + 1}^h}}{{I_t^h}})^2} | (21) |
式(20)为一般产品生产部门的实物性投资品需求方程,相对价格
(五)土地转卖商
在现实经济中,政府拍卖土地,房地产商竞拍,但不是所有房地产商会把拍卖获得的土地都直接用于新房生产。事实上,不少房地产商会把这些土地再转卖给生产新房的其他房地产商,使得土地买卖的一级市场价格与二级市场价格不再相等,从而产生摩擦成本。这类房地产商实际上是一个“土地转卖商”。该厂商以价格
由
| q_t^l = [1 + \frac{{{\omega _l}}}{2}{(\frac{{{L_t}}}{{{L_{t - 1}}}} - 1)^2} + {\omega _l}(\frac{{{L_t}}}{{{L_{t - 1}}}} - 1)\frac{{{L_t}}}{{{L_{t - 1}}}}]Q_t^l - \beta {\omega _l}{{\rm{E}}_{\rm{t}}}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}(\frac{{{L_{t + 1}}}}{{{L_t}}} - 1){(\frac{{{L_{t + 1}}}}{{{L_t}}})^2}]Q_{t + 1}^l | (22) |
(六)政府部门
土地供给
| \log ({{{L_t}}/ {\bar L}}) = {\rho _L}\log ({{{L_{t - 1}}} / {\bar L}}) - {\varepsilon _{Lt}},{\rm{ }}{\varepsilon _{Lt}} \sim {N(0,\sigma _L^2)} | (23) |
其中,
政府拍卖土地的一级市场价格为
| {G_t} = Q_t^lL_t | (24) |
(七)一般均衡与经济动力系统
一般均衡时,劳动力、产品、房地产与实物性资产等各个市场出清。加总后,模型中整个经济的资源约束为:
| {C_t} + q_t^hH_t^{new} + Q_t^pI_t^p + Q_t^hI_t^h = {Y_t} + Q_t^lL_t | (25) |
其中,新房生产部门和一般产品生产部门的总产出
| {Y_t} = Y_t^h + Y_t^p | (26) |
其中,新房生产部门的产出
| Y_t^h = r_t^hK_t^h + {w_t}N_t^h | (27) |
全国房地产部门的新商品房销售额
| V_t^{hnew} = q_t^hH_t^{new} = r_t^hK_t^h + {w_t}N_t^h + q_t^lL_t | (28) |
全国的总劳动
| {N_t} = N_t^h + N_t^p | (29) |
全国的总投资
| {I_t} = I_t^p + I_t^{hd} | (30) |
其中,房地产部门的开发投资
| I_t^{hd} = I_t^h + I_t^l | (31) |
| I_t^l = Q_t^l{L_t} | (32) |
此外,土地价值以外的总实物性资产
| {K_t} = K_t^h + K_t^p | (33) |
| V_{t + 1}^h = q_t^hH_{t + 1} | (34) |
各个经济部门、各个市场的均衡条件及所有外生冲击过程共同构成了一个经济动力系统(由式(11)以外的上述其他等式组成)。在这个经济系统中,共有33个变量、22个参数和4个外生冲击。根据这个动力系统,可以计算得到模型的稳态值。受篇幅限制,文中没有给出动力系统稳态值的详细求解过程。
三、数据描述与参数校准
(一)数据描述
由下文可知,本文需要利用全国和京沪两地的土地购置费、新商品房销售额和房地产开发投资数据。房地产部门和京沪两地的地区生产总值数据来自Wind资讯。将原始的季度或月度数据统一整理成季度数据,并在校准或估计前做季度调整和剔除价格因素。Chang等(2016)基于国家统计局等权威部门的原始数据,整理得到与美国数据具有可比性的中国宏观经济季度数据。②因此,我们可以直接选取Chang等(2016)中的全国国民生产总值和消费的季度数据。我们还选取了其中的消费者价格指数(CPI)、固定资产投资(FAI)价格指数以及GDP平减指数来剔除名义变量中的价格因素。具体而言,真实消费等于名义消费除以CPI,真实产出等于名义国民生产总值除以GDP平减指数,真实土地购置费、房地产开发真实投资和新商品房真实价值分别等于名义土地购置费、房地产开发名义投资和新商品房销售额除以FAI价格指数。根据数据可得性,本文选取了2002年第1季度至2016年第4季度共60个季度的数据。
(二)参数校准
假设一期对应于一个季度。将22个模型参数分成四个集合:3类投资调节成本参数
| 参数符号 | 参数名称 | 校准值 | 校准依据 |
|
{a_n}
|
闲暇负效用常数 | 1 | 标准化为1 |
|
\beta
|
主观折现因子 | 0.994 | 2002Q1−2016Q4的一年期存款年平均利率为2.56% |
|
\alpha
|
中间产品生产资本份额 | 0.50 | Chow和Li(2002)、Song等(2011)等 |
|
\delta
|
实物性资产折旧率 | 0.025 | 国外标准文献 |
|
{A_{ss}}
|
稳态时的全要素生产率 | 1 | 标准化为1 |
|
{Z_{ss}}
|
稳态时的投资专用技术 | 1 | 标准化为1 |
|
{\omega _p}
|
一般产品生产部门的投资调节成本常数 | 0.18 | Liu等(2013) |
|
{\omega _h}
|
新房生产部门的投资调节成本常数 | 0.18 | Liu等(2013) |
|
{\omega _l}
|
土地转卖中的调节成本常数 | 0.18 | Liu等(2013) |
|
{\delta _h}
|
房产折旧率 | 0.01 | Iacoviello和Stefano(2010) |
|
\bar L
|
土地供给常数 | 1 | 标准化为1 |
|
\gamma
|
全国新房生产中的土地份额 | 0.211 | 2016Q1−Q4全国和京沪两地的土地购置费与新商品房销售额的加权平均比值① |
|
{\alpha _h}
|
全国新房生产中与资本份额相关的参数 | 0.884 | 2016Q1−Q4全国和京沪两地的土地购置费与房地产开发投资的加权平均比值 |
|
{a_h}
|
全国的家庭房产需求偏好强度 | 0.818 | 2016Q1−Q4全国和京沪两地的新商品房销售额与全国总产出的加权平均比值 |
|
{\gamma ^{JH}}
|
京沪两地新房生产中的土地份额 | 0.284 | 2016Q1−Q4京沪两地的土地购置费与新商品房销售额的平均比值 |
|
\alpha _h^{JH}
|
京沪两地新房生产中与资本份额相关的参数 | 0.715 | 2016Q1−Q4京沪两地的土地购置费与房地产开发投资的平均比值 |
|
a_h^{JH}
|
购买京沪两地新房的家庭房产需求偏好强度 | 1.084 | 2016Q1−Q4京沪两地的新商品房销售额与全国总产出的平均比值 |
四、房地产部门结构参数的贝叶斯估计
由上文可知,如果本文的模型设定基本正确,那么全国的土地购置费、新商品房销售额和房地产开发投资这3个房地产业的统计数据可能存在一定的瞒漏报或虚重报等质量问题。下文中,我们首先利用这些可能存在系统性偏差的数据对模型中上述3个试校准的参数进行贝叶斯估计,然后通过方差分解来探讨政府的土地供给政策、家庭的房产需求偏好、一般产品生产部门的全要素生产率和投资专用技术这4个冲击的重要性。
(一)系统性偏差数据的处理
假设某个变量的统计报告值为
| {{b_t^r} / {b_t}} = x_t^bX_t^b | (35) |
进一步地,假设
| {{{g_{b_t^r}}}/ {{g_{{b_t}}}}} = ({g_{x_{}^b}}{g_{X_{}^b}})({g_{x_t^b}}{g_{X_t^b}}) | (36) |
其中,
进一步地,假设
| {\tilde g_{b_t^r}} = {\tilde g_{{b_t}}} + \varepsilon _{{b_t}},{\rm{ }}\varepsilon _{{b_t}} = \log ({g_{x_t^b}}{g_{X_t^b}})\sim N(0,\sigma _{{g_b}}^2) | (37) |
其中,
对于全国的土地购置费、新商品房销售额和房地产开发投资这3个房地产业可能存在系统性偏差的可观测变量,则有:
| {{\tilde g}}_{{b}_{t}^{r}} = {{\tilde g}}_{{b}_{t}} + {{\varepsilon }}_{{b}_{t}} | (38) |
其中,
此外,对于没有系统性偏差的全国GDP和消费变量,则有:
| {\tilde g_{Y_t^r}} = {\tilde g_{Y_t}} | (39) |
| {\tilde g_{C_t^r}} = {\tilde g_{C_t}} | (40) |
(二)房地产部门统计数据季度增长的描述性统计
表2显示了2002年第2季度至2016年第4季度房地产部门统计数据的季度增长情况。从中可以看到,全国的土地购置费、新商品房销售额和房地产开发投资的季度增长率都显著高于GDP和消费的季度增长率,约为后者的两倍。京沪两地的新商品房销售额和房地产开发投资的季度增长率仅略高于地区生产总值的季度增长率,但土地购置费的季度增长率显著高于地区生产总值的季度增长率,约为后者的两倍。另外,房地产部门的各个变量波动程度都明显大于其他产品部门,土地购置费和新商品房销售额的波动程度显著大于房地产开发投资的波动程度,京沪等一线城市房地产部门的各个变量波动程度显著大于全国其他城市。
| 土地购置费季度增长 | 新商品房销售额季度增长 | 房地产开发投资季度增长 | 产出季度增长 | 消费季度增长 | ||
| 全国 | 均值 | 0.0449 | 0.0488 | 0.0402 | 0.0225 | 0.0233 |
| 标准差 | 0.1147 | 0.2118 | 0.0427 | 0.0065 | 0.0084 | |
| 京沪两地 | 均值 | 0.0420 | 0.0300 | 0.0218 | 0.0204 | − |
| 标准差 | 0.3156 | 0.2145 | 0.1126 | 0.0498 | − | |
| 资料来源:Wind资讯。 | ||||||
(三)房地产部门结构参数的贝叶斯估计
下文中,我们利用上文的季度增长数据,采用贝叶斯方法来估计参数
表3总结了重要参数的估计结果,其中中间三列分别为先验分布、先验均值和众数,最右边一列为模型估计的后验均值及其90%的置信区间,这些值都是利用Metropolis-Hastings算法模拟200 000次得到的。从中可以看到,参数
本文采用类似的方法,还估计了京沪两地新房生产函数中的结构参数,结果(受篇幅限制未报告)显示:参数
| 待估参数 | 先验分布 | 先验均值 | 众数 | 后验均值与90%的置信区间 |
|
\gamma
|
Beta | 0.211 | 0. 2207 | 0.2289 [0.1953,0.2663] |
|
{\alpha _h}
|
Beta | 0.884 | 0.8805 | 0.8680 [0.8312,0.9052] |
|
{a_h}
|
Gamma | 0.818 | 0.8087 | 0.8426 [0.7123,0.9818] |
|
{\omega _p}
|
Gamma | 0.18 | 0.3046 | 0.2707 [0.1233,0.4162] |
|
{\omega _h}
|
Gamma | 0.18 | 0.5070 | 0.9383 [0.5562,1.2170] |
|
{\omega _l}
|
Gamma | 0.18 | 0.1766 | 0.1875 [0.0579,0.3103] |
|
{\rho _L}
|
Beta | 0.90 | 0.9506 | 0.9128 [0.8763,0.9380] |
|
{\rho _{{a_h}}}
|
Beta | 0.90 | 0.9046 | 0.9011 [0.8683,0.9339] |
|
{\rho _A}
|
Beta | 0.90 | 0.9408 | 0.9313 [0.9006,0.9584] |
|
{\rho _Z}
|
Beta | 0.90 | 0.8737 | 0.8569 [0.8174,0.8952] |
|
{\sigma _L}
|
Inverse Gamma | 0.01 | 0.1129 | 0.0350 [0.0021,0.1113] |
|
{\sigma _{{a_h}}}
|
Inverse Gamma | 0.01 | 0.0046 | 0.0084 [0.0025,0.0155] |
|
{\sigma _A}
|
Inverse Gamma | 0.01 | 0.0068 | 0.0056 [0.0043,0.0071] |
|
{\sigma _Z}
|
Inverse Gamma | 0.01 | 0.0102 | 0.0138 [0.0096,0.0177] |
|
{\sigma _{{g_{{I^l}}}}}
|
Inverse Gamma | 0.01 | 0.1092 | 0.1135 [0.0956,0.1305] |
|
{\sigma _{{g_{{V^{hnew}}}}}}
|
Inverse Gamma | 0.01 | 0.2071 | 0.2145 [0.1817,0.2480] |
|
{\sigma _{{g_{{I^{hd}}}}}}
|
Inverse Gamma | 0.01 | 0.0351 | 0.0547 [0.0351,0.0726] |
如果本文的模型设定基本正确,我们可以利用上文估计得到的全国和京沪两地的新商品房生产函数来初步估算房地产部门统计数据的系统性偏差。结果显示:全国和京沪两地的新商品房销售额分别瞒漏报约8%和3%,土地购置费分别瞒漏报约23%和6%,而房地产开发投资分别虚重报约28%和23%。比较而言,全国的新商品房销售额和土地购置费比京沪两地瞒漏报得更多,房地产开发投资比京沪两地虚重报得更多,这比较符合直觉。当然,受现实统计数据和理论模型设定的限制,我们应谨慎对待这些初步估算结果。
(四)方差分解:各种冲击的重要性
为了考察土地供给政策等冲击对我国宏观经济波动的影响,需要进一步做方差分解。从对房地产部门的影响看,在四个冲击中,土地供给政策冲击影响供给侧,家庭房产需求偏好冲击影响需求侧,而产品部门的全要素生产率冲击和投资专用技术冲击既影响需求侧,也影响供给侧。那么,究竟哪个冲击占优,需要比较其对产品和房地产部门投资收益率的影响。
表4报告了上述四种不同性质的冲击下全国和京沪两地的方差分解结果。全国参数模拟和估计的方差分解结果显示,土地供给政策冲击主要影响全国地价波动,也影响全国土地财政和新房生产波动。对全国土地财政和新房生产波动影响最大的是产品部门的投资专用技术冲击。方差分解结果还显示,对全国房价波动影响最大的也是产品部门相对于房产部门升级更快或更慢的投资专用技术冲击。
与全国的结果相比,京沪参数模拟和估计的方差分解结果显示,土地供给政策冲击仍是影响京沪地价波动的重要因素,对京沪两地的房价、土地财政和新房生产波动的影响相对较小。对京沪两地的地价、房价、土地财政和新房生产波动影响最大和第二大的分别是产品部门的全要素生产率和投资专用技术冲击。
| 土地供给政策冲击 | 房产需求偏好冲击 | 全要素生产率冲击 | 投资专用技术冲击 | |
| 总产出 | 4.08(0.02) | 0.10(0.01) | 70.96(99.76) | 24.86(0.21) |
| 房产产出 | 39.19(6.99) | 0.92(1.88) | 2.44(57.95) | 57.45(33.18) |
| 产品产出 | 0.46(0.00) | 0.01(0.00) | 61.10(99.54) | 38.43(0.45) |
| 消费 | 0.25(0.02) | 0.01(0.01) | 6.34(76.98) | 93.41(22.98) |
| 房产投资 | 2.08(0.37) | 0.04(0.11) | 1.48(61.31) | 96.40(38.22) |
| 产品投资 | 0.37(0.02) | 0.01(0.01) | 10.72(94.06) | 88.90(5.91) |
| 土地财政 | 34.76(5.58) | 0.99(1.91) | 2.62(58.83) | 61.63(33.69) |
| 新房生产 | 45.59(6.66) | 0.02(0.12) | 1.38(63.98) | 53.01(29.24) |
| 房价 | 1.37(0.20) | 1.67(3.16) | 3.30(64.21) | 93.67(32.43) |
| 地价 | 89.50(26.57) | 0.16(1.48) | 0.42(45.75) | 9.91(26.20) |
| 注:括号内外的数值分别对应于京沪两地和全国的参数模拟和估计结果,方差分解结果用百分数表示。 | ||||
五、土地供给增减的宏观经济效应与不同城市的土地供给政策变化
本文的第二个目的是分析中国房地产部门的土地供给政策变化效应以及与宏观经济基本面联系紧密的供给侧结构性改革。因此,本节首先分析土地供给增减的宏观经济效应,包括短期效应和长期效应,然后重点探讨一二线城市土地供给政策变化的长效机制和三四线城市这一政策变化的短期效果。
(一)土地供给增减的宏观经济效应
1. 传导机制的理论分析
由上文模型中政府部门的设置可知,如果土地供给函数式(23)中的
2. 短期效应
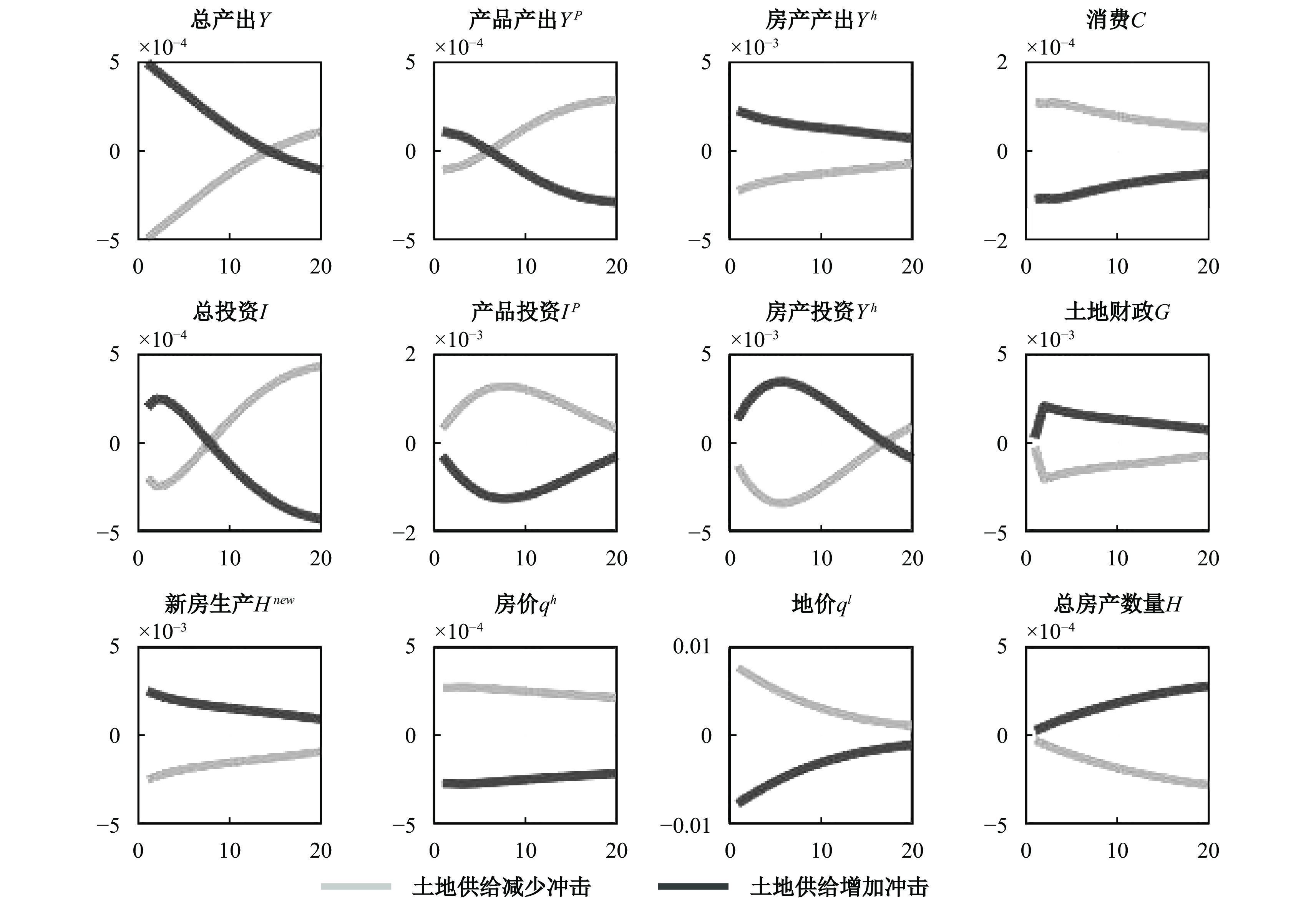
图3中深色实线表示政府土地供给增加时的脉冲反应,可以看到,土地供给增加会使房地产部门和产品部门的实物性资产的收益率增加,房地产部门的实物性投资、新房数量、产出和住房总量都相应增加,政府的土地财政收入或支出(即房地产部门的土地购置费)也增加,而地价和房价都因供给的增加而下降。为使产品部门的实物性资产的收益率增加,其实物性投资和家庭部门的消费都因挤出效应的存在而减少,产品部门的产出也减少。整体上看,房地产部门增加的产出大于产品部门减少的产出与家庭部门减少的消费之和,因此总产出增加。图3中浅色实线表示政府土地供给减少时的脉冲反应,可以看到,土地供给减少会引致房地产部门的实物性投资和新房生产都下降,地价和房价上升。由于房地产部门投资下降,在替代效应下,家庭部门的消费和产品部门的实物性投资增加。这与上述传导机制的理论分析结论一致。
|
| 图 3 政府土地供给增减的脉冲反应 |
3. 长期效应
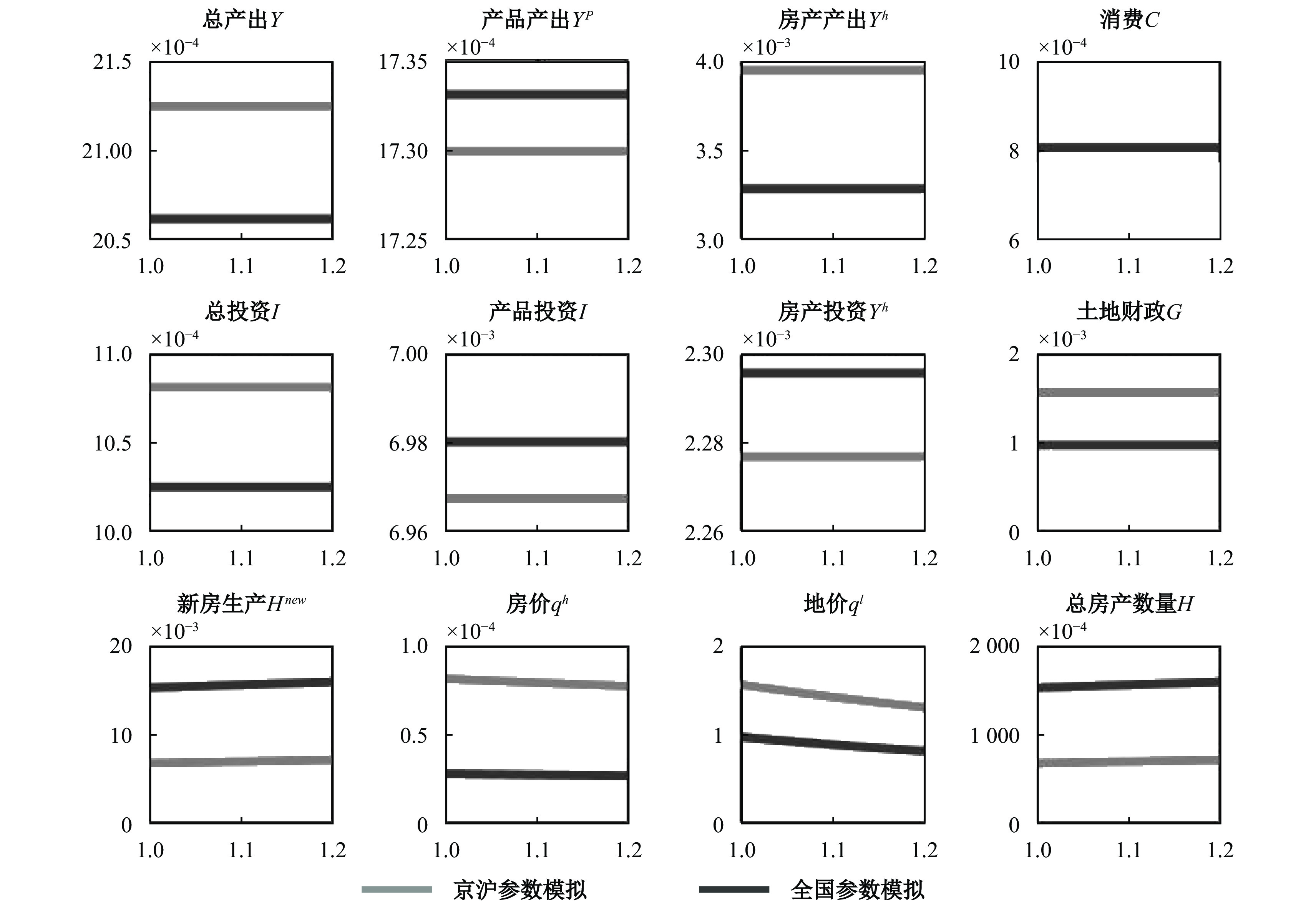
图4中深色实线的模拟结果显示,如果全国土地供给增加20%,那么长期新房生产将增加20%,总房产数量增加4.2%,地价和房价分别下降20%。由于长期土地供给的增加幅度等于地价的下降幅度,长期的土地财政收入或支出(即房地产部门的土地购置费)不变。此外,长期土地供给的增加也不会引起消费、投资和产出的变化。相反,如果长期土地供给减少20%,那么新房生产将减少20%,地价和房价上升20%。同样,长期土地供给的减少也不会引起土地财政、消费、投资和产出的变化。这表明,长期来看,除了房地产部门外,土地供给的增减对宏观经济几乎没有影响。
(二)一二线城市土地供给政策变化的长效机制
根据上文中京沪两地参数模拟和估计的方差分解结果,京沪两地的土地供给增减政策冲击对当地的地价、房价、土地财政和新房生产波动的影响较小,因此应重点关注京沪等一二线城市土地供给增减政策的长期影响。图4中浅色实线的模拟结果暗示,如果一二线城市的政府土地供给长期增加20%,那么新房生产长期会增加20%,地价和房价分别下降20%;长期来看,土地供给的增减对投资、消费和产出等宏观经济变量没有显著影响。本文认为,一二线城市政府在长期应尽量增加土地供给以降低地价和房价。图4中浅色实线反映的一二线城市情况与全国情况相同,但两者的数值大小不同。图4结果显示,一线城市的平均房价是全国平均水平的3倍左右。中国一二线城市一直面临地价和房价过高的问题,这主要是京沪等一二线城市大幅减少土地供给所导致的。
(三)三四线城市土地供给政策变化的短期效果
根据上文中全国参数模拟和估计的方差分解结果,应重点关注全国特别是三四线城市的土地供给增减政策冲击,因为它是影响地价、房价、土地财政和新房生产波动的重要因素。这表明在三四线城市,应采取与一二线城市不同的土地供给政策,即一二线城市的土地供给政策应重点关注长效机制,而三四线城市则应聚焦于短期房价和地价的稳定。金融危机后,为了保持经济稳定增长,三四线城市政府短期增加大量土地供给,与图3中深色实线反映的土地供给增加时的情形一致。
中国2016—2017年的“去库存”包括去除三四线城市的商品房库存。由上文可知,商品房库存过多的重要原因是2008—2009年金融危机后,特别是从2011—2012年开始的“新常态”下,三四线城市过多地依赖房地产部门来稳定经济增长。图3中浅色实线的脉冲反应结果表明,三四线城市政府在短期应适当减少土地供给以稳定地价和房价,引导资源从房地产部门重新流回产品部门。
|
| 图 4 政府土地供给增加的长期宏观经济效应 |
六、基本结论与政策建议
中国的土地制度、家庭购房偏好和新房生产函数与欧美国家不同,作为从宏观视角研究中国房地产经济的起点,需要利用中国数据校准或估计出一个参数更加可信的新房总量生产函数。本文基于一个包含两个生产部门的DSGE模型,尝试做了这项工作。基本模型分析表明,在全国新房生产中,土地、资本和劳动份额分别为23%、67%和10%。这一结果与Iacoviello和Stefano(2010)关于美国新房生产函数中结构参数的估计结果(资本、土地和劳动份额分别约为20%、10%和70%)差距巨大。因此,我们不能直接借用欧美国家新房生产函数中的结构参数。而在京沪两地的新房生产中,土地份额为28.44%,接近三成;资本份额为51.24%,略超五成;劳动份额为20.32%,约占两成。由于资本在国内基本可以自由流动,京沪等一线城市的土地和劳动力价格比全国平均水平要高,因此新房生产中的土地和劳动份额比全国高是合理的。另外,中国家庭对京沪等一线城市的房产需求偏好参数约为1.09,明显大于全国平均水平0.84。
如果模型设定基本正确,本文初步估算了房地产部门统计数据中可能存在的系统性偏差。结果显示,全国和京沪两地的新商品房销售额分别瞒漏报约8%和3%,土地购置费分别瞒漏报约23%和6%,而房地产开发投资分别虚重报约28%和23%。比较而言,全国的新商品房销售额和土地购置费比京沪两地瞒漏报得更多,房地产开发投资比京沪两地虚重报得更多,这比较符合直觉。当然,受现实统计数据和理论模型设定的限制,我们应谨慎对待这些初步估算结果。
基于模拟分析结果,本文强调对于当前的土地供给应“分城施策”,三四线城市短期内应适当减少土地供给以稳定地价和房价,而一二线城市长期应尽量增加土地供给以降低地价和房价。2020年3月12日,国务院印发《关于授权和委托用地审批权的决定》,进一步深化“放管服”改革,赋予省级人民政府更大的用地自主权,这更加有利于地方政府实施本文所提出的“分城施策”建议。
* 作者感谢上海交通大学安泰经济与管理学院许志伟老师和两位匿名审稿人的建议性意见!当然,文责自负。
① 由于研究目的不同,国内有关房地产经济的其他宏观文献大多没有设定标准新房总量生产函数。例如,蔡明超等(2011)以及陈彦斌和邱哲圣(2011)的研究中没有房地产部门生产函数;侯成琪和龚六堂(2014)在房地产部门生产函数中将土地做了一个类似于全要素生产率的设定,其仅作为土地供给冲击存在;陈彦斌等(2015)设定的房地产部门生产函数中不包含劳动要素。
② 作者每年大约在8月份更新前一年的数据,可以从以下网址下载:http://www.nber.org/data-appendix/c13592/或https://www.frbatlanta.org/cqer/research/china-macroeconomy.aspx。
③ 仅采用全国数据出现校准失败,推断出全国数据可能存在一定程度上的瞒漏报或虚重报情况,从而引入比较准确的京沪两地数据来修正初始校准值。下同。
| [1] | 蔡明超, 黄徐星, 赵戴怡. 房地产市场反周期宏观调控政策绩效的微观分析[J]. 经济研究, 2011(S1): 80–89. |
| [2] | 陈彦斌, 郭豫媚, 陈伟泽. 2008年金融危机后中国货币数量论失效研究[J]. 经济研究, 2015(4): 21–35. |
| [3] | 陈彦斌, 邱哲圣. 高房价如何影响居民储蓄率和财产不平等[J]. 经济研究, 2011(10): 25–38. |
| [4] | 高然, 龚六堂. 土地财政、房地产需求冲击与经济波动[J]. 金融研究, 2017(4): 32–45. DOI:10.3969/j.issn.1009-3109.2017.04.005 |
| [5] | 郭庆旺, 贾俊雪. 中国全要素生产率的估算: 1979−2004[J]. 经济研究, 2005(6): 51–60. |
| [6] | 侯成琪, 龚六堂. 货币政策应该对住房价格波动作出反应吗——基于两部门动态随机一般均衡模型的分析[J]. 金融研究, 2014(10): 15–33. |
| [7] | 梅冬州, 崔小勇, 吴娱. 房价变动、土地财政与中国经济波动[J]. 经济研究, 2018(1): 35–49. |
| [8] | 王云清, 朱启贵, 谈正达. 中国房地产市场波动研究——基于贝叶斯估计的两部门DSGE模型[J]. 金融研究, 2013(3): 101–113. |
| [9] | 许志伟, 林仁文. 我国总量生产函数的贝叶斯估计——基于动态随机一般均衡的视角[J]. 世界经济文汇, 2011(2): 87–102. DOI:10.3969/j.issn.0488-6364.2011.02.006 |
| [10] | 许志伟, 吴化斌. 企业组织资本对中国宏观经济波动的影响[J]. 管理世界, 2012(3): 23–33. |
| [11] | 赵扶扬, 王忏, 龚六堂. 土地财政与中国经济波动[J]. 经济研究, 2017(12): 46–61. |
| [12] | 周彬, 周彩. 土地财政、企业杠杆率与债务风险[J]. 财贸经济, 2019(3): 19–36. |
| [13] | An S, Schorfheide F. Bayesian analysis of DSGE models[J]. Econometric Reviews, 2007, 26(2−4): 113–172. DOI:10.1080/07474930701220071 |
| [14] | Bernanke B S, Gertler M, Gilchrist S. The financial accelerator in a quantitative business cycle framework[A]. Taylor J B, Woodford M. Handbook of macroeconomics (Vol.1)[M]. Amsterdam: Elsevier, 1999. |
| [15] | Chang C, Chen K J, Waggoner D F, et al. Trends and cycles in China’s macroeconomy[A]. Eichenbaum M, Parker J A. NBER Macroeconomics Annual 2015[M]. University of Chicago Press, 2016. |
| [16] | Chen K J, Wen Y. The great housing boom of China[J]. American Economic Journal: Macroeconomics, 2017, 9(2): 73–114. DOI:10.1257/mac.20140234 |
| [17] | Chow G C, Li K W. China’s economic growth: 1952-2010[J]. Economic Development and Cultural Change, 2002, 51(1): 247–256. DOI:10.1086/344158 |
| [18] | Hansen G D. Indivisible labor and the business cycle[J]. Journal of Monetary Economics, 1985, 16(3): 309–327. DOI:10.1016/0304-3932(85)90039-X |
| [19] | Iacoviello M, Stefano N. Housing market spillovers: Evidence from an estimated DSGE model[J]. American Economic Journal: Macroeconomics, 2010, 2(2): 125–164. DOI:10.1257/mac.2.2.125 |
| [20] | Ireland P N. A method for taking models to the data[J]. Journal of Economic Dynamics and Control, 2004, 28(6): 1205–1226. DOI:10.1016/S0165-1889(03)00080-0 |
| [21] | Kydland F E, Prescott E C. Time to build and aggregate fluctuations[J]. Econometrica, 1982, 50(6): 1345–1370. DOI:10.2307/1913386 |
| [22] | Liu Z, Wang P F, Zha T. Land-price dynamics and macroeconomic fluctuations[J]. Econometrica, 2013, 81(3): 1147–1184. DOI:10.3982/ECTA8994 |
| [23] | Miao J J, Wang P F. Asset bubbles and credit constraints[J]. American Economic Review, 2018, 108(9): 2590–2628. DOI:10.1257/aer.20160782 |
| [24] | Piazzesi M, Schneider M. Housing and macroeconomics[A]. Taylor J B, Woodford M. Handbook of macroeconomics (Vol.2)[M]. Amsterdam: Elsevier, 2016. |
| [25] | Song Z, Storesletten K, Zilibotti F. Growing like China[J]. The American Economic Review, 2011, 101(1): 196–233. DOI:10.1257/aer.101.1.196 |
| [26] | Wei S J, Zhang X B. The competitive saving motive: Evidence from rising sex ratios and savings rates in China[J]. Journal of Political Economy, 2011, 119(3): 511–564. DOI:10.1086/660887 |


