
2019第45卷第11期
2. 国家发改委宏观经济研究院 产业所,北京 100038
2. Academy of Macroeconomic Research, National Development and Reform Commission, Beijing 100038, China
一、引 言
近20年,我国劳动生产率总体上大幅提高,但在各地区和各城市间仍存在较大差异。根据《中国城市统计年鉴》数据,2015年我国中小城市劳动力的平均产出为56 256元,明显低于大城市的70 577元。传统的新古典经济学理论认为,要素投入和集聚经济的差别是导致劳动生产率差异的原因。新经济地理学者强调运输成本的高低和规模经济的大小会对不同地区和城市的市场规模和劳动生产率产生差异化影响。后续研究通过正规理论模型分析指出,劳动者与工作岗位的技能匹配程度影响劳动生产率(Duranton和Puga,2004)。反观我国劳动技能匹配状况,人保部数据显示2014年4季度城市劳动力市场求人倍率为1.15,各类用工总需求的15%无法得到满足。
城市规模的大小决定着本地劳动力市场规模,进而极大地影响着技能匹配水平和企业生产率。大城市各种专业化行业比较齐全,劳动者技能与岗位技能需求愈相匹配。从日常观察可见,双双拥有高学历和专业技能的夫妻倾向选择在大城市工作和生活,因为大城市内各类专业技能易于匹配,双方可以拥有各自的事业、获得较高的收入。理论和实证研究还表明,随着城市规模的增长和功能分工的演变,大城市逐渐成为管理、研发和先进服务业中心,而外围中小城市则主要承担专业化制造和加工功能(Duranton和Puga,2005;赵勇和白永秀,2012)。与中小城市相比,大城市具有吸纳高技能劳动力的优势,高技能劳动力和高技术企业有更各得其所的技能匹配和更高的生产率。
交通条件直接影响着劳动力流动性和技能匹配水平。在我国一些发达地区,城市交通条件的改善显著提高了大城市职工的通勤距离。2017年GDP排名前十的城市职工平均通勤里程都在8公里以上,其中排名前三的城市的平均通勤距离更是突破了12公里。全国其他地区城市交通条件的改善同样有助于提高劳动力流动性、扩大劳动力市场规模、缓解技能错配、提高劳动生产率。根据《第一财经周刊》中国城市分级标准,2016年,我国三、四线城市的道路面积较去年增长8.6%(高于一、二线城市的6.2%),而三、四线城市的月人均出行次数增长了23.1%,增速是一、二线城市的近三倍。①便利的交通和通勤条件显著提高了劳动力的出行效率,也为更多城市提供了与大城市劳动力集聚同等的劳动力蓄水池效益。
企业职工培训是改善技能匹配水平、提高生产率的另一重要途径。例如,福特汽车、摩托罗拉等企业每年人才培训支出在10亿美元以上,韩国每年人均就业培训费为223万韩元。② 我国沿海地区外资企业也很注重职工技能培训,为此专门在我国建立了培训基地。相比之下,国内企业的员工培训经费投入很低。《中国企业人力资源管理调查报告》的数据显示,培训经费占公司销售收入千分之三以上的企业仅占企业数的8.7%,然而,占销售收入千分之零点五以下的企业则有48.2%。
行业技术水平和行业间技术相似性是影响技能匹配的另一个重要原因。根据人力资源和社会保障部数据,技能劳动者数量仅占中国就业人员总量的约19%,而高技能人才只占5%,技能人才供需矛盾突出。根据《制造业人才发展规划指南》,现阶段新信息技术产业、高档数控和机器人、电力装备、新材料和生物医药等十大重点领域技工总缺口高达三千万。特定行业技工缺口的扩大不仅降低了技能匹配的总体水平,也造成技术人才的频繁流动。由于有些行业人才流失率居高不下,以致企业不看好技能培训的投资回报。根据行业技术水平和城市类型系统地分析交通条件和企业培训的影响将有助于增强地区经济结构调整的针对性。
本文的目的和贡献是分析交通条件和城市规模如何通过技能匹配影响企业生产率。我们将技能匹配引入Venables(2007)理论模型,利用中国企业面板数据检验交通条件与城市规模通过改变技能匹配水平对企业生产率的影响机制及其行业差异,弥补文献的缺失,为制定和评价城市发展政策提供若干统计依据。本文各节内容安排如下。第二节是文献综述;第三节构建理论框架和计量模型;第四节说明指标和数据;第五节报告和解释计量估计结果;第六节是结论。
二、文献综述
我们把与本文密切相关的文献分为三组:集聚经济与交通条件,交通条件与劳动力流动,劳动技能匹配机制的分析和检验。以下分别综述三组文献。
自马歇尔(Marshall,1890)勾画出集聚经济效应以来,后续文献−尤其是Duranton 和Puga(2004)−分析了集聚经济的三个微观机制−劳动力蓄水池、中间投入的规模经济和技术外溢,并初步构建了理论模型。其中:劳动力集聚有利于厂商雇用专业职工,也有利于劳动者找到与个人技能匹配的岗位,因而成为集聚经济的一个重要来源。改善交通条件将降低通勤成本,扩大地方劳动力市场,促进人口和产业集聚,产生集聚经济效益。为了确定交通条件影响城市生产率的空间范围,Graham等(2009)使用英国企业面板数据和非线性计量模型检验了不同行业的集聚经济效益和影响距离。该研究显示,英国生产性服务业和建筑业的集聚产出弹性分别为0.08和0.03,而制造业和消费性服务业的产出弹性仅为0.02;估计还显示生产性与消费性服务业和建筑业的距离衰减指数分别为1.8和1.6,远大于制造业的1.0,意味着与制造业相比,服务业和建筑业的集聚效益在空间上更加受制于距离和交通条件。Lin和Truong(2012)在一项类似研究中利用中国1999—2009年278个地级及以上等级城市的面板数据检验交通距离对集聚效应和城市生产率的影响,用就业密度表示集聚,发现就业集聚的人均产出弹性为0.109,且集聚经济随着交通条件的改善而增长,产出弹性可增至0.17。除了类似的大量正面分析以外,城市经济学也指出,交通密度的增长和经济活动的过度集中会造成集聚不经济。为了研究城市密度、生产率和交通拥堵间的关系,Graham(2007)选择距离与成本两个变量来识别道路交通拥堵效应,使用英国制造业、建筑业和服务业厂商及其区位数据和超越对数需求函数估计交通拥堵对各业厂商集聚效应的影响,发现某些行业厂商集聚收益随城市密度的增加而明显递减,交通拥堵降低了高度城市化地区的集聚收益。近年来,我国研究者也定量研究了城市生产率因交通拥堵受到的损失。柯善咨和郑腾飞(2015)根据拥堵外部性和居民与厂商最优化原理构建理论模型,利用中国266个地级及以上城市2003—2012年数据检验交通密度对生产率的影响,证实城市劳动生产率随着车辆密度的增加出现了显著的倒U形变化。
现有研究表明,交通条件影响着劳动力在部门间和区域间的流动和配置,改善交通条件有利于促进经济结构调整、提高整体经济效率。Gollin和Rogerson(2014)利用一般均衡模型和数值模拟方法分析非洲撒哈拉以南地区劳动生产率和交通成本是否会造成农业人口变动,模拟结果显示,如果农业全要素生产率和交通成本分别增加和降低10%,农业部门人口可降低20%。林理升和王晔倩(2006)在新经济地理框架内探讨运输成本和劳动力流动对制造业区域分布的作用机制,认为运输成本的差异造成了沿海地区制造业的选址优势,而劳动力流动成本则阻碍了沿海地区产业集聚的进一步深化。张光南和宋冉(2013)采用中国各省工业数据分析交通条件对要素投入的影响,结果显示改善交通基础设施能显著降低劳动力流动成本,促使劳动密集生产技术替代资本密集技术,并减少中间品投入,从而降低了生产成本。
本文与劳动技能匹配研究密切相关,而劳动技能匹配水平直接受到劳动力市场规模和交通条件的影响。Helsley和Strange(1990)的早期研究曾构建了包括劳动者、厂商和土地开发商三个经济主体的模型,其理论分析表明劳动力市场规模越大,劳动者与工作岗位的匹配质量越高。基于上述理论,Duranton和Puga(2004)在理论框架中引入了劳动力市场竞争,构建了包含均衡企业数和匹配成本的厂商模型用以分析集聚经济的来源。由于存在规模经济,企业数量的增长比例小于劳动力增长比例,劳动力市场竞争加剧,从而提高了匹配质量和劳动生产率。由于交通成本制约了劳动者−特别是城市低收入者−的工作搜寻强度,所以降低交通成本会改善劳动力流动性、扩大劳动力市场有效规模、提高技能匹配水平。为检验交通条件对工作搜寻强度(进而对劳动技能匹配)的影响,Gautier和Zenou(2010)使用劳动力市场稳态均衡模型和 1981—1982年美国全国调查数据分析了白人与黑人青年的工作搜寻强度(时间和距离)与产出水平,发现拥有私家车使白人比黑人在单位距离时间内搜寻更多的工作,接近资本市场或公共交通则有助于减少劳动市场产出的差异。研究者还发现交通成本对工作搜寻强度的影响因收入而异。Phillips(2014)根据2010年华盛顿地区雇主-家庭调查数据,设计了交通补助的随机实验,检验交通成本对低收入者工作搜寻强度的影响。该研究估计接受补助的实验组比控制组的工作搜寻强度高19%,而且交通补贴对偏远地区求职者的作用更加明显。现有研究还发现,交通成本对不同技能水平的劳动者具有筛选效应。劳动力流动性也因技能水平而异。Torfs和Zhao(2015)的研究表明,由于存在劳动力流动成本,只有高技能劳动力才有能力迁往大城市,而低技能劳动者只能在本地搜寻工作。高技能劳动力外流使当地就业环境恶化,进而降低低技能劳动者的匹配质量。个别文献还研究了交通条件通过改善匹配效率对经济增长的影响。Tikoudis等(2012)的分析显示了交通基础设施通过改善贸易条件和提高匹配效率两种途径影响产出,该研究构建了两区域空间迭代模型,采用模拟实验分析了匹配效应对经济增长的影响,定量估计认为交通基础设施通过改善劳动力匹配效率可以提高人均产出10%左右。上述有关匹配机制的理论研究和实证检验为分析交通条件与生产率之间的关系提供了一个重要思路。
综上所述,相关领域的学者们初步探讨了技能匹配如何受劳动力市场规模和交通条件影响,但是理论分析中并未涉及劳动力市场规模和交通条件对技能匹配的协同或替代作用,实证检验中依赖比较简易的模型,也忽略了交通条件与技能匹配对不同技术水平行业和不同规模城市中企业效率的影响。本文试图弥补这些研究的不足,文中理论和实证研究的逻辑是:技能匹配影响劳动生产率,即存在技能匹配效应;交通条件和城市规模协同作用于技能匹配效应。
三、理论框架
本节将技能匹配引入Venables(2007)的交通条件−城市规模−生产率理论框架,分析城市交通条件、城市规模和劳动技能匹配对企业生产率的影响,进而设置计量模型。
假设同行业的厂商生产同质产品,令x为劳动者技能与工作岗位完全匹配时的劳动生产率。大量研究表明,在相当大的规模范围内城市集聚经济大于集聚非经济,所以假设企业生产率是城市劳动力规模N的增函数x(N),x'>0。令m表示匹配成本,即劳动者技能与岗位所需技能的差别,反映技能匹配状况。假设某城市拥有足够大的技能多样化的劳动力市场,而且有完善的交通条件,厂商和劳动力的搜寻成本为0(或作为某一基点),那么这里的厂商无需内部培训投入即可实现技能匹配。而其他城市的职工和厂商的搜寻成本则大于0(或大于上述基点),他们需努力搜寻方可实现技能的供求匹配。然而,这些厂商和职工也可以通过降低招聘门槛和接受较低起薪,把搜寻成本全部投到内部培训上,培训投入越大,岗位技能差距导致的生产率损失越小,所以培训投入量是匹配成本的反向测度。又因城市劳动力规模N的扩大会促进职工与岗位之间的技能匹配,降低匹配成本m,所以匹配成本为N的减函数,m(N),m'<0。
假设城市空间是半径为
| $y\left( N \right) = x\left( N \right) - m\left( N \right) - c(z) - \rho (z),\;\;\;\;\;\;z \in \left[ {0,\hat z} \right]$ | (1) |
在市区半径外居住与工作的职工不支付通勤和城市地租,且假设其从事简易工作(如农业或简单的加工装配),技能匹配成本为常数
| $x\left( N \right) - m\left( N \right) - c(\hat z) = \overline x - \overline m $ | (2) |
设距离市中心为z的职工密度是
| $c\left( {\hat z} \right) = c{\left[ {N\left( {1 + \theta } \right)/k} \right]^{\lambda /\left( {1 + \theta } \right)}}$ | (3) |
式(2)和式(3)是
| $x\left( N \right) - m\left( N \right) - \left( {\overline x - \overline m } \right) = c{N^{\gamma - 1}},\;\;\text{其中:}\gamma = \frac{\lambda }{{1 + \theta }} + 1$ | (4) |
若不计匹配成本,则简化的空间均衡为
下面考察存在匹配成本时的城市均衡规模和劳动生产率。注意到
| $\left[ {\left( {{x'} - {m'}} \right) - \left( {\gamma - 1} \right)c{N^{\gamma - 2}}} \right]\frac{{dN}}{{dc}} = {N^{\gamma - 1}}$ | (5) |
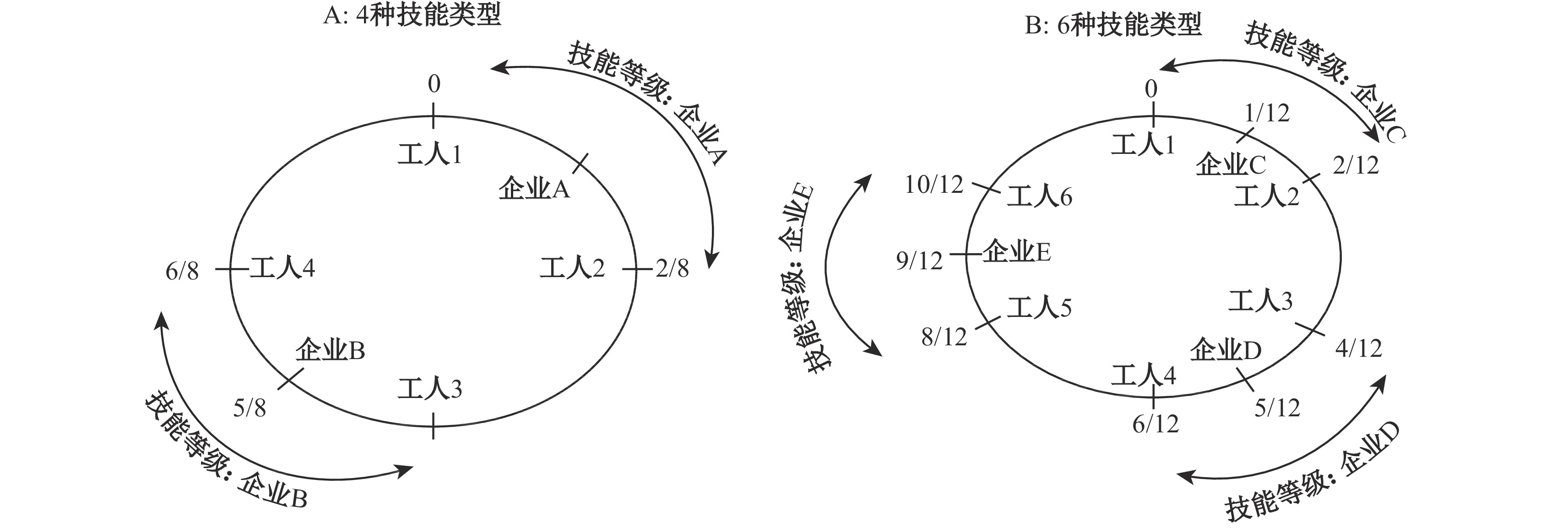
借鉴Helsley和Strange(1990)的技能空间单位圆周的表达形式(见图1),用单位圆周上均匀分布的位置表示每个厂商岗位的不同技能要求和每个劳动者的特有技能。图1A假设劳动市场中有A和B两个技术要求不同的厂商和4个具有不同技能的职工,其中工人1和工人2为厂商A所雇佣,工人3和工人4为厂商B所雇佣,平均每人的技能匹配差距为1/8。同理,图1B假设有三个企业和6名工人,技能匹配差距下降为1/12。不失一般性,劳动者技能与岗位需求技能间的差距用单位圆周上两者之间的距离μ表示,增加的匹配成本则可表示为μm(N)。
|
| 图 1 劳动技能匹配 |
设有n个企业进入市场,所以每个企业在技能空间圆周上占互不重复的1/n。在对称均衡条件下,各企业的基本工资(x)相同。假设每个企业都将为争夺技术工人而展开竞争,其有效竞争对手主要是岗位技能要求差异仅为1/n的左右两侧竞争者。工人的净收入等于工资减去匹配成本。工人都力图获得最高净收入。当与企业h的差距为μ的工人获得的工资x(h)等于从h的竞争对手获得的工资x时,可得:
| $ x\left( h \right) - \mu m\left( N \right) = x - \left( {\frac{1}{n} - \mu } \right)m\left( N \right) $ | (6) |
其中:[(1/n)–μ)]m(N)是h的竞争者雇佣该工人所增加的匹配成本。对式(6)变换整理可得:
| $\mu = \frac{1}{{{\rm{2}}n}} + \frac{1}{{{\rm{2}}m\left( N \right)}}\left[ x\left( h \right){ - x} \right]$ | (7) |
企业h将会雇佣与其技能要求差别不大于μ(μ≤1/2n)的工人,根据式(7)可得雇佣数为:
| $l\left( h \right) = 2\bar N\mu = \frac{{\bar N}}{n} + \left[ {x\left( h \right) - x} \right]\frac{{\bar N}}{{m\left( N \right)}}$ | (8) |
式(8)表明,企业h相对工资 [x(h)−x] 越高、劳动力市场
| $Y = \frac{1}{n}\left[ {Nx\left( N \right) - Nm\left( N \right) - {(N^\gamma }c/\gamma) + \left( {\bar N - N} \right)\left( {\bar x - \bar m} \right)} \right]$ | (9) |
值得注意的是,
利用式(9)对c求导得交通条件改善对产出的影响有:
| $\frac{{dY}}{{dc}} = \frac{1}{n}\left[ {N\left( {{x'} - {m'}} \right) + \left( {x(N) - m(N) - (\bar x - \bar m)} \right) - c{N^{\gamma - 1}}} \right]\frac{{dN}}{{dc}} - \frac{{{N^\gamma }}}{{n\gamma }}$ | (10) |
上式综合了交通条件通过几个途径影响劳动生产率的机制。第一,上式最后一项
第二,交通条件的改善使城市规模扩大(
第三,因为错配损失随着城市规模的增大而减小
根据方程式(4),均衡状态下的城市劳动生产率优势和城市交通成本抵消,所以式(10)中的其他各项
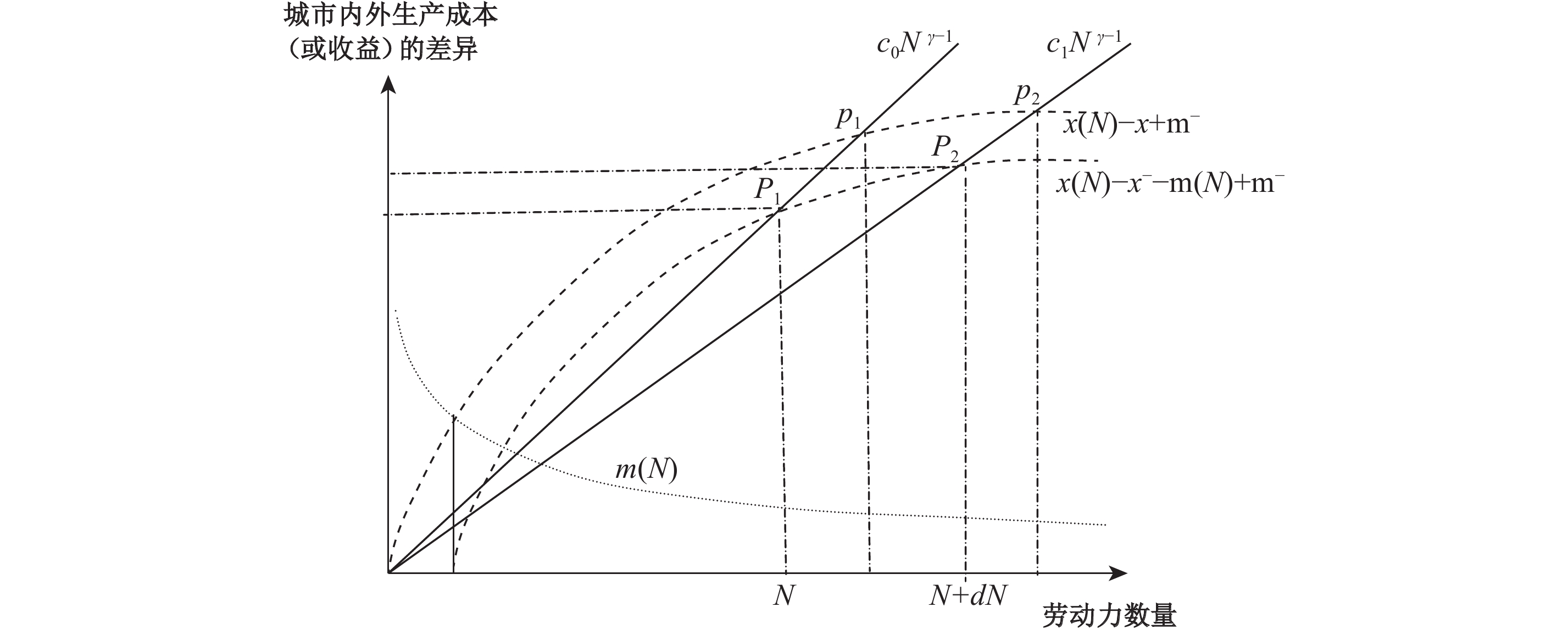
|
| 图 2 交通条件、城市规模和劳动技能匹配对生产率的影响 |
图2中的横轴和纵轴分别衡量城市规模和城市内外生产率的差别。纵轴原点表示城市外的平均净生产率,即平均生产率减去匹配成本,
四、计量模型设定与数据说明
(一)计量模型设定。根据以上分析,由于集聚经济和交通条件的改善均有助于劳动生产率的增长,城市规模、交通条件和技能匹配直接影响劳动生产率,但是技能错配会降低生产率。更为重要的是,劳动力在找工作时,城市规模和交通条件的改善会提高匹配程度;而且,给定城市规模和交通条件,企业可以通过培训投入来改善现有的技能匹配水平。因此,交通条件、城市规模和企业培训对企业生产率的直接影响和协同影响是本文考察的重点。同时需要说明,搜寻和培训是前后两个阶段的行为,其目的都是实现技能匹配,但是两者的作用可以替代(已达到技能匹配时)也可以叠加(尚未达到匹配时)。理论模型的构建过程力求刻画技能匹配机制,避免遗漏重要的相关变量,但均衡模型的最终结果不在于区分搜寻和培训所处的阶段,而在于揭示各变量对生产率的可能的贡献。计量模型检验的是均衡模型,所以城市规模、交通条件和企业培训投入变量的参数估计都是包含了上述两个阶段变化的最终结果。
为了降低估计偏误,文中还引入了其他控制变量。根据已有研究(周黎安等,2007;孙晓华和王呁,2014;钟昌标等,2015),企业生产率还与企业内部特点和外部环境的诸多因素相关,因此,计量模型引入企业规模size和年龄age,城市财政科研支出比重kn,城市每万人口中大学生数st和企业所在行业indh以及企业所在城市cityi虚拟变量作为控制变量。我们根据上述理论框架设置相应的计量模型有:
| $\begin{aligned} \ln {Y_{ijt}} = & {\beta _0} + {\beta _{\rm{1}}}\ln {C_{it}} + {\beta _2}\ln {N_{it}} + {\beta _{\rm{3}}}\ln {m_{ijt}} + {\beta _4}\ln {m_{ijt}}\ln {N_{it}} + {\beta _5}\ln {m_{ijt}}\ln {C_{it}} + {\beta _6}\ln {N_{it}}\ln {C_{it}} \\ & + {\beta _7}\ln {m_{ijt}}\ln {C_{it}}\ln {N_{it}} + {\beta _8}{\left( {\ln {N_{it}}} \right)^2} + {\beta _9}\ln {X_t} + \sum\limits_{h = 1}^H {{\lambda _h}in{d_h}} + \sum\limits_{i = 1}^n {{\lambda _i}cit{y_i}} + \sum\limits_{t = 1}^T {{\lambda _t}yea{r_t}} + {\varepsilon _{ijt}} \end{aligned}$ | (11) |
其中:各变量的下标i和j识别城市和企业,下标t是年份;被解释变量Y表示企业生产率,解释变量Ci是用路网密度表示的城市i的交通条件,Ni是用人口表示的城市i的规模,m是用企业培训投入测度的技能匹配。随后四个(组)变量是交互项。交互项参数β4和β5表示技能匹配水平分别与城市规模和交通条件对企业生产率的协同影响。第六项β6表示交通条件和城市规模对企业生产率的协同作用。交互项参数β7表示交通条件和企业培训对生产率的影响是否随着城市规模的变化而变化。已有研究发现城市生产率随非农业人口规模呈非线性变化(如,柯善咨和赵曜,2014)。为此,在计量方程(11)的基础上引入城市规模的二次项。变量Xt表示控制变量,包括企业和城市的四个连续变量以及各个行业、城市和年份的虚拟变量indh、cityi和yeart。
本文进一步分析交通条件和企业培训对不同类型产业生产率的影响。不同技术类型产业对要素和市场有不同的需求,意味着不同类型的产业偏好不同规模的城市。④为了检验交通条件与企业培训对不同产业生产率的影响是否存在城市规模差异,本文根据2014年国务院印发的《关于调整城市规模划分标准的通知》,将城市按规模划分为三类:人口<100万的中小城市用虚拟变量N1=1表示,人口介于100万和500万之间的大城市用虚拟变量N2=1表示(该变量在回归中略去),人口>500万的特大城市用虚拟变量N3=1表示,每个城市只属于一类,模型中其他两个虚拟变量值为0。重新设定的计量模型如下所示:
| $ \begin{aligned} \ln {Y_{ijt}} = & {\beta _0} + {\beta _{\rm{1}}}\ln {C_{it}} + {\beta _2}\ln {N_{it}} + {\beta _{\rm{3}}}\ln {m_{ijt}} + {\beta _4}\ln {m_{ijt}}\ln {N_{it}} + {\beta _5}\ln {m_{ijt}}\ln {C_{it}} + {\beta _6}\ln {N_{it}}\ln {C_{it}} \\ & + \sum\limits_{k = 1}^3 {\left( {{\beta _{{\rm{7k}}}}N_t^k\ln {m_{ijt}}\ln {C_{it}}} \right)} + {\beta _8}{\left( {\ln {N_{it}}} \right)^2} + {\beta _9}\ln {X_t} + \sum\limits_{h = 1}^H {{\lambda _h}in{d_h}} + \sum\limits_{i = 1}^n {{\lambda _i}cit{y_i}} + \sum\limits_{t = 1}^T {{\lambda _t}yea{r_t}} + {\varepsilon _{ijt}} \end{aligned}$ | (12) |
其中:第七项的变量Nk是城市规模类型的虚拟变量,k=1,2,3。参数β7k测度交通条件和匹配水平对第k类的城市规模中企业生产率的协同影响。
(二)变量和数据说明。本文数据来自国家统计局发布的《中国工业企业数据库》和《中国城市统计年鉴》。《中国工业企业数据库》中只有2004—2007年四年序列中报告了企业劳动培训支出数据,这成为本文时间序列的约束条件。工业企业数据库中有些指标存在异常值,本文样本剔除了职工人数、总资产或固定资产净值和销售额缺失的观测值。根据谢千里等(2008)的方法,剔除职工人数少于8人的观测值。本文还剔除了企业年龄大于100的个别可疑记录。由于工业企业数据库中各年收集的统计指标个数差别较大,本文选取在样本期间内持续存在的变量。稳健性检验还将使用被解释变量高低端各1%截尾后的样本。由于从2004年起,国家统计局不再收集工业增加值和工业总产值数据,本文参照聂辉华等(2012)的方法,根据会计准则估算,工业增加值=产品销售额−期初存货+期末存货−工业中间投入+增值税。劳动生产率用企业增加值与企业职工数的比值表示。
下面扼要说明各解释变量及其测度。方程(11)和(12)中的技能匹配水平m是本研究的关键变量。但是,对技能匹配的任何国内外研究都没有发现直接的统计数据。然而,现实中无论企业劳动技能匹配水平如何,职工培训都可以使职工劳动技能与企业需要更加匹配,从而提高生产效率,这也是企业培训投入的根本动力。企业培训投入未必和企业原技能匹配水平相关,既可能是技能匹配差的企业增加培训投入,也有可能是其他因素导致企业培训投入增加。因此,用技能培训投入表示匹配水平并不能揭示培训投入的原因,但是计量检验可以发现所有企业培训投入的平均收益。本文用每个职工平均技能培训投入(变量Match)表示匹配水平,该指标统计数据的最长时间序列为2004—2007年四年。Street是路网密度,用每平方公里建成区面积上的道路长度表示。城市规模Pop用市辖区人口表示。该变量还用于构建三个城市规模虚拟变量N1、N2和N3。企业规模Size用企业职工数测度。企业年龄Age是从注册到本研究样本年份之间的年数。高等教育St以大学在校生数占总人口的比重表示。科研环境Kn以科技支出占财政支出的比重表示。表1为这些变量的描述统计量。其中:一些企业教育培训支出(Match)为0,在取对数时,为了防止0值造成缺失记录,我们借鉴文献中惯用方法,先平移所有数据(Match +1),再取对数。
| 变量 | 均值 | 标准差 | 极小值 | 极大值 |
| Prod(企业劳动生产率,元/人) | 95 166 | 104 177 | 2 301 | 697 923 |
| TFP(全要素生产率对数值) | 3.2842 | 1.0277 | −3.5339 | 4.6493 |
| Street(路网密度,km/km2) | 8.04 | 3.62 | 1.07 | 22.40 |
| Match(培训投入,千元/人) | 0.132 | 0.62 | 0 | 61.910 |
| Pop(城市规模,万人) | 270.37 | 315.96 | 14.08 | 1 526.02 |
| Size(企业规模,人) | 243.48 | 936.10 | 8 | 108 525 |
| Age(企业年龄,年) | 8.64 | 8.79 | 1 | 99 |
| St(每万人大学生数,人/万人) | 471 | 333.96 | 1 | 2 284 |
| Kn(科技支出占财政支出比重) | 0.0149 | 0.0452 | 1.32e-06 | 0.328 4 |
五、计量检验和分析
(一)交通基础设施、城市规模和培训投入对中国企业生产率影响的计量检验。除了虚拟变量,文中变量均采用对数形式。所有模型的Hausman检验都拒绝了随机效应原假设,表明未控制的企业特征与某些解释变量相关,必须控制这些企业的固定效应(FE)才能得到一致性参数估计。此外,一些地区推行的特定产业政策影响相关产业的企业生产率,⑤ 所以回归模型引入了省份与产业固定效应的交互项(29×29个虚拟变量,其中部分变量因共线性而被自动删除)以控制地区层面的特定产业政策差异。为了检验交通条件、城市规模和技能匹配对企业生产率的影响,我们逐步引入城市路网密度、城市规模和技能匹配(用企业培训投入测度)的交互项,检验三个不同的固定效应模型。对中国诸多城市的大量企业来说,城市规模和培训投入两变量对企业生产率有独立的作用。同时,城市规模和培训投入这两个变量的变化相互作用,很可能影响各自对企业生产率的作用。如果城市人口增长显著增强了企业培训投入对生产率的作用(即交互项的计量结果是显著的正参数),根据经济学一般逻辑,城市人口规模是企业培训投入的互补因素。相反,如果城市人口增长削弱了企业培训投入对生产率的作用(交互项有显著的负参数),根据经济学逻辑,城市人口规模和企业培训投入就很可能是替代因素。我们进而推测其机制,合乎逻辑和常理的解释是,具有城市人口规模优势的企业不需要大量内部培训即可获得较好的技能匹配,而城市人口规模越小的企业越需要依靠内部培训才可获得所需的技能匹配。我们根据同样逻辑解释交通条件和技能培训交互项的实证结果。同时,为了控制城市规模可能带来的内生性问题,所有回归方程中使用城市规模滞后一期的数据。表2报告了方程(11)的FE模型估计结果。
| 1.lnprod | 2.lnprod | 3.lnprod | 4.lnprod | |
| lnStreet | 0.0776***(0.0083) | 0.0647***(0.0088) | −0.2812***(0.0315) | −0.2422***(0.0326) |
| lnMatch | 0.0029***(0.0005) | 0.0207***(0.0032) | 0.0294***(0.0032) | 0.0374***(0.0037) |
| lnStreet×lnMatch | −0.0041***(0.0008) | −0.0074***(0.0008) | −0.0096***(0.0010) | |
| lnPop×lnMatch | −0.0014***(0.0005) | −0.0014***(0.0005) | −0.0040***(0.0008) | |
| lnStreet×lnPop | 0.0653***(0.0059) | 0.0629***(0.0060) | ||
| lnPop×lnStreet×lnMatch | 0.0010***(0.0002) | |||
| lnPop | 1.6870***(0.0811) | 1.5544***(0.1246) | 1.5185***(0.0818) | 1.5041***(0.0819) |
| (lnPop)2 | −0.1493***(0.0074) | −0.1446***(0.0109) | −0.1333***(0.0075) | −0.1319***(0.0075) |
| lnSize | 0.2356***(0.0036) | 0.1850***(0.0036) | 0.2310***(0.0036) | 0.2307***(0.0036) |
| lnAge | 0.1962***(0.0045) | 0.0497***(0.0051) | 0.1841***(0.0045) | 0.1832***(0.0045) |
| lnSt | 0.1991***(0.0061) | 0.0080(0.0078) | 0.2253***(0.0065) | 0.2246***(0.0065) |
| lnKn | 0.0482***(0.0015) | 0.0449***(0.0031) | 0.0480***(0.0015) | 0.0483***(0.0015) |
| Constant | −4.2243***(0.2242) | −2.3870***(0.3535) | −3.8506***(0.2254) | −3.8592***(0.2254) |
| 地区产业差异 | 控制 | 控制 | 控制 | 控制 |
| Observations | 319 925 | 319 925 | 319 925 | 319 925 |
| R-squared | 0.1154 | 0.1155 | 0.1158 | 0.1159 |
| 注:括号内为标准误,***、**和*分别表示p<0.01、p<0.05 和p<0.1。下表同。 | ||||
我们设置和检验四个回归方程。模型1检验劳动培训效应,不含交通和培训投入的交互项。模型2加入培训投入(lnMatch)分别与交通条件(lnStreet)和城市规模(lnPop)形成交互项。根据理论分析,这两个交互项均有助于提高技能匹配。模型3加入交通条件与城市规模的交互项,检验交通条件与城市规模对企业生产率的协同作用。为了检验交通条件与培训投入对企业生产率的影响是否因城市规模而异,模型4引入城市规模与交通条件和培训投入的三重交互项(lnPop×lnStreet× lnMatch)。
我们先扼要分析控制变量。所有模型中企业规模(lnSize)的系数显著为正,表明企业规模越大,企业生产率越高。企业年龄(lnAge)的显著性说明随着企业经营时间的增加和经验的积累,企业生产率可能从“干中学”中获得增长。与预期一致,每万人中大学生数(lnSt)促进了企业生产率的提高,因为提升人力资本可以创造有利的商业环境。科研环境(lnKn)在各模型中的正参数表明在科技实力雄厚的地区,企业可以利用公共投资和技术溢出来提高生产率。
以下考察交通条件和培训投入对企业生产率的影响。模型1和2中交通条件(lnStreet)对企业生产率的影响均显著为正。培训投入(lnMatch)在各模型中的参数估计也显著为正,表明愿意为了提高职工技能配置效率而投入培训的企业能获得更高的效率。模型2是引入交通条件、城市人口规模和培训投入交互项后的估计结果。交通条件与培训投入的交互项(lnStreet× lnMatch)系数显著为负,似有违常理。但结合lnMatch的含义,这一估计结果与理论和常识相符。一方面,交通条件的改善提高了经济活动频率,减小了劳动者技能与岗位不匹配造成的损失,故而降低了技能培训的潜在收益。另一方面,技能培训缩小了劳动技能与工作岗位所需技能的差距,从而降低了交通基础设施改善匹配的收益。这说明交通条件和技能培训两者对企业生产率的作用具有一定的替代性。城市规模和培训投入交互项(lnPop × lnMatch)的负参数估计表明城市规模和培训投入之间也存在一定的替代关系,因为劳动力规模lnPop的扩大提高了职工与岗位间的技能匹配效率,从而降低了技能培训的潜在收益。模型3引入交通条件与城市规模的交互项。结果显示,交通条件的参数估计显著为负,交通条件和城市规模交互项(lnStreet×lnPop)的参数估计是0.0653,且通过显著性检验。在均值处(lnPop=5.60,lnMatch=0.0925),交通条件对企业生产率的作用弹性约为0.0837。由于城市规模的一次项和二次项系数一正一负,结果还是表明交通条件的改善有助于扩大城市最优规模。⑥
模型4检验交通条件与培训投入对企业生产率的协同作用是否因城市规模不同而异。由于lnStreet×lnMatch的参数显著为负,而交互项lnPop×lnStreet×lnMatch的系数显著为正,因而随着lnPop的增加,lnStreet×lnMatch会逐渐变小。该结果意味着城市交通与技能培训间的替代效应因城市规模大小而异,城市劳动力市场规模越大,技能匹配越好,城市交通与技能培训替代效应也越小。
(二)交通条件、城市规模和培训投入对不同技术行业和不同规模城市企业生产率的影响。不同产业具有各自的技术特点。本节根据《高技术产业统计分类目录》和OECD产业分类标准划分高、中、低技术三类产业,附表1列出了每类包含的两位码行业。高技术产业技术含量高,技术更新快,产品附加值高,需要专业知识型劳动者,同时必须支付较高的薪酬;相反,低技术产业倾向于采用成熟和稳定的技术,雇工进行更多的常规生产,职工的薪酬也相对较低;中等技术产业的技术含量则介于高、低技术产业之间。各类产业因技术特征和对要素投入的要求不同而有不同的区位偏好。大城市具有较大的专业劳动力市场和产品市场、较完整的上下游相关产业和较迅速的技术信息传播,因而成为高技术产业的首选之地,而中小城市则因土地和一般劳力等要素价格较低而成为低技术产业的集聚地。交通条件的改善不仅有利于产品运输和信息传播,也有利于劳动力流动。表3报告了方程(12)的分产业固定效应回归结果。
| 高技术 | 中技术 | 低技术 | |
| lnStreet | −0.6262***(0.2177) | −0.0732(0.0764) | −0.1718*(0.0934) |
| lnMatch | 0.0298(0.0264) | 0.0507***(0.0079) | 0.0445***(0.0095) |
| lnStreet×lnMatch | −0.0054(0.0035) | −0.0092***(0.0011) | −0.0059***(0.0013) |
| lnPop×lnMatch | −0.0145***(0.0047) | −0.0049***(0.0015) | −0.0049***(0.0018) |
| lnStreet×lnPop | 0.1154***(0.0399) | 0.0213(0.0145) | 0.0494***(0.0181) |
| N1×lnStreet×lnMatch | −0.0079** (0.0033) | −0.0027***(0.0009) | 0.0013 (0.0010) |
| N3×lnStreet×lnMatch | 0.0079** (0.0035) | 0.0036***(0.0011) | 0.0016 (0.0014) |
| lnPop | 2.6191***(0.5507) | 1.9522***(0.1782) | 2.3910*** (0.1975) |
| (lnPop)2 | −0.2309***(0.0474) | −0.1581***(0.0154) | −0.2057*** (0.0173) |
| lnSize | 0.2272***(0.0157) | 0.2535*** (0.0049) | 0.1988***(0.0057) |
| lnAge | 0.1257***(0.0187) | 0.1576***(0.0062) | 0.2294*** (0.0074) |
| lnSt | 0.2243***(0.0278) | 0.2364***(0.0091) | 0.2122*** (0.0104) |
| lnKn | 0.0304***(0.0056) | 0.0520***(0.0020) | 0.0446*** (0.0024) |
| Constant | −6.8244***(1.5889) | −5.5849***(0.5126) | −6.1113*** (0.5609) |
| 地区产业差异 | 控制 | 控制 | 控制 |
| Observations | 22 825 | 174 415 | 122 685 |
| R-squared | 0.1205 | 0.1032 | 0.1010 |
| MEM1 | 0.0031 | 0.0378 | 0.0812 |
| MEM2 | 0.0042 | 0.0381 | 0.0811 |
| MEM3 | 0.0052 | 0.0385 | 0.0812 |
| 分类 | 产业(SIC代码) |
| 高技术产业 | 核燃料加工(2530)、信息化学品制造(2665)、医药制造业(27)、医疗仪器设备及器械制造(368)、航空航天器制造(376)、通信设备、计算机及其他电子设备制造业(40)、通用仪器仪表制造(411)、专用仪器仪表制造(412)、光学仪器制造(4141)、复印和胶印设备制造(4154)、计算器及货币专用设备制造(4155)、其他仪器仪表的制造及修理(4190) |
| 中技术产业 | 文教体育用品制造业(24)、化学原料及化学制品制造业(26,不含信息化学品制造2665)、化学纤维制造业(28)、塑料制品业(30)、非金属矿物制品业(31)、有色金属冶炼及压延加工业(33)、金属制品业(34)、通用设备制造业(35)、专用设备制造业(36,除医疗仪器设备及器械制造368)、交通运输设备制造业(37,除航空航天器制造376)、电气机械及器材制造业(39)、眼镜制造(4142)、文化、办公用机械制造(415,除复印和胶印设备制造4154、计算器及货币专用设备制造4155)、工艺品及其他制造业(42) |
| 低技术产业 | 农副食品加工业(13)、食品制造业(14)、饮料制造业(15)、烟草制品业(16)、纺织业(17)、纺织服装鞋帽制造业(18)、皮革、毛皮、羽毛(绒)及其制品业(19)、木材加工及木竹藤棕草制品业(20)、家具制造业(21)、造纸及纸制品业(22)、印刷业和记录媒介的复制(23)、石油加工、炼焦及核燃料加工业(25,不含核燃料加工2530)、橡胶制品业(29)、黑色金属冶炼及压延加工业(32)、废弃资源和废旧材料回收加工业(43) |
为了测度交通条件和培训投入的协同作用在特大、大、中小三个规模等级城市组间的差异化影响,三类产业方程都引入了城市规模虚拟变量(N1和N3)与lnStreet×lnMatch交互项。所有方程的估计结果都显示,高、中、低技术产业的控制变量(lnSize,lnAge,lnSt,lnKn)与表2中总体样本模型的控制变量参数估计本质上非常相似。下面着重分析三类产业模型的交通条件、培训投入和城市规模及其交互项的计量估计结果。
三类技术产业的三个培训投入参数估计表明,企业培训对中低技术产业的生产率有促进作用,而对高技术产业的生产率影响不显著。估计结果意味着中低技术产业的职工经过企业培训较易掌握本企业所需的技能,而高技术产业的技术密集度和复杂程度较高,企业技能培训未必产生立竿见影的效果。交通条件、城市规模和培训投入交互项的参数估计与表2基本一致。城市规模虚拟变量(N1和N3)和lnStreet×lnMatch的交互项一负一正,且在中、高技术产业通过了显著性检验,表明交通条件对中小城市中、高技术产业技能培训的替代作用明显高于大城市。而在低技术产业则未通过显著性检验,表明交通条件和技能培训对低技术产业生产率的影响并不存在城市规模差异。
表3中的MEM1、MEM2和MEM3分别给出了培训投入均值处(
(三)稳健性检验。为了检验上述结论的稳健性,我们用厂商全要素生产率TFP替换劳动生产率重估上述模型。虽然劳动生产率的差别是TFP差别的重要决定因素,但是其他要素(例如资本)的效益差别也影响着TFP,所以我们主要关注两组方程参数估计值的正负和显著性,而非每个估计值的大小。TFP可以用不同的方法测度。鲁晓东和连玉君(2012)分析和比较了TFP的最小二乘估计、固定效应估计、OP估计和LP估计,发现最小二乘法和固定效应估计法都不能解决同时性偏差问题,而OP估计无法处理投资额为0的样本。因而,本文使用LP法估计企业的全要素生产率。实证结果可能受一些极端值的影响,为检验上述方程的稳健性,我们还使用被解释变量lntfp高低端各1%截尾样本重估方程。表4报告了交通条件和企业培训对全国所有制造业和三类技术产业企业生产率影响的估计结果。
| 全国样本 | 高技术行业 | 中技术行业 | 低技术行业 | |
| lnStreet | −0.1999***(0.0524) | −0.6708***(0.2090) | −0.1833**(0.0724) | −0.2437***(0.0883) |
| lnMatch | 0.0306***(0.0035) | 0.0204(0.0253) | 0.0402***(0.0075) | 0.0338***(0.0090) |
| lnStreet×lnMatch | −0.0095***(0.0009) | −0.0054(0.0033) | −0.0090***(0.0011) | −0.0058***(0.0013) |
| lnPop×lnMatch | −0.0033***(0.0007) | −0.0102**(0.0045) | −0.0029**(0.0014) | −0.0029*(0.0017) |
| lnStreet×lnPop | 0.0505***(0.0100) | 0.1267***(0.0383) | 0.0408***(0.0137) | 0.0594***(0.0171) |
| lnPop×lnStreet×lnMatch | 0.0009***(0.0002) | |||
| N1×lnStreet×lnMatch | −0.0036(0.0034) | −0.0022**(0.0009) | 0.0004(0.0010) | |
| N3×lnStreet×lnMatch | 0.0063**(0.0031) | 0.0026**(0.0011) | 0.0010(0.0014) | |
| lnPop | 2.2784***(0.1200) | 2.1709***(0.5276) | 2.0482***(0.1688) | 2.5843***(0.1867) |
| (lnPop)2 | −0.1923***(0.0104) | −0.1922***(0.0454) | −0.1679***(0.0146) | −0.2233***(0.0164) |
| lnSize | 0.3133***(0.0034) | 0.3623***(0.0150) | 0.3377***(0.0046) | 0.2723***(0.0053) |
| lnAge | 0.2078***(0.0043) | 0.1715***(0.0179) | 0.1818***(0.0059) | 0.2547***(0.0070) |
| lnSt | 0.2417***(0.0063) | 0.2416***(0.0266) | 0.2574***(0.0086) | 0.2178***(0.0098) |
| lnKn | 0.0397***(0.0014) | 0.0240***(0.0054) | 0.0451***(0.0019) | 0.0337***(0.0023) |
| Constant | −4.5072***(0.3443) | −4.4005***(1.5226) | −4.2274***(0.4858) | −4.7296***(0.5303) |
| 地区产业差异 | 控制 | 控制 | 控制 | 控制 |
| Observations | 313 526 | 22 368 | 170 927 | 120 231 |
| R-squared | 0.1541 | 0.1128 | 0.1624 | 0.1493 |
与前节回归结果相比,所有控制变量参数估计比较稳定。企业培训对全国企业TFP有显著的正向作用(lnMatch>0);交通条件和城市规模对企业培训具有替代作用(lnStree× lnMatch <0,ln Pop× lnMatch <0);城市劳动力市场规模的扩大,提高劳动技能匹配水平,降低城市交通对技能培训的替代效应(ln Pop×lnStreet×lnMatch>0;N1×lnStreet× lnMatch<0;N3×lnStreet× lnMatch>0)。
(四)企业培训内生性检验。企业培训支出有利于提高生产率,而企业培训支出也可能取决于生产率水平,企业培训可能具有内生性。现实中,生产率高的企业有更多的财力进行企业职工培训,而生产率低的企业则在提高职工技能上有更强烈的紧迫感。因此,两类企业在技能培训方面的内生性有正负抵消的趋势。无论内生性是正或是负,因为企业今年的生产率很难影响去年的培训支出,使用滞后一期的技能培训能进一步削弱内生影响。表5报告了估计结果,其中滞后一期变量加前缀“L.”标识。
| 全国样本 | 高技术行业 | 中技术行业 | 低技术行业 | |
| lnStreet | −0.1835***(0.0347) | −0.1381(0.1321) | −0.2287***(0.0471) | −0.1162**(0.0582) |
| L.lnMatch | 0.6002***(0.2144) | 1.0832(0.7378) | 0.4133(0.2825) | 0.8070**(0.4012) |
| lnStreet×l. lnMatch | −0.2596**(0.1039) | −0.4622(0.3555) | −0.2072(0.1349) | −0.3663*(0.1980) |
| lnPop×l.lnMatch | −0.1119***(0.0396) | −0.2067*(0.1253) | −0.0551(0.0521) | −0.1871**(0.0771) |
| lnStreet×lnPop | 0.0441***(0.0066) | 0.0273(0.0242) | 0.0546***(0.0089) | 0.0305***(0.0113) |
| lnPop×lnStreet×l.lnMatch | 0.0046**(0.0019) | |||
| N1×lnStreet×l.lnMatch | −0.0103(0.0117) | −0.0080***(0.0028) | −0.0013(0.0075) | |
| N3×lnStreet×l.lnMatch | 0.0098**(0.0046) | 0.0060**(0.0024) | 0.0020(0.0030) | |
| lnPop | 1.3976***(0.1223) | 1.4406***(0.1759) | 1.3378**(0.5559) | 1.4099***(0.1829) |
| (lnPop)2 | −0.1141***(0.0107) | −0.1149***(0.0153) | −0.1177**(0.0480) | −0.1164***(0.0162) |
| lnSize | 0.1795***(0.0042) | 0.2044***(0.0179) | 0.1999***(0.0058) | 0.1489***(0.0066) |
| lnAge | 0.2179***(0.0062) | 0.1928***(0.0251) | 0.1936***(0.0084) | 0.2577***(0.0099) |
| lnSt | 0.0891***(0.0079) | 0.1161***(0.0346) | 0.0869***(0.0110) | 0.0810***(0.0121) |
| lnKn | 0.0560***(0.0014) | 0.0348***(0.0053) | 0.0622***(0.0019) | 0.0507***(0.0023) |
| Constant | −2.4333***(0.3413) | −2.5267(1.5654) | −2.7544***(0.4932) | −2.1705***(0.5054) |
| 地区产业差异 | 控制 | 控制 | 控制 | 控制 |
| Observations | 239 423 | 17 112 | 130 205 | 92 106 |
| R-squared | 0.1121 | 0.1084 | 0.1087 | 0.1096 |
在总样本模型中,企业培训的一次项为正,与交通条件和城市规模交互项的参数估计显著为负,分别为−0.2596和−0.1119。分行业估计结果与总体模型相类似,仅显著性有所降低。总体而言,使用企业培训滞后一期的估计结果与基准回归结果的性质一致。
六、结论与启示
本文将拓展了Venables(2007)的理论模型,利用全国工业企业数据库和城市数据检验交通条件、城市规模和企业培训对企业生产率的影响。检验结果显示:交通条件、城市规模和企业培训均有助于提高企业生产率;改善交通条件和扩大城市规模能弱化技能培训投入对企业生产率的影响。对高、中、低技术产业的计量检验发现:交通条件和企业培训对企业生产率的影响存在着行业差异和城市规模差异。改善交通条件有助于提高特大城市高技术产业企业的生产率,吸引高技术产业向特大城市集聚,同时低技术产业企业应从特大城市向其他城市转移。
本文的研究结果为制定和评价区域发展和结构调整政策提供了若干实证依据。首先,在中国,很少有企业具备正规的培训体系或对职工培训进行充分的投资。因此,各地和各行业主管部门应制定和实施优惠政策、鼓励企业增加培训支出。其次,落后地区在城市化进程中应努力改善城市公共交通基础设施,促进劳动力流动。在国家人口规模和土地资源有限的情况下,应优先发展中等规模的城市以接近最优规模,扩大城市劳动力市场,纠正劳动市场技能错配。其三,随着各地交通条件的普遍改善,高技术产业具有向特大城市集聚、低技术产业从特大城市向其他城市转移的内在趋势,这在我国各地经济结构的调整中具有积极意义。各地区在产业结构调整中应根据各自产业特点和城市规模因势利导,减少阻力,积极引进(和迁出)相关产业,促使大城市成为高技术产业中心,同时引导其他城市成为生产成本较低、产出效率较高的成熟产业的基地。
① 数据来源于《中国城市统计年鉴》和《2016智能出行大数据报告》。
② 中国企业报道:http://www.ceccen.com/toutia oxinwen/1458701214.html;搜狐网、商务部网站。
③
④ 高新技术产业需要大量高技能人才和便利的交通和信息交往,因此往往集聚在大城市。技术成熟的传统产业需要成本较低的土地、原材料和一般劳动力,因而偏好在要素成本较低的二、三线城市。
⑤ 例如,国务院关于印发“十三五”国家战略性新兴产业发展规划的通知指出,山东半岛城市群重点发展生物医药、高端装备制造、新一代信息技术、新材料等产业,而福建重点发展海峡西岸地区生物、海洋、集成电路等产业,以及东北地区大力发展机器人及智能装备、光电子、生物医药及医疗器械等产业。
⑥ 令含城市人口规模的各项lnPop、lnPop×lnMatch、lnStreet×lnPop、lnPop×lnStreet× lnMatch和lnPop二次项的系数分别为a1、a2、a3、a4和b,则城市最佳规模的一阶条件为(a1+a2lnMatch+a3lnStreet+a4lnMatch×lnStreet)/(-2b)。由于回归结果中,a3和a4的参数估计均显著为正、b显著为负,故lnStreet值越大,城市最优规模也越大。
⑦ 高技术行业中交通条件和技能培训交互项(lnStreet× lnMatch)的t=1.55(即P=0.121,否定零假设的概率87.9%),所以参数估计有一定意义。
| [1] | 柯善咨, 赵曜. 产业结构、城市规模与中国城市生产率[J]. 经济研究, 2014(4): 76–88,115. DOI:10.3969/j.issn.1673-291X.2014.04.034 |
| [2] | 柯善咨, 郑腾飞. 中国城市车辆密度、劳动生产率与拥堵成本研究[J]. 中国软科学, 2015(3): 65–79. DOI:10.3969/j.issn.1002-9753.2015.03.007 |
| [3] | 林理升, 王晔倩. 运输成本、劳动力流动与制造业区域分布[J]. 经济研究, 2006(3): 115–125. DOI:10.3969/j.issn.1005-913X.2006.03.047 |
| [4] | 鲁晓东, 连玉君. 中国工业企业全要素生产率估计: 1999—2007[J]. 经济学(季刊), 2012(2): 541–558. |
| [5] | 聂辉华, 江艇, 杨汝岱. 中国工业企业数据库的使用现状和潜在问题[J]. 世界经济, 2012(5): 142–158. |
| [6] | 孙晓华, 王昀. 企业规模对生产率及其差异的影响——来自工业企业微观数据的实证研究[J]. 中国工业经济, 2014(5): 57–69. |
| [7] | 谢千里, 罗斯基, 张轶凡. 中国工业生产率的增长与收敛[J]. 经济学(季刊), 2008(3): 809–826. |
| [8] | 张光南, 宋冉. 中国交通对" 中国制造”的要素投入影响研究[J]. 经济研究, 2013(7): 63–75. DOI:10.3969/j.issn.1002-5863.2013.07.030 |
| [9] | 赵勇, 白永秀. 中国城市群功能分工测度与分析[J]. 中国工业经济, 2012(11): 18–30. |
| [10] | 钟昌标, 黄远浙, 刘伟. 外资进入速度、企业异质性和企业生产率[J]. 世界经济, 2015(7): 53–72. |
| [11] | 周黎安, 张维迎, 顾全林, 等. 企业生产率的代际效应和年龄效应[J]. 经济学(季刊), 2007(4): 1297–1318. |
| [12] | Brandt L, Luhang W, Yifan Z. Productivity in Chinese industry: 1998-2013[J]. Working Paper, 2017. |
| [13] | Duranton G, Puga D. Micro-foundations of urban agglomeration economies[J]. Handbook of Regional and Urban Economics, 2004, 4: 2063–2117. DOI:10.1016/S1574-0080(04)80005-1 |
| [14] | Duranton G, Puga D. From sectoral to functional urban specialisation[J]. Journal of Urban Economics, 2005, 57(2): 343–370. DOI:10.1016/j.jue.2004.12.002 |
| [15] | Gautier P A, Zenou Y. Car ownership and the labor market of ethnic minorities[J]. Journal of Urban Economics, 2010, 67(3): 392–403. DOI:10.1016/j.jue.2009.11.005 |
| [16] | Gollin D, Rogerson R. Productivity, transport costs and subsistence agriculture[J]. Journal of Development Economics, 2014, 107: 38–48. DOI:10.1016/j.jdeveco.2013.10.007 |
| [17] | Graham D J. Variable returns to agglomeration and the effect of road traffic congestion[J]. Journal of Urban Economics, 2007, 62(1): 103–120. DOI:10.1016/j.jue.2006.10.001 |
| [18] | Graham D J, Gibbons S, Martin R. Transport investment and the distance decay of agglomeration benefits[R]. Centre for Transport Studies, 2009. |
| [19] | Helsley R W, Strange W C. Matching and agglomeration economies in a system of cities[J]. Regional Science and Urban Economics, 1990, 20(2): 189–212. DOI:10.1016/0166-0462(90)90004-M |
| [20] | Marshall A. Principles of economics: An introductory volume[M]. London: Macmillan, 1890. |
| [21] | Phillips D C. Getting to work: Experimental evidence on job search and transportation costs[J]. Labour Economics, 2014, 29: 72–82. DOI:10.1016/j.labeco.2014.07.005 |
| [22] | Tikoudis I, Sundberg M, Karlström A. The effects of transport infrastructure on regional economic development: A simu- lated spatial overlapping generations model with heterogenous skill[J]. Journal of Transport and Land Use, 2012, 5(2): 77–101. |
| [23] | Torfs W, Zhao L Q. Everybody needs good neighbors? Labor mobility costs, cities and matching[J]. Regional Science and Urban Economics, 2015, 55: 39–54. DOI:10.1016/j.regsciurbeco.2015.08.005 |
| [24] | Venables A J. Evaluating urban transport improvements: Cost-benefit analysis in the presence of agglomeration and income taxation[J]. Journal of Transport Economics and Policy, 2007, 41(2): 173–188. |


