一、引　言

2008年国际金融危机以来，各国宏观调控重拾相机抉择范式。美国迅速调整政策导向，相机实施了多轮量化宽松政策，有力支持了经济复苏。时至今日，学术界对于相机抉择和事前承诺范式孰优孰劣仍莫衷一是，但相机调控的灵活性和针对性较强，这对于经济走出衰退泥潭无疑具有重要作用。2017年中国《政府工作报告》中关于货币政策的表述首次强调要加强相机调控，2018年国务院常务会议再次重申宏观政策要根据形势变化相机预调微调。在经济传导机制梗阻和政策目标多元化背景下，相机调控符合中国当前的国情（陈彦斌，2016）。

多数研究认为，按规则行事蕴含一种事前承诺机制，使得货币政策可信度较高，从而有助于稳定公众预期，促进经济稳定。只有少数学者如Blanchard和Fischer（1989）认为相机抉择可能比动态一致解更有效率。自20世纪90年代货币政策透明度研究兴起以来，规则似的或受约束的相机货币政策概念开始出现。Svensson（1999）认为，在实现事先确定的目标时，通胀目标制允许央行相机抉择，从而将规则和相机抉择的优点结合起来。特别是在2008年金融危机后，许多学者建议放宽通胀目标制的目标区间，以增大货币政策的相机抉择灵活性和操作空间。卞志村和高洁超（2015）发现，相机型规则有利于产出缺口稳定，而承诺型规则有利于通货膨胀稳定，两者各有优劣。程均丽（2010）认为，在异质性预期下，受约束的相机政策或相机式规则要优于承诺。近年来，各国货币政策表现出越来越明显的相机抉择倾向（Taylor，2014）。本文将基于新凯恩斯模型刻画货币政策的相机抉择和事前承诺范式，深入系统地评价两者的经济稳定效应，识别符合中国现实经济运行要求的货币政策范式。研究发现，一定约束条件下的相机抉择型政策可以产生比事前承诺政策更佳的经济稳定效果，尤其是在利率调整上的灵活性优势更加突出。

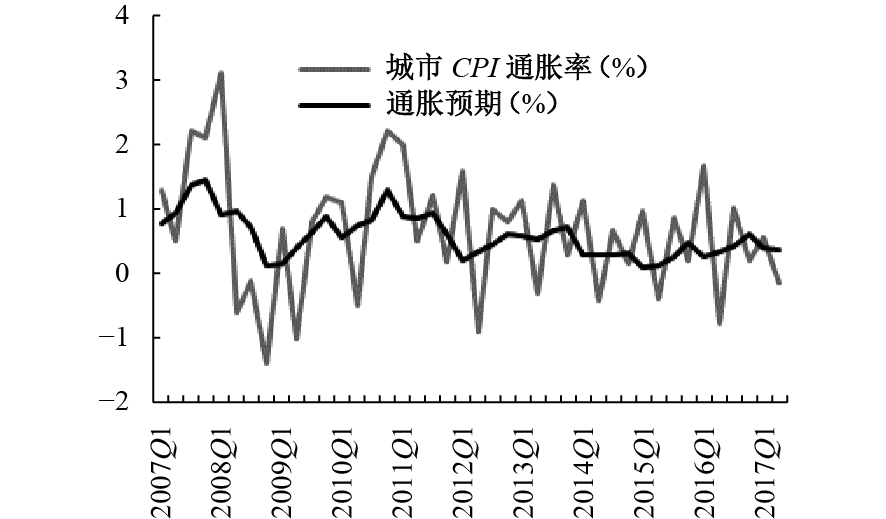
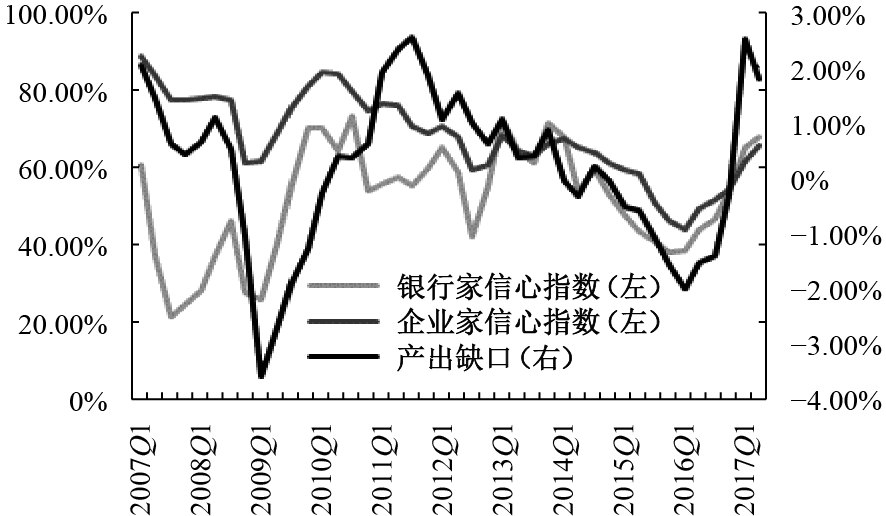
国内外已有相关文献大多采用基于理性预期假设的新凯恩斯框架进行分析。而中国作为一个新兴转轨国家，在经济结构调整、经济波动不确定性增加以及市场摩擦广泛存在的背景下，不同主体的预期存在显著差别，且预期的整体理性程度尚待提高。基于理性预期假设的货币政策分析所得结论显然难以适用于目前的现实。从图1中可以发现，公众预期尽管能捕捉到实际通胀走向，但是在诸多节点上预测误差很大，我国居民的预期总体来看具有保守的适应性特征，现实的公众预期并非完全理性。^①图2显示，企业家的宏观经济信心指数的波动性明显低于银行家，而平均水平高于银行家。以产出缺口来衡量经济周期波动，可以发现银行家和企业家对宏观经济形势冷热的预期能够大致捕捉到经济周期波动的基本趋势，但准确度不高。比如，2014年底产出缺口就转入持续的负区间，银行家信心指数迟滞1个季度后相应降至50%以下，但企业家信心指数降至50%以内则多迟滞了3个季度。因此，单纯采用基于理性预期假设的新凯恩斯模型来研究中国货币政策问题尚不合时宜。本文将包含理性和适应性特征的异质性预期引入三部门DSGE模型中，比较理性预期和异质性预期下货币政策范式的经济稳定效应，使分析更加贴近中国现实。^②

注：图1中的通胀预期由C-P概率法计算得到，具体参见卞志村和张义（2012），所需信息来自中国人民银行的《城镇储户问卷调查报告》。图2中的信心指数反映银行家和企业家对本季度和下个季度宏观经济形势的自信程度，数值在50%以上反映预期宏观经济向好，反之则表示预期经济形势变差，数据来自中国人民银行的企业家调查问卷和银行家调查问卷。

自Muth（1961）、Lucas（1972）以及Sargent和Wallace（1976）等倡导理性预期革命以来，理性预期假设被广泛运用于宏观经济学研究。但理性预期假说过分强调公众预期的理性化，与诸多经验证据并不吻合。Branch（2004）以及Branch和Evans（2011）认为经济主体的预期并非是理性的同质预期，Cowan等（2009）也认为通胀预期的异质性广泛存在于各私人部门。许多实证研究发现理性预期假设难以解释现实中通胀预期的有限理性特征，公众预期同时包含理性预期和适应性预期成分（Pfajfar和Zakelj，2011；Hommes等，2015；肖争艳和陈彦斌，2004；刘凤良等，2012）。Orphanides和Williams（2005）指出异质性预期会延长经济波动的周期。Huang等（2009）在新凯恩斯模型中同时引入理性预期和适应性预期机制，发现相对于理性预期，适应性预期会放大技术冲击所引起的经济波动。随着市场化程度的不断提高，货币政策的实施效果越来越有赖于经济主体能否形成较为理性的一致预期，经济主体通过适应性形成的有限理性预期应被视作制定货币政策的基本要素（Sargent，1993）。

国内学者对有限理性预期下的货币政策定量研究起步较晚。卞志村和高洁超（2014）以及郭豫媚和周璇（2018）通过引入适应性学习过程，放松了新凯恩斯模型的理性预期假设，并分析了有限理性预期下货币政策调控的有效性问题。但他们对适应性学习机制中关键学习参数的设定具有一定的主观性，难以准确反映现实经济的理性程度和异质性情况。许志伟等（2015）利用实际数据估计了包含理性预期和适应性预期的异质性新凯恩斯模型，发现公众预期中的适应性成分较高，有限理性的异质性预期使通货膨胀对货币政策反应的敏感性减弱、持久性提高。杨源源等（2017）也发现异质性预期比理性预期更容易放大总供给和总需求冲击，并引致较大的央行福利损失；此外，他们还进一步比较了数量型和价格型货币政策工具的调控效果。这些文献拓展了异质性预期在新凯恩斯模型中的应用，但普遍存在货币政策仍采用外生规则形式、忽视货币当局的最优决策范式的影响等问题。为此，本文基于货币当局损失函数、动态IS曲线约束和NKPC约束，利用最优化方法推导出内生利率规则，并将其分解为相机抉择和事前承诺两种范式。模拟分析表明，预期的理性程度提高总体上可以改进福利，但我国当前的公众预期中仍存在较明显的适应性成分，其比例达到32%；在此条件下，货币政策不宜盲目转向事前承诺范式，否则可能导致宏观政策的经济稳定效果减弱、引起更大的福利损失，这一点被已有的货币政策范式研究所忽略。

随着供给侧结构性改革的持续推进，中国经济增长的引擎将由过去的外需和投资拉动逐渐转向创新驱动，因此经济波动中的需求冲击贡献和供给冲击贡献将此消彼长，这一变化是否会对货币政策的经济稳定效果产生影响？货币政策应如何做出相应调整？对此，本文将在货币政策范式分析中引入这两类冲击，识别相应的经济波动效应。此外，当前中国货币政策框架的一个重要调整是一改过去多年来的稳健基调，2016年底召开的中央经济工作会议首次提出“货币政策要保持稳健中性”。^③除了延续以往的稳健基调外，这一调整着重强调了货币政策的中性立场。从货币理论来看，中性货币政策要求维持政策利率在自然利率水平附近，避免利率政策本身的过度调整影响经济自主配置资源。因此，与以往的货币政策基调相比，稳健中性要求将货币政策自身调整这一因素纳入货币政策设计中，防止政策调整幅度过大影响经济金融稳定。

关于最优货币政策规则的现有研究普遍没有考虑利率调整成本及其变动可能对金融稳定造成的影响，因而所得结论难以适应未来货币政策稳健中性的取向。Woodford（2012）提出，除了产出缺口和通胀外，央行损失函数还应包括能够反映金融稳定的某种衡量指标。部分文献注意到利率波动可能对金融稳定造成影响，从而稳定利率可作为货币政策维护金融稳定的一个渠道。为此，本文在推导相机抉择和事前承诺范式时，通过将利率目标引入中央银行损失函数中，刻画包含中性基调的货币政策范式，并模拟分析范式和基调转变的经济稳定效应，为完善中国货币政策框架提供有价值的参考。研究发现，货币政策应考虑稳定利率这一因素，保持稳健中性基调可防止不必要的利率扰动影响金融稳定，从而大幅降低福利损失。这也从理论上支持了2016年中央经济工作会议提出的“货币政策要保持稳健中性”基调的科学性。

二、模型构建

本文将构建一个包含家庭、企业和货币当局在内的三部门DSGE模型。其中，家庭提供劳动，消费商品并进行储蓄；中间品企业雇佣劳动进行生产，并出售给最终品企业；货币当局的目标是使包含产出缺口波动、通胀波动和利率波动的三因素损失函数最小，通过在动态IS曲线约束和NKPC约束下最优化其利率调控规则来熨平经济金融波动。此外，模型中的预期机制分别基于理性预期和异质性预期来刻画，以比较不同预期形成机制下货币政策调控效果的变化情况。

（一）家庭。假定经济中存在连续统的家庭，他们消费、储蓄并向企业提供劳动。家庭的效用函数和预算约束如下：

其中， $\beta $ 为主观贴现因子， ${C_t}$ 为消费， $\varsigma $ 为消费跨期替代弹性的倒数， ${N_t}$ 为劳动， $\gamma $ 为劳动供给弹性的倒数， ${D_t}$ 为储蓄， $R_t^D$ 为无风险的储蓄毛利率， ${\Pi _t}$ 包括企业的经营利润和家庭支付的税收等。

在预算约束下最大化家庭效用函数，可得最优跨期消费和最优劳动供给的一阶条件 ${E_t}\displaystyle\frac{{{P_t}C_{t + 1}^{ - \varsigma }}}{{{P_{t + 1}}}} = \displaystyle\frac{{C_t^{ - \varsigma }}}{{\beta R_t^D}}$ 和 $\displaystyle\frac{{{W_t}}}{{{P_t}}} = N_t^\gamma C_t^\varsigma $ ，经对数线性化处理后可得：

其中， ${\hat X_t}$ 表示变量 ${X_t}$ 对自身稳态的偏离， ${\pi _t}$ 为通货膨胀率。由于本文的模型不考虑投资和资本，均衡状态下有 ${\hat c_t} = {\hat y_t}$ ，将其代入（3）式可得反映经济总需求的动态IS曲线：

其中， ${d_t} = {\rho _d}{d_{t - 1}} + {\sigma _d}\varepsilon _t^d$ ， $\varepsilon _t^d\sim iidN(0, 1)$ ，表示经济的总需求冲击。假设货币当局通过利率调控直接影响无风险储蓄利率，则有 $\hat R_t^D = {\hat i_t}$ 。

（二）企业

1. 最终品企业。假设最终品市场为完全竞争结构，代表性的最终品企业购买中间品 ${Y_{j, t}}$ 来生产最终品： ${Y_t} = {\left( {\int_0^1 {Y_{j, t}^{\frac{{\theta - 1}}{\theta }}dj} } \right)^{\frac{\theta }{{\theta - 1}}}}$ ，其中 $\theta > 1$ 表示各种中间品之间的不变替代弹性，中间品需求函数为 ${Y_{j, t}} = {\left( {\displaystyle\frac{{{P_{j, t}}}}{{P{}_t}}} \right)^{ - \theta }}{Y_t}$ 。由零利润条件可得最终品价格方程： ${P_t} = {\left( {\int_0^1 {P_{j, t}^{1 - \theta }dj} } \right)^{\frac{1}{{1 - \theta }}}}$ 。

2. 中间品企业。假设中间品市场为垄断竞争结构，由区间 $\left( {0, 1} \right)$ 上的连续统企业构成，忽略短期内资本存量的影响，假设代表性企业的生产函数为 ${Y_{j, t}} = {A_t}{N_{j, t}}$ ，其中 ${A_t}$ 为中性技术。厂商通过选择劳动要素来最小化成本函数 $\left( {\displaystyle\frac{{{W_t}}}{{{P_t}}}} \right){N_{j, t}} - {\lambda _{j, t}}({Y_{j, t}} - {A_t}{N_{j, t}})$ ，其中 ${\lambda _{j, t}}$ 为拉格朗日乘子。通过优化求解可得企业的真实边际成本： $M{C_{j, t}} = \displaystyle\frac{{{W_t}}}{{{P_t}{A_t}}}$ 。

采用Calvo（1983）的黏性价格假设，假定每一期有 $ 1 - \omega $ 比例的企业可以重新调整产品价格。价格总水平按 $P_t^{1 - \theta } = \left( {1 - \omega } \right){\left( {P_t^*} \right)^{1 - \theta }} + \omega {\left( {{P_{t - 1}}} \right)^{1 - \theta }}$ 的形式演进，其中 $P_t^*$ 表示所有在 $t$ 期可以最优化其产品价格的企业重新选择的价格，通过优化求解可得最优价格 $P_t^*$ 的欧拉方程：

对价格总水平演进方程和（6）式进行对数线性化处理，可得反映经济总供给的新凯恩斯菲利普斯曲线（NKPC）：

其中， ${s_t} = {\rho _s}{s_{t - 1}} + {\sigma _s}\varepsilon _t^s$ ， $\varepsilon _t^s\sim iidN(0, 1)$ ，表示经济的总供给冲击， $\delta = \left( {\varsigma + \gamma } \right)\left( {1 - \omega } \right)\left( {1 - \beta \omega } \right)/\omega $ 。

（三）货币当局。与多数DSGE文献直接给定利率规则的表达式不同，本文在经济的总需求约束（动态IS曲线）和总供给约束（NKPC）下，通过优化方法推导货币当局的最优利率规则。传统基于通胀和产出缺口的双因素损失函数假设货币当局只关注实际经济波动，忽视了货币政策调整本身所引致的成本，不符合稳健中性的政策取向，而且基于双因素损失函数推导最优货币政策规则时并不受经济总需求约束（卡尔∙瓦什，2012），这显然有悖于现实。为此，本文借鉴Woodford（2003）的思路，构建包含通胀、产出缺口和利率在内的三因素损失函数，以综合考虑货币当局对经济波动和利率稳定的关注。利率波动也会引起损失，因而利率调整受到限制，此时经济的总需求约束可以对货币当局的最优决策产生实质性影响。三因素损失函数如下：

其中， $f\left( \cdot \right)$ 为线性函数，参数 $\vartheta $ 和 $\sigma $ 分别表示产出缺口和利率在损失函数中的权重。

借鉴McCallum和Nelson（2000）以及Evans和Honkapohja（2006）的建模方式，在最优利率规则的推导中，将货币政策范式分为相机抉择型和事前承诺型，以比较不同范式下利率规则的有效性。

1. 相机抉择。在经济总需求和总供给约束下，货币当局每期都会对损失函数进行最优化，得到当期最优的利率调控规则。此时，最优货币政策决策变为如下的单期优化问题：

经计算，可得到相机抉择型货币政策规则：

与基于双因素损失函数得到的结果不同，在利率波动进入货币当局损失函数后，利率调整不仅着眼于抑制产出缺口和通胀波动，同时也要尽量降低自身波动。这类似于中央银行的利率平滑操作，利率稳定的一个重要目的就是防止金融市场过度波动。反映在最优利率规则上就是（10）式中的通胀预期、产出缺口预期、需求冲击和供给冲击前面的系数相对于双因素损失函数下的结果都要更小，这表明相同条件下利率调整幅度降低。

2. 事前承诺。在总需求和总供给约束下，货币当局通过最小化当期和未来损失函数的贴现值，得到最优货币政策。为简便考虑，假定货币当局的预期贴现因子与公众相同。此时，最优货币政策决策变为如下的跨期优化问题：

经计算，可得到事前承诺型货币政策规则：

（12）式表明，在利率波动进入货币当局的损失函数后，基于事前承诺的利率调整会使最优利率规则内生地表现出平滑机制，而基于双因素损失函数的最优利率规则没有这一特征。与（11）式的相机抉择相比，基于事前承诺的利率调整不仅表现出平滑机制，而且还对上一期通胀做出反应，因此历史通胀会影响当期利率调整。

（四）预期机制。为避免参数过多而导致参数估计不可识别以及参数校准过于主观，本文参照Gelain等（2013）、许志伟等（2015）等在模型中引入理性预期和简单适应性预期加权设定的方式，刻画更加贴近现实的异质性预期，并以理性预期情形为基准，模拟异质性预期下货币政策调控效果的变化情况。

1. 理性预期。理性预期假说认为公众具有高度理性，能够通过自我学习和调整，最终实现对经济变量的无偏和一致估计，公众能够准确预测随机冲击以外的经济变量的基本走势。为简便考虑，与多数DSGE文献的做法一致，采用如下完美信息条件下的理性预期假定：

其中，期望因子 $E_t^R\left( \cdot \right)$ 表示理性预期。

2. 异质性预期。本文构建的异质性预期同时包含了理性预期机制和适应性预期机制。借鉴Gelain等（2013）的预期设置方式，在适应性预期下，公众对未来的预期由过去形成的预期以及过去预期与实际值偏差的加成得到：

其中，期望因子 $E_t^A\left( {\cdot } \right)$ 表示适应性预期。参数 $\lambda $ 表示对预期偏误的纠正，衡量过去预期与实际值偏差对未来预期的影响权重，数值增大说明未来预期受到过去实际值的影响上升、受过去预期的影响下降。由此，通过加权平均可以得到如下异质性预期：

其中，期望因子 $E_t^H\left( \cdot \right)$ 表示异质性预期。参数 $\kappa $ 和 $ {1 - \kappa } $ 分别表示异质性预期中的适应性预期成分和理性预期成分的比例。

三、参数校准和估计

（一）参数校准。在贝叶斯估计之前，必须对模型中的部分参数进行校准，否则无法识别模型中的全部参数。在参数校准过程中，同时确保模型存在唯一稳定均衡解。与多数文献一样，将家庭主观贴现因子 $\beta $ 的季度值校准为0.99。参照马勇和陈雨露（2014）的估计结果，取居民消费跨期替代弹性的倒数 $\varsigma = 0.451$ 。研究中国问题的已有文献对劳动供给弹性的倒数 $\gamma $ 取值差异较大，王国静和田国强（2014）注意到这一问题，以他们的估计结果将 $\gamma $ 设定为2.2329。借鉴郭豫媚等（2016）的研究，取价格调整的粘滞程度参数 $\omega = 0.75$ 。

（二）数据选择。由于模型系统包含需求冲击和供给冲击2个外生冲击，本文选择产出（以实际GDP衡量）和通货膨胀（以CPI变化率衡量）这两个观测变量，数据来自中经网统计数据库，时间区间为2000年第1季度至2017年第1季度。其中，真实产出由CPI平减得到，变量采用X-12方法进行季节调整，利用一阶差分去除趋势。^④此外，使用金融机构1年期法定存款基准利率的季度数据表示无风险存款利率。

（三）先验分布设置。适应性预期中纠错参数 $\lambda $ 的设定与许志伟等（2015）类似，令其服从均值为0.3、标准差为0.2的Beta分布。异质性预期中的适应性预期成分参数 $\kappa $ 介于0和1之间，设其服从均值为0.5、标准差为0.2的Beta分布。将货币当局损失函数中的产出缺口权重参数 $\vartheta $ 设为0.5，令其服从标准差为0.2的Normal分布。参照Woodford（2003）的研究，设定货币当局损失函数中的利率权重参数 $\sigma $ 服从均值为0.236、标准差为0.2的Normal分布。参考王国静和田国强（2014）、马勇和陈雨露（2014）等文献，将需求和供给冲击的持久性参数 ${\rho _d}$ 和 ${\rho _s}$ 分别设为服从均值为0.5、标准差为0.2的Beta分布，将标准差 ${\sigma _d}$ 和 ${\sigma _s}$ 分别设为服从均值为0.01的Inv_Gamma分布。参数的先验分布及贝叶斯估计结果见表1。

四、货币政策模拟分析

（一）模型评价。首先，对模型与实际经济的拟合程度进行评价，甄别何种货币政策范式和预期形成机制对现实经济的解释力度更强。表2从标准差、一阶自相关系数以及与产出缺口的相关系数三个维度报告了模型与实际经济的拟合程度。整体来看，对于与产出缺口的相关系数，Model2和Model4的表现与实际经济特征出入很大，表明事前承诺范式不符合中国经济运行现实；对于一阶自相关系数和标准差，Model1和Model3的拟合效果较为接近，表明中国经济运行呈现出相机抉择特征。进一步从表1的贝叶斯估计结果来看，Model3估计出的异质性预期中的适应性预期成分参数 $\kappa $ 和适应性预期中的纠错参数 $\lambda $ 在95%的置信区间内显著不为零，分别达到32%和21%。这与许志伟等（2015）估计出中国公众预期中的适应性成分约为80%的结论比较接近，进一步表明中国的预期机制的确存在较强的适应性特征。因此，中国的货币政策表现出明显的相机抉择倾向，宏观经济预期呈现出理性预期和适应性预期混合的异质性特征。

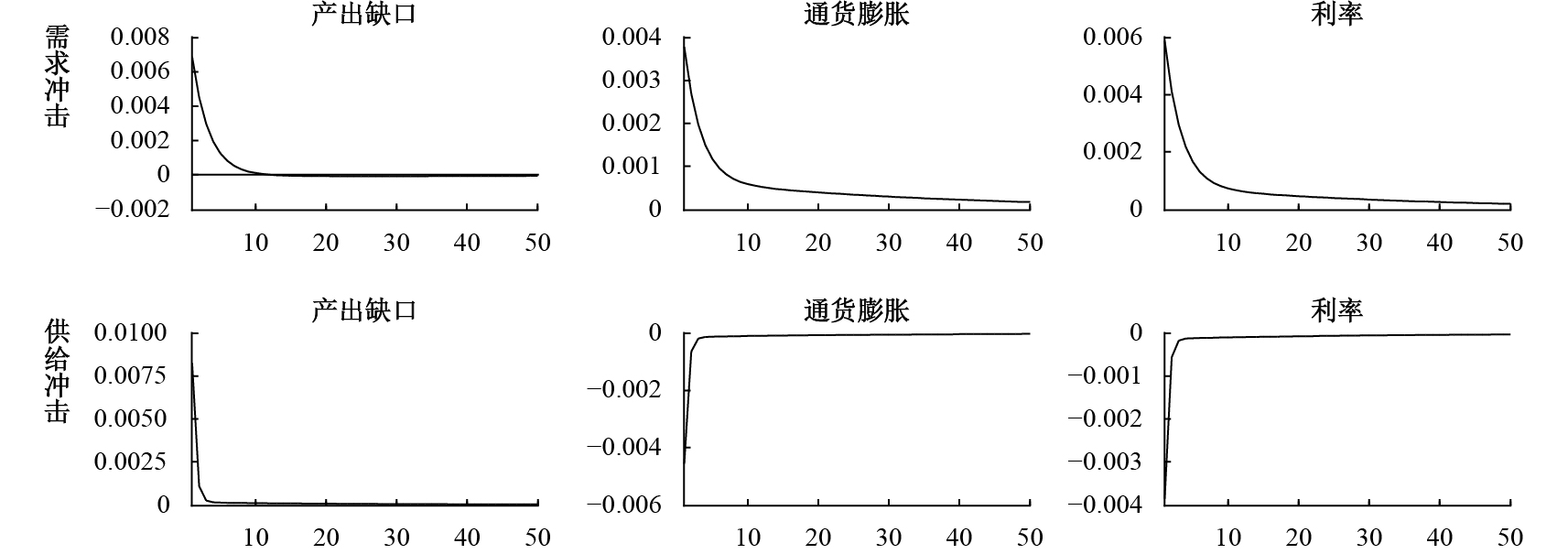
图3显示了异质性预期下相机抉择模型的动态。在正向需求冲击下，产出缺口、通货膨胀和利率都呈现出正向偏离稳态的响应轨迹；而在正向供给冲击下，产出缺口呈现正向反应，通货膨胀和利率均为负向反应。从变量回归稳态的速度看，在需求冲击下，产出缺口大约需10期收敛至稳态，而通货膨胀和利率的收敛速度明显偏慢、显示出较强的粘滞性特征；在供给冲击下，产出缺口只需约4期即可完全收敛至稳态，通货膨胀和利率的收敛速度也明显快于需求冲击时的情况。

表3显示了异质性预期下相机抉择模型的方差分解结果。从中可以看到，需求冲击对解释各经济变量的贡献权重均明显高于供给冲击，甚至可达到80%以上。这表明当前需求冲击是引起中国经济波动的主要力量，供给冲击的驱动力量十分有限。而由图3可知，需求冲击下主要经济变量回归稳态的速度明显慢于供给冲击时的情况，这种粘滞性特征也是引起当前中国宏观政策的经济稳定效果不断弱化的一个重要原因。可以预见在逐渐摆脱外需依赖、大力推进供给侧结构性改革的进程中，未来需求冲击驱动中国经济周期将会受到明显抑制，而供给冲击的驱动作用则会不断增强。这将有助于提升经济吸收外部冲击后的恢复能力，从而改善宏观政策调控的经济稳定效果。

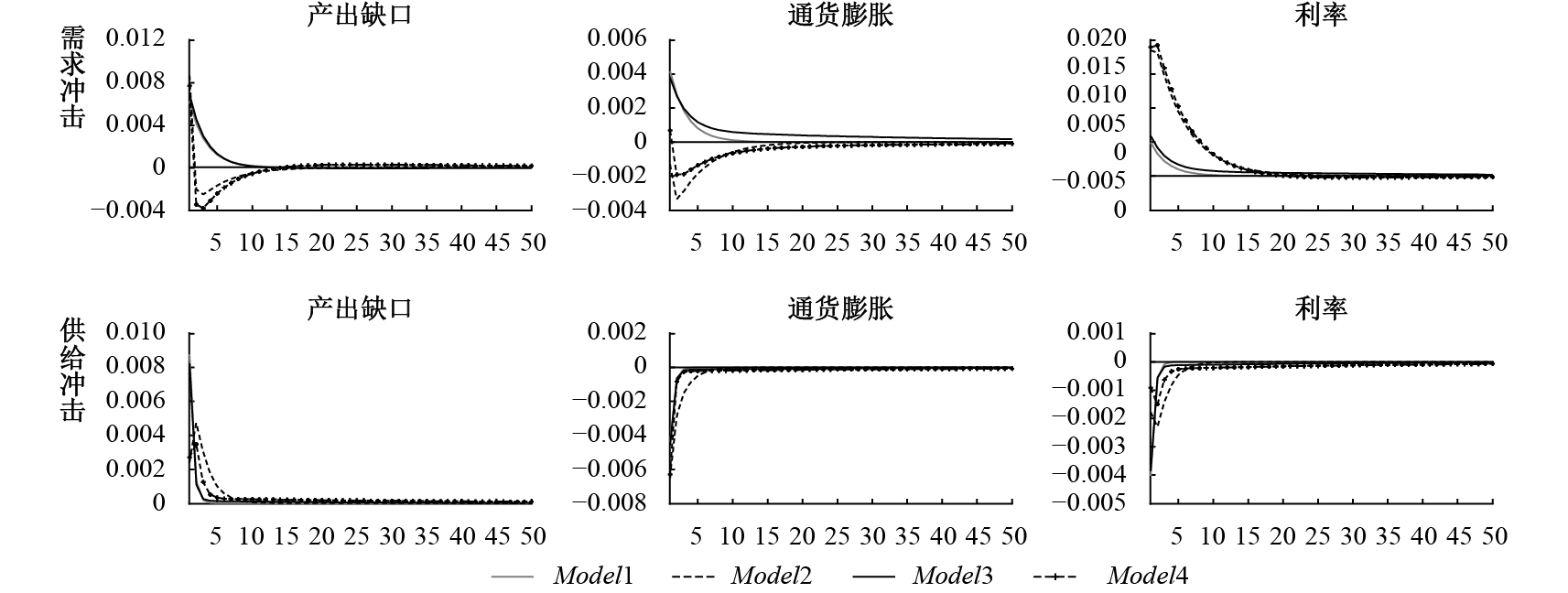
（二）预期和范式转变对货币政策稳定经济效果的影响。我们将分析当预期由异质性预期转变为理性预期，或者相机抉择范式转变为事前承诺范式时，货币政策的经济稳定效果会如何变化？模拟结果见图4。

1. 需求冲击。从产出缺口的动态响应路径来看，异质性预期下的相机抉择模型向稳态收敛的速度最快，这符合近年来我国始终将“稳增长”作为宏观调控的重中之重的基本事实；而无论是在理性预期还是异质性预期下，事前承诺下的波动幅度都偏高，收敛速度也更慢。从通货膨胀的动态响应路径来看，理性预期下的相机抉择模型收敛速度最快，异质性预期下的粘滞程度大、难以迅速向稳态回归，尤其是异质性预期下的相机抉择模型。利用2000年第1季度至2017年第1季度的实际数据分析发现，通货膨胀对稳态的偏离明显高于产出缺口，再次印证了当前我国异质性预期下的相机抉择调控具有“重产出、轻通胀”的特征。从利率的动态响应路径来看，相机抉择下的收敛速度最快，其中理性预期下的粘滞程度又低于异质性预期，而事前承诺下的波动幅度大、粘滞程度高、难以迅速向稳态回归，其中理性预期下的情况稍优于异质性预期。

由于异质性预期中的适应性成分具有预期粘性特征，其调整受过去经济表现的影响较大，如果货币政策此时采取事前承诺范式，则利率调整惯性将增大，由此引起经济变量的调整会更加缓慢，从而经济恢复稳态的速度也会变慢。由上文的方差分解结果可知，当前我国的经济波动主要由需求冲击所驱动，而在需求冲击下，异质性预期下的事前承诺模型的整体收敛效果最差。因此，在当前我国预期呈现明显异质性的背景下，货币政策不宜盲目转向事前承诺范式，否则可能导致宏观政策的经济稳定效果锐减，引起更大的福利损失。这也从理论上印证了2017年《政府工作报告》提出加强相机型调控的合理性与必要性。另外，无论货币政策采取相机抉择还是事前承诺，预期的理性程度提高整体上能够改进福利。理性预期本质上是一种前瞻性预期，可以减小过去货币政策调控绩效在未来的非合意影响，因此与货币政策范式转型相比，着力提高公众预期的理性程度更加科学、紧迫。

2. 供给冲击。从产出缺口的动态响应路径来看，与事前承诺相比，相机抉择下的粘滞程度更低、回归稳态的速度更快，而理性预期下的事前承诺模型的粘滞程度最高、收敛速度最慢。从通货膨胀的动态响应路径来看，相机抉择下的波动幅度最小、收敛速度最快，而理性预期下的事前承诺模型粘滞性最强。从利率的动态响应路径来看，理性预期下的相机抉择模型收敛速度最快，其次是异质性预期下的相机抉择，而事前承诺虽然在异质性预期下的波动幅度小于理性预期，但其粘滞性更强、难以迅速回归稳态。这与需求冲击情形下的结果是基本吻合的，表明“理性预期+相机抉择”组合的利率稳定效果最佳，而“异质性预期+事前承诺”组合的利率稳定效果最差。这再次说明在公众预期没有明显改善的条件下，货币政策不宜盲目转向事前承诺范式。

对比两类冲击下的结果可以发现，各主要经济变量吸收供给冲击后回归稳态的速度和程度要明显优于需求冲击。这表明不仅是公众预期和货币政策范式，导致经济波动的外部冲击对货币政策的经济稳定效果具有直接的重要影响。因此，深入推进供给侧结构性改革、扭转国内经济对外需的依赖，可以为宏观政策调控提供有利的外部环境。抑制需求波动、平稳转换经济驱动力、着力改善公众预期、科学实施相机型调控是提升我国货币政策调控绩效的重要路径，而不宜盲目转向事前承诺范式。

值得注意的是，一般认为“理性预期+事前承诺”的组合应优于“理性预期+相机抉择”，但上述模拟结果否定了这一点。其原因在于，本文构建的相机抉择范式是在既定的央行单期损失函数和一定约束下得到的，本质上是一种“相机抉择型规则”，而不同于理论上纯粹的无约束的相机抉择。这样就使相机抉择在保持较大灵活性的同时兼具规则约束，从而可以产生更好的经济稳定效果。同时，由于假设央行的货币政策操作具有稳定利率的倾向，从利率的动态响应路径中可以看到，相机抉择在利率调整上的灵活性优势更加突出。

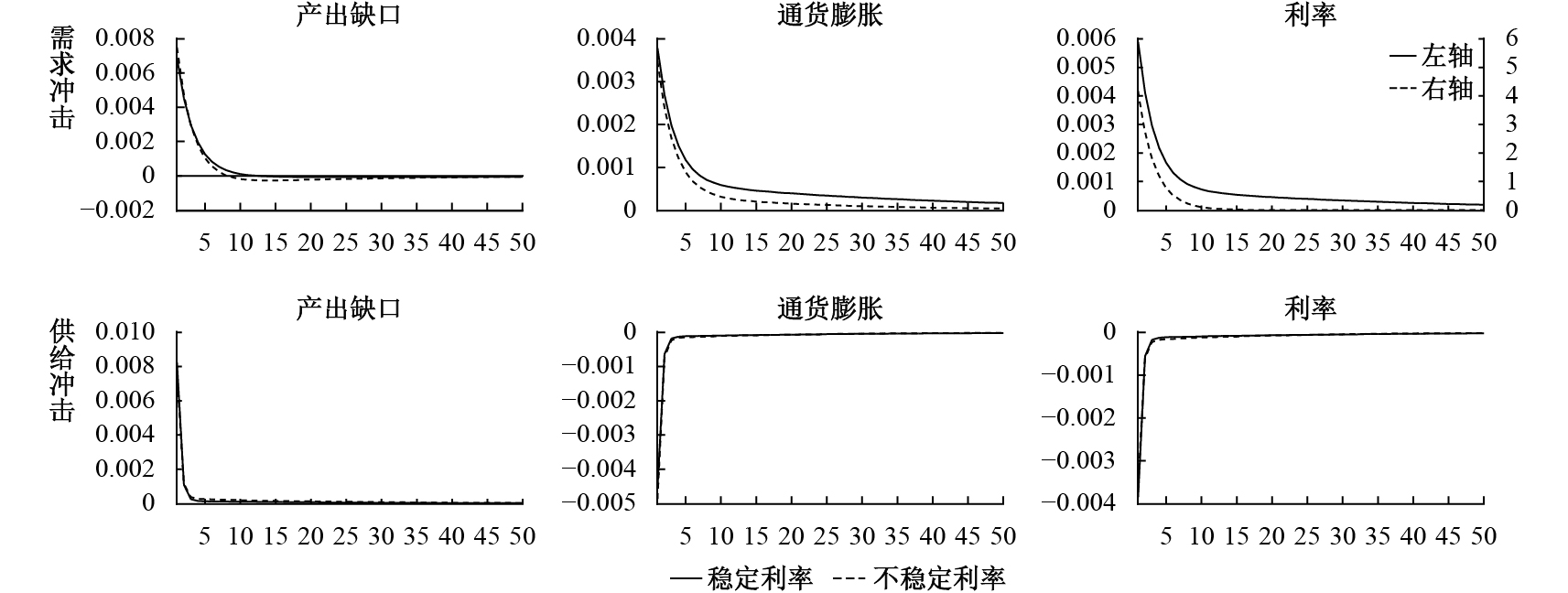
（三）稳定利率操作的福利效应。本文的贝叶斯估计结果显示，货币当局损失函数中的利率权重参数 $\sigma $ 为0.4034，表明中国的货币政策实施确实考虑了利率稳定因素，反映了货币政策的中性基调及其对金融稳定的关注。为分析是否纳入稳定利率操作对货币政策调控效果的影响，取 $\sigma $ =0.001，表示货币政策不采取稳定利率操作，并与 $\sigma $ =0.4034的基准情形进行比较分析。^⑤由图5可知，在需求冲击下，不采取稳定利率操作会导致利率波动大幅增加，而对产出缺口和通货膨胀波动的抑制效果更好；在供给冲击下，是否采取稳定利率操作的经济波动效应差别很小。

参照Woodford（2003）的做法，本文进一步通过计算福利损失来定量评估稳定利率操作对货币政策调控效果的综合影响。令 $Loss = {E_t}\sum\limits_{s = 0}^{50} {{\beta ^s}(\pi _{t + s}^2} + \vartheta \hat y_{t + s}^2 + \sigma \hat i_t^2)$ ，测算经济充分回归稳态过程中经济波动的福利损失。由表4可知：（1）不采取稳定利率操作会导致需求冲击下的福利损失大幅上升，而供给冲击下的福利损失明显更低，总体上不采取稳定利率操作时的整体福利损失高于稳定利率操作；（2）无论货币政策是否采取稳定利率操作，需求冲击导致的福利损失都显著高于供给冲击，而不采取稳定利率操作时的福利损失在供求冲击间的分布差距更大。因此，在当前以需求冲击为主导的情况下，采取稳定利率操作能使福利损失大幅下降。这也从理论上支持了2016年中央经济工作会议提出的“货币政策要保持稳健中性”基调的科学性。此外，无论是否采取稳定利率操作，扭转需求冲击对我国经济的主导驱动力，都将显著降低经济的福利损失。

五、结论和政策建议

本文将异质性预期引入新凯恩斯模型，基于包含利率稳定目标的三因素损失函数，推导出相机抉择和事前承诺两种货币政策范式，对比分析了不同的外生冲击下预期理性程度变化和货币政策范式转变的经济波动效应，并探讨了稳定利率操作对货币政策调控有效性的影响。贝叶斯估计与模型评价结果显示，当前中国货币政策表现出明显的相机抉择倾向，货币政策实施在一定程度上考虑了利率稳定目标；宏观经济预期呈现出理性预期和适应性预期混合的异质性特征；需求冲击是当前引起经济波动的主要力量。模拟分析结果表明，提升预期的理性程度整体上能够增进福利，而且无论是在理性预期还是异质性预期下，需求冲击所导致的经济波动向稳态收敛的时间都要明显长于供给冲击；事前承诺并不一定优于相机抉择，当预期呈现有限理性的异质性特征时，事前承诺的货币政策反而引起经济波动的幅度更大、恢复稳态的时间更长；货币政策忽视利率稳定目标将导致更大的整体福利损失，而需求冲击下的福利损失又显著高于供给冲击。

本文建议：（1）中央银行应着力提高预期管理水平以提升公众预期的理性程度，因为无论在何种外生冲击或货币政策范式下，提高预期理性程度总体上都能够增进福利。（2）在当前公众预期呈现异质性特征的背景下，相机型调控具有合理性，货币政策不宜盲目向事前承诺范式转型，异质性预期下采取事前承诺政策反而会导致经济出现更大波动。（3）在当前经济波动主要由需求冲击驱动的条件下，货币政策应采取稳定利率操作，保持稳健中性的政策基调有助于防止不必要的利率扰动影响金融稳定，从而显著降低福利损失。（4）逐步摆脱外需依赖，大力推进供给侧结构性改革，有助于提升宏观调控的经济稳定效果，在驱动经济周期的主要动力由需求面转向供给面后，经济恢复稳态的时间有望大幅缩短。

① 尽管中国处于经济转型期，存在大量的非预期冲击，但是不可否认，经济主体预期的理性程度还不够高。许多研究显示我国是有限理性预期，适应性成分仍比较明显（张蓓，2009；范从来和高洁超，2016）。

② 本文的异质性预期是指代表性主体的预期中同时包含理性成分和适应性成分，而非不同类型行为主体的预期。

③ 当前，迫于不断升级的中美贸易摩擦，中国货币政策有重回稳健的态势，但毋庸置疑，稳健中性才是货币政策的长期取向。2018年10月，中国人民银行网站在沟通交流栏目中重申了稳健中性的货币政策取向保持不变。

④ 根据匿名审稿人的意见，采用HP滤波处理数据会存在DSGE模型变量与原始数据不匹配的问题，本文采用一阶差分滤去变量中的时间趋势；此外，还使用GDP平减指数代替CPI进行贝叶斯稳健性估计，所得结果与原文保持了较高的一致性。

⑤ 由于 $\sigma $ 取0时经济总需求方程无法对货币政策制定形成实际约束，为比较需求冲击下货币政策是否采取稳定利率操作带来的经济波动效应变化，取 $\sigma $ =0.001，近似表示不采取稳定利率操作。