
2019第45卷第1期
一、引 言
就业作为经济调控的重要目标之一,不仅关系着国家的经济发展,还关系着社会的安定团结。据国家统计局的统计,2013—2016年城镇新增就业连续四年保持在1 300万人以上,全国城镇登记失业率均在4%以上,31个大城市的城镇调查失业率更是保持在5%左右。这意味着在我国经济高速发展的同时,就业情况并不乐观。据本文统计,2007—2015年我国污染密集型行业与非污染密集型行业的平均就业量均由增长转为下降趋势。①
在我国就业增长面临很大挑战的同时,我国的环境污染问题也日趋严重。据《中国环境统计年鉴2015》显示,2015年工业废气排放总量为685 190亿m3,二氧化硫排放总量为1 859.1万吨,烟尘排放总量为1 538万吨。据《2015年中国气候公报》披露,2015年我国共出现11次大范围、持续性霾过程。如此范围广、污染程度重的雾霾天气严重危及人民的身体健康。治理污染、保护环境已成为制约我国经济和社会发展的关键问题。十九大报告明确指出,必须加大环境治理力度,着力解决突出环境问题,实行最严格的生态环境保护制度,形成绿色发展方式和生活方式。那么,如何协调生态环境保护与就业增长就成为政策制定者和学者们关注的热点问题。对该问题的解答,对于我们有效地协调环境管制和经济发展的关系,促进人与自然的和谐发展具有重要的现实意义。根据本文统计,2007—2015年污染密集型行业的年平均行业就业人数远高于非污染密集型行业的就业人数。由此可知,我国环境管制对就业的影响至关重要。
目前,关于环境管制与就业关系的讨论,部分文献以某一污染行业为例,研究环境管制与就业的关系。Gray等(2014)和Liu等(2017)分别以美国造纸业和中国江苏地区纺织印染企业为例,研究发现环境管制使得就业量有小幅下降。Ferris等(2014)以电力行业为例,但是研究结果与上述文献并不一致,发现公共事业可以利用法规的灵活性最大限度地减少其对就业的总体影响。然而,在环境规制的作用下,污染行业的劳动力可能转移到其他行业。因此,针对于某一具体行业的研究可能忽略了劳动力在部门间的转移再分配问题,会夸大或低估环境管制对就业的影响。例如,Tsuyuhara(2015)扩大了研究行业范围,发现能源税并没有对就业造成不利影响,而且使劳动力从污染重的能源密集型行业转移到劳动效率更高的清洁生产行业。Walker(2013)以美国清洁空气法案为例,研究发现环境规制产生了明显的劳动力部门间再分配成本。Greenstone(2002)也针对美国清洁空气法案,研究发现环境管制潜在地提高了企业的生产成本,损失了就业。但是,Berman和Bui(2001)针对洛杉矶地区的空气质量监管,研究发现成本的提高并没有减少劳动力的需求,可能还有微弱的促进作用。
具体到中国,现有文献大多集中于行业层面的分析,探讨产业层面宏观因素对就业的影响。陈诗一(2010)基于方向性距离函数的动态行为分析模型,对中国工业38个两分位行业未来40年的节能减排双赢情景进行预测,发现节能减排一开始会造成较大的潜在生产损失,但这种损失会逐年降低,最终会低于潜在产出增长,从而实现双赢。陆旸(2011)在VAR模型的基础上,采用行业数据模拟了中国的减排与就业“双重红利”问题,认为通过税收体系改革还难以在短期内获得减排和就业的“双重红利”,但是改革税收体系以发展中国低碳经济不失为一种次优选择。
但是,上述研究大多忽略了环境管制类型之间的经济效应差异,集中于研究末端环境管制对就业的影响。事实上,不同类型的环境管制政策,其作用机制和效果存在较大的差异(Jaffe和Stavins,1995;Milliman和Prince,1989)。一般而言,环境管制政策可以划分为末端环境治理和前端污染治理两种类型。末端环境治理是以“先污染、后治理”为基本思想,通过对污染物的稀释、掩埋等处理方式,以达到污染物排放标准。末端环境治理的方式不仅导致治污成本的快速攀升(刘伟明,2014),而且不能从根本上消除污染,为未来的环境保护和经济发展留下隐患。而前端污染治理将“末端治理”为主的环保战略调整为以“前端预防”和“全程预防”为主的环保战略(殷杉,2003),将污染处理转变为对生产全过程的控制,从源头上削减污染物的产生。从直观上看,两种政策都将环境成本内部化,在一定程度上增加了企业的生产成本,可能会降低企业的产出数量,从而进一步加剧一国范围内的失业问题。但事实上,相比于末端环境管制,前端污染治理要求淘汰技术落后、资源消耗高、环境污染重的生产工艺设备,优先采用能源利用效率高、污染排放量少的生产工艺,更多地涉及企业资本投入的增加,从而对就业产生多渠道影响。
前端污染治理政策中最具代表性的是清洁生产政策,其包含三个要求:采用清洁的能源、生产过程清洁化和生产清洁的产品。这不仅有利于减少污染物的产生,而且能够激励企业积极进行开发、研制和更新清洁的生产技术,从而有利于提高能源、原材料的利用率,提升企业的生产率,实现经济与环境的协调发展。鉴于此,本文采用2000—2006年中国工业企业数据库,以省份层面的清洁生产政策为例,基于拟断点回归方法研究前端污染治理对就业的影响,并探讨其作用的微观机制。研究发现,前端污染治理对我国就业有显著的提升作用,进一步对内在机制分解显示:(1)前端污染治理引导企业更新先进清洁的生产设备,加大研发投入,通过企业生产效率的提升,扩大了企业的生产规模,最终吸纳了更多的劳动力。(2)技术的进步并没有形成资本对劳动的替代,即替代效应并没有起作用。(3)从市场动态角度来看,前端污染治理使得具有一定规模的高效率企业得以进入和存活,从而提高了整个市场的就业量。此外,前端污染治理对就业的影响具有异质性,主要提升了污染密集型行业、大规模企业和国有企业的就业水平。
与已有文献相比,本文的贡献主要体现在以下两个方面:首先,在研究视角上,本文以清洁生产政策为例,考察前端污染治理对我国微观企业就业的影响。②现有关于环境管制的文献虽然探讨了其对就业的影响,但大多集中于考察末端环境管制对就业的影响(Berman和Bui,2001;Greenstone,2002;陈媛媛,2011;王勇等,2013;Ferris等,2014;赵连阁等,2014;Liu等,2017)。与本文研究最为密切的文献为张彩云等(2017),其虽然采用了企业级数据,考察了全国范围内的清洁生产政策对就业的影响;但该文献主要是针对重点污染行业的就业考察,没有将就业在行业内的再分配效应纳入分析框架。为此,本文一方面将研究视角转向前端污染治理,探究其作用的微观传导机制;另一方面从微观企业角度进行分析,不仅涵盖了行业间的就业再分配效应,而且能更有效地反映企业微观主体的就业调整和变动。这对我们正确地认识和判断前端污染治理政策的作用,有效调整就业方向、制定合理的环境政策具有重要现实指导意义。其次,在研究方法上,本文采用拟断点回归方法的原因在于:一方面,由于各省实施清洁生产政策的年份并不一致,因此我们可以根据政策时间的差异,界定相应的对照组和处理组;另一方面,实施清洁政策的省份与邻近省份,在经济和自然条件等方面都是基本一致的,只是由于行政区域分界线两边清洁政策的实施存在差异,从而造成了就业差异。因此,本文采用拟断点回归方法,既能利用断点回归更接近于准自然实验的优势,以此来界定处理组和对照组,又能利用倍差法将可能存在的省份间不可观测的因素差分掉,更好地控制内生性的问题,从而更加有效地识别前端污染治理对就业的影响。
本文的其余部分安排如下:第二部分为理论分析和清洁生产政策介绍;第三部分为计量模型;第四部分对数据、指标构建和特征化事实进行说明;第五部分为计量结果分析,包括基本回归结果、内在机制分解、有效性检验以及异质性分析;最后部分为本文的结论与启示。
二、理论分析和清洁生产政策
(一)理论分析
本文在Berman和Bui(2001)关于环境管制与就业的局部静态均衡模型(Brown和Christensen,1981)基础上,考察前端污染治理对就业的影响及其微观机制。Brown和Christensen(1981)的局部静态均衡模型可以将不变要素设置为外生约束,如环境管制,而不仅是求解成本最小化。因此,依据Berman和Bui(2001)的理论分析框架,减排成本为不变要素投入,包括减排的资本投入和用于减排的劳动力、原材料等投入。生产经营用的劳动力、中间品和资本投入为可变要素。
在市场完全竞争的假设下,企业的可变成本函数为:
| $CV = F(Y,{P_1}, \cdots ,{P_L},{Z_1}, \cdots ,{Z_M})$ | (1) |
其中,Y是产出,
| $L{\rm{ = }}\alpha {\rm{ + }}{\rho _Y}Y + \sum\limits_{k = 1}^L {{\gamma _k}{P_k} + } \sum\limits_{q = 1}^M {{\beta _q}{Z_q}} $ | (2) |
由此,环境管制(ER)对就业需求的影响可表示为:
| $\frac{{dL}}{{dER}} = {\rho _Y}\frac{{dY}}{{dER}} + \sum\limits_{k = 1}^L {{\gamma _k}\frac{{d{P_k}}}{{dER}}} + \sum\limits_{q = 1}^M {{\beta _q}\frac{{d{Z_q}}}{{dER}}} $ | (3) |
式(3)右边第一项表示环境管制通过产出渠道影响就业。传统观点认为环境管制会提高企业的生产成本,降低产出。但是,如果环境管制能够刺激企业进行投资,降低企业的边际成本,那么产出反而会随着环境管制的实施而提升,最终增加企业的就业(Berman和Bui,2001;Morgenstern等,2002)。就末端治理而言,其处理污染的方式大多为转移和掩埋,污染治理成本的增加,往往会对产出产生负向作用。不同于末端治理,前端污染治理将污染治理与生产过程相结合,通过强制和激励相结合的手段,引导和激励企业淘汰污染严重的生产设备,采用更加清洁先进的生产工艺。伴随着一系列技术的改进,前端污染治理反而会提升企业的生产规模,刺激就业。因此,本文提出如下研究假说:
假说1:前端污染治理提升了企业的技术和生产效率,从而对就业产生正向的生产规模效应。
同时,式(3)右边第一项还存在一种极端情况,即部分已存在企业退出了市场,产出Y为0,而新进入的企业均具有较高的产出Y。因此,从市场动态角度看,环境管制通过增加企业的成本,提高了市场的进入门槛,使得高效率的企业得以进入和存活,而这些高效率企业通常更具有规模优势,能够吸纳更多的就业。因此,本文提出如下研究假说:
假说2:前端污染治理通过企业的进入退出机制,使得更具规模优势的高效率企业进入和存活,从而吸纳更多的就业,形成市场选择效应。
在要素市场完全竞争的情形下,受环境管制的厂商对市场价格的作用微乎其微。因此,式(3)右边第二项约等于0。式(3)右边第三项反映了环境管制所采取的治污措施以及治污措施与劳动力之间的边际技术替代率对就业的影响。显然,治污成本会随着环境管制程度的加深而提高,即dz/dER为正值,但是
假说3:在前端污染治理下,劳动力与资本的替代效应取决于劳动力与治污措施之间的替代性,且有待进一步的经验检验。
(二)清洁生产政策
根据工业和信息化部的《工业清洁生产政策汇编》,2001—2005年我国部分省份相继颁布了清洁生产政策,但是各省颁布的政策存在一定的差异。研究证据表明,严格的环境管制和执法依然是企业改善环境的首要驱动力(Greenstone和Hanna,2014)。为此,本文依据强制进行清洁生产审核的时间来调整政策的实施时间。此外,在拟断点回归框架下,控制组选取的范围限定为与实验组相邻的未实施该政策的省份。因此,本文依据是否存在未实施清洁生产政策的相邻控制组省份来选取实验组省份。最终,以强制进行生产审核和存在相应的控制组为标准,发现2001—2005年共有15个省份实施了清洁生产政策。③
同时,拟断点回归模型涉及样本“带宽”范围的选取。④根据我国的地理特征,部分省份边界处地势险要,两侧的企业可能处于隔绝状态,可比性差。有必要选择一个较小的带宽以保证实验组企业和对照组企业的特征相似性,同时尽可能多地保留样本量,因此本文选取50 km带宽作为基本带宽。在这一带宽范围内,恰好剔除了处于复杂地势的新疆边界线,从而保证了边界线内外企业特征的相似性。最终,在50 km带宽范围内,本文共得到10个实施清洁生产政策的省份。
三、计量模型
拟断点回归方法(Pseudo-regression Discontinuity Model)将断点回归方法与双重差分方法相结合,不仅可以利用断点两边分组的随机性,而且可以利用双重差分排除不可观测因素的影响。在拟断点回归框架下,核心变量包括指派变量(assignment variable或forcing variable)、处理变量(treatment variable)和结果变量(outcome variable)。其中,处理变量由指派变量是否超过某断点决定。本文将实验组企业与省份边界线的距离设为正值,将对照组企业与省份边界线的距离设为负值,处于边界线上的企业距离则为0,即为断点。我们根据该距离组建了指派变量x。处理变量D完全由指派变量x是否超过断点值来决定:
| $D = \left\{ \begin{gathered} 1\;\;\;\;\;\;\;if\;\;x \geqslant 0 \\ 0\;\;\;\;\;\;if\;\;x < 0 \\ \end{gathered} \right.$ | (4) |
本文采用拟断点回归模型估计前端污染治理对企业就业的影响。回归函数形式如下:
| ${y_{itz}} = \alpha + \beta {D_{iz}} \times pos{t_t} + {\lambda _t} + {\lambda _c} + {\varepsilon _{it}}$ | (5) |
其中,
此外,根据数据特征,本文运用边界断点回归模型检验前端污染治理的市场选择效应。Hahn等(2001)提出使用局部线性回归(local linear regression)估计断点回归模型,这样能够使估计值更加接近真实处理效应,减少了估计的偏误。因此,本文的边界断点回归模型采用局部线性回归方法,即将下列函数最小化:
| $\mathop {min}\limits_{\left\{ {\alpha ,\beta ,\delta ,\gamma } \right\}} \sum\limits_{i = 1}^n K \left[ {\left( {{x_i} - c} \right)/h} \right]{\left[ {{y_i} \\ - \alpha - \beta \left( {{x_i} - c} \right) - \delta {D_i} - \gamma \left( {{x_i} - c} \right){D_i}} \right]^2}$ | (6) |
其中,
四、数据、指标构建和特征化事实
(一)数据说明
本文数据分为三个部分:第一部分数据是来自工业与信息化部的《工业清洁生产政策汇编》。该文件包括了2010年前实施清洁生产政策的省份信息,并且各省份实施清洁生产政策的时间各不相同。为保证本文的样本量,我们选取了2001—2005年实施地方清洁生产政策的省份作为实验对象。第二部分数据是关于行业层面的变量,主要来自相关年份的《中国统计年鉴》,包括行业煤炭消费量(万吨标准煤)、行业固定资产(亿元)、行业全部从业人员(万人)和行业工业总产值(亿元)。⑤第三部分数据是来自2000—2006年工业企业库的数据。该数据涵盖了全部国有企业及销售额在500万元以上的非国有工业企业信息,包括企业所有制、企业所在地、行业类别和企业就业人数等方面的信息。我们参考Brandt等(2012)的做法,对数据库进行了如下处理:(1)构建面板数据;(2)采用永续盘存法估算企业的实际资本存量;(3)删除企业员工少于8人、流动资产大于总资产、总固定资产大于总资产的样本;(4)根据企业的注册类型和注册资本调整企业的所有制属性;(5)统一将行业代码调整为国民经济行业分类标准(GB/T4754-2002);(6)采用2004年经济普查数据库中的工业总产值填补了该数据库2004年缺失的工业总产值。需要说明的是,各个省份从2001年开始相继实施清洁生产的相关政策。在拟断点回归框架下,处理组与其相应的对照组是相邻的两个省份;而随着时间的推移,越来越多的对照组变为处理组,尤其是到了2006年,可选用的对照组急剧减少,这严重影响了本文的样本量。为了保证样本量,本文将实验对象限定为2006年前实施清洁生产政策的省份,并且将2006年实施清洁生产政策的省份从样本中剔除,从而将数据时间跨度限定为2000—2006年。
(二)指标构建
1. 指派变量构建
在拟断点回归中,本文的指派变量为企业与省份边界线之间的距离。本文依据企业地址信息,通过百度地图计算距离变量(x)。首先,依据百度地图将企业的地址转换为企业的经纬度;其次,通过百度地图获取省份边界的经纬度,这些省份包括实施清洁生产政策的省份以及与其相邻的未实施清洁生产政策的省份;最后,测算企业的经纬度与省份边界不同经纬度之间的距离,取其中的最小值作为企业与省份边界线之间的距离。本文将实施清洁生产政策省份内的企业距离设置为正数,将未实施清洁生产政策省份内的企业距离设置为负数,则省份边界上的距离值为0,即为断点。
2. 企业层面变量
本文以企业特征变量作为经营活动的考察指标,具体包括企业流动资产比率(liq_ratio)、固定资产周转率(fixed_turnover)、负债率(lia_asset)和企业利润率(profit_ratio)。其中,企业流动资产比率为流动资产与总资产的比值;固定资产周转率为销售产值与固定资产净值年平均余额的比值,反应了企业的固定资产利用效率;负债率为企业总负债与总资产之比,衡量公司利用债权人资金进行经营活动的能力;利润率为销售利润与销售收入的比值,反映了企业的利润完成情况和经营管理水平。
(三)特征化事实
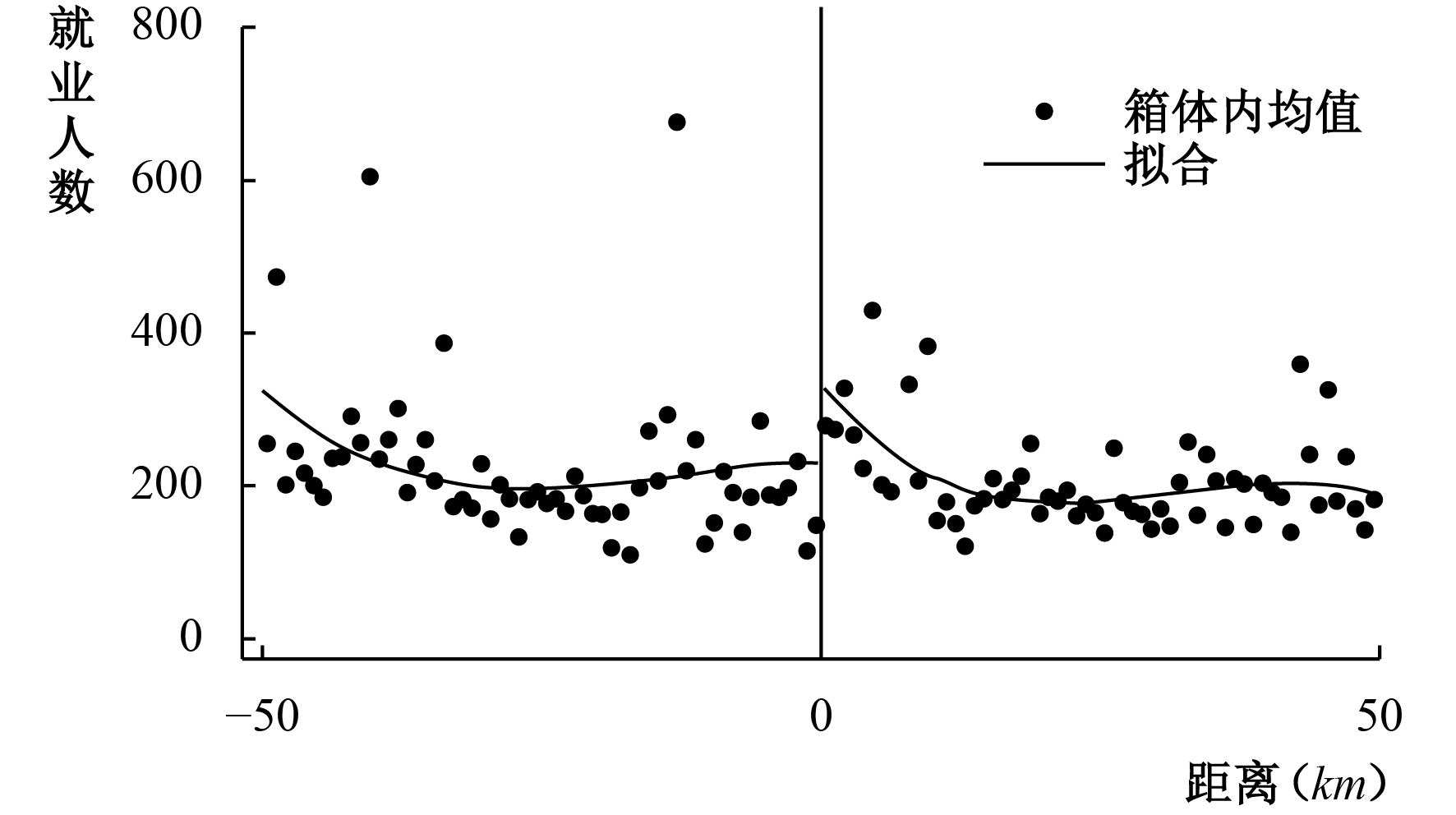
在进行计量分析之前,我们首先通过图1来对比分析在断点左右两边50 km区域内企业就业水平的差异。图1中的散点代表在箱体范围内企业就业的平均值,使用平均值能更好地避免原始数据的噪音。图中的曲线代表对断点前后的所有散点进行非线性回归所得到的因变量的拟合值。从图中可以看出,在断点处,实验组企业的就业水平有明显向上跳跃的倾向。这意味着企业可能因外生政策冲击而增加了就业吸纳量,或者因企业自身的经营活动需要而扩大了就业规模。
|
| 图 1 企业就业水平在断点处的变化 |
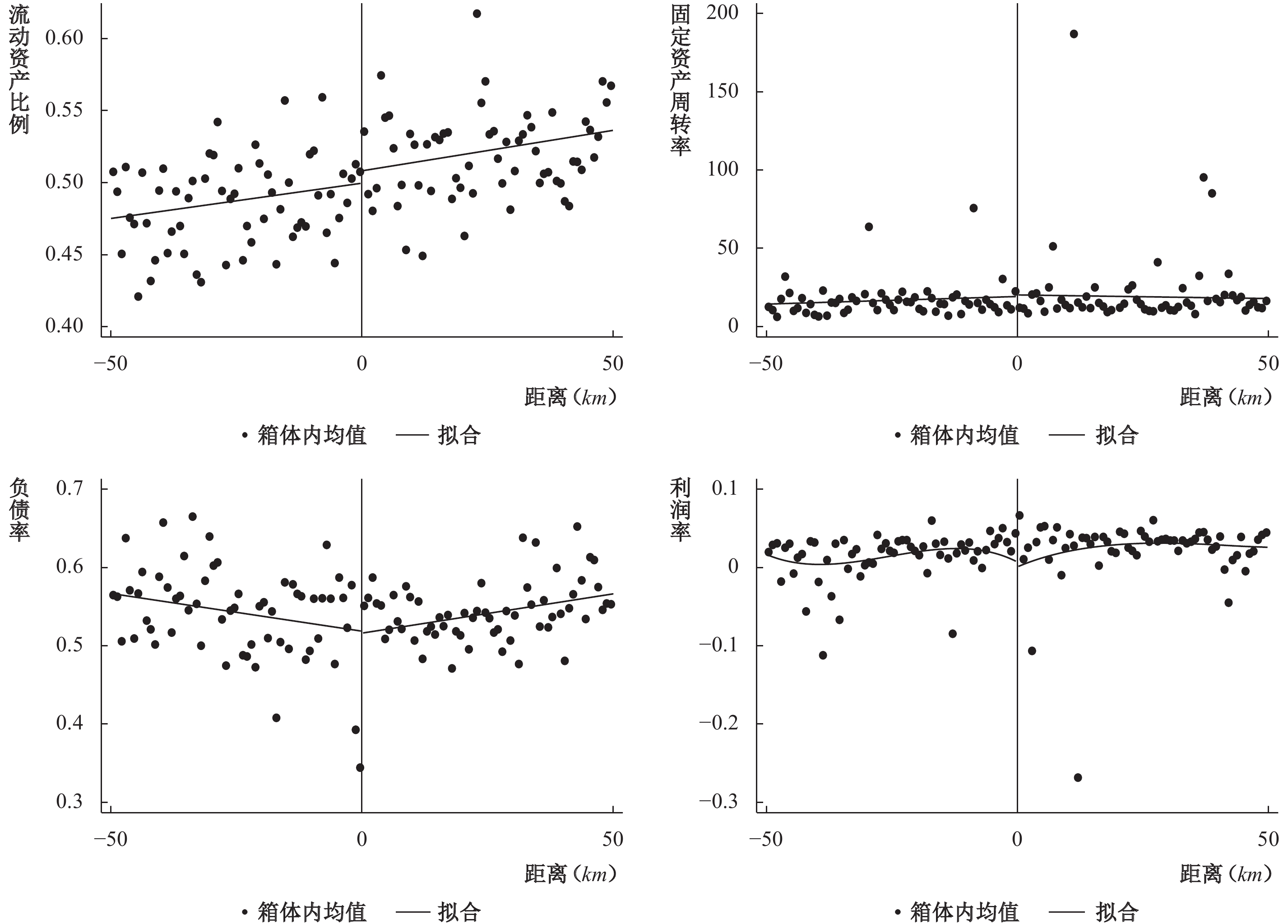
鉴于此,本文通过考察企业特征变量在断点处的变化来判断企业的经营活动在断点处的变化情况,并以此来初步推断引发企业就业规模变化的原因。图2是企业特征变量在断点左右50 km区域内的变化图,散点代表在箱体内变量的均值,曲线代表对断点前后的所有散点进行回归所得到的变量拟合值。从图中可以看出,这些变量在断点处并没有明显的跳跃。这说明在断点处,企业的经营活动并没有发生明显改变,这很有可能是因为清洁生产政策的实施引发了就业规模的扩大。
|
| 图 2 企业特征变量在断点处的变化 |
五、计量结果
(一)基本结果
本部分通过经验研究验证前端污染治理对就业的影响。表1为其相应的回归结果。首先,模型(1)中D×post的系数在统计水平上显著为正,并保持在0.139的水平上。这说明前端污染治理政策的实施扩大了企业的就业规模。其次,模型(2)将能够代表企业特征的变量和企业所有制的类别变量(ownership)作为协变量加入其中。这主要是因为在拟断点回归模型中加入协变量,不仅可以控制企业特征变量对估计结果的干扰,而且还可以降低回归结果的抽样变异性,令估计值更接近真实值。此外,模型(3)进一步加入了行业的虚拟变量,以考察在控制了行业差异后,前端污染治理对就业的影响。模型(4)在模型(3)的基础上,加入了省份时间趋势,以控制各省的时间趋势,从而排除实验组与对照组省份的发展不一致对回归结果的干扰。模型(1)—模型(4)均采用50 km作为基本带宽,模型(5)将带宽更改为25 km。模型(1)—模型(5)的回归系数均在统计水平上显著为正,说明前端污染治理对就业的提升作用是稳健的。
| (1) | (2) | (3) | (4) | (5) | |
| D×post | 0.139** (0.057) |
0.139* (0.069) |
0.120* (0.058) |
0.087** (0.034) |
0.130*** (0.033) |
| liq_ratio | −0.162
(0.094) |
−0.164* (0.079) |
−0.166* (0.080) |
−0.221** (0.101) |
|
| fixed_turnover | −0.000*** (0.000) |
−0.000*** (0.000) |
−0.000*** (0.000) |
−0.000*** (0.000) |
|
| lia_asset | 0.265*** (0.058) |
0.243*** (0.058) |
0.248*** (0.060) |
0.319*** (0.072) |
|
| profit_ratio | 0.000
(0.000) |
0.000
(0.000) |
0.000
(0.000) |
0.000
(0.000) |
|
| ownership | −0.103** (0.042) |
−0.109*** (0.035) |
−0.111*** (0.035) |
−0.103** (0.039) |
|
| _cons | 5.199*** (0.048) |
5.307*** (0.093) |
5.749*** (0.184) |
318.276*** (8.141) |
273.269*** (17.051) |
| 年份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 省份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 行业固定效应 | 控制 | 控制 | 控制 | ||
| 省份时间趋势 | 控制 | 控制 | |||
| 样本量 | 86 923 | 83 067 | 83 067 | 83 067 | 36 735 |
| adj. R2 | 0.057 | 0.076 | 0.146 | 0.150 | 0.156 |
| 注:(1)*、 **和***分别代表在10%、5%和1%水平上显著;(2)括号内为稳健集聚(省份水平)标准误。下表同。 | |||||
(二)影响机制分解
前端污染治理可以通过多种渠道影响企业的就业水平。根据本文的理论分析,本部分就前端污染治理政策对就业的规模效应、市场选择效应和替代效应进行一一验证。
1. 规模效应
首先,本文采用拟断点回归方法验证前端污染治理的规模效应。根据本文的理论分析,如果前端污染治理是通过正向的规模效应提升了企业的就业水平,那么企业的生产率水平也会得到相应提升。本部分就企业生产率水平和生产规模进行一一验证。此外,为排除市场选择效应这一影响渠道,本部分将样本限定为政策实施前一年存在且在政策实施后一年一直存在的企业,采用平衡面板数据。其中,企业全要素生产率(tfp)依据Olley和Pakes(1996)方法计算得到。对生产率的考察结果参见表2中的模型(1)—模型(3)。模型(1)与模型(2)选用50 km带宽,模型(3)更换为25 km带宽。从回归结果来看,模型(1)—模型(3)的回归系数均在统计水平上显著为正。这说明前端污染治理政策通过技术升级提高了企业的生产效率。
| (1) | (2) | (3) | (4) | (5) | (6) | |
| D×post | 0.015** (0.007) |
0.016** (0.007) |
0.018** (0.007) |
0.130* (0.067) |
0.133* (0.066) |
0.184*** (0.052) |
| liq_ratio | 0.056*** (0.012) |
0.056*** (0.013) |
−0.032
(0.065) |
−0.006
(0.074) |
||
| fixed_turnover | 0.000** (0.000) |
0.000** (0.000) |
0.000* (0.000) |
0.000
(0.000) |
||
| lia_asset | −0.035*** (0.012) |
−0.041*** (0.010) |
0.088
(0.083) |
0.226*** (0.066) |
||
| profit_ratio | 0.025
(0.016) |
0.198*** (0.047) |
0.123
(0.106) |
0.986* (0.490) |
||
| ownership | 0.008*** (0.002) |
0.006** (0.002) |
−0.040
(0.034) |
−0.039
(0.035) |
||
| _cons | 0.754*** (0.002) |
0.721*** (0.011) |
0.725*** (0.014) |
10.040*** (0.039) |
10.118*** (0.101) |
10.094*** (0.116) |
| 年份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 省份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 18 189 | 17 160 | 7 589 | 19 508 | 18 396 | 8 142 |
| adj. R2 | 0.110 | 0.133 | 0.150 | 0.051 | 0.057 | 0.093 |
但是,企业效率的提升并不意味着企业生产规模的扩大。只有效率提升效应大于成本增加效应时,前端污染治理才会对就业形成正向规模效应。为此,我们进一步将被解释变量更换为企业产出的对数值(lnoutput),以检验企业生产规模的变化。结果参见表2中的模型(4)—模型(6)。模型(6)在模型(5)的基础上将带宽从50 km更换为25 km。从回归结果来看,D×post的系数均在统计水平上显著为正。这说明前端污染治理不仅有利于企业生产效率的提升,而且生产效率的提升效应大于成本增加效应,从而扩大了企业的生产规模,增加了就业量。
2. 市场选择效应
其次,本文通过进入退出机制来验证前端污染治理的市场选择效应。对于企业进入退出市场的界定,本文采用“三年判断准则”。⑥根据数据特征,存在间断存在企业,如果将这些企业纳入新进入企业可能导致分析偏误,本文将其划分为持续存在企业。此外,该部分样本无法运用拟断点回归模型,均采用断点回归模型,并用企业生产率衡量新进入企业和退出企业的市场表现。表3中的模型(1)—模型(4)为新进入企业和退出企业的生产率回归结果。从回归结果来看,虽然退出企业的生产效率没有显著变化,但控制实验组中新进入企业明显具有更高的生产效率。这意味着前端污染治理使得效率高的企业得以进入和存活,从而提高了市场的整体生产效率。⑦
为深入分析市场选择效应,有必要进一步考察新进入企业与退出企业的生产效率与其生产规模是否具有一致的变化趋势,这直接关系着企业的就业量。为此,我们将被解释变量更换为企业产出的对数值。具体回归结果参见表3中的模型(5)—模型(8)。从回归结果来看,实验组新进入企业明显具有更大的生产规模,能够吸纳更多的就业;而退出企业在生产规模上并没有显著变化,这与退出企业的生产率表现相一致。这说明前端污染治理对就业的市场选择效应主要表现为提高企业进入门槛,使新进入企业具有更高的生产效率和生产规模,从而吸纳更多的就业。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| 样本 | 新进入企业 | 退出企业 | 新进入企业 | 退出企业 | ||||
| 带宽( km) | 58 | 43 | 112 | 103 | 40 | 25 | 72 | 104 |
| 就业的跳跃 | 0.143** | 0.124* | 0.024 | 0.046 | 0.220*** | 0.158* | 0.065 | −0.008 |
| (0.072) | (0.070) | (0.044) | (0.048) | (0.081) | (0.087) | (0.178) | (0.117) | |
| 核分布函数 | triangular | uniform | triangular | uniform | triangular | uniform | triangular | uniform |
| 带宽准则 | mse | mse | mse | mse | mse | mse | mse | mse |
| 协变量 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 有效样本量 | 9 779 | 6 872 | 9 858 | 4 093 | 6 395 | 3 724 | 5 254 | 8 765 |
| 样本量 | 63 348 | 63 348 | 23 274 | 23 274 | 63 348 | 63 348 | 23 274 | 23 274 |
3. 替代效应
由前端污染治理引发的技术改进不仅会提升企业的生产效率,产生正向的规模效应,从而促进就业,还会从反方向形成资本对劳动的替代效应,造成就业损失。因此,我们采用资本与劳动之比的变化来考察要素间的替代关系,并将被解释变量更换为企业的资本劳动比值(k/l),即固定资产净值年平均余额与全部从业人员年平均人数的比值。具体估计结果参见表4。在表4中,模型(1)与模型(2)选用50 km带宽,模型(3)与模型(4)将带宽更换为25 km。从回归结果来看,模型(1)—模型(4)中D×post的系数均在统计水平上不显著。这说明前端污染治理引致的技术改进并没有产生资本对劳动的替代效应,即没有造成就业损失。
| (1) | (2) | (3) | (4) | |
| D×post | −0.106
(3.014) |
0.426
(3.512) |
−1.946
(2.943) |
−1.176
(3.817) |
| liq_ratio | −145.293*** (10.460) |
−141.371*** (8.739) |
||
| fixed_turnover | −0.154*** (0.051) |
−0.254*** (0.062) |
||
| lia_asset | 3.245
(2.821) |
5.423
(5.019) |
||
| profit_ratio | −0.013*** (0.000) |
−0.013*** (0.000) |
||
| ownership | −6.067*** (1.402) |
−4.970** (1.818) |
||
| _cons | 76.778*** (1.564) |
162.311*** (6.627) |
86.397*** (1.452) |
169.006*** (6.637) |
| 年份固定效应 | 控制 | 控制 | 控制 | 控制 |
| 省份固定效应 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 84 997 | 81 344 | 37 383 | 35 913 |
| adj. R2 | 0.024 | 0.173 | 0.026 | 0.179 |
综上所述,前端污染治理主要通过规模效应和市场选择效应提升了企业的就业水平。前端污染治理激励企业通过研发和技术升级以控制生产过程中的污染,虽然研发和设备投入增加了企业的生产运营成本,但是企业的生产效率也得到了提升,并且生产率提升效应要大于成本增加效应,最终使得企业扩大了生产规模,吸纳了更多的劳动力,形成正向的规模效应。而且从市场动态角度看,前端污染治理使得具有一定规模的高效率企业进入,提高了市场的生产效率和规模,进而使整个市场吸纳了更多的就业。此外,企业技术的改进,并没有产生资本对劳动的替代效应,从而避免了就业损失。
(三)有效性检验
拟断点回归模型结合了断点回归与倍差法的思想,该模型的成立暗含着如下假设:断点附近的分组是随机的;实验组和对照组中企业的经营活动具有相似性;政策实施前实验组和对照组具有相同的就业趋势。为此,本部分对以上假设进行一一验证,并就断点位置、预期效应和“两控区”政策干扰加以检验。
1. 协变量的连续性检验
如果企业特征变量在断点处发生了明显的跳跃,那么就业在断点处的跳跃就不能完全归因于前端污染治理政策的实施,本文的因果推断也就失去了效力。为此,我们一方面在特征化事实中已通过画箱体内平均值的散点图和拟合曲线鉴定了企业特征变量在断点处的连续性,另一方面本部分进一步运用拟断点回归模型,将被解释变量更换为企业特征变量,并依次检验其在断点处的连续性。表5报告了拟断点回归模型下企业特征变量在断点处的D×post系数估计值。列(1)控制了年份和省份固定效应,列(2)加入了企业所有制变量和行业固定效应。列(3)与列(4)在列(1)与列(2)的基础上将带宽从50 km更换为25 km。结果显示,所有回归结果均在统计水平上不明显。这说明特征变量在断点处是连续的,即本文的估计结果有效。
| (1) | (2) | (3) | (4) | |
| liq_ratio | 0.008(0.008) | 0.009(0.008) | 0.006(0.010) | 0.009(0.010) |
| fixed_turnover | 1.479(2.556) | 1.409(2.494) | 3.753(3.731) | 3.568(3.880) |
| lia_asset | 0.002(0.031) | −0.003(0.025) | −0.011(0.028) | −0.014(0.023) |
| profit_ratio | −0.541(0.522) | −0.592(0.604) | −0.662(0.925) | −0.766(1.048) |
2. 个体对指派的精确控制检验
在采用拟断点回归模型时,如果个体事先知道分组规则,并通过自身的努力控制指派变量,那么个体则可以自行选择进入处理组或控制组,导致在断点附近的内生分组失去随机性,进而引起拟断点回归失效。为此,我们需要检验个体能否精确操控指派。本文采用McCrary(2008)的方法,检验指派变量在断点处的连续性。若密度函数分布不连续,则可能存在对指派的精确操控,否则可认为没有精确操控。图3是指派变量的密度函数图。从图中可以看出,企业与省份边界之间的距离变量在断点处并没有显著跳跃。这说明指派变量在断点处的分布是连续的,个体并不能精确操控指派变量,即本文的回归结果有效。

|
| 图 3 指派变量的密度函数图 |
3. 平行趋势检验
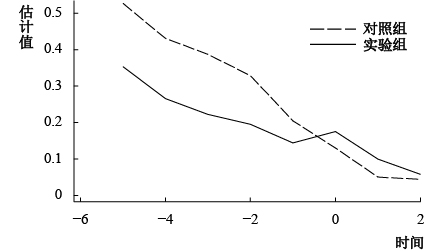
拟断点回归模型兼具断点回归和双重差分法的特征。因此,我们的模型不仅要满足断点回归的假设条件,也有必要检验企业就业的时间趋势,以保证双重差分法的平行趋势假定成立。如果在实施清洁生产政策前,实验组和对照组并不具有相同的就业趋势,那么双重差分法的回归结果就会失效。为此,我们将年份拆分成每一年的虚拟变量,分别对实验组和对照组进行回归估计,根据其估计系数画出对应的就业时间趋势图。从图4可以看出,在政策实施前,实验组和对照组的就业趋势基本是平行的;在政策实施当年,实验组的就业趋势从下降变为上升,与对照组的就业趋势呈反向变化。这说明本文的双重差分法满足平行趋势假定。
|
| 图 4 就业的时间趋势 |
4. 断点位置检验
在拟断点回归中,我们将−25 km和20 km处假定为断点进行回归,比较真实断点与假定断点处的回归结果差异。⑧具体回归结果参见表6中的模型(1)和模型(2)。在表6中,断点位置−25 km表示将−50 km至−25 km的区域与−25 km至0 km的区域相比较,由于在−25 km这一假设断点处并没有真正实施清洁生产政策,因此在−25 km这一断点处的回归系数应该不存在显著变化。从回归结果来看,−25 km和25 km处D×post的系数均在统计水平上不显著。这说明在省份边界处的确存在断点特征,满足拟断点回归的基本假设。
| (1) | (2) | (3) | (4) | (5) | (6) | |
| 断点位置检验 | 预期效应检验 | “两控区”政策冲击检验 | ||||
| D×post | −0.044
(0.079) |
0.045
(0.040) |
0.198** (0.088) |
0.231** (0.093) |
0.146* (0.078) |
0.168** (0.070) |
| D×pre1 | 0.090
(0.093) |
0.079
(0.082) |
||||
| D pre2 | 0.061
(0.072) |
0.035
(0.065) |
||||
| D×pre3 | −0.002
(0.083) |
0.018
(0.067) |
||||
| TCZ | −0.114
(0.072) |
−0.164** (0.063) |
||||
| liq_ratio | −0.022
(0.133) |
−0.276** (0.102) |
−0.162
(0.094) |
−0.233** (0.108) |
−0.174
(0.102) |
−0.208* (0.117) |
| fixed_turnover | −0.000*** (0.000) |
−0.000** (0.000) |
−0.000*** (0.000) |
−0.000*** (0.000) |
−0.000*** (0.000) |
−0.000*** (0.000) |
| lia_asset | 0.250*** (0.039) |
0.273** (0.099) |
0.265*** (0.058) |
0.327*** (0.073) |
0.258*** (0.071) |
0.288*** (0.088) |
| profit_ratio | 0.003* (0.002) |
0.000
(0.000) |
0.000
(0.000) |
0.000
(0.000) |
0.000
(0.000) |
0.000
(0.000) |
| ownership | −0.121*** (0.034) |
−0.088
(0.070) |
−0.104** (0.042) |
−0.088* (0.049) |
−0.103* (0.048) |
−0.087
(0.058) |
| _cons | 5.153*** (0.134) |
5.322*** (0.127) |
5.286*** (0.098) |
5.193*** (0.149) |
5.329*** (0.107) |
5.257*** (0.164) |
| 年份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 省份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 36 496 | 46 571 | 83 067 | 36 735 | 71 181 | 31 213 |
| adj. R2 | 0.064 | 0.078 | 0.077 | 0.084 | 0.082 | 0.096 |
| 注:(1)模型(1)与模型(2)的断点位置分别在−25 km和25 km处,其他模型的断点位置均在0 km处;(2)模型(3)与模型(5)选用的带宽为50 km,模型(4)与模型(6)选用的带宽为25 km。 | ||||||
5. 预期效应
在清洁生产政策开始正式实施前,当地企业可能会预期到清洁生产政策的实施,并在该政策实施前就开始采取措施。为此,我们将政策实施前的预期效应加入模型,进一步检验本文的估计结果是否存在偏误。回归结果参见表6的模型(3)和模型(4)。其中,D×pre1、D×pre2和D×pre3分别是政策实施前一年、前两年和前三年的时间虚拟变量与实验组虚拟变量的交互项。从回归结果可以看出,模型(3)与模型(4)中D×post的估计结果均在统计水平上显著为正,而且D×pre1、D×pre2和D×pre3的系数均在统计水平上不显著。这说明前端污染治理对就业的影响并没有受预期效应的影响,所估计的回归系数是可信的。
6. “两控区”政策影响的检验⑨
在本文的样本期间内,政府不仅颁布实施了地方清洁生产政策,而且早在1998年就颁布实施了“两控区”政策,考虑到实施“两控区”政策的城市与地方清洁生产政策的省份有交叉,我们有必要排除“两控区”政策措施对前端污染治理的就业效应的干扰。鉴于此,本文将“两控区”城市的虚拟变量加入回归模型,以进一步验证前端污染治理对企业就业的影响。具体回归结果参见表6中的模型(5)和模型(6)。其中,变量TCZ表示“两控区”城市的虚拟变量。从回归结果来看,D×post的系数值在统计水平上均显著为正。这意味着,在控制了“两控区”政策的影响后,前端污染治理依然有利于扩大企业的就业水平,而且这一结果是稳健的。
(四)异质性分析
为了进一步拓展分析前端污染治理对就业影响的异质性,本部分将D×post项与exposure相交乘,构建三重差分项,通过三重差分方法考察其对不同污染密集度行业和不同规模企业的影响差异。其中,exposure为企业异质性指标,包括行业污染密集度和企业规模。此外,我们还分样本考察前端污染治理对不同所有制企业的影响异质性。
1. 不同污染密集度的行业异质性
与非污染密集型行业相比,污染密集型行业的污染程度更高,对清洁生产政策更加敏感。因此,有必要考察前端污染治理对不同污染程度行业的影响异质性。其中,我们依据2003年、2005年和2006年的行业年均污染密集度刻画行业的污染密集程度。其中,行业污染密集度用行业煤炭消费量与行业工业总产值的比值表示。原因在于:一方面,根据2013年IEA Coal Information的报告,全国范围内约有80%的电力和70%的能源来自煤炭,煤炭的污染排放量远高于其他化学染料的污染排放量;另一方面,这一指标得到了经验研究的检验(Hering和Poncet,2014)。具体回归结果参见表7中的模型(1)和模型(2)。从回归结果可以看出,D×post×exposure的系数均在统计水平上显著为正。这说明随着行业污染程度的加深,前端污染治理对就业的提升作用也越明显。这意味着,相较于非污染密集型行业,污染密集型行业的生产效率和生产规模提升得更加明显,就业也随之增加。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| D×post×exposure | 0.061*** (0.019) |
0.063** (0.025) |
0.063*** (0.012) |
0.064*** (0.010) |
|||
| D×post | 0.130** (0.049) |
−0.018
(0.084) |
0.099* (0.052) |
||||
| liq_ratio | −0.133
(0.097) |
−0.201* (0.113) |
−0.102
(0.087) |
−0.166
(0.118) |
0.139
(0.138) |
−0.028
(0.147) |
−0.160** (0.072) |
| fixed_turnover | −0.000*** (0.000) |
−0.000*** (0.000) |
−0.000** (0.000) |
−0.000** (0.000) |
−0.001*** (0.000) |
−0.001
(0.000) |
−0.000
(0.000) |
| lia_asset | 0.265*** (0.057) |
0.323*** (0.072) |
0.260*** (0.057) |
0.321*** (0.073) |
0.065* (0.032) |
0.470*** (0.071) |
0.325*** (0.058) |
| profit_ratio | 0.000
(0.000) |
0.000
(0.000) |
0.000** (0.000) |
0.000** (0.000) |
0.000
(0.000) |
0.031*** (0.006) |
−0.002
(0.020) |
| ownership | −0.096** (0.041) |
−0.080
(0.048) |
−0.099** (0.042) |
−0.085* (0.048) |
|||
| _cons | 5.299*** (0.099) |
5.221*** (0.153) |
5.159*** (0.096) |
5.073*** (0.147) |
4.746*** (0.073) |
4.915*** (0.114) |
4.782*** (0.100) |
| 年份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 省份固定效应 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 | 控制 |
| 样本量 | 82 869 | 36 689 | 83 067 | 36 735 | 16 698 | 2 262 | 59 339 |
| adj. R2 | 0.078 | 0.085 | 0.093 | 0.101 | 0.035 | 0.075 | 0.061 |
| 注:(1)模型(1)、模型(3)、模型(5)—模型(7)选用的带宽为50 km,模型(2)与模型(4)选用的带宽为25 km;(2)对于所有制影响差异,模型删除了企业所有制协变量,且限于篇幅,未报告25 km带宽的结果(备索)。 | |||||||
2. 企业规模的异质性
企业规模不同,其技术改进所产生的效益也有较大的差异。规模越大,企业进行研发创新和技术改进的分摊成本越小,而技术改进所带的规模效益却越大,由此获利更多。鉴于此,我们利用企业规模与D×post的交互项,考察前端污染治理对不同规模企业就业量的影响。企业规模采用企业的固定资产净值年平均余额的对数值表示。具体回归结果参见表7中的模型(3)和模型(4)。从回归结果来看,D×post×exposure的系数均在1%的统计水平上显著为正。这说明随着企业规模的上升,前端污染治理对就业的提升作用越大,即大企业的就业增长要快于小企业的就业增长。
3. 不同企业所有制的影响差异
对于不同所有制的企业,环境管制对就业的影响也存在差异。相比于外商企业和民营企业,国有企业不仅与政府之间有着密切的联系,还会承担部分的社会职能。而就业问题不仅关系着民生,而且也是政府宏观调控的目标之一。前端污染治理对不同所有制企业就业的影响也可能有差异,可能对国有企业的影响会更加明显。基于此,本文依据企业所有制的差异,将样本划分为国有企业、外商企业和民营企业,分别考察前端污染治理对企业就业的影响差异。具体回归结果见表7。模型(5)和模型(7)分别采用国有企业和民营企业样本,D×post系数在统计水平上显著为正,而模型(6)中外资企业的就业没有发生变化。这进一步验证了在前端污染治理中,国有企业的就业显著增加,而民营企业次之。
六、结论与启示
随着环境质量的不断恶化,我国相继实施了不同的环境管制政策,进而也引发了关于环境保护与经济发展的一系列争论。其中的一个焦点问题是:环境管制会增加企业的生产和运营成本,追求利润最大化的企业是否会因此削减生产规模,从而造成就业损失?现有文献大多关注末端环境管制的经济效应,而忽略了前端污染治理的经济效应差异。本文将研究视角从末端环境管制转向前端污染治理,以清洁生产政策为例,运用拟断点回归方法考察前端污染治理在改善环境问题的同时,是否也会引起我国的失业问题,并详尽地探讨了其背后的影响机制和影响的异质性。
本文的研究结果表明:(1)总体而言,前端污染治理对企业就业起到了正向提升作用,说明前端污染治理并没有造成就业损失,反而对就业有促进作用。此外,经过一系列的有效性检验,我们还证明了本文的结果是有效的和稳健的。(2)从影响机制来看,前端污染治理主要通过正向的规模效应和市场选择效应提升了企业就业。该政策激励企业更新生产设备,虽然增加了企业的生产运营成本,但是企业的生产效率也得到提升,并且生产率提升效应要大于成本增加效应,最终导致企业扩大生产规模,吸纳了更多的劳动力,从而形成正向的规模效应。同时,前端污染治理使得具有一定规模的高效率企业得以进入和存活,整个市场吸纳了更多的就业量,从而形成正向的市场选择效应。此外,企业的技术改进,并没有产生资本对劳动的替代效应,从而避免了就业损失。(3)前端污染治理对企业就业的影响具有显著的异质性,其主要作用于污染密集型行业、大规模企业和国有企业。
本文的结论对于制定合理的环境政策,有效调整就业方向,实现环境改善、经济可持续发展和缓解就业压力具有重要的政策涵义。前端污染治理着重于对企业生产过程的全控制,激励企业改进生产技术,加大研发投入,从而有利于增强企业的创新能力和核心竞争力。因此,继续深化和推行前端污染治理政策不仅可以缓解就业压力,而且是实现环境和经济可持续发展的一项重要举措。本文研究还显示,前端污染治理对就业的影响具有异质性。这就要求政府在制定清洁生产政策时,要考虑行业间的差异,要通过一定的优惠激励政策,将非污染密集型行业纳入政策影响范围内。此外,政府要加大对小规模企业的技术升级引导,充分发挥前端污染治理政策的规模效应,缓解就业压力。
① 本文的污染密集型行业划分参照国务院2007年《第一次全国污染源普查方案》,明确我国11个重污染行业分别是:造纸及纸制品业,农副食品加工业,化学原料及化学制品制造业,纺织业,黑色金属冶炼及压延工业,食品制造业,电力、热力的生产和供应业,皮革、毛皮、羽毛(绒)及其制品业,石油加工、炼焦及核燃料加工业,非金属矿物制品业,有色金属冶炼及压延加工业。限于篇幅,本文未报告我国污染密集型行业与非污染密集型行业的就业统计数据(备索)。
② 此处的企业就业是指企业吸纳就业的能力;为了表达方便,以下都简称为企业就业。
③ 限于篇幅,本文未报告2001—2005年实施清洁生产政策的省份清单(备索)。
④ 带宽是指用于回归的观测值距离断点处的“窗”的宽度。这一宽度限定了断点两侧观测值的选取范围。如本文选取50km带宽,即指只选取距离断点50km内的观测值作为样本。
⑤ 为了保持行业代码的一致性,本文所用的《中国统计年鉴》时间跨度为2003—2006年,其中2004年的行业工业总产值为缺失值。
⑥ 三年判断准则是指通过对企业进行三年的观察来判断企业的状态:新进入企业是指前一期不存在,而当期和后一期均存在的企业;在位企业是指三期均存在的企业;退出企业是指前一期和当期存在,而后一期不存在的企业;仅存在一年的企业是指仅在当期存在的企业。
⑦ 采用50km带宽以及更换核函数为epanechnikov的回归结果均与表3保持一致。限于篇幅,未报告详细结果(备索)。
⑧ 断点位置检验是采用Lu 等(2016)的方法,将断点两边−100km至75km的区域划分为长度均为25km的7个等分区域,将相邻两个区域的边界假定为断点进行回归。由于篇幅限制,本文仅报告了假定断点为−25km和25km处的回归结果,其他假定断点处的回归结果均与其保持一致(备索)。
⑨ 1998年我国实施了“两控区”(特指酸雨控制区和二氧化硫污染控制区)的环境政策。
| [1] | 陈诗一. 节能减排与中国工业的双赢发展: 2009—2049[J]. 经济研究, 2010(3): 129–143. |
| [2] | 陈媛媛. 行业环境管制对就业影响的经验研究: 基于25个工业行业的实证分析[J]. 当代经济科学, 2011(3): 67–73. DOI:10.3969/j.issn.1002-2848.2011.03.009 |
| [3] | 刘伟明. 环境污染的治理路径与可持续增长: " 末端治理”还是" 源头控制”?[J]. 经济评论, 2014(6): 41–53. |
| [4] | 陆旸. 中国的绿色政策与就业: 存在双重红利吗?[J]. 经济研究, 2011(7): 42–54. DOI:10.3969/j.issn.1004-7778.2011.07.017 |
| [5] | 王勇, 施美程, 李建民. 环境规制对就业的影响——基于中国工业行业面板数据的分析[J]. 中国人口科学, 2013(3): 54–64. |
| [6] | 殷杉. " 末端治理”与" 前端预防”环保理念的差异分析[J]. 青岛科技大学学报(社会科学版), 2003(3): 32–34. DOI:10.3969/j.issn.1671-8372.2003.03.007 |
| [7] | 张彩云, 王勇, 李雅楠. 生产过程绿色化能促进就业吗——来自清洁生产标准的证据[J]. 财贸经济, 2017(3): 131–146. |
| [8] | 赵连阁, 钟搏, 王学渊. 工业污染治理投资的地区就业效应研究[J]. 中国工业经济, 2014(5): 70–82. |
| [9] | Berman E, Bui L T M. Environmental regulation and labor demand: Evidence from The South Coast Air Basin[J]. Journal of Public Economics, 2001, 79(2): 265–295. DOI:10.1016/S0047-2727(99)00101-2 |
| [10] | Brandt L, Van Biesebroeck J, Zhang Y F. Creative accounting or creative destruction? Firm-level productivity growth in Chinese manufacturing[J]. Journal of Development Economics, 2012, 97(2): 339–351. DOI:10.1016/j.jdeveco.2011.02.002 |
| [11] | Brown R S, Christensen L R. Estimating elasticities of substitution in a model of partial static equilibrium: An application to U.S. agriculture, 1947-1979[A]. Berndt E R, Field B C. Modeling and measuring natural resource substitution[M]. Cambridge, MA: MIT Press, 1981. |
| [12] | Ferris A, Shadbegian R, Wolverton A. The effect of environmental regulation on employment: An examination of the 1990 Clean Air Act Amendments and its impact on the electric power sector[R]. Working Paper # 14-03, 2014. |
| [13] | Gray W B, Shadbegian R J, Wang C B, et al. Do EPA regulations affect labor demand? Evidence from the pulp and paper industry[J]. Journal of Environmental Economics and Management, 2014, 68(1): 188–202. DOI:10.1016/j.jeem.2014.06.002 |
| [14] | Greenstone M. The impacts of environmental regulations on industrial activity: Evidence from the 1970 and 1977 Clean Air Act Amendments and the census of manufactures[J]. Journal of Political Economy, 2002, 110(6): 1175–1219. DOI:10.1086/342808 |
| [15] | Greenstone M, Hanna R. Environmental regulations, air and water pollution, and infant mortality in India[J]. American Economic Review, 2014, 104(10): 3038–3072. DOI:10.1257/aer.104.10.3038 |
| [16] | Hahn J, Todd P, Van Der Klaauw W. Identification and estimation of treatment effects with a regression-discontinuity design[J]. Econometrica, 2001, 69(1): 201–209. DOI:10.1111/ecta.2001.69.issue-1 |
| [17] | Hering L, Poncet S. Environmental policy and exports: Evidence from Chinese cities[J]. Journal of Environmental Economics and Management, 2014, 68(2): 296–318. DOI:10.1016/j.jeem.2014.06.005 |
| [18] | Imbens G, Kalyanaraman K. Optimal bandwidth choice for the regression discontinuity estimator[J]. The Review of Economic Studies, 2012, 79(3): 933–959. DOI:10.1093/restud/rdr043 |
| [19] | Jaffe A B, Stavins R N. Dynamic incentives of environmental regulations: The effects of alternative policy instruments on technology diffusion[J]. Journal of Environmental Economics and Management, 1995, 29(3): S43–S63. DOI:10.1006/jeem.1995.1060 |
| [20] | Lee D S, Lemieux T. Regression discontinuity designs in economics[J]. Journal of Economic Literature, 2010, 48(2): 281–355. DOI:10.1257/jel.48.2.281 |
| [21] | Liu M D, Shadbegian R, Zhang B. Does environmental regulation affect labor demand in China? Evidence from the textile printing and dyeing industry[J]. Journal of Environmental Economics and Management, 2017, 86: 277–294. DOI:10.1016/j.jeem.2017.05.008 |
| [22] | Lu Y, Wang J, Zhu L. Place-based policies, creation, and displacement: Evidence from China’s economic zone program[R]. Working Paper, 2016. |
| [23] | McCrary J. Manipulation of the running variable in the regression discontinuity design: A density test[J]. Journal of Econometrics, 2008, 142(2): 698–714. DOI:10.1016/j.jeconom.2007.05.005 |
| [24] | Milliman S R, Prince R. Firm incentives to promote technological change in pollution control[J]. Journal of Environmental Economics and Management, 1989, 17(3): 247–265. DOI:10.1016/0095-0696(89)90019-3 |
| [25] | Morgenstern R D, Pizer W A, Shih J S. Jobs versus the environment: An industry-level perspective[J]. Journal of Environmental Economics and Management, 2002, 43: 412–436. DOI:10.1006/jeem.2001.1191 |
| [26] | Olley G S, Pakes A. The dynamics of productivity in the telecommunications equipment industry[J]. Econometrica, 1996, 64(6): 1263–1297. DOI:10.2307/2171831 |
| [27] | Tsuyuhara K. Environmental regulation and labor market reallocation: A general equilibrium analysis[R]. Working Paper, 2015. |
| [28] | Walker W R. The transitional costs of sectoral reallocation: Evidence from the Clean Air Act and the workforce[J]. The Quarterly Journal of Economics, 2013, 128(4): 1787–1835. DOI:10.1093/qje/qjt022 |


