文章信息
 | 财经研究 2018年44卷第4期 |
- 姚海祥, 魏嘉辉, 马庆华,
- Yao Haixiang, Wei Jiahui, Ma Qinghua.
- 人口预期寿命与退休年龄
- Life expectancy and retirement age
- 财经研究, 2018, 44(4): 62-75
- Journal of Finance and Economics, 2018, 44(4): 62-75.
-
文章历史
- 收稿日期:2017-10-12

2018第44卷第4期
一、引 言
随着中国经济社会的发展,医疗水平不断提高,人口预期寿命也变得越来越长。2016年中国统计年鉴显示,在过去的30多年间,中国人口预期寿命从1981年的67.77岁增长到了2015年的76.34岁。在国务院发布的《国家人口发展规划(2016−2030年)》中,更是预测了在2030年,中国人口预期寿命将达到79岁。预期寿命的延长加剧了中国的人口老龄化现状,并给中国的养老事业带来了越来越大的压力。殷俊等(2012)曾建立了养老金精算模型,估算中国养老金未来90年的收入和支出水平,认为在过去的养老保险政策下也许难以实现养老金收支的平衡。为了缓解长寿带来的养老金支付压力,目前中国正拟出台延迟退休政策来应对寿命延长导致的人口老龄化问题。
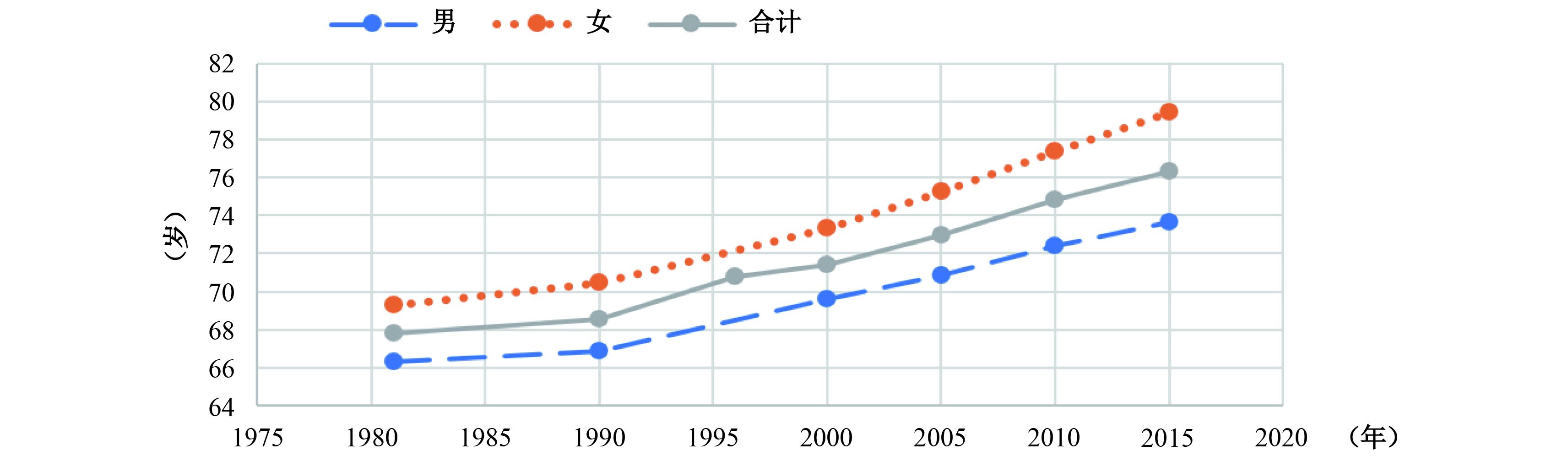
|
| 图 1 中国人口预期寿命延长情况(1981—2015年) |
是否应该延迟退休,仍然存在很多争议。赞成者一般认为延迟退休能够增加劳动力的供给,提高社会的产出,由此给老年生活提供更多的保障。Lacomba和Lagos(2006)认为,延迟退休在一定程度上也许能够提高劳动力的供给水平,同时提高养老金的收入,进而缓解长寿带来的养老压力。Kalwij等(2010)使用OECD中22个国家从1960−2008年的统计数据,发现老年人就业与年轻人不存在替代的关系。林宝(2014)在考虑实际的就业状况和保障机制后,提出了具体的延迟退休方案,并测算了延迟退休将有效改善职工养老保险资金的平衡状况。但也有相当一部分学者认为,延迟退休并不一定能缓解长寿带来的养老压力。Michello和Ford(2006)认为美国提出的延迟退休政策和提出的降低失业率的目标是相矛盾的。Casamatta和Paoli(2012)通过对不同行业的失业率、人均寿命和法定退休年龄进行比较,模拟出了最优的退休年龄,并发现现行的退休年龄下的失业率会比延迟退休后的更低。张熠(2011)建立了连续时间养老金收支模型,考察延迟退休对养老金余额的影响,提出了延迟退休年龄是由很多复杂因素决定的,而延迟退休不一定能减轻政府在养老保险方面的负担。阳义南等(2014)构建了关于养老金的期望精算现值模型,通过赋值模拟计算不同退休年龄能得到的具体养老金,结果发现延迟退休可能减少也可能增加养老金给付,主要取决于参保人的性别和参保年龄。Weller(2006)、Aubert和Duc(2013)出于公平性的考虑,认为延迟退休可能会不利于不同群体之间的收入再分配。总的来说,退休行为由很多复杂的因素决定,是否应该延迟退休,如何延迟退休,仍然存在很大的争议。
然而,从国际对比的角度来看,按照中国目前的人口预期寿命,现行的法定退休年龄处于世界上的低水平。世界上大多数国家都通过法律规定了退休的年龄,从2013年世界银行HDNSP养老金数据库中可以得到151个国家的法定退休年龄和各国人口预期寿命的样本。①从样本中发现,男性最低平均退休年龄为61岁,女性最低平均退休年龄为59岁;男性平均预期寿命为69岁,女性平均预期寿命为74岁。而根据2016中国统计年鉴,中国男性平均预期寿命为73.64,女性平均预期寿命为79.43;男性最低退休年龄为60岁,女性最低退休年龄为50岁。可以用平均法定退休年龄与预期寿命的比值来衡量法定退休年龄的高低:
由表1可见,无论是男性还是女性,中国最低退休年龄和预期寿命之比均低于国际水平。利用以上数据作单变量回归,令RAM表示男性退休年龄,RAF表示女性退休年龄,LEM表示男性预期寿命,LEF表示女性预期寿命。由此可以分别得到:
| 解释变量 | 被解释变量:RAM、RAF | |||
| 参数OLS估计 |
|
我国RAM预测值
(基于2016年数据) |
||
| 截距 | 斜率 | |||
| LEM | 43.17338***(18.15) | 0.26067***(7.64) | 0.2766 | 62.36912 |
| LEF | 45.16143***(16.04) | 0.19295***(5.12) | 0.1439 | 60.48745 |
| 注:括号中为t值,*表示p<0.1,**表示p<0.05,***表示p<0.01。 | ||||
| $RAM = 43.17338 + 0.26067LEM$ | (1) |
| $RAF = 45.16143 + 0.19295LEM$ | (2) |
从回归结果看,在国际上这种人口预期寿命和法定退休年龄的线性关系下,中国男性退休年龄应为62.37岁,女性退休年龄应为60.49岁。实际上,目前已经有部分国家直接或间接地建立起了人口预期寿命和退休年龄之间的调整机制。例如,丹麦以保持退休后剩余的寿命为基础,随着预期寿命的变化而调整法定退休年龄;英国则以保持养老金缴费年数和领取年数不变的原则来调整退休年龄。所以,有部分专家学者认为可以参考和借鉴国外的相关经验,建立人口预期寿命和法定退休年龄之间的调节机制。王晓军等(2015)参照国际法定退休年龄和人口预期寿命数据,通过实证分析发现,人口预期寿命和法定退休年龄是正相关的,并认为国际上的退休经验值得我们参考和借鉴。综上所述,我国是否也应该建立这种预期寿命和退休年龄之间的弹性调整机制,由此看来具有非常高的研究价值。
本文的研究基于交叠世代模型(Overlapping generations model,OLG)。交叠世代模型最初由Samuelson(1958)提出,之后由Diamond(1965)扩展为跨期动态模型,是基于一般均衡的框架,考察微观主体行为对整个宏观经济的影响,非常适合用来研究退休的相关问题。目前国内外已经有很多文献使用了交叠世代模型来分析养老保险政策的问题。在经典形式的两期交叠世代模型上,Casamatta(2000)研究了存在不同个体劳动生产率的交叠世代模型。杨再贵(2008)分析了交叠世代模型中各参数对养老金余额以及各期消费和效用的影响,研究认为养老金个人缴费由于对储蓄有完全替代的作用,即养老金个人缴费率对人均资本没有影响,而公共养老金缴费率的增加会使人均资本下降。胡仕强等(2011)通过建立随机的交叠世代模型,提出了两种养老金改革方案,包括无养老金体制和减少社会统筹、增加个人账户,并通过赋值模拟说明这两种方案下都能得出人均资本和长寿之间的关系是正相关的。也有学者在交叠世代模型中将人力资本因素加入考虑,将其扩展成三个时期的形式,研究存在内生增长的模型形式。Pecchenino和Pollar(2002)就在基础的两期交叠世代模型基础上加入了对儿童时期的人力资本投资,将其扩展成了三期模型来分析人口老龄化问题。乐菡(2016)在交叠世代模型中加入学习期,把传统的两期模型扩展成了三期,并分析研究了养老金发放水平的影响因素,发现寿命的延长会使个人养老金发放水平上升,而公共养老金发放水平必须减少才能使整个经济框架均衡。如果从效用函数的角度进行划分,交叠世代模型还可以被区分为利己模型和利他模型。杨丹妮等(2013)在交叠世代模型中嵌入了老一辈人对年轻一辈人的单方向利他因素,来研究模型中各变量的关系。刘庆彬等(2011)在模型中加入了是否赡养老人的不确定性,包括赡养老人的利他形式和不赡养老人的利己形式,来研究政府是否提供保险对经济增长的影响。总而言之,国内外还有许多文献利用交叠世代模型研究了养老保险,这里暂且先不作过多的论述。
过去已有部分文献探讨了建立人口预期寿命和法定退休年龄的调节机制,如王晓军等(2015),但很少有文献从理论模型的角度展开论证。也有部分文献利用交叠世代模型研究过预期寿命和退休年龄的关系,但没能解出两者间的具体算法,如曾燕(2013)、康传坤(2014)。而本文在两期交叠世代模型的基础上,加入退休因素,从个人行为、企业行为、政府行为、资本市场均衡四个方面建立整个宏观经济学框架,基于社会计划者的角度,通过最优化求解和赋值模拟的方法,解出人口预期寿命和退休年龄之间的调整算法,并根据算法给出两者相应的调整对照表。根据计算的结果,建议在2030年前逐步延迟退休年龄至65岁。本文的结论希望能丰富和发展交叠世代模型在延迟退休问题上的应用,同时在这一问题上给予政府一定的参考价值。
二、理论模型
假设在封闭的经济环境下,存在为数众多的企业、个人以及唯一的政府。在时期的设置上,暂时不考虑积累知识或者人力资本的青年期,而假设个人一生中只经历两个时期:第一个时期是参加工作的中年期,第二个时期是工作一段时间后退休的老年期。通常OLG模型假设一期约为25~30年,本文令30年为一期,把21~50岁作为中年期,51~80岁作为老年期。同时,假设时期
在中年时期,中年人参与工作获得工资,并按一定比例缴纳养老金后用作消费和储蓄。用
| ${C_{1t}} = \left( {1 - \tau } \right){w_t} - {s_t},$ | (3) |
其中:
在老年时期内,个人存在两种状态,分别是参加工作和退休。假设没有人愿意度过没有工资收入的真空期,都会坚持工作直到法定退休年龄。②设每个时期的时间为1,从老年期开始计算,退休的时间为

|
| 图 2 个人一生状态的设置 |
在老年时期,个人在退休前会继续参加工作并获得工资,而退休后不会有任何工资收入。整个老年时期的消费需要依靠退休前参加工作的工资收入和积累的储蓄,以及退休后政府发放的养老金提供。根据《国务院关于完善企业职工基本养老保险制度的决定》(国发[2005]38号)中的规定,把政府发放的养老金分为两部分:一是个人账户养老金,由个人按工资比例缴纳;二是公共账户养老金,由企业按工资比例缴纳。假设在中年期,个人参加工作要按工资比例缴纳个人账户养老金,而在老年期不需要。④同时,中年时期所积累的储蓄和缴纳的个人账户养老金,在老年时期领取时会获得一定的利率回报。另外,为了模型计算简单,假设老年人死亡之前会把所有的资源消费完。用
| ${C_{2t + 1}} = \beta {w_{t + 1}} + \left( {1 + {r_{t + 1}}} \right)\left( {{s_t} + {I_t}} \right) + \left( {d - \beta } \right){Q_{t + 1}},$ | (4) |
其中:
假设个人一生的效用由中年时期和老年时期的消费组成,用对数函数来描述消费所获得的效用,那么个人一生的效用可以用以下的函数表示:
| ${U_t} = \ln C_{1t} + \theta d\ln {{(C_{2t + 1}/d)}}$ | (5) |
其中:
(一)个人行为。个人的目标是在中年、老年时期的预算约束下实现效用最大化:
| $\left\{ \begin{array}{l}{{{Max}} _{\left\{ {{s_t}} \right\}}}{U_t} = \ln C_{1t} + \theta d\ln \frac{{C_{2t + 1}}}{d},\\s.t{.}C_{1t} = \left( {1 - \tau } \right){w_t} - {s_t},\\C_{2t + 1} = \beta {w_{t + 1}} + \left( {1 + {r_{t + 1}}} \right)\left( {{s_t} + {I_t}} \right) + \left( {d - \beta } \right){Q_{t + 1}}\end{array} \right. $ | (6) |
个人一生效用最大化问题实际上是在预算约束下个人如何分配中年消费
| $\theta d\left( {1 + {r_{t + 1}}} \right)C_{1t} = C_{2t + 1}$ | (7) |
式(7)表明,一生效用最大化时,老年时期的一单位消费所得到的效用等价于
(二)企业行为。假设企业在完全竞争的环境下生产完全同质的产品,该产品可以满足所有人的消费需求,并令其价格为1。用包含技术进步的Cobb-Douglas生产函数来表示企业的生产行为:
| ${Y_t} = AK_t^\alpha {\left( {{N_t} + \beta {N_{t - 1}}} \right)^{1 - \alpha }}$ | (8) |
其中:
| ${\pi _t} = {Y_{{t}}} - {r_t}{K_t} - \left( {{N_t} + \beta {N_{t - 1}}} \right)\left( {1 + \eta } \right){w_t}$ | (9) |
其中:
| ${\pi _t} = AK_t^\alpha {\left( {{N_t} + \beta {N_{t - 1}}} \right)^{1 - \alpha }} - {r_t}{K_t} - \left( {{N_t} + \beta {N_{t - 1}}} \right)\left( {1 + \eta } \right){w_t}$ | (10) |
为了求解企业利润最大化,在式(10)中分别对资本
| ${r_t} = \alpha A{M^{1 - \alpha }}k_t^{\alpha - 1}$ | (11) |
| ${w_t} = {{\left( {1 - \alpha } \right)A{M^{ - \alpha }}k_t^\alpha }}/{{(1 + \eta )}}$ | (12) |
这里
(三)政府行为。在模型中,政府部门的作用是管理养老金的缴纳和发放。按照目前我国养老保险政策有关规定,城镇居民按一定的工资比例缴纳个人账户养老金,企业按照一定的工资比例缴纳公共账户养老金。个人账户养老金由个人在工作时缴纳,退休后再发放。而公共养老金是“现给现付”的,由当期的中年人和还在参加工作的老年人缴纳给当期已经退休的老年人。
假设个人养老金按工资比例
| ${I_t} = \tau {w_t}$ | (13) |
公共部分养老金由当期参加工作的中年人和老年人所在的企业按工资比例
| $\left( {d - \beta } \right){N_t}{Q_{t + 1}} = \left( {{N_{t + 1}} + \beta {N_t}} \right)\eta {w_{t + 1}}$ | (14) |
式(14)简单变换一下,每一位还存活的老年人平均可以得到的公共账户养老金为:
| ${Q_{t + 1}} = {{\left( {1 + n + \beta } \right)\eta {w_{t + 1}}}}/{{(d - \beta )}}$ | (15) |
对
| ${{\partial {Q_{t + 1}}}}/{{\partial d}} = - {{\left( {1 + n + \beta } \right)\eta {w_{t + 1}}}}/{{{{\left( {d - \beta } \right)}^2}}} < 0$ | (16) |
式(16)说明,在工资和退休年龄保持不变的前提下,随着人均寿命的提高,同一时期内退休的老年人数增加,分配到每一个老年人手中的公共账户养老金就会减少。此时,如果政府仍然需要维持原来的公共养老金发放水平,就可能会造成养老金收支的不平衡,出现收不抵支的缺口。
(四)资本市场。Blanchard和Fischer(1988)具体推导了资本市场均衡的条件。假设资本完全折旧,资本市场均衡要求上一期的总储蓄构成了下一期期初的资本存量,由此可以得出市场均衡条件:
| ${N_{t + 1}}{k_{t + 1}} = {N_t}\left( {{s_t} + {I_t}} \right)$ | (17) |
该等式左边表示
| ${s_t} = \left( {1 + n} \right){k_{t + 1}} - {I_t}$ | (18) |
把式(13)代入式(18),可以得到:
| ${s_t} = \left( {1 + n} \right){k_{t + 1}} - {{\tau \left( {1 - \alpha } \right)A{M^{ - \alpha }}k_t^\alpha }}/{{(1 + \eta )}}$ | (19) |
式(19)表示个人储蓄关于人均资本的函数,但由于其中存在两个时间段的人均资本
(五)动态均衡。由式(11)−(13)、式(15)和式(19),可分别得到利率
| $\begin{array}{l}\theta d\left( {1 + \alpha A{M^{1 - \alpha }}k_{t + 1}^{\alpha - 1}} \right)\left[ {\displaystyle\frac{{\left( {1 - \alpha } \right)A{M^{ - \alpha }}k_t^\alpha }}{{1 + \eta }} - \left( {1 + n} \right){k_{t + 1}}} \right] - \displaystyle\frac{{\beta \left( {1 - \alpha } \right)A{M^{ - \alpha }}k_{t + 1}^\alpha }}{{1 + \eta }}\\[12pt] - \left( {1 + \alpha A{M^{1 - \alpha }}k_{t + 1}^{\alpha - 1}} \right)\left( {1 + n} \right){k_{t + 1}} - \displaystyle\frac{{\left( {1 + n + \beta } \right)\eta \left( {1 - \alpha } \right)A{M^{ - \alpha }}k_{t{{ + }}1}^\alpha }}{{1 + \eta }} = 0\end{array}$ | (20) |
为了构造经济框架的一般均衡,假设方程(20)存在唯一、稳定且无振动的解,令这个解为
(六)社会福利最大化。政府部门与个人、企业部门不同,是非盈利的机构。除了管理养老金的缴纳和发放外,政府也是养老保险政策的制定者,可以决定退休年龄,也就是常说的社会计划者(Social Planner)。从社会计划者角度出发,政府的工作是实现社会福利的最大化。取单个人的一生中效用函数作为代表性个体的福利函数,把从第0代开始到第
| $V = \theta d\ln \frac{{C_{20}}}{d} + \sum\limits_{i = 0}^\infty {{\xi ^i}\left[ {\ln C_{1i} + \theta d\ln \frac{{C_{2i + 1}}}{d}} \right]} $ | (21) |
其中:
| ${N_i}{k_i} + {Y_i} = {N_{i + 1}}{k_{i + 1}} + {N_i}C_{1i} + {N_{i - 1}}C_{2i}$ | (22) |
把式(8)代入式(22),并且进一步化简可以有:
| ${k_i} + A{M^{1 - \alpha }}k_i^\alpha = \left( {1 + n} \right){k_{i + 1}} + C_{1i} + {{C_{2i}}}/{{(1 + n)}}$ | (23) |
假设社会计划者能够通过控制退休年龄进而控制稳态下的人均资本存量,从而使社会福利达到最大。令社会福利函数式(21)在约束条件式(23)的约束下最大化,于式(21)中对稳态下的人均资本
| $k = {\left[ {{{(1 + n - \xi) }}/{{\alpha A\xi }}} \right]^{\frac{1}{{\alpha - 1}}}}M$ | (24) |
其中:
于是,将式(24)代入至式(20)中,可以得到表示人均资本处于动态均衡的方程式:
| $\begin{array}{l}\theta d\left( {1 + \alpha A{M^{1 - \alpha }}k^{\alpha - 1}} \right)\left[ {\displaystyle\frac{{\left( {1 - \alpha } \right)A{M^{ - \alpha }}k^{\alpha - 1}}}{{1 + \eta }} - \left( {1 + n} \right)} \right] - \displaystyle\frac{{\beta \left( {1 - \alpha } \right)A{M^{ - \alpha }}k^{\alpha - 1}}}{{1 + \eta }}\\[10pt] - \left( {1 + \alpha A{M^{1 - \alpha }}k^{\alpha - 1}} \right)\left( {1 + n} \right) - \displaystyle\frac{{\left( {1 + n + \beta } \right)\eta \left( {1 - \alpha } \right)A{M^{ - \alpha }}k^{\alpha - 1}}}{{1 + \eta }} = 0\end{array}$ | (25) |
本文意在得出个人效用最大化和社会福利最大化下的最优退休年龄,以及人口寿命变化对最优退休年龄的影响。把稳态下的人均资本式(24)代入到稳态下关于人均资本的方程式(25)中,可以得到稳态下的最优退休年龄的关系式:
| $\beta = \frac{{\theta d\left( {1 + n} \right)\left[ {\left( {1 - \alpha } \right)\left( {1 + n - \xi } \right) - \alpha \xi \left( {1 + \eta } \right)\left( {1 + n} \right)} \right] - \eta \xi \left( {1 - \alpha } \right)\left( {1 + n - \xi } \right)\left( {1 + n} \right) - \alpha \xi \left( {1 + \eta } \right){{\left( {1 + n} \right)}^2}}}{{\xi \left( {1 + \eta } \right)\left[ {\alpha \left( {1 + n} \right)\left( {1 + \theta d} \right) + \left( {1 - \alpha } \right)\left( {1 + n - \xi } \right)} \right]}}$ | (26) |
下面通过比较静态分析的方法,考察人口寿命变化对稳态下的退休年龄的影响,再通过算法优化和赋值模拟的方法,研究人口寿命变化在模型中是如何对最优退休年龄产生影响的。
三、比较静态和影响机制分析
目前对延迟退休政策是否有效的探讨主要集中在延迟退休是否会对就业和工资产生挤出的问题上。而本文从社会福利最大化的角度出发,通过计算得到了稳态下的工资、利率与退休年龄无关的结论。
(一)稳态下的利率、工资与最优退休年龄。将稳定状态下的人均资本式(24)分别代入到利率式(11)与工资式(12)中,可以得到稳定状态下的利率和工资:
| $r = {{(1 + n - \xi )}}/{\xi }$ | (27) |
| $w = {{\left( {1 - \alpha } \right)A}}/{{(1 + \eta) }}{\left[ {{{(1 + n - \xi )}}/{{\alpha A\xi }}} \right]^{\frac{\alpha }{{\alpha - 1}}}}$ | (28) |
其中:
对于稳态下的工资和退休年龄无关,根据式(12),可以得到:
| ${{\partial {w_t}}}/{{\partial \beta }} = - {{\left( {1 - \alpha } \right)\alpha A{M^{ - \alpha - 1}}k_t^\alpha }}/{{\left( {1 + \eta } \right)\left( {1 + n} \right)}} < 0$ | (29) |
当退休年龄提高时,会使得同一时期中参加工作的人数增加,进而导致工资下降,此时经济会偏离稳态水平,出现了我们所说的挤出效应。然而,当经济恢复到均衡状态中,根据式(24)有:
| ${{\partial k}}/{{\partial \beta }} = {\left[ {{{(1 + n - \xi )}}/{{\alpha A\xi }}} \right]^{\frac{1}{{\alpha - 1}}}}{{(2 + n)}}/{{(1 + n)}} > 0$ | (30) |
退休年龄的提高,会提高稳态下的人均资本水平。由式(12)可知,工资是由人均资本和退休年龄共同决定的。退休年龄的提高会产生工资下降的趋势,但又由于人均资本的提高带来了总产出的提高,进而增加了企业对劳动力的需求,又使工资回到了原来的水平。实际上本文认为,在短时间内,延迟退休的确可能会产生一定的挤出效应。然而从长期来看,这种挤出效应也许只是暂时的。当经济恢复到稳定状态时,延迟退休会提高劳动力的供给水平,带来更多的产出,增加人均GDP,由此为经济社会带来更多的就业机会,因此抵消了挤出的效应。类似地,Lacomba和Lagos(2006)认为长期以来延迟退休确实能增加劳动力的供给,而不是挤出就业和工资。Kalwij等(2010)通过22个国家和40多年的统计数据实证分析表明,老年人继续参加工作并不会对年轻人就业产生挤出,相反甚至可能会刺激年轻人的就业。
而对于稳态下的利率与退休年龄无关,从式(11)可以得到:
| ${{\partial {r_t}}}/{{\partial \beta }} = {{\alpha \left( {1 - \alpha } \right)A{M^{ - \alpha }}k_t^{\alpha - 1}}}/{{(1 + n)}} > 0$ | (31) |
随着退休年龄的提高,企业获得劳动力相对比较容易,会出现工资下降的趋势,企业获得资本相对会变得困难,利率出现暂时上涨的趋势。但根据式(11)可以知道,利率也是由退休年龄和人均资本共同决定的。而根据式(30),长期来看,在经济恢复到稳定状态的过程中,由于人均资本的提高,可能使企业获得资本变得容易,使利率又回复到了原来的水平。
所以,总的来说,由于本文考察的是一般均衡的模型框架,存在社会计划者的前提下,当退休年龄发生变化时,工资和利率的变化可能只是暂时的,最终将恢复到稳态水平。所以得出稳态下工资、利率和退休年龄可能是无关的结论。
(二)人口预期寿命最优退休年龄。化简式(26)的稳态下的最优退休年龄,可得以下函数:
| $\beta = {({e}/{g})} - {{\left[({eh}/{g}) - f\right]}}/{{(gd + h)}}$ | (32) |
其中系数
| $\left\{ \begin{aligned}& e = \theta \left( {1 + n} \right)\left[ {\left( {1 - \alpha } \right)\left( {1 + n - \xi } \right) - \alpha \xi \left( {1 + n} \right)\left( {1 + \eta } \right)} \right]\\& f = - \eta \xi \left( {1 - \alpha } \right)\left( {1 + n - \xi } \right)\left( {1 + n} \right) - \alpha \xi \left( {1 + \eta } \right){\left( {1 + n} \right)^2}\\& g = \alpha \theta \xi \left( {1 + n} \right)\left( {1 + \eta } \right)\\& h = \xi \left( {1 + \eta } \right)\left[ {\left( {1 + n} \right) - \left( {1 - \alpha } \right)\xi } \right]\end{aligned} \right.$ | (33) |
式(32)对人口预期寿命
| ${{\partial \beta }}/{{\partial d}} = {{(eh - gf)}}/{{{{\left( {gd + h} \right)}^2}}} > 0$ | (34) |
即当
| ${{{\partial ^2}\beta }}/{{\partial {d^2}}} = - {{(egh - {g^2}f)}}/{{{{\left( {gd + h} \right)}^4}}} < 0$ | (35) |
即随着预期寿命的延长,最优退休年龄提高的速度是下降的。从式(32)的函数形式上看,退休年龄
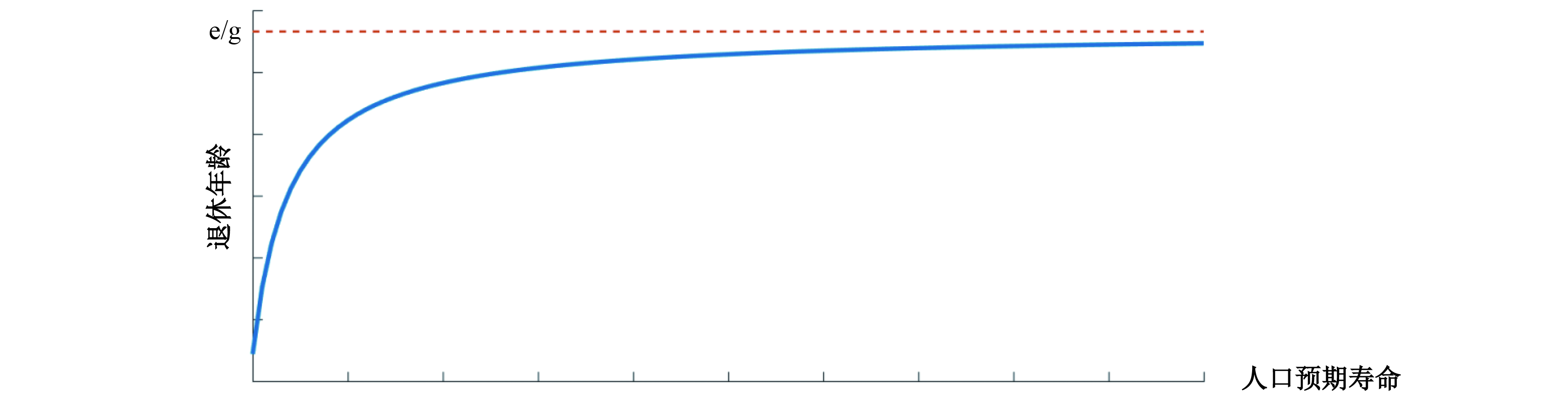
|
| 图 3 人口预期寿命和退休年龄的调整机制 |
从模型上看,随着人口预期寿命的提高,提高退休年龄一方面会增加个人一生的收入,由此可进行更多的消费;另一方面,为了应对人口寿命的延长,提高退休年龄还能增加劳动力的供给,增加社会上的总产出,并由此增加一个时期内可消费的总资源,实现社会福利的最大化。而当预期寿命缩短时,人们会相应地减少储蓄,此时降低退休年龄,能够保持人们的储蓄水平,增加资本存量,使总产出保持较高水平,由此实现社会福利的最大化。所以出现了人口预期寿命和退休年龄的正相关关系。然而,由于老年时期参加工作所获得的工资可能大多用于当期的消费,而不是储蓄,所以随着人口预期寿命的延长,提高退休年龄的过程中增加了较多的劳动力供给,而形成了较少的资本。当劳动力供给处于高水平时,想要通过继续提高退休年龄来增加社会产出的效果是较小的,从而一个时期内可消费资源的增加也是较少的。所以,随着预期寿命的延长,模型中最优退休年龄的提高幅度是减少的。
从现实生活中看,由于预期寿命和退休年龄的不断提高可能会持续增加劳动者的财富,而当财富积累到一定程度时,仅通过短期的投资回报就足够保障老年消费的需要,此时如果继续提高退休年龄,也许只会因为占用闲暇而降低效用。所以,这时候无论寿命如何延长,最优的退休年龄也不应该继续提高,而最终可能会趋向于一个稳定值。另外,本模型中没有考虑劳动者的身体健康问题。如果加入健康因素,建立一个随着年龄增长而减少劳动力供给的函数,可能更能支撑本结论,出现这样一个极限的退休年龄,这也是我们未来继续展开研究的方向之一。
四、赋值模拟和退休年龄测算
式(26)是模型求解出来的关于退休年龄的解析式,存在以下参数:人口预期寿命
(一)参数估计。
1. 人口预期寿命
2. 代际折现率
3. 资本收入份额
4. 效用折现率
(二)敏感性分析。以上参数中,资本收入份额和效用折现率难以准确测算,有必要分别进行敏感性分析。
1. 对参数资本收入份额
| 参数设置 | 最优退休年龄 |
|
|
|
|
|
|
|
|
|
由表3可见,设置的资本收入份额越高,最优退休年龄越低。一方面,这是因为当资本收入份额较高时,个人的老年消费生活会更依赖资本积累而不是参加工作赚取工资;另一方面,当资本收入份额较高时,社会总产出更多地由资本提供而非劳动力,此时退休年龄应设置更低。
2. 对参数效用折现率
| 参数设置 | 最优退休年龄 |
|
|
|
|
|
|
|
|
|
由表4可见,设置的效用折现率越高,最优退休年龄越高。效用折现率反映了老年时期的消费生活对中年期的重要程度,当效用折现率较高时,人们会更加关注老年时期的消费,此时提高退休年龄,能获得更多的收入,保障老年消费生活。
(三)人口预期寿命和退休年龄调整机制。基于模型的求解和参数估计,下面给出人口预期寿命和退休年龄的调整公式,以供政府参考。基于以上参数估计,得到以下参数估计表:
|
|
|
|
|
|
|
| 0.35 | 0.6001 | 0.2 | 0.08 | 0.1600 | 0.2284 |
以男性为例,将表5参数代入至式(26)中,假设退休年龄为RA,预期寿命为LE,通过换算可以得到人口预期寿命和退休年龄的调整公式:
| $RA = 204.5733 - {{47.6894}}/{{(0.0668LE + 4.9784)}}$ | (36) |
由式(36)可见,在社会资源约束下,不考虑健康因素时,极限退休年龄为204.57岁。实际上,假如人口预期寿命不断延长,相信老年人的健康状况也会变得越来越好,从而可参加工作的年限也会远远高于目前。由此,可以得到关于人口预期寿命和退休年龄的调整对照表:
| 预期寿命 | 退休年龄 | 预期寿命 | 退休年龄 | 预期寿命 | 退休年龄 | 预期寿命 | 退休年龄 |
| 68.69 | 55 | 72.62 | 59 | 76.78 | 63 | 81.18 | 67 |
| 69.65 | 56 | 73.64 | 60 | 77.86 | 64 | 82.32 | 68 |
| 70.63 | 57 | 74.67 | 61 | 78.95 | 65 | 83.48 | 69 |
| 71.62 | 58 | 75.72 | 62 | 80.06 | 66 | 84.65 | 70 |
《国家人口发展规划(2016−2030年)》预测中国2030年人口预期寿命达到79岁。根据本模型的结论,建议在2030年前根据寿命的延长逐步延迟退休年龄至65岁。
五、长寿风险造成的福利损失
长寿风险是指由于无法准确预期到自己未来的寿命,而可能无法做出保障老年生活的最优决策的风险。下面假设人口预期寿命在某一时期突然延长,而政府没有来得及根据上述调整机制调整退休年龄,考察这种情况下可能会带来的损失。
假设在
| 调整退休年龄 |
|
|
|
|
|
|
|
|
0.7880 | 0.3333 | 0.0948 | 0.2647 | 0.3359 | −2.8958 |
|
|
0.9667 | 0.5016 | 0.1032 | 0.2939 | 0.3040 | |
| 不调整退休年龄 |
|
|
|
|
|
|
|
|
0.7880 | 0.3333 | 0.0948 | 0.2647 | 0.3359 | −2.9565 |
|
|
0.9667 | 0.3333 | 0.0681 | 0.2647 | 0.2738 |
由表7可知,不存在调整机制时,在
通过对比可以发现,当不存在人口预期寿命和退休年龄的调整机制时,在保持养老金收支平衡的前提下,由于退休年龄没能及时根据人口寿命的延长而调整,平均发放的养老金可能会减少,这使得当代人单位时间的老年消费下降幅度相对较大,进而影响消费所获得的效用。如果此时政府想要维持养老金的发放水平,则可能导致养老金的收不抵支。而当存在人口预期寿命和退休年龄的调整机制时,由于退休年龄随着寿命的延长而提高,一方面增加了老年时期的收入,另一方面延迟了发放养老金的时间,使得老年时期的平均消费下降幅度相对较小。
根据表7还可以得到,当人口预期寿命从73.64岁增长到79岁时,如果不根据人口预期寿命而调整退休年龄,可能导致老年人单位时间得到的养老金减少
六、结论与政策启示
本文在两期交叠世代模型的基础上,加入退休因素,在市场完全竞争、充分就业和政府能够控制退休年龄的假设前提下,从社会计划者的角度,研究了经济处于稳态水平时人口预期寿命变化和退休年龄之间的函数关系。分析结果显示,人口预期寿命与社会福利最大化下的退休年龄可能是正相关的,并且呈现出负反比例函数的形式。同时,使用赋值模拟和参数估计的办法,计算出了人口预期寿命和退休年龄的调整公式,并由此给出了两者的调整对照表。最后通过反事实检验,发现如果不建立人口预期寿命和退休年龄之间的调整机制,突然的预期寿命变化可能造成社会福利损失。
基于研究的结论,本文建议政府建立人口预期寿命和退休年龄之间的调整机制。同时,根据《国家人口发展规划(2016−2030年)》中预测的人口预期寿命,在2030年前逐步将退休年龄延长至65岁。本文认为,人口预期寿命延长将给老年人的生活带来一定的压力。而根据人口预期寿命对退休年龄作出适当地调整也许能够提高老年人每年获得的养老金水平,进而缓解老年的消费压力。实际上,世界上已有很多国家建立起了退休年龄与平均预期寿命之间直接或间接的机制,中国可以学习和借鉴国际上的这种经验,并结合我国实际情况,制定适合我国未来人口寿命变化趋势的养老保险政策。
本文还存在一些不足之处。首先,本文模型的构建基于退休年龄由政府决定的假设,实际上个人是可以自由决定退休的,无法决定的只是养老金的发放时间,这在一定程度上不符合实际情况。但相信现实生活中,法定退休年龄是具有一定指导意义的,这让大部分人最终选择在法定的退休年龄退休,而非提前几年或推迟几年,因为很多人为了保险起见,不愿意度过完全没有工资收入的真空期。而法定退休年龄的指导作用到底有多大,相信会是另一个值得研究的方向。其次,本文没有考虑劳动者的身体健康情况,劳动者的身体情况将影响实际的劳动力供给,进而会对人口预期寿命和退休年龄之间的调整机制产生影响。第三,本文通过赋值模拟的方法测算出了人口预期寿命和退休年龄的调整公式,但参数估计过程中部分参数存在一定的量化困难,由此得到的调整算法的准确性还有待进一步检验。以上不足之处也将是我们未来继续研究的方向。
① 限于篇幅,这里不贴出具体数据。可以自行查阅世界银行数据库http://web.worldbank.org,其中各国法定退休年龄数据更新至2013年。
② 本文采用了退休年龄完全由政府控制的外生方式建模,而实际上政府能够决定的仅为领取退休金的法定退休年龄,而非实际的退休年龄。这在一定程度上不符合实际情况。但相信现实生活中,法定退休年龄是具有一定的指导意义的,这让大部分人最终选择在法定的退休年龄退休。
③ 按照假设,60岁退休可以计算出β=(60−50)/30=0.3333,73.64岁的人口预期寿命可以计算出d=(73.64−50)/30=0.788。
④ 在老年时期,缴纳的个人账户养老金会在退休后全部发回。按照模型假设,延迟退休参加工作与实际退休同属一个时期,不存在利率的回报,所以这里提前把个人账户养老金的缴纳和发放相抵消了。
⑤ 具体求解过程见附录。
⑥ 稳态条件求解过程略,但备索。
⑦ 其中i趋向于无穷。
⑧ 社会福利最大化求解过程略,但备索。
⑨ 详细证明过程略,但备索。
⑩ 模型中设置的利率r为一个时期所有储蓄的回报。假设个人每年做同样的储蓄,可以通过等比数列求和的方法计算利率r。
| [1] | 白重恩, 钱震杰. 我国资本收入份额影响因素及变化原因分析——基于省际面板数据的研究[J]. 清华大学学报(哲学社会科学版), 2009(4): 137–147. |
| [2] | 胡仕强, 许谨良. 长寿风险、养老金体制与资本积累[J]. 财经研究, 2011(8): 125–134. |
| [3] | 黄健元, 石晶晶. 基于BP算法的人口平均寿命预测[J]. 统计与决策, 2007(6): 60–62. |
| [4] | 康传坤. 人口老龄化背景下养老保险与退休年龄关系的研究[D]. 成都: 西南财经大学, 2014. |
| [5] | 乐菡. 基于三期OLG模型的老龄社会城镇职工基本养老保险发放水平影响因素研究——以上海市为例[J]. 老龄科学研究, 2016(1): 20–33. |
| [6] | 李志生, 吕勇斌, 刘恒甲. 长寿风险的识别与量化研究: 来自中国的数据[J]. 统计与决策, 2011(16): 72–74. |
| [7] | 连祥卿. 人口老龄化对劳动年龄人口的影响[J]. 同济医科大学学报, 1990(1): 55–58. |
| [8] | 林宝. 延迟退休年龄对养老金资金平衡的影响[J]. 财经问题研究, 2014(12): 41–46. DOI:10.3969/j.issn.1000-176X.2014.12.007 |
| [9] | 林忠晶, 龚六堂. 退休年龄、教育年限与社会保障[J]. 经济学(季刊), 2007(1): 211–230. |
| [10] | 马贤磊, 曲福田. 成本效益分析与代际公平: 新代际折现思路[J]. 中国人口•资源与环境, 2011(8): 22–28. |
| [11] | 王晓军, 赵明. 寿命延长与延迟退休: 国际比较与我国实证[J]. 数量经济技术经济研究, 2015(3): 111–128. |
| [12] | 魏翔. 基于闲暇时间−效用函数的居民消费研究——对中国数据的实证检验[J]. 经济科学, 2006(4): 104–113. |
| [13] | 谢世清. 长寿风险的创新解决方案[J]. 保险研究, 2011(4): 70–75. |
| [14] | 许伟, 陈斌开. 银行信贷与中国经济波动: 1993−2005[J]. 经济学(季刊), 2009(3): 969–994. |
| [15] | 阳义南, 曾燕, 瞿婷婷. 推迟退休会减少职工个人的养老金财富吗?[J]. 金融研究, 2014(1): 58–70. |
| [16] | 杨再贵. 企业职工基本养老保险、养老金替代率和人口增长率[J]. 统计研究, 2008(5): 38–42. |
| [17] | 殷俊, 黄蓉. 人口老龄化、退休年龄与基础养老金长期偿付能力研究[J]. 理论与改革, 2012(4): 73–76. |
| [18] | 曾燕, 郭延峰, 张玲. 基于长寿风险与OLG模型的延迟退休决策[J]. 金融经济学研究, 2013(4): 83–93. |
| [19] | 张熠. 延迟退休年龄与养老保险收支余额: 作用机制及政策效应[J]. 财经研究, 2011(7): 4–16. |
| [20] | Aubert P, Duc C, Ducoudré B. French retirement reforms and intragenerational equity in retirement duration[J]. De Economist, 2013, 161(3): 277–305. DOI:10.1007/s10645-013-9212-6 |
| [21] | Casamatta G, Cremer H, Pestieau P. The political economy of social security[J]. Scandinavian Journal of Economics, 2000, 102(3): 503–522. DOI:10.1111/sjoe.2000.102.issue-3 |
| [22] | Casamatta G, De Paoli C. Choosing the legal retirement age in presence of unemployment[J]. Recherches Économiques de Louvain / Louvain Economic Review, 2012, 78(1): 5–25. DOI:10.3917/rel.781.0005 |
| [23] | Chai J J, Horneff W, Maurer R. Optimal portfolio choice over the life cycle with flexible work, endogenous retirement, and lifetime payouts[J]. Review of Finance, 2011, 15(4): 875–907. DOI:10.1093/rof/rfr016 |
| [24] | Hugonnier J, Pelgrin F, St-Amour P. Health and (other) asset holdings[J]. The Review of Economic Studies, 2013, 80(2): 663–710. DOI:10.1093/restud/rds033 |
| [25] | Kalwij A, Kapteyn A, De Vos K. Retirement of older workers and employment of the young[J]. De Economist, 2010, 158(4): 341–359. DOI:10.1007/s10645-010-9148-z |
| [26] | Lacomba J A, Lagos F. Population aging and legal retirement age[J]. Journal of Population Economics, 2006, 19(3): 507–519. DOI:10.1007/s00148-005-0044-9 |
| [27] | Michello F A, Ford W F. The unemployment effects of proposed changes in social security’s " normal retirement age”[J]. Business Economics, 2006, 41(2): 38–46. DOI:10.2145/20060205 |
| [28] | Pecchenino R A, Pollard P S. Dependent children and aged parents: Funding education and social security in an aging economy[J]. Journal of Macroeconomics, 2002, 24(2): 145–169. DOI:10.1016/S0164-0704(02)00024-1 |
| [29] | Weller C E. Raising the retirement age for social security: Implications for low wage, minority, and female workers[R]. Working Paper: Center for American Progress, Washington, DC, 2005. |
| [30] | Zhang J S, Zhang J, Lee R. Mortality decline and long-run economic growth[J]. Journal of Public Economics, 2001, 80(3): 485–507. DOI:10.1016/S0047-2727(00)00122-5 |
 2018, Vol. 44
2018, Vol. 44


