
2. 江西财经大学 产业经济研究院,江西 南昌 330013;
3. 上海国家会计学院,上海 201702;
4. 上海财经大学 中国产业发展研究院,上海 200433
2. Institute of Industrial Economics,Jiangxi University of Finance and Economics,Nanchang 330013,China;
3. Shanghai National Accounting Institute,Shanghai 201702,China;
4. Institute of China Industrial Development,Shanghai University of Finance and Economics,Shanghai 200433,China
一、引 言
亚当•斯密曾在《国富论》(p.443)中指出,“钱来的容易去得快,在任何地方,消费的一般状况,与其说是受消费能力的支配,不如说受赚钱难易程度的支配”。本来这段话是用来描述垄断行业利润是如何被西方皇室奢侈挥霍的,但是对于国家的经济实践来说,产业政策特别是财政补贴带给企业的无疑是一笔不属于自己辛苦赚取的财富,也可能被相对容易地消费掉(刘海洋等,2012),从而带来一系列的资源错配。同时,中国的产业政策导向也在发生改变,十八届三中全会明确提出要保证市场对资源配置的决定地位。但是,在某些改革落后的产业领域仍然存在着各种影响企业决策的政策,所以有必要关注中国产业政策对各种经济结果的影响路径,探究产业政策对企业决策、生产和绩效的影响,这是当前供给侧结构性改革中十分重要的话题,可以为政策的进一步优化提供指导意见。本文从产业政策出发,探讨学界忽视已久的问题,即产业政策会带来企业间的工资差距吗?从直觉上说,产业政策的施行牵扯到资源分配问题,会直接影响企业间的效率差异,而企业的效率则关系职工的工资,建立产业政策与企业工资差异的关系需要以企业效率作为纽带。既有文献主要从企业出口、全要素生产率、创新产出和企业风险承担等角度来评估政府补贴、研发政策的经济效果(邵敏和包群,2012;肖兴志和王伊攀,2014;Aghion等,2015;毛其淋和许家云,2016),本文首次从企业员工平均工资这一视角对政府补贴的经济效果进行了评估。本文的贡献在于厘清了补贴政策对企业工资的影响机制,并运用1998−2007年中国工业企业数据进行了经验分析,为减少产业政策带来的扭曲和保证企业工资内涵式增长提供了相应的启示。
产业政策对企业效率究竟有何种作用?至今,学界仍有争议。新古典强调市场机制的自由运行,政府不应过多地干预市场,而这成为了产业政策失效时攻击政府的有力武器。但是,市场也并非万能,有时候完全靠市场可能无法实现国家层面的战略意图。战后日韩经济腾飞的经验就表明,产业政策对保护幼小(新兴)产业及提升传统产业起到过巨大作用。但基于各国产业演变的事实与经验研究又表明,产业政策并不总是有利于企业或者行业总体效率的提升(Harris和Robinson,2004;Kiyota和Okazaki,2010)。在中国,产业政策在改革开放近四十年间扮演重要贡献的同时也出现了诸多负面的影响,受数据可得性的限制,学界对产业政策的研究多聚焦于政府的研发或者补贴政策。邵敏和包群(2011)考察补贴政策的选择对象以及补贴程度的研究发现,地方政府在补贴对象和补贴程度上分别具有“扶持强者”“保护弱者”的特征;韩超(2014)在其基础上有所突破,利用Heckman两步估计考察了战略新兴行业;韩超等(2017)则细致地考察了多种产业政策及其与补贴的交互作用对企业(行业)绩效的影响。该系列文章有一个共同特点就是考虑了补贴政策的选择性问题。肖兴志和王伊攀(2014)通过建立企业政府模型,探讨了政府补贴对于企业创新的激励或者粉饰业绩的机制,虽然他们的研究以创新为结果,但仍是用研发投入衡量创新结果;张杰等(2015)将研究对象聚焦到了企业出口产品质量上,他们发现政府的财政补贴对出口产品质量具有抑制效应,而市场竞争则是促进效应;毛其淋和许家云(2016)探讨了政府补贴对企业风险承担的影响,他们认为适度的补贴提高了企业风险承担水平,而高额度政府补贴反而会降低企业风险承担水平;谭诗羽等(2017)则将研究视角转向了国产化政策,发现国产化政策显著提升了汽车零部件企业的生产率,主要得益于下游整车厂商对上游零部件厂商的纵向技术转移和溢出,随着市场竞争程度的下降,零部件企业也产生了技术改进的惰性。
出现违背政策初衷结果的原因大多在于产业政策更多地干预了市场竞争,政府代替了市场并限制了市场竞争;而促进市场竞争的政策看起来更有效率。因此,近期学者开始更多地考虑什么样的产业政策能够促进市场竞争,从而让企业在竞争中得到效率提升。江飞涛和李晓萍(2010)探讨了产业政策对竞争的作用,并提出了中国产业政策的缺陷和改进方向,他们认为,“中国式”的选择性产业政策具有强烈的行政干预性,限制了市场的竞争,从而造成了市场价格的严重扭曲,是不可为继的。Aghion等(2015)实证分析了具有维持或者提升市场竞争程度的产业政策是如何影响企业效率的。黄先海等(2015)扩展了上述发现,并指出了中国产业政策的三种优化设计方向。虽然有关产业政策对企业效率影响的研究颇多,但政府的产业政策目标不仅限于此,应让更多的劳动者共享企业发展的成果。产业政策会对企业的效率产生作用,而企业效率又与职工的最终收入有着密切联系,所以有必要将产业政策对企业效率的影响往前推进一步,即研究产业政策的施行是否会造成企业间的工资差距?这就将产业政策和收入差距问题联系在了一起,而收入差距问题是学界长期的研究热点,尤其是改革开放以来,随着中国分配政策的转变,市场机制逐步在资源配置中起决定性作用,作为初次分配结果的工资收入不均衡问题也日益突出,如果产业政策导致企业间存在过高的工资差距,那么最终造成的就是不同群体间的收入不均衡,会进一步影响国内的有效需求,从而影响经济增长,因此研究产业政策与工资差距的关系非常重要。已有很多文献研究了企业间的工资差距,比如出口企业相对于非出口企业来说有工资溢价(金祥荣等,2012;马述忠和王笑笑,2015)。Bernard和Jensen(1999)认为,出口企业的生产率优势能获得更多利润,因而支付更高的工资。而垄断企业比非垄断企业的平均工资要高(陆正飞等,2012;岳希明和蔡萌,2015),这部分研究给出的结论十分一致,为了缩小垄断部门与非垄断部门间的收入差距须破除行政垄断(崔友平,2015)。综上所述,虽然已有文献围绕产业政策以及企业间工资差距问题进行了大量研究,但是对于产业政策如何影响企业工资差距尚缺乏深入探讨,本文为企业工资差距影响因素分析提供了新的视角。由企业效率差异导致的收入差距是市场机制作用的客观结果,而当这种效率差异来自产业政策时,那么由于政府“有形之手”越界造成的效率变化就可能传导至企业间的工资差距上。
二、理论机制探讨
(一)产业政策、创新与工资。本文基于Aghion等(2015)的研究构建理论假说,在一个有两家企业参与竞争的伯川德模型中,企业既可以在同一行业内生产,也可以在不同行业。同一行业内的两个企业为了规避竞争会加大创新投入,从而有利于其占领市场,排挤对手;企业也可能选择异于竞争对手的行业寻求差异化发展。而对于政府来说,为了达到某些行业发展目的,希望更多的企业加入。此时,政府可以通过使用政策补助诱使企业加入到这一行业中来。企业为了占领市场会加大创新投资,这样产业政策就可以最大限度地激励企业创新,释放市场活力。Aghion等(2015)称这样的政策为“竞争兼容型政策”(competition-friendly),即在竞争性行业中,政府的产业政策不能只为少数企业“搭台唱戏”,而应该更加均等化,这样潜在的进入者才会加入。因此,只有符合以下条件才能说产业政策是有助的,能够提升企业效率:(1)产业政策诱使企业参与高强度的竞争;(2)产业政策并不会阻碍行业竞争甚至可能促使竞争。当然,上述发现也得到了经验数据的验正(Aghion等,2015;黄先海等,2105)。一旦政府的产业政策有效,那么目标行业的企业由于创新发展而带来的绩效提升必然有益于整个行业的工资水平提升。以补贴政策为例,补贴政策可以通过允许更多企业获得补助,从而激励潜在进入者进入市场,对行业在位者和进入者而言,只有将更大的精力投入到创新上,才能在更加激烈的竞争中生存下去,并实现提升企业生产率和创新水平的效果,员工的工资待遇也会随之提升,获得政策带来的福利水平改进。下面通过更为具体的理论模型来表达产业政策是如何影响企业间工资差距的。
(二)基本模型。假定市场中存在消费者和企业两个主体,与Melitz(2003)的设定一样,异质性企业在垄断竞争行业中生产差异化产品,假定差异化产品的真实消费指数Q采取CES形式,即:
| $Q = {\left[ {\int_{j \in J} {q{{(j)}^\beta }dj} } \right]^{1/\beta }},\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}\end{array}}\end{array}0 < \beta < 1$ | (1) |
其中,j代表差异化产品 ,J是行业产品的集合,q(j)表示对产品j的消费,
| ${\rm Max}\begin{array}{*{20}{c}}{}\end{array}U = {\left[ {\int_{j \in J} {q{{(j)}^\beta }dj} } \right]^{1/\beta }}s.t.\begin{array}{*{20}{c}}{}\end{array}\int_{j \in J} {p(j)q(j)dj} \le E$ | (2) |
那么,企业j的需求函数可以表示为(3)式,P表示差异化产品的总价格指数。
| $p(j) = {E^{1 - \beta }}{P^\beta }q{(j)^{ - (1 - \beta )}}$ | (3) |
| $P \equiv {\left[ {\int_{j \in J} {p{{(j)}^{ - \beta /(1 - \beta )}}dj} } \right]^{ - (1 - \beta )/\beta }}$ | (4) |
其中,U=Q为消费者效用,p(j)是产品j的价格,E=PQ为行业总消费额。
假设企业在获得政策补助后,会根据他们所感知的市场竞争程度权衡资源的分配,有以下两种途径使用这笔补助:作为生产的部分SP与研发的部分SR,SP+SR=1。其中生产部分被用于支付工人的工资和福利,投入品购买以及投资等各项费用,相当于直接的财政转移补贴了企业生产;而用于研发的部分是帮助企业降低生产成本、提高产品质量和管理效率等一系列旨在提高企业生产力的费用,这部分则间接通过企业效率影响人均工资水平,可以视为产业政策的竞争效应。因为设定劳动为唯一的投入要素,假设生产部分用于支付工资的占比为
| $R(j) = r(j) + (1 - \phi ){S_p}(j) = p(j)q(j) + (1 - \phi ){S_p}(j) = Aq{(j)^\beta } + (1 - \phi ){S_p}(j),\begin{array}{*{20}{c}}{}\end{array}A = P{Q^{1 - \beta }}$ | (5) |
其中,R(j)为加入了政策补助后企业j的总收益,r(j)则为企业通过销售产品所获销售收益。接下来,构造简单的生产函数:
| $y = \theta {h^\gamma },\begin{array}{*{20}{c}}{}\end{array}0 < \gamma < 1$ | (6) |
其中,h代表企业雇佣的人数,假设企业在没有摩擦的劳动力市场上搜寻h个雇员所需要的成本为b(
对于企业与雇员间的收益分配问题,本文利用讨价还价博弈(Bargaining Game)解决。在讨价还价之前,对参与者双方来说,企业和雇员的信息是充分的。一方面,企业为了生产而进行的沉没成本(sunk cost)投资是需要雇佣劳动力生产补偿的,所以他们需要雇员;另一方面,作为劳动力市场上的求职者,时刻面临失业选项(outside option wage=0)的冲击,所以他们需要工作。①因此,本文沿用Stole和Zwiebel(1996a,b)的设定,w(
①为了简化模型,本文取博弈双方的谈判权重,即谈判力(bargaining power)对等。实际上,本文接下来考虑的产业政策会扭曲这一关系(刘海洋等,2012),但这不影响本文的最后结论。
| $\partial [r(\theta ,h) - w(\theta ,h)h] /\partial {\rm{h}} = w(\theta ,h)$ | (7) |
| $w(\theta ,h) = {\beta \gamma}\cdot {r(\theta ,h)} /[(1 + \beta \gamma) h]$ | (8) |
可见,企业和雇员讨价还价的结果就是分别以1/(1+
| $\pi (\theta ) \equiv \mathop {\max }\limits_{h \ge 0} \left\{ {A{\theta ^\beta }{h^{\gamma \beta }}/(1 + \beta {\rm{ }}\gamma ) + (1 - \phi ){S_p} - b(\theta )h - {f_d}} \right\}$ | (9) |
| $\beta \gamma \cdot r(\theta )/(1{\rm{ + }}\beta \gamma ) = b(\theta )h$ | (10) |
再根据(8)式和(10)式以及政策因素的加入,可以得到如下的企业平均工资表达式:
| $\bar W(\theta ,h){\rm{ = }}\beta \gamma \cdot r(\theta ,h)/[(1{\rm{ + }}\beta \gamma ) \cdot h]{\rm{ + }}\phi {S_p}/h = b(\theta ) + \phi {\bar s_p}$ | (11) |
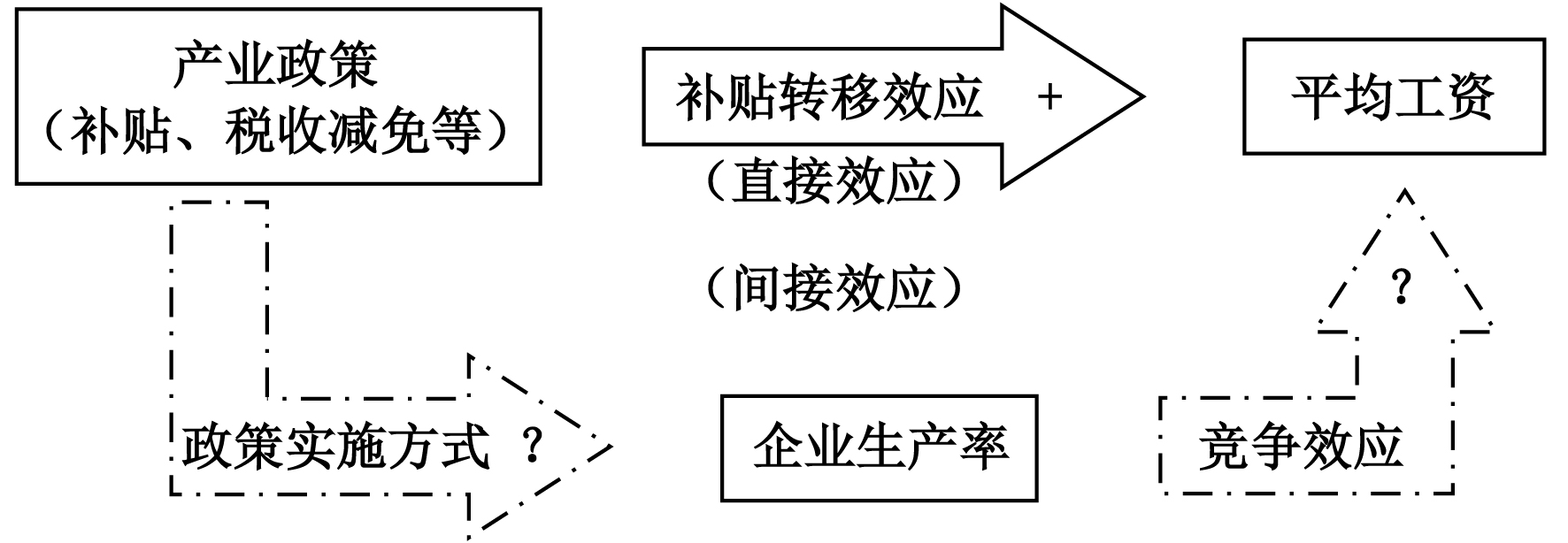
(三)影响机制探讨。企业平均工资表达式(11)表明,企业平均工资是随企业生产率的提高而增加的,效率高的企业雇佣能力更大的劳动力与之匹配,从而维持或者进一步提高其生产率。因此,企业为雇用到能力素质一流的劳动力,需要支付更高的工资(Bernard和Jensen,1995,1997;Helpman等,2012)。在考虑了产业政策变量之后,企业可能会将投入生产的政策补助用于发放工资,这相当于产业政策的直接补贴效应,也就是说即使两个企业拥有同样的效率,但是产业政策会扭曲这两个企业的工资差距。另外,基于Aghion等(2015)的分析,企业的创新研发投入强度SR是受产业政策导向影响的。一旦产业政策具有竞争兼容性,那么企业会将更多的政策补助用于创新而非生产,这样将会增大企业创新成功的概率或者达到降低生产成本的效果,从而传导为企业人均工资的提升。大量的经验研究也验证了上述发现,研发能够提升企业生产率(周亚虹等,2012;汤学良等,2015)。而员工的平均工资和企业生产率是正向关联的(Bernard和Jensen,1999),随着生产率的提高,工资也会相应提高。因此,企业将政策补助用于创新的部分能够通过效率这一中间渠道影响平均工资水平。综上所述,本文提出以下待检验的假说。
|
| 图 1 产业政策对工资的影响机制 资料来源:作者绘制。 |
假说:产业政策对企业工资的影响通过补贴效应和竞争效应两个渠道实现。其中,补贴转移效应为正,竞争效应的符号取决于产业政策对企业所处行业竞争程度的影响。当产业政策是以竞争兼容方式实施时,该类政策通过激励企业竞争提升工资水平,此时竞争效应为正;反之,产业政策会抑制企业创新,使企业效率降低,工资水平过低,此时竞争效应为负。产业政策对企业工资的总效应最终取决于两个效应之间的强弱关系。图1简洁地概括了这一假说,接下来通过计量模型检验上述假说。
三、实证策略、数据与变量
(一)实证策略。在阐述了产业政策对企业工资影响机制的基础上,本文依据(11)式构建如下线性方程,作为本文实证分析的基本计量方程,即:
| $\ln wag{e_{i\!jt}} = {\beta _0} + {\beta _1}industry\_polic{y_{i\!jt}} + {\beta _2}tf{p_{i\!jt}} + {{\beta }_3}{othercontro}{{l}_{i\!jt}} + \delta {D_{ijt}} + {\mu _{i\!jt}}$ | (12) |
其中,lnwageijt为行业j中企业i在t时期的平均工资,industry_policyijt为企业i在当年获得的补贴,tfpijt为企业的全要素生产率(Total Factor Productivity,TFP),othercontrolijt是影响企业工资的其他控制变量,Dijt为企业所有制、年份、地区和行业等虚拟变量,µijt为扰动项。
本文首先考虑在基本回归中只添加补贴这一核心解释变量,然后逐次添加其他控制变量,最后加入另一个关键变量全要素生产率,在这一过程中观察政策变量系数
| ${t\!f\!p_{i\!jt}} = {\gamma _0} + {\gamma _1}industry\_polic{y_{i\!jt}} + {{\bf{\gamma }}_2}{controlvariable}{{s}_{i\!jt}} + \sigma {D_{i\!jt}} + {\varepsilon _{i\!jt}}$ | (13) |
其中,tfpijt为行业j中企业i在t时期的全要素生产率,industry_policyijt为企业i在当年获得的政策补助,controlvariablesijt是影响全要素生产率的其他控制变量,Dijt表示企业所有制、年份、地区和行业等虚拟变量,
(13)式的
(二)数据来源与变量选择。本文研究对象为中国工业企业,数据来源于《中国工业企业数据库(1998−2007)》。该数据每年由国家统计局负责对年销售产值高于500万元的“规模以上”制造业企业进行调查,时间跨度长、企业样本量大,数据较为权威,且主要以企业财务指标为主,为科学地测算企业全要素生产率提供了便利。为了保证用于实证分析数据的质量,本文参考Cai和Liu(2009)、Brandt等(2012)以及一般公认会计准则,对原始数据库中财务指标的异常或缺失、从业人数小于8、销售收入小于500万元的样本进行了剔除,最终得到一个跨度10年,企业观测数量超过180万的非平衡面板数据集,该数据能够客观反映连续10年的中国工业企业变迁。
本文重点关注产业政策对企业平均工资的影响,被解释变量是企业平均工资(lnwage),用企业本年应付职工工资总额除以企业员工人数,再取自然对数得到,考虑到经济发展的周期性波动,工资总额数据使用消费价格指数(以1998年为基期)进行平减;政府的产业政策形式是多种多样的,除了行政管制和行政协调这类直接规制手段,实际操作中采用更多的是政府财政补贴、减免税和增值税等间接的经济手段。本文选取研究中最为常见的补贴强度(syratio)为核心解释变量,通过企业所获补贴金额与企业工业总产值之比来衡量。另外一个重要的解释变量企业生产效率,用全要素生产率(tfp)刻画,Olley和Pakes(1996)提供了TFP的估算方法,该方法能有效解决最小二乘法(OLS)存在的偏误问题。
除了关注的产业政策和反映企业绩效水平的全要素生产率之外,还有其他因素可能影响企业的平均工资,参照已有文献,选择如下控制变量:(1)企业规模,规模大的企业可以获得规模经济,从而有更高的平均工资。本文采用企业总资产的对数值来表示企业规模。(2)出口状态,出口企业往往代表了高技术、高品质产品,能够获得参与国际市场的工资溢价,本文用当年企业出口交货值是否大于零表示企业的出口状态。(3)人均资本,人均资本反映企业的技术水平与生产效率,人均资本高的企业往往有更高的工资。用实际资本存量与员工人数之比来刻画人均资本。(4)企业年龄,用数据报告年份减去企业创建年份计算。(5)考虑一些行政垄断对工资的影响,需要控制企业所有制性质,依据路江涌(2008)的方法,将企业分为国有企业(state)、民营企业(private)和外资企业(foreign);同时控制了年份、地区和行业虚拟变量。这些变量能够较好地控制企业的微观特征、时间、区域和行业效应。表1给出了主要变量的描述性统计。
| 变量 | 计算方法 | 均值 | 标准差 | 最小值 | 最大值 |
| 补贴强度(syratio) | 补贴值/企业工业总产值 | 0.0035 | 0.0802 | 0 | 59 |
| 平均工资(lnwage) | 平减后工资总额/员工总数,取对数 | 2.2643 | 0 .7311 | −7.8043 | 11.2286 |
| 全要素生产率(tfp) | OP方法估计所得,取对数 | 3.3924 | 1.1722 | −7.6345 | 11.3585 |
| 企业规模(size) | 企业总资产,取对数 | 9.5839 | 1.4223 | 0 .6939 | 18.6644 |
| 出口状态(export) | 企业出口交货值大于0为1,否则为0 | 0.2798 | 0.4489 | 0 | 1 |
| 人均资本(percapital) | 实际资本存量/员工总数 | 86.8893 | 246.1540 | 0.0012 | 93 316.3300 |
| 企业年龄(age) | 数据报告年份减去企业创建年份 | 10.0825 | 11.5230 | 0 | 449 |
| 资料来源:作者使用Stata软件计算;下表统同。 | |||||
四、实证结果分析
(一)基本回归结果。表2汇报了基本回归方程(12)的结果,其中第(1)栏只考虑政策补助这一核心变量,虽然第(1)栏的结果为正,但是并不显著;而第(2)至第(5)栏在依次添加了其他控制变量之后,政策补助的系数稳定为负,且显著。当表2第(6)栏加入了tfp变量之后,政策补助系数则变为正。这一系数方向的变化证明了产业政策对企业工资水平的直接影响为正,一旦控制了所有主要变量之后,政策补助的估计系数为0.0551,这表明企业补助占产出的比重每增加1%,会使受补贴的企业工资水平增加0.0551%。因此,政策补助这一额外财富的增加会扭曲企业间的工资差异,表现为产业政策的转移效应。第(6)栏中其他控制变量对企业工资水平的影响基本符合预期:大企业、有出口经历的企业都会有工资溢价,而人均资本对工资的影响为正,这表明单位员工的技术水平高并能使用更多的资本,从而通过更多的资本收益获取更多工资;企业全要素生产率对工资的影响最为突出,企业全要素生产率每增加1%,企业平均工资可以提高16.88%。可以看出,企业效率是员工待遇的主要来源,更有效率的企业员工工资更高,这一发现使得政策补助通过企业效率途径影响工资水平更受关注。第(7)栏,进一步加入了补贴与企业效率的交互项,随着企业效率的提升,工资水平同时提高,这表明补贴和效率的共同作用是正向的。
| 解释变量: | (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
|
注:*表示 |
|||||||
| 0.0090 (0.0056) |
−0.0130** (0.0055) |
−0.0122** (0.0055) |
−0.0135** (0.0054) |
−0.0130** (0.0054) |
0.0551*** (0.0052) |
0.0659*** (0.0056) |
|
| 0.1024*** (0.0003) |
0.1011*** (0.0003) |
0.0873*** (0.0003) |
0.0919*** (0.0004) |
0.0743*** (0.0003) |
0.0743*** (0.0003) |
||
| 0.0243*** (0.0011) |
0.0344*** (0.0011) |
0.0384*** (0.0011) |
0.0331*** (0.0011) |
0.0332*** (0.0011) |
|||
| 0.0003*** (0.0000) |
0.0003*** (0.0000) |
0.0003*** (0.0000) |
0.0003*** (0.0000) |
||||
| −0.0029*** (0.0000) |
−0.0008*** (0.0000) |
−0.0008*** (0.0000) |
|||||
| 0.1688*** (0.0004) |
0.1688*** (0.0004) |
||||||
| 0.0088*** (0.0016) |
|||||||
| 0.0273*** (0.0012) |
|||||||
| 0.2067*** (0.0015) |
|||||||
| 1 841 804 | 1 841 804 | 1 841 804 | 1 841 804 | 1 841 804 | 1 841 804 | 1 841 804 | |
| 0.3017 | 0.3363 | 0.3365 | 0.3439 | 0.3456 | 0.3973 | 0.3973 | |
| 解释变量 | tfp | New product | rd |
| syratio | −0.1961***(0.0077) | −0.0757**(0.0378) | 1.0000***(6.76e-07) |
| size | 0.0443***(0.0005) | 0.6805***(0.0043) | 1.7651***(0.0044) |
| export | 0.0073***(0.0017) | 1.6563***(0.0112) | 1.4306***(0.0106) |
| percapital | −0.0001***(0.0000) | −0.0003***(0.0000) | 0.9994***(0.0000) |
| age | −0.0064***(0.0001) | 0.0251***(0.0005) | 1.0083***(0.0003) |
| tfp_lag | 0.6382***(0.0007) | 0.1613***(0.0037) | 1.1410***(0.0036) |
| N | 1 249 028 | 1 131 726 | 1 247 702 |
| adj. R2 | 0.5938 | 0.1526 | 0.1614 |
| 注:当研发(rd)作为被解释变量时,报告的数值为Logit模型各个解释变量的几率比;tfp_lag为滞后一期效率。 | |||
当然,补贴变量的估计系数在加入全要素生产率之后的改变,让我们有理由怀疑补贴与企业的生产效率有着很强的负向关联。补贴可能通过抑制企业全要素生产率间接导致企业工资水平下降,表3报告了回归方程(13)的结果。
表3中的第(1)栏显示补贴的提高反而抑制了企业全要素生产率。按照本文前述理论的分析,企业生产率在平均意义上并没有提高,这可能是因为企业并没有将这部分补助更多地用于创新投入,通过表3中第(2)、(3)栏可以发现,补助的提升并没有提高企业选择研发的概率,反映企业创新结果的新产品产值也随之下降,这表明企业并没有将补助更多地用于创新。这些发现的另一种解释与邵敏和包群(2012)所描述的国内大量企业“为补贴而补贴”类似,即企业获得补贴之后并没有将这部分补助用于提升企业效率而是作为生产资料的补充。因此,当企业长期没有创新、没有新产品推向市场并且效率低下时,企业员工的工资水平自然会受到影响。也就是说,财政补助如果没有促进企业竞争性,那么反而加深了企业的“惰性”,最终使这种补助效果适得其反,不但没有起到激励企业成长,反而导致生产效率低下,更会严重扭曲企业间的工资差距。
(二)内生性处理。虽然基本模型尽可能多地考虑了企业异质性对工资差异的影响,但是仍然存在可能的内生性问题,从而导致回归结果的偏误较大,基本模型中可能遗漏了企业那些不随时间变化的特征。例如,企业是否是高科技企业。一方面,高科技企业的工资相对较高;另一方面,“中国式”产业政策也更倾向给这些企业补助。所以,这一遗漏的企业特征造成了产业政策的内生问题。因此本文采用面板数据的固定效应模型(Fixed Effects)和随机效应模型(Random Effects)对产业政策影响工资差距的机制进行了再检验。
基本模型可能存在的另一个内生性问题来自全要素生产率与企业工资间的双向因果关系。根据Yeaple(2005)的研究发现,工资是员工能力的信号,高工资意味着企业拥有更高能力的工人,这样有利于TFP的提升,因此TFP存在内生性。在解决这一问题时,本文选取平减后的中间投入品价值作为TFP的工具变量,并采用GMM-FE估计同时解决上述两类内生性问题。同时,参考韩超(2014)以及韩超等(2017)的研究,企业的补贴可能是由其自身特征带来的,假使企业是亏损企业,那么也许寻求补贴或者补贴的结果仅仅是为了弥补亏损或者掩盖不好的业绩,因此直接效应的考虑可能还需要考虑企业接受补贴的各种情况。本文采用Heckman两步法解决这一自选择问题。即在第一步通过企业的上一期绩效以及特征估计其获得补贴的概率,再根据这一修正的结果去对企业工资进行回归。具体回归结果见表4,为了便于比较,表中同样列示了混合回归的结果。
| 解释变量 | 被解释变量:Lnwage | |||||
| (1)Panel-Pooled | (2)Panel-Fe | (3)Panel-Re | (4)IV | (5)GMM | (6)Heckman | |
| syratio | 0.0659*** | 0.0345*** | 0.0461*** | 0.0548** | 0.0484*** | 0.0297*** |
| (0.0056) | (0.0131) | (0.0168) | (0.0218) | (0.0157) | (0.0056) | |
| size | 0.0743*** | 0.0829*** | 0.0748*** | 0.0777*** | 0.0756*** | 0.0617*** |
| (0.0003) | (0.0036) | (0.0025) | (0.0014) | (0.0035) | (0.0022) | |
| export | 0.0332*** | 0.0177*** | 0.0309*** | 0.0342*** | 0.0117*** | 0.0316*** |
| (0.0011) | (0.0020) | (0.0017) | (0.0015) | (0.0024) | (0.0033) | |
| percapital | 0.0003*** | 0.0003*** | 0.0003*** | 0.0003*** | 0.0003*** | 0.0003*** |
| (0.0000) | (0.0001) | (0.0000) | (0.0000) | (0.0001) | (0.0000) | |
| age | −0.0008*** | −0.0008*** | −0.0016*** | −0.0012*** | −0.0007*** | 0.0003*** |
| (0.0000) | (0.0001) | (0.0001) | (0.0001) | (0.0001) | (0.0001) | |
| tfp | 0.1688*** | 0.1510*** | 0.1615*** | 0.1365*** | 0.2406*** | 0.1594*** |
| (0.0004) | (0.0010) | (0.0008) | (0.0061) | (0.0182) | (0.0013) | |
| syratio·tfp | 0.0088*** | 0.0004 | 0.0037 | 0.0098 | −0.0013 | 0.0044*** |
| (0.0016) | (0.0035) | (0.0049) | (0.0064) | (0.0045) | (0.0014) | |
| private | 0.0273*** | 0.0101*** | 0.0279*** | 0.0334*** | 0.0069*** | 0.0211*** |
| (0.0012) | (0.0023) | (0.0016) | (0.0017) | (0.0022) | (0.0039) | |
| foreign | 0.2067*** | 0.0152*** | 0.1628*** | 0.2106*** | 0.0128*** | 0.2142*** |
| (0.0015) | (0.0043) | (0.0027) | (0.0019) | (0.0041) | (0.0050) | |
| K-P rk LM | 4 252.0860 | 1 259.2690 | ||||
| K-P rk Wald F | 303.3190 | 113.6300 | ||||
| N | 1 841 804 | 1 841 804 | 1 841 804 | 1 841 804 | 1 703 020 | 1 308 708 |
| adj. R2 | 0.3973 | 0.1888 | 0.3963 | 0.3954 | 0.1788 | |
对比表4中第(1)栏和第(2)栏的政策补助变量系数,采用面板固定效应模型比混合回归的估计系数小,这说明基本回归方程(12)遗漏了企业不随时间变化的特征,第(3)栏的随机效应模型进一步验证了这一发现;对比第(1)栏和第(4)栏,tfp变量的系数变小说明由tfp带来的内生性会使混合估计结果偏大,引入工具变量能够降低这一影响。最后,GMM-FE方法同时控制了syratio和tfp这两个变量的内生性,通过第(5)栏可以发现,相关变量的系数均比第(1)栏有所减小。最后,与基本结果相比,Heckman两步估计的结果中,补贴政策以及全要素生产率的估计系数减小了,但方向没有变化。
(三)稳健性检验。
(1)考虑不同的回归方法。表4分别用了混合回归、固定效应模型、随机效应模型、工具变量法、GMM和Heckman两步估计方法,这六种方法得出的结论基本一致,核心解释变量政策补助的估计系数并没有发生方向上的改变,这些处理内生性的方法也进一步验证了基本回归结果的稳健性。(2)考虑将被解释变量替换成员工福利,同时参照谭诗羽等(2017)的方法,加入了另一个产业政策变量税收减免(tax_holiday)作为解释变量。职工的最终薪酬应该包括基本工资和所得福利,而在现实中,企业获得额外补助也可以直接以福利的形式转移给职工。具体的回归结果见表5,同样列示了各个内生性处理的结果。表5中GMM-FE估计显示,政策补助每增加1%,会使受补贴企业员工平均福利增加0.0630%,其他结果与表4相比未有差异。
| 解释变量 | 被解释变量:Lnbenefit | |||||
| (1)Panel-Pooled | (2)Panel-Fe | (3)Panel-Re | (4)IV | (5)GMM | (6)Heckman | |
| syratio | 0.1155*** | 0.0653** | 0.0844** | 0.0955** | 0.0630** | 0.0404*** |
| (0.0434) | (0.0294) | (0.0339) | (0.0401) | (0.0302) | (0.0104) | |
| tax_holiday | 0.0012 | 0.0023*** | 0.0010 | 0.0011 | 0.0023*** | 0.3153*** |
| (0.0027) | (0.0002) | (0.0022) | (0.0026) | (0.0004) | (0.0514) | |
| size | 0.0836*** | 0.0969*** | 0.0824*** | 0.0900*** | 0.0981*** | 0.0635*** |
| (0.0024) | (0.0046) | (0.0034) | (0.0022) | (0.0047) | (0.0038) | |
| export | −0.0151*** | 0.0063* | −0.0147*** | −0.0127*** | 0.0072* | 0.0002 |
| (0.0025) | (0.0037) | (0.0029) | (0.0026) | (0.0043) | (0.0058) | |
| percapital | 0.0004*** | 0.0003*** | 0.0003*** | 0.0003*** | 0.0003*** | 0.0004*** |
| (0.0000) | (0.0001) | (0.0001) | (0.0000) | (0.0001) | (0.0000) | |
| age | 0.0003*** | −0.0007*** | −0.0008*** | −0.0004*** | −0.0007*** | 0.0010*** |
| (0.0001) | (0.0002) | (0.0001) | (0.0002) | (0.0002) | (0.0002) | |
| tfp | 0.1982*** | 0.1717*** | 0.1868*** | 0.1372*** | 0.1574*** | 0.1947*** |
| (0.0010) | (0.0016) | (0.0012) | (0.0123) | (0.0347) | (0.0024) | |
| syratio·tfp | 0.0208* | 0.0081 | 0.0136 | 0.0224** | 0.0084 | 0.0177*** |
| (0.0119) | (0.0077) | (0.0092) | (0.0107) | (0.0077) | (0.0027) | |
| private | 0.0338*** | 0.0129*** | 0.0333*** | 0.0449*** | 0.0135*** | 0.0324*** |
| (0.0021) | (0.0037) | (0.0026) | (0.0030) | (0.0037) | (0.0069) | |
| foreign | −0.0105*** | −0.0209** | −0.0382*** | −0.0012 | −0.0205** | −0.1421*** |
| (0.0036) | (0.0089) | (0.0046) | (0.0037) | (0.0085) | (0.0093) | |
| K-P rk LM | 3 786.9490 | 1 012.5850 | ||||
| K-P rk Wald F | 267.3570 | 87.3460 | ||||
| N | 1 505 487 | 1 505 487 | 1 505 487 | 1 505 487 | 1 363 576 | 1 027 266 |
| adj. R2 | 0.177 | 0.062 | 0.1761 | 0.173 | 0.0618 | |
五、进一步讨论:具有竞争兼容度的产业政策效应
上文的回归结论是产业政策平均意义上的作用,但是并没有区分出产业政策的施行方式,即产业政策究竟是以更竞争性的方式还是更集中的方式施加。Aghion等(2015)和黄先海等(2015)均考察了产业政策的竞争兼容度(ComHerf_subsidy)对企业生产效率的影响。因此,本文继续追问产业政策竞争兼容度对企业工资的作用。本文借鉴前者所使用的赫芬达尔指数来构造产业政策的竞争兼容度,具体的计算方法如下:
| $ComHerf\_subsid{y_{ijrt}} = 1 - {\sum\limits_{h \in j,h \notin i} {\left( {\frac{{subsid{y_{hjrt}}}}{{sum\_subsid{y_{jrt}}}}} \right)} ^2}$ | (14) |
按照不同年份不同地区不同行业划分市场,对于在t年r地区j行业的企业i来说,其所要面对的政策竞争兼容度(ComHerf_subsidyijrt)由1减去该企业所处市场的赫芬达尔指数得到。需要指出的是,在计算赫芬达尔指数时排除了企业i自身所接受的补助。通过上述方法估算得到的指标能够给每一个企业带来其所面临的市场竞争程度,不但刻画了产业政策施加的离散性和均匀性,而且由于每个企业自身所获补助并没有参与分式的分子与分母部分,可以有效规避产业政策的内生性问题。由理论分析可知,当市场中的企业感受到了产业政策的高竞争程度时,为了在竞争中不落下风,企业必然将更多的精力投入到效率提升上(沈坤荣和孙文杰,2009;Aghion等,2015),具体表现为生产成本的降低或者产品质量的提高(李丹丹和王平田,2016),从而在市场竞争中处于优势,这种优势也会通过企业的工资表现出来。表6是基本回归模型(12)加入了产业政策竞争兼容度之后的回归结果。
| 解释变量 | (1) | (2) | (3) | (4) |
| lnwage | lnwage | tfp_op | lnbenefit | |
| syratio | −0.0125(0.0121) | 0.0482***(0.0149) | −0.1440***(0.0087) | 0.0511***(0.0197) |
| CompHerf_subsidy | 0.3106***(0.0029) | 0.0150***(0.0040) | 0.0840***(0.0059) | 0.0177**(0.0070) |
| size | 0.0723***(0.0038) | 0.1231***(0.0018) | 0.0947***(0.0052) | |
| export | 0.0128***(0.0023) | 0.0323***(0.0031) | 0.0090**(0.0042) | |
| percapital | 0.0004***(0.0001) | −0.0001***(0.0000) | 0.0004***(0.0001) | |
| age | −0.0007***(0.0001) | 0.0061***(0.0001) | −0.0007***(0.0002) | |
| tfp | 0.2320***(0.0167) | 0.1422***(0.0338) | ||
| private | 0.0067***(0.0022) | 0.0388***(0.0033) | 0.0134***(0.0037) | |
| foreign | 0.0127***(0.0041) | 0.0220***(0.0062) | −0.0218**(0.0085) | |
| N | 1 834 249 | 1 695 469 | 1 244 992 | 1 357 734 |
| adj. R2 | 0.1556 | 0.1757 | 0.2878 | 0.0617 |
表6第(1)栏是只考虑政策补助变量和产业政策竞争兼容度变量的回归结果,可以发现政策补助变量虽然不显著,但还是对企业工资有负向影响,这和基本回归结果是一致的。政策的竞争兼容度对企业工资有显著的正向作用,结合第(2)栏,在控制了影响企业工资水平的其他变量特别是企业的全要素生产率之后,产业政策竞争兼容度的估计系数变小了,这说明产业政策竞争兼容度和企业效率之间具有显著的正向作用,这一发现得到了第(3)栏回归结果的验证,这表明产业政策的竞争兼容度越高,由此带来的企业效率提升也越大,这会增加企业的平均工资水平。第(4)栏则将被解释变量替换成企业平均福利,结果与以工资为被解释变量时基本一致。
六、结论与政策启示
在中国劳动者收入不均衡问题日益严重的经济环境下,本文探讨了产业政策与企业间工资差距的关系。通过引入产业政策的异质性模型,得到了产业政策影响企业工资的机制:企业获得补贴可以直接将其中的一部分作为福利转移给职工,这是正向的补贴效应;如果此时市场的竞争程度不是很高,那么企业不会留足补贴用于提升企业效率,由效率下降造成的工资下降则是负向的竞争效应。本文使用中国制造业企业数据对上述结论进行了实证检验。结果显示:(1)在没有控制企业的效率之前,财政补贴对工资的影响为负,这是财政补贴的总效应。而一旦将企业效率控制在同一水平,受补贴的企业工资水平显著高于未收补贴的企业,这说明补贴的直接转移效应为正。将全要素生产率、新产品产值作为被解释变量之后,补贴对其有负向影响,因此通过企业效率传导的竞争效应为负,而竞争效应显然超过了直接转移效应。(2)进一步考虑具有竞争兼容度的产业政策之后,提升行业竞争程度的产业政策同时提高了企业工资水平,无论是补贴的转移效应,还是竞争效应都为正,这种工资的提高则是由企业效率带来的质的飞跃。
以上结论为产业政策制定提供了启示。首先,企业补贴是政府转移支付行为,相当于收入的二次分配,但如果这个转移支付会通过企业效率导致工资的下降,就违背了产业政策的初衷。即使效率相同的两个企业,有财政支持的企业将会比没有支持的企业平均工资更高,因此这直接关系到了政策补助的公平性问题。通过分析,过去“中国式”的产业政策没有兼顾公平,最终也破坏了效率,产业政策的不合理施行给我国的基本工资制度改革带来了阻碍,不能拿一部分企业的收益去补助另外一部分,相关政策制定者如何在坚持效率优先的同时兼顾公平是需要慎重权衡的。本文认为,产业政策应该在那些竞争程度更高的行业内施行,或者产业政策应覆盖得更加离散均衡,从而诱使企业去参与更为激烈的市场竞争,使最终企业间工资的差距是有效市场竞争的结果,这样的产业政策对企业工资的影响才能与我国分配制度在内涵上一致。
其次,对于存在大量“僵尸企业”的行业,产业政策的制定应更谨慎。这些行业中的企业由于长期得到大量补贴,缺乏竞争意识。产业政策应从提升这些企业的效率出发,使其生产重新焕发生机,进行技术或者产品革新,对于这部分企业的补贴可以转为给技术人才的工资补助,一来可以为企业吸引人才,帮助企业提高效率,另一方面也能避免直接补贴带来的负面效应。同时,政府也可以帮助这部分企业组织员工培训(worker training),将补贴金以员工教育费的形式发放(吴万宗和汤学良,2016),既可以提升劳动力技能,促进企业效率提升;又能为员工的职业生涯提供更多保障,一旦企业倒闭,得到技能培训的下岗职工也可以更加灵活地适应劳动力市场。
最后,本文以补贴为内容研究了产业政策与企业工资的关系,而产业政策的财政手段还有很多,比如税收减免。当前,我国全面深化改革进入了关键时期,政府也推出了“减税降费”等政策为企业减负。本文研究的补贴是在给企业收益做加法,而税收减免则是给企业成本做减法,二者对企业效率以及工资的影响机制是否一致,如何科学地使用这些政策手段促进企业效率以及工资的提升,都是未来需要进一步探讨的话题。
* 本文曾在2016年华中科技大学举办的第十六届“中国经济学年会”上宣讲过,感谢与会专家的建议;同时感谢外审专家和编辑部老师对本文提供的宝贵意见。
| [1] | 韩超, 肖兴志, 李姝. 产业政策如何影响企业绩效: 不同政策与作用路径是否存在影响差异?[J]. 财经研究, 2017(1): 122–133. |
| [2] | 刘海洋, 孔祥贞, 马靖. 补贴扭曲了中国工业企业的购买行为吗? ——基于讨价还价理论的分析[J]. 管理世界, 2012(10): 119–129. |
| [3] | 毛其淋, 许家云. 政府补贴、异质性与企业风险承担[J]. 经济学(季刊), 2016(4): 1533–1562. |
| [4] | 邵敏, 包群. 地方政府补贴企业行为分析: 扶持强者还是保护弱者?[J]. 世界经济文汇, 2011(1): 56–72. |
| [5] | 谭诗羽, 吴万宗, 夏大慰. 国产化政策与全要素生产率——来自汽车零部件制造业的证据[J]. 财经研究, 2017(4): 82–95. |
| [6] | 肖兴志, 王伊攀. 战略性新兴产业政府补贴是否用在了" 刀刃”上? ——基于254家上市公司的数据[J]. 经济管理, 2014(4): 19–31. |
| [7] | Aghion P, Cai J, Dewatripont M. Industrial policy and competition[J]. American Economic Journal: Macroeconomics, 2015, 7(4): 1–32. |
| [8] | Helpman E, Itskhoki O, Redding S. Inequality and unemployment in a global economy[J]. Econometrica, 2010, 78(4): 1239–1283. DOI:10.3982/ECTA8640 |
| [9] | Yeaple S R. A simple model of firm heterogeneity, international trade, and wages[J]. Journal of International Economics, 2005, 65(1): 1–20. DOI:10.1016/j.jinteco.2004.01.001 |
 2018, Vol. 44
2018, Vol. 44




