文章信息
 | 财经研究 2017年43卷第10期 |
- 陈利锋.
- Chen Lifeng.
- 劳动力市场结构性改革的宏观经济效应:一个模拟分析
- Macroeconomic effects of labor market structural reform:a simulation analysis
- 财经研究, 2017, 43(10): 4-17
- Journal of Finance and Economics, 2017, 43(10): 4-17.
-
文章历史
- 收稿日期:2017-03-12

2017第43卷第10期
2. 中国社会科学院 经济研究所,北京 100836;
3. 广东财经大学 国民经济研究中心,广东 广州 510320
2. Institute of Economics, Chinese Academy of Social Sciences, Beijing 100836, China;
3. National Economics Research Center, Guangdong University of Finance and Economics, Guangzhou 510320, China
一、引言与文献综述
劳动力市场的稳定是宏观经济政策的重要目标之一。然而,2002年以来,劳动力成本上升、用工荒、金融危机等因素不断对我国劳动力市场形成冲击,进而引起我国劳动力市场波动和失业的增加。促进社会就业一直是我国政府工作的重要组成部分,一系列保障和促进社会就业的政策相继出台,在一定程度上缓解了我国的就业问题。然而,依靠经济增长促进就业的政策思路并未使我国的失业问题得到真正缓解,“高增长与低就业”并存已经成为我国劳动力市场的事实(中国经济增长前沿课题组,2015)。那么,应该采用何种政策机制以实现我国劳动力市场的稳定呢?
以往的研究尝试从提高劳动力流动性的角度来寻找实现劳动力市场稳定的政策机制。①其内在机理为:通过劳动力市场的结构性改革来提高劳动力的流动性,进而促进就业与缓解失业(Faia等,2014)。与发达国家不同,我国的劳动力市场结构具有典型的发展中国家的特征:非正规部门和非正规就业广泛存在(La Porta和Shleifer,2014)。吴要武(2014) 等估算的结果发现我国非正规就业的规模已经超过正规就业。更重要的是,我国劳动就业具有显著的部门差异特征。具体表现为:(1) 从就业收入上看,魏下海和余玲铮(2012) 等发现我国正规就业的收入远超非正规就业;(2) 正规就业在社会地位、岗位培训、带薪休假等显性和隐性福利方面均优于非正规就业。正规就业的诸多优越性造成求职者倾向于追求正规部门的就业岗位,阻碍了劳动力的自由流动(吴要武,2014;钱先航等,2015),进而引起劳动力市场的低迷、宏观经济波动和社会福利损失的增加(Fiess等,2010;沈晓栋,2015)。因此,基于劳动力市场结构的视角,缩小部门间差异是实现劳动力自由流动进而稳定劳动力市场的重要前提。基于我国劳动力市场的现实需要,进行结构性改革是一个必然的选择(张平,2012)。近年来,我国政府积极推进的一系列针对正规部门的养老社保机制改革、机关事业单位改革,鼓励正规部门的就业者“有进有出”。这些措施客观上降低了正规部门的雇佣成本和就业者的议价能力。因此,建立相应的模型对这些改革的宏观经济效应进行量化分析将是一个重要的研究话题。
① Ravenna和Walsh(2012) 在包含搜寻与匹配的模型中讨论了这一话题,研究结果表明,劳动力的流动对劳动力市场乃至经济周期性波动均具有重要的影响;Davis和Haltiwanger(2014) 考察了劳动力的流动性与宏观经济表现,结果表明劳动力流动性越差的经济,失业与产出的波动更大。彭国华(2015) 则指出,劳动力的自由流动可以有效促进技能与岗位的匹配,进而实现就业增加。
事实上,国外的研究者如Blanchard和Giavazzi(2003) 较早对劳动力市场结构性改革的影响进行了考察,研究发现这一改革对改善持续失业问题具有显著成效。金融危机后,欧美国家学者从劳动力市场制度出发,重新审视劳动力市场“缓慢复苏”的现实,劳动力市场结构性改革重新成为研究的热点。Alessandra和Delacroix(2009) 等采用静态模型对劳动力市场结构性改革的长期效应进行了分析,尽管其结论具有一定的启发性,但静态分析法显然无法有效地剖析劳动力市场结构性改革的动态效应与短期效应;Thomas和Zanetti(2009)、Christoffel等(2009)、Campolmi和Faia(2011)、Cacciatore等(2015) 以及Cacciatore和Fiori(2016) 等则建立动态随机一般均衡(即DSGE)模型对劳动力市场结构性改革的短期效应和长期效应进行了考察,研究结果无一例外地表明:劳动力市场结构性改革的长期效应表现为失业的下降和产出的增加,而短期效应则表现为失业的上升和产出的下降。换言之,以往研究均表明,劳动力市场结构性改革具有显著的“以短期疼痛换取长期收益”(Short Term Pain for Long Term Gain)特征(Cacciatore和Fiori,2016)。
现有相关研究在探讨劳动力市场结构性改革的宏观经济效应方面进行了有益的尝试,但是,这些研究均忽略了我国劳动力市场所具有的特征:非正规就业的大量存在,因而其所建立的研究范式在分析我国劳动力市场结构性改革时可能并不适合。②基于此,本文建立了一个包含正规部门与非正规部门的DSGE模型。与以往的研究类似,本文所建立的模型仍包含了名义刚性和垄断竞争等元素。所不同的是,其名义刚性和垄断势力存在跨部门差异。这是因为,我国非正规部门企业数量相对较多且规模相对较小,而正规部门企业数量和规模则正好相反。更重要的是,这一模型框架与我国的现实情况类似,两类部门具有不同的雇佣成本,并且两类部门就业者具有不同的议价能力。据此,我们考察了两种劳动力市场的结构性改革:①第一种劳动力市场结构性改革旨在降低正规部门的雇佣成本,而第二类劳动力市场的结构性改革则倾向于降低正规部门就业者的议价能力。同时,通过比较不同货币政策机制下两类劳动力市场结构性改革的效应,来剖析我国劳动力市场结构性改革过程中的货币政策机制选择。
② Charlot等(2015) 基于包含非正规性的发展中国家经济,建立搜寻与匹配模型,并考察了相应的非正规性规制政策的宏观经济效应。但这一研究并未对非正规部门的行为进行刻画,并且主要集中于考察非正规性对财政政策宏观经济效应的影响。陈利锋(2015) 则采用动态转移方法考察了降低正规部门雇佣成本所引起的劳动力市场动态转移特征。但这一研究对非正规部门的刻画并不全面,并且使用的方法主要为比较静态分析。
① 我国政府近年推行的劳动力市场结构性改革主要针对的是正规部门就业与非正规部门就业之间的差距,比如公务员事业单位养老机制的改革、事业单位就业人员实行合同制、鼓励事业单位就业者创业等。公务员事业单位养老机制改革降低了正规部门的雇佣成本,依据本文的界定,应属于第一类劳动力市场结构性改革;而事业单位就业人员合同制改革以及鼓励事业单位就业者创业等改革则有助于降低正规部门就业者的议价能力,因而属于第二类劳动力市场结构性改革。
本文的探索之处在于:第一,在构建DSGE模型时,考虑了我国劳动力市场非正规就业的广泛存在以及两类部门在雇佣成本和就业者议价能力上存在显著差异的事实;第二,分析了我国劳动力市场结构性改革的短期效应和长期效应,并比较了该两种效应的差异;第三,比较了不同货币政策机制下两种劳动力市场结构性改革的宏观经济效应,从而可以分析我国劳动力市场结构性改革过程中的货币政策配套。
本文研究发现,如果以货币政策为基准的泰勒规则下,那么两类劳动力市场结构性改革均呈现出“以短期疼痛换取长期收益”的特征:在短期,两类劳动力市场结构性改革均引起失业的增加和产出的减少;但在长期,这两类劳动力市场结构性改革均引起失业的减少和产出的增加。我们进一步考察了基于泰勒规则拓展的Evans规则下两类劳动力市场结构性改革的宏观经济效应。研究发现,Evans规则显著降低了两类劳动力市场结构性改革在短期中给宏观经济带来的“疼痛”。这表明,在推行降低正规部门雇佣成本与议价能力等两类劳动力市场结构性改革的过程中,货币政策当局可以尝试推行考虑失业的Evans规则。
二、模型与设定
(一)劳动力市场。任意时期t,模型中正规部门就业NtF与非正规部门就业NtI满足:
| $N_t^s = \left( {1 - {\delta ^s}} \right)N_{t - 1}^s + H_t^s\left( {s = F;I} \right)$ | (1) |
其中:δs为两类部门的离职率;Hts为两类部门新雇佣的就业人员。定义Ut为失业,我们将其定义为:Ut=1-NtF-NtI。经济中的待业劳动力数量为:
| ${J_t} = {U_{t - 1}} + {\delta ^F}N_{t - 1}^F + {\delta ^I}N_{t - 1}^I = 1 - \left( {1 - {\delta ^F}} \right)N_{t - 1}^F - \left( {1 - {\delta ^I}} \right)N_{t - 1}^I$ | (2) |
上式意味着,待业的劳动力包括失业以及两类部门解雇或离职的劳动力。劳动力在两类部门获得雇佣机会的概率(以下简称就业机会)满足:Xts=Hts/Jt。与Blanchard和Gali等(2010) 相同,并设定两类部门中的企业雇佣劳动力需耗费雇佣成本HCts,并且HCts与相应部门提供的就业机会正相关。不同的是,基于研究目的考虑,我们设定两类部门雇佣成本函数的系数Bts具有随时间可变的特征,即HCts=Bts(Xts)γs。
(二)家庭。我们设定模型中的家庭具有同质性特征,并且其优化行为表现为最大化效用函数:Uth=E0∑t=0∞βtlnCt,β为折现算子,Ct为消费。现有的包含搜寻与匹配的相关研究如Gertler等(2016) 等均采用这一效用函数。大多数基于名义刚性建模的NK-DSGE模型在效用函数设定上暗含了就业者的效用低于失业者的假定(Christiano等,2016),而本文所采用的设定则克服了这一不足。家庭消费的产品源自两类部门,定义Cts为家庭消费的两类部门产品数量,v为总消费中正规部门消费品所占的权重,η为两类部门产品的替代弹性,那么模型中的总消费和物价水平满足:
| ${C_t} = {\left[ {{v^{\frac{1}{\eta }}}{{\left( {C_t^F} \right)}^{\frac{{\eta - 1}}{\eta }}} + {{\left( {1 - v} \right)}^{\frac{1}{\eta }}}{{\left( {C_t^I} \right)}^{\frac{{\eta - 1}}{\eta }}}} \right]^{\frac{\eta }{{\eta - 1}}}}$ | (3) |
| ${P_t} = {\left[ {v{{\left( {P_t^F} \right)}^{1 - \eta }} + \left( {1 - v} \right){{\left( {P_t^I} \right)}^{1 - \eta }}} \right]^{\frac{1}{{1 - \eta }}}}$ | (4) |
基于以上设定,家庭的预算约束为:
| $\begin{array}{l} {P_t}\left( {{C_t} + {I_t}} \right) + {B_t}/{R_t} \le \left( {1 - {\tau _F}} \right)W_t^FN_t^F + W_t^IN_t^I + \\ {B_{t - 1}} + {P_t}R_t^k{K_t} + {W^u}{U_t} + {O_t} \end{array}$ |
其中:It为投资,Bt为债券,Rt为名义利率,Rtk为实际租金率,τF为正规部门税率,WtF和WtI分别为两类部门的名义工资率,Wu为失业者获得的收入,Ot为其他来源的收入,Kt为物质资本。与Gali等(2007) 等现有的研究相同,我们设定模型中的物质资本由家庭的物质资本投资行为形成,且满足:
| ${K_{t + 1}} = \left( {1 - \delta } \right){K_t} + {K_t}S\left( {{I_t}/{K_t}} \right)$ | (5) |
上式中,稳态时投资调整成本函数S(·)满足:S(δ)=δ,S′(δ)=1。
(三)最终产品生产者。最终产品生产者的生产技术为:Yts(i)=Zts(i),Yts(i)和Zts(i)为两类部门第i个最终产品生产者的产出和中间品投入。这一技术被称为一一对应(One-to-One)技术。显然,本文的设定意味着最终产品生产者的产出存在差异性,进而导致其具有产品定价上的垄断势力。
我们设定最终产品生产者依据Calvo(1983) 的方式设定产品价格,也即:
| $P_t^s\left( i \right) = {\left[ {\left( {1 - \theta _p^s} \right){{\left( {P_t^{s*}} \right)}^{ - 1/\Lambda _t^{sp}}} + \theta _p^s{{\left( {P_{t - 1}^s\left( i \right)} \right)}^{ - 1/\Lambda _t^{sp}}}} \right]^{ - \Lambda _t^{sp}}}$ | (6) |
其中:θps为两类部门名义价格刚性;Pts*为最优价格;εtsp=ln(1+Λtsp)为价格加成冲击,其稳态值为εps,这一参数可以表示两类部门不同最终产品的替代弹性。非正规部门企业数量相对较多,其垄断势力相对较小,故εpF<εpI。最终产品生产者依据利润最大化原则调整产品价格,因此,决定其价格调整决策的一阶条件为:
| ${E_t}\sum _{k = 0}^\infty {\left( {\beta \theta _p^s} \right)^k}{\left( {\Lambda _{t + k}^{sp}} \right)^{ - 1}}Y_{t + k}^s\left[ {\left( {P_{t + k}^{s*}/{P_{t + k}}} \right) - \left( {1 + \Lambda _{t + k}^{sp}} \right)MC_{t + k}^s} \right] = 0$ | (7) |
其中:MCts代表了两类部门最终产品生产者的实际边际成本,其源自生产投入,因而MCts应等于两类部门中间品的实际价格,即MCts=Ptsz/Pt,Ptsz为两类部门中间品的价格。
(四)正规部门中间品生产者。正规部门中间品生产者的技术为:ZtF(j)=AtF[Kt(j)]αF[NtF(j)]1-αF,εtFa=lnAtF为正规部门技术冲击。生产者最大化利润ΩtF为:
| $\begin{array}{l} \Omega _t^F\left( j \right) = \left( {P_t^{Fz}/{P_t}} \right)Z_t^F\left( j \right) - \left( {W_t^F\left( j \right)/{P_t}} \right)N_t^F\left( j \right) - \\ R_t^kK_t^F\left( j \right) - HC_t^FH_t^F\left( j \right) + \beta {E_t}{\Lambda _{t,{\rm{ }}t + 1}}\Omega _{t + 1}^F\left( j \right) \end{array}$ |
对应的一阶条件为:
| $R_t^k = {\alpha _F}\left( {P_t^{Fz}/{P_t}} \right)\left( {Z_t^F\left( j \right)/K_t^F\left( j \right)} \right) = {\alpha _F}\left( {P_t^{Fz}/{P_t}} \right)\left( {Z_t^F/K_t^F} \right)$ | (8) |
| $\begin{array}{l} \left( {W_t^F\left( j \right)/{P_t}} \right) = \left( {1 - {\alpha _F}} \right)\left( {P_t^{Fz}/{P_t}} \right)\left( {Z_t^F\left( j \right)/N_t^F\left( j \right)} \right) - HC_t^F\\ + \beta \left( {1 - {\delta ^F}} \right){E_t}{\Lambda _{t,{\rm{ }}t + 1}}HC_{t + 1}^F \end{array}$ | (9) |
式(8) 为最优物质资本投入;式(9) 为最优劳动力投入,其意为最优劳动力投入应满足实际工资等于劳动的实际边际产品价值与劳动力未离职或未被解雇而节省的雇佣成本之差。显然,节省的雇佣成本满足:HCtF-β(1-δF)EtΛt, t+1HCt+1F。为分析便利,我们定义正规部门劳动的实际边际产品价值为:
| $MRPN_t^F\left( j \right) = \left( {1 - {\alpha _F}} \right)\left( {P_t^{Fz}/{P_t}} \right)\left( {Z_t^F\left( j \right)/N_t^F\left( j \right)} \right)$ | (10) |
(五)非正规部门中间品生产者。非正规部门中间产品生产者的技术为:
| $Z_t^I\left( j \right) = A_t^I{\left[ {N_t^I\left( j \right)} \right]^{1 - {\alpha _I}}}$ | (11) |
其中:εtIa=lnAtI为非正规部门技术冲击。与正规部门相似,非正规部门中间品生产者选择最优的劳动力投入以最大化如下利润函数:
| $\begin{array}{l} \Omega _t^I\left( j \right) = \left( {P_t^{Iz}/{P_t}} \right)Z_t^I\left( j \right) - \left( {W_t^I\left( j \right)/{P_t}} \right)N_t^I\left( j \right) - \\ HC_t^IH_t^I\left( j \right) + \beta {E_t}{\Lambda _{t,{\rm{ }}t + 1}}\Omega _{t + 1}^I\left( j \right) \end{array}$ |
对应的一阶条件为:
| $\begin{array}{l} W_t^I\left( j \right)/{P_t} = \left( {1 - {\alpha _I}} \right)\left( {P_t^{Iz}/{P_t}} \right)\left( {Z_t^I\left( j \right)/N_t^I\left( j \right)} \right) - \\ HC_t^I + \beta \left( {1 - {\delta ^I}} \right){E_t}{\Lambda _{t,{\rm{ }}t + 1}}HC_{t + 1}^I \end{array}$ | (12) |
类似地,我们可以定义家庭成员在非正规部门就业的边际产品价值为:
| $MRPN_t^I\left( j \right) = \left( {1 - {\alpha _I}} \right)\left( {P_t^{Iz}/{P_t}} \right)\left( {Z_t^I\left( j \right)/N_t^I\left( j \right)} \right)$ | (13) |
(六)工资议价过程。定义
| $\begin{array}{l} V_t^F = \left( {1 - {\tau _F}} \right)\left( {W_t^F/{P_t}} \right) + \beta {E_t}{\Lambda _{t,{\rm{ }}t + 1}}\left\{ {\left[ {\left( {1 - {\delta ^F}} \right) + {\delta ^F}X_{t + 1}^F} \right]V_{t + 1}^F} \right.\\ \left. { + {\delta ^F}X_{t + 1}^IV_{t + 1}^I + {\delta ^F}\left( {1 - X_{t + 1}^F - X_{t + 1}^I} \right)V_{t + 1}^U} \right\} \end{array}$ |
上式表明,正规部门就业的收益为税后工资收入与预期收益之和,而正规部门就业的预期收益包括:(1)t+1期(也即未来)未被解雇获得的收益(1-δF)VFt+1;(2)t+1期被解雇但重新得到本部门就业机会而获得的收益δFXt+1FVt+1F;(3)t+1期被解雇后得到非正规部门就业机会获得的收益δFXt+1IVt+1I;(4)t+1期被解雇后失业的收益δF(1-Xt+1F-Xt+1I)Vt+1U。类似地,非正规部门就业的收益为工资收入与预期收益之和,而非正规部门就业的预期收益则包括:(1)t+1期未被解雇获得的收益(1-δI)Vt+1I;(2)t+1期被解雇但重新得到本部门就业机会而获得的收益δIXt+1IVt+1I;(3)t+1期被解雇后获得正规部门就业机会而获得的收益δIXt+1FVt+1F;(4)t+1期被解雇后失业的收益δI(1-Xt+1F-Xt+1I)Vt+1U。具体地,VtI可以表述为如下形式:
| $\begin{array}{l} V_t^I = {\frac{{W_t^I}}{P}_t} + \beta {E_t}{\Lambda _{t,{\rm{ }}t + 1}}\left\{ {\left[ {\left( {1 - {\delta ^I}} \right) + {\delta ^I}X_{t + 1}^I} \right]V_{t + 1}^I + } \right.\\ \left. {{\delta ^I}X_{t + 1}^FV_{t + 1}^F + {\delta ^I}\left( {1 - X_{t + 1}^F - X_{t + 1}^I} \right)V_{t + 1}^U} \right\} \end{array}$ |
失业的收益VtU包括失业救助Wu和预期收益,而失业的预期收益则包括:(1)t+1期获得正规部门就业机会得到的收益Xt+1FVt+1F;(2)t+1期获得非正规部门就业机会得到的收益Xt+1IVt+1I;(3)t+1期继续失业获得的收益(1-Xt+1F-Xt+1I)Vt+1U。因此,VtU满足:
| $V_t^U = {W^u} + \beta {E_t}{\Lambda _{t,{\rm{ }}t + 1}}\left[ {X_{t + 1}^FV_{t + 1}^F + X_{t + 1}^IV_{t + 1}^I + \left( {1 - X_{t + 1}^F - X_{t + 1}^I} \right)V_{t + 1}^U} \right]$ |
定义StF=VtF-VtU和StI=VtI-VtU分别为两类部门的就业剩余,而企业剩余Jts则等于雇佣成本(Blanchard和Gali等,2010)。因此,家庭与两类部门中间产品生产者的目标为选择最优工资以实现联合收益的最大化,其联合利益可以表述为:(Sts)
| $\begin{array}{l} \lambda _t^F\left( {1 - {\tau _F}} \right)HC_t^F = \left( {1 - {\tau _F}} \right)\left( {W_t^F/{P_t}} \right) - {W^u} + \beta \left( {1 - {\delta ^F}} \right){E_t}{\Lambda _{t,{\rm{ }}t + 1}}\\ \quad \quad \quad \quad \quad \quad \quad \left[ {\left( {1 - X_{t + 1}^F} \right)\left( {1 - {\tau _F}} \right)\lambda _{t + 1}^FHC_{t + 1}^F - X_{t + 1}^I\lambda _{t + 1}^IHC_{t + 1}^I} \right] \end{array}$ | (14) |
| $\begin{array}{l} \lambda _t^IHC_t^I = \frac{{W_t^I}}{{{P_t}}} - {W^u} + \beta \left( {1 - {\delta ^I}} \right){E_t}{\Lambda _{t,{\rm{ }}t + 1}}\\ \left[ {\left( {1 - X_{t + 1}^I} \right)\lambda _{t + 1}^IHC_{t + 1}^I - X_{t + 1}^F\lambda _{t + 1}^FHC_{t + 1}^F} \right] \end{array}$ | (15) |
(七)加总与市场出清。经济中的总产出为两类部门产出的加总,也即:
| ${Y_t} = Y_t^F + Y_t^I$ | (16) |
依据支出法可知,模型中的总产出用于满足消费、投资和支付雇佣成本,也即:
| ${Y_t} = {C_t} + {I_t} + HC_t^FH_t^F + HC_t^IH_t^I$ | (17) |
(八)政府部门。模型中的政府扮演两方面的角色:财政政策当局与货币政策当局。首先,作为财政政策当局,其依据如下规则行事:
| ${W^u}{U_t} = {\tau _F}\left( {W_t^F/{P_t}} \right)N_t^F$ | (18) |
作为货币政策当局,货币政策满足如下规则:
| $\left( {{R_t}/R} \right) = {\left( {{R_{t - 1}}/R} \right)^{{\rho _R}}}{\left[ {{{\left( {{Y_t}/Y} \right)}^{{r_y}}}{{\left( {\Pi _t^p/{\Pi ^p}} \right)}^{{r_p}}}} \right]^{1 - {\rho _R}}}{\rm{exp}}\left( {\varepsilon _t^r} \right)$ | (19) |
(九)外生冲击。模型中的外生冲击如两类部门的雇佣成本规模εtsb=lnBts、两类部门价格加成冲击εtsp以及两类部门就业者议价能力冲击εts
| $\varepsilon _t^x = \left( {1 - {\rho _x}} \right){\varepsilon ^x} + {\rho _x}\varepsilon _{t - 1}^x + e_t^x\left( {x = Fb,{\rm{ }}Ib,{\rm{ }}Fp,{\rm{ }}Ip,{\rm{ }}F\vartheta ,{\rm{ }}I\vartheta } \right)$ | (20) |
其中:εx为εtx的稳态值;ρx用于反映冲击的持续性;扰动项etx服从均值为0、标准差为σx的白噪声。为了与现实相符,设定BF>BI,即稳态时正规部门具有更大的雇佣成本规模。非正规部门企业规模小且数量大,对市场和价格的控制能力较差,因而垄断势力相对较弱。基于这一事实,我们设定εFp<εIp,即非正规部门不同最终产品之间的替代性更强。另外,正规部门尤其是体制内部门存在的行政性用人体制,导致正规部门就业者的议价能力相对较强。基于此,我们设定稳态时正规部门的议价能力参数
| $\varepsilon _t^x = {\rho _x}\varepsilon _{t - 1}^x + e_t^x\left( {s = Fa,{\rm{ }}Ia,{\rm{ }}r} \right)$ | (21) |
三、动态模拟分析
(一)参数的校准与估计。为了保证模型的可识别性,首先对一些参数进行校准。反映家庭时间偏好特征的参数β,与国内的相关研究相同,本文将其设定为0.98;物质资本折旧率δ,参考陈利锋(2016) 的取值,设定为0.04;两类部门稳态雇佣成本规模参数BF和BI,分别设定其取值为2.5和0.5;稳态时正规部门劳动者的议价能力参数
模型中的其他参数采用贝叶斯方法进行估计。数据的样本空间为2002年第1季度至2015年第4季度,数据包括消费、名义利率、通货膨胀和产出。消费数据采用取自然对数后的全国消费总额;名义利率采用取自然对数后的同业拆借利率;通胀采用经环比处理的CPI;产出则采用取自然对数后的GDP数据。所有观测序列全部进行季节调整,并经CF滤波剔除包含的趋势。
本文参考现有相关研究对结构性参数的先验均值与先验分布进行设定。具体过程如下:(1) 两类部门名义价格刚性参数。我们将正规部门名义价格刚性参数θpF的先验均值设定为0.7。另外,借鉴陈利锋(2016和2017a)等,将非正规部门名义价格刚性参数θpI的先验均值设定为0.5。(2) 两类部门不同最终产品的替代弹性系数。我们将正规部门最终产品的替代弹性系数εpF的先验均值设定为1,而将非正规部门最终产品的替代弹性系数εpI的先验均值设定为2。(3) 两类部门资本的产出弹性系数。卞志村和杨源源(2016) 等指出,我国资本的产出弹性约为0.6。基于此,我们将正规部门资本产出弹性系数αF的先验均值设定为0.6。由于非正规部门的生产规模相对较小,劳动力所占的份额相对较大,因而我们将αI的先验均值设定为0.4。(4) 两类部门雇佣成本对就业机会的弹性系数。国内现有研究并未对这两个参数进行有效的估计,我们使用Charlot等(2015) 的估计结果,将γF和γI的先验均值分别设定为1.5和0.8。(5) 两类部门离职率。Blanchard和Gali等(2010) 对美国离职率的估计值为0.12。依据这一结果,我们将两类部门的离职率δF和δI的先验均值全部设定为0.1。(6) 货币政策参数。依据王君斌等(2013),我们将ρR的先验均值设定为0.8。同时,依据以往关于泰勒规则的研究,我们将ry和rp的先验均值分别设定为0.5和1.5。参数估计的详细结果见表 2。
| 参数 | 先验 | 后验 | |||
| 均值 | 分布 | 均值 | 置信域 | 极大似然估计值 | |
| θpF | 0.7 | Beta | 0.7840 | (0.6080, 0.9220) | 0.8412 |
| θpI | 0.5 | Beta | 0.5251 | (0.3632, 0.6393) | 0.5066 |
| εpF | 1.0 | Gamma | 1.5144 | (0.8901, 2.1703) | 1.4660 |
| εpI | 2.0 | Gamma | 2.5606 | (1.6428, 3.3241) | 2.4797 |
| αF | 0.6 | Beta | 0.5511 | (0.3984, 0.6908) | 0.5968 |
| αI | 0.4 | Beta | 0.3803 | (0.2924, 0.4698) | 0.3623 |
| γF | 1.5 | Gamma | 1.4251 | (1.1235, 1.7371) | 1.5171 |
| γI | 0.8 | Beta | 0.8228 | (0.7049, 0.9500) | 0.8425 |
| δF | 0.1 | Beta | 0.0719 | (0.0677, 0.1088) | 0.0693 |
| δI | 0.1 | Beta | 0.1024 | (0.0711, 0.1291) | 0.1010 |
| ρR | 0.8 | Beta | 0.7584 | (0.7479, 0.7672) | 0.7570 |
| ry | 0.5 | Beta | 0.4765 | (0.3365, 0.5983) | 0.4716 |
| rp | 1.5 | Gamma | 1.3533 | (1.2863, 1.4571) | 1.3426 |
(二)劳动力市场结构性改革:降低正规部门雇佣成本。由于雇佣成本发生于劳动力的雇佣过程,因而这一改革直接影响了两类部门新雇佣的就业。为便于分析,我们考虑的是正规部门雇佣成本下降10%所带来的动态影响。
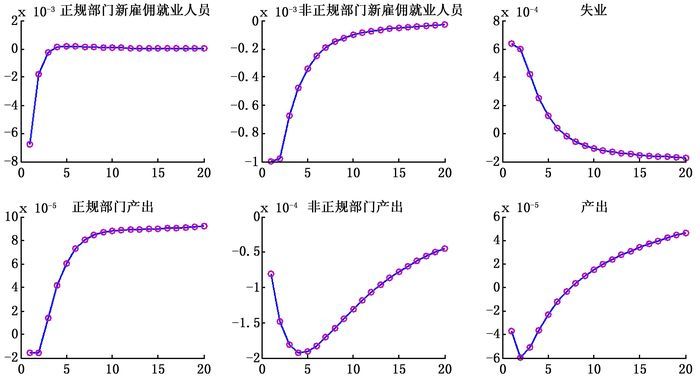
图 1显示,从长期效应看,正规部门雇佣成本下降引起本部门新雇佣就业人员增加和非正规部门新雇佣就业人员减少。原因在于,正规部门雇佣成本的下降会使该部门可以以相对较低的成本雇佣更多的劳动力,而正规部门相对较高的福利待遇则吸引了非正规部门的就业者、失业者进入正规部门,进而使正规部门新雇佣的劳动力数量增加;与之相对应,非正规部门新雇佣的劳动力数量相对减少。因此,基于长期效应可知,降低正规部门的雇佣成本促进了就业的正规化。类似地,降低正规部门的雇佣成本降低了失业,并分别引起了正规部门产出、总产出的增长以及非正规部门产出的下降。这一结果表明,通过劳动力市场结构性改革,降低正规部门的雇佣成本,不仅有利于缓解失业,而且有利于促进产出的增长。更重要的是,这一改革有助于就业的正规化和降低我国经济的非正规性特征。
|
| 图 1 降低正规部门雇佣成本的效应 |
图 1还表明,从短期效应看,这一改革引起了两类部门的新雇佣就业人员、产出、总产出的下降和失业的上升。原因可能在于,这一改革推行后,非正规部门企业预期未来劳动力将大量进入正规部门,进而导致本部门产出的下降。因此,非正规部门企业将减少劳动力的雇佣。类似地,由于劳动力市场相关法律在正规部门获得较好的贯彻执行,政府对正规部门具有较强的规制能力,因而劳动力一旦为正规部门企业所雇佣,企业在解雇劳动力时所付出的成本将相对较高。这一改革发生后,正规部门生产企业预期未来可以以相对较低的成本雇佣更多的就业,因而导致其在短期内减少劳动力的雇佣。两类部门新雇佣就业的下降直接导致了这一改革初期失业的增加,同时也引起了短期内两类部门产出的下降;而失业的增加则降低了我国的短期总产出水平。
综上,由图 1可见,降低正规部门的雇佣成本,有助于促进就业的正规化,并且可以降低我国经济的非正规性特征。而比较这一改革的短期效应和长期效应则可以发现,这一改革在短期中会引起产出的减少和失业的增加,而在长期中则会引起产出的增加和失业的减少,换言之,这一改革具有以“短期疼痛换取长期收益”的特征。
(三)劳动力市场结构性改革:降低正规部门就业者的议价能力。与降低正规部门雇佣成本不同,降低正规部门就业者的议价能力则直接影响了现有正规部门的就业者。通过这一改革,降低正规部门就业者的议价能力,有助于降低正规部门就业者的收益;同时,也有助于降低行政性用人体制所产生的扭曲,实现劳动力的自由流动。当然,这一改革也间接降低了正规部门的雇佣成本。类似地,我们同样考察正规部门就业者的议价能力下降10%所带来的宏观经济效应。
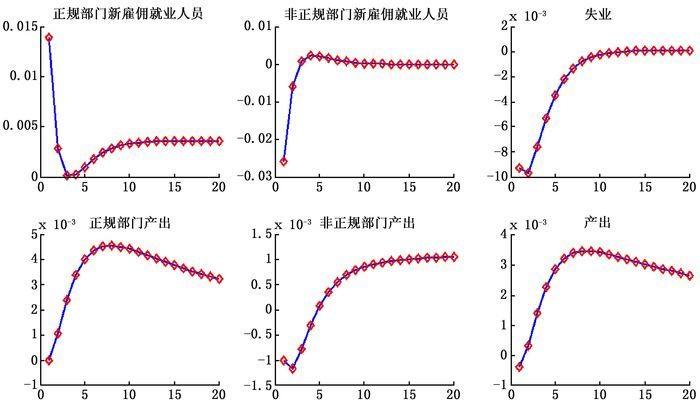
图 2给出了这一改革所形成的冲击对两类部门的新雇佣就业人员、失业、产出和总产出等宏观经济变量的动态冲击效应。首先,从长期效应看,这一改革引起了两类部门的新雇佣就业人员、产出、总产出的增加以及失业的下降。原因可能在于,这一改革降低了正规部门就业者的议价能力,相对降低了该部门就业者通过议价能力获得的超额收益,进而也相对降低了正规部门现有就业者的就业收益与雇佣成本,推动了正规部门新雇佣就业数量的上升。同时,这一改革也使得非正规部门就业的吸引力相对上升,劳动力部门间的重新配置,进而引起非正规部门新雇佣就业数量的增加。两类部门新雇佣数量的增加直接降低了失业,并且提高了两类部门的产出水平,由此也引起了总产出的增加。相对而言,正规部门新雇佣就业数量和产出增长的幅度大于非正规部门。因此,从长期效应看,这一改革方式促进了我国就业的正规化,降低了经济的非正规性程度。
|
| 图 2 降低正规部门就业者议价能力的效应 |
与图 1相比,可以发现这一改革方式的长期效应与第一种改革方式存在显著差异,具体表现在两个方面:(1) 第二种改革方式引起了非正规部门新雇佣就业的增加,而第一种改革方式则引起了非正规部门新雇佣就业的减少;(2) 相对于第一种改革方式,第二种改革方式的宏观经济效应相对更大,图 2中第二种改革对各宏观经济变量的冲击效应大于图 1中第一种改革方式的冲击效应。
图 2还显示了第二种改革方式的短期冲击效应。显然,这一改革引起了正规部门的新雇佣就业、产出的增加以及非正规部门的新雇佣就业、产出、总产出和失业的减少。原因在于,这一改革方式降低了正规部门就业者的就业收益,相应增加了企业的收益,因而使正规部门企业增加劳动力的雇佣;而正规部门就业的增加则推动了产出的增加。在这一改革方式下,非正规部门就业给企业带来的收益相对下降,因而导致企业减少劳动力的雇佣,进而导致了非正规部门产出的减少;非正规部门产出的减少甚至超过了正规部门产出增加的幅度,进而在短期中甚至导致了总产出的减少。不过,总产出的减少趋势并未持续较长时间,在冲击发生后的第二个时期,总产出开始出现增加的趋势。
比较图 2和图 1还可以发现两种劳动力市场改革方式在短期效应上的差异。首先,第二种改革方式下,正规部门的新雇佣就业与产出在短期并未呈现下降的趋势;第二,第二种改革方式下,总产出在短期呈现出更为短暂的下降趋势;第三,第二种改革方式下,失业即使在短期中也并未表现出上升的趋势。
综上,基于图 2,降低正规部门就业者的议价能力,有助于促进就业的正规化,并降低我国经济的非正规性。这与第一种改革方式相同。但是,这一改革方式下,即使在短期中失业也并未表现出上升的趋势,并且产出仅仅表现出非常短暂的下降。因此,与第一种改革方式不同,这一改革方式并不具有明显的“以短期疼痛换取长期收益”的特征。
四、货币政策与劳动力市场结构性改革的效应
与Gali等(2016) 等类似,我们引入一个被称为“Evans规则”的货币政策。这一政策机制来源于Evans(2011),其主张将失业作为货币盯住的目标,货币政策当局可以依据失业的变化积极地调整名义利率,进而达到稳定劳动力市场和宏观经济的目的。具体地,这一政策机制可以近似表述为如下形式:
| ${R_t}/R = {\left( {{R_{t-1}}/R} \right)^{{\rho _R}}}{\left[ {{{\left( {{Y_t}/Y} \right)}^{{r_y}}}{{\left( {\Pi _t^p/{\Pi ^p}} \right)}^{{r_p}}}{{\left( {{U_t}/U} \right)}^{{r_u}}}} \right]^{1 - {\rho _R}}}{\rm{exp}}\left( {\varepsilon _t^r} \right)$ | (22) |
其中:U度量了货币政策当局盯住的失业水平;ru反映了货币政策当局对失业的敏感程度,进而也反映了货币政策当局对失业的容忍程度。本文将这一参数的取值分别设定为-0.5,并分别剖析两种劳动力市场结构性改革的效应。
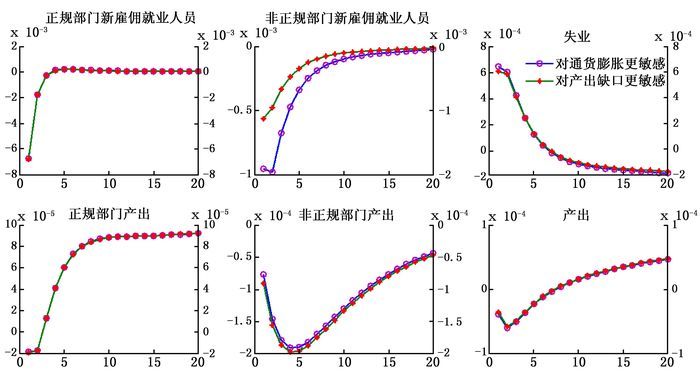
图 3显示的是Evans规则下第一种劳动力市场结构性改革的效应。显然,Evans规则下,第一种劳动力市场改革冲击在短期内引起了正规部门新雇佣就业人员的下降,但在长期内引起了上升。这与图 1一致。相对而言,Evans规则下,第一种劳动力市场改革冲击仅引起短期中正规部门新雇佣就业人员较小幅度的下降。
|
| 图 3 降低正规部门雇佣成本的效应:Evans规则 |
图 3表明,无论是短期效应还是长期效应,Evans规则下第一种劳动力市场结构性改革均引起了正规部门的产出和总产出的上升;对应地,这一改革还引起了非正规部门的新雇佣就业人员、产出和失业的下降。因此,与图 1对照可见,Evans规则显著改变了第一种劳动力市场结构性改革的效应,使得基准政策机制下这一劳动力市场结构性改革所具有的“以短期疼痛换取长期收益”的特征不复存在。
另外,基于冲击效应大小的角度比较图 3和图 1还可以发现,Evans规则下,第一种劳动力市场结构性改革引起了失业更大幅度的减少,进而引起总产出相对较大幅度的增加。因此,在劳动力市场结构性改革过程中,政府通过降低正规部门的雇佣成本,如果我国央行使用Evans规则作为配套,那么相对于基准政策机制而言,Evans规则下降低正规部门雇佣成本的改革方式具有更好的政策效果:既可以更大幅度地降低失业,也可以更好地保证经济增长。
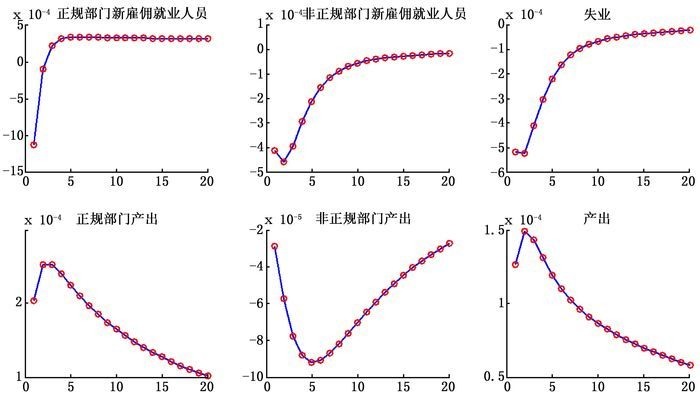
我们进一步分析Evans规则下第二种劳动力市场结构性改革的效应。图 4显示,与图 2相比,Evans规则并未改变第二种劳动力市场结构性改革的短期和长期宏观经济效应。不过,基于改革效应大小的角度,相对于基准货币政策机制而言,Evans规则下仍显著改变了第二种劳动力市场结构性改革的宏观经济效应。通过观测这一改革的长期效应可以发现:Evans规则下,第二种劳动力市场结构性改革引起了两类部门的新雇佣就业人员、产出和总产出更大幅度的上升以及失业更大幅度的下降。因此,基于这一改革的长期效应可以认为,Evans规则下这一改革具有更好的效果。
|
| 图 4 降低正规部门就业者议价能力的效应:Evans规则 |
最后,通过观测Evans规则下第二种劳动力市场结构性改革的短期效应,可以发现:(1) 第二种劳动力市场结构性改革引起了正规部门的新雇佣就业人员数量、产出以及非正规部门的产出和总产出更大幅度的上升;(2) 第二种劳动力市场结构性改革引起了失业更大幅度的下降;(3) 第二种劳动力市场结构性改革即使在短期也并未引起总产出的下降;(4) 第二种劳动力市场结构性改革引起非正规部门新雇佣就业人员数量相对较小幅度的下降。因此,基于改革的短期效应同样可以发现,Evans规则的引入改善了第二种劳动力市场结构性改革的效果。
综上,比较不同货币政策机制下两种劳动力市场结构性改革的效应可以发现,无论政府使用哪一种劳动力市场结构性改革方式,Evans规则的引入均相对改善了劳动力市场结构性改革的宏观经济效应。因此,这一结论意味着,在我国劳动力市场结构性改革过程中,如果货币政策当局采用Evans规则作为配套性货币政策,劳动力市场结构性改革将具有更好的宏观经济效应。
五、结论
基于国内外关于劳动力市场结构性改革的相关研究,本文在NK-DSGE模型框架中对我国劳动力市场结构性改革的宏观经济效应进行了考察。我们得到如下结论:
(1) 基准货币政策机制下,第一种劳动力市场结构性改革(即降低正规部门雇佣成本)具有显著的“以短期疼痛换取长期收益”的特征,而第二种劳动力市场结构性改革(即降低正规部门就业者的议价能力)的特征并不明显;并且就改革效应的大小而言,第二种劳动力市场结构性改革的效应大于第一种劳动力市场结构性改革。因此,在基准货币政策机制下,为了降低改革所带来的短期“疼痛”,第二种劳动力市场结构性改革可能优于第一种劳动力市场结构性改革。(2) Evans规则下,两种劳动力市场结构性改革冲击效应的模拟结果表明:第一种劳动力市场结构性改革“以短期疼痛换取长期收益”的特征不复存在;两种改革效应比较的结果显示,第二种劳动力市场结构性改革仍具有相对较大的冲击效应。因此,即使我国央行执行Evans规则,第二种劳动力市场结构性改革仍具有相对较好的效果。(3) 通过比较基准政策机制与Evans规则下两种劳动力市场结构性改革的效应可以发现,Evans规则显著改善了两种劳动力市场结构性改革的效应。因此,在我国劳动力市场结构性改革过程中,无论政府采用哪一种改革方式,Evans规则均可以作为配套的货币政策。
以劳动力为代表的生产要素无法自由流动是造成中国就业难题的一个重要原因。目前,政府正积极地推进供给侧结构性改革,作为供给侧结构性改革的一个重要构成部分,劳动力市场的结构性改革是促进劳动力自由流动进而缓解失业问题的有效举措。基于本文的研究结论,无论在哪一种货币政策机制下,相对于旨在降低正规部门聘用成本的第一类劳动力市场结构性改革而言,旨在降低正规部门议价能力的第二类劳动力市场结构性改革对中国劳动力市场和宏观经济所产生的冲击效应相对较大,第二类劳动力市场结构性改革具有相对较好的效果。导致正规部门就业者具有较高议价能力的原因除了就业者自身的条件之外,行政性用人体制扮演着非常重要的角色。行政性用人体制直接导致了正规部门的失业呆滞,使我国通过经济增长促进就业的措施难以有效发挥作用。因此,在推行第二类劳动力市场结构性改革时,需要改革行政性用人体制,提高劳动力市场尤其是正规部门就业的市场化程度,减少政府对正规部门用人的干预和管制。惟有如此,才能有效地推进第二类劳动力市场结构性改革,促进劳动力的自由流动和缓解当前的就业难题。
另外,就本文的研究结论而言,无论政府推行哪一类劳动力市场结构性改革,采用Evans规则作为配套性货币政策,将具有相对较好的宏观经济效应。这一结论意味着,在我国劳动力市场结构性改革过程中,中国人民银行应该在货币政策方面采用Evans规则作为配套。Evans规则要求中国人民银行将失业作为货币政策盯住目标的对象之一,并且依据失业的动态变化及时进行货币政策的调整。目前,城镇登记失业率是官方公布的数据,但是这一数据与中国劳动力市场所表现出来的失业数据存在较大的差异,因而并不能作为Evans规则的决策参考依据。在中国劳动力市场结构性改革过程中,货币政策当局如果推行Evans规则作为辅助,则需要对失业进行精确的测算和科学的界定。同时,目前中国货币政策仍然是以为经济增长服务为目标(Chen等,2016),就本文的研究结论而言,在劳动力市场结构性改革过程中,基于稳定劳动力市场的角度,调整货币政策盯住的目标,将失业作为货币政策盯住的对象之一,这样才能有效地缓解劳动力市场结构性改革带来的“短期疼痛”并充分实现劳动力市场结构性改革的目标。
最后,本文尝试在封闭经济NK-DSGE模型中考虑了劳动力市场结构性改革对我国劳动力市场以及宏观经济产生的短期效应与长期效应,进而考察了劳动力市场结构性改革过程中的配套性货币政策机制选择。当然,作为尝试,本文仍可能存在一些不足之处,主要包括:(1) 现实经济中仍存在其他不同形式的劳动力市场结构性改革,而本文主要分析了针对雇佣成本和议价能力的改革;(2) 本文在考察劳动力市场结构性改革的过程中,设定不同部门劳动力在技能上可以具有替代性,并且失业并不影响劳动者的技能。但现有相关研究表明,劳动者的技能并不具有完全替代性,并且失业会造成技能的退化。这一机制将影响正规部门失业者的就业决策。关于这一方面的研究可以参考陈利锋(2017b)等。
| [1] | 卞志村, 杨源源. 结构性财政调控与新常态下财政政策工具选择[J]. 经济研究, 2016(3): 66–80. |
| [2] | 陈利锋. 异质性雇用成本、社会福利与劳动力市场结构性改革[J]. 财经研究, 2015(1): 49–61. |
| [3] | 陈利锋. 内部人势力、失业呆滞与货币政策——基于包含非正规部门的NK-DSGE模型[J]. 经济科学, 2016(6): 47–62. |
| [4] | 陈利锋. 失业呆滞、劳动力市场结构性改革与货币政策[J]. 华中科技大学学报(社会科学版), 2017a(4): 67–76. |
| [5] | 陈利锋. 技能退化、干中学与失业的持续性[J]. 贵州财经大学学报, 2017b(5): 1–14. |
| [6] | 彭国华. 技术能力匹配、劳动力流动与中国地区差距[J]. 经济研究, 2015(1): 99–110. |
| [7] | 钱先航, 曹廷求, 曹先芳. 既患贫又患不安:编制与公共部门的收入分配研究[J]. 经济研究, 2015(7): 57–71. |
| [8] | 沈晓栋. 中国非正规部门规模估算与宏观效应量化分析[M]. 北京: 中国统计出版社, 2015. |
| [9] | 王君斌, 郭新强, 王宇. 中国货币政策工具选取、宏观效应与规则设计[J]. 金融研究, 2013(8): 1–15. |
| [10] | 魏下海, 余玲铮. 中国城镇正规就业与非正规就业工资差异的实证研究——基于分位数回归与分解的发现[J]. 数量经济技术经济研究, 2012(1): 78–90. |
| [11] | 吴要武. 中国城镇非正规就业问题研究[M]. 北京: 中国社会科学出版社, 2014. |
| [12] | 张平. "结构性"减速下的中国宏观政策和制度机制选择[J]. 经济学动态, 2012(10): 3–9. |
| [13] | 中国经济增长前沿课题组. 突破经济增长减速的新要素供给理论、体制与政策选择[J]. 经济研究, 2015(11): 4–19. DOI:10.3969/j.issn.1002-5863.2015.11.001 |
| [14] | Batini N, Kim Y, Levine P, et al.Informal labour and credit markets:A survey[R].IMF Working Paper, 2010. |
| [15] | Blanchard O, Gali J. Labor markets and monetary policy:A new Keynesian model with unemployment[J]. American Economic Journal:Macroeconomics, 2010, 2(2): 1–30. |
| [16] | Cacciatore M, Duval R, Fioro G, et al.Short-term pain for long-term gain:Market deregulation and monetary policy in small open economies[R].NBER Working Paper No.w21784, 2015. |
| [17] | Cacciatore M, Fioro G. The macroeconomic effects of markets deregulation[J]. International Finance, 2015, 183(3): 343–360. |
| [18] | Cacciatore M, Fioro G. The macroeconomic effects of goods and labor markets deregulation[J]. Review of Economic Dynamics, 2016, 20: 1–24. DOI:10.1016/j.red.2015.10.002 |
| [19] | Campolmi A, Faia E. Labour market institution and inflation volatility in the Euro area[J]. Journal of Economic Dynamics and Control, 2011, 35(5): 793–812. DOI:10.1016/j.jedc.2010.07.001 |
| [20] | Charlot O, Malherbet F, Terra C. Informality in developing economies:Regulation and fiscal policies[J]. Journal of Economic Dynamics and Control, 2015, 51: 1–27. DOI:10.1016/j.jedc.2014.09.031 |
| [21] | Chen K, Higgins P, Waggoner D F.China pro-growth monetary policy and its asymmetric transmission[R].NBER Working Paper No.w22650, 2016. |
| [22] | Christiano L, Eichenbaum M, Trabandt M. Unemployment and business cycle[J]. Econometrics, 2016, 84(4): 1523–1569. DOI:10.3982/ECTA11776 |
| [23] | Davis S, Haltiwanger J.Labor market fluidity and economic performance[R].NBER Working Papers No.w20479, 2014. |
| [24] | Evans C.The Fed's dual mandate responsibilities and challenges facing U.S. monetary policy[R].Federal Reserve of Chicago Working Paper No.r111019c, 2011. |
| [25] | Faia E, Wolfgang L, Cristian M. Labor selection, turnover cost and optimal monetary policy[J]. Journal of Money, Credit and Banking, 2014, 46(1): 115–144. DOI:10.1111/jmcb.2014.46.issue-1 |
| [26] | Fiess N, Fugazza M, Maloney W. Informal self-employment and macroeconomic fluctuations[J]. Journal of Development Economics, 2010, 91(2): 211–226. DOI:10.1016/j.jdeveco.2009.09.009 |
| [27] | Gali J.Insider-outsider labor markets, hysteresis and monetary policy[R].UPF Department of Economic Working Paper No.1506, 2016. |
| [28] | Gertler M, Huckfeldt C, Trigari A.Unemployment fluctuations, match quality, and the wage cyclicality of new hires[R].NBER Working Paper No.w22341, 2016, . |
| [29] | La Porta R, Shleifer A. Informality and development[J]. Journal of Economic Perspectives, 2014, 28(3): 109–126. DOI:10.1257/jep.28.3.109 |
 2017, Vol. 43
2017, Vol. 43


