文章信息
 | 财经研究 2017年43卷第1期 |
- 于斌斌.
- Yu Binbin.
- 产业结构调整如何提高地区能源效率?——基于幅度与质量双维度的实证考察
- How Does Industrial Restructuring Improve Regional Energy Efficiency? An Empirical Study Based on Two Dimensions of Magnitude and Quality
- 财经研究, 2017, 43(1): 86-97
- Journal of Finance and Economics, 2017, 43(1): 86-97.
-
文章历史
- 收稿日期:2016-03-22

2017第43卷第1期
2.浙江理工大学 浙江省生态文明研究中心,浙江 杭州 310018
2.Center for Ecological Civilization,Zhejiang Province,Zhejiang Sci-tech University,Hangzhou 310018,China
伴随着工业化与城市化的快速推进以及能源供需矛盾的日益紧张,“新常态”下中国经济发展将会面临越来越严重的能源环境约束问题;加上煤炭资源所具有的价格优势,这让中国在很长时间内将不会改变以煤炭为主的能源消费格局(林伯强等,2012)。这意味着,通过进一步优化能源结构来实现节能减排的空间不大,而提高能源效率才是解决问题最重要、最现实的途径。但长期以来,高投入、高能耗、高污染、高排放的粗放型发展模式,让中国成为全球最大的能源生产国和消费国,同时也成为温室气体和大气污染物排放大国(关伟和许淑婷,2015)。随着世界各国对于全球温室效应及气候异常现象的关注,中国政府在节能减排问题上将会面临更大的国际压力。在此背景下,中国政府制定了限制温室气体排放的措施,承诺在2020年碳排放强度较2005年降低40%-45%。
对于实现节能减排的战略目标,已经形成共识的三大路径是产业结构调整、能源结构优化和技术进步。其中,产业结构调整对于降低碳排放强度的贡献度在70%以上(王文举和向其凤,2014)。原因主要在于产业结构既是各类经济投入与产出的“资源转换器”,又是各种污染物种类和数量的“环境控制器”:一方面,产业结构的组合类型和调整强度决定了经济效益和能源利用效率;另一方面,生态环境承载力直接制约着区域产业结构及其转化方向。
需要指出的是,随着区域产业转移和能源跨区域流动(如西气东输、北煤南运和西电东送等工程项目)的不断推进,产业结构调整与能源效率改善的空间联系更加紧密,已超越了地理意义上的“近邻”关系;而且,现有研究大多没有对产业结构调整做出系统性考察,仅从产业结构变动的角度(如二、三产比重)进行分析(黄亮雄等2012),尚未深入到产业结构优化升级对能源效率影响的本质。鉴于此,本文将从调整幅度和调整质量两个维度来分析中国城市产业结构调整与能源效率的演变特征及相互关系,并运用空间计量方法研究调整幅度与调整质量对能源效率的影响作用及其空间溢出效应,最后进一步分东、中、西三类地区进行考察。本文采用从业人员在产业部门之间的重新配置强度来反映产业结构的调整幅度;利用产业部门之间比例关系变动所引致的生产率变化来表示产业结构的调整质量;运用线性数据转换函数法将非期望产出纳入到DEA-Malmquist指数中来度量能源效率。研究发现,产业结构的调整幅度、调整质量与能源效率之间都存在显著的空间相关性及交互耦合关系,并且更重要的是,与调整幅度相比,调整质量才是改善能源效率的主要动力来源,尤其是东部地区。这意味着,与单纯推进“腾笼换鸟”或“退二进三”的政策引导相比,伴随产业部门比例关系变迁的生产率提升才是改善能源效率的有效途径。
本文可能的贡献在于:首先,在数据选择上,采用2003-2013年中国285个地级及以上城市的统计数据,相比于省级数据,得出的研究结论更加真实可靠。因为中国不少省区的经济规模、人口数量和地理面积已不亚于一些国家,省级层面的分析将省内各市设定为同质化单元,尚未考虑到中国区际市场分割现象的存在。其次,在研究方法上,本文选择空间杜宾模型(SDM),不仅避免了传统计量方法将研究单元视为均质且相互独立的弊端,还可以对产业结构调整对能源效率的影响作用及空间溢出效应进行比较分析,从而提高了实证检验结果的可信度和稳健性。最后,在研究内容上,本文重点关注的是产业结构调整的幅度与质量对能源效率的影响作用及其空间溢出效应。这是因为产业结构调整不仅包含了产业部门之间比例关系的变化,还包括与这一比例关系相匹配的生产率水平的提升。
二、 文献回顾能源效率作为能源经济学的一个热点问题日益受到学术界的关注,而对于能源效率的测量,主要有单要素能源效率和全要素能源效率两种方法。单要素能源效率主要是以经济产出与能源投入比或能源投入与经济产出比来度量。前者被称为能源生产率,测度的是单位能源的经济产出;后者是通常所说的能源强度,测度的是单位GDP的能源消耗量。单要素能源效率的优点是定义直观、方法简单、应用方便,而且通过不同的因素分解方法可以考察产业结构、技术进步和规模效应等因素对能源效率变化的贡献度。但是单要素能源效率并没有考虑到劳动、资本等生产要素对经济产出的贡献度及不同生产要素之间的替代作用。
与单要素能源效率相比,全要素能源生产率讨论的是能源及其他生产要素的利用效率,能更好地反映能源与经济之间的相互关系,已被国内外学者普遍采用(魏楚和沈满洪,2008;师博和沈坤荣,2008;Arabi等,2014)。全要素能源效率主要通过对生产可能集(或生产技术)进行定义,利用各生产单位的要素投入与经济产出的相关数据构造出前沿生产边界,并分析各生产单位与前沿生产边界之间的关系,以确定该生产单位的资源是否得到充分利用或是否存在帕累托改进空间。对全要素能源效率的测算方法主要有非参数估计的数据包络分析(DEA)与参数估计的随机前沿函数分析(SFA)。由于DEA模型无需设定具体函数形式,其适用范围比参数估计的SFA更为广泛。随着学术界对中国环境污染和生态破坏问题的重视,基于非期望产出(如排放量、工业废水排放量和工业烟尘排放量等)的DEA模型在全要素能源效率评价中得到了越来越普遍的应用(Hu,2014;Lu等,2014)。
关于产业结构变化对能源效率的影响,一种观点认为,产业结构调整将有助于提高能源效率。魏楚和沈满洪(2008)运用DEA模型测算和分解了中国1995-2006年省级层面的能源效率及其演化趋势,结果表明“退二进三”的产业结构调整能改善能源技术效率。程叶青等(2013)的分析也发现,优化产业结构是减少碳排放强度和实现节能减排目标的重要途径。肖挺和刘华(2014)通过产业结构均衡和产业结构优化两个维度讨论了1998-2012年间中国产业结构调整对二氧化硫排放的影响效应,结果发现产业结构均衡化调整有助于减少工业二氧化硫排放并提高了能源效率。王文举和向其风(2014)构建了产业结构调整的动态投入产出模型,并利用投入产出表预测了中国在2020年节能减排的潜力,发现产业结构调整对实现中国碳强度目标的贡献度可达60%左右。另一种观点指出,产业结构调整对能源效率的提升作用很小,甚至存在负面影响。Liao等(2007)通过Törnqvist-Sato-Vartia指数法将中国1997-2002年间的能源强度变化分解为生产效率效应和部门结构效应,结果发现生产效率对能源强度下降的贡献度最大,而结构调整对其影响较小。此外,王玉潜(2003)分析了1987-1997年间中国能耗强度变动的原因,指出产业结构调整对单位产出能耗下降的影响是负面的。吴琦和武春友(2010)则利用超效率DEA方法测度了中国在1978-2007年间的能源技术效率,发现第三产业每提高1个百分点,能源技术效率将会降低1.25个百分点。林伯强和杜克锐(2014)针对指数分解法(IDA)和生产理论分解法(PDA)的不足,重构了一个分析框架证实了产业结构变化阻碍了中国能源强度的下降。
在上述关于产业结构调整对能源效率影响的研究中,大多数学者主要着眼于产业部门之间相对比值的变化来反映产业结构的变化,进而考察其对能源效率的影响,因而并未得出一致性的研究结论。但Dinda(2004)的研究发现,提高能源效率与优化生态环境的重要途径是推动产业结构向知识技术密集型产业转型;Lan等(2012)研究发现,实现节能减排主要源于产业部门生产率的提高,而不是产业结构比例的调整。这说明,产业结构调整幅度的增大并不意味着实现了能源效率改善,而只有当产业结构调整能降低对资源环境的依赖和破坏且带来生产效率的持续增进时,这种结构调整才是可取的。
进一步梳理文献发现,现有研究仅从时间维度检验了产业结构调整与能源效率之间的相互关系,较少从空间维度来探索二者的互动关系,更忽视了产业结构调整与能源效率提升所产生的空间溢出效应。在“两个大局”战略思想的制度安排下,“两个大局”战略思想是指中西部支持东部沿海地区优先发展、东部沿海发展以后支持中西部地区发展。中国经济发展采取的是非均衡发展道路,空间关联性应成为理解中国产业结构调整与能源效率相关关系的重要切入点。于斌斌(2014、2015)运用空间计量方法检验了中国区域之间产业结构调整存在显著的空间溢出效应,而程叶青等(2013)和潘雄锋等(2014)等学者证实了中国能源效率在省际之间也存在明显的空间相关性和空间依赖性。由于中国不同区域间产业结构和能源效率差异较大,忽视区域之间的相互影响会显著降低实证检验结果的可信性和稳健性。
三、 研究设计(一) 测算方法与变量说明。本文采用DEA-Malmquist指数法对中国城市能源效率进行估算。选取劳动力、资本存量和能源消费量作为投入要素指标,选择期望性产出实际GDP以及非期望性产出废水排放量、二氧化硫排放量和烟尘排放量为产出要素指标。
1.投入指标。(1)劳动力投入。该指标采用各个城市的从业人数来表示。(2)资本存量。利用社会固定资产投资来替代,并采用永续盘存法估计:${k_{j,t}} = \left( {1 - \delta } \right){K_{j,t - 1}} + {I_{j.t}}$>。其中,K、I分别表示资本存量和新增社会固定资产投资,j和t表示地区和年份,σ表示固定资产折旧率,参照单豪杰(2008)的处理方法,设定折旧率为10.96%。(3)能源消费。由于中国总能源投入数据被明显低估且电力消耗数据更加准确,本文借鉴秦炳涛(2014)的做法,采用全年全市用电量来反映能源消费水平。
2.产出指标。(1)实际GDP。以2003年为基期,根据各个城市所在省份的GDP平减指数进行平减消除价格因素的影响。(2)废水排放量。本文将利用Seiford和Zhu(2002)提出的线性数据转换函数法对生产过程中的废水排放量进行处理。具体处理方法为:设第i个城市第j年度的废水排放量为${Q_{ij}},{Q_{ij}} = {\left( {{Q_{i1}},{Q_{i2}}, \cdots ,{Q_{ij}}} \right)^T} > 0,(i = 12 \cdots ,n)$;取η=max(Qij)+C,其中C为任意大于0的常数,这里取值为1;通过线性数据转换后,废水排放量可表示为Qij*=-Qij+η。(3)二氧化硫排放量和烟尘排放量。这两类非期望性产出也采取上述线性数据转换函数法进行处理。
3.产业结构调整。本文借鉴Findeisen和Südekum(2008)的方法,通过测算从业人员在行业间重新配置的强度来反映产业结构的调整幅度(StrI),其计算公式表示为:
| $StrI = \left\{ {\left[ {\sum\limits_{i = 1}^n {\left| {e\left( {i,t + 1} \right) - e\left( {i,t} \right)} \right|} } \right] - \left| {e\left( {t + 1} \right) - e\left( t \right)} \right|} \right\}/e\left( t \right)$ | (1) |
其中,e(i,t+1)和e(i,t)分别表示一个城市的i产业在t+1期和t期的就业人数,e(t+1)和e(t)分别为该城市在t+1期和t期的总就业人数;StrI≥0,即只有当城市所有行业就业人数随总就业人数同比例增减时,StrI=0。该指数反映了劳动力跨行业配置的幅度。
产业结构调整质量(StrH)。产业结构调整是产业结构从低级向高级发展的过程,从技术角度可以把产业结构调整质量表述为:资源要素从低效率部门转移到高效率部门,使得效率高的产业部门比例持续增加,最终引致不同产业部门的生产率共同提高。这意味着产业结构调整质量包括数量(比例关系)和质量(生产率)两部分内容,其计算公式表示为:
| $Str{H_{it}} = \sum\limits_{j = 1}^J {({S_{ijt}} \times {F_{ijt}})} $ | (2) |
其中,i、j和t分别表示城市、行业和时间;J为行业总数;Sijt为i城市j产业的增加值在t时间占所有行业总增加值的比重;Fijt为i城市j产业的劳动生产率。一个经济体系中劳动生产率越高的产业在总产业中占比越大,其产业结构调整质量StrH就越大。
4.控制变量。(1)经济发展水平(Eco)。经济发展水平的提高会带来生产率增长、技术创新和产业结构升级,从而进一步促进能源效率提升。采用人均GDP并取对数来反映一个城市的经济发展水平。(2)人力资本(Hum)。人力资本的累积是提高生产效率和促进产业结构升级的重要途径。借鉴于斌斌(2015)的做法,采用平均受教育年限来代理人力资本变量。(3)外商直接投资(FDI)。FDI的流入不仅可以增加该地区的资本存量,还能促进当地和其他地区节能技术的普及与应用(Hübler和Keller,2010)。按历年人民币汇率的平均价格对FDI进行折算,并以FDI占GDP的比重来反映一个城市的外商直接投资水平。(4)政府干预程度(Gov)。采用财政支出占财政收入的比重来表示。
(二) 空间相关性检验。本文采用Moran’sI指数来检验产业结构调整、能源效率是否存在空间相关性,其计算公式为:
| $MoransI = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{W_{ij}}} } ({Y_i} - \bar Y)({Y_j} - \bar Y)/{S^2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{W_{ij}}} } $ | (3) |
其中,${S^2} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({Y_i} - \bar Y)}^2}} ,\bar Y = \frac{1}{n}\sum\limits_{i = 1}^n {{Y_i}} $,Yi、Yj分别表示第i、j个城市的观测值,n为观测值数量,Wij是空间权重矩阵。本文采用标准统计量Z来检验Moran’sI指数的显著性水平,其计算公式为:
| $Z(MoransI) = \frac{{MoransI - E\left( {MoransI} \right)}}{{\sqrt {VAR(Moran'sI)} }}其中E\left( {MoransI} \right) = - \frac{1}{{n - 1}}$ | (4) |
(三)空间面板计量模型设定。关于处理面板数据的空间计量方法,Anselin等(1996)提出了空间误差模型(SEM)和空间滞后模型(SLM)。如果LM检验结果拒绝了OLS模型,并且同时存在空间误差和空间滞后,则应选择SDM模型(Elhorst,2010),其基本形式为:
| ${Y_{it}} = \delta \sum\limits_{j = 1}^n {{W_{ij}}{Y_{it}} + \beta {X_{it}}} + \gamma \sum\limits_{j = 1}^n {{W_{ij}}{X_{it}}} + {\mu _i} + {\lambda _i} + {\varepsilon _{it}},{\varepsilon _{it}} \sim N(0,{\sigma ^2}I)$ | (5) |
其中,Yit和Xit分别为被解释变量和解释变量,$\delta \sum\limits_{j = 1}^n {{W_{it}}{Y_{it}}} $和$\gamma \sum\limits_{J = 1}^n {{W_{ij}}{X_{it}}} $分别为被解释变量和解释变量的空间滞后项,W为空间权重矩阵。由于二元邻接矩阵认为不相邻区域间不存在空间相关性,本文采用距离权重矩阵,见下式:
| ${W_{ij}} = \left\{ \begin{array}{l} {e^{ - \alpha {d_{ij}}}},i \ne j\\ 0,i = j \end{array} \right.$ | (6) |
其中,Wij是包含i行和j列元素的空间权重矩阵,对角线上都为0;α为距离系数,dij是地理单元i和j之间的地理距离,这里用城市之间最短距离的倒数来替代。
当存在空间滞后项时,Monfort和Nicolini(2009)指出使用点估计方法检验空间溢出效应会导致偏误,应使用微积分方法将总效应划分为直接效应和间接效应,以表示解释变量对本地区与其他地区的平均影响。因此,将SDM模型改写成如下向量形式:
| ${y_t} = {\left( {I\delta W} \right)^{ - 1}}\left( {\beta {X_t} + \gamma W{X_t}} \right) + {\left( {1 - \delta W} \right)^{ - 1}}{\varepsilon _t}$ | (7) |
以第k个解释变量为自变量对式(5)进行求导,可以得到如下偏微分矩阵:
| ${\left[ {\frac{{\partial y}}{{\partial {X_{1k}}}} \ldots \frac{{\partial y}}{{\partial {X_{Nk}}}}} \right]_t} = {\left( {1 - \delta W} \right)^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{\beta _k}}&{{w_{12}}{\lambda _k}}& \ldots &{{w_{1N}}{\lambda _k}}\\ {{w_{21}}{\lambda _k}}&{{\beta _k}}& \ldots &{{w_{2N}}{\lambda _k}}\\ \vdots & \vdots & \ddots & \vdots \\ {{w_{N1}}{\lambda _k}}&{{w_{N2}}{\lambda _k}}& \ldots &{{\beta _k}} \end{array}} \right]$ | (8) |
由式(8)可知,若一个地区的解释变量发生变化,则该地区和其他地区的被解释变量都会发生变化。直接效应和间接效应在偏微分矩阵中分别反映为对角线元素的平均值和非对角线元素的平均值。当λk=0时产生的间接效应为局部效应,是W矩阵内相邻区域对本地区的影响效应;当δ=0时产生的间接效应为全局效应,是W矩阵内、外所有地区对本地区的影响效应。但是,局部效应和全局效应在实证研究中很难区分。
(四)数据来源。本文的数据来源于《中国城市统计年鉴》(2004-2014年)、《中国区域经济统计年鉴》(2004-2014年)和《中国统计年鉴》(2004-2014年),采用插值法补充个别城市所缺失的数据。为统一口径,本文最终选择除拉萨(缺少数据)、巢湖、毕节、铜仁、三沙和海东之外的285个地级及以上城市数据进行分析。①
① 在2011-2013年间,国务院撤销了安徽的巢湖市,在贵州升格毕节和铜仁两个地级市,并在海南成立三沙市以及在青海设立地级海东市,使中国地级及以上城市数量变为290个。
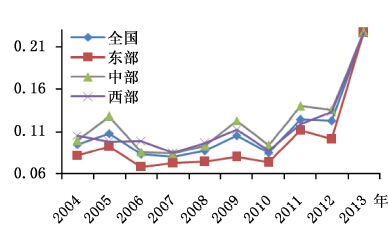
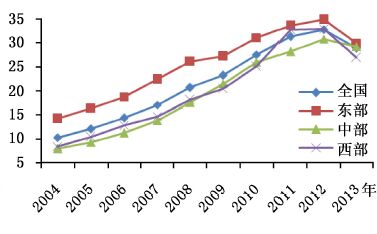
四、 中国城市产业结构调整与能源效率变化的特征性事实(一)产业结构调整与能源效率的演变特征。在产业结构调整幅度与调整质量的变化数量上,②西部地区的产业结构调整幅度最大,中部次之,而东部最小;与之相反的是,东部产业结构调整质量最高,而中西部则相对较低,详见图 1和图 2。从变化趋势上,在2004-2013年间,产业结构调整幅度呈“波浪式”变化趋势,但值得注意的是,全国及东中西地区的产业结构调整幅度分别从2012年的0.12、0.11、0.14、0.13同时上升到2013年0.22,上升幅度接近1倍;全国及东中西部地区的产业结构调整质量在2004-2012年间都逐年上升,并以2013年初为拐点开始出现小幅下降。这说明,在“两个大局”战略思想的引导下,东部地区经济起步较早,其产业结构质量明显优于中西部地区,但在“西部大开发”、“中部崛起”等区域一体化战略的影响下,中西部地区通过承接产业转移和优化内部产业结构等方式加快了产业结构调整幅度。但“十八大”以后,中国经济逐渐进入了“新常态”发展阶段,其典型特征是“三期叠加”(增长速度换挡期、产业结构调整阵痛期、前期刺激政策消化期)和“三重冲击”(资本积累速度下降、人口红利消失和“干中学”技术进步效应削减)。正是由于中国长期依赖“三高一低”的产业发展模式,使得“结构红利”和“人口红利”消耗殆尽,短期内即便进行高强度的产业结构调整,也难以实现产业升级。
② 本文将北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东、海南11个省(市)作为东部地区,把山西、内蒙古、吉林、黑龙江、安徽、江西、河南、湖北、湖南9个省作为中部地区,把广西、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆11个省(市)作为西部地区。
|
| 图 1 中国产业结构调整幅度的变化情况 |
|
| 图 2 中国产业结构调整质量的变化情况 |
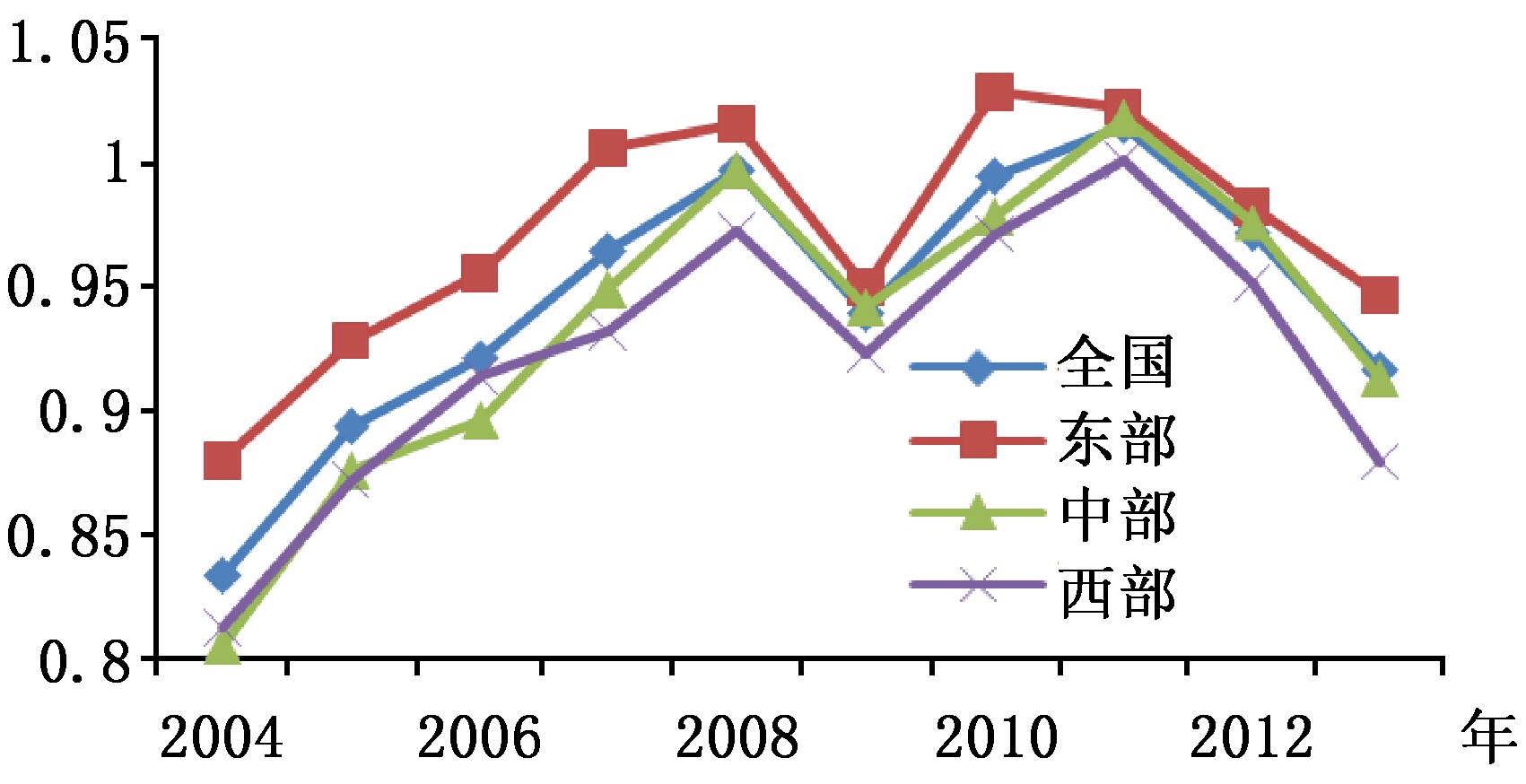
从区域差异上,东部地区的能源效率明显高于中西部地区及全国平均水平(详见图 3)。在2004-2013年间,全国及东中西地区的能源效率都呈“M”形,并以2008、2009和2011年为拐点。在东部,能源效率从2004年的0.88逐年上升至2008年的0.99,随后出现“断崖式”下降,到2009年降为0.93,然后又开始逐渐上升,到2010年达到最大值1.03,随之又开始下降至2013年的0.92;在中部,能源效率从2004年的0.80上升至2008年的0.97,到2009年下降至0.92,2011年上升至1.02后再下降至2013年的0.91;在西部,能源效率从2004年的0.81上升至2008年的0.97,到2009年下降至0.92,2011年上升至1.00后下降到2013年的0.88。原因可能在于:2008年金融危机爆发以后,国内外市场需求紧缩使得国内投资锐减(如FDI转移或撤资)与产能过剩的矛盾日益突出,导致能源效率在2009年大幅下降;随后,在2010年,国家提出“加快转变经济发展方式”的战略性调整,通过产业转移和创新驱动等战略提高了能源效率;但伴随经济发展逐渐进入“新常态”,能源效率随之从2012年开始下降。
|
| 图 3 中国能源效率的变化情况 |
(二)产业结构调整与能源效率的空间相关性。由表 1可知,在2004-2013年间,产业结构调整幅度在2007、2008和2012年没有通过空间相关性的显著性检验。而产业结构调整质量的空间相关性在2004-2013年间都通过了显著性检验,这说明中国城市产业结构调整质量在区域之间都存在明显的空间依赖性;能源效率的检验结果亦是如此。
| Year | 2004年 | 2005年 | 2006年 | 2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 |
| StrI | 0.0517*** [4.0133] | 0.0557*** [4.3427] | 0.0256** [2.1797] | 0.0125 [1.1606] | 0.0040 [0.5232] | 0.0288** [2.3645] | 0.0412*** [3.2461] | 0.0872*** [6.6516] | 0.01716 [1.4838] | 0.1268*** [9.4945] |
| StrH | 0.2064*** [15.6984] | 0.1710*** [13.3755] | 0.1611*** [12.6319] | 0.1751*** [13.7853] | 0.1493*** [11.6868] | 0.1406*** [10.7416] | 0.1297*** [9.9451] | 0.0940*** [7.3713] | 0.1171*** [8.9446] | 0.1246*** [9.5993] |
| EnE | 0.1830*** [13.5422] | 0.1586*** [11.7678] | 0.1637*** [12.1442] | 0.1730*** [12.8218] | 0.1599*** [11.8694] | 0.1615*** [11.9887] | 0.1587*** [11.7812] | 0.1438*** [10.7024] | 0.1629*** [12.0858] | 0.1542*** [11.4561] |
| 注:*、**、***分别表示通过10%、5%、1%水平下的显著性检验;方括号内为Z统计量。 | ||||||||||
从LISA集聚图可以看出由于篇幅限制,本文并未给出产业结构调整幅度、调整质量与能源效率的LISA集聚图,如有需要可向作者索要。:(1)在2004年,产业结构调整幅度的高值集聚区主要零星分散在中南部地区,如安徽、湖南、江西和山西等地区的个别城市,到2013年逐渐向山东西南部、江苏大部等东部沿海地区以及山西地区转移。究其原因主要在于:一方面,从2004年开始,国家开始实施“中部崛起计划”,重点依托现有产业基础,发挥承“东”启“西”的产业功能,从而大大提高了中部地区的产业结构调整幅度;另一方面,东部沿海地区在加快低端产业向中西部地区转移的同时,大力发展战略性新兴产业,推进产业高端化发展,从而扩大了东部沿海地区及部分内陆地区的产业结构调整幅度。(2)在2004年,产业结构调整质量的高值集聚区主要集中在长三角、珠三角和山东半岛等地区,到2013年高值区数量逐步减少并向陕西北部和内蒙古中部地区转移,如鄂尔多斯、呼和浩特等城市。在“两个大局”制度的安排下,东部沿海地区发展迅速,并一直占据中国经济总量与质量的制高点,但随着生产成本、用工成本的上升以及产业同质化、低端化的影响,东部沿海地区存在较为严重的产能过剩现象,而中部地区则在承接东部地区产业转移的同时,不断优化自身的产业结构,从而导致东部沿海地区的产业结构调整质量高值区不断向中部地区转移。(3)在2004年,能源效率高值集聚区以长三角地区和山东半岛等地区为主,到2013年,能源效率高值集聚区转移到了与东南沿海城市接壤的东南部地区。这一结论正好验证了前文的分析:在2004年,由于东部沿海地区占据产业结构调整质量的高值区,随之成为能源效率的高值区;到2013年,伴随节能减排政策与结构战略性调整的压力,能源效率高值区开始向中部地区转移。
(三)产业结构调整与能源效率的耦合关系。本文采用以变异系数为基础的耦合度模型对产业结构调整与能源效率两个系统的耦合关系进行分析,其计算公式为:
| $C = {\left\{ {\frac{{{S_i}\left( x \right)E\left( y \right)}}{{\left[ {\frac{{{S_i}\left( x \right) + E{{\left( y \right)}^2}}}{2}} \right]}}} \right\}^k}$ | (9) |
其中,Si(x)和E(y)表示产业结构调整指数和能源效率。k为区别系数,其取值范围为[2,5]。为了加强区分度,我们设定k=4。为了更容易甄别能源效率分别与产业结构调整幅度、质量的耦合关系,借鉴关伟与许淑婷(2015)的做法,构建耦合协调指数$R = \sqrt {C \times \left[ {0.6E\left( x \right) + 0.4{S_i}(x)} \right]} $。在对耦合度和耦合协调度计算之前,对数据采用min-max标准化方法进行标准化处理,并利用中值分段法对耦合度和耦合协调度分段(见表 2)。
| 耦合度 | 耦合阶段 | 耦合协调度 | 协调耦合阶段 | 综合耦合阶段 |
| 0c≤0.3 | 分离阶段 | 0<R≤0.3 | 低协调耦合阶段 | 低协调分离阶段 |
| 0.3c≤0.5 | 拮抗阶段 | 0.3<R≤0.5 | 中协调耦合阶段 | 中协调拮抗阶段 |
| 0.5c≤0.8 | 磨合阶段 | 0.5<R≤0.8 | 高协调耦合阶段 | 高协调磨合阶段 |
| 0.8c≤1 | 耦合阶段 | 0.8<R≤1 | 极协调耦合阶段 | 极协调耦合阶段 |
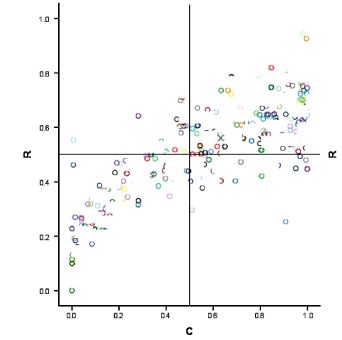
中国城市产业结构调整与能源效率的耦合情况如图 4和图 5所示,其中产业结构的调整幅度、调整质量和能源效率分别取2004-2013年的平均值。综合来看,中国城市产业结构调整幅度与能源效率的耦合度和耦合协调度要明显优于产业结构调整质量与能源效率的耦合度和耦合协调度。产业结构调整幅度与能源效率的耦合分布显示,处于高协调磨合阶段和极协调耦合阶段的城市数占全国城市总数的49.47%,典型的有宜昌、娄底和扬州等城市;而产业结构调整质量与能源效率的耦合分布则显示,有89.82%的城市处于低协调分离阶段和中协调拮抗阶段,例如鸡西、黑河和双鸭山等资源型城市。这意味着产业结构调整幅度与能源效率改善的关系更加密切,尤其是产业结构由“硬化”(如重工业)向“软化”(如轻工业、服务业)的调整幅度越大对提高能源效率的作用就越明显。原因主要在于不同行业的能源密度差异较大,例如化工、冶金、建筑等行业的单位产值能耗约为3-4吨标准煤,是精密仪器、电子及通讯设备等制造业的50倍以上(关伟和许淑婷,2015)。需要说明的是,耦合度模型的测度结果只能说明产业结构的调整幅度和调整质量与能源效率关系的紧密程度,并不能解释产业结构调整是否提高了能源效率,这需要进一步采用空间计量模型进行分析。
|
| 图 4 调整幅度与能源效率的耦合分布 |
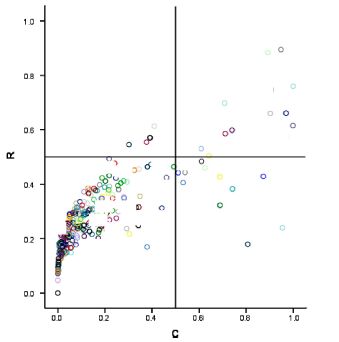
|
| 图 5 调整质量与能源效率的耦合分布 |
(一) 全国层面的实证分析。检验发现,Wald spatial lag和LR Spatial lag的值分别为89.24和54.35,都在1%的显著水平上拒绝了的原假设,而且Wald spatial error和LR spatial error的值依次为73.25和44.26,也都在1%的显著水平上拒绝了γ+ρβ=0的原假设。由此本文选择SDM模型为最终分析模型。Hausman检验结果支持采取固定效应模型。
SDM模型的计量结果表明,一个地区能源效率的改善不仅受本地区产业结构调整的影响,还受周边地区产业结构调整的影响。具体而言,产业结构调整幅度对能源效率的影响为负但未通过显著性检验,而产业结构调整质量提高则有利于能源效率改善且通过了1%的显著性检验。与SDM模型不同的是,在SEM和SLM模型中,产业结构调整幅度对能源效率的负向影响通过了1%的显著性检验。主要原因在于SEM和SLM模型并没有考察产业结构调整幅度对能源效率影响的空间溢出效应。
本文进一步通过直接效应、间接效应和总效应对空间溢出效应的大小进行比较。由表 4可以看出,产业结构调整幅度的直接效应为正但未通过显著性检验,而其间接效应和总效应都为负且通过了1%和5%的显著性检验。这说明,产业结构调整幅度增强对本地区能源效率改善并不显著,但其他地区提高产业结构调整幅度对本地区能源效率改善具有明显的抑制效应。其原因是在区域产业结构调整过程中,一个地区对产业的“腾龙换鸟”倾向于将低能效、高能耗、高排放的落后产业向周边地区或其他地区转移。由产业结构调整质量的估计结果可知,产业结构调整质量的直接效应、间接效应和总效应对能源效率改善都存在显著的促进效应。这意味着提高产业结构调整质量不仅可以改善本地区的能源效率,还能促进周边地区能源效率的提升。可能的原因在于,某一地区在推动产业结构升级的过程中,可以通过信息、技术溢出等途径改善周边地区的能源效率,也可能会引发邻近地区的学习与模仿效应,导致邻近区域之间呈现能源效率改善的“俱乐部收敛”趋势。
 | SEM | SLM | SDM |
| StrI | -0.1139***(-4.5575) | -0.0830***(-3.5940) | -0.0116(-0.0902) |
| StrH | 0.0020***(8.6930) | 0.0016***(7.2278) | 0.0012***(4.0488) |
| Eco | 0.0368***(5.6048) | 0.0170**(2.2984) | 0.0266***(31.2561) |
| Hun | 0.0047(0.5629) | -0.0016(-0.2042) | -0.0038(-0.8027) |
| FDI | -0.0140(-1.2708) | -0.0124(-1.1744) | -0.0075*(-1.8172) |
| Gov | -0.1903***(-4.9698) | -0.1878***(-5.1264) | -0.0896***(-8.0700) |
| W·StrI | -0.0791**(-2.1962) | ||
| W·StrH | 0.0004(0.0019) | ||
| W·Eco | 0.0188***(17.8059) | ||
| W·Hum | -0.0161(-1.2445) | ||
| W·FDI | -0.2681***(-4.0276) | ||
| W·Gov | -1.3312***(8.0906) | ||
| ρ或λ | 0.6690***(15.4702) | 0.7189(9.9033) | 0.7410***(4.9543) |
| Agj-R2 | 0.7271 | 0.8005 | 0.8353 |
| LogL | 1735.3351 | 1702.2139 | 2621.7933 |
| LR | 56.7361*** | 61.2615*** | 60.7165*** |
| 观测值 | 2850 | 2850 | 2850 |
| 注:*、**、***分别表示通过10%、5%、1%水平的显著性检验;括号内为T值检验。下表同。 | |||
 | 直接效应 | 间接效应 | 总效应 |
| StrI | 0.1002(1.2038) | -0.3523***(-3.1623) | -0.2435**(-2.1837) |
| StrH | 0.0065***(2.9384) | 0.0117**(1.9978) | 0.0056***(3.2465) |
| Eco | 0.2389***(3.1078) | 0.1395***(2.9044) | 0.1572***(4.6283) |
| Hun | 0.1826*(1.7265) | -0.0928(-0.7463) | -0.0252(-1.2708) |
| FDI | 0.2073**(2.3417) | -0.5295***(-3.0928) | -0.3405*(-1.7702) |
| Gov | -2.0115***(-4.9253) | -1.4248***(-3.9406) | -1.2834***(-3.1098) |
在控制变量方面,一个地区的经济发展水平不仅对本地区能源效率具有显著的正向影响,而且对周边地区能源效率也存在显著的促进效应和空间溢出效应。提高人力资本水平和外商直接投资仅对能源效率的直接效应显著为正,但二者对能源效率的间接效应和总效应并没有通过显著性检验。这可能是由于人力资本市场与外商直接投资区际分割现象的存在。政府干预程度的估计结果显示,政府干预程度的提高对本地区和周边地区的能源效率改善都存在显著的抑制效应。可能的原因在于:一方面,各级地方政府强调的是本地区的经济发展,往往忽视与周边地区产业发展政策与环境污染治理的统筹协调;另一方面,地方政府之间以邻为壑、环境倾销等短视行为导致了区域之间的环境冲突。
(二)按东、中、西地区分组的分析。由表 5可知,东、西部地区的估计结果与全国层面的比较接近,与产业结构调整幅度相比,提高产业结构调整质量才有助于能源效率的提升。但东部地区产业结构调整幅度和调整质量的系数绝对值都要相应地大于全国层面的估计结果,而西部地区则正好相反。这说明,在经济发达、基础设施完善的东部地区,产业结构调整幅度过大会抑制能源效率改善,而提高产业结构调整质量对能源效率的正向作用更加明显;对于西部地区而言,产业结构层次较低、产业结构相对滞后,过快的产业结构调整必然会引致“三高一低”企业入驻,引致了能源消费提高和环境污染。从中得到的启示有:一是产业结构不断优化升级,逐渐形成了规模经济、促进劳动分工和技术进步,促进了能源效率不断提升;二是产业结构分化变迁在推动工业化和城市化发展的同时,使能源消费进一步增加,加剧了要素市场扭曲、能源供需失衡和能源消费不合理等问题的发生。对于东部地区而言,提高能源效率更应该注重产业全要素生产率的提升,而不是简单地“退二进三”或“腾龙换鸟”。
 | 东部 | 中部 | 西部 | |
| 直接效应 | StrI | -0.0865*(-1.9070) | 0.0458***(3.1105) | -0.0965*(-1.9376) |
| StrH | 0.0212***(4.8772) | 0.0012(0.0350) | 0.0013***(4.2113) | |
| Eco | 0.0006(0.0681) | 0.0343***(17.5438) | -0.0009(-0.1035) | |
| Hun | 0.1176**(2.0912) | 0.0075(0.8507) | -0.0132(-1.5070) | |
| FDI | -0.0106(-1.0204) | -0.0838**(-10.4451) | 0.1449(0.6271) | |
| Gov | -0.1212***(-2.8355) | -0.1528(-1.3989) | 0.2617*(1.7217) | |
| 间接效应 | StrI | -1.0242***(-5.1268) | -0.4593***(-4.2336) | -0.4031***(-2.9422) |
| StrH | 0.0125***(2.7341) | 0.1374**(2.2050) | 0.0060***(2.9726) | |
| Eco | -0.0093(-0.2896) | 0.0098***(4.6672) | 0.0229(0.8336) | |
| Hun | 0.4727***(3.6088) | -0.0445(-1.0535) | 0.3801***(2.6251) | |
| FDI | -0.0461(-0.4769) | -0.0763(-1.4213) | 6.3469***(3.0060) | |
| Gov | -1.1568**(-2.0422) | 0.5079(0.4795) | 7.0506**(2.5403) | |
| 总效应 | StrI | -1.1106***(-5.6019) | 0.1283(0.9974) | -0.4996***(-3.1441) |
| StrH | 0.0113**(2.4566) | 0.0116*(1.6938) | 0.0074***(3.6266) | |
| Eco | -0.0087(-0.2690) | 0.3762***(3.9471) | 0.0220(0.8103) | |
| Hun | 0.4651***(3.4999) | 0.0289(1.1904) | 0.3669**(2.4983) | |
| FDI | -0.0567(-0.5792) | -0.1235**(2.3355) | 6.4918***(3.0007) | |
| Gov | -1.0355*(-1.8081) | 0.8398(0.7742) | 7.3123***(2.6186) | |
中部地区的估计结果显示,扩大产业结构调整幅度对本地区能源效率改善具有显著的促进作用,但不利于其他地区的能源效率提升;与之相反的是,提高中部地区产业结构调整质量对其他地区能源效率的影响显著为正。这一结论为中部地区继续通过承接产业转移来改善本地区的能源效率提供了论据支撑,但承接效果应以提升产业结构调整质量为目的。
从控制变量的估计结果可知,提高经济发展水平对中部地区的能源效率具有显著为正的空间溢出效应。人力资本水平提升有助于东、西部地区的能源效率改善,这可能由东部地区产业结构和能源结构优化升级对于高端人才的旺盛需求以及西部地区本身人才匮乏所致。外商直接投资对中部地区能源效率存在显著为负的直接效应,而对西部地区则具有显著为正的间接效应。可能的原因在于,外商直接投资在中部地区的流入会弱化这些地区的环境监管而引起能耗强度的提高,但是却能促进西部地区节能技术的应用(张宇和蒋殿春,2013)。政府干预程度对东部与西部地区能源效率的空间溢出效应截然相反,即对东部地区具有显著的负向效应,而对西部地区则存在明显的正向作用。
六、 主要结论与政策启示本文利用中国285个地级及以上城市2004-2013年面板数据,从调整幅度和调整质量两个维度分析了产业结构调整与能源效率变化的演变特征及相关关系,并运用空间杜宾模型检验了调整幅度、调整质量对能源效率的影响作用及空间溢出效应。研究发现:(1)在2004-2013年间,伴随着产业结构调整幅度与调整质量的变化,能源效率呈现“M”形变化趋势,而且调整幅度、调整质量与能源效率都存在显著的空间相关性和耦合互动关系。(2)从全国层面的分析来看,一个地区提高调整质量不仅有利于本地区能源效率提升,还对周边地区的能源效率改善存在显著的促进作用,而加快调整幅度并不利于本地区及周边地区的能源效率提升。(3)进一步分地区进行讨论时发现,提高调整质量对东、中、西各地区能源效率的改善均存在显著的促进作用及空间溢出效应,而加快调整幅度仅有利于中部地区的能源效率提升。(4)控制变量的估计结果显示,经济发展水平、人力资本、外商直接投资和政府干预程度对能源效率改善的影响作用及其空间溢出效应存在区域差异。
本文的政策含义有:第一,应以各区域自身的资源禀赋特征为基础,推进产业结构调整,从而构建适合区域特点的能源效率提升路径。第二,不断调整与优化产业转移的空间关联结构,提高能源区域配置效率,实现产业结构调整与能源效率改善的协调发展。第三,消除不同地区间产业转移与能源流动的“市场分割”,充分重视市场机制在生产要素和商品流动中的作用。
| [1] | 关伟, 许淑婷. 中国能源生态效率的空间格局与空间效应[J]. 地理学报, 2015(6): 980–992. |
| [2] | 秦炳涛. 中国区域能源效率研究——地级市的视角[J]. 世界经济文汇, 2014(1): 95–104. |
| [3] | 王文举, 向其凤. 中国产业结构调整及其节能减排潜力评估[J]. 中国工业经济, 2014(1): 44–56. |
| [4] | 于斌斌. 产业结构调整与生产率提升的经济增长效应——基于中国城市动态空间面板模型的分析[J]. 中国工业经济, 2015(12): 83–98. |
| [5] | Arabi B, Munisamy S, Emrouznejad A, et al. Power industry restructuring and eco-efficiency changes: A new slacks-based model in Malmquist-Luenberger Index measurement[J]. Energy Policy, 2014, 68: 132–145. DOI:10.1016/j.enpol.2014.01.016 |
| [6] | Elhorst J P. Applied spatial econometrics: Raising the bar[J]. Spatial Economic Analysis, 2010, 5(1): 9–28. DOI:10.1080/17421770903541772 |
| [7] | Findeisen S, Südekum J. Industry churning and the evolution of cities: Evidence for Germany[J]. Journal of Urban Economics, 2008, 64(2): 326–339. DOI:10.1016/j.jue.2008.02.003 |
| [8] | Hu B. Measuring plant level energy efficiency in China's energy sector in the presence of allocative inefficiency[J]. China Economic Review, 2014, 31: 130–144. DOI:10.1016/j.chieco.2014.08.011 |
 2017, Vol. 43
2017, Vol. 43


