文章信息
 | 财经研究 2016年42卷第12期 |
- 刘玉博, 汪恒.
- Liu Yubo, Wang Heng.
- 内生环境规制、FDI与中国城市环境质量
- Endogenous Environmental Regulation, FDI and Environmental Quality in Chinese Cities
- 财经研究, 2016, 42(12): 119-130
- Journal of Finance and Economics, 2016, 42(12): 119-130.
-
文章历史
- 收稿日期:2016-08-01

2016第42卷第12期
2.上海财经大学 经济学院,上海 200433
2.School of Economics, Shanghai University of Finance and Economics, Shanghai 200433, China
党的十八届五中全会通过的“十三五规划建议”提出,要牢固树立创新、协调、绿色、开放、共享五大发展理念,其中,“绿色”强调改善生态环境,“开放”着力实现合作共赢。在全球经济一体化背景下,随着中国对外开放程度的不断加深,许多局部“绿色”环境问题正通过外商直接投资等“开放”途径转变为全球性问题(盛斌和吕越,2012)。根据联合国贸易和发展会议(UNCTAD)发布的《世界投资报告(2015)》,2014年中国吸引FDI达1 276亿美元,首次超过美国成为全球最大的外商直接投资目的国;同时,《中国环境统计年鉴(2015)》显示,中国2014年二氧化硫排放量达1 974万吨,其中工业排放占比为88.15%,居世界第一。那么,中国如此大规模的FDI是否影响了国内的环境质量呢?本文试图从理论和实证上解答这一问题,以期澄清认识,为“绿色”和“开放”发展理念下的外资政策提供理论依据和经验支持。
目前,FDI对东道国环境质量的影响在理论研究和经验研究层面均存在争议。Copeland和Taylor (1994)提出了“污染避难所”假说,认为发达国家污染性产业转移至制度宽松的发展中国家,致使东道国的环境恶化。与此相反,Birdsall和Wheeler (1993)、Eskeland和Harrison (2003)等提出的“技术外溢”假说认为,发达国家的企业拥有更高效的污染处理技术,通过技术溢出有助于改善发展中国家的环境质量。实际上,“污染避难所”假说和“技术外溢”假说均获得了一定的实证支持,如Esty和Geradin (1998)以及Xing和Kolstad (2002)都认为东道国宽松的污染规制吸引了外资流入;而Dietzenbacher和Mukhopadhyay (2007)认为印度没有成为“污染避难所”,而是在对外开放中不断获利。在以中国为案例的研究中,两大假说的适用性亦无定论。He (2006)、郭红燕和韩立岩(2008)以及林季红和刘莹(2013)等学者支持“污染避难所”假说,认为较低的排污成本是FDI流入的主导因素;而Zeng和Eastin (2007)、Liang (2008)以及包群等(2010)等认为外商投资企业拥有较高的污染治理水平,可通过示范效应改善中国的环境质量。另有学者分析了FDI的投资动机(盛斌和吕越,2012)和外资企业的生产效率(Kirkulak等,2011)等问题,也都认为“污染避难所”的效果有限。
关于开放条件下FDI环境效应的研究,关系到中国绿色发展的可持续性。本文借鉴Grossman和Krueger (1995)分解环境效应的开创性思路,将其引入Copeland-Taylor模型,从理论上分解FDI对环境质量的异质性影响,并利用2007-2009年286个地级城市面板数据进行实证检验。研究表明:FDI通过技术效应和收入效应改善了环境质量,而通过规模效应和结构效应恶化了环境质量;FDI对环境的改善效果存在门槛值,即当FDI比重超过0.12时,FDI的增加将导致环境质量的恶化。
本文的主要创新之处为:第一,构建了一个FDI影响东道国环境质量的理论模型,弥补了现有文献以实证检验为主的缺憾;第二,在模型设计中,本文将环境规制内生化,避免因忽视居民收入增加对环境质量的作用而造成的对FDI环境效应的低估;第三,以气象仪器测量获得的污染物浓度表征城市环境质量,更契合本文的理论模型设计,也可以避免使用“污染排放量”这一常用指标造成的偏误。
二、 理论模型 (一) 基础模型构建1.生产函数。假设完全竞争的经济体中有N个企业,生产两种最终产品X和Y,其中产品X在生产过程中产生污染,Y不产生污染。令产品X为资本密集型,①存在两种基本生产要素,即资本(K)和劳动(L),两者供给无弹性,边际报酬分别为r和w。令Z代表X在生产过程中产生的污染排放量。厂商拥有污染减排技术,但减排本身有成本。假设厂商选择潜在产出量F的θ比率(0≤θ≤1)进行污染治理。θ越大,用于污染治理的比例越高,同时用于生产X的生产资料越少。产品X与污染Z联立生产的技术函数如下:
①资本密集型产业与污染密集型产业之间的关系已得到文献验证,比如,Antweiler等(2001)通过比较美国不同产业的资本密集程度和污染密集程度证明了两者之间的正相关关系。产品Y为劳动密集型。
| $ X=\left({1 - \theta } \right)F\left({{K_x}, {L_x}} \right) $ | (1) |
| $ Z=\emptyset \left(\theta \right)F\left({{K_x}, {L_x}} \right) $ | (2) |
其中,F是非递减且线性同次凹函数,代表厂商的潜在产出水平;Ø代表污染治理函数,Ø(0)=1,Ø(1)=0,且d(Ø)/d(θ) < 0。给定Ø(θ)的具体形式为:Ø(θ)=(1-θ)1/α,其中,0 < α < 1。联立式(1)和式(2)可得:
| $ X={Z^a}{\left[{F\left({{K_x}, {L_x}} \right)} \right]^{1 - a}} $ | (3) |
观察式(3),可将污染Z视为一种投入要素,进入生产函数。根据“技术外溢”假说,外资厂商拥有更清洁的生产技术和更有效的污染处理手段,①为此本文进一步假定式(3)在FDI投资的厂商和其他厂商中的形式分别为:
①“技术外溢”假说是比较符合现实的,除了前述文献中对“技术外溢”假说的支持外,林立国和楼国强(2014)利用上海的数据也证明外资企业的单位排放量的确小于其他类型的企业,而且这一现象与污染税税率无关。
| $ {X_f}={Z^{{a_f}}}{\left[{F\left({{K_x}, {L_x}} \right)} \right]^{1 - {a_f}}} $ | (4) |
| $ {X_d}={Z^{{a_d}}}{\left[{F\left({{K_x}, {L_x}} \right)} \right]^{1 - {a_d}}} $ | (5) |
其中,0 < αf < αd < 1,表示外商生产等量的X会产生更少的污染排放Z,也可以理解为需要投入更少的Z,即外资拥有更清洁的生产技术。
2.厂商的最优决策。假设厂商每产生一单位污染物所要付出的代价是τ,生产潜在产出F的总成本为cF(w, r)F,因此生产产品X的厂商最优化问题为:
| $ \begin{array}{*{20}{c}} {ma{x_{{Z_i}, {F_i}}}{\pi _i}={X_i} - \tau {Z_i} - {c^F}{F_i}}\\ {s.t.{X_i} \le {Z^{{\alpha _i}}}F_i^{1 - {\alpha _i}}} \end{array} $ | (6) |
其中,i=(f, d),分别代表外资厂商和其他厂商。求解可得厂商的单位净产出污染排放量为:
| $ {e^i}=\frac{{{Z_i}}}{{{X_i}}}=\frac{{{a_i}}}{\tau } \le 1 $ | (7) |
进一步可以得到全社会生产X的单位净产出的污染排放量为:
| $ e=\sum\limits_{i=f, d} {{q^i}{e^i}={e^d}}+{q^f}\left({{e^f} - {e^d}} \right) $ | (8) |
其中,qf代表FDI占总资本的比重;qd代表其余资本占总资本的比重。由于ef-ed < 0,因此qf越大,则e越小,即FDI占总资本的比重越高,则全社会的单位净产出污染排放量就越低。利用式(7),可进一步将式(8)简化为:
| $ e=e\left({{q^f}, \tau } \right) $ | (9) |
其中,
3.政府的最优决策。设代表性消费者的间接效用函数为:
| $ V\left({I, Z} \right)=u\left(I \right)- \gamma Z $ | (10) |
其中,I为人均国民收入,u为递增凹函数。γZ可看作代表性消费者为污染所支付的成本,γ为常数。设一国人口总量为M,国民总收入为G,则有I=G/M。国民总收入由个人部门总收入R(K, L)和政府收入(政府对污染排放Z的征税)构成,也即:
| $ G\left({K, L, Z} \right)=R\left({K, L} \right)+\tau Z $ | (11) |
假定政府希望通过选择污染税税率以最大化代表性消费者效用,则政府最优化问题为:
| $ \begin{array}{*{20}{c}} {ma{x_\tau }V}\\ {s.t.I=G\left({K, L, Z} \right)/M} \end{array} $ | (12) |
使消费者效用最大化的一阶条件为:
| $ {V_I}{\rm{ \times }}\left({dI/dZ} \right)+{V_Z}=0 $ | (13) |
变形可得:
| $ dI/dZ=- {V_Z}/{V_I} $ | (14) |
式(14)右边衡量的是污染排放与收入之间的边际替代率,即一个代表性消费者愿意为减少一个单位的污染排放而放弃多少个单位的收入,称之为边际损害,记为MD。
结合式(10)、式(11)和式(14),可得到:
| $ \tau=M{\rm{ \times }}MD=\sigma \left(I \right) $ | (15) |
由于效用函数是凹的,可知MD>0,其中,消费者的边际损害函数MDI=γ/u′。①
式(15)表明,污染税税率由政府最大化代表性消费者效用内生决定,这与Xu (2000)和Dasgupta等(2001)发现环境规制与收入水平高度相关的研究结论一致。另外,陆旸(2009)等也认为环境规制由收入水平内生决定,因而将人均收入水平作为环境规制的衡量指标。国内绝大多数学者,如盛斌和吕越(2012)、杨仁发(2015)等将污染税的税率视为外生给定,但这样做至少存在三个问题:①中国各地的真实污染税税率与各地的发展水平相关。如“十一五”期间,中国较为发达的省份减排任务也更大,相对来说完成的情况也更好(见环境保护部公告http://www.zhb.gov.cn/gkml/hbb/qt/201108/t20110829_216607.htm),这说明经济发展程度与环境诉求之间存在正向相关关系。②近年来中国厂商的实际污染排放量由排放额度而非污染税税率决定,这导致名义污染税税率无法反映真实的污染排放规制水平。③国民收入水平变动对环境治理效果存在影响,污染税税率外生的假设实际上忽略了这一相关关系。以上三点均可能造成实证估计结果偏误。
(二) FDI与环境质量1.环境质量的决定因素。定义经济规模S为两部门生产产品的总和,也即:S=X+Y。由式(7)可得:
| $ Z=eX=e\varphi S $ | (16) |
其中,φ为X在总产出S中的比重,视为产业结构。式(16)表明,污染排放总量取决于污染密集型产业的单位排放密度e、整个经济的产业结构φ和经济体规模S。两边同时取对数,再对时间进行求导可得:
| $ \tilde Z=\tilde e+\tilde \varphi+\tilde S $ | (17) |
其中,上标“~”表示变动的百分比。由基础模型构建部分可知,污染税影响污染排放强度e,进而影响X的产出水平。将X和Y写成e、K和L的函数,可得:
| $ \begin{array}{*{20}{c}} {X=X\left({e, K, L} \right)}\\ {Y=Y\left({K, L} \right)} \end{array} $ | (18) |
由于K和L是线性同次的,可以将φ写成:
| $ \varphi=X\left({X+Y} \right)=\varphi \left({e, k} \right) $ | (19) |
其中,k=K/L,表示人均资本量。参考盛斌和吕越(2012)的研究成果,可知:əφ/əe>0,əφ/ək>0。
2.FDI对环境质量的直接影响。对式(9)、式(15)和式(19)两边同时取全微分后变形可得:
| $ \tilde e={\varepsilon _{e, {q_f}}}\widetilde {{q_f}}+{\varepsilon _{e, \tau }}\tilde \tau $ | (20) |
| $ \tilde \tau={\varepsilon _{\tau, I}}\tilde I $ | (21) |
| $ \tilde \varphi={\varepsilon _{\varphi, e}}\tilde e+{\varepsilon _{\varphi, k}}\tilde k $ | (22) |
根据式(20)、式(21)和式(22),可将式(17)写为:
| $ \tilde Z={\delta _1}\tilde S+{\delta _2}\tilde k+{\delta _3}\tilde I+{\delta _4}\widetilde {{q_f}} $ | (23) |
其中,δ1=1,δ2=εφ, k,δ3=εe, τετ, I(1+εφ, e),δ4=εe, qf(1+εφ, e)。
式(23)的右边第一项反映经济规模变化所带来的污染排放量的变化,称为规模效应,δ1=1>0,意味着经济规模越大,污染排放量越多;第二项反映资本密集度变化所带来的污染排放量的变化,称为结构效应,δ2=εφ, k>0,表示人均资本存量越高,环境质量越差;第三项反映居民收入变化所带来的污染排放量的变化,称为收入效应,δ3=εe, τετ, I(1+εφ, e) < 0,意味着随着人均收入水平的提高,污染排放量逐渐下降;第四项反映了生产技术变化所带来的污染物排放量的变化,称为技术效应。现考察δ4的符号:式(8)证明εe, qf < 0,即外资比例与污染产业单位排放密度呈反向变动关系,同时εφ, e>0,即污染产业单位排放密度与污染产业的比重正向相关,因此可得δ4 < 0,意味着外资比例越高,污染排放量越小。
3.FDI对环境质量的间接影响。基于式(23),方程两边同时对外商投资FDI求导再乘以FDI,变形可得:
| $ \begin{array}{l} \frac{{dZ}}{Z}\frac{{FDI}}{{dFDI}}={\delta _1}\frac{{dS}}{S}\frac{K}{{dK}}\frac{{FDI}}{K}\frac{{dK}}{{dFDI}}+{\delta _2}\frac{{dk}}{{dK}}\frac{{dK}}{{dFDI}}\frac{{FDI}}{K}\frac{K}{k}\\ \;\;\;\;\;\;\;\;+{\delta _3}\frac{{dI}}{I}\frac{K}{{dK}}\frac{{FDI}}{K}\frac{{dK}}{{dFDI}}+{\delta _4}\left({d\left({\frac{{FDI}}{K}} \right)/dFDI} \right)K \end{array} $ | (24) |
根据罗长远(2007)的估计,dFDI/dK=0.98,即每增加一单位FDI将带来0.98单位固定资产投资的增加。不妨令dFDI/dK=1,将其代入式(24),可得:
| $ \frac{{dZ}}{Z}\frac{{FDI}}{{dFDI}}={\delta _1}{\varepsilon _{s, K}}{q_f}+{\delta _2}{\varepsilon _{k, K}}{q_f}+{\delta _3}{\varepsilon _{I, K}}{q_f}+{\delta _4}\left({1 - {q_f}} \right) $ | (25) |
其中,εs, K为经济规模的资本产出弹性;εk, K为人均资本的资本产出弹性,εk, K=1;εI, K为收入水平的资本产出弹性。由式(25)可知,污染排放对FDI的弹性由四个部分构成:刻画规模效应的δ1εs, kqf、刻画结构效应的δ2qf、刻画收入效应的δ3εI, kqf和刻画技术效应的δ4(1-qf)。这四种效应的影响方向表现如下:(1)由于εs, K>0,且δ1>0,因此污染排放量对FDI弹性的规模效应为正,即FDI的增加将通过扩大经济规模增加污染排放;(2)由于δ2=εφ, k>0,因此污染排放量对FDI弹性的结构效应为正,即FDI的增加将通过提高污染产业比重恶化环境质量;(3)由于εI, K>0,且δ3 < 0,进而可得δ3εI, k < 0,因此引入FDI提高了居民收入水平,从而间接地降低了污染排放,改善了环境质量;(4)由于δ4 < 0,因此FDI倾向于降低单位产出污染,并通过技术外溢提升东道国的环境质量。
4.FDI影响环境质量的门槛效应。①将式(25)变形,写成qf的一次函数,也即:
①作者感谢审稿人的意见。当然,文责自负。
| $ \frac{{dZ}}{Z}\frac{{FDI}}{{dFDI}}={\delta _4}+\left({{\delta _1}{\varepsilon _{Y, K}}+{\delta _2}+{\delta _3}{\varepsilon _{Y, K}} - {\delta _4}} \right){q_f} $ | (26) |
令
| $ {q_f}=- {\delta _4}/\left({{\delta _1}{\varepsilon _{Y, K}}+{\delta _2}+{\delta _3}{\varepsilon _{Y, K}} - {\delta _4}} \right) $ | (27) |
由于δ4 < 0,因此,为保证qf>0,必须满足以下条件:
| $ \begin{array}{l} {\delta _1}{\varepsilon _{Y, K}}+{\delta _2}+{\delta _3}{\varepsilon _{Y, K}} - {\delta _4} > 0\\ \ln {Z_{it}}={\delta _0}+{\delta _1}\ln {S_{it}}+{\delta _2}\ln {k_{it}} \end{array} $ |
由(
本文以全国286个地级市为样本进行实证分析。同时考虑到中国地级市市辖区工业化程度较高、经济发展较快且容易成为外资进驻地等特点,本文又以市辖区作为样本观测的空间尺度。相关数据包含以下4种类型:
1.污染排放数据。本文采用污染物浓度代表环境质量,而非其他文献中较常使用的污染物排放量数据。这主要出于以下两点考虑:(1)污染物浓度更容易被消费者感知而进入消费者的效用函数,这契合本文的理论模型。(2)污染物排放量数据由环保行政部门统计,人为测量误差较大,且容易出现信息不对称的问题,导致估计偏误;相对而言,环境质量浓度数据由仪器直接测量,精确度更高。污染物浓度数据来源于《中国环境质量报告》中二氧化硫、二氧化氮和PM10的城市年均浓度数据,①可获得数据周期为2007-2009年,包括286个地级市市辖区数据。②
①文章主要用二氧化硫浓度作为衡量城市环境的指标,这是具有中国特色的。中国是全球最大的煤炭消费国和生产国,也是世界上二氧化硫排放最多的国家。“十一五”规划及以后,二氧化硫被当成大气污染的标杆污染物进行治理,即在本文的样本观测期内,二氧化硫排放受到政府的管制,需征收污染税。同时,二氧化硫作为很多工业产品的副产品,地域性特征明显,排放治理技术相对成熟,这些特点使得二氧化硫浓度指标的选取优于PM2.5。
②目前已披露的全国污染物浓度数据主要来源于国家环境保护部编写的《中国环境质量报告》,该书在2007-2014年间每年出版一本,但仅在2007-2009年披露全国各城市的空气质量数据,2010年之后仅报告全国城市空气质量概况。鉴于污染物浓度数据具有较强的应用性和准确度,本文利用可获得的2007-2009年数据进行计量回归。由于各地FDI规模和比重具有连贯性,因此回归结果对各地的引资实践具有现实意义。
2.城市资本存量。本文借鉴柯善咨和向娟(2012)的处理方法,设定最大、最小两种折旧率估计中国各城市市辖区1995-2009年资本存量的上下限,并取均值作为各城市市辖区的总资本存量。③
③以总资本存量除以市辖区就业人员数量,得到各城市市辖区的人均资本存量。各城市市辖区的就业人员数量为《中国城市统计年鉴》中市辖区在岗职工数、私营企业和个体劳动者就业人员数加总而得。
3.经济发展水平。在计算经济规模、人均收入和人均资本存量时,用到城市市辖区GDP、面积、人口总量、实际利用外资额和固定资产投资额等数据,这些数据来源于《中国城市统计年鉴》《中国统计年鉴》《中国经济统计年鉴》。数据中涉及美元与人民币汇率的,按照当年人民币汇率值平均中间价折算;解释变量中名义变量以1995年为基期进行平减。
4.其他控制变量。主要包括年均气温、年均降雨量和年均风速等气象数据,以及代表城市资源禀赋的哑变量。气象数据来源于国家气象中心的气象数据集,该数据集收集了2004-2012年825个气象站点每日的气象情况(包括气温、降雨量、风速和风向等)。本文选取年均温度、年均降雨量和年均风速作为部分控制变量的指标。另外,根据《全国资源型城市可持续发展规划(2013-2020年)》换算出资源型城市哑变量。
四、 实证检验与结果分析 (一) 计量模型设定与实证结果分析根据式(23),本文设定计量模型如下:④
④基于计量模型的设计习惯,FDI比重不再取对数。理论模型中的弹性概念δ4将由
| $ \ln {Z_{it}}={\delta _0}+{\delta _1}\ln {S_{it}}+{\delta _2}\ln {k_{it}}+{\delta _3}\ln {I_{it}}+{{\ddot \delta }_4}q_{it}^f+contro{l_{it}}+{\mu _i}+{\varepsilon _t}+{\varepsilon _{it}} $ | (28) |
其中,Z为二氧化硫浓度;S为单位面积产出,k为人均资本存量,I为人均国民收入,qf为外资占比;Control为其他控制变量,包括资源型城市哑变量、气候变量和科技水平等;μi为个体固定效应;εt为时间固定效应;εit为随机扰动项。i代表城市,t代表时间。在模型设定时,模型检测聚类标准误与普通标准误相差较小,Hausman检验拒绝个体异质性μi与解释变量不相关的原假设,因此应该使用固定效应模型,而非随机效应模型。另外,加入城市个体效应进行Linktest检验,拟合值平方项系数不显著,因此不存在模型设定误差。
回归结果见表 1。列(1)和列(2)为普通最小二乘法的回归结果;列(3)报告了随机效应模型的回归结果;列(4)为固定效应模型的估计结果。其中,列(2)-列(4)加入了年份虚拟变量以控制时间趋势。
| (1) | (2) | (3) | (4) | |
| Pool_1 | Pool_2 | RE | FE | |
| 单位面积GDP对数 | 0.106***(2.85) | 0.093***(2.70) | 0.157***(4.13) | 0.530***(8.20) |
| 人均劳动资本对数 | -0.089(-1.42) | -0.002(-0.03) | 0.100*(1.78) | 0.165*(1.69) |
| 人均GDP对数 | 0.031(0.35) | 0.024(0.30) | -0.155***(-2.59) | -0.260***(-4.61) |
| 外资比重 | -1.245**(-2.06) | -1.910***(-3.17) | -1.407***(-3.25) | -0.829**(-2.25) |
| 科技人员占比 | -0.685(-0.19) | -2.286(-0.70) | -0.568(-0.17) | -1.434(-0.24) |
| 资源型城市哑变量 | 0.035(0.64) | 0.026(0.51) | ||
| 气候变量 | 控制 | 控制 | ||
| 年份固定效应 | 控制 | 控制 | 控制 | |
| 个体固定效应 | 控制 | 控制 | ||
| 常数项 | -2.571***(-3.17) | -3.211***(-4.14) | -3.869***(-5.35) | -6.447***(-5.07) |
| 观测值 | 396 | 396 | 424 | 424 |
| R2 | 0.205 | 0.286 | 0.338 | 0.389 |
| 注:*、**和***分别表示在10%、5%和1%的水平上显著;回归结果已进行聚类处理;括号内为t统计量。下同。 | ||||
估计结果较好地验证了理论模型的结论。由列(4)可知,以单位面积GDP代表的经济规模和以人均GDP代表的人均收入的系数都在1%水平上显著,人均劳动资本存量和外资比重的系数分别在10%和5%水平上显著。结果表明,FDI的比重每提高一个百分点,二氧化硫浓度降低约0.83%,这意味着,在平均水平上,FDI的比重每提高1%,二氧化硫浓度将降低约0.04%,①说明外资比重的提高可以改善中国的城市空气质量。同时,人均GDP每提高一个百分点,二氧化硫浓度将下降约0.26%;人均资本存量每提高一个百分点,二氧化硫浓度将增加约0.16%;单位面积GDP每提高一个百分点,二氧化硫浓度将增加约0.53%。
①
根据式(25),分别计算FDI对城市环境质量影响的四种效应。qf为外资占比,可由统计数据直接计算获得;δ1、δ2、δ3和δ4由表 3中列(4)的系数估计结果获得;εk, K=1,同时可假设经济规模和人均收入的资本产出弹性相同,即εs, K=εI, K=εY, K。下面将选取3个不同的资本产出弹性值分别计算外资对环境质量的三种效应。第一个参照吕冰洋(2008)的结论,将该值设定为0.6;第二个参照Antweiler等(2001)的结论,将该值设定为1/3;第三个根据白重恩和钱震杰(2009)的方法,将每年的GDP减去生产税净额和劳动份额后作为资本收入,再除以减去生产税净额后的GDP,得到每年各城市的资本收入份额,作为资本产出弹性。基于不同的资本产出弹性值,我们分别计算出FDI对环境质量影响的四种效应。
| εY, K=0.6 | εY, K=1/3 | εY, K(均值0.4671) | |
| 规模效应 | 0.017 | 0.009 | 0.013 |
| 结构效应 | 0.009 | 0.009 | 0.009 |
| 收入效应 | -0.008 | -0.005 | -0.006 |
| 技术效应 | -0.041 | -0.041 | -0.041 |
| 总效应 | -0.024 | -0.028 | -0.026 |
| 注:限于数据可得性,第三种资本收入弹性的计算未包含2008年的结果。 | |||
| (1) | (2) | (3) | (4) | |
| FE_1 | FE_2 | FE_3 | Ⅳ | |
| 单位面积GDP对数 | 0.533***(11.59) | 0.529***(8.36) | 0.593***(9.89) | 0.531***(4.30) |
| 人均劳动资本对数 | 0.162*(1.67) | 0.247**(1.96) | ||
滞后期人均劳动 资本对数 | 0.446**(2.43) | 0.421**(2.27) | ||
| 人均GDP对数 | -0.262**(-2.51) | -0.245***(-4.28) | -0.266***(-2.68) | -0.290*(-1.96) |
| 外资比重 | -0.652*(-1.88) | -0.428(-0.41) | ||
| FDI占资本存量比重 | -3.524***(-2.75) | |||
| 规模以上外资工业 企业产值比重 | -0.719*(-1.71) | |||
| 科技人员占比 | 5.759(1.45) | -1.667(-0.28) | 5.281(1.32) | -5.663(-0.91) |
| 常数项 | -10.029***(-3.86) | -6.538***(-5.20) | -10.109***(-4.11) | -7.257***(-3.45) |
| 观测值 | 190 | 426 | 191 | 189 |
| R2 | 0.498 | 0.390 | 0.493 | 0.467 |
表 2表明,四种效应的符号和相对大小与理论预期一致,并且四种效应中,技术效应占主导。在总效应中,外商直接投资比重平均每提高一个百分点,大约能使中国城市市辖区的二氧化硫浓度下降0.03%左右,其中FDI通过规模效应和结构效应使得二氧化硫浓度平均上升约0.02%,但收入效应和技术效应会使其平均下降约0.05%。因此,从结果上看,尽管外资带来了经济规模的扩大和污染产业的扩张,间接导致环境质量下降,但引进外资同时提高了居民收入水平,并产生技术溢出,从而改善了环境质量,且改善程度大于恶化程度。
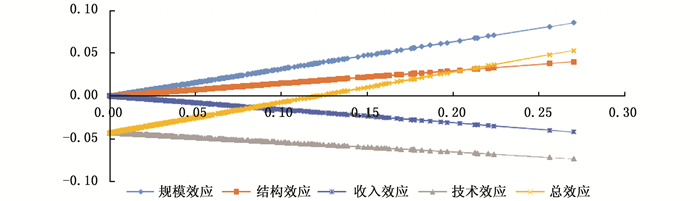
(三) FDI对环境质量影响的变动趋势与门槛效应根据式(25),FDI对环境质量的规模效应、结构效应、收入效应和技术效应的表达式分别为δ1εY, Kqf、δ2qf、δ3εY, Kqf和δ4(1-qf),总效应表达式为δ4+(δ1εY, K+δ2+δ3εY, K-δ4)qf,均为qf的一次函数。不失一般性,εY, K取值为0.6,代入表 1中列(4)的相应变量的系数值,可得:δ1εY, K>0,δ2>0,δ3εY, K < 0,δ4 < 0,δ1εY, K+δ2+δ3εY, K-δ4>0。由此可进一步画出总效应和四种分解效应与qf之间的函数关系图(如图 1所示)。①
①四种效应和总效应曲线的斜率由模型系数决定,不受单一城市当年FDI比重的影响。
|
| 图 1 中国城市FDI对城市环境质量影响的效应分解 |
由式(27)可得FDI影响环境质量的门槛效应,当FDI比重处于较低水平(约为0.12),即qf <
②与四种效应或总效应的斜率类似,该门槛值为-δ4/(δ1 εY, K+δ2+δ3 εY, K-δ4),由模型系数决定,不受单一城市当年FDI比重的影响。在模型系数较为稳健的情况下,可为目前的FDI政策提供经验支持。
①数据来源于《中国城市统计年鉴(2014)》与《中国统计年鉴(2015)》。
(四) 稳健性检验表 3为改变模型自变量参数设定后的回归结果。列(1)考察了滞后一期的人均劳动资本对二氧化硫浓度的影响,各关键解释变量系数的大小和显著性均无明显变化。列(2)将关键解释变量FDI比重更换为当年FDI占资本存量的比重。更换后的解释变量系数的符号与原解释变量相同,但由于FDI占资本存量的比重比原解释变量小,因此变量的回归系数较原模型的估计结果大。回归结果符合预期,且在1%水平上显著。列(3)在列(1)的基础上,将FDI比重更换为当年规模以上外资企业的工业总产值比重,模型回归系数的符号和大小符合预期,且统计性显著。另外,考虑到FDI比重与当期环境规制政策可能存在内生性关系,列(4)以滞后一期FDI比重为工具变量进行检验,回归结果依然较为稳健。
另外,本文选取二氧化氮浓度和PM10替代二氧化硫浓度作为被解释变量,进行敏感性分析。由于二氧化氮和PM10的产生渠道主要为生活源,与本文基于生产过程建立的理论模型前提不同,因此预期实证结论与原模型可能存在较大差异。计量回归结果见表 4。
| 二氧化硫 | 二氧化氮 | PM10 | 二氧化氮+PM10 | |
| (1) | (2) | (3) | (4) | |
| 单位面积GDP对数 | 0.530***(8.20) | 0.244***(3.37) | 0.172***(3.04) | 0.182***(3.64) |
| 人均劳动资本对数 | 0.165*(1.69) | 0.217(1.05) | 0.044(0.49) | 0.077(0.86) |
| 人均GDP对数 | -0.260***(-4.61) | 0.103(1.01) | -0.029(-0.49) | 0.001(0.02) |
| 外资比重 | -0.829**(-2.25) | -0.364(-0.66) | -0.679*(-1.74) | -0.541(-1.50) |
| 科技人员比重 | -1.434(-0.24) | 4.672(0.79) | 4.150(1.00) | 4.845(1.36) |
| 2008年哑变量 | -0.132***(-4.84) | -0.098***(-2.88) | -0.079***(-4.31) | -0.081***(-4.62) |
| 2009年哑变量 | -0.308***(-7.90) | -0.159***(-2.81) | -0.136***(-4.75) | -0.139***(-5.11) |
| 常数项 | -6.447***(-5.07) | -9.026***(-3.06) | -4.006***(-3.07) | -4.481***(-3.47) |
| 观测值 | 424 | 424 | 424 | 424 |
| R2 | 0.389 | 0.113 | 0.196 | 0.228 |
表 4中列(1)为原模型的计量回归结果,作为参照。列(2)和列(3)分别是二氧化氮浓度和PM10作为因变量的回归结果,列(4)为两者相加作为因变量的回归结果,均与原模型具有较大的差异。正如前文所述,二氧化氮和PM10与二氧化硫的产生渠道有较大不同。本文的理论构建是基于对生产过程中污染物排放进行分析,二氧化硫几乎完全从生产过程中产生,与生活消费相关性很小,符合模型设计。根据2015年《中国环境统计年鉴》的相关数据,生活二氧化硫的排放仅占总排放量的11.85%。相较之下,二氧化氮和PM10的产生渠道与居民生活关联较大。仅以汽车排污为例,2014年中国机动车尾气氮氧化物排放量占全年排放总量的30.21%,同时,汽车尾气排放同样是PM10的重要来源,生活中汽车保有量的增加也将持续增加二氧化氮和PM10的排放量。二氧化氮和PM10作为因变量并不适用于本文以生产过程为背景构建的理论模型,因此与本文原计量模型的回归结果有较大差异,回归结论的可信度不高。
总体而言,改变模型自变量设定对本文的实证结论并无明显影响,表明模型的计量回归具有较好的稳健性;改变模型因变量设定后,与原模型回归结论有较大差异,这与不同污染物的产生渠道和模型的适用背景有关,这也从侧面印证了本文的实证模型与理论构建的一致性。
五、 结论与建议本文通过理论分析和实证检验研究了FDI对中国环境质量的作用机制和影响效应。模型引入内生化污染税税率,避免了忽视居民收入水平变动对于环境质量的重要影响,继而避免对环境效应的估计偏误。理论研究发现,FDI通过四种路径影响环境质量:一是由经济规模变化带来的规模效应,二是由资本结构变化带来的结构效应,三是由居民收入水平变化带来的收入效应,四是由外资单位产出污染排放水平变化带来的技术效应。进一步地,通过理论推导揭示了上述四种效应对环境质量存在异质性影响:引入FDI将扩大经济规模,并增加污染产业占比,通过规模效应和结构效应间接地增加污染排放,从而导致环境恶化;同时,引入FDI将提高人均收入水平,并增加技术外溢,通过收入效应和技术效应降低污染排放,从而改善环境质量。基于理论模型,本文利用2007-2009年中国286个地级城市的污染物浓度等数据进行实证检验。虽然可获得的数据存在一定的滞后,但较好地验证了本文理论模型的结论和应用性,可为引资政策提供经验支持。实证结果表明,FDI通过规模效应和结构效应使二氧化硫浓度平均上升约0.02%,但收入效应和技术效应会使其下降约0.05%,因此FDI比重平均每提高一个百分点大约会使中国城市市辖区的二氧化硫浓度下降约0.03%。这说明引入FDI能够总体上改善中国目前的环境质量。同时,FDI对环境的改善存在门槛值,即当FDI比重大于0.12时,在其他条件不变的情况下,FDI比重的增加将导致中国环境质量的恶化。
本文的政策启示包括以下几点:(1)当前仍可适当扩大引进外资的规模以改善环境质量。本文的研究结论表明,目前中国引入FDI可以总体上改善环境质量,但存在门槛值,该值约为0.12。《中国统计年鉴(2015)》相关数据表明,2014年中国FDI比重的均值约为0.02,与门槛值存在较大差距,这意味着现阶段仍可积极引进外资以提高中国环境质量。同时,FDI比重门槛值的存在,意味着引进外资的规模不可无限扩大。为持续改善中国环境质量,在现阶段引入外资的同时,应积极推进国内传统制造业的“绿色”改造,鼓励开发减排技术,降低在清洁生产技术上对外资的依赖。(2)优先引进具有高水平污染处理技术的外资企业,实现“开放”和“绿色”双重发展目标。研究表明,FDI的规模效应和结构效应将恶化环境质量,技术效应是FDI总体上改善中国环境质量的重要原因。因此,引进FDI的重点应放在使用清洁能源、拥有较高污染处理技术的外资企业,最大限度地发挥FDI技术外溢对环境质量的改善作用。从产业发展的角度来看,中国应注重从引进传统的工业化、资本密集型的外资向引进高端制造业、服务业及知识密集型的外资转变。(3)谨慎地使用约束城市规模的政策工具,权衡经济规模扩张与人均收入水平提高对环境质量的相反作用效果。按照世界银行的标准,目前中国已属于“中等偏上收入”国家,但人均GDP水平仍然较低,2014年末约为7 485美元(约合人民币46 531元),仅相当于美国1975年的水平。考虑到经济规模扩张与人均收入水平的正向关系,一方面要谨慎地使用以资源环境承载力控制增长速度或约束城市规模的政策工具,以保持中国较高的经济增长速度,增加居民收入,提高环境质量的改善效果;另一方面要转变要素驱动式经济扩张模式,注重经济结构的调整和创新技术的应用,以降低经济规模扩张带来的环境污染程度。
| [1] | 郭红燕, 韩立岩. 外商直接投资、环境管制与环境污染[J]. 国际贸易问题, 2008(8): 111–118. |
| [2] | 林季红, 刘莹. 内生的环境规制:"污染天堂假说"在中国的再检验[J]. 中国人口·资源与环境, 2013(1): 13–18. |
| [3] | 盛斌, 吕越. 外国直接投资对中国环境的影响——来自工业行业面板数据的实证研究[J]. 中国社会科学, 2012(5): 54–75. |
| [4] | Antweiler W, Copeland B R, Taylor M S. Is free trade good for the environment?[J]. American Economic Review, 2001, 91(4): 877–908. DOI:10.1257/aer.91.4.877 |
| [5] | Birdsall N, Wheeler D. Trade policy and industrial pollution in Latin America:Where are the pollution havens?[J]. The Journal of Environment Development, 1993, 2(1): 137–149. DOI:10.1177/107049659300200107 |
| [6] | Copeland B R, Taylor M S. North-South trade and the environment[J]. The Quarterly Journal of Economics, 1994, 109(3): 755–787. DOI:10.2307/2118421 |
| [7] | Dietzenbacher E, Mukhopadhyay K. An empirical examination of the pollution haven hypothesis for India:Towards a green Leontief paradox?[J]. Environmental and Resource Economics, 2007, 36(4): 427–449. DOI:10.1007/s10640-006-9036-9 |
| [8] | Esty D C, Geradin D. Environmental protection and international competitiveness:A conceptual framework[J]. Journal of World Trade, 1998, 323(3): 5–46. |
| [9] | He J. Pollution haven hypothesis and environmental impacts of foreign direct investment:The case of industrial emission of sulfur dioxide (SO2) in Chinese provinces[J]. Ecological Economics, 2006, 60(1): 228–245. DOI:10.1016/j.ecolecon.2005.12.008 |
| [10] | Liang F H. Does foreign direct investment harm the host country's environment? Evidence from China[EB/OL]. http://ssrn.com/abstract=1479864, 2008-11-28. |
| [11] | Xing Y, Kolstad C D. Do lax environmental regulations attract foreign investment?[J]. Environmental and Resource Economics, 2002, 21(1): 1–22. DOI:10.1023/A:1014537013353 |
| [12] | Zeng K, Eastin J. International economic integration and environmental protection:The case of China[J]. International Studies Quarterly, 2007, 51(4): 971–995. DOI:10.1111/isqu.2007.51.issue-4 |
 2016, Vol. 42
2016, Vol. 42


