
2.兰州大学 经济学院,甘肃 兰州 730000
2.School of Economics, Lanzhou University, Lanzhou 730000, China
随着我国经济的快速发展,大量人口从农业部门转移到非农业部门,城镇化率快速提升,2015年以常住人口统计的我国城镇化率已达到了56.1%,而以户籍人口统计的城镇化率则依然偏低。我国存在大量的流动人口,2014年末我国流动人口2.53亿,而其中绝大部分是农民工,农民工问题已成为我国重要的经济和社会现象。近年来农民工结构也在发生变化,新生代农民工逐渐成为主力军,其工作和消费理念与父辈存在较大差异。同时,我国正处于产业结构调整期,产业空间转移和产业结构变动对劳动力空间流动的影响也不容忽视,这些新变化对当前劳动力迁移研究提出了新要求。在此背景下,“十三五”规划建议提出要推动城乡协调发展,深化户籍制度改革,推进以人为核心的新型城镇化。户籍制度改革破茧待出。随着改革的不断深入,对农村劳动力流动的束缚将大为降低,这将深刻影响当前劳动力流动模式,因此,亟需研究户籍制度改革对我国农村劳动力流动的影响。
关于农民工问题产生的根源,陆铭(2011)等将其归结为我国户籍制度和土地产权制度对人口自由流动的束缚。随着我国经济的发展,农村产生大量的剩余劳动力,同时在城市工作机会和较高收入水平的吸引下(王格玮,2004),农民来到城市打工,而现行户籍制度对农村居民转变为城镇居民有着各种限制,大大增加了农民工在城市落户的难度,于是就形成了中国农民工现象,农民工在城乡之间的流动呈现出“候鸟式”(李克强,2014)或“钟摆式”(肖文韬,2004)特征。由于户籍制度阻碍了劳动力要素的优化配置,降低了经济效率,户籍制度改革的呼声越来越高,尽管政府在一定程度上放松了户籍制度对人口流动的限制,但孙文凯等(2011)指出,由于政府改革力度不够,户籍制度改革的作用有限。此外,都阳等(2014)对户籍制度改革的收益进行了量化,认为户籍制度改革可以带来可观的净收益。
这些研究大多从定量角度进行分析,很难预测户籍制度改革对人口流动和经济发展的影响,对此亟需在新的理论框架下进行深入研究。目前为止,国内外劳动力迁移理论的研究出现了几种趋势。一是研究异质性劳动力迁移的理论(Takatoshi, 2002;Costinothe和Vogel, 2010;孙晓芳, 2013;Pennock, 2014等)着重剖析不同技能水平劳动力的迁移问题;二是研究劳动力国际迁移的理论(Kim和Park, 2012;Baruffaldi和Landoni, 2012)认为随着全球一体化的深入推进,由于劳动力的流动受国际贸易、家庭纽带等因素的影响,劳动力的跨国迁移变得越来越频繁;三是集聚经济条件下劳动力迁移的理论,以新经济地理学理论(Krugman, 1991;Ottaviano和Puga,1998;Meliz, 2003、2008等)和协同集聚理论(Ellison和Glaeser, 1997;Helsley, 2014;Behrens, 2014)为代表,其中新经济地理学理论认为生产集聚和规模经济导致的空间工资差异引起劳动力空间迁移,而协同集聚理论则认为是异质性多产业在同一城市地域靠近,而非单一产业在区域空间的集聚。
国内已有学者尝试将新经济地理学理论用于我国户籍制度改革的研究。张杰飞等(2009)将Harris-Todaro模型与新经济地理模型相结合,通过农村居民的务农收入和农民工进城的期望收入之间的差异来表述农民工的迁移决策,认为在促进农业技术进步的同时,逐步放松户籍制度才能取得最佳的经济效果。安虎森等(2011)在Pfluger(2004)模型中加入住房部门和非熟练劳动力的异质性移民行为,指出城市高房价与户籍制度具有“门槛效应”,在城乡市场开放度高于某个“临界值”时,户籍制度促使城乡收入差距的扩大。倪鹏飞等(2014)结合刘易斯二元经济模型和新经济地理模型,将农民工和农业劳动力进行区分,研究了国际贸易与我国城市化的滞后关系,认为国际贸易顺差强化了我国城市化的滞后问题。梁琦等(2013)基于伯伦斯和村田提出的可变替代弹性效用函数和新经济地理学异质性企业理论,融入城市通勤成本和劳动力的户籍成本,认为户籍改革和劳动力流动可以优化我国城市层级体系。朱江丽和李子联(2016)则借鉴Pflüger (2004)、Pflüger和Südekum (2008)的简化自由企业家模型,融合了Tabuchi和Thisse (2002)、Murata (2003)以及Russek(2010)的劳动力异质性理论,指出户籍改革将引致农村劳动力与企业家的比例以及农村劳动力迁移成本的下降,进而影响地区经济发展。
这些研究多以新经济地理学异质性理论为基础,同时融入了我国户籍制度的某些特征,基本上涉及劳动力迁移的核心内容,但未考虑到我国户籍制度和土地产权制度之间的联动性,尚未建立起完全符合中国人口流动特征的劳动力迁移模型,不能预测户籍制度改革对农村劳动力空间流动的影响。而Fujita等(1999)以Krugman和Venables(1995a)建立的中间投入品模型为基础,并将外生技术进步率和Krugman和Venables(1995b)中的农业部门边际收益递减生产函数引入模型,建立了多国多产业新经济地理学模型。该模型同时融合了中间产品需求、劳动力要素流动和技术进步等特征,与实际情况更加吻合,具有重要理论价值和应用价值。本研究就以Fujita等(1999)建立的新经济地理学多国多产业模型为基础,吸收现有研究中合理成分,以中国户籍制度演变对人口流动模式的影响为纽带,融入我国户籍制度和土地产权制度特征,将不同阶段人口流动模式糅合在同一个模型中,建立我国户籍制度演变模型,并借此模拟户籍制度和土地产权制度改革对我国农村劳动力流动的影响。
二、 中国户籍制度演变理论模型综合国内外研究,劳动力流动模式主要有三类:一是完全不流动,这非常类似国家之间和我国改革开放之前的人口流动模式(蔡昉,2001);二是完全自由流动,这是大多数国家内部的人口流动模式(邓曲恒等,2007),也是我国户籍制度改革的目标;三是流动受到限制,劳动力在城乡之间呈现“候鸟式”流动特征(“城镇化进程中农村劳动力转移问题研究”课题组,2011),正如我国目前的人口流动模式,由于户籍制度限制,农民工很难在工作地落户,城市对农民工存在“户籍歧视”(吴贾等2015等),同时其打工收入主要部分通过“移民汇款”的方式汇到户籍所在地(严超,2011;胡枫等,2013),提高了原籍亲属的收入水平。这几种劳动力流动模式,我们在新中国成立以来的不同发展阶段都经历过。
依照户籍制度变迁对人口流动的影响,新中国成立以来的户籍制度可分为三个阶段(人口研究编辑部,2008;袁媛,2015等):第一阶段,人口自由迁徙阶段,时间为1958年之前;第二阶段,人口迁移流动受到严格控制阶段,时间为1958-1978年;第三阶段,人口迁移流动逐步松动阶段,时间为1978年以后至今,此时农村人口可以向城市流动,但由于在城市落户难度非常大,人口流动呈现出“候鸟式”特征。此外,随着我国户籍制度改革的不断深入,我国人口流动模式将进入第四个阶段,即人口自由迁徙阶段,与1958年之前人口流动模式相同。下面将建立我国户籍制度演变的理论模型。
(一) 基本假设1.假设有两个地区R1和R2。起初R2为核心地区,R1为边缘地区,即所有现代产业都位于地区R2,此外地区R1存在土地产权制度和户籍制度约束,地区R2没有。
2.假设经济系统农业部门A和现代产业部门M。其中农业部门规模收益递减,使用土地和劳动进行生产。现代部门规模收益递增,生产差异化产品,生产中需要投入可变投入和固定投入,二者均为劳动力和中间投入品组合的Cobb-Douglas函数,其中劳动所占份额为α,中间投入品组合所占份额为1-α,且中间投入品组合为CES型。
3.假定只有劳动力一种流动要素,每个地区劳动力是同质的,且劳动力数量为Ωr,r=1, 2。劳动力不能在地区间流动,但是能在同一地区不同部门间流动。地区2劳动力在部门间完全自由流动,而地区1劳动力在不同部门之间流动情况见下面各阶段对应模型。
4.假定外生的技术进步率L,技术进步率主要影响劳动力的生产效率,而对土地数量没有影响。另外,假设每个地区的技术效率跟本国工业化程度有关,工业化程度越高,技术效率水平也越高。我们采用S型增长曲线①对之进行修正,每个地区的技术进步率Lr=L×θ/(1+e-a(xr-b)+c),a、b和c为参数,x为本地区非农产业就业人口与农业就业人口之比,θ=(1+e-a(0-b)+c),那么,各地区有效劳动力数量为Lr×Ωr,r=1, 2。
5.为了简化,假设农产品没有运输成本,而工业产品为冰山型运输成本,并且工业品在本地区内部运输没有成本。
(二) 基本模型1.消费者行为。所有消费者具有相同的偏好,具有相同的效用函数,上层效用函数为柯布-道格拉斯型,下层效用函数为CES型:
| $ U=C_{A}^{(1-u)}{{({{C}_{M}})}^{u}}, {{C}_{M}}={{(\int{_{_{0}}^{n}}c{{(j)}^{\rho }}dj)}^{\frac{1}{\rho }}}, 0<\rho <1 $ | (1) |
其中:μ为常数,为消费者对现代产业部门产品的支出份额,1-μ则为对农产品的支出份额。CA为农产品需求量,CM表示消费者对工业品组合需求量,c(j)为第j种产品的消费量,ρ表示消费者多样性偏好。
当消费者所有收入用于消费时,得到消费者预算约束方程为:
| $ {{P}_{A}}{{C}_{A}}+G{{C}_{M}}=Y, G={{[\int _{0}^{n}p{{(j)}^{1-\sigma }}dj]}^{\frac{1}{1-\sigma }}}$ | (2) |
其中:PA为农产品价格,G为工业品组合价格指数,p(j)为第j种产品的价格;则根据消费者效用最大化原理,可以得出消费者需求函数为:
| $ c(j)=uYp{{(j)}^{-\sigma }}/{{(G)}^{1-\sigma }}[\sigma \text{=}\frac{1}{(1-\rho )}\text{ }\!\!]\!\!\text{ } $ | (3) |
2.生产者行为。
(1)农业部门。当前土地产权制度赋予农民两种权利,农用地承包权和宅基地使用权。根据假设,农业部门生产函数A[(Ωr-λr)Lr]=K/η×[(Ωr-λr)Lr/K]η,Ωr、λr、Lr和K分别为r地区的劳动总数量、现代部门工人数量、技术进步率和土地要素投入量,η为参数。技术进步率Lr只改变有效劳动数量,而对土地数量没有影响,它等价于放大了地区r劳动力数量Lr倍。由农业部门生产函数对农业劳动力数量Ωr-λr求导,得到边际产出为:
| $ \text{MP=}{{\text{A}}^{'}}\text{ }\!\![\!\!\text{ (}{{\Omega }_{r}}\text{-}{{\lambda }_{r}}\text{)}{{\text{L}}_{r}}\text{ }\!\!]\!\!\text{ }={{[({{\Omega }_{r}}-{{\lambda }_{r}})/K]}^{\eta -1}}\times \text{L}_{r}^{\eta } $ | (4) |
将农业部门生产函数除以Ωr-λr,得平均产出为:
| $ AP-A[\text{(}{{\Omega }_{r}}\text{-}{{\lambda }_{r}}\text{)}{{\text{L}}_{r}}]/\text{(}{{\Omega }_{r}}\text{-}{{\lambda }_{r}}\text{)}=(\frac{1}{\eta })\times {{[({{\Omega }_{r}}-{{\lambda }_{r}})/K]}^{\eta -1}}\times \text{L}_{r}^{\eta } $ | (5) |
由于Lr≥1,0 < η < 1,发现AP>MP,那么土地租金R=AP-MP。定义农村劳动力边际工资wA=MP×pA,平均工资wA=AP×pA。这部分土地租金的处理,涉及对农用土地产权制度不同的改革路径。如果将土地租金留在农村,农村劳动力的收入即为wA。
如果农村迁移劳动力将土地租金带入城市,则留守农民平均收入为农业总产出减去外迁农民工带走租金后留守农民的平均收入。其中,农业总收入为wA(Ωr-λr),外迁农民工带走租金为R(Ωr-λr)[ΩA-(Ωr-λr)]/ΩA,则留守农民的平均收入wI和外迁农民工的租金收入wR分别为:
| $ {{w}_{1}}=\overline{{{w}_{A}}}-R\times ({{\lambda }_{r}}+{{\Omega }_{A}}-{{\Omega }_{r}})/{{\Omega }_{A}}\times {{p}_{A}};{{w}_{R}}=R\times \text{(}{{\Omega }_{r}}\text{-}{{\lambda }_{r}}\text{)}/{{\Omega }_{A}}\times {{p}_{A}} $ | (6) |
其中:ΩA为土地产权制度改革前有地农民数量,λr+ΩA-Ωr即为非农化的农民工数量。由于假设地区2没有土地产权制度约束,地区2土地租金归农业工人所有,所以地区2农业工人的边际工资为wA,平均工资为wA。
至于农村建设用地的处理问题,在地区1假定土地产权制度改革完成后,农民放弃宅基地能获得一个平均补贴,记为Θ;而在土地制度改革完成之前或不放弃宅基地时Θ=0,而地区2不存在Θ。
(2)现代部门。由前面假设,现代部门企业成本函数C(x)=PP(F+amx),其中am为单位产出需要的可变投入组合量,x为产出水平,PP为劳动和投入品组合的价格指数。由于劳动和中间投入品组合形式为柯布-道格拉斯形式,所以要素组合的价格PP=wα(G)1-α,其中w和G分别为工人的劳动工资水平和工业产品组合的价格指数。
根据企业利润最大化原理及零利润条件,可以得到工业品价格和企业均衡产量为:
| $ p={{P}_{P}}{{\alpha }_{m}}(1-\frac{1}{\sigma });{{q}^{*}}=F(\sigma -1)/{{\alpha }_{m}} $ | (7) |
3.短期均衡。当市场达到短期均衡时,市场能够实现出清,此时产品供给等于需求。由工业品价格指数表达式可知,各地区工业品价格指数为:
| $ {{G}_{r}}={{[\sum\limits_{s=1}^{2}{{{n}_{s}}}{{({{p}_{s}}{{T}_{sr}})}^{1-\sigma }}]}^{\frac{1}{1-\sigma }}} $ | (8) |
由要素组合的价格PP表达式,经过标准化后地区r的工业品价格可以表示为:
| $ {{p}_{r}}=w_{r}^{\alpha }G_{r}^{1-\alpha } $ | (9) |
由(3)式所求需求函数可知,地区s对地区r生产产品的需求量为:
| $ {{q}_{r, s}}={{({{p}_{r}})}^{-\sigma }}{{({{T}_{r, s}}/{{G}_{s}})}^{(1-\sigma )}}{{E}_{s}} $ | (10) |
达到短期均衡时市场出清,各地区对r地区生产产品的需求量qr等于产品供给量,则:
| $ {{q}_{r}}\equiv \sum\limits_{s=1}^{2}{{{q}_{r,s}}}={{({{p}_{r}})}^{-\sigma }}{{({{T}_{r,s}}/{{G}_{r}})}^{(1-\sigma )}}{{E}_{r}}+{{({{p}_{r}})}^{-\sigma }}{{({{T}_{r,s}}/{{G}_{s}})}^{(1-\sigma )}}{{E}_{s}}=q* $ | (11) |
其中:Es为地区s购买地区r产品时的支出,Tr, s为r地区产品运到s地区的冰山交易成本。选择适当的计量单位,可以将地区r每个厂商的均衡产出水平q*标准化为1/α。
各国用于工业品的支出为:
| $ {{E}_{r}}=u[{{Y}_{r}}-{{\Omega }_{r}}\overline{Y}]+(1-\alpha ){{n}_{r}}{{p}_{r}}{{q}_{r}} $ | (12) |
其中:第一项为地区r居民对工业品支出,第二项为地区r企业对中间投入品需求量,这是由于企业总收入中α用来发工资,1-α用来购买中间投入品。Y为购买生活必需品部分,即收入低于Y时,全部用来购买生活必需品。
现代产业部门工资支出为:
| $ {{L}_{r}}{{\lambda }_{r}}{{w}_{r}}=\alpha {{n}_{r}}{{p}_{r}}{{q}_{r}}={{n}_{r}}{{p}_{r}} $ | (13) |
其中:wr为地区r现代部门的效率工资水平,Lrλr为有效劳动力数量,现代部门工资水平刚好等于企业总收入用于劳动力工资支出的部分。
各国的收入水平为:
| $ {{Y}_{r}}={{L}_{r}}{{\lambda }_{r}}{{w}_{r}}+A[\text{(}{{\Omega }_{r}}\text{-}{{\lambda }_{r}}\text{)}{{\text{L}}_{r}}] $ | (14) |
其中:第一项为现代部门工人的工资收入,第二项为农业部门总收入。
由(9)式和(13)式代入(8)式可求出价格指数的表达式;由(9)式代入(11)式可以确定工资方程;由(13)式代入(12)式可确定支出方程;(14)式即为收入方程,处理后结果如下:
价格指数方程为:
| $ {{({{G}_{r}})}^{1-\sigma }}={{L}_{1}}{{\lambda }_{1}}{{({{T}_{1r}})}^{1-\sigma }}{{({{w}_{1}})}^{1-\sigma \alpha }}{{({{G}_{1}})}^{-\sigma (1-\alpha )}}+{{L}_{2}}{{\lambda }_{2}}{{({{T}_{2r}})}^{1-\sigma }}{{({{w}_{2}})}^{1-\sigma \alpha }}{{({{G}_{2}})}^{-\sigma (1-\alpha )}} $ | (15) |
工资方程为:
| $ {{[{{({{w}_{r}})}^{\alpha }}{{({{G}_{r}})}^{1-\alpha }}]}^{\sigma }}/\alpha ={{({{T}_{r1}}/{{G}_{1}})}^{1-\sigma }}{{E}_{1}}+{{({{T}_{r2}}/{{G}_{2}})}^{1-\sigma }}{{E}_{2}} $ | (16) |
收入方程为:
| $ {{Y}_{1}}={{L}_{1}}{{\lambda }_{1}}{{w}_{1}}+A[\text{(}{{\Omega }_{1}}\text{-}{{\lambda }_{1}}\text{)}\times {{\text{L}}_{1}}];{{Y}_{2}}={{L}_{2}}{{\lambda }_{2}}{{w}_{2}}+A[\text{(}{{\Omega }_{2}}\text{-}{{\lambda }_{2}}\text{)}\times {{\text{L}}_{2}}] $ | (17) |
支出方程为:
| ${{E}_{1}}=u[{{Y}_{1}}-{{\Omega }_{1}}\overline{Y}]+{{L}_{1}}{{\lambda }_{1}}{{w}_{1}}(1-\alpha )/\alpha ;{{E}_{2}}=u[{{Y}_{2}}-{{\Omega }_{2}}\overline{Y}]+{{L}_{2}}{{\lambda }_{2}}{{w}_{2}}(1-\alpha )/\alpha $ | (18) |
技术进步率方程:
| ${{L}_{r}}=L\times \theta /(1+{{e}^{-a({{x}_{r, -b}})}}+c), {{x}_{1}}/({{\Omega }_{1}}\text{-}{{\lambda }_{1}}), {{x}_{2}}={{\lambda }_{2}}/({{\Omega }_{2}}\text{-}{{\lambda }_{2}})$ | (19) |
下面将以上述方程为基础,结合我国户籍制度所处不同阶段人口流动的特征,构建户籍制度演变模型。
(三) 我国户籍制度演变模型及长期均衡1.第一阶段:1950年到1958年之前,人口自由流动。此时,假定地区1劳动力在农业部门和现代部门间自由流动,且不存在户籍歧视。当地区1现代部门潜在工资水平与农业部门工资水平相等时,地区1农业部门劳动力开始向现代部门转移,核心区产业也开始向地区1转移。我们设定产业转移活动一直持续到地区1产业份额和城市化率达到一定水平时,经济活动开始进入到第二阶段,此时地区1从农业部门向现代部门转移的劳动力数量为k1,此阶段两个地区的价格指数方程、工资方程、收入方程、支出方程及技术进步率方程如(15)式至(19)式。此时两个地区的农业部门效率单位工资水平分别为:
| $\overline{W_{A}^{1}}=\frac{A[({{\Omega }_{1}}\text{-}{{\lambda }_{1}})\times {{L}_{1}}]}{({{\Omega }_{1}}\text{-}{{\lambda }_{1}})\times {{L}_{1}}};\overline{W_{A}^{2}}=\frac{A[({{\Omega }_{2}}\text{-}{{\lambda }_{2}})\times {{L}_{2}}]}{({{\Omega }_{2}}\text{-}{{\lambda }_{2}})\times {{L}_{2}}}$ | (20) |
当达到长期均衡时,各地区不同部门的劳动力工资水平要满足以下均衡条件:
第一,刚开始时,制造业部门聚集在发达地区2,还没有向地区1转移时,发达地区内部各部门的工资水平相等,地区1部门间效率工资水平满足WA1≥w1。那么,均衡条件为:
WA2=w2;λ1=0,且WA1L1+Yf≥w1L1
当w1L1≥WA1L1+Yf时,经济活动进入第二步,此时技术进步率临界值记为L1。
第二,当地区1的现代部门的人均工资水平与农业部门的人均工资水平相等时,地区1农业部门劳动力开始向现代部门转移,同时产业也开始由地区2向地区1转移。此时,产业向地区1转移的均衡条件为:
WA2=w2;w1L1=WA1L1+Yf,且λ1≤k1(λ1≠0)
当λ1≥k1时,经济进入第二阶段,此时技术进步率记为L2。
2.第二阶段:1958年到1978年,户籍制度严格限制农村人口向城市流动。这一阶段地区1农村劳动力不能再向现代部门流动。假设这期间外生技术进步率L增加量为t1,在这一阶段开始时,地区1已经有k1数量的农村劳动力转移到城市现代部门。那么只需将(15)式至(20)式中的λ1换成k1,其他变量都不需改变,在此不再赘述。
此时地区1的农村劳动力停止向城市转移,当达到长期均衡时,相关方程满足如下条件:
WA2=w2,且L≤L2+t1(t1为1958年起户籍制度开始实施到1978年改革开放时的技术进步率增量值)。这时地区1农业部门转移到城市现代部门的劳动力数量λ1即为k1。
当L≥L2+t1时,经济进入到第三阶段,此时外生技术进步率的临界值记为L3。
3.第三阶段:从1978年到未来某一年开始进行户籍制度改革时。该阶段户籍制度对农民工的流动限制主要表现为“移民汇款”和“户籍歧视”,该部分需对二者进行处理。其中对“移民汇款”处理,假定农民工收入中有一部分用作最低生活保障,记为Y,剩余部分中有一个比例返回家乡,这个比例记为β,称为汇款系数,当β=1时,表示农民工非常节俭顾家,更接近老一代农民工的行为特征;当β=0时,自我意识比较强,与新一代农民工的行为更接近。对“户籍歧视”的处理有两种方式,一是假设农民工工资比城市劳动力工资少wf;二是假设农民工在基本迁移成本Yf之外还存在一个迁移成本wf,这两种处理方式的结果都是降低农民工净收入,本研究在建模过程中采用后者。当β=0,wf=0时,农民工跟城市居民完全一样,农村劳动力自由流动,这是户籍制度改革完成之后的理想状态。
此时地区1人口处于半流动状态,进入“候鸟式”劳动力流动模式,即农村劳动力可以向城市现代部门转移,但是不能在城市定居,是非永久性的迁移,地区1农村劳动力只根据城乡短期收入差距来做迁移决策。此时农民工迁移存在基本迁移成本Yf用以弥补迁移时交通、食宿等支出,同时还有一个户籍歧视迁移成本wf;农民工不仅通过移民汇款提高了农村收入水平,并且将土地租金留在农村,归农村劳动力所有。假设这期间技术进步率增量为t2,Δλ1为地区1农业部门新转移劳动力数量。此时只需将(15)式至(20)式中的λ1换成k1+Δλ1,其他变量都不需改变,在此不再赘述。
当达到长期均衡时,相关方程要满足如下条件:
WA2=w2;w1×L1=[WA1×(Ω1-k1-Δλ1)×L1+βw1L1×Δλ1]/(Ω1-k1)+Yf+wf
上述第二个等式右边括号中第一项为地区1从事农业劳动力的收入,第二项为从农业中新转移出来的农民工在城市打工的汇款收入,等式右边第一项就是地区1农村劳动力人均收入。此时外生技术进步率还要满足:L≤L3+t2(t2为1978年改革开放时起,到将来某一年户籍制度改革完成时的技术进步率增量值)。此时地区1农业部门转移到城市现代部门的劳动力总数量即为k1+Δλ1。
当L≥L3+t2时,经济进入到第四阶段,此时技术进步率的临界值记为L4,此阶段开始时,现代部门劳动力的就业数量k1+Δλ1值记为k2。
4.第四个阶段:户籍改革完成时到其后任意一年。此时假设户籍制度改革的最终目标是人口的自由迁徙,此阶段模拟户籍制度改革完成后,人口流动处于完全自由流动状态时的情况。此时劳动力是永久性迁移,需根据城乡长期收入差距做出迁移决策。这时不再存在“户籍歧视”和“移民汇款”现象,当地区1农村劳动力搬到城市时存在一个搬迁成本Γf。这一阶段刚开始时,已经有k2单位的劳动力进入城市现代产业部门,将Δλ1记为该阶段从农村新转移劳动力数量。此时人口流动模式就又回到1950年到1958年状态。需将(15)式至(20)式中的λ1换成k2+Δλ1,其他变量都不需改变,在此不再赘述。
当达到长期均衡时,均衡方程要分以下两种情况:
(1)租金留在农村WA2=w2;V(0)=∫0+∞[w1(t)L1-wA1(t)]e-ρtdt+Θ-Γf-Yf=0
(2)租金带入城市WA2=w2;V(0)=∫0+∞{[w1(t)L1+wR(t)]-wI(t)}e-ρtdt+Θ-Γf-Yf=0。
其中:V(0)为农村迁移劳动力收入贴现后的迁移净收益;ρ为贴现因子,表示农村迁移劳动力的时间偏好。此时农业部门转移到城市现代部门的总劳动力数量即为k2+Δλ1。
由前分析,我们已经在理论上建立了中国户籍制度的演变模型,而所建模型的实用性和合理性究竟如何?为此我们先对模型进行模拟,并用中国的实际数据变化来加以验证,以检验模型的实用性;然后模拟户籍制度和土地产权制度的改革等对农村劳动力转移的影响,探索户籍制度改革的方式与路径。
三、 户籍制度演变下农村人口转移与我国城镇化经验数据比较前面所建模型中的方程都是隐函数形式,不能直接进行求解,因此需借助matlab软件对方程进行数值模拟,在此对本部分及以下部分的模拟参数值进行说明。
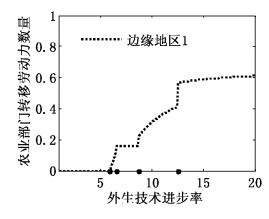
区内运输成本和区间运输成本,由于假设工业品在同一地区内部不存在运输成本,所以T11=T22=1。而本文的地区间运输成本是广义的运输成本,不仅包括税收等制度成本,也包括货物的直接运输成本。目前我国税收占GDP的比重约为20%,2012年中国物流费用占GDP的比重约为18%,计算出国内地区间运输成本(冰山成本)约为1.62。此外,许统生等(2011)计算了中国对主要贸易伙伴国的制造业贸易成本,中日之间为1.7513,中韩为1.7550,中美为1.8083,中德为1.8995。一般来讲,一国内部运输成本要低于国家间运输成本,综合考虑,工业品地区间运输成本取值为T12=1.67。工业品替代弹性σ,方虹等(2010)指出国内外研究对工业品替代弹性σ的估计值在5-10之间,本文为σ=6。此外,1/K是人均土地数量指标,K取值0.42,倒数为2.38,约等于中国的人均耕地数量。k1为我国刚实行户籍制度时的城镇化率,1958年我国城镇化率约为16%,所以k1=0.16。t1为我国从1958年到1978年的技术进步率增量,t2为改革开放至今的技术进步率增量,文中以时间跨度来估算这两个时期的技术进步率增量,t1和t2取值分别为2和3.8。农业生产函数参数η、劳动力生活必需品支出Y、中间投入品中劳动所占比例α和工业品支出份额μi的取值,参考了藤田昌久等(1999)研究产业扩散时所取的参数值。最后,根据研究需要及有关参数含义,对其余参数进行适当赋值,其中a=1,b=1.1,c=5.5,Ω1=Ω2=1,Yf=0.2,wf=0.1,β=1。以下模拟图中横轴四个点,分别代表L1、L2、L3和L4,其含义见上述对应模型。图 1(a)、图 2、图 4和图 5中的Θ-Γf=0,并且土地租金留在农村。
|
| 图 1a 地区1农业部门劳动力转移情况 数据来源:中国统计年鉴。 |
|
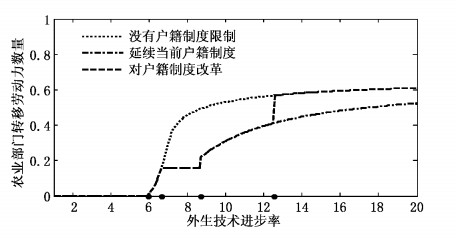
| 图 2 不同户籍制度改革路径的比较 |
|
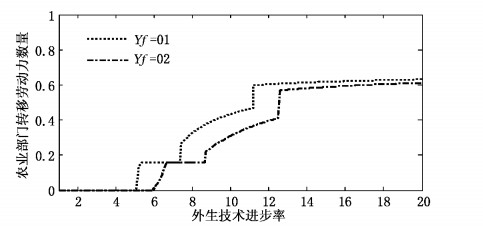
| 图 4 劳动力流动成本对农村劳动力转移的影响 |
|
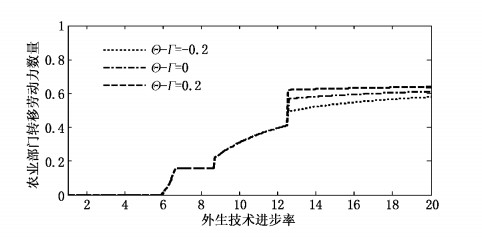
| 图 5 宅基地补偿金与城市迁入成本对农村劳动力转移的影响 |
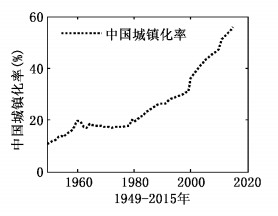
图 1(a)为随着户籍制度的变迁地区1农业部门转移劳动力数量的模拟情况,图 1(b)为新中国成立以来我国城镇化率的实际变化情况。从图 1(b)中发现,新中国成立以来我国城镇化率不断地上升,这是由于现代部门快速发展、产业规模扩张和吸纳大量农业劳动力的缘故。随后城镇化率出现下降,并逐渐稳定下来直到1978年改革开放。1958年我国的户籍制度正式确立,且经济的冒进发展、全国范畴的返乡动员和随后的三年自然灾害,城镇化率在1960年前后出现波动。之后户籍制度被严格执行,农村人口很少向城市转移,城市的城镇化率变化主要取决于城乡人口的自然增长率变化,如果城乡人口的自然增长率能够稳定,那么城镇化率也会相对稳定。改革开放以后,农村人口流动限制放松,加上经济体制改革,使城市现代部门快速发展,对劳动力需求量增加,城镇化率有较大提高。由图 1(b)可见,在改革开放初期,我国城镇化率短期内快速上升,这是相关政策释放红利的结果,之后人口流动就进入“候鸟式”流动状态模式。
|
| 图 1b 新中国成立以来中国城镇化率 数据来源:中国统计年鉴。 |
图 1(a)中,曲线第四段模拟的是当前户籍制度改革条件下农村劳动力的转移情况,这是对户籍制度改革后农村劳动力流动的预测,在图 1(b)中没有对应部分。通过对中国城镇化率的实际变化与理论模拟轨迹的比较,发现模拟结果与实际情况基本吻合,能够解释中国农村人口向城市转移的规律和趋势,模型具有很好的现实解释力。
四、 户籍制度改革对农村劳动力流动影响模拟分析 (一) 不同户籍制度改革路径对农村劳动力转移影响的比较在前述建立的三种不同劳动力流动模式下农村劳动力转移的模型中,再将我国户籍制度变迁对劳动力转移的影响模型化,由此在不同劳动力流动模式下,我国农村劳动力转移会沿着怎样的路径走下去?为此,我们将重点讨论三种情况:不存在户籍制度约束时我国农村劳动力转移的轨迹;维持当前“候鸟式”劳动力流动模式下我国农村劳动力转移的轨迹;当前户籍制度改革条件下我国农村劳动力转移的轨迹。模拟结果见图 2所示。
图 2模拟的是地区1将土地租金留在农村条件下的户籍制度改革路径,而将土地租金留在农村意味着农村人口城市化过程中要将土地退回集体。由图可见,没有户籍制度约束时,曲线位置最高,农村劳动力转移数量也最多,相应经济发展水平也最高;维持目前户籍制度不变时,农民工在城乡之间仍然处于“候鸟式”流动,农村转移劳动力数量最少,其与劳动力完全自由流动时相比存在一个巨大的缺口,该缺口就是经济效率的损失,也是户籍制度改革红利的期望极大值;对当前户籍制度进行改革时,曲线经过跳跃与第一条路径重合,将户籍制度对劳动力流动限制带来的效率损失完全弥补回来。从图中模拟结果看,人口流动模式的两次变革都带来了改革红利。这主要是因为,第一,对人口流动的限制阻碍了要素的自由流动,抑制了经济活力和经济发展;第二,当农村人口不能向城市部门自由流动时,农村劳动力收入水平很难提升,消费品和中间投入品市场规模的提升就受到限制,规模经济不能充分发挥,抑制了现代部门的扩张。而随着户籍制度改革的完成,经济活力短期内得到激发,地区1现代部门快速扩张,大量农村人口被吸纳到现代部门。上述三条劳动力转移路径具有重要意义,它们揭示了我国户籍制度改革将会带来何种影响。由于模拟时不考虑改革过程及所经历的时间,由图可见曲线在人口流动模式转换处发生了突变,这种转变瞬间完成。而现实改革往往具有复杂性和长期性,因此改革的途径和手段要精准,尽可能减少户籍制度改革带来的负面效应,从而使改革效益最大化。
(二) 不同土地产权制度改革路径对农村劳动力转移影响的比较现有土地产权制度将土地分为国有土地和集体土地,而集体土地与农村户籍人口紧密关联,户籍制度改革必定牵涉土地产权制度。目前土地产权制度改革形式多样,但归根结底还是土地收益的分配问题。这里我们讨论两种土地租金分配方式:一是城市化农民将土地租金带入城市,即城市化农民仍然拥有土地承包权;二是将土地租金留在农村,即城市化农民要放弃土地承包权,不能再享用土地租金。这两种土地租金的处理方式涉及不同农用土地的改革路径。为此,我们还要模拟土地租金不同处理方式对农村劳动力转移的影响。
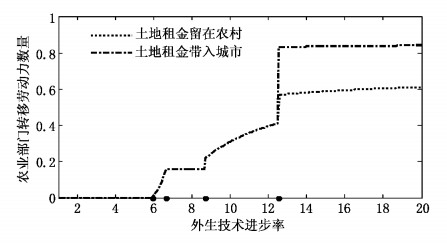
图 3模拟的是地区1不同土地产权制度的改革路径,两条曲线模拟参数完全相同。由图可见,户籍制度改革后短期内都引起了农村劳动力的快速转移,这是由于放松了人口流动限制,释放了改革红利,促进了地区1现代部门的发展,能够吸纳更多的农村劳动力。然而比较两条路径发现,把土地租金留在农村的曲线位置要低得多,而图 3中将土地租金留在农村的曲线正是图 2中对户籍制度进行改革的那条曲线。显然,将土地租金带入城市时的人口转移路径甚至远超过图 2中没有户籍制度限制时的曲线位置,这说明将土地租金带入城市时更能够促进地区1的经济发展和农村劳动力转移。根据“推-拉”理论,农村劳动力跨部门转移是由城市与农村的工资差别所引起,而城市化的农民将土地租金带入城市,提高了其收入水平,间接降低了农村劳动力的迁移成本,增强了城市的拉力因素。因此,户籍制度和土地产权制度的协同改革非常重要,两者同时推进,将大大促进经济发展和农民工的市民化。目前国内研究大都将户籍制度改革和土地产权制度改革分离开来,这显然不能达到最佳的改革效果,由此可以得出如下结论。
|
| 图 3 土地产权制度改革对农村劳动力转移的影响 |
结论1:户籍制度改革和土地产权制度改革必须同步进行,将土地租金带入城市更有利于农民工的市民化。
(三) 劳动力流动成本对农村劳动力转移的影响图 4中两条曲线为不同劳动力流动成本下地区1从农业部门转移的劳动力数量,除劳动力流动成本不同外,所模拟两条曲线的其余参数值都相同。由图可见两条曲线总体变化趋势相一致,都能够反映出我国户籍制度演变对农村劳动力转移的影响。图 4中的曲线变化趋势与地区1的产业份额变化相一致,这是由于地区1的产业份额变化反映出地区1的工业化进程,而地区1的劳动力从农业部门向现代部门转移则反映出地区1的城市化过程,城市化与工业化相互影响,所以尽管两条曲线对应的劳动力转移成本不同,但趋势则相同。除此之外,还发现两条曲线上都存在两个跳跃点,这反映出户籍制度变化对劳动力流动的影响,随着每次户籍制度对劳动力流动束缚的放松,都会带来发展红利,促使农村人口短期内大量转移至城市现代部门。
图 4中劳动力流动成本较低的曲线始终高于另一曲线,这反映了劳动力流动成本对农村劳动力转移的影响:一方面,劳动力转移成本较低时,产业从地区2向地区1转移的时间更早,地区1开始工业化的时机相对提前,使得农村劳动力向现代部门的转移提前,提高了地区1劳动力的整体收入水平,扩大了消费品市场规模,加快了地区的工业化和城市化。同时地区1一旦开始工业化,需要大量的中间投入品,强化了产业关联度和前后向联系,进一步放大地区1的市场规模,能够使工业生产中的规模经济效应充分发挥。此外,工业化增强了地区1的整体技术水平,提高了劳动效率,促进了地区1的经济发展和人口转移。由图 4可以看出,在相同技术效率水平下,劳动力流动成本较低时,从农村转移到城市的劳动力数量要多一些,那么降低劳动力流动成本将促进农村劳动力转移,并带来可观的效益。该结果具有重要的政策含义,即我国政府在实行户籍制度改革时,可以让农民工“带着土地”进城,这样农民即使进城仍可继续享有土地收益,通过提高农民收益就相应降低了农民工转移的成本,这将提高我国的城市化水平,促进经济发展。由此可得如下结论。
结论2:劳动力转移成本的存在,不利于劳动力从农村部门向城市转移,转移成本越大这种阻碍就越大。
(四) 宅基地补偿金与城市迁入成本对农村劳动力转移的影响当前,我国农民工的迁移大多是非永久性迁移,其迁移决策取决于城乡收入差距和流动成本,而流动成本只考虑食宿及交通费用等。而户籍制度改革完成后,农村劳动力在城乡自由迁移,迁移将具有永久性,这时的迁移决策取决于迁移的长期收益和迁移成本,而迁移成本包括城市安居成本,如购房成本等。此外,我国农民具有宅基地使用权,随着农村土地产权制度改革的深入,农村土地将可以进行流转、抵押等,那么农村迁移人口可以从中获得一定的收益。这里我们模拟宅基地补偿金和城市迁入成本净值对农村劳动力迁移行为的影响。
图 5中曲线模拟的是将土地租金留在农村时户籍制度改革的曲线,由于将土地租金带入城市,因而曲线形状相似,在此不再赘述。三条曲线代表不同宅基地补偿金与城市迁入成本净值。由图中可见,当净值小于0时,表示宅基地补偿金不足以弥补在城市定居的成本,此时户籍制度改革后曲线位置最低,户籍制度改革对经济促进作用较小,现代部门吸纳的农村劳动力较少,改革红利最低;当净值等于0时,表示宅基地补偿金正好弥补在城市定居的成本,曲线位置居中,相关改革效果处于中等水平;而当净值大于0时,表示宅基地补偿金高于城市定居成本,曲线位置最高,此时相关改革对经济促进作用最大,经济系统释放大量红利。从曲线变化规律可以推断,如果维持宅基地补偿金不变,随着城市房价的逐步提高,曲线会逐渐向下滑动,当房价高到一定程度时,曲线将回落到维持户籍制度不变时的位置,此时房价上涨完全吞噬掉户籍制度改革释放的红利。因此,我国宅基地改革、城市住房制度改革及城市房价调控政策非常有必要。
国内外通过房价收入比来判断房价合理与否,一般来讲,房价收入比的国际正常区间为3到6倍,而我国房价收入比2000年为6.3倍,2015年则增加到7.2倍,尤其是一些大城市的房价收入比更是大得惊人。据统计,2016年北京房价收入比为44.4倍,上海为42.3倍,深圳为33.7倍,广州、天津、杭州等城市则在20倍左右,其余城市多在10倍以下。总体上我国房价收入比还算合理,但是近年来快速上涨势头显然不利于人口转移,如果房价继续上涨,将吞噬掉户籍制度和土地产权制度改革带来的红利,甚至会使相关改革变得无效。由此,我们有结论3。
结论3:要提高我国农民工的市民化水平,必须加强宅基地流转,并降低城市房价。
五、 结论本文以中国户籍制度演变对农村劳动力流动影响为纽带,将我国户籍制度变迁和土地产权制度改革模型化。研究建立了符合我国人口流动特征的劳动力迁移模型,并模拟了户籍制度改革对我国农村劳动力流动的影响,这不仅解决了户籍制度改革中的重大现实问题,还丰富和完善了劳动力迁移理论,具有重要的应用价值和理论价值。研究发现,户籍制度对劳动力要素的束缚抑制了产业转移,使经济系统遭受较大损失。同时模拟不同的户籍制度和土地产权制度的改革路径发现,不同的土地产权制度改革路径将极大地影响户籍制度的改革效果,由此推断,农民工市民化时应保留其农用土地的承包权和宅基地的使用权,让其带着土地转移,如此他们就可以从农用土地承包权和宅基地使用权中获得一定收益,间接降低了迁移成本,更有利于农民工市民化,并释放更多的改革红利。此外,研究还表明,如果要提高我国农民工的市民化水平,还需加强宅基地流转,降低城市房价。本研究为地方政府有关农民工市民化的决策提供了全新思路,即户籍制度改革将释放巨大红利,如果政策得当,整个经济系统都会享受到农民工市民化带来的红利,这足以弥补市民化带来的成本,农民工市民化并不是增加了地方政府负担。因此,地方政府在对待户籍制度改革和农民工市民化问题上应该更加积极主动。
由于本文研究框架的复杂性,建模过程中假定劳动力和企业同质,这虽然能够解释户籍制度改革对农村劳动力流动的影响,但是不能够非常精确地刻画出农村劳动力迁移的个性化特征。因此,今后研究将试着把劳动力异质性、企业异质性等因素纳入到研究框架中,进一步完善和深化有关劳动力迁移的理论。
| [1] | 安虎森, 颜银根, 朴银哲. 城市高房价和户籍制度:促进或抑制城乡收入差距扩大?——中国劳动力流动和收入差距扩大悖论的一个解释[J]. 世界经济文汇 , 2011 (4) : 41–54. |
| [2] | “城镇化进程中农村劳动力转移问题研究”课题组. 城镇化进程中农村劳动力转移:战略抉择和政策思路[J]. 中国农村经济 , 2011 (6) : 4–25. |
| [3] | 邓曲恒, 古斯塔夫森. 中国的永久移民[J]. 经济研究 , 2007 (4) : 137–148. |
| [4] | 都阳, 蔡昉, 屈小博, 等. 延续中国奇迹:从户籍制度改革中收获红利[J]. 经济研究 , 2014 (8) : 4–13. |
| [5] | 胡枫, 史宇鹏. 农民工汇款与输出地经济发展——基于农民工汇款用途的影响因素分析[J]. 世界经济文汇 , 2013 (2) : 80–95. |
| [6] | 梁琦, 陈强远, 王如玉. 户籍改革、劳动力流动与城市层级体系优化[J]. 中国社会科学 , 2013 (12) : 36–59. |
| [7] | 陆铭. 玻璃幕墙下的劳动力流动——制度约束、社会互动与滞后的城市化[J]. 南方经济 , 2011 (6) : 23–37. |
| [8] | 倪国华, 蔡昉. 农户究竟需要多大的农地经营规模?——农地经营规模决策图谱研究[J]. 经济研究 , 2015 (3) : 159–171. |
| [9] | 倪鹏飞, 颜银根, 张安全. 城市化滞后之谜:基于国际贸易的解释[J]. 中国社会科学 , 2014 (7) : 107–124. |
| [10] | 人口研究编辑部. 户籍制度50年[J]. 人口研究 , 2008 (1) : 43–50. |
| [11] | 孙文凯, 白重恩, 谢沛初. 户籍制度改革对中国农村劳动力流动的影响[J]. 经济研究 , 2011 (1) : 28–41. |
| [12] | 严超, 常志霄. 中国省际劳动力迁移对地区经济增长的影响研究——基于1995-2005年数据的实证分析[J]. 经济科学 , 2011 (6) : 19–29. |
| [13] | 袁媛. 我国户籍制度改革中的路径依赖研究[J]. 农村经济 , 2015 (1) : 19–23. |
| [14] | 张杰飞, 李国平, 柳思维. 中国农业剩余劳动力转移理论模型及政策分析:Harris-Todaro与新经济地理模型的综合[J]. 世界经济 , 2009 (3) : 82–95. |
| [15] | 章莉, 李实, WilliamA, DarityJr. 中国劳动力市场上工资收入的户籍歧视[J]. 管理世界 , 2014 (11) : 35–46. |
| [16] | 章莉, 李实. 中国劳动力市场就业机会的户籍歧视及其变化趋势[J]. 财经研究 , 2016 (1) : 4–16. |
| [17] | 张伟进, 胡春田, 方振瑞. 农民工迁移、户籍制度改革与城乡居民生活差距[J]. 南开经济研究 , 2014 (2) : 30–53. |
| [18] | 朱江丽, 李子联. 户籍改革、人口流动与地区差距——基于异质性人口跨期流动模型的分析[J]. 经济学(季刊) , 2016 (2) : 797–816. |
| [19] | Forslid R, Ottaviano G I P. An analytically solvable core-periphery model[J]. Journal of Economic Geography , 2003, 3 (3) : 229–240. DOI:10.1093/jeg/3.3.229 |
| [20] | Fujita M, Krugman P, Venables A J. The spatial economics: Cities, regions, and international trade[M]. MA: MIT Press, 1999 . |
| [21] | Krugman P, Venables A J. The seamless world: A spatial model of international specialization[R]. NBER Working Paper No.5220, 1995. |
| [22] | Krugman P, Venables A J. Globalization and the inequality of nations[J]. Quarterly Journal of Economics , 1995, 110 (4) : 857–880. DOI:10.2307/2946642 |
| [23] | Pflüger M, Südekum J. A synthesis of footloose-entrepreneur new economic geography models:When is agglomeration smooth and easily reversible?[J]. Journal of Economic Geography , 2008, 8 (1) : 39–54. |
| [24] | Pflüger M, Südekum J. Integration, agglomeration and welfare[J]. Journal of Urban Economics , 2008, 63 (2) : 544–566. DOI:10.1016/j.jue.2007.03.006 |
| [25] | Russek S. Differential labour mobility and agglomeration[J]. Papers in Regional Science , 2010, 89 (3) : 587–606. DOI:10.1111/j.1435-5957.2009.00269.x |
| [26] | Tabuchi T, Thisse J F. Taste heterogeneity, labor mobility and economic geography[J]. Journal of Development Economics , 2001, 69 (1) : 155–177. |
| [27] | Todaro M P. A model of labor migration and urban unemployment in less developed countries[J]. American Economic Review , 1969, 59 (1) : 138–148. |
| [28] | Venables A J. Equilibrium locations of vertically linked industries[J]. International Economic Review , 1996, 37 (2) : 341–59. DOI:10.2307/2527327 |
 2016, Vol. 42
2016, Vol. 42




