文章信息
 | 财经研究 2016年42卷第9期 |
- 陈杰, 周倩.
- Chen Jie, Zhou Qian.
- 中国城市规模和产业结构对城市劳动生产率的协同效应研究
- The Synergy Effects of City Size and Industrial Structure on Urban Labor Productivity in China
- 财经研究, 2016, 42(9): 75-86
- Journal of Finance and Economics, 2016, 42(9): 75-86.
-
文章历史
- 收稿日期:2016-03-12

2016第42卷第9期
2.上海财经大学 高等研究院, 上海 200433;
3.上海财经大学 公共政策与治理研究院, 上海 200433
2.Institute for Advanced Research, Shanghai University of Finance and Economics, Shanghai 200433, China;
3.Institute of Public Policy and Governance, Shanghai University of Finance and Economics, Shanghai 200433, China
经过30多年的高速增长, 中国经济增速在近年来有所放慢, 引起各界高度关注, 并引发不少忧虑。中国要维持经济中高速增长的前提是要深刻理解中国劳动生产率的影响机制, 从而为持续提升中国经济潜在增长率找到方向。“城镇化是现代化的必由之路”, 中国城镇化率已经超过56%, 城市经济对中国经济增长的贡献程度达到90%以上。为此, 提升城市劳动生产率成为中国突破“中等收入陷阱”、实现全面小康的关键所在, 这也是新常态下城镇化模式转型的根本要求。
在经济学文献中, 关于城市劳动生产率的讨论往往与“城市最优规模”假说相紧密联系(Henderson, 1974;Black和 Henderson,1999;Gabaix和Ioannides,2004), 验证城市是否存在“规模红利”是经济增长文献中的重要命题(Abdel-Rahman和Fujita, 1990;Duranton和Puga, 2005)。同时, 大量研究表明, 技术进步和城市劳动生产率也深受城市产业结构的影响(Pavitt,1984;Drucker和Feser,2012)。中国的实证研究也证实, 恰当的产业结构调整对劳动生产率具有“结构红利”效应(毛丰付和潘加顺, 2012), 而工业与服务业如果比重失衡将对城市生产率产生抑制作用(顾乃华等, 2006;江静等, 2007;袁志刚和高虹, 2015)。结合这些理论背景, 可见城市规模和产业结构都是影响城市劳动生产率的重要因素, 但也有理由相信城市集聚的“规模红利”会随着城市产业结构的不同而有较大差异, 同样有理由相信产业结构对城市劳动生产率“结构红利”在不同规模的城市也可能迥然不同。新近文献中也有提出“城市规模-产业结构”对城市劳动生产率具有协同效应的假说(柯善咨和赵曜, 2014), 但对城市规模、产业结构和城市劳动生产率三者之间的关联特征以及在不同情境下的关联特点, 现有文献中还缺乏系统的研究。
本文以城市劳动生产率为研究对象, 以城市规模和产业结构对城市劳动生产率的协同效应为分析视角, 分析城市规模、产业结构与城市劳动生产率这三者之间的相互关联。相对已有文献, 本文除了运用了更新和时间跨度更长的地级市面板数据外, 主要的贡献在于:系统地考察了城市规模的“规模红利”和产业结构的“结构红利”之间互动关系的非线性特征, 包括城市规模对城市劳动生产率的边际溢出效应是如何受到产业结构的影响, 以及产业结构对城市劳动生产率的作用在不同规模的城市中又有怎样的不同表现。本文还应用了空间面板模型来控制城市之间的相互影响与空间溢出效应, 也控制了关键变量与被解释变量之间可能的内生性, 在多种模型设定下, 主要结果都十分接近, 保障了结果的稳健性。这些模型设定上的新尝试, 也是对文献的推进与发展。
从学术价值上, 本文的研究结果可以与早前Au和Henderson(2006a、b)等基于中国20世纪90年代城市数据的经典文献研究结果作对照, 从而看出2000年以来市场化和快速城镇化情境是如何影响一个转型经济体的城市规模及城市体系的演变。当然, 关于城市规模及城市体系合理性的讨论并不局限于中国或转型经济, 在发达经济体和各国都有大量文献讨论(Gabaix和Ioannides,2004;Parkinson等, 2015)。但中国巨大的城市规模、快速的城市化进程和高速的经济增长, 给予城市规模问题研究一个特殊的实验性场景来深入挖掘, 也提升了这个问题的实践价值。从政策应用价值上看, 本文的研究结果可以用来评价当前中国整体上城市规模是否合理、城市体系是否健康, 同时发现不同类型的城市产业结构是否需要进一步调整。具体而言, 本文依据计量模型分别对当前中国城市规模的最优容纳规模和产业结构的最优结构做了最新测度, 以此判断目前具体哪些城市需要进一步调整城市规模和优化产业结构, 可为中国城镇化发展的政策实践提供科学依据。
二、 研究设计与计量模型本文采用2000-2013年地级市面板数据进行研究, 较目前可比文献的数据更新更长。城市发展在空间上相互影响, 尤其在中国这样人口高密度、主要城市群又高度集中在有限地区的国家中, 有理由相信城市经济指标具有高度的空间依赖性和聚簇性, 城市经济体之间的空间联动发展会十分显著。为此, 能否在计量上有效控制城市数据的空间相关性与空间依赖性, 对准确测量城市规模的边际收益, 具有十分重要的意义, 但之前的文献都基本忽略了这点。本文应用了空间面板模型来控制城市发展在空间上的相互影响与溢出效应, 可以让研究结果更加稳健和可靠。本文在差分 GMM、系统GMM和空间计量模型结果的基础上实际测算出在现有条件下的城市最优规模以及最优产业结构配置, 并由此计算出每个城市在现有条件下可以增加的劳动力吸纳规模比例和产业结构可调整比例, 从而为改进城市治理政策、提高城市发展水平提供了理论依据。
(一) 数据描述。本文数据来自2000-2013年全国281个省会、计划单列市及地级市数据。本文剔除了北京和上海这两个不宜与其他城市比较的特大城市, 也剔除了拉萨市、陇南市、中卫市等数据缺失严重的城市。这样, 样本覆盖了281个城市14年、一共3 934个样本值。数据来自《中国城市统计年鉴》、《中经网统计数据库》、《中国经济与社会发展统计数据库》和同花顺数据库等, 个别缺失数据使用插值法填补。表 1是各变量指标数据的描述性统计。
| 变量名称 | 含义 | 单位 | 均值 | 方差 | 最小值 | 最大值 |
| lnpgdp | 市辖区人均GDP对数值 | ln(元) | 9.266 | 0.819 | 6.497 | 11.990 |
| emp | 市辖区就业人员数 | 十万人 | 2.269 | 3.229 | 0.081 | 45.740 |
| empsq | 市辖区就业人员数平方项 | 十万人%$\hat{2}$ | 15.570 | 62.800 | 0.007 | 2092.15 |
| ms | 市辖区第二与第三产业增加值之比 | 1 | 1.561 | 0.906 | 0.193 | 10.859 |
| empms | emp×ms | 十万人×% | 3.238 | 4.057 | 0.041 | 41.025 |
| lncapemp | 劳均资本量(cap/emp)对数值 | ln(万元/十万人) | 7.627 | 1.048 | 2.423 | 10.918 |
| fdicap | FDI与资本量比值 | % | 0.146 | 0.236 | 0.000 | 2.155 |
| lnedu | 滞后两期的当地高校毕业生人数的对数值 | ln(人) | 9.296 | 2.532 | 0.000 | 15.750 |
| lngreen | 建成区绿化覆盖率的对数值 | ln(%) | 3.468 | 0.421 | 0.0583 | 6.253 |
| road | 市辖区人均铺装道路面积 | 平方米 | 8.709 | 6.206 | 0.0400 | 85.20 |
| lnbook | 单位市辖区人口拥有公共图书馆藏量的对数值 | ln(册/百人) | 3.845 | 0.944 | 0.113 | 6.999 |
| lnbus | 单位市辖区人口拥有公共汽车数的对数值 | ln(辆/万人) | 1.577 | 0.798 | 0 | 4.745 |
| lndist | 与最近最大港口城市距离的对数值 | ln(公里) | 5.989 | 1.007 | 1.966 | 7.906 |
| 注:每个指标的样本均为3 934个。价值变量均以2000年为基期作价格平减。 | ||||||
图 1a是地级及以上城市市辖区的劳动生产率与城市规模的散点图并做了二次型拟合, 发现有比较明显的倒 U形曲线轨迹。但图 1b地级及以上城市市辖区的劳动生产率与产业结构虽然出现了一阶导数大于0、二阶导数小于0的趋势, 但在样本区间里尚未出现完整的倒U形曲线。
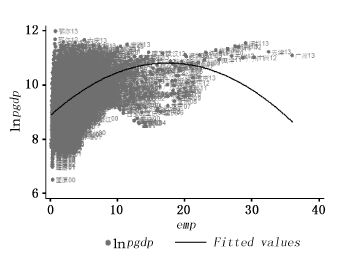
|
| 图 1a 城市人均GDP与城市规模的关系 |
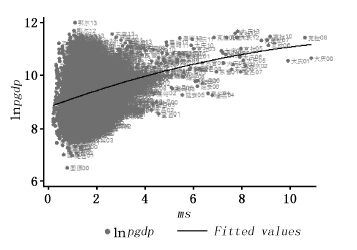
|
| 图 1b 城市人均GDP与产业结构的关系 |
(二) 计量模型。根据现有经典文献对城市劳动生产率决定因素的讨论, 结合上述机制分析和数据分析, 本文把城市劳动生产率表述为:
| $Y=f\left( emp,empsq,ms,mssq,empms,K,U,D \right)$ | (1) |
其中:Y为城市劳动生产率。参照现有文献(Au和Henderson, 2006a、b;毛丰付和潘加顺, 2012;柯善咨和赵曜, 2014; 梁婧等, 2015), 本文将采用人均国内生产总值(PGDP)这一变量来度量城市劳动生产率。式(1)认为, 影响城市劳动生产率的因素包括:emp-城市规模, ①empsq城市规模的平方项, ms-产业结构, mssq-产业结构的平方项, empms-城市规模与产业结构的交互项, K-城市的资本存量与资本特征, U-城市的基础设施水平, D-城市的地理特征。
①城市规模可以采用市辖区常住人口、户籍人口等指标, 但本文为了与文中城市劳动生产率的概念直接对应而采用市辖区就业人员数指标。
根据式(1)及前述对城市劳动生产率影响因素的理解, 本文将基本计量模型设定为:
| $\begin{align} & lnpgd{{p}_{it}}={{\beta }_{0}}+{{\beta }_{1}}em{{p}_{it}}+{{\beta }_{2}}emps{{q}_{it}}+{{\beta }_{3}}m{{s}_{it}}+{{\beta }_{4}}mss{{q}_{it}}+{{\beta }_{5}}empm{{s}_{it}}~ \\ & +{{\beta }_{6}}lncapem{{p}_{it}}+{{\beta }_{7}}fdica{{p}_{it}}+{{\beta }_{8}}lned{{u}_{it}}+{{\beta }_{9}}lngree{{n}_{it}}+{{\beta }_{10}}roa{{d}_{it}} \\ & +{{\beta }_{11}}lnboo{{k}_{t}}+{{\beta }_{12}}lnbu{{s}_{it}}+{{\beta }_{13}}lndis{{t}_{it}}+{{\delta }_{it}}+{{\varepsilon }_{it}}~ \\ \end{align}$ | (2) |
其中:被解释变量即为市辖区人均GDP数据的对数值lnpgdp, 该数据以2000年为基期做平减。关键解释变量同式(1), 其中emp是市辖区就业人员数, 表示城市规模;empsq是城市规模emp的平方项, 本文根据机制分析和图 1a的数据分析, 认为城市规模与劳动生产率之间很可能存在倒U形的曲线关系, 为验证这一观点而采用本指标;ms是市辖区第二产业增加值与第三产业增加值的比值, 用于度量产业结构, mssq是其平方项, 其构造类似于empsq项, 交互项empms用于考察emp与ms的交互作用对劳动生产率的影响。
式(2)的其他控制变量包括:与物质资本相关的变量有劳均资本存量lncapempit和外商实际投资额与资本量的比值fdicapit。由于中国没有公开发布的城市资本量数据, 因此本文将对这一数据进行测算;人力资本变量——用滞后两期的当地高校毕业生人数的对数lnedu作为当地人力资本的代理变量。与城市劳动生产率相关的基础设施水平变量包括lngreen、road、lnbook和lnbus, 参见表 1的定义解释。dist是各城市与其最近最大港口城市(上海市、天津市和广州市)的距离, 这代表着不同城市的地理位置特征, lndist是对dist变量取对数的结果。除以上变量外, 城市自身的特征还有很多, 比如自然资源禀赋、地形地貌、社会风俗、历史文化等方面的不同, 都会对城市劳动生产率产生影响。所有这些影响将采用地区固定效应方法加以控制。
(三) 协同效应及最优规模的推导。为了推导出城市最优规模的量化表达式, 令式(2)对劳动力empit分别求一阶和二阶导数有:
| $(lnpgd{{p}_{it}})/\left( em{{p}_{it}} \right)={{\beta }_{1}}+2{{\beta }_{2}}em{{p}_{it}}+{{\beta }_{5}}m{{s}_{it}}~$ | (3) |
| ${{\partial }^{2}}(lnpgd{{p}_{it}})/{{\left( em{{p}_{it}} \right)}^{2}}=2{{\beta }_{2}}~$ | (4) |
首先看一阶条件式(3), 无论二阶导数是否等于0(即β2=0与否), 城市劳动生产率与城市规模之间的关系都受β1和β5msit值的共同影响。探测β5的大小和方向, 考察城市规模-产业结构对劳动生产率的联合作用, 是本文的工作焦点之一。再看二阶条件式(4), 当二阶导数小于0时(即β2<0), 则存在使劳动生产率最大化的城市最优规模。这个条件下当一阶导数为0时, 即可取得城市规模的极大值点(即本文所指的城市最优规模)。
根据式(3)和式(4), 城市最优规模的表达式及其限定条件为:
| $em{{p}^{*}}_{it}=\left( {{\beta }_{1}}+{{\beta }_{5}}m{{s}_{it}} \right)/\left( -2{{\beta }_{2}} \right),{{\beta }_{2}}<0,{{\beta }_{1}}+{{\beta }_{4}}m{{s}_{it}}>0$ | (5) |
上式可计算求得各城市最优规模的量化表达式。可以看出, 城市最优规模受产业结构的影响, 随着产业结构的变化, 城市最优规模会发生相应变化。因此, 讨论最优规模需要界定特定的产业结构。在特定的产业结构下, 城市最优规模与当前城市规模的差值就是各城市劳动力吸纳规模, 这个差值与当前各城市规模的比值即为各个城市劳动力吸纳规模比例。基于同样思路, 可以计算出最优产业结构配置和产业结构可调整比例。表达式为:
| $\Delta emp\% = \left( {em{p^*}_{it} - em{p_{it}}} \right)/\left( {em{p_{it}}} \right)$ | (6) |
| $\Delta ms\% = \left( {m{s^*}_{it} - m{s_{it}}} \right)/m{s_{it}}$ | (7) |
此外, 尽管Au和Henderson(2006a、b)以及柯善咨和赵曜(2014)的研究认为城市规模增大的边际收益会随产业结构向服务业转变而增加, 却没有充分考察和验证其转换边界。本文认为, 产业结构在哪个城市规模边界上更有利于吸纳更多劳动力并增强城市规模对劳动生产率的外溢影响, 具有很强的政策应用价值。为此, 本文借用Hansen(2000)的门槛回归面板方法, 更加直接地验证产业结构在城市规模对劳动生产率的影响中的非线性作用。同时, 本文也探索城市规模大小在产业结构对劳动生产率影响中的非线性效应, 探究其转换边界。本文还进一步使用差分 GMM和系统GMM方法, 通过引入因变量的滞后项来克服模型可能存在的内生性问题, 并可作为空间回归模型的稳健性回归。
(四) 模型设定与检验。
1.差分GMM和系统GMM模型的设定。本文将使用差分GMM模型和系统GMM模型的方式来尝试解决内生性问题。参考相关文献, 本文引入因变量的二至四阶滞后项、城市规模的二至三阶滞后项和产业结构的二至三阶滞后项作为工具变量, 检验结果见表 2。差分GMM估计共使用了90个工具变量, 结果显示, 扰动项的差分存在一阶自相关、但不存在二阶及三阶自相关, 可以使用差分GMM。Sargan检验的过度识别结果显示, 在1%的显著性水平上, 无法拒绝“所有工具变量均有效”, 故认为工具变量的设定有效。系统GMM的检验结果类似。
| DGMM | SGMM | |
| 工具变量个数 | 90 | 126 |
| AR(1) | 0.0001 | 0.0001 |
| AR(2) | 0.8448 | 0.9460 |
| AR(3) | 0.2292 | 0.2204 |
| Sargan | 214.591*** | 233.259*** |
| P值 | 0.0000 | 0.0000 |
| 注:(1)AR(1)、AR(2)和AR(3)结果列示的是其对应P值。(2)Sargan检验用于检验工具变量的有效性, 这里报告了其统计值和P值。 | ||
2.门槛模型的设定。为有效和全面考察关键变量之间的非线性关系, 本文运用门槛模型。相比主观的人为划分数据的不同区段, 门槛模型的优势是可以根据数据自身属性内生地划分门槛区段, 这样可以更加敏锐地刻画不同区段内城市规模或产业结构对劳动生产率的影响关系。本文借助Hansen(2000)的门槛面板模型, 其基本公式是:
| ${{y}_{it}}={{\mu }_{i}}+\beta {{\prime }_{1}}{{x}_{it}}I\left( {{q}_{it}}\le \gamma \right)+\beta {{\prime }_{2}}{{x}_{it}}I\left( {{q}_{it}}>\gamma \right)+{{e}_{it}}~$ | (8) |
其中:qit是门槛变量, γ是未知门槛值, eit~iid(0,δ2)为随机扰动项, I(·)为指标函数。门槛值及其个数由样本数据内生决定, 对应于任意门槛值γ, 可以通过残差平方和S1(r)=ei(γ)′ei(γ)得到各参数的估计值。最优的门槛值$\hat{\gamma }$是使S1(γ)在所有残差平方和中达到最小, 即$\hat{\gamma }$=argminS1(γ)。满足此式的观测值即为门槛值。类似地, 双门槛模型为:
| ${{y}_{it}}={{\mu }_{i}}+\beta {{\prime }_{1}}{{x}_{it}}I\left( {{q}_{it}}\le {{\gamma }_{1}} \right)+\beta {{\prime }_{2}}{{x}_{it}}I\left( {{\gamma }_{1}}\le {{q}_{it}}\le {{\gamma }_{2}} \right)+\beta {{\prime }_{3}}{{x}_{it}}I\left( {{q}_{it}}>{{\gamma }_{2}} \right)+{{e}_{it}}$ | (9) |
应用门槛模型首先需要确定模型中门槛值的个数。相关检验使用F统计量值和Hansen自抽样法(Bootstrap)的P值, 结果见表 3。结果显示, 不管是将城市规模emp设置为门槛变量还是将产业结构ms设置为门槛变量, 单一门槛和双重门槛的F值和P值都非常显著, 三重门槛检验结果不显著。所以, 本文将使用双重门槛模型。同时, 由“门槛估计值”及其相应的“95%置信区间”数据, 本文判断, 城市规模emp作为门槛变量的两个门槛值分别为1.078和12.222, 而产业结构ms作为门槛变量的两个门槛值分别是0.544和2.308。
| emp作为门槛值 | F值 | P值 | 门槛估计值 | 95%置信区间 |
| 单一门槛模型 | 117.457*** | 0.000 | 1.257 | [1.000, 10.897] |
| emp作为门槛值 | F值 | P值 | 门槛估计值 | 95%置信区间 |
| 双重门槛模型 | 214.480*** | 0.000 | ||
| 12.222 | [12.222, 12.222] | |||
| 1.078 | [0.957, 1.539] | |||
| 三重门槛模型 | 0.000 | 0.892 | 6.747 | [6.747, 9.198] |
| emp作为门槛值 | F值 | P值 | 门槛估计值 | 95%置信区间 |
| 单一门槛模型 | 25.786*** | 0.000 | 2.299 | [0.457,2.388] |
| 双重门槛模型 | 67.221*** | 0.000 | ||
| 0.544 | [0.471, 0.561] | |||
| 2.308 | [2.285, 3.020] | |||
| 三重门槛模型 | 0.000 | 0.703 | 2.000 | [0.561, 7.237] |
| 注:(1)* * *、* *和*分别表示在1%、5%和10%的显著性水平下显著, 下同。(2)P值是采用Bootstrap法反复抽样500次得到的结果。 | ||||
3.空间模型设定与选择。鉴于传统计量模型无法控制城市间的空间效应, 具体包括空间误差效应(SEE, Spatial Error Effect)和空间滞后效应(SLE, Spatial Lag Effect), 而这又对度量城市劳动生产率及其影响因素的溢出效应至关重要, 所以本文借鉴最新的空间计量经济研究成果(Mutl和Pfaffermayr, 2011;Elhorst, 2012), 将空间效应纳入分析框架。分别参照Mutl和Pfaffermayr(2011)对静态空间面板模型的研究成果以及Elhorst(2012)对动态空间面板模型的研究成果, 分别构建静态空间面板模型和动态空间面板模型。在进行空间面板模型回归之前, 需要先确定空间权重矩阵, 以选定具体的空间面板模型形式。
空间面板模型权重矩阵的确定一般有:(1)0-1变量矩阵。一般将临近样本城市间赋值为1, 其他则为0。(2)地理距离矩阵。城市间的直线距离或地球表面距离构成基础矩阵Wg, 再对其进行标准化。(3)经济社会矩阵。采用地区间人均实际GDP的差额的倒数作为测度地区间“经济距离”指标的基础矩阵Wgdp, 其与地理距离矩阵相乘得到权重矩阵W =Wgdp×Wg, 再对W做标准化处理即为经济社会矩阵W*(Elhorst, 2010)。
通过空间面板数据的Moran-I检验来判断空间效应, 并利用LM-Lag检验与LM-error检验以及相应的稳健性检验来判断究竟采用空间滞后模型(SLM)还是空间误差模型(SEM);使用Hausman检验来判断采用固定效应还是随机效应, 使用LR检验判定个体固定效应和时期固定效应的适用性, 如果两者均显著, 则使用双向效应。这些检验的统计量均根据面板混合回归的残差来构造。
由表 4 Moran-I检验值可见, 城市劳动生产率与城市规模、产业结构等变量之间存在很强的空间相关性;列(1)和列(2)显示, 空间误差效应(SLE)比空间滞后效应(SEE)更为强烈, 但无论是空间误差效应还是空间滞后效应都非常显著。在这种检验结果下, 可以选择空间误差模型(SEM)也可以选择空间滞后模型(SLM), 所以本文将分别采用这两种模型进行估计。表 4中Hausman检验对应表 5最后两列模型, 结果显示固定效应要优于随机效应。而LR个体固定效应和时期固定效应均显著, 所以本文将采取双向效应。本文借鉴Elhorst(2010)采用极大似然法进行回归估计。
| (1) | (2) | |
| Moran I | 61.8518*** | 40.2676*** |
| LM-lag检验 | 2.9454* | 3.4521** |
| Robust LM-lag检验 | 17.1426*** | 4.5616** |
| LM-error检验 | 1327.3276*** | 580.8135*** |
| Robust LM-error检验 | 1341.5248*** | 585.0298*** |
| Hausman检验值 | 331.89*** | 207.25*** |
| LR个体固定效应 | 6187.1560*** | 6075.1970*** |
| LR时期固定效应 | 4516.2069*** | 4082.5776*** |
| 注:(1)括号内是z统计量, * * *表示在1%的显著性水平下显著。(2)所有检验结果均列出其对应检验统计量的值, 其中, LR个体固定效应的自由度是281, LR时期固定效应的自由度是14。(3)列(1)和列(2)的自变量分别对应表 5的列(5)和列(6)。 | ||
本文主要回归结果见表 5。由表 5可见, 列(1)和列(2)分别是差分GMM和系统GMM面板回归结果, 列(3)和列(4)是门槛面板回归模型结果, 应用了稳健性标准误差。为了多角度考察产业结构在城市规模对劳动生产率影响中的非线性作用, 以及城市规模在产业结构对劳动生产率影响中的非线性作用, 本文分别设置核心变量为城市规模(emp)、门槛变量为产业结构(ms), 以及设置核心变量为ms、门槛变量为emp这两种情况。在门槛模型(3)中, 只有产业结构ms水平的估计系数随城市规模emp的变化而变化, 其他参数的估计系数均保持固定不变;列(4)则反之, 城市规模emp的估计系数随产业结构ms的变化而变化, 其他参数的估计系数均保持固定不变;列(5)和列(6)分别是空间误差模型(SEM)和空间滞后模型(SLM)的回归结果。
| lnpgdp | ||||||
| (1)DGMM | (2)SGMM | (3)门槛1 | (4)门槛2 | (5)SEM | (6)SLM | |
| emp | 0.057*** | 0.046*** | 0.021*** | 0.052*** | 0.051*** | |
| (4.51) | (3.91) | (15.49) | (12.10) | (12.03) | ||
| emp | 0.069*** | |||||
| (ms<0.544) | (5.34) | |||||
| emp | 0.166*** | |||||
| (0.544≤ms≤2.308) | (6.79) | |||||
| emp | 0.086*** | |||||
| (ms>2.308) | (5.59) | |||||
| empsq | -0.001*** | -0.001*** | -0.006*** | -0.002*** | -0.002*** | |
| (-5.22) | (-4.27) | (-10.83) | (-10.01) | (-10.06) | ||
| ms | 0.071*** | 0.110*** | 0.087*** | 0.041*** | 0.042*** | |
| (3.76) | (6.07) | (3.14) | (7.07) | (7.26) | ||
| ms | 0.099*** | |||||
| (emp<1.078) | (4.84) | |||||
| ms | 0.190*** | |||||
| (1.078≤emp≤12.222) | (9.05) | |||||
| ms | -0.289*** | |||||
| (emp>12.222) | (-4.08) | |||||
| mssq | -0.007*** | -0.006*** | -0.005 | -0.001*** | -0.001*** | |
| (-3.04) | (-3.36) | (-1.37) | (-3.08) | (-2.71) | ||
| empms | -0.014** | -0.011** | -0.014 | -0.030*** | -0.002** | -0.001*** |
| (-2.50) | (-1.98) | (-1.43) | (-3.38) | (-2.17) | (-4.24) | |
| lncapemp | 0.166*** | 0.172*** | 0.376*** | 0.400*** | 0.139*** | 0.133*** |
| (20.69) | (21.95) | (32.73) | (39.60) | (22.20) | (20.99) | |
| fdicap | 0.244*** | 0.228*** | 0.358*** | 0.380*** | 0.107*** | 0.095*** |
| (9.12) | (4.07) | (10.80) | (11.69) | (6.69) | (5.87) | |
| lnedu | 0.007*** | 0.007 | 0.002 | 0.004 | 0.002 | 0.002 |
| (2.79) | (0.96) | (0.33) | (0.69) | (0.99) | (1.19) | |
| lngreen | 0.097*** | 0.103*** | 0.123*** | 0.112*** | 0.192** | 0.180** |
| (6.89) | (3.38) | (7.81) | (7.11) | (2.21) | (2.10) | |
| road | 0.009*** | 0.017*** | 0.015*** | 0..012*** | 0.244*** | 0.233*** |
| (10.26) | (3.08) | (6.01) | (5.79) | (3.51) | (3.38) | |
| lnbook | 0.043*** | 0.043*** | 0.054*** | 0.053*** | 0.228*** | 0.211*** |
| (6.27) | (2.62) | (5.45) | (5.46) | (5.27) | (4.92) | |
| lnbus | 0.152*** | 0.152*** | 0.137*** | 0.129*** | 0.424*** | 0.459*** |
| (15.50) | (5.32) | (7.91) | (7.60) | (6.83) | (7.39) | |
| lndist | -0.085*** | -0.072*** | -0.041*** | -0.044*** | ||
| (-9.48) | (-8.23) | (-10.79) | (-11.32) | |||
| L.lnpgdp | 0.762*** | 0.750*** | 0.843*** | |||
| (79.85) | (73.39) | (95.31) | ||||
| Constant | 1.099*** | 1.075*** | 5.285*** | 5.287*** | ||
| (5.02) | (4.90) | (57.47) | (58.05) | |||
| N | 3372 | 3653 | 3934 | 3934 | 3653 | 3653 |
| R2 | 0.415 | 0.685 | 0.735 | 0.764 | 0.951 | 0.949 |
| Δemp% | 29.327 | 29.694 | 26.093 | 25.002 | ||
| Δms% | 37.677 | 38.363 | 38.178 | 33.886 | ||
| 注:(1)括号内是t统计量, * * *、* *和*分别表示在1%、5%和10%的显著性水平下显著。(2)因篇幅限制, 列(5)和列(6)仅列示主体效应, 省略直接效应、间接效应和总效应等;列(5)的空间滞后项是 L.lnpgdp, 即被解释变量的滞后。(3)Δemp%一行代表给定2013年产业结构的条件下, 样本城市在达到最优规模之前的吸纳比例, 其单位是%;Δms%一行代表给定2013年城市规模的条件下, 样本城市在达到最优产业结构配置之前的可调整比例, 其单位是%。 | ||||||
表 5回归结果表明, 本文设定的计量模型所产生的结果稳健性较高。限于篇幅限制, 文章简略讨论非核心变量的回归结果。总体来说, 这些控制变量的效应均基本符合经济学经典理论的预期, 如劳均资本存量lncapemp和人力资本lnedu都显著为正, 说明劳均物质资本和人力资本都有提高劳动生产率的关键性作用。此外, 建成区绿化覆盖率的对数lngreen、人均铺装道路面积road、人均公共图书馆藏量册数的对数lnbook、人均公共汽车辆数的对数lnbus等变量的系数均基本显著为正值, 说明基础设施对城市劳动生产率确实具有正向溢出作用。地理因素lndist表明劳动生产率与大港口城市的距离呈负向相关关系, 这说明与大港口城市的距离越远, 所获得的辐射力越小。
本文重点关注城市规模和产业结构对城市劳动生产率的联合作用。主要发现为:
(1) 城市规模项(市辖区劳动力规模)的一次项emp的系数均显著为正, 二次项empsq的系数均显著为负。这证明了中国城市规模与劳动生产率之间确实存在倒U形曲线关系, 这个结果与之前文献(Au和Henderson, 2006a、b;毛丰付和潘加顺, 2012;柯善咨和赵曜, 2014;梁婧等, 2015)相一致。可以认为, 在城市规模达到最优规模前, 中国城市劳动生产率随城市规模的扩张而提高, 在城市规模达到最优容纳峰值后, 城市劳动生产率随城市规模的扩张而降低, 也即城市扩张对城市劳动生产率的边际收益随着城市规模的上升而下降。但由于样本中的城市大多数未达到该倒U形曲线的顶点位置, 也即中国大部分城市都仍有继续大量吸纳劳动力的潜在能力。因此, 打破对人口集聚的制度约束, 进一步加快劳动力流动, 进一步释放“规模红利”, 仍然是推动城市劳动生产率提高的必须措施。
(2) 产业结构的一次项ms的系数均显著为正, 二次项mssq的系数均显著为负。这说明产业结构与城市劳动生产率之间也存在先上升后下降的倒U形曲线关系。然而如本文的图 1b所示, 虽然存在一阶导数为正、二阶导数为负的趋势, 但超越峰值点的城市很少, 本文基于计量模型的推断也发现仅有少数城市二产比重已经过度。总体来看, 对中国绝大多数城市而言, 第二产业比重越大, 城市劳动生产率越高, 也即目前中国产业中第二产业相对第三产业来说, 对提高劳动生产率有更积极的作用, 这与上述相关代表性文献也一致。中国绝大多数城市的第二产业对劳动生产率的贡献度仍未得到充分发掘, 尚未出现下降的拐点, 仍有很大的提升空间。这意味着, 对中国绝大多数城市而言, 工业化进程尚未完全完成, 仍要以工业和制造业强市, 尚不能过早提倡“去工业化”。
(3) 交叉项empms的系数在各面板回归模型结果中一致性为负, 且基本均统计上高度显著。这说明, 随着产业结构ms的变动(第二产业比重上升), 城市规模emp对劳动生产率的边际促进作用趋于下降;另一角度的解读是, 随着城市规模emp的上升, 如果产业结构ms趋向下降(第三产业相对壮大发展), 那会增强城市规模对劳动生产率的边际外部效益。该发现与柯善咨和赵曜(2014)“城市规模扩张的边际收益不仅受城市规模影响, 而且随着产业结构(城市生产服务业-制造业结构比例)的上升而增加”的结果相一致。
但交互项只有一个变量, 对城市规模与产业结构之间互动关系所能揭示的信息有限, 本文为此试图从多个角度来考察“城市规模-产业结构”协同效应的非线性特征。这表现在列(3)和列(4)的门槛模型回归结果中: 由于门槛回归起到了考察核心变量非线性效应的作用, 所以列(I)中不再列入empsq项, 列(II)不再列入mssq项。 在列(3) 由门槛变量产业结构ms将城市规模划分成的三区段中, 城市规模emp对劳动生产率的正向促进作用系数均十分显著, 但随着产业结构的逐步变化(ms从<0.544, 增加到≥0.544但<2.308, 再到≥2.308), 城市规模对劳动生产率的边际收益系数也呈现一个先上升后下降的关系。这进一步说明, 当一个城市工业比重不够高, 城市“规模红利”不会特别显著;而当这个城市开始进入工业化阶段, 产业结构的“重化”程度提高, 借助于制造业强大的就业乘数效应和技术进步的引领作用, 在相当大范围内会持续增强城市规模对城市生产率的外溢作用和“规模红利”。但如果产业结构继续“重化”, 制造业没有得到服务业的合理搭配, 则城市规模的“规模红利”反而会降低, 即重工业城市如果产业结构向三产适度调整将在提高生产率上有很大收益。总结而言, 城市的“规模红利”在工业化高潮阶段最显著, 在工业化之前和工业化尾声都相对较弱。同样, 在列(4)中, 在由门槛变量城市规模emp划分的三区段中, ms系数也出现先上升后下降的特点。这说明在中等规模城市中提高二产比重对促进生产率的作用最大, 小城市中能得到的结构红利相对比较有限, 但对大城市尤其是特大城市, 增加二产比重反而很可能对劳动生产率有抑制作用。如本文发现, 在城市规模大于122万人的城市中, 这些城市为深圳市、成都市、广州市、杭州市、天津市、东莞市、南京市、重庆市、西安市、佛山市、武汉市、苏州市、沈阳市、郑州市和厦门市。 继续提高二产比重, 将对城市劳动生产率产生较为严重的负向影响。换言之, 这部分城市提高三产比重可以起到提升城市劳动生产率的作用。本文使用门槛回归来考察城市规模项emp和产业结构ms之间互动关系的非线性, 总体结论上与列(1)至列(6)的交叉项empms系数一致性为负相一致, 但比简单利用交互项来考察, 视角更丰富, 揭示信息更全面、更细致。
以上发现具有重要的政策含义。城市规模与产业结构之间需要十分合理的匹配。基于制造业的乘数效应, 城市的“规模红利”在城市经历工业化高潮时最为显著, 在工业化启动阶段存在一个门槛效应, 在工业化尾声则会出现下降。这与经典文献(Black和Henderson, 1999;Duranton和Puga, 2005)和直觉观察也相一致。另一方面, 城市在从小城市到中等城市的发展过程中, 主要依赖工业来驱动劳动生产率的提高, 同时创造就业机会和吸引人口, 大多数城市不能跨越城市经济的自身发展规模, 跨过工业化就发展第三产业。从国际上看, 在国家层面工业化发展不足就进入服务业驱动, 劳动生产率提高缓慢, 往往也被认为是“中等收入陷阱”的一个主要成因(王小鲁, 2000、2010)。但当城市规模发展到了一定阶段, 城市自身的发展规律需要产业结构增加第三产业比重, 形成合理的二产、三产分工格局, 这样城市规模才能更好发挥对城市劳动生产率的溢出作用。否则, 如果大城市、特大城市仍然产业结构过度工业化, 则会一方面因为服务业配套不足的制约, 另一方面因为妨碍城市“规模红利”的释放, 而对城市劳动生产率产生负面作用。
基于空间面板模型的回归结果, 参照式(6), 在设定产业结构为2013年水平的前提下, 计算得到样本城市劳动力吸纳规模比例数据。类似地, 计算产业结构可调整比例, 结果分别列于表 5列(3)至列(6)的最后两行。可以看出, 这两项指标的计算结果相差并不大, 但由于实际经济发展中, 劳动生产率存在一定的惯性效应, 结合回归模型的设定, 本文更倾向于采纳列(6)的结果, 即样本城市在既定产业结构水平下, 较之2013年数据, 总体上城市还可容纳约25%的城市规模;而产业结构可调整比例则约为34%。本文与梁婧等(2015)认为中国2009年城市已经大部分达到最优规模区的结果存在差异, 主要原因有:(1)部分关键变量的不同选取和模型设定存在差异;(2)计算最优规模的方式有所不同。
本文依据空间滞后模型( SLM )即表 5中列(6)的结果提出, 中国目前只有极个别样本城市略超出最优规模, 它们是广州市、天津市、大庆市、深圳市、杭州市、克拉玛依市、重庆市、成都市、武汉市、嘉峪关市和西安市等11个城市, 仅约占样本总数的3.91%;接近最优规模的城市包括郑州市、攀枝花市、厦门市、南京市、吕梁市、鹤壁市、沈阳市、宁波市、合肥市、南昌市、大连市和长沙市等12个城市, 约占样本总数的4.27%;劳动力吸纳规模比例在10%-30%之间的城市最多, 为134个, 约占总数的47.69%;劳动力吸纳规模比例在30%-50%之间的城市为93个, 约占总数的33.10%;大于50%吸纳比例的城市为31个, 约占总数的11.03%。本文认为, 迫切需要发展服务业以拉动劳动生产率提高的城市有广州市、天津市、深圳市、杭州市、大庆市和克拉玛依市, 约占样本城市的2.14%;接近最优产业结构配置比例的城市有重庆市、成都市、武汉市、西安市和郑州市等18个城市, 约占总数的6.41%。制造业增加值相对服务业比重可继续上升10%-30%的城市有141个, 约占总数的50.18%;该比重可继续上升30%-50%的城市有89个, 占总数的31.67%;而可继续上升50%以上的城市有27个, 约占总数的9.61%。
本文还进行了多项稳健性检验, 如将样本分为东中西部三大地区、或按2000年人口规模分为三组、或按2000年人均GDP分为三组等, 在不同的分样本中, 都得到了基本一致的结论。限于篇幅这里没有反映, 但可供索取。
四、 结论及政策建议本文研究发现:(1)中国城市劳动生产率与城市规模之间呈倒 U形关系, 即城市规模在达到最优规模之前具有“规模红利”。(2)城市劳动生产率与产业结构也同样呈现倒U形关系, 即合理的产业结构调整将产生“结构红利”。(3)城市规模与产业结构的交互项为负, 说明过高的工业比重将妨碍城市“规模红利”的发挥, 产业的“结构红利”也取决于城市规模。(4)城市规模对劳动生产率的边际收益与产业结构呈现先上升后下降的特点, 城市的“规模红利”在工业化高潮阶段最显著, 之前和之后都相对逊色;同时, 产业结构“重化”对劳动生产率的拉动作用与城市规模也呈现先上升后下降的特点, 二产对中等城市的效率促进作用明显高于小城市, 但在大城市中提高三产比重、降低二产比重反而能带来劳动生产率上更多的“结构红利”。
应用计量模型研究发现:就中国281个样本城市来看, 在2013年的产业结构和经济发展水平下, 各城市平均还将能吸纳大约25%的城市规模, 达到或超过最优规模的城市比例不到6%。这说明, 虽然中国目前有个别特大城市和大城市已经出现规模不经济, 但绝大多数中等城市规模偏小, 人口增长潜力巨大, 城市“规模红利”还有待发掘, 未来中国城市化的重点应该是做大做强中等城市, 充分发挥中等城市的规模经济效应。研究结果也预示中国经济潜在增长率率仍然存在不小的上升空间, 在城市部门仍有很大的劳动生产率红利潜力待开发。研究还发现, 目前对中国绝大多数城市, 第二产业仍然起到了拉动经济增长的作用, 绝大多数城市还并未充分发挥第二产业的潜力, 工业化进程尚未完全完成, 不宜过早提倡“去工业化”。平均而言, 产业结构可继续向上调整的比例约为34%, 工业化仍具有相当大的发展空间。综合来说, 合理调整城市规模与产业结构, 将会提高潜在生产率和释放更多的经济发展动力, 这应成为当前供给侧结构性改革的重要组成部分。
综上我们提出如下建议, 分层级、因地制宜和因势利导地采取促进人口流动的措施, 在继续充分发挥特大城市和大城市的集聚力和辐射力的同时, 做大做强中等城市, 充分释放城市规模红利。这首先需要加快户籍制度改革, 切实以提高户籍人口城镇化率作为新型城镇化的指引方向, 促进流动人口的市民化。力推城市群发展, 推动城市加强与周边各类城市广泛和多样化的合作协同, 以最大化彼此的利益。另一方面, 引导城市产业结构顺应市场需求及时加快调整。其关键点是, 像OECD(2014)等国际组织给中国建议的那样, 开放民营资本进入城市各类服务行业, 充分竞争, 有利于吸纳更多外来人口, 为服务业比重上升创造机会, 真正扩大内需, 同时增加城市三产对二产的支持能力。城市体系的合理优化、劳动力的更自由流动和产业结构的市场化调整, 不仅会带来更强的城市竞争力、更高的劳动产出效率和更持久的经济潜在增长率, 也有利于实现“十八大”所说的包容性增长的践行。
| [1] | 干春晖, 郑若谷, 余典范. 中国产业结构变迁对经济增长和波动的影响[J]. 经济研究 , 2011 (5) : 4–16. |
| [2] | 江静, 刘志彪, 于明超. 生产者服务业发展与制造业效率提升——基于地区和行业面板数据的经验分析[J]. 世界经济 , 2007 (8) : 52–62. |
| [3] | 柯善咨, 赵曜. 产业结构、城市规模与中国城市生产率[J]. 经济研究 , 2014 (4) : 76–88. |
| [4] | 梁婧, 张庆华, 龚六堂. 城市规模与劳动生产率:中国城市规模是否过小?——基于中国城市数据的研究[J]. 经济学(季刊) , 2015 (3) : 1053–1072. |
| [5] | 刘伟, 张辉. 中国经济增长中的产业结构变迁和技术进步[J]. 经济研究 , 2008 (11) : 4–15. |
| [6] | 毛丰付, 潘加顺. 资本深化、产业结构与中国城市劳动生产率[J]. 中国工业经济 , 2012 (10) : 32–44. |
| [7] | 孙三百, 黄薇, 洪俊杰. 劳动力自由迁移为何如此重要?——基于代际收入流动的视角[J]. 经济研究 , 2012 (5) : 147–159. |
| [8] | 王小鲁. 中国城市化路径与城市规模的经济学分析[J]. 经济研究 , 2010 (10) : 20–32. |
| [9] | 杨学成, 汪冬梅. 我国不同规模城市的经济效率和经济成长力的实证研究[J]. 管理世界 , 2002 (3) : 9–12. |
| [10] | 于斌斌, 金刚. 中国城市结构调整与模式选择的空间溢出效应[J]. 中国工业经济 , 2014 (2) : 31–44. |
| [11] | 袁志刚, 高虹. 中国城市制造业就业对服务业就业的乘数效应[J]. 经济研究 , 2015 (7) : 30–41. |
| [12] | 郑若谷, 干春晖, 余典范. 转型期中国经济增长的产业结构和制度效应——基于一个随机前沿模型的研究[J]. 中国工业经济 , 2010 (2) : 58–67. |
| [13] | Baum-Snow N, Pavan R. Inequality and city size[J]. Review of Economics & Statistics , 2013, 95 (5) : 1535–1548. |
| [14] | Buettner T, Holm-Hadulla F. City size and the demand for local public goods[J]. Regional Science and Urban Economics , 2013, 43 (1) : 16–21. DOI:10.1016/j.regsciurbeco.2012.10.003 |
| [15] | Drucker J, Feser E. Regional industrial structure and agglomeration economies:An analysis of productivity in three manufacturing industries[J]. Regional Science and Urban Economics , 2012, 42 (1) : 1–14. |
| [16] | Gabaix X,Ioannides Y M.The evolution of city size distributions[A].Henderson J V,Thisse J.Handbook of regional and urban economics[C].Amsterdam:Elsevier 2014. |
| [17] | Giesen K, Suedekum J. City age and city size[J]. European Economic Review , 2014, 71 : 193–208. DOI:10.1016/j.euroecorev.2014.07.006 |
| [18] | Parkinson M, Meegan R, Karecha J. City size and economic performance:Is bigger better,small more beautiful or middling marvellous?[J]. European Planning Studies , 2015, 23 (6) : 1054–1068. DOI:10.1080/09654313.2014.904998 |
| [19] | Schläpfer M, Bettencourt L M A, Grauwin S, et al. The scaling of human interactions with city size[J]. Journal of The Royal Society Interface , 2014, 11 (98) : 1742–5662. |
| [20] | Tsekeris T, Geroliminis N. City size,network structure and traffic congestion[J]. Journal of Urban Economics , 2013, 76 (1) : 1–14. |
 2016, Vol. 42
2016, Vol. 42


