文章信息
- 周建 , 赵琳
- Zhou Jian , Zhao Lin
- 人民币汇率波动与货币政策调控难度
- RMB Exchange Rates Fluctuations and the Difficulty in Monetary Policy Regulation
- 财经研究, 2016, 42(2): 85-96
- Journal of Finance and Economics, 2016, 42(2): 85-96.
-
文章历史
- 收稿日期:2015-08-25
2.上海财经大学 高等研究院 上海 200433
2.Institute for Advanced Research, Shanghai University of Finance and Economics, Shanghai 200433, China
一、引言与文献回顾
2005年7月21日,我国按照主动性、可控性、渐进性原则改革人民币汇率形成机制,实行以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度,人民币对美元汇率总体上呈现出爬行上升的趋势。随着我国外汇市场的不断成熟,交易主体的自主定价和风险管理能力日渐增强。为增强人民币汇率双向浮动弹性,中国人民银行自2007年5月21日起将银行间即期外汇市场人民币兑美元交易价的日浮动幅度由3‰扩大至5‰,2015年8月11日进一步宣布完善人民币兑美元中间价。人民币汇率的波动性逐渐增大,不仅呈现出升值的趋势,也表现出贬值的特征。2014年12月15日,人民币兑美元即期汇率收盘报6.1912,创下2014年7月25日以来最低水平,人民币对美元汇率出现自汇率制度改革以来罕见的长达四个月的贬值,从而使人民币汇率的走势呈现出动荡局势。从实际运行效果来看,中国外汇市场总体运行平稳,呈现出弹性增强、双向浮动的特征。
有关汇率波动对宏观经济和国民经济福利的影响机制,现代国际经济理论长期以来存在两种对立的观点。一种观点的起源可以追溯到Friedman(1953)和Mundell(1961),他们认为相互依赖的经济体之间受到不对称的真实冲击时,灵活的名义汇率变化可以通过相对价格的迅速调控来抵消冲击的不利影响,帮助经济恢复均衡,因此汇率被视为一种积极的凯恩斯主义调控工具。近年来,持上述观点具有代表性的研究是Makin和Rohde(2012),他们构建了一个理论模型来评价开放小国的汇率机制选择,认为当经济更多地受到真实宏观经济冲击时,浮动汇率可以减少产出和就业波动,而当经济更多地受到货币等名义冲击时,固定汇率有助于价格、产出和就业的稳定。与上述观点相对立,Obstfeld和Rogoff(1996)认为汇率稳定可以降低国际贸易的交易成本和资本流入的风险,从而有利于经济增长,汇率波动本身则制造而不是减弱了宏观经济波动。近年来也有部分学者支持上述观点,如麦金农(2005)和Schnabl(2007)积极主张开放小国以汇率盯住作为稳定经济的货币名义锚;McKinnon和Schnabl(2006)提出经济赶超国家实施固定汇率制度更有利于提高劳动者的真实工资;Cavoli(2009)认为汇率波动大对新兴市场经济体的负面作用更加显著,因为其金融和实体经济的脆弱性更大,造成了“浮动恐慌”现象。此外,还有大量学者在汇率其他相关理论和政策分析方面做了较为充分的研究。例如,Albuquerque和Portugal(2006)检验了巴西汇率与通货膨胀的波动关系,De Grauwe和Schnabl(2005)对欧元的加盟方案进行了前景展望,Ghosh等(2003)研究了汇率的区制选择及后果。这些研究为汇率理论与实践提供了一定指导和借鉴。
从中国实践来看,人民币汇率波动幅度增大不仅意味着人民币汇率形成机制更加市场化和国际化,也意味着人民币汇率波动弹性的不确定性增加。人民币汇率波动会加大中国货币政策的调控难度吗?根据经济学理论,汇率波动大会通过传递效应产生更高的价格不确定性,从而影响通胀预期产生价格冲击,由此带来的经济影响对中国货币政策的设计和制定提出了严峻的挑战。
单纯研究人民币汇率波动或中国货币政策的文献已有很多。关于人民币汇率波动的已有研究大多集中于讨论汇率波动的特征、来源以及汇率对国际贸易和资本流动的影响等。如陈创练和杨子晖(2012)指出,人民币汇率波动的长期来源是商品市场,而短期波动则取决于货币市场因素。赵文胜和张屹山(2012)认为货币政策冲击是汇率波动的一个主要来源。关于汇率波动对贸易的影响,多数研究认为汇率对贸易的各种影响具有不对称性。潘红宇(2007)研究了汇率波动对向美国、欧盟和日本出口的影响,发现汇率波动与中国对美国和欧盟的出口存在长期负向关系,与对日本的出口无关,而短期内汇率波动只影响中国对美国的出口。韩青(2010)讨论了汇率波动对贸易量的影响,认为汇率波动对中国出口供给的影响是显著的,但不会显著影响出口需求。顾国达等(2007)发现汇率对中国劳动密集型企业和资本密集型企业的影响幅度不同,汇率波动会改变中国的出口结构。赵永亮等(2011)研究了汇率波动对产出水平及波动的影响。张瑜和李书华(2013)研究了汇率波动对FDI流入的影响,认为汇率波动增大会阻碍市场导向型FDI的流入,且这种阻碍作用随行业技术密集度的提高而增强。
有关人民币汇率波动的另一重要研究领域是汇率波动对价格的影响,主要集中于研究汇率波动对价格波动的传递效应。如毕玉江和朱钟棣(2007)基于不完全竞争市场结构,研究了中国商品出口价格的汇率传递效应,结果显示中国商品出口价格的汇率传递是不完全的,且不同商品之间存在较大差异。陈学彬等(2007)分析了中国总出口和各行业出口品的汇率传递率以及不同行业出口商的盯市能力。陈六傅和刘厚俊(2007)研究了人民币汇率的价格传递效应。项后军和潘锡泉(2011)对比了汇率和货币供应量对通货膨胀的传递效应,指出汇率的传递是不完全的,货币政策抑制通胀的作用比汇率政策要好。
有关中国汇率和货币政策问题的研究大多集中于分析汇率对货币政策决策方式和独立性的影响等。如陈晓莉(2008)以及邓永亮和李薇(2010)研究了汇率变动对货币政策的影响,认为货币政策的制定需要考虑汇率政策因素。陈雨露和周晴(2004)研究了浮动汇率制度下的货币政策操作问题,认为在以货币供应量作为调控手段的情况下,货币政策规则主要采用相机抉择的方式。王胜和郭汝飞(2012)基于开放经济的货币政策模型,研究了汇率不完全传递条件下的最优货币政策问题,认为随着汇率波动幅度的增加,最优货币政策对国内生产冲击的反应逐渐增强,汇率波动幅度也逐渐增加。陈浪南和柳阳(2012)研究了不同汇率制度下货币政策的净出口需求效应,证明了随着汇率波动幅度的增大,货币政策的净出口需求效应会出现非线性的变化。苏应蓉和李楠(2014)从理论上分析了汇率波动对利率政策的影响机理,但没有给出经验的量化分析。李文乐等(2011)的研究表明,货币政策与人民币汇率波动之间存在显著的均值与波动溢出效应。
从以上国内外相关文献可以看出,有关中国汇率和货币政策关系的研究主要围绕人民币汇率波动对货币政策的决策方式以及人民币汇率对货币供应量、出口等宏观经济变量的影响进行分析,几乎没有就人民币汇率波动对中国货币政策实现预期调控目标(包括稳定产出、控制通胀和稳定汇率等多重目标)有何影响进行过深入研究,这一研究问题面临的主要困难在于如何系统有效地刻画人民币汇率波动与中国货币政策之间的内在影响机制。因此,本文试图利用动态随机一般均衡(DSGE)模型对该问题进行探索性分析,探究人民币汇率波动对中国宏观经济波动及货币政策调控的作用机理。
二、理论模型本文借鉴Smets和Wouters(2003)的分析框架,将其扩展为一个小型开放经济体模型,在非抛补利率平价的分析中加入汇率因素,从而使汇率波动和宏观经济波动联系起来,建立人民币汇率波动与中国宏观经济波动和货币政策作用机制的模型。本文模型中包括代表性家庭、厂商、货币当局三个行为主体。代表性家庭是厂商的最终所有者,并向中间厂商提供生产所需的两种要素:劳动力和资本。因此,家庭的收入来源包括工资和资本收益,家庭的效用来自消费和闲暇,家庭在收支平衡的约束下实现无限期的效用最大化。中间厂商投入劳动和资本生产异质化的中间产品,追求利润最大化。最终厂商通过CES形式的生产函数把中间产品加总成同质化的最终产品,最终产品的一部分出口到国外,其他则在国内市场流通,用于消费和投资。消费品由国内市场流通的最终产品和进口品组成。货币当局按照一个经验的利率规则进行宏观经济调控,以实现稳定产出、控制通胀和稳定汇率的政策目标。
(一)家庭。家庭以连续分布的变量τ表示,τ分布在区间[0, 1]上。家庭积累实物资本,并将其租借给厂商。此外,家庭持有国内和国外的政府债券使自己的消费行为免受收入波动的影响。劳动力的异质性决定了劳动力供给市场是垄断竞争的,其效用函数为:
| $E\sum\limits_{t = 0}^\infty {{\beta ^t}} \varepsilon _t^B[\frac{1}{{1 - {\sigma _C}}}{(C_t^\tau - {H_t})^{(1 - {\sigma _C})}} - \frac{{\varepsilon _t^L}}{{1 + {\sigma _L}}}{(l_t^\tau )^{(1 + {\tau _L})}} + \frac{{\varepsilon _t^M}}{{1 - {\sigma _M}}}{(\frac{{M_t^\tau }}{P})^{(1 - {\sigma _M})}}]\;$ | (1) |
其中,β是效用的折现因子,$C_t^\tau $和$l_t^\tau $分别是家庭τ在t期的消费量和劳动量,Ht=hCt-1反映消费行为惯性,Mt/Pt是实际现金持有量,σC是消费替代弹性的倒数,σL是劳动对实际工资的弹性的倒数,σM是货币持有对利率的弹性的倒数,$\varepsilon _t^B$、${\varepsilon _t^L}$和${\varepsilon _t^M}$分别是偏好冲击、劳动力供给冲击与货币需求冲击。家庭收入除了用于当期消费和投资外,一部分作为现金持有以满足需求,另一部分以国内政府债券和国外政府债券的形式存在,其预算约束为:
| $\begin{array}{*{20}{c}} {PtCt + PtIt + {{(\varepsilon {{_t^R}^P})}^{ - 1}}{B_{t + 1}} + {{({\Gamma _{B*}}R_t^*)}^{ - 1}}{S_t}B_{(t + 1)}^* + {M_{t + 1}}}\\ { = WtLt + [{r_{K,t}} - \psi ({z_t})]{P_t}{K_t} + \tau {P_t}{K_t} + {D_t} + {B_t} + {S_t}B_t^* + Mt\;} \end{array}$ | (2) |
其中,货币持有Mt、国内债券Bt和国外债券${B_t^*}$是家庭财富的三种形式,Rt和${R_t^*}$分别是国内和国外的基准利率,Pt是t时期的价格水平,It和Kt分别是投资量和资本存量,Wt和Lt分别是总工资水平和总的劳动力数量,rK,t是真实资本收益率,τ是资本折旧率。ψ(zt)是资本利用率zt变动产生的成本,有ψ(zt)≡γz,1(zt-1)+$\frac{{{\gamma _{Z,2}}}}{2}$(zt-1)2,γz,1>0,γz,2>0,即该成本函数是一个凸函数。Dt是来自中间厂商的分红,St是汇率,${\varepsilon {{_t^R}^P}}$是外生的国内债券的风险贴水冲击,${{\Gamma _{B*}}}$是持有的国外债券的溢价。在式(2)的约束下,我们可以得到代表性家庭的消费和实际现金需求决定方程:
| $Et[\beta \frac{{{\lambda _{(t + 1)}}}}{{{\lambda _t}}}\frac{{{R_t}{P_t}}}{{{P_{(t + 1)}}}}] = 1,\varepsilon _t^M{(\frac{{{M_t}}}{{{P_t}}})^{( - {\sigma _M})}} = {({C_t}{\rm{ }} - {H_t})^{ - {\sigma _C}}} - \frac{1}{{1 + {i_t}}} $ | (3) |
其中,λt=$\varepsilon _t^M{({C_t}{\rm{ }} - {H_t})^{ - {\sigma _C}}}$是消费的边际效用,Rt=1+it=1/bt是债券的名义收益率。给定工资水平,对家庭的劳动需求为:$l_t^\tau = {\left( {\frac{{\omega _t^\tau }}{{{W_t}}}} \right)^{ - \frac{{1 + {\lambda _\omega }}}{{{\lambda _\omega }}}}}{L_t}$,其中1+λw是工资加成率。${L_t} = {\left[ {\int\limits_0^1 {{{(l_t^\tau )}^{\frac{1}{{1 + {\lambda _\omega }}}}}} {d_\tau }} \right]^{1 + {\lambda _\omega }}}$和${W_t} = {\left[ {\int\limits_0^1 {{{(w_t^\tau )}^{\frac{{ - 1}}{{{\lambda _\omega }}}}}} {d_\tau }} \right]^{ - {\lambda _\omega }}}$分别由每个家庭按照Dixit-Stiglitz函数形式加总得到。工资的变动服从Calvo机制,即家庭不能连续地调整价格,而只是在接收到某种价格调整信息时才调整价格,价格变化具有一定的粘性。假定每一期调整价格的厂商比例为1-ξw。在t期接收到价格调整信息的家庭把工资调整到同一最优水平$W_t^\tau = {\tilde w_t}$,没有接收到价格调整信息的家庭则根据前一期的通货膨胀水平来调整工资,即:
| $W_t^\tau = {({P_{t - 1}}/{P_{t - 2}})^{{\gamma _w}}}W_{t - 1}^\tau $ | (4) |
在预算约束方程(式(2))、市场对劳动力的总需求和总工资水平的约束下,家庭最大化一生效用的折现值(式(1)),可得最优工资的一阶条件:
| $\frac{{{{\tilde w}_t}}}{{{P_t}}}{E_t}\sum\limits_{i = o}^\infty {{\beta _i}\xi _w^i} {(\frac{{{P_t}/{P_{t - 1}}}}{{{P_{t + i}}/{P_{t + i - 1}}}})^{{\gamma _w}}}\frac{{l_{t + i}^\tau U_{t + i}^C}}{{1 + {\lambda _w}}} = {E_t}\sum\limits_{i = o}^\infty {{\beta _i}\xi _w^i} l_{t + i}^\tau U_{t + i}^L$ | (5) |
其中,${U_{t + i}^C}$和$U_{t + i}^L$分别表示消费和劳动的边际效用。结合式(4)可以得到:
| $W_t^{ - 1/{\lambda _w}} = {\xi _w}{({W_{t - 1}}{({P_{t - 1}}/{P_{t - 2}})^{{\gamma _w}}})^{ - 1/{\lambda _w}}} + (1 - {\xi _w})({\tilde w_t}) - 1/{\lambda _w}\;\;$ | (6) |
家庭是生产用资本的提供者,以租借率$r_t^k$把资本提供给中间厂商。家庭采用两种方式来补充总资本的供给:一是投资,新增投资经过一期才能转化为可用资本,且存在投资的变动成本;二是调整现有资本的使用率zt。资本积累方程是:Kt+1=Kt(1-τ)+(1-S(εtI))It,其中${S\left( {\varepsilon _t^I{I_t}/{I_{t - 1}}} \right) = \frac{{\varepsilon _t^I}}{2}{{\left( {\frac{{{I_t}}}{{{I_{t - 1}}}} - 1} \right)}^2}}$反映投资的调整成本,εtI是资本调整的冲击。在预算约束和资本积累约束下,家庭通过选择投资水平和资本利用率来实现效用最大化。设Qt是单位新增投资品的影子价格,则有:
| $Qt = Et(\beta \frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}({Q_{(t + 1)}}(1 - \tau ) + {z_{t + 1}}r_{(t + 1)}^k - \psi ({z_{(t + 1)}})))$ | (7) |
| ${Q_t}S'(\frac{{\varepsilon _t^I{I_t}}}{{{I_{t - 1}}}})\frac{{\varepsilon _t^I{I_t}}}{{{I_{t - 1}}}} + \beta {E_t}{Q_{t + 1}}\frac{{{\lambda _{t + 1}}}}{{{\lambda _t}}}S'(\frac{{\varepsilon _{t + 1}^I{I_{t + 1}}}}{{{I_t}}})\;\frac{{\varepsilon _{t + 1}^I{I_{t + 1}}}}{{{I_t}}}\frac{{{I_{t + 1}}}}{{{I_t}}} = 1\;$ | (8) |
| $\gamma _t^k = \psi '({z_t})$ | (9) |
(二)厂商。国内市场中存在三种类型的厂商:一是生产异质化中间产品的中间厂商,在垄断竞争市场上出售其产品,这些中间产品是最终厂商的投入;二是进口厂商,进口国外生产的产品,并重新制定进口品在国内市场的价格,出售给最终厂商;三是最终厂商,把国内生产的产品和进口品作为投入,生产同质化的最终产品,在完全竞争市场上出售,最终产品用于消费、投资、出口和财富积累(持有现金和购买债券)。
1.中间厂商。中间厂商采用扩展的柯布-道格拉斯生产函数进行生产,即:
| $y_t^j = {A_t}{({\tilde K_{j,t}})^a}L_{j,t}^{1 - a} - \phi $ | (10) |
其中,At是生产率冲击,服从AR(1)过程${{{\tilde K}_{j,t}} = {z_t}{K_{_{j,t} - 1}}}$是有效资本的数量,Lj,t是家庭提供的异质化劳动,a表示资本产出弹性,Φ是生产的固定成本。厂商最小化其生产成本,可得一阶条件:$\frac{{{W_t}{L_{j,t}}}}{{r_i^k{{\tilde K}_{j,t}}}} = \frac{{1 - a}}{a}$。厂商的边际成本为:
| $m{c_{H,t}} = \frac{1}{{\varepsilon _t^a}}W_t^{1 - a}{(r_t^k)^a}({{\rm{a}}^{ - {\rm{a}}}}{(1 - {\rm{a}})^{ - (1 - {\rm{a}})}})\;$ | (11) |
中间厂商在中间产品的交易中处于垄断竞争地位,国内产品的总价格指数变动方程为:
| ${\left( {{P_{H,t}}} \right)^{ - 1/{\lambda _p}}} = {\xi _P}{({P_{_{H,t - 1}}}{({P_{_{H,t - 1}}}/{P_{_{H,t - 2}}})^{{\gamma _P}}})^{ - 1/{\lambda _p}}} + (1 - {\xi _P})(\tilde P_{_{H,t}}^j) - 1/{\lambda _p}\;(12)$ | (12) |
其中,ξp是不按照最优价格进行价格调整的中间厂商的比例,$\tilde P_{_{H,t}}^j$是最优的国内价格水平。令Λt,t+i是t期到t+i期的贴现因子,则有以下一阶条件:
| ${Et\sum\limits_{i = 0}^\infty {{\beta ^i}\xi _P^{^i}{\Lambda _{t,t + 1}}y_{t + i}^j(\frac{{\tilde P_{_{H,t}}^j}}{{{P_{H,t}}}}{{(\frac{{{P_{H,t - 1 + i}}/{P_{H,t - 1}}}}{{{P_{H,t + i}}/{P_{H,t}}}})}^{{\gamma _p}}} - (1 + {\lambda _p})m{c_{_{H,t + i}}}) = 0\; } }$ | (13) |
2.国内进口厂商。本文假定汇率的波动不能完全传导给进口价格。进口厂商以价格${P_{IM,t + k}^*}$(以外国货币表示)进口产品j,它需要确定进口品的最优国内价格${P_{IM}^{new}(j)}$,其优化问题为:
$\begin{array}{*{20}{c}} {Max{E_t} = \left\{ {\sum\limits_{k = 0}^\infty {{\beta ^k}{\Lambda _{t,t + k}}\xi _{IM}^{^k}(P_{IM}^{new}(j) - {S_{t + k}}P_{IM,t + k}^*(j))IM_{t + k}^C(j)} } \right\}}\\ \;\\ {s.t.IM_{t + k}^C(j) = {{(\frac{{P_{IM}^{new}(j)}}{{{S_{t + k}}P_{IM,t + k}^*}})}^{ - \lambda w}}IM_{(t + k)}^C} \end{array}$
其中,${\xi _{IM}^{^k}}$是t期设定的最优价格${P_{IM}^{new}(j)}$在t+k期仍保持不变的概率。βkΛt,t+k是随机贴现因子,Λt,t+k反映了t+k期的贴现风险,${IM_{t + k}^C(j)}$是t+k期消费品的进口数量。求解以上优化问题,得到最优价格${P_{IM}^{new}(j)}$的决定方程:
| ${P_{IM}^{new}(j) = \frac{{{\lambda _{IM}}}}{{{\lambda _{IM}} - 1}}\frac{{{E_t}\left\{ {\sum\nolimits_{k = 0}^\infty {{\beta ^k}{\Lambda _{t,t + k}}\xi _{IM}^k({S_{t + k}}P_{IM,t + k}^*)IM_{t + k}^C(j))} } \right\}}}{{{E_t} - \left\{ {\sum\nolimits_{k = 0}^\infty {{\beta ^k}{\Lambda _{t,t + k}}\xi _{IM}^k(IM_{t + k}^C(j))} } \right\}}}\;}$ | (14) |
对数线性化之后的进口品总价格水平的波动根据Calvo机制进行调整。
3.最终厂商。最终厂商以国内中间产品和进口品为投入,采用CES生产函数生产最终产品。国内的最终产品用于消费、投资和出口,国内的总消费由国内最终消费品和进口品组成,假设国内产品和进口产品之间不能完全替代,则国内总消费由式(15)决定:
| ${{C_t} = {{(v_{C,t}^{\frac{1}{{\mu C}}}{{(H_t^C)}^{1 - \frac{1}{{\mu C}}}} + {{(1 - {v_{C,t}})}^{\frac{1}{{\mu C}}}})}^{\frac{{\mu C}}{{\mu {C^{ - 1}}}}}}\;\;}$ | (15) |
其中,${H_t^C}$和${IM_{t}^C}$分别表示国内最终产品和进口的国外最终产品,vC,t 是消费的国内产品比例,μC是国内外最终产品之间的替代弹性。设定最终消费品的基准价格为1,则国内最终产品的价格$P_t^d$和国外最终产品的价格$Q_t^p$之间存在以下关系:
| ${w^{\mu c}}{({p_{H,t}})^{1{ - ^{\mu c}}}} + {\left[ {(1 - w){\xi _t}} \right]^{\mu c}}P_{IM,t}^{1 - \mu c} = 1\;$ | (16) |
我们进一步可以得到国内消费品和进口品的需求方程:
| $H_T^c = {v_{C,t}}{(\frac{{{P_{H,t}}}}{{{P_t}}})^{ - \mu c}}{C_t},IM_t^C = (1 - {v_{C,t}}){(\frac{{{P_{IM,t}}}}{{{P_t}}})^{ - \mu c}}{C_t}\;$ | (17) |
(三) 政府。政府采用如下的利率规则作为货币政策的执行规则:
| $\begin{array}{*{20}{c}} {{{\hat R}_t} = {\rho _R}{{\hat R}_{t - 1}} + (1 - {\rho _R})\left\{ {{{\bar \pi }_t} + {r_\pi }({{\bar \pi }_{t - 1}} - {{\bar \pi }_t}) + {r_Y}{{\hat Y}_t}} \right\} + {r_{\Delta \pi }}({{\bar \pi }_t} - {{\bar \pi }_{t - 1}})}\\ { + {r_{\Delta y}}({{\hat Y}_t} - {{\hat Y}_{_{t - 1}}}) + {r_{\Delta S}}({{\hat S}_t} - {{\hat S}_t}_{ - 1}) + \varepsilon _t^R\;\;} \end{array}$ | (18) |
其中,变量上面的符号“^”表示该变量相对于稳态值的对数偏离,ρR反映了利率的平滑程度,${{{\bar \pi }_t}}$是政府在t期的通胀目标,Y是总产出水平,rπ和rY分别表示利率对通胀目标变化和产出的敏感程度,rΔπ、rΔY和rΔS分别表示利率对通胀变化、产出变化和汇率变化的响应程度,${\varepsilon _t^R}$是利率冲击,服从AR(1)过程。如式(18)所示,货币政策的制定除了考虑通胀波动和产出波动之外,也把汇率波动作为政策目标之一,这样的设定更符合我国现行的有管理的浮动汇率制度的特征,汇率的变动能够影响货币政策的制定和实施效果。
根据以上设定,可以得到市场出清条件。家庭可以购买国内和国外政府发行的债券,以债券的形式实现国际资本流动,使非抛补利率平价条件成立,由此可以确定国内利率、国外利率和汇率之间的关系。本文采用的非抛补利率平价等式为:
| $\begin{array}{*{20}{c}} {{{\hat R}_t} - {{\hat R}^*}_{t - 1} = (1 - {{\tilde \varphi }_s}){E_t}{{\hat S}_{t + 1}} - {{\tilde \varphi }_s}{{\hat S}_t} - {{\tilde \varphi }_a}{{\hat a}_t} + {{\tilde \varphi }_t}}\\ {\;\;} \end{array}$ | (19) |
其中,at=StBt/Pt表示本国持有的国外净资产,${{{\tilde \varphi }_s}}$和${{{\tilde \varphi }_a}}$分别表示对汇率变动和国外净资产变动的调整系数,${{{\tilde \varphi }_t}}$是风险贴水冲击。变量上面的符号“^”表示该变量的对数线性化形式。假设国外经济平稳运行,稳态时对数线性化之后的国外经济变量服从AR(1)过程。
对于以上模型,本文参考刘斌(2008)等多个成熟的DSGE模型,并结合中国经济的实际运行数据,对模型的参数进行了校准(受篇幅限制未列出,如有需要可向作者索要)。
三、实证结果及分析本文在对以上模型进行对数线性化处理和参数校准的基础上,分析汇率对货币政策调控难度的影响。首先,通过脉冲响应分析来检验汇率对宏观经济波动是否产生了显著影响;然后,检验汇率波动对货币政策的效果是否产生了显著影响;最后,分析汇率波动对宏观经济波动的贡献。
(一)汇率波动的宏观经济影响1.人民币汇率波动对主要宏观经济变量产生了显著影响。从理论模型来看,人民币汇率升值主要从两个方面对中国经济波动产生影响:一是通过影响直接贸易价格,影响出口和进口行为,并进一步影响其他经济变量;二是通过影响利率波动(资金价格),影响其他主要经济变量。
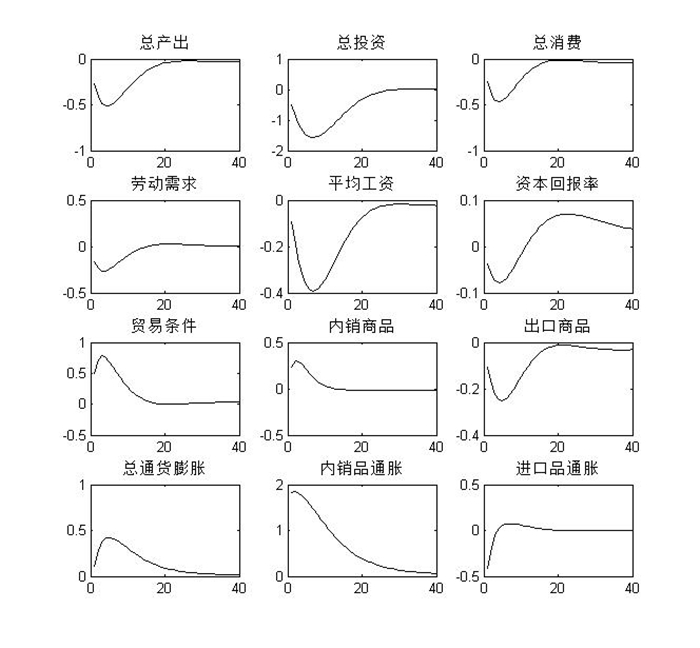
从图 1中可以看出,人民币升值的影响主要体现在以下几个方面:(1)贸易方面。人民币升值导致出口价格上升和进口价格下降,从而使贸易条件(出口价格和进口价格的比值)得到改善。但出口价格上升抑制了部分边际需求,导致出口额下降。在发生人民币升值冲击后,到第3个季度左右贸易条件变量达到最大值,随后开始长时间的下降,大约在第20个季度下降至零;出口商品在发生人民币升值冲击后立即下降,至第4个季度下降至最低点,当人民币汇率发生1个标准差冲击时,出口商品最低减少0.2%,在第5个季度后出口商品的降幅开始逐渐减小,直至第20个季度左右恢复至稳态水平。同时,人民币升值会立即造成内销商品增加,较快达到最大值,随后大约在第10个季度恢复至稳态水平。以上结果表明人民币升值对我国贸易条件、出口商品和内销商品均有显著的影响,但影响幅度、影响方向和时滞存在差异。人民币汇率发生1个标准差冲击对贸易条件变量的影响最大,最高达到正向0.7%左右,影响时滞为20个季度左右;对内销商品的影响最高达到正向0.3%左右,影响时滞约为10个季度;对出口商品的影响最高达到负向0.22%左右,影响时滞大约为20个季度。(2)国内需求方面。人民币升值使国内需求(消费、投资等)普遍下滑,进而造成总产出下滑。从图 1中可以看出,人民币升值对投资的影响最大,人民币汇率发生1个标准差冲击导致投资的最大降幅达到1.5%,从传导机制来看,这主要是因为人民币升值对利率产生了影响,导致资本品价格扭曲、资本收益出现短期下降,从而对投资行为造成较大的负面影响。人民币升值对我国总产出和消费的影响不如对投资的影响大,人民币汇率发生1个标准差冲击导致总产出和消费的最大降幅达到0.5%左右。此外,劳动需求也出现下降,并进一步影响了总工资水平。人民币汇率1个标准差的冲击导致劳动需求和总工资水平的最大降幅为0.25%和0.4%左右。(3)价格水平方面。在发生人民币汇率冲击的前期,国内通胀水平出现温和上升,大约第5个季度达到最大值,随后逐渐衰减,直至第40个季度左右其冲击作用消失为零。总体上,人民币升值对我国通货膨胀的影响呈现出“倒勾型”态势,即短期上升至最高点,然后逐渐拖尾缓慢下降至零。这表明,如果人民币升值发生在我国经济周期运行的底部,国内经济的滞胀风险将显著增加。
|
| 图 1 人民币汇率波动对主要经济变量的影响 |
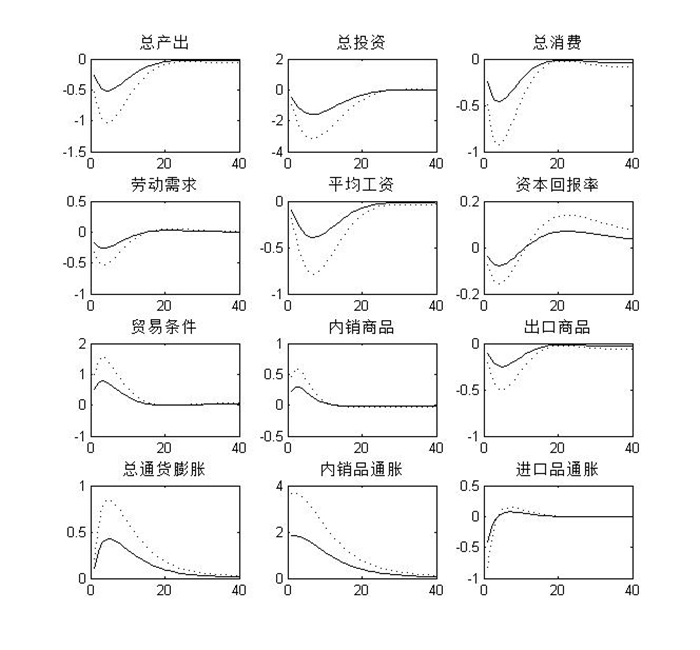
2.人民币汇率波动增大将增加主要宏观经济变量的波动幅度。图 2中的实线和虚线分别表示人民币汇率波动为1单位和2单位标准差时,其他经济变量的冲击响应情况。可以看到,汇率波动的增大导致每个变量的波动幅度增加。以产出为例,当汇率波动从1单位标准差增加到2单位标准差时,产出的波动增大,最多下滑1%。而对于进出口,汇率波动增大使出口的国内商品价格大幅上升,贸易条件(出口价格和进口价格的比值)进一步得到改善。从脉冲响应的时滞来看,除了资本回报率之外,其他变量对人民币升值的响应幅度逐渐减小至零,而资本回报率则先降后升,在长期出现微幅上升。
|
| 图 2 不同幅度的人民币汇率波动影响 |
1.货币政策冲击对经济产生了多方面显著影响。利率上升对主要经济变量产生了较为显著的影响,主要体现在以下几个方面(受篇幅限制,未给出相关脉冲响应图):(1)与人民币升值的影响不同,利率上升引起进口品的价格短暂上涨,但在长期其影响衰减为零。这主要是通过利率平价条件产生影响,即利率上升导致人民币预期贬值,使得出口价格下降而进口价格上升,贸易条件(出口价格和进口价格的比值)恶化。而出口价格下降通过刺激边际需求起到了刺激出口的作用,出口的繁荣也进一步促使原来内销的部分产品转向出口,造成内销商品小幅下降。(2)与人民币升值相同,利率上升会导致国内需求下滑,即紧缩性货币政策能有效抑制国内需求。利率上升会使家庭增加储蓄,减少边际消费。而对厂商来说,利率上升增加了投资成本,压缩了投资收益,导致其投资积极性减弱。消费需求和投资需求的双重下滑导致总需求下滑。(3)利率上升陡然引起通胀水平上升,而后呈现出逐渐下降的趋势,并缓慢恢复至稳态水平。这表明意在控制价格上涨的紧缩性货币政策在实施瞬间不仅没有降低价格水平,反而引起了价格水平的突发性上涨。同时,在冲击大小相同时,货币政策冲击对各个变量的影响程度大于人民币升值的影响程度。
2.汇率波动增大将减弱货币政策的有效性。为了分析汇率波动增大对货币政策的影响,本文研究了人民币汇率波动分别为1单位和2单位标准差时,各主要经济变量对货币政策冲击(利率上升)的响应情况(受篇幅限制,未给出脉冲响应图)。可以发现,人民币汇率波动增大会在一定程度上减弱中国货币政策的调控效果,但是对每个变量的冲击响应影响程度有所不同。(1)人民币汇率波动增大将显著干扰货币政策对宏观经济需求的调控力度。当人民币汇率波动幅度增加时,货币政策对各种需求的影响显著减弱,主要表现为:利率对总产出、总投资、总消费、总出口等需求的调控效果明显减弱。从影响幅度来看,当人民币汇率波动幅度为1单位标准差(2单位标准差)时,利率对总产出、总投资、总消费和总出口的最大影响程度分别为相应变量的-1.45%(-0.6%)、-5%(-2.5%)、-1.48%(-0.75%)和-2.4%(-1.9%),在人民币不同升值幅度下,利率对以上宏观经济需求变量的作用力度存在显著差异。从影响时滞来看,虽然人民币汇率的波动幅度增大时,利率对总产出、总投资、总消费、总出口等需求的影响程度存在显著差异,但是在发生利率冲击后,以上各变量在不同时点的变化特征是一致的,两者并不存在明显的差异。综合来看,人民币汇率波动幅度增大会显著减弱货币政策对需求变量的调控效果,但不会影响相关需求变量在不同时点的冲击响应特征。可见,在更加开放的国际经济环境下,人民币汇率波动通过影响中国货币政策对若干宏观经济需求变量的调控效果而不是时滞变化特征,减弱了中国货币政策的实施效果。因此,必须紧密结合开放环境下人民币汇率波动的特征来科学地制定货币政策,否则可能难以达到预期的调控效果,从而失去有效性。(2)当人民币汇率波动幅度发生变化时,中国货币政策对通货膨胀的调控效果几乎不会受到显著影响。总通胀水平、内销品通胀水平和进口品通胀水平对货币政策的响应几乎不受汇率波动的影响,当人民币汇率波动幅度分别为1个和2个标准差时,总通膨水平、内销品通胀水平和进口品通胀水平对利率冲击的响应曲线几乎重合,没有出现大的差异。(3)汇率波动幅度增大会减弱利率上升对出口的负面影响,缓解货币政策对出口的负面冲击,但导致贸易条件(出口价格和进口价格的比值)进一步恶化。因此,汇率波动幅度增大是通过出口品价格下降来缓解出口下滑的,这是一种以价换量式的缓解。
(三)汇率波动对宏观经济波动的贡献本文进一步分析了汇率波动对宏观经济波动的贡献,方差分解结果显示(受篇幅限制未列示):(1)利率冲击是经济波动的主要因素,可以解释大部分变量的波动。特别是利率冲击对总产出、消费和资本收益率波动的贡献高达60.83%、60.96%和51.2%,对劳动、工资和通胀波动的贡献均在30%以上,对资本存量和投资波动的贡献在20%以上。因此,中国货币政策对各种宏观经济变量的波动具有至关重要的影响。(2)除了利率冲击外,每个变量的波动有不同的驱动因素。如投资冲击可以解释较多的投资和资本波动,政府支出冲击可以解释9.5%的消费波动和13.28%的利率波动,而通胀冲击是引起利率波动的另一主要因素,投资冲击对资本收益率波动的贡献高达15.29%。(3)生产率冲击对各变量的影响具有较大差异。生产率冲击对劳动、资本收益率、利率和通胀波动的贡献较大,均在10%以上,特别是对劳动和利率波动做出了较大的贡献,而对投资波动的贡献相对较小,为4.85%。(4)汇率冲击对其他变量波动的影响有限,其贡献不超过5%,大多在2%-3%左右。总体上看,相对于其他冲击,汇率冲击对中国宏观经济波动的贡献有限。因此,虽然人民币汇率波动会造成中国宏观经济波动,但是还不能成为中国宏观经济波动的重要之源。
四、结 论本文弥补了现有相关文献的研究不足,采用动态随机一般均衡(DSGE)模型,深入研究了人民币汇率波动增大是否加大了中国货币政策的调控难度,主要得到以下结论:
1.人民币汇率波动对中国主要宏观经济变量产生了显著影响。人民币升值导致出口价格上升和进口价格下降,从而贸易条件得到改善。但出口价格上升抑制了部分边际需求,导致出口额下降。人民币升值使国内需求普遍下滑,进而造成总产出下滑。人民币升值对投资的影响最为严重,其对我国总产出和消费的影响不如对投资的影响大。此外,劳动需求也出现下降,并进一步影响了总工资水平。在发生人民币升值冲击的前期,国内通胀水平出现温和上升,大约第5个季度通胀水平达到最大值,随后逐渐衰减。总体上,人民币升值对我国通胀的影响呈现出“倒勾型”态势。汇率波动增大导致了每个变量更大的波动。从脉冲响应的时滞来看,除资本回报率之外,其他变量对人民币升值的响应幅度逐渐衰减,并在长期衰减为零;而资本回报率先降后升,在长期出现微幅上升。
2.货币政策利率冲击对经济体产生了多方面显著影响。与人民币升值的影响不同,利率上升带来了进口品价格的短暂上涨,但在长期其影响衰减为零。与人民币升值相同的是,利率上升会导致国内需求下滑,紧缩性货币政策能够有效抑制国内需求。利率冲击陡然引起通胀水平上升,而后呈现出逐渐下降的趋势,并缓慢恢复至稳态水平。
3.人民币汇率波动增大将减弱中国货币政策的有效性。人民币汇率波动增大会在一定程度上减弱中国货币政策的调控效果,但是对每个变量的冲击响应影响程度有所不同。人民币汇率波动增大将显著干扰货币政策对宏观经济需求的调控力度。在人民币汇率的不同波动幅度下,我国利率政策对主要需求变量的调控效果具有显著的差异。人民币汇率波动增大会显著减弱货币政策对需求变量的调控效果,但不会影响相关需求变量在不同时点的变化特征。因此,在从盯住汇率制度向更灵活的浮动汇率制度转变的过程中,人民币汇率波动是通过影响中国货币政策对若干宏观经济需求变量的调控效果而不是时滞变化特征,减弱了中国货币政策的调控效果。
以上结论表明,必须紧密结合开放环境下人民币汇率波动的差异性特征来科学地设计和制定货币政策。当人民币汇率波动增大时,相对于通货膨胀,中国货币政策更应着重关注政策改变对国内需求的影响。同时,从国际贸易来看,当人民币汇率波动增大时,利率上升对出口的负面影响会减弱,但贸易条件(出口价格和进口价格的比值)进一步恶化。这表明,就进出口而言,中国货币政策应细化出口目标的量化标准,具体需要区分国内外进出口品的价格体系目标和出口量的目标差异,就其所关注的重点进行政策调整。当人民币汇率波动增大时,中国货币政策的调控难度显著增加。此时,货币政策管理当局应合理充分地考虑其政策调控目标;同时,在国内需求、通货膨胀、进出口等多种目标存在冲突且不能都实现的情况下,还应明确政策调控的首要目标和次要目标,确保调控目标的层次性和多样性,以保障宏观经济的发展重点。
| [1] | 毕玉江,朱钟棣.人民币汇率变动对中国商品出口价格的传递效应[J].世界经济,2007,(5):3-15. |
| [2] | 陈创练,杨子晖."泰勒规则"、资本流动与汇率波动研究[J].金融研究,2012,(11):60-73. |
| [3] | 陈浪南,柳阳.不同汇率制下我国货币政策的净出口需求非线性效应的实证研究[J].国际金融研究,2012,(12):4-11. |
| [4] | 陈六傅,刘厚俊.人民币汇率的价格传递效应——基于VAR模型的实证分析[J].金融研究,2007,(4):1-13. |
| [5] | 陈晓莉.汇率变动对货币政策操作变量的影响——理论分析及对中国的检验[J].经济科学,2008,(5):40-47. |
| [6] | 陈学彬,李世刚,芦东.中国出口汇率传递率和盯市能力的实证研究[J].经济研究,2007,(12):106-117. |
| [7] | 陈雨露,周晴.浮动汇率制度下货币政策操作模式及中国货币状况指数[J].世界经济,2004,(7):24-28. |
| [8] | 邓永亮,李薇.汇率波动、货币政策传导渠道及有效性——兼论"不可能三角"在我国的适用性[J].财经科学,2010,(4):1-9. |
| [9] | 顾国达,张正荣,张钱江.汇率波动、出口结构与贸易福利——基于要素流动与世界经济失衡的分析[J].世界经济研究,2007,(2):3-8. |
| [10] | 韩青.汇率波动与国际贸易量的不确定性关系——基于中国的经验证据[J].经济学(季刊),2010,(2):447-466. |
| [11] | 李文乐,王彬,王继晖.人民币汇率波动与货币政策调控——基于新凯恩斯垄断竞争模型框架的理论分析与实证[J].当代经济科学,2011,(4):54-66. |
| [12] | 刘斌.我国DSGE模型的开发及在货币政策分析中的应用[J].金融研究,2008,(10):1-21. |
| [13] | 罗纳德·麦金农.美元本位下的汇率——东亚高储蓄两难[M].王信,何为,译. 北京:中国金融出版社,2005. |
| [14] | 潘红宇.汇率波动率与中国对主要贸易伙伴的出口[J].数量经济技术经济研究,2007,(2):73-81. |
| [15] | 苏应蓉,李楠.汇率波动对利率政策经济绩效的影响机理分析[J].宏观经济研究,2014,(2):45-53. |
| [16] | 王胜,郭汝飞.不完全汇率传递与最优货币政策[J].经济研究,2012,(S2):131-143. |
| [17] | 项后军,潘锡泉.汇率变动、货币政策与通货膨胀[J].统计研究,2011,(5):3-12. |
| [18] | 张瑜,李书华.汇率波动对外商直接投资的影响——基于一般均衡和面板平滑模型的分析[J].世界经济研究,2013,(8):52-57. |
| [19] | 赵文胜,张屹山.货币政策冲击与人民币汇率动态[J].金融研究,2012,(8):1-15. |
| [20] | 赵永亮,干杏娣,熊德平.人民币实际有效汇率升值对中国产出影响的实证研究[J].世界经济研究,2011,(6):16-21. |
| [21] | Albuquerque C R, Portugal M S. Testing nonlinearities between Brazilian exchange rate and inflation volatilities[R]. RBE Working Paper, 2006. |
| [22] | Cavoli T. Is fear of floating justified? The East Asia experience[J]. Journal of Policy Modeling, 2009, 31(1): 1-16. |
| [23] | De Grauwe P, Schnabl G. Nominal versus real convergence with respect to EMU accession——EMU entry scenarios for the new member states[J]. Kyklos, 2005, 58(4): 481-499. |
| [24] | Friedman M. The case for flexible exchange rates[A].Friedman M. Essays in positive economics[C].Chicago:University of Chicago Press, 1953. |
| [25] | Ghosh A, Gulde A M, Wolf H. Exchange rate regimes: Choices and consequences[M]. Cambridge, MA: MIT Press, 2003. |
| [26] | Makin A J, Rohde N. Has Australia's floating exchange rate regime been optimal?[J]. Economic modeling, 2012, 29(4): 1338-1343. |
| [27] | Mckinnon R, Schnabl G. China's exchange rate and international adjustment in wages, prices, and interest rates[J]. CESifo Studies, 2006, 52(2): 276-303. |
| [28] | Mundell R. A theory of optimum currency areas[J]. American Economic Review, 1961, 51(4):657-665. |
| [29] | Obstfeld M, Rogoff K. Foundations of international macroeconomics[M]: Cambridge: MIT Press, 1996. |
| [30] | Schnabl G. Exchange rate volatility and growth in small open economies at the EMU periphery[R]. ECB Working Paper No.773, 2007. |
| [31] | Smets F, Wouters R. An estimated dynamic stochastic general equilibrium model of the Euro area[J]. Journal of the European Economic Association, 2003, 1(5): 1123-1175. |
 2016, Vol. 42
2016, Vol. 42


